Log-Lattices for Atmospheric Flows
Abstract
:1. Foreword by B. Dubrulle
2. Introduction
3. Log-Lattice Framework
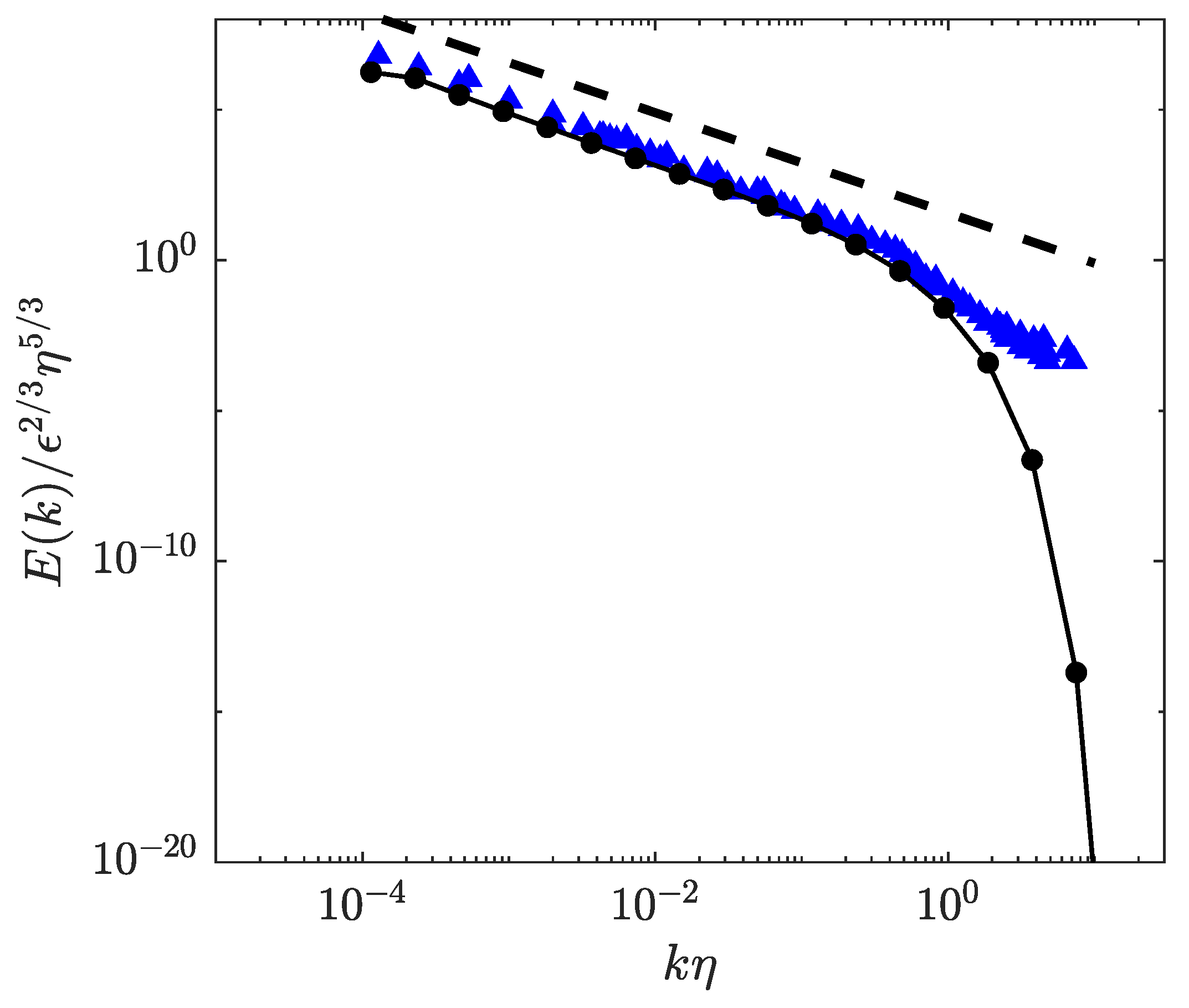
3.1. Energy Spectra
3.2. Generalizations
3.3. Limitations of Log-Lattices
4. Homogeneous Rotating Convections on Log-Lattices
4.1. Definitions
4.2. Non-Dimensional Numbers
- The Rayleigh number , which characterizes the forcing by the temperature gradient.
- The Prandtl number , which is the ratio of the fluid viscosity to its thermal diffusivity.
- The Nusselt number that characterizes the mean total heat flux is the z direction is .
- The Ekman number , measuring the importance of the rotation with respect to the diffusive process.
- The Rossby number , measuring the importance of the rotation with respect to buoyancy. In terms of other variables, we have .
- The friction coefficient , which provides the intensity of the Rayleigh damping.
4.3. Equations on Log-Lattice
4.4. Convection Onset
Onset at Zero Rotation
4.5. Onset at Large Rotation
4.6. Phenomenology When
4.6.1. Non-Rotating Case
- (I):
- When , we are in the laminar case. The fluid is at rest, , and the heat flux is only piloted by the Fourier law, so that and .
- (II):
- Above the critical threshold for instability, when , convection sets in, starts becoming positive, and we have , where is an exponent characterizing the (super)-critical transition to convection.
- (III):
4.6.2. Rotating Case
4.6.3. Log-Lattice Simulation Details
5. Results
5.1. Non-Rotating Case
5.2. Rotating Case
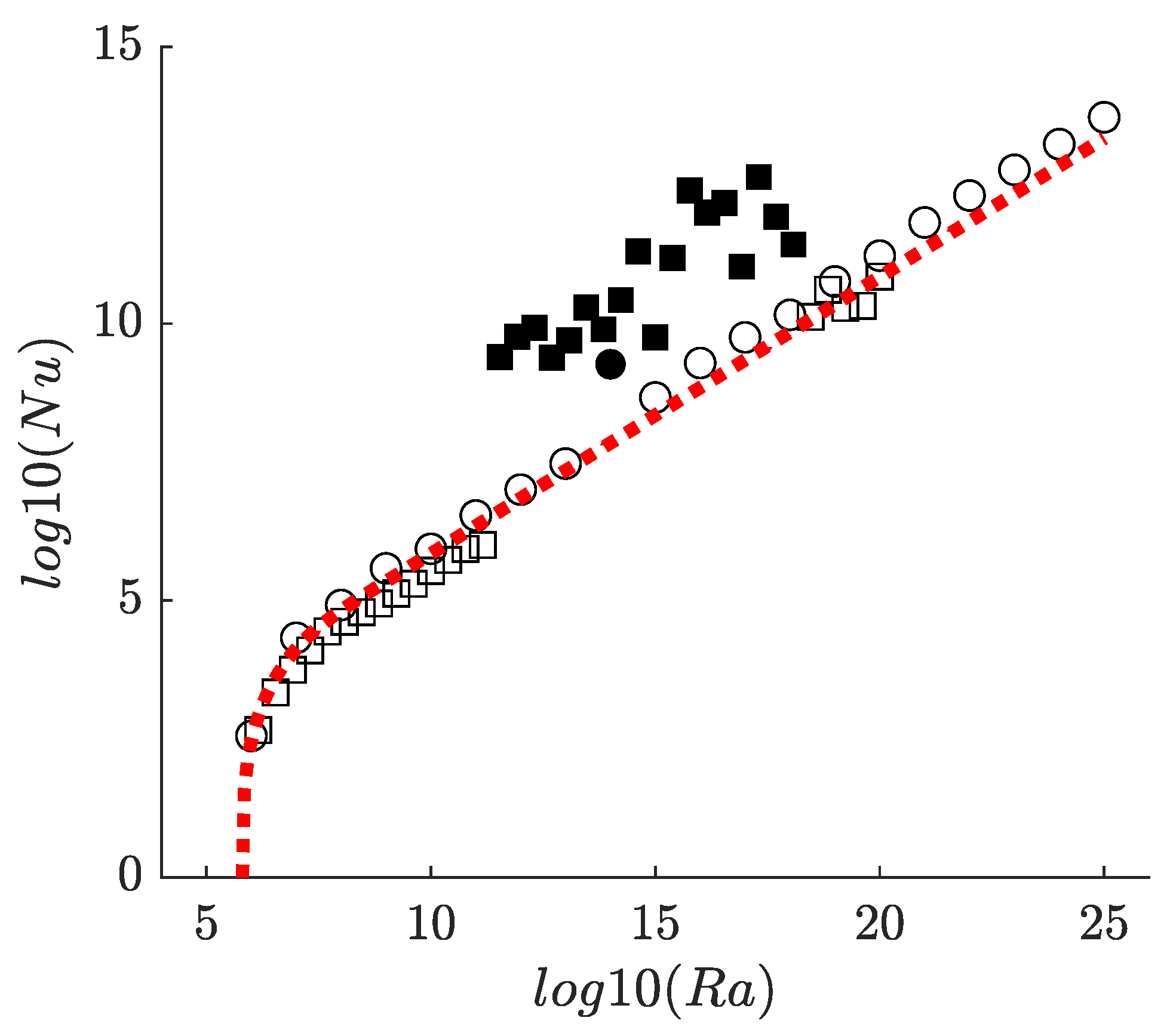
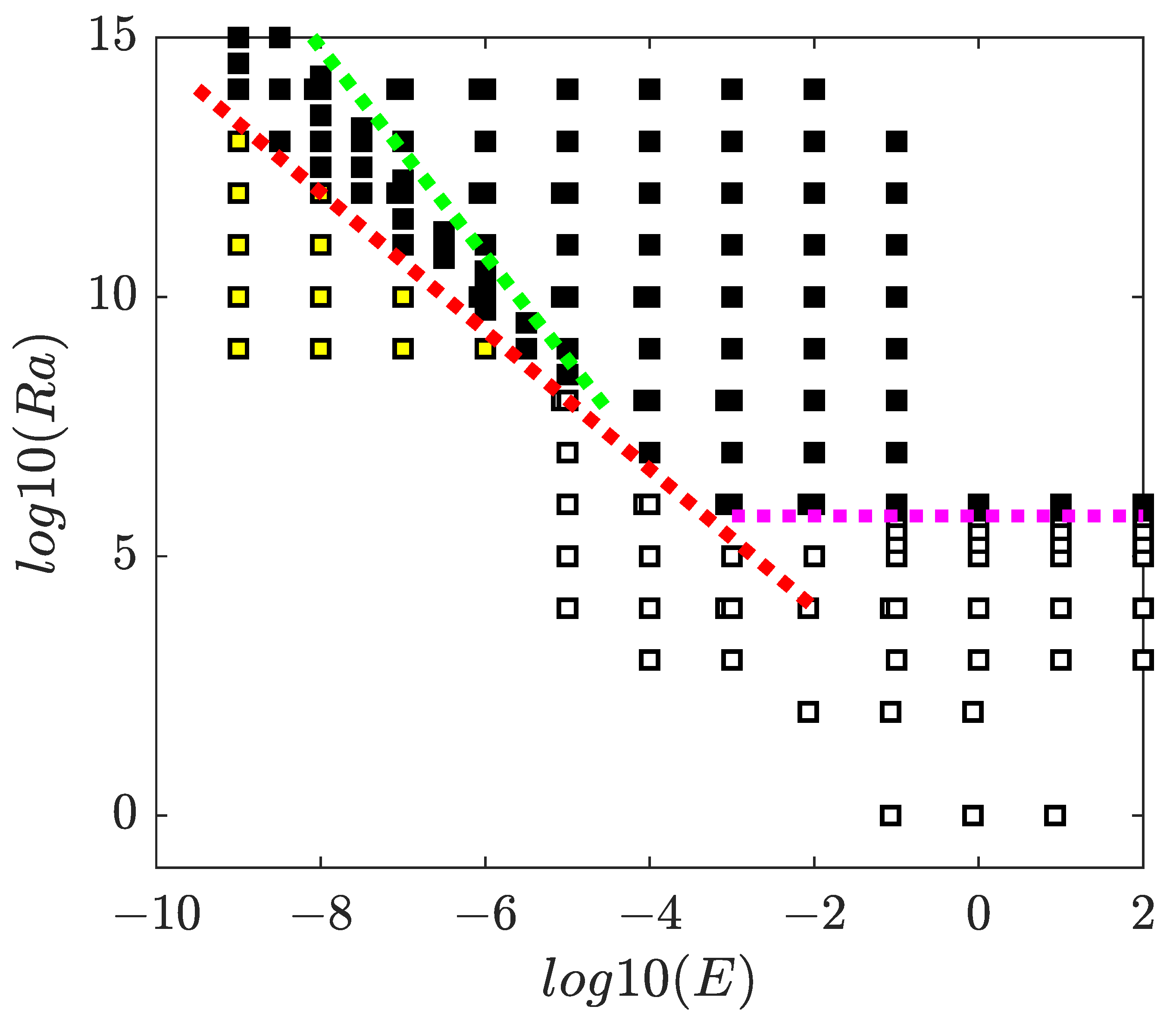
Parameter Space and Critical Rayleigh Number
5.3. Influence of Friction
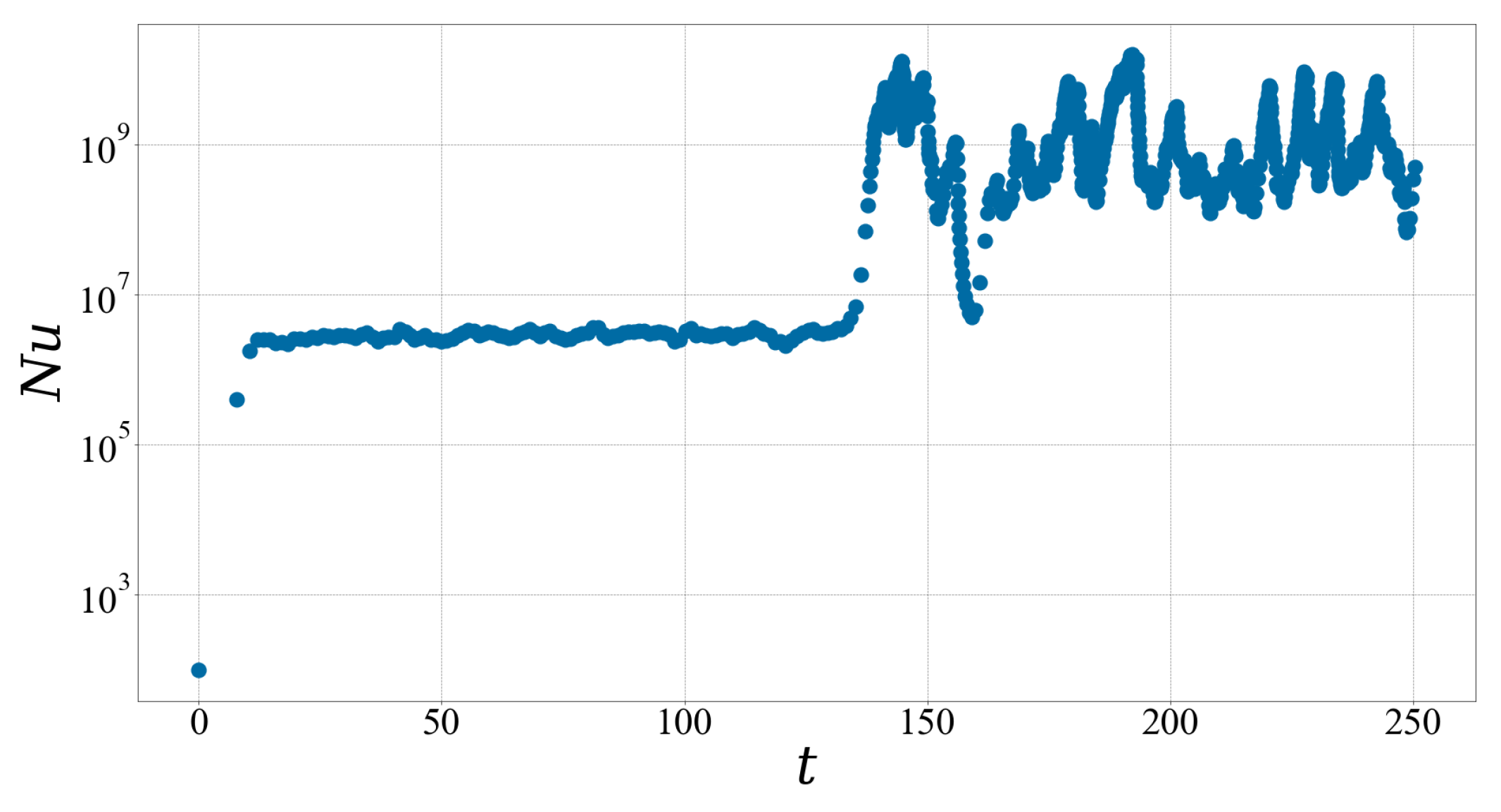
5.3.1. Laminar vs. Turbulent Regime
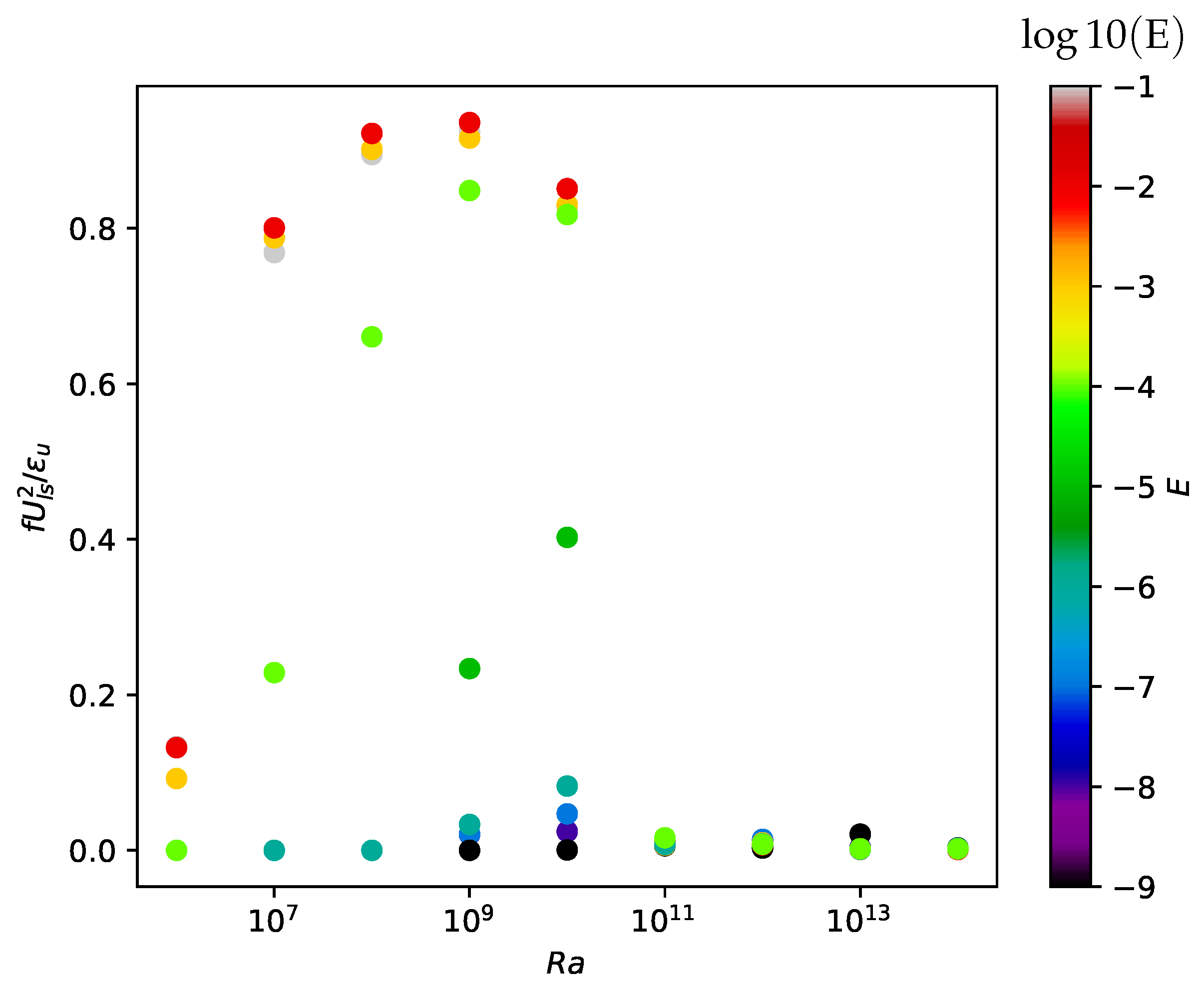
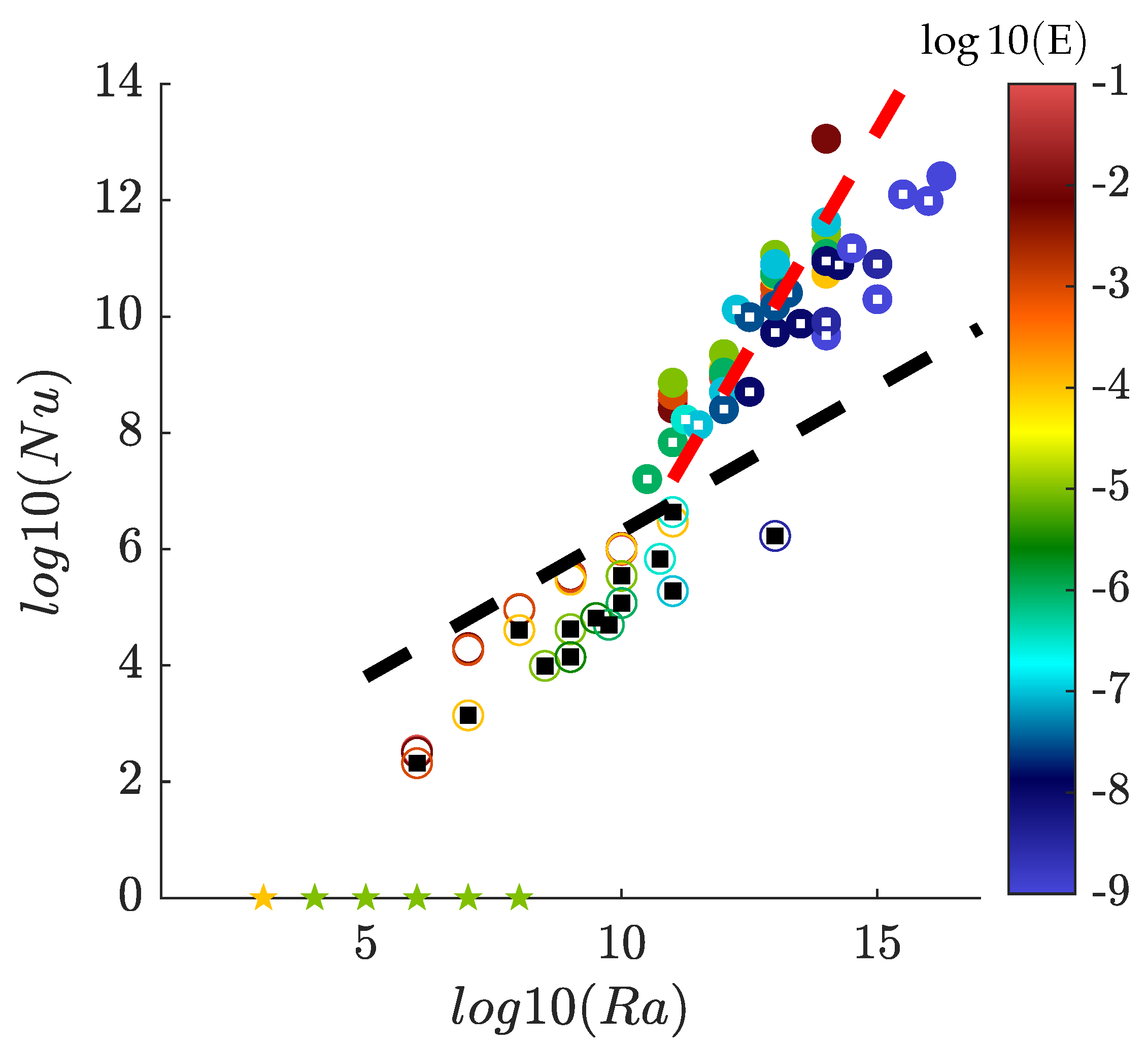
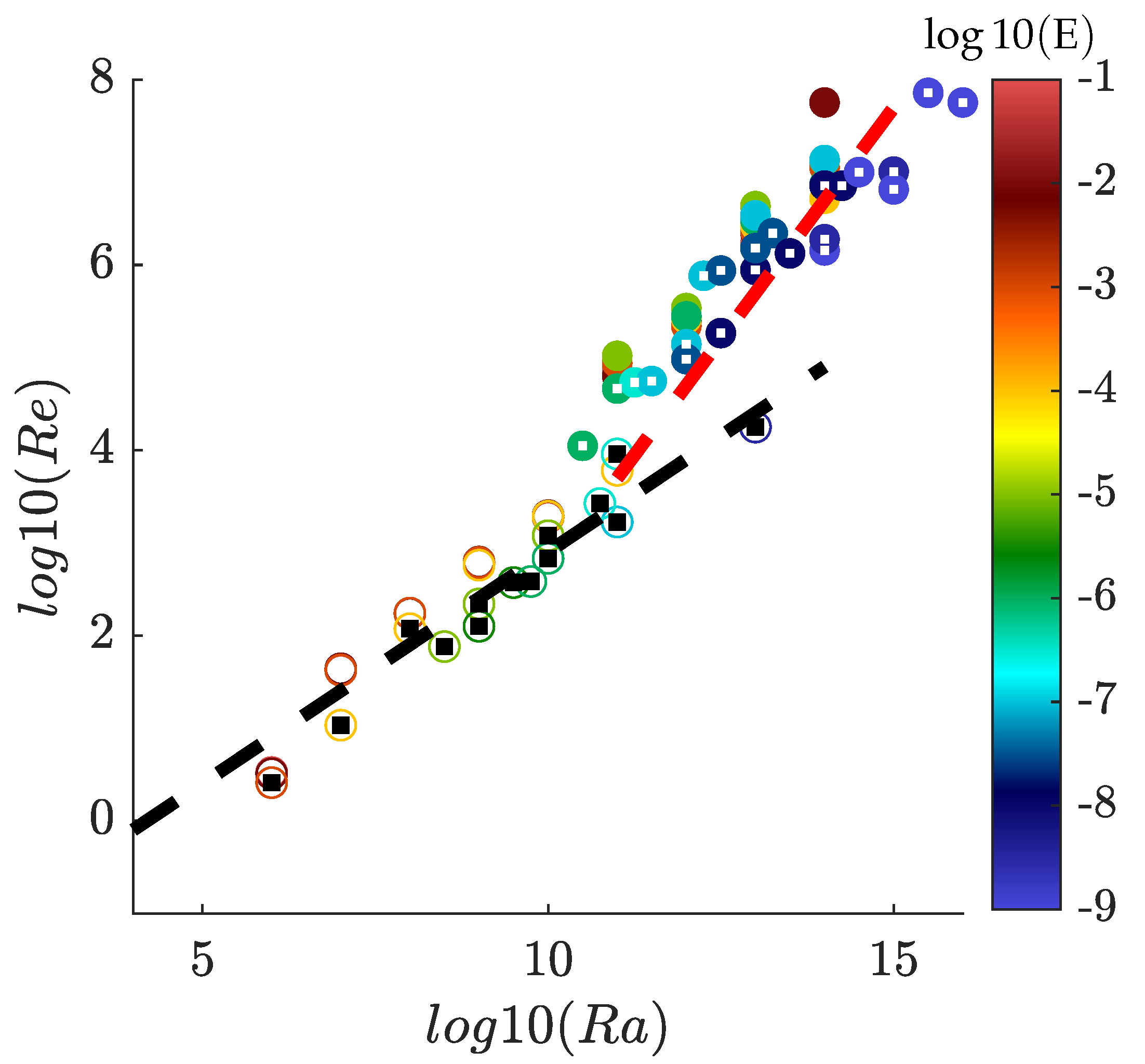
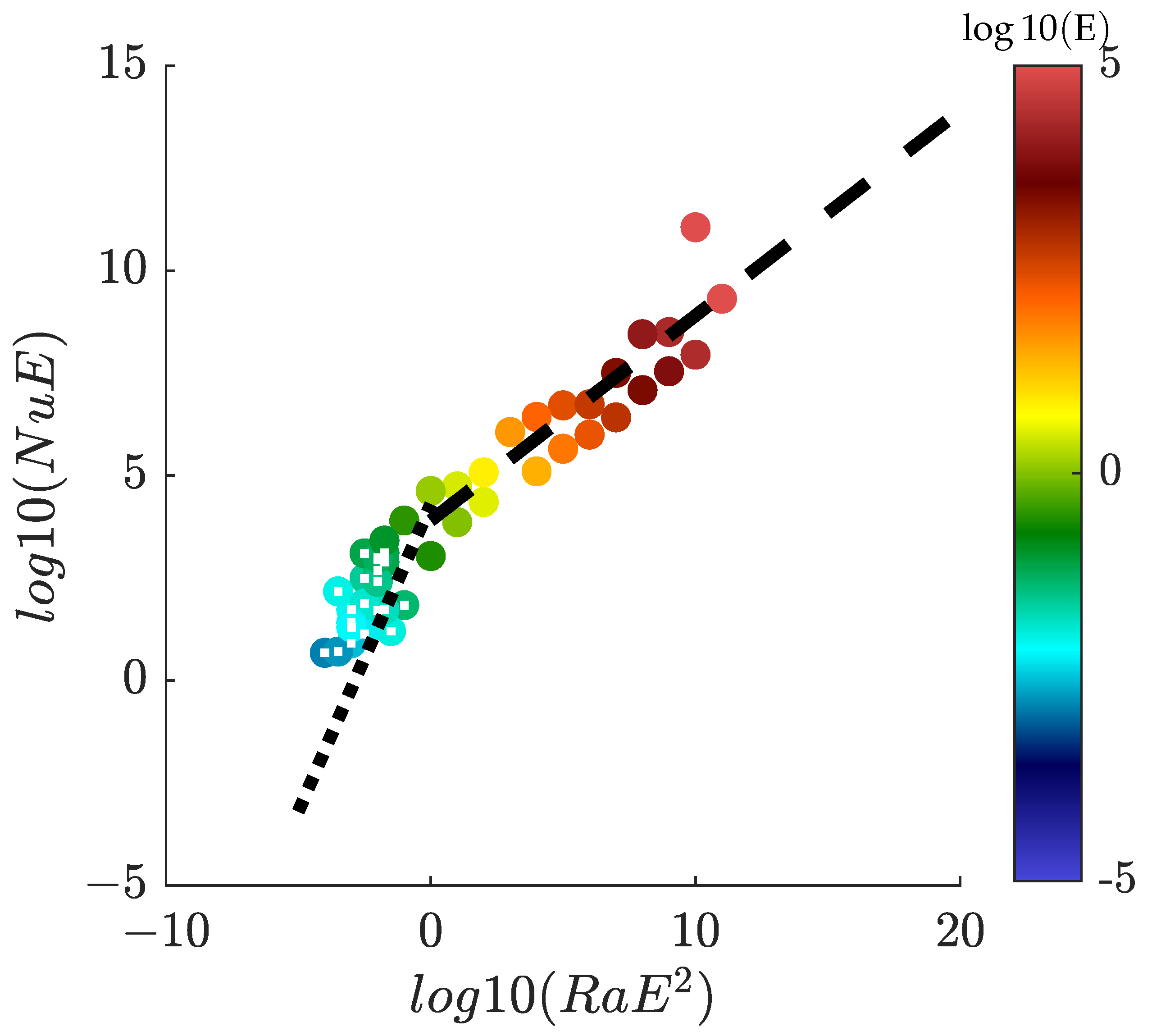
5.3.2. Influence of Rotation and Onset of Rotation-Dominated Regimes
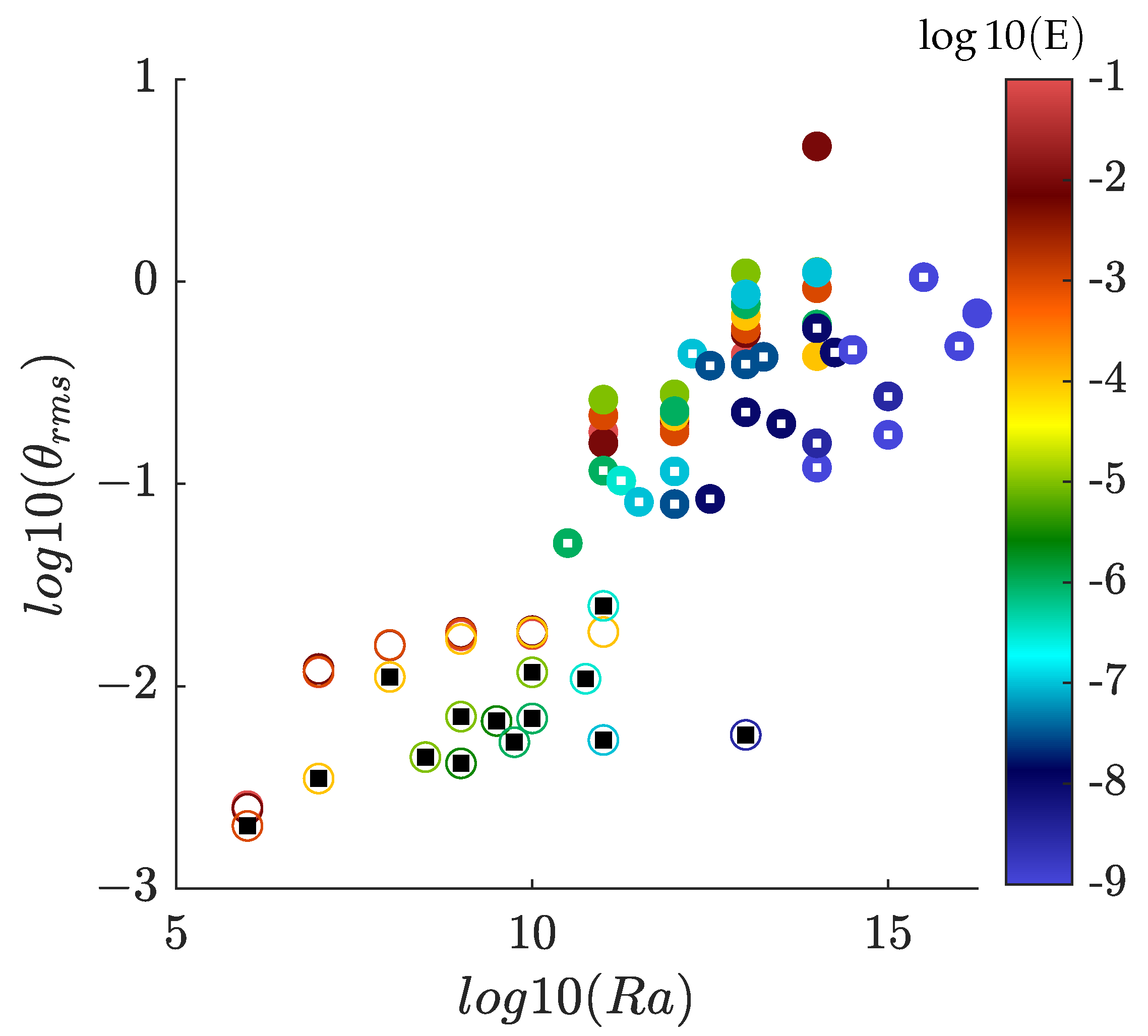
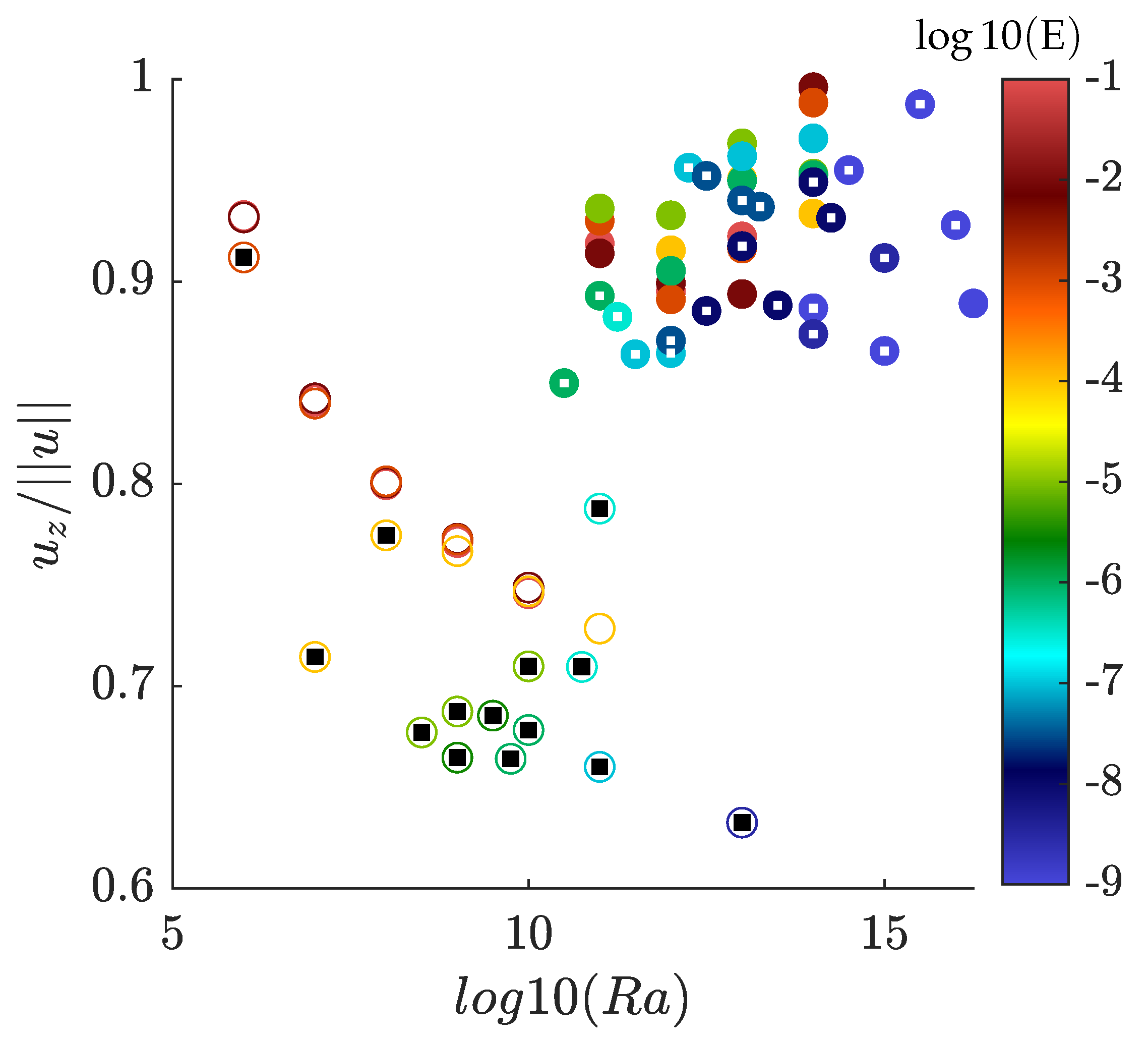
5.3.3. Temperature Fluctuation and Anisotropy
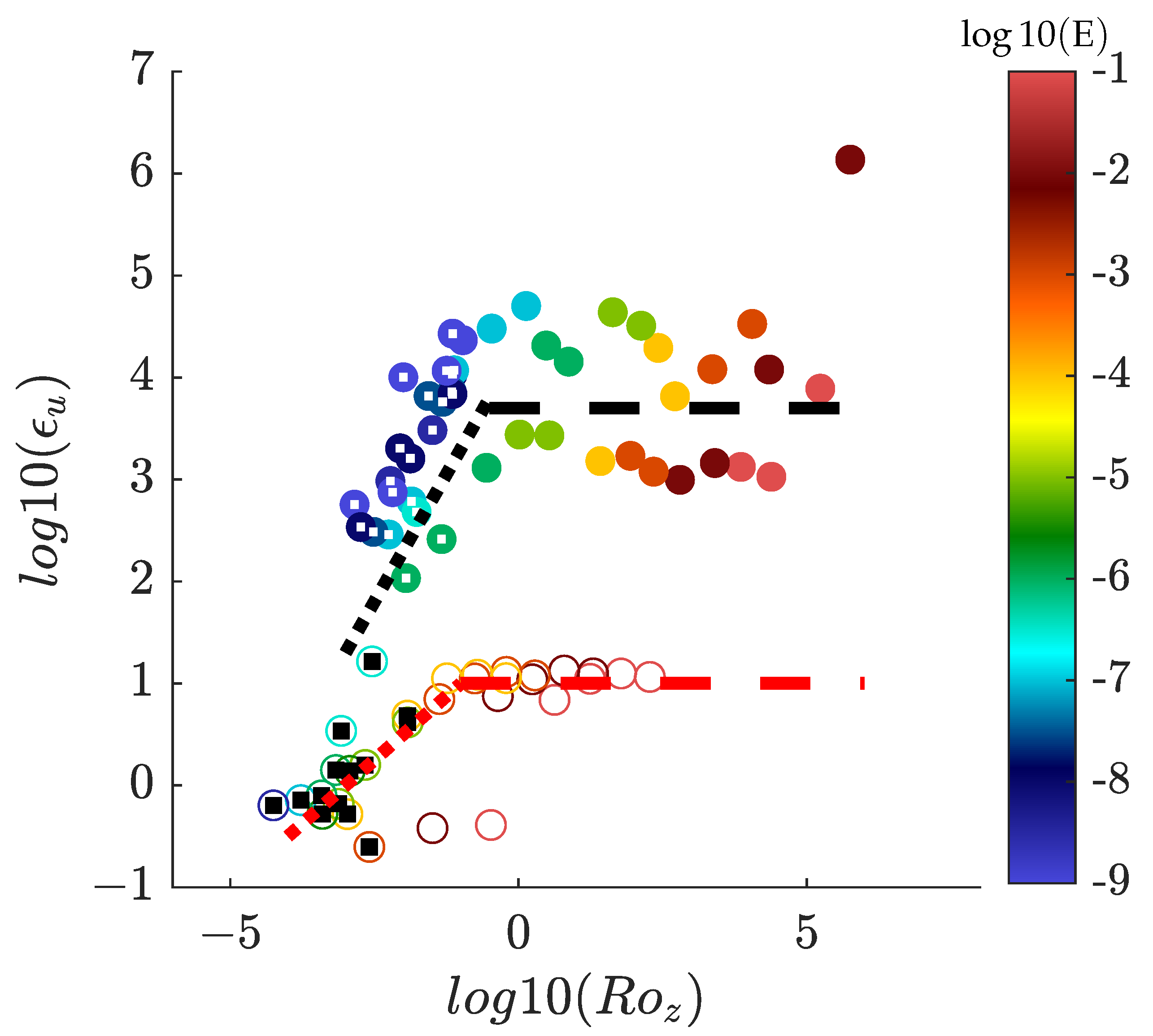
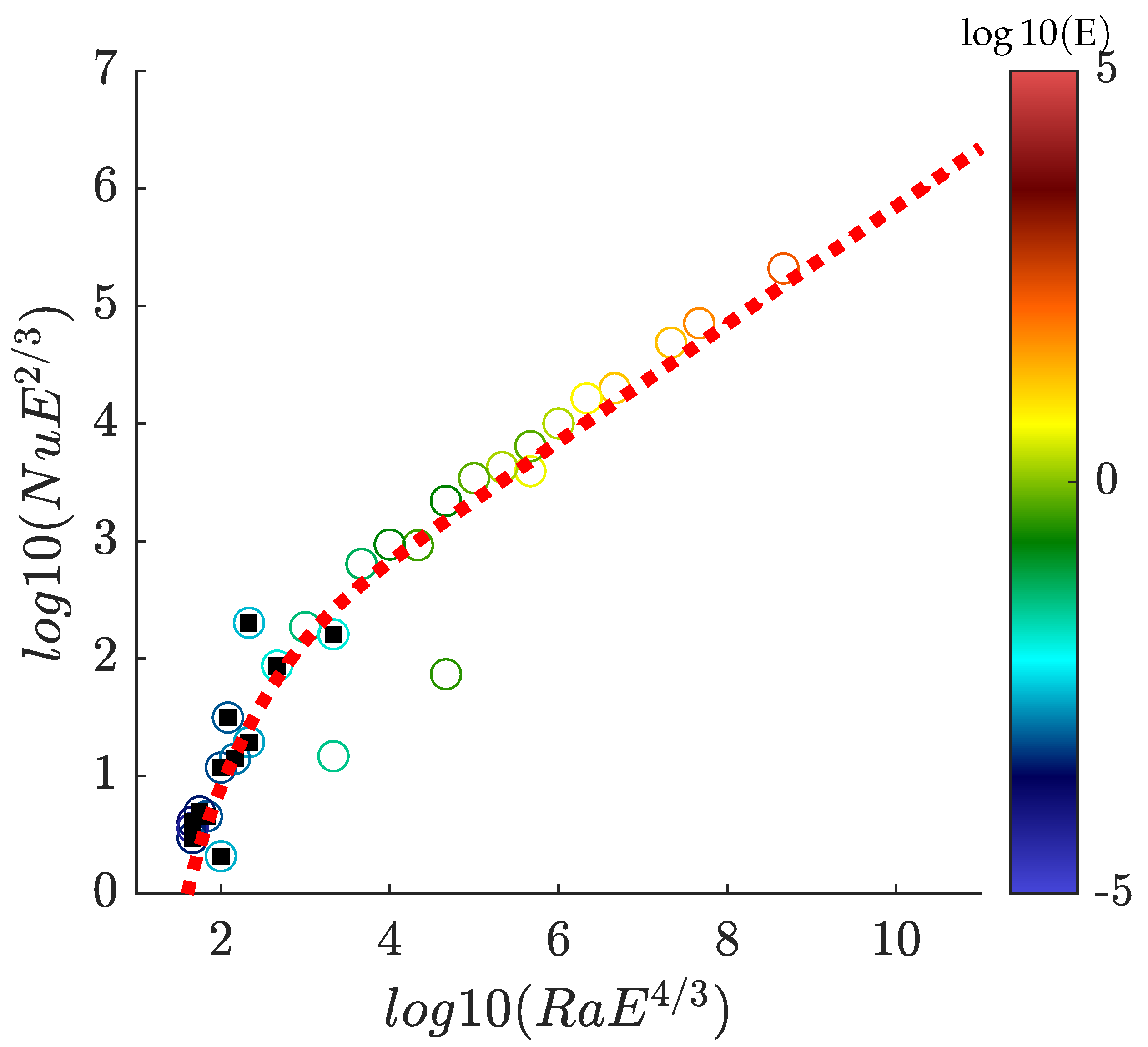
5.3.4. Laminar and Turbulent Scaling Laws and GT Regimes
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Grant, H.L.; Stewart, R.W.; Moilliet, A. Turbulence spectra from a tidal channel. J. Fluid Mech. 1962, 12, 241–268. [Google Scholar] [CrossRef]
- Frisch, U. Turbulence, the Legacy of A. N. Kolmogorov; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Dubrulle, B. Beyond Kolmogorov cascades. J. Fluid Mech. 2019, 867, P1. [Google Scholar] [CrossRef]
- Herring, J.R. Some Contributions of Two-Point Closure to Turbulence. In Proceedings of the Frontiers in Fluid Mechanics; Davis, S.H., Lumley, J.L., Eds.; Springer: Berlin/Heidelberg, Germany, 1985; pp. 68–87. [Google Scholar]
- Dubrulle, B.; Daviaud, F.; Faranda, D.; Marié, L.; Saint-Michel, B. How many modes are needed to predict climate bifurcations? Lessons from an experiment. Nonlinear Process. Geophys. 2022, 29, 17–35. [Google Scholar] [CrossRef]
- Campolina, C.S.; Mailybaev, A.A. Fluid dynamics on logarithmic lattices. Nonlinearity 2021, 34, 4684–4715. [Google Scholar] [CrossRef]
- Meneguzzi, M.; Politano, H.; Pouquet, A.; Zolver, M. A Sparse-Mode Spectral Method for the Simulation of Turbulent Flows. J. Comput. Phys. 1996, 123, 32–44. [Google Scholar] [CrossRef]
- Grossmann, S.; Lohse, D.; L’vov, V.; Procaccia, I. Finite size corrections to scaling in high Reynolds number turbulence. Phys. Rev. Lett. 1994, 73, 432–435. [Google Scholar] [CrossRef]
- Frisch, U.; Pomyalov, A.; Procaccia, I.; Ray, S.S. Turbulence in Noninteger Dimensions by Fractal Fourier Decimation. Phys. Rev. Lett. 2012, 108, 074501. [Google Scholar] [CrossRef] [PubMed]
- Lanotte, A.S.; Benzi, R.; Malapaka, S.K.; Toschi, F.; Biferale, L. Turbulence on a Fractal Fourier Set. Phys. Rev. Lett. 2015, 115, 264502. [Google Scholar] [CrossRef] [PubMed]
- Barral, A.; Dubrulle, B. Asymptotic ultimate regime of homogeneous Rayleigh-Bénard convection on logarithmic lattices. J. Fluid Mech. 2023, 962, A2. [Google Scholar] [CrossRef]
- Pikeroen, Q.; Barral, A.; Costa, G.; Campolina, C.; Mailybaev, A.; Dubrulle, B. Tracking complex singularities of fluids on log-lattices. Nonlinearity 2023. submitted. [Google Scholar]
- Laval, J.P.; Dubrulle, B.; Nazarenko, S. Nonlocality and intermittency in three-dimensional turbulence. Phys. Fluids 2001, 13, 1995–2012. [Google Scholar] [CrossRef]
- Costa, G.; Barral, A.; Dubrulle, B. Reversible Navier–Stokes equation on logarithmic lattices. Phys. Rev. E 2023, 107, 065106. [Google Scholar] [CrossRef] [PubMed]
- Campolina, C.S. Fluid Dynamics on Logarithmic Lattices. Ph.D. Thesis, IMPA, Rio de Janeiro, Brazil, 2022. [Google Scholar]
- Calzavarini, E.; Lohse, D.; Toschi, F.; Tripiccione, R. Rayleigh and Prandtl number scaling in the bulk of Rayleigh-Bénard turbulence. Phys. Fluids 2005, 17, 055107. [Google Scholar] [CrossRef]
- Calzavarini, E.; Doering, C.R.; Gibbon, J.D.; Lohse, D.; Tanabe, A.; Toschi, F. Exponentially growing solutions in homogeneous Rayleigh-Bénard convection. Phys. Rev. E 2006, 73, 035301. [Google Scholar] [CrossRef]
- Calzavarini, E.; Lohse, D.; Toschi, F. Homogeneous Rayleigh-Bénard Convection. In Proceedings of the Progress in Turbulence II; Oberlack, M., Khujadze, G., Günther, S., Weller, T., Frewer, M., Peinke, J., Barth, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 181–184. [Google Scholar]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Spiegel, E.A. A Generalization of the Mixing-Length Theory of Turbulent Convection. Astrophys. J. 1963, 138, 216. [Google Scholar] [CrossRef]
- Kraichnan, R.H. Turbulent Thermal Convection at Arbitrary Prandtl Number. Phys. Fluids 1962, 5, 1374–1389. [Google Scholar] [CrossRef]
- Grossmann, S.; Lohse, D. Scaling in thermal convection: A unifying theory. J. Fluid Mech. 2000, 407, 27–56. [Google Scholar] [CrossRef]
- Ecke, R.E.; Shishkina, O. Turbulent Rotating Rayleigh–Bénard Convection. Annu. Rev. Fluid Mech. 2023, 55, 603–638. [Google Scholar] [CrossRef]
- Cheng, J.S.; Stellmach, S.; Ribeiro, A.; Grannan, A.; King, E.M.; Aurnou, J.M. Laboratory-numerical models of rapidly rotating convection in planetary cores. Geophys. J. Int. 2015, 201, 1–17. [Google Scholar] [CrossRef]
- Plumley, M.; Julien, K. Scaling Laws in Rayleigh-Bénard Convection. Earth Space Sci. 2019, 6, 1580–1592. [Google Scholar] [CrossRef]
- Iyer, K.P.; Scheel, J.D.; Schumacher, J.; Sreenivasan, K.R. Classical 1/3 scaling of convection holds up to Ra = 1015. Proc. Natl. Acad. Sci. USA 2020, 117, 7594–7598. [Google Scholar] [CrossRef] [PubMed]
- Dubrulle, B.; Valdettaro, L. Consequences of rotation in energetics of accretion disks. Astron. Astrophys. 1992, 263, 387–400. [Google Scholar]
- Campagne, A.; Machicoane, N.; Gallet, B.; Cortet, P.P.; Moisy, F. Turbulent drag in a rotating frame. J. Fluid Mech. 2016, 794, R5. [Google Scholar] [CrossRef]
- Bouillaut, V.; Miquel, B.; Julien, K.; Aumaître, S.; Gallet, B. Experimental observation of the geostrophic turbulence regime of rapidly rotating convection. Proc. Natl. Acad. Sci. USA 2021, 118, e2105015118. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pikeroen, Q.; Barral, A.; Costa, G.; Dubrulle, B. Log-Lattices for Atmospheric Flows. Atmosphere 2023, 14, 1690. https://doi.org/10.3390/atmos14111690
Pikeroen Q, Barral A, Costa G, Dubrulle B. Log-Lattices for Atmospheric Flows. Atmosphere. 2023; 14(11):1690. https://doi.org/10.3390/atmos14111690
Chicago/Turabian StylePikeroen, Quentin, Amaury Barral, Guillaume Costa, and Bérengère Dubrulle. 2023. "Log-Lattices for Atmospheric Flows" Atmosphere 14, no. 11: 1690. https://doi.org/10.3390/atmos14111690
APA StylePikeroen, Q., Barral, A., Costa, G., & Dubrulle, B. (2023). Log-Lattices for Atmospheric Flows. Atmosphere, 14(11), 1690. https://doi.org/10.3390/atmos14111690







