Physical Model of D-Region Ionosphere and Preliminary Comparison with IRI and Data of MF Radar at Kunming
Abstract
1. Introduction
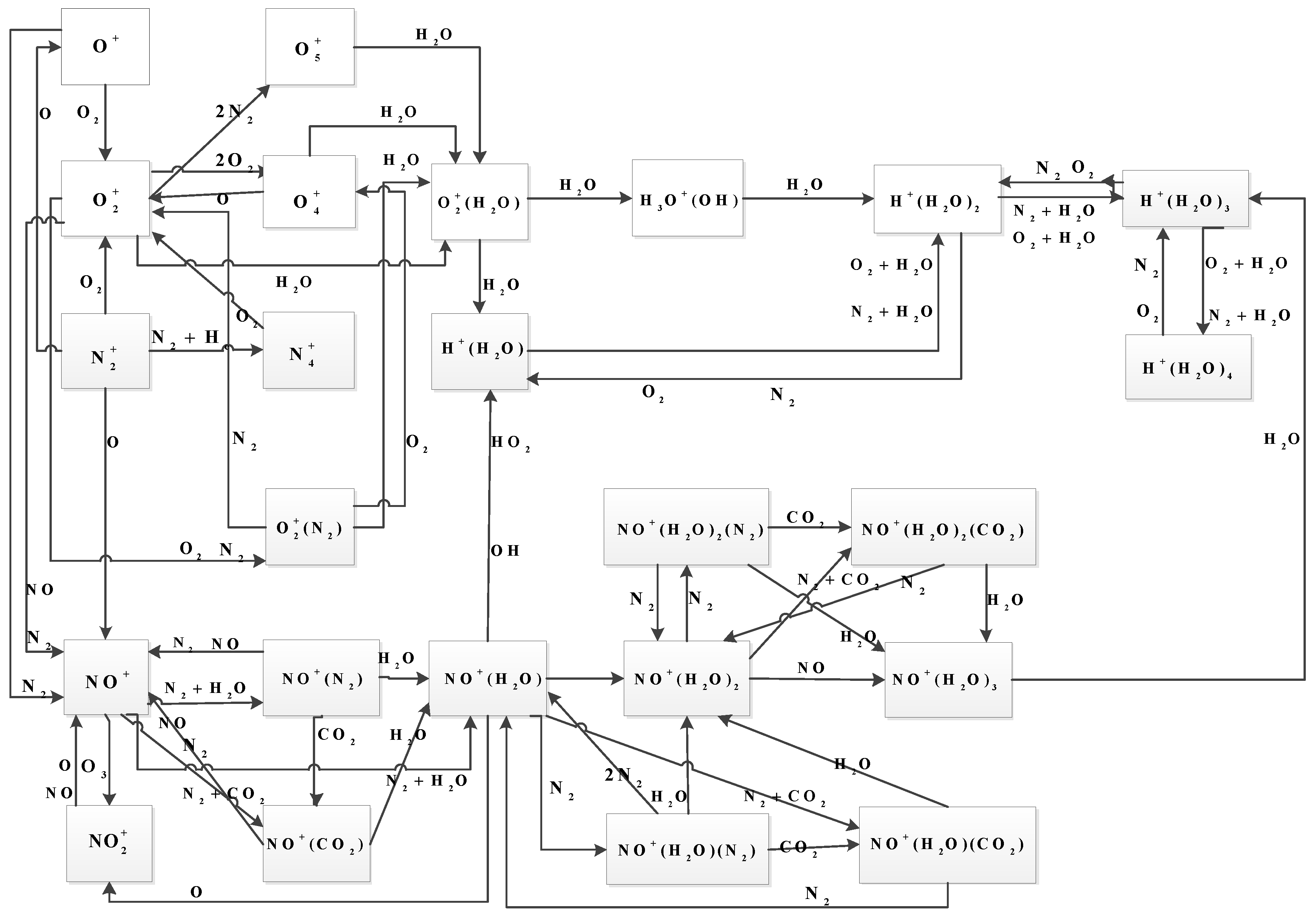
2. Model Description
3. Model Output and Comparative Analysis
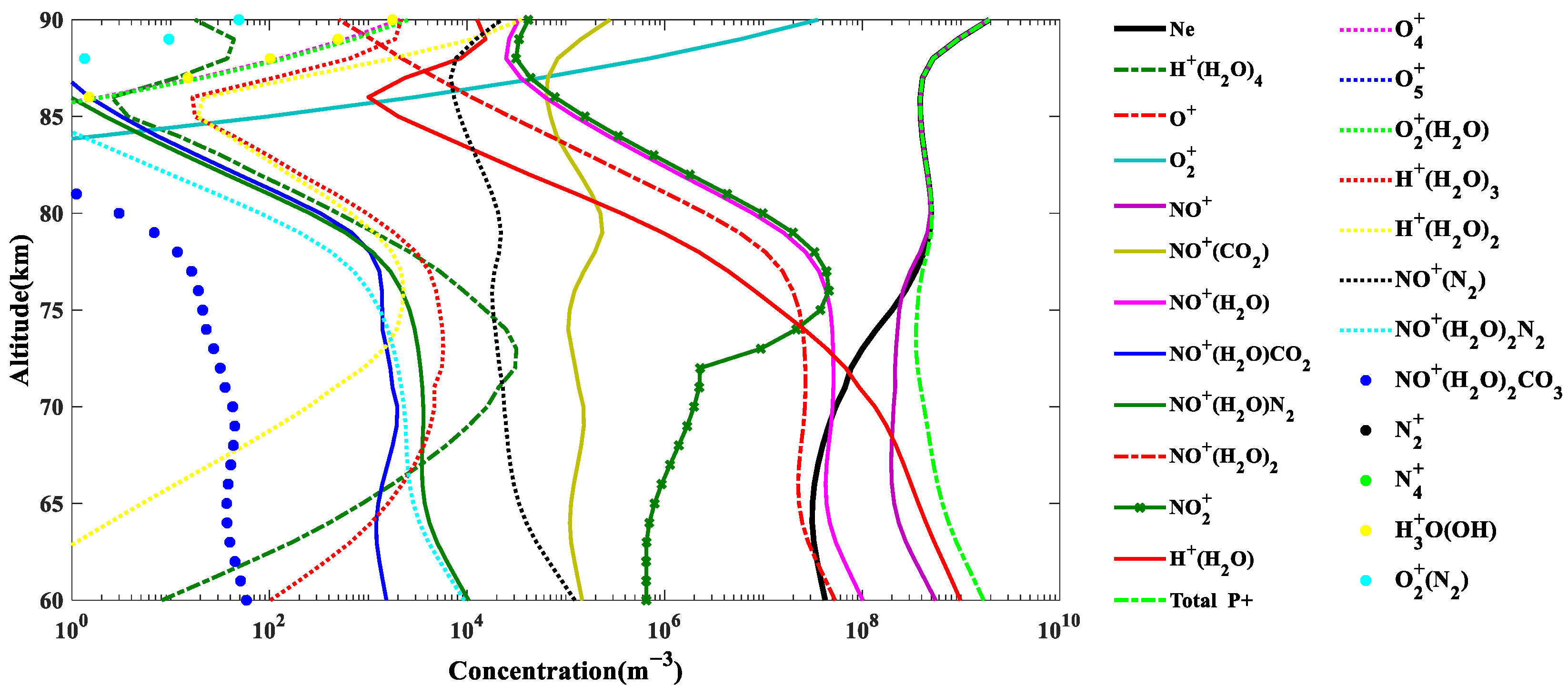
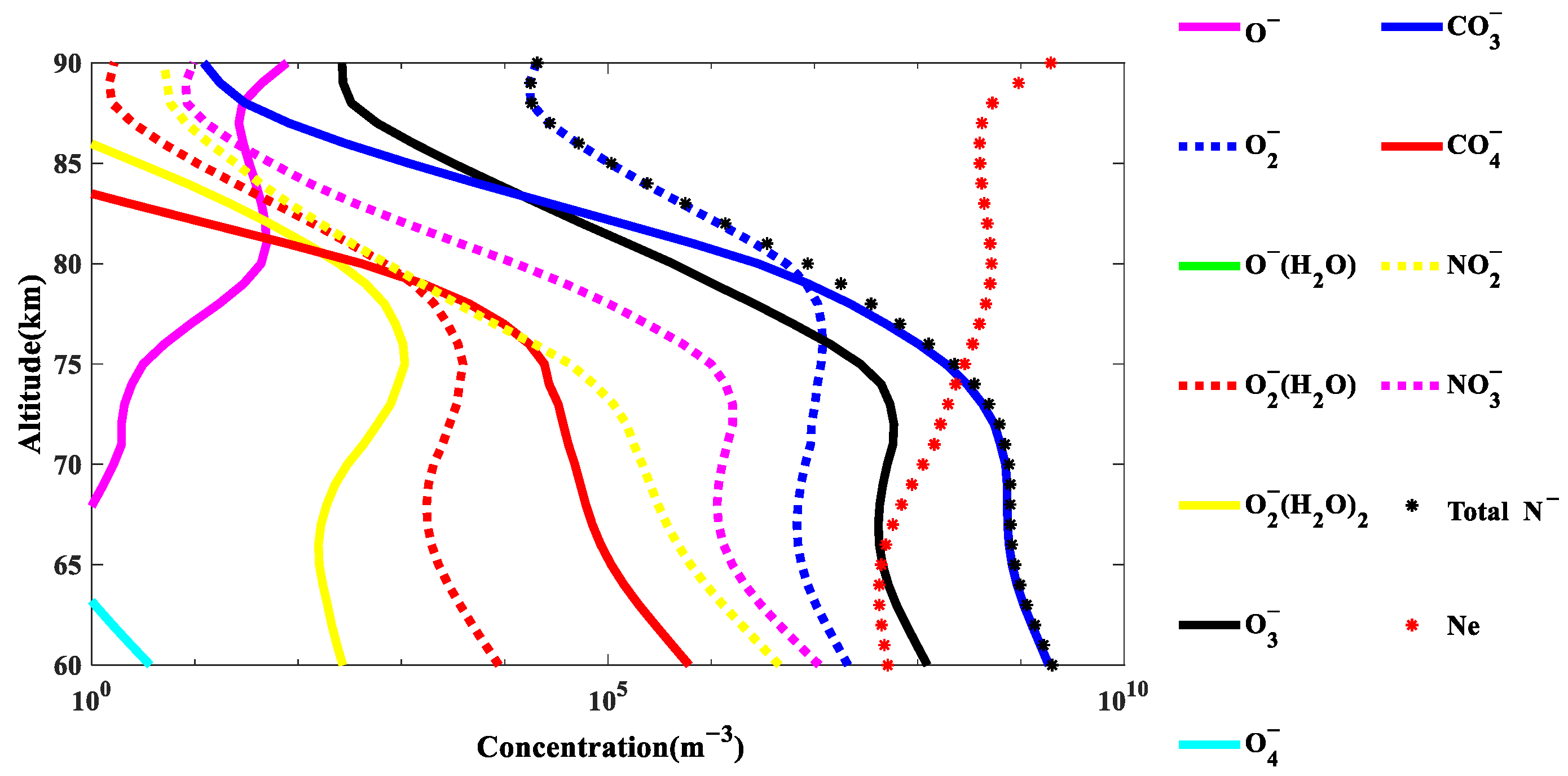
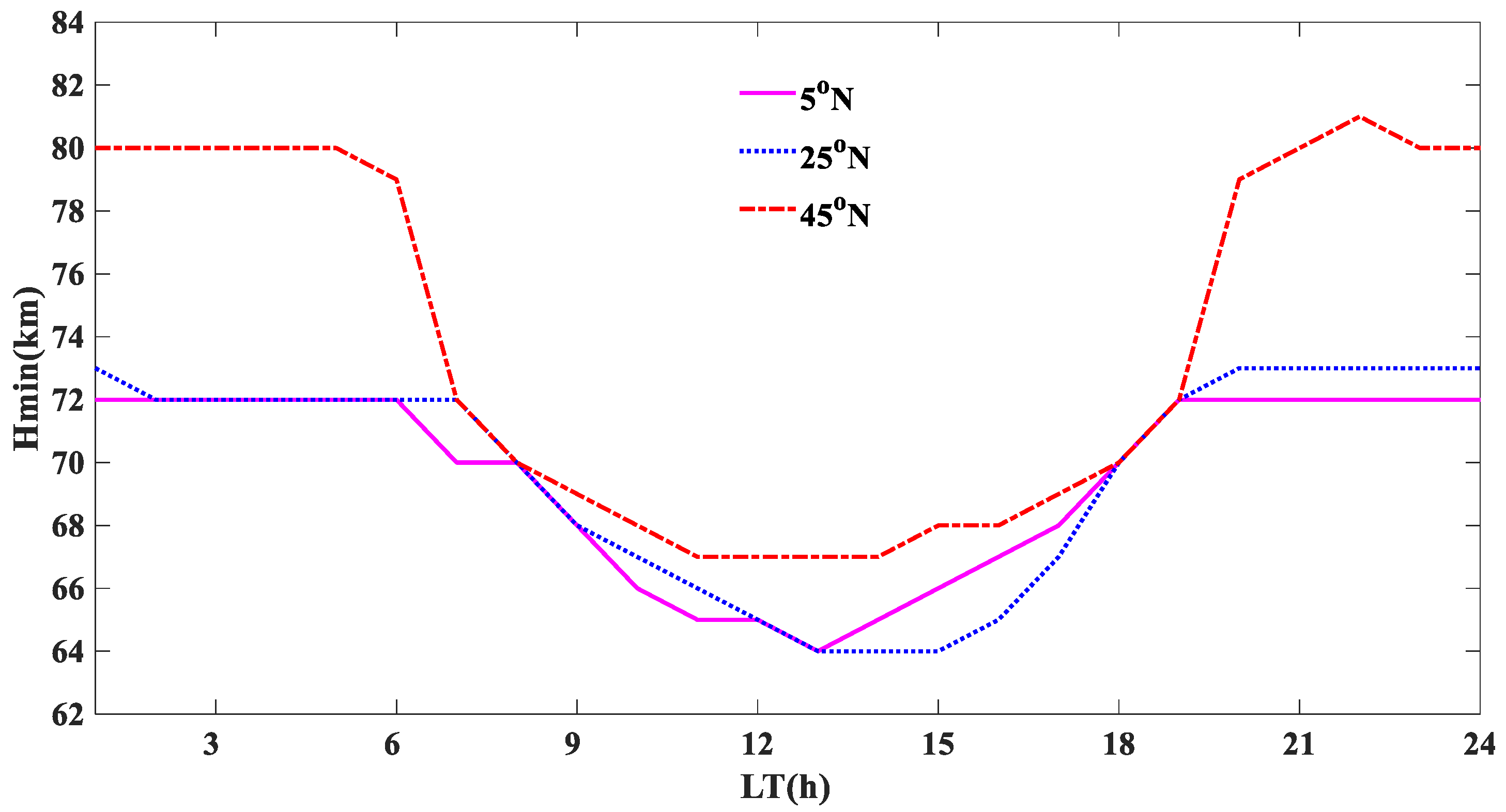
3.1. Model Output
3.2. Kunming MF Radar Data
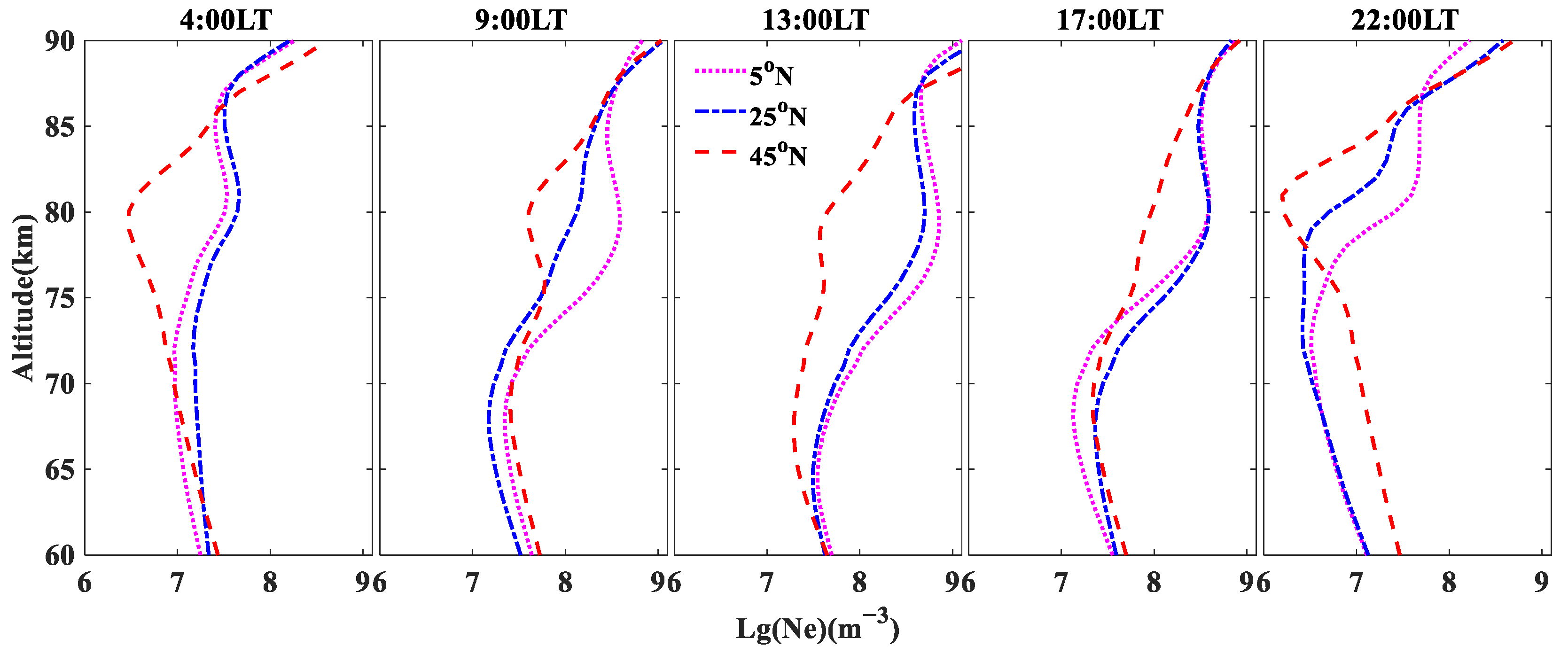
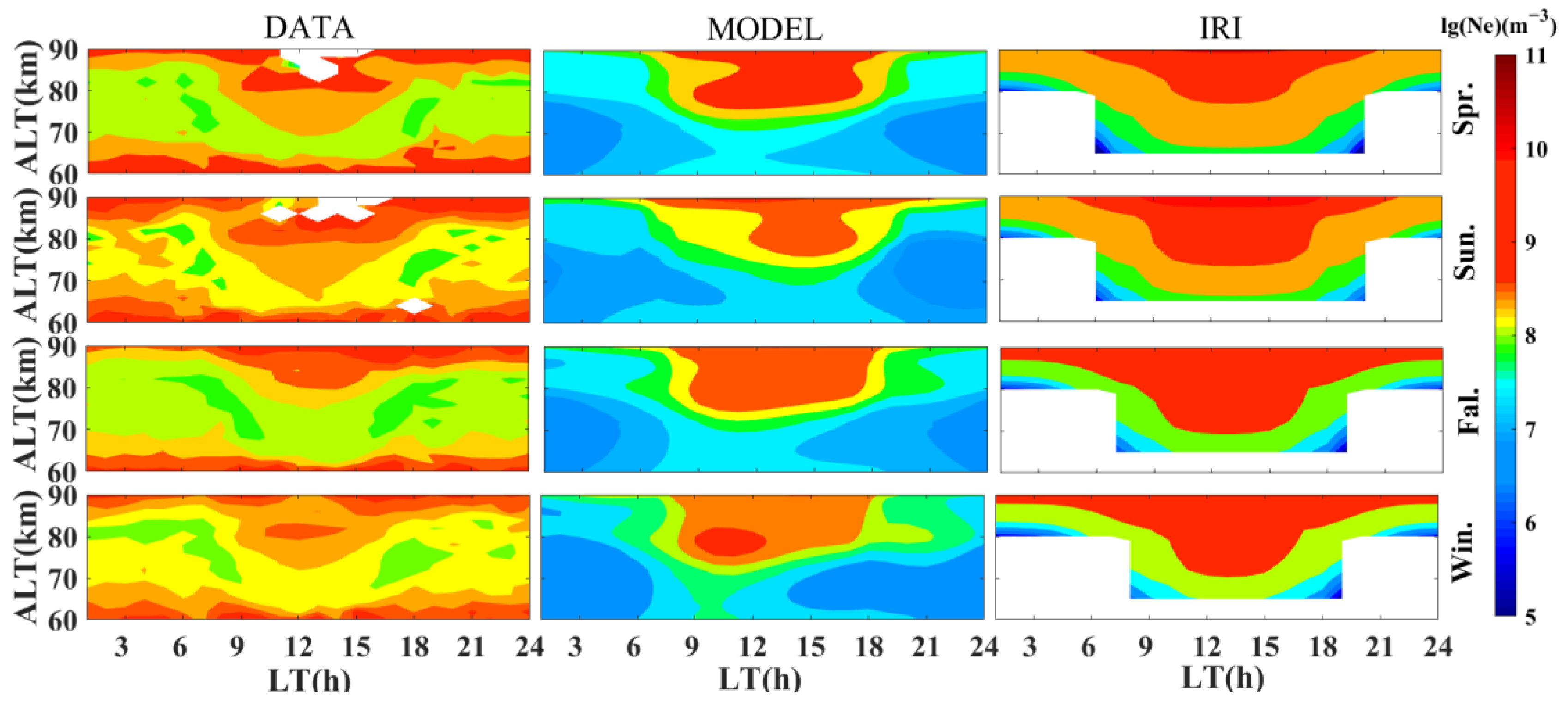
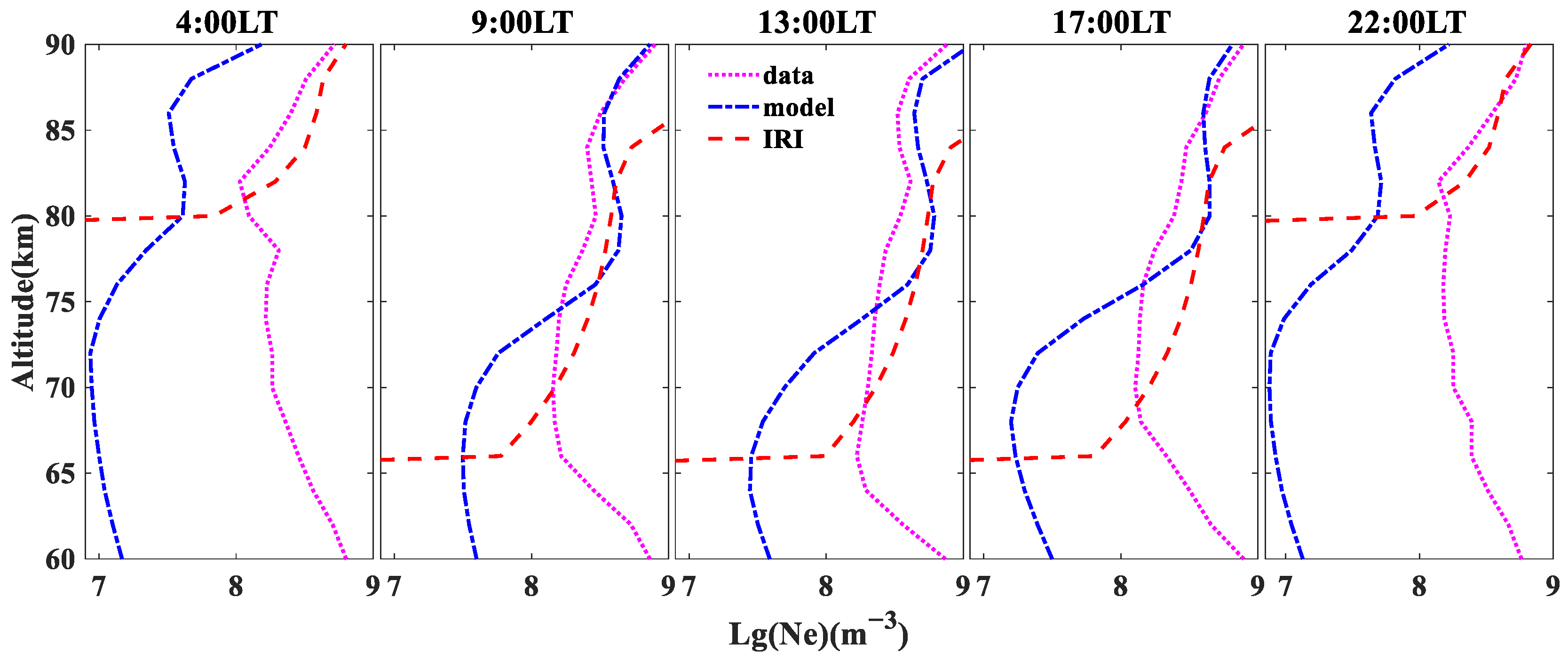
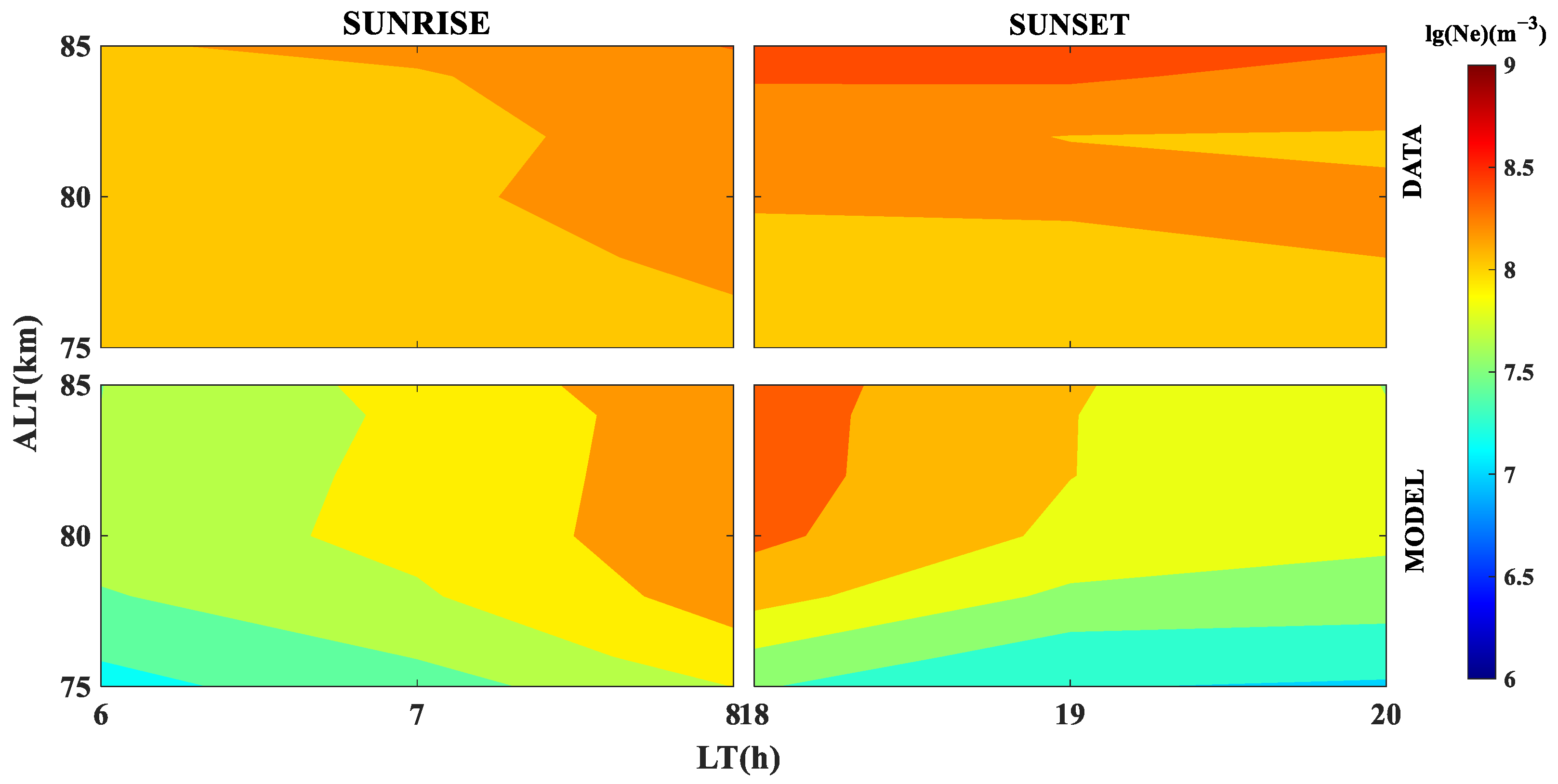
3.3. Comparison with IRI and Observed Data
4. Summary and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Djuth, F.T.; Sulzer, M.P.; Elder, J.H.; Wickwar, V.B. High-resolution studies of atmosphere-ionosphere coupling at Arecibo Observatory. Radio Sci. 1997, 32, 2321–2344. [Google Scholar] [CrossRef]
- Yi, W.; Reid, I.M.; Xue, X.; Younger, J.P.; Murphy, D.J.; Chen, T.; Dou, X. Response of neutral mesospheric density to geomagnetic forcing. Geophys. Res. Lett. 2017, 44, 8647–8655. [Google Scholar] [CrossRef]
- Pancheva, D.; Shiokawa, K.; Knizova, P.; Wan, W. Recent progress in the vertical coupling in the atmosphere-ionosphere system Preface. J. Atmos. Sol.-Terr. Phys. 2012, 90, V–VI. [Google Scholar] [CrossRef]
- Mitra, A.P. The D-region of the ionosphere. Adv. Space Res. 1978, 2, 12–21. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, S. Solar flare effects on D-region ionosphere using VLF measurements during low- and high-solar activity phases of solar cycle 24. Earth Planets Space 2018, 70, 29. [Google Scholar] [CrossRef]
- Mathews, J.D.; Breakall, J.K.; Ganguly, S. The measurement of diurnal variations of electron concentration in the 60–100 km ionosphere at Arecibo. J. Atmos. Terr. Phys. 1982, 44, 441–448. [Google Scholar] [CrossRef]
- Thomson, N.R.; Clilverd, M.A.; Rodger, C.J. Ionospheric D region VLF-measured electron densities compared with rocket-based FIRI-2018 model. J. Geophys. Res. Space Phys. 2022, 127, e2022JA030977. [Google Scholar] [CrossRef]
- Velásquez-García, L.; Izquierdo-Reyes, J.; Kim, H. Review of in-space plasma diagnostics for studying the Earth’s ionosphere. J. Phys. D Appl. Phys. 2022, 55, 263001. [Google Scholar] [CrossRef]
- Bilitza, D. Electron density in the D-region as given by the IRI. Int. Ref. Ionos.-IRI 1981, 79, 7–10. [Google Scholar]
- Singer, W.; Bemer, J.; Taubenheim, J. Improvement of the solar-cycle variation of IRI lower ionosphere models by means of radio wave propagation data. Adv. Space Res. 1984, 4, 79–88. [Google Scholar] [CrossRef]
- Mukhtarov, P.; Pancheva, D. Model of the electron density height profile in the lowest D-region. Adv. Space Res. 1995, 15, 179–182. [Google Scholar] [CrossRef]
- Danilov, A.; Rodevich, A.; Smirnova, N. Problems with incorporating a new D-region model into the IRI. Adv. Space Res. 1995, 15, 165–169. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, V.; Galkin, I.; Reinisch, B.; Huang, X. International Reference Ionosphere 2016: From ionosphere climate to real time weather predictions. Space Weather 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Friedrich, M.; Pock, C.; Torkar, K. FIRI-2018, an updated empirical model of the lower ionosphere. J. Geophys. Res. Space Phys. 2018, 123, 6737–6751. [Google Scholar] [CrossRef]
- Gokov, A.M.; Tyrnov, O.F.; Buts, Y.V.; Kovalenko, E.N. Empirical modeling of variations of electron density in the undisturbed mid-latitude D-region of the ionosphere. Telecommun. Radio Eng. 2020, 79, 335–342. [Google Scholar] [CrossRef]
- McCormick, J.C.; Cohen, M.B.A. New Four-Parameter D-Region Ionospheric Model: Inferences from Lightning-Emitted VLF Signals. J. Geophy. Res. 2021, 126, e2021JA029849. [Google Scholar] [CrossRef]
- Thomson, N.R.; Clilverd, M.A.; Rodgers, C.J. Midlatitude ionospheric D region: Height, sharpness and solar zenith angle. J. Geophys. Res. 2017, 122, 8933–8946. [Google Scholar] [CrossRef]
- Pavlov, A.V. Photochemistry of ions at D-region altitudes of the ionosphere: A review. Surv. Geophys. 2013, 35, 259–334. [Google Scholar] [CrossRef]
- Torkar, K.M.; Friedrich, M. Tests of an ion-chemical model of the D-and lower E region. J. Atmos. Terr. Phys. 1983, 45, 369–385. [Google Scholar] [CrossRef]
- Tomko, A.A.; Ferraro, A.J.; Lee, H.S.; Mita, A.P. A theoretical model of D-region ion chemistry modifications during high power radio wave heating. J. Atmos. Terr. Phys. 1980, 42, 275–285. [Google Scholar] [CrossRef]
- Smimova, N.V.; Ogloblina, O.F.; Vlaskov, V.A. Modeling of the lower ionosphere. Pure Appl. Geophys. 1988, 127, 354–357. [Google Scholar]
- Verronen, P.T.; Andersson, M.E.; Marsh, D.R.; Kovács, T.; Plane, J.M. WACCM-D: Whole Atmosphere Community Climate Model with D-region ion chemistry. J. Adv. Model. Earth Syst. 2016, 8, 954–975. [Google Scholar] [CrossRef]
- Turunen, E.; Matveinen, H.; Tolvanen, J.; Ranta, H. D-region ion chemistry model. In STEP Handbook of Ionospheric Models; Utah State University: Logan, UT, USA, 1996; pp. 1–25. [Google Scholar]
- Sentman, D.D. Plasma chemistry of sprite streames. J. Geophys. Res. 2008, 113, D11112. [Google Scholar] [CrossRef]
- Kotovsky, D.A.; Moore, R.C. Photochemical response of the nighttime mesosphere to electric fieldheating—Recovery of electron density enhancements. Geophys. Res. Lett. 2016, 43, 952–960. [Google Scholar] [CrossRef]
- Megner, L.; Rapp, M.; Gumbel, J. Distribution of meteoric smoke—Sensitivity to microphysical properties and atmospheric conditions. Atmos. Chem. Phys. 2006, 6, 4415–4426. [Google Scholar] [CrossRef]
- Baumann, C.; Rapp, M.; Anttila, M.; Kero, A.; Verronen, P.T. Effects of meteoric smoke particles on the D region ion chemistry. J. Geophys. Res. Space Phys. 2015, 120, 10823–10839. [Google Scholar] [CrossRef]
- Nicolet, M. Aeronomical aspects of mesospheric photodissociation: Processes resulting from the solar H Lyman-alpha line. Planet Space Sci. 1985, 33, 69–80. [Google Scholar] [CrossRef]
- Strobel, D.F.; Young, T.R.; Meier, R.R.; Coffey, T.P.; Ali, A.W. The nighttime ionosphere: E region and lower F region. J. Geophys. Res. 1974, 79, 3171–3178. [Google Scholar] [CrossRef]
- Titherige, J.E. Modelling the peak of the ionospheric E-layer. J. Atmos. Solar-Terr. Phys. 2000, 62, 93–114. [Google Scholar] [CrossRef]
- Huba, J.D.; Joyce, G.; Fedder, J.A. Sami2 is Another Model of the Ionosphere (SAMI2): A new low-latitude ionosphere model. J. Geophys. Res. Space Phys. 2000, 105, 23035–23053. [Google Scholar] [CrossRef]
- Burns, C.J.; Turunen, E.; Matveinen, H.; Ranta, H.; Hargreaves, J.K. Chemical modeling of the quiet summer D- and E-regions using EISCAT electron density profiles. J. Atmos. Terr. Phys. 1991, 53, 115–134. [Google Scholar] [CrossRef]
- Albritton, D.J. Ion-neutral reaction-rate constants measured in flow reactors through 1977. At. Data Nucl. Data Tables 1978, 22, 1–101. [Google Scholar] [CrossRef]
- Emmert, J.T.; Drob, D.P.; Picone, J.M.; Siskind, D.E.; Jones, M., Jr.; Mlynczak, M.G.; Bernath, P.F.; Chu, X.; Doornbos, E.; Funke, B.; et al. NRLMSIS2.0: A whole-atmosphere empirical model of temperature and neutral species densities. Earth Space Sci. 2021, 8, e2020EA001321. [Google Scholar] [CrossRef]
- Richards, P.G.; Fennelly, J.A.; Torr, D.G. EUVAC: A solar EUV Flux Model for aeronomic calculations. J. Geophys. Res. Space Phys. 1994, 99, 8981–8992. [Google Scholar] [CrossRef]
- Muratama, Y.; Igarashi, K.; Rice, D.D. Medium frequency radars in Japan and Alaska for upper atmosphere observations. IEICS Trans. Commun. 2000, E83-B, 1996–2003. [Google Scholar]
- Yang, K.J. About layer C in ionospheric zone D. Chin. J. Geophys. 1986, 29, 1–7. (In Chinese) [Google Scholar]
- Thomson, N.R. Daytime tropical D region parameters from short path VLF phase and amplitude. J. Geophys. Res. 2010, 115, A09313. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, J.Q.; Ma, Q.M.; Huang, Q.; Xiao, F. A method for determining D region ionosphere reflection height from lightning sky-waves. J. Atmos. Sol.-Terr. Phys. 2021, 221, 1364–6826. [Google Scholar] [CrossRef]
- Baumann, C.; Kero, A.; Raizada, S.; Rapp, M.; Sulzer, M.P.; Verronen, P.T.; Vierinen, J. Arecibo Measurements of D-Region Electron Densities during Sunset and Sunrise in August 2016 [dataset]. Ann. Geophys. Discuss. 2022, 40, pp. 519–530. [CrossRef]
- Baumann, C.; Kero, A.; Raizada, S.; Rapp, M.; Sulzer, M.P.; Verronen, P.T.; Vierinen, J. Arecibo measurements of D-region electron densities during sunset and sunrise: Implications for atmospheric composition. Ann. Geophys. Discuss. 2022, 1–17. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, M.; Xu, T.; Sun, S.; Zhou, C.; Hu, Y.; Ge, S.; Li, N.; Deng, Z.; Zhang, Y.; Liu, X. Physical Model of D-Region Ionosphere and Preliminary Comparison with IRI and Data of MF Radar at Kunming. Atmosphere 2023, 14, 235. https://doi.org/10.3390/atmos14020235
Zhu M, Xu T, Sun S, Zhou C, Hu Y, Ge S, Li N, Deng Z, Zhang Y, Liu X. Physical Model of D-Region Ionosphere and Preliminary Comparison with IRI and Data of MF Radar at Kunming. Atmosphere. 2023; 14(2):235. https://doi.org/10.3390/atmos14020235
Chicago/Turabian StyleZhu, Mengyan, Tong Xu, Shuji Sun, Chen Zhou, Yanli Hu, Shucan Ge, Na Li, Zhongxin Deng, Yuqiang Zhang, and Xiaolei Liu. 2023. "Physical Model of D-Region Ionosphere and Preliminary Comparison with IRI and Data of MF Radar at Kunming" Atmosphere 14, no. 2: 235. https://doi.org/10.3390/atmos14020235
APA StyleZhu, M., Xu, T., Sun, S., Zhou, C., Hu, Y., Ge, S., Li, N., Deng, Z., Zhang, Y., & Liu, X. (2023). Physical Model of D-Region Ionosphere and Preliminary Comparison with IRI and Data of MF Radar at Kunming. Atmosphere, 14(2), 235. https://doi.org/10.3390/atmos14020235






