Frost Mitigation Techniques for Tunnels in Cold Regions: The State of the Art and Perspectives
Abstract
:1. Introduction
2. Theory of Tunnel Design in Cold Regions
2.1. Freezing and Thawing Depth
2.2. Frost Heaving Force
2.3. Classifications of the Surrounding Rock and Cold Regions
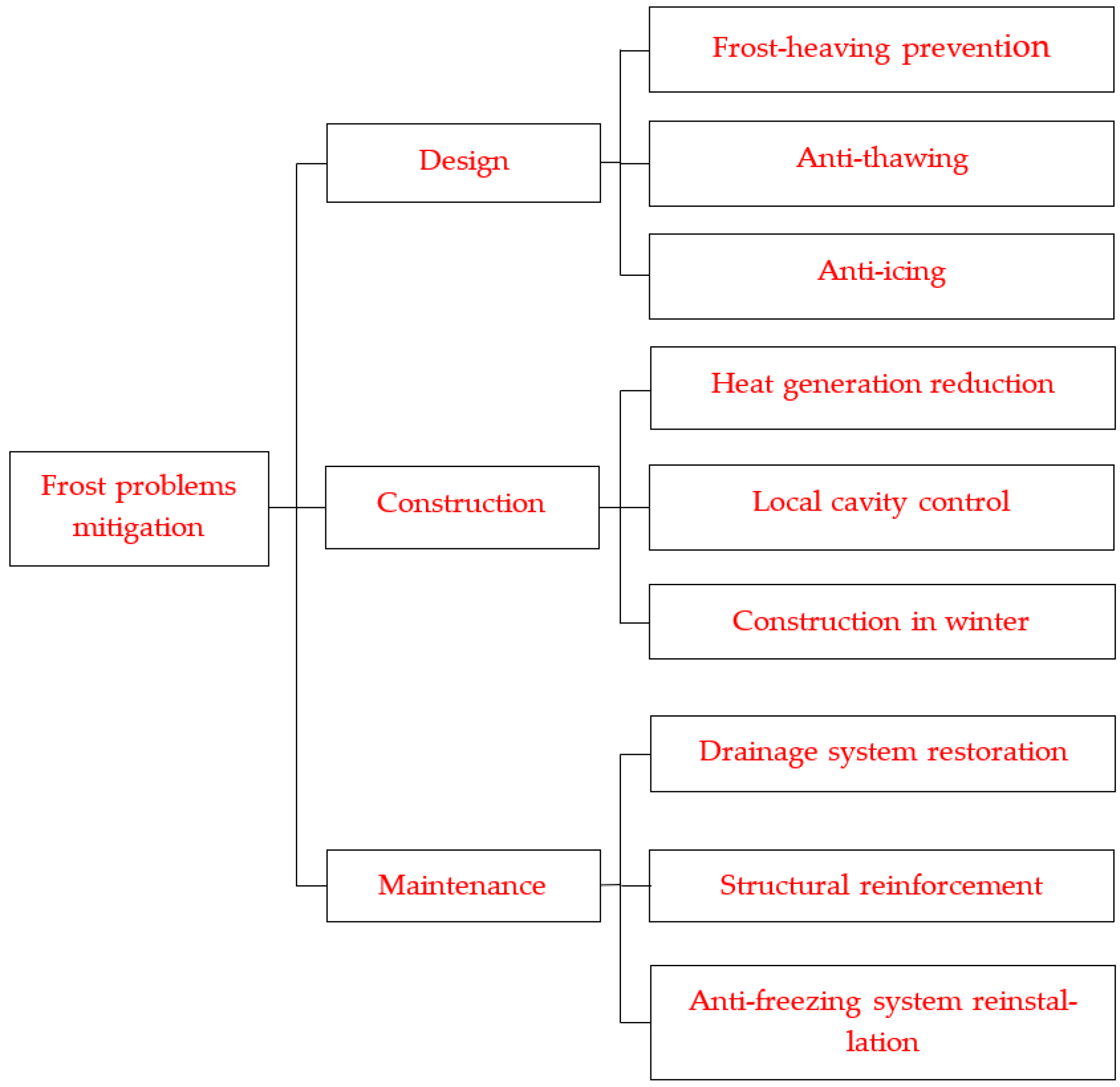
3. Techniques for Frost Problem Mitigation in Tunnel Design
3.1. Frost Heaving Prevention
3.1.1. Insulation Layer
3.1.2. Heating and Other Measures
3.2. Anti-Thawing Measures
3.3. Anti-Icing Measures
4. Tunnel Construction Techniques for Frost Problem Mitigation
5. Tunnel Maintenance Techniques for Frost Problem Mitigation
6. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tao, Q. Study on Electric Film Heating and Thermal Insulation Technology for Tunnels in Cold Regions. Railw. Eng. 2022, 62, 130–134. [Google Scholar]
- Wan, J.G. Review on and Present Situation and Prospect of Antifreezing Technologies for Tunnels in Cold Areas in China. Tunn. Constr. 2021, 41, 1115–1131. [Google Scholar] [CrossRef]
- Inokuma, A.; Inano, S. Road tunnels in Japan: Deterioration and countermeasures. Tunn. Undergr. Space Technol. 1996, 11, 305–309. [Google Scholar] [CrossRef]
- Jin, H.; Hwang, Y. A Study on Current Extent of Damage of Road Tunnel Lining in Cold Regions (Gangwon-do). J. Korean Geoenviron. Soc. 2017, 18, 49–58. [Google Scholar] [CrossRef]
- Gao, Y.; Zhu, Y.Q.; Zhao, D.P.; Geng, J.Y.; Xin, H. Study on classified suggestion of tunnel in cold region and thermal insulation-considered drainage technology. Chin. J. Rock Mech. Eng. 2018, 37, 3489–3499. [Google Scholar] [CrossRef]
- Aursand, P.O. Frost heave in highway tunnels in Nordland County, Norway. Proc. Int. Conf. Bear. Capacit. Roads Railw. Airfields 2013, 2, 993–1001. [Google Scholar]
- Asakura, T.; Kojima, Y. Tunnel maintenance in Japan. Tunn. Undergr. Space Technol. 2003, 18, 161–169. [Google Scholar] [CrossRef]
- Kang, F.Z.; Qi, F.L.; He, S.H.; Jiang, B. Application of ground penetrating radar to disease detection of Kunlun Mountain tunnel. Chin. J. Rock Mech. Eng. 2010, 29, 3641–3646. [Google Scholar]
- Liu, H.J.; Zheng, J.Y.; Cheng, C.G.; Huang, L.H. Rehabilitation project of the Dabanshan highland road tunnel. J. Chong-Qing Univ. 2011, 34, 138–143+150. [Google Scholar]
- Lv, K.C.; Ji, Z.; Ma, C.C.; Xu, P. Causes and Prevention for Tunnel Lining Crack in Cold Region. Highway 2012, 1, 196–200. [Google Scholar]
- Yu, W.; Zhang, T.; Lu, Y.; Han, F.; Zhou, Y.; Hu, D. Engineering risk analysis in cold regions: State of the art and perspectives. Cold Reg. Sci. Technol. 2019, 171, 102963. [Google Scholar] [CrossRef]
- Zhou, L.C.; Zheng, Y.F.; Li, Z. Study on Mechanism of Circumferential Cracks in cold-region Tunnels. Glob. Geol. 2010, 13, 75–78. [Google Scholar] [CrossRef]
- Jensen, S.F.; Ayele, Y.Z.; Barabadi, A. Fire safety aspects for underwater tunnels in cold climate. In Proceedings of the 27th International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 25–30 June 2017. [Google Scholar]
- Lai, J.; Wang, X.; Qiu, J.; Zhang, G.; Chen, J.; Xie, Y.; Luo, Y. A state-of-the-art review of sustainable energy based freeze proof technology for cold-region tunnels in China. Renew. Sustain. Energy Rev. 2018, 82, 3554–3569. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, J. Research status and progress of tunnel frost damage. J. Traffic Transp. Eng. 2019, 6, 297–309. [Google Scholar] [CrossRef]
- Chen, L.; Yu, W.; Zhang, T.; Yi, X. Asymmetric talik formation beneath the embankment of Qinghai-Tibet Highway triggered by the sunny-shady effect. Energy 2023, 266, 126472. [Google Scholar] [CrossRef]
- Zhang, M.; Pei, W.; Lai, Y.; Niu, F.; Li, S. Numerical study of the thermal characteristics of a shallow tunnel section with a two-phase closed thermosyphon group in a permafrost region under climate warming. Int. J. Heat Mass Transf. 2017, 104, 952–963. [Google Scholar] [CrossRef]
- Shui, W.; Gao, G.; Han, X.; Lv, K. Analysis on thermal conductivity and frost depth of enclosing rock of tunnel in cold region. Undergr. Space 2002, 22, 343–346. [Google Scholar]
- Pei, W.; Yu, W.; Li, S.; Zhou, J. A new method to model the thermal conductivity of soil–rock media in cold regions: An example from permafrost regions tunnel. Cold Reg. Sci. Technol. 2013, 95, 11–18. [Google Scholar] [CrossRef]
- Liu, W.; He, P.; Zhang, Z. A calculation method of thermal conductivity of soils. J. Glaciol. Geocryol. 2002, 24, 770–773. [Google Scholar]
- Côté, J.; Konrad, J.-M. A generalized thermal conductivity model for soils and construction materials. Can. Geotech. J. 2005, 42, 443–458. [Google Scholar] [CrossRef]
- Lai, Y.M.; Liu, S.Y.; Wu, Z.W.; Yu, W.B. Approximate analytical solution for temperature fields in cold regions circular tunnels. Cold Reg. Sci. Technol. 2002, 34, 43–49. [Google Scholar] [CrossRef]
- Zhang, Y.; He, S.; Li, J. Analytic solutions for the temperature fields of a circular tunnel with insulation layer in cold region. J. Glaciol. Geocryol. 2009, 31, 113–118. [Google Scholar]
- Zhang, G.; Xia, C.; Yin, Z. Analytical solution to axial and radial temperature of tunnel in cold region. J. Tongji Univ. (Nat. Sci.) 2010, 38, 1117–1123. [Google Scholar]
- Feng, Q.; Jiang, B. Analytical calculation on temperature field of tunnels in cold region by Laplace integral transform. J. Min. Saf. Eng. 2012, 29, 391–395. [Google Scholar]
- Xia, C.; Lv, Z.; Li, Q.; Huang, J.; Bai, X. Transversely isotropic frost heave of saturated rock under unidirectional freezing condition and induced frost heaving force in cold region tunnels. Cold Reg. Sci. Technol. 2018, 152, 48–58. [Google Scholar] [CrossRef]
- Lai, Y.; Wu, Z.; Zhu, Y.; Zhu, L. Nonlinear analysis for the coupled problem of temperature, seepage and stress fields in cold-region tunnels. Tunn. Undergr. Space Technol. 1998, 13, 435–440. [Google Scholar] [CrossRef]
- Lai, Y.-M.; Wu, Z.; Zhu, Y.; Zhu, L. Nonlinear analysis for the coupled problem of temperature and seepage fields in cold regions tunnels. Cold Reg. Sci. Technol. 1999, 29, 89–96. [Google Scholar] [CrossRef]
- Zhang, X.F.; Lai, Y.M.; Yu, W.B.; Zhang, S.J. Nonlinear analysis for the three-dimensional temperature fields in cold region tunnels. Cold Reg. Sci. Technol. 2002, 35, 207–219. [Google Scholar] [CrossRef]
- Zhang, X.; Lai, Y.; Yu, W.; Zhang, S. Numerical analysis for the three-dimension temperature fields in cold region tunnels. J. China Railw. Soc. 2003, 25, 84–90. [Google Scholar]
- Lai, Y.; Zhang, X.; Yu, W.; Zhang, S.; Liu, Z.; Xiao, J. Three-dimensional nonlinear analysis for the coupled problem of the heat transfer of the surrounding rock and the heat convection between the air and the surrounding rock in cold-region tunnel. Tunn. Undergr. Space Technol. 2005, 20, 323–332. [Google Scholar] [CrossRef]
- Yang, G.; Zhou, C.; Tian, Y. Numerical simulation and analysis of moisture-heat coupling for soft rock tunnel in cold regions. Yantu Lixue (Rock Soil Mech.) 2006, 27, 1258–1262. [Google Scholar]
- Zhang, Q.; Gao, G.; Yang, G. Three-dimensional finite difference analysis of the temperature field of cold-region tunnels. J. Univ. Sci. Technol. Suzhou Eng. Technol. 2006, 19, 15–20. [Google Scholar]
- Tan, X.; Chen, W.; Tian, H.; Cao, J. Water flow and heat transport including ice/water phase change in porous media: Numerical simulation and application. Cold Reg. Sci. Technol. 2011, 68, 74–84. [Google Scholar] [CrossRef]
- Tan, X.; Chen, W.; Wu, G.; Yang, J. Numerical simulations of heat transfer with ice–water phase change occurring in porous media and application to a cold-region tunnel. Tunn. Undergr. Space Technol. 2013, 38, 170–179. [Google Scholar] [CrossRef]
- Tan, X.; Chen, W.; Wu, G.; Yang, J. Study of airflow in a cold-region tunnel using a standard k − ε turbulence model and air-rock heat transfer characteristics: Validation of the CFD results. Heat Mass Transf. 2012, 49, 327–336. [Google Scholar] [CrossRef]
- Tan, X.; Chen, W.; Yang, D.; Dai, Y.; Wu, G.; Yang, J.; Yu, H.; Tian, H.; Zhao, W. Study on the influence of airflow on the temperature of the surrounding rock in a cold region tunnel and its application to insulation layer design. Appl. Therm. Eng. 2014, 67, 320–334. [Google Scholar] [CrossRef]
- Zhou, X.; Zeng, Y.; Fan, L. Temperature field analysis of a cold-region railway tunnel considering mechanical and train-induced ventilation effects. Appl. Therm. Eng. 2016, 100, 114–124. [Google Scholar] [CrossRef]
- Jin, H.; Kim, T.; Hwang, Y. Analysis of Temperature Change of Tunnel Lining with Heating Element. J. Korean Geoenviron. Soc. 2017, 18, 5–12. [Google Scholar] [CrossRef]
- Lai, Y.; Hui, W.; Wu, Z.; Liu, S.; Den, X. Analytical viscoelastic solution for frost force in cold-region tunnels. Cold Reg. Sci. Technol. 2000, 31, 227–234. [Google Scholar] [CrossRef]
- Lai, Y.; Wu, Z.; Zhu, Y.; Zhu, L. Elastic visco-plastic analysis for earthquake response of tunnels in cold regions. Cold Reg. Sci. Technol. 2000, 31, 175–188. [Google Scholar] [CrossRef]
- Gao, G.; Chen, Q.; Zhang, Q.; Chen, G. Analytical elasto-plastic solution for stress and plastic zone of surrounding rock in cold region tunnels. Cold Reg. Sci. Technol. 2011, 72, 50–57. [Google Scholar] [CrossRef]
- Feng, Q.; Jiang, B.-S.; Zhang, Q.; Wang, L.-P. Analytical elasto-plastic solution for stress and deformation of surrounding rock in cold region tunnels. Cold Reg. Sci. Technol. 2014, 108, 59–68. [Google Scholar] [CrossRef]
- Feng, Q.; Liu, W.-W.; Jiang, B.-S. Analytical solution for the stress and deformation of rock surrounding a cold-regional tunnel under unequal compression. Cold Reg. Sci. Technol. 2017, 139, 1–10. [Google Scholar] [CrossRef]
- Huang, S.; Liu, Q.; Cheng, A.; Liu, Y. A statistical damage constitutive model under freeze-thaw and loading for rock and its engineering application. Cold Reg. Sci. Technol. 2018, 145, 142–150. [Google Scholar] [CrossRef]
- Wang, J.Y.; Hu, Y.F. A discussion on frost-heaving force on tunnel lining. J. Glaciol. Geocryol. 2004, 26, 112–119. [Google Scholar]
- Fan, L.; Zeng, Y.; He, C.; Cheng, X. Magnitude and Distribution of Frost Heave Force for Cold Region Strong Rock Tunnels. China Railw. Sci. 2007, 28, 44–49. [Google Scholar]
- Kang, Y.; Liu, Q.; Zhao, J.; Zhang, F. Research on frost deformation characteristics of rock and simulation of tunnel frost deformation in cold region. Chin. J. Rock Mech. Eng. 2012, 31, 2518–2526. [Google Scholar]
- Tan, X.; Chen, W.; Wu, G.; Zheng, P. Study of thermo-hydro-mechanical-damage (THMD) coupled model in the condition of freeze-thaw cycles and its application to cold region tunnels. Chin. J. Rock Mech. Eng. 2013, 32, 239–250. [Google Scholar] [CrossRef]
- Huang, J.; Xia, C.; Han, C.; Huang, M. Analytical solution of frost heave force acting on cold-region tunnel liner considering anisotropy frost heave of surrounding rock. Yanshilixue Yu Gongcheng Xuebao 2015, 34, 3766–3774. [Google Scholar] [CrossRef]
- Huang, J.; Xia, C.; Han, C.; Li, Z. Distribution and simplified calculation method of the frost heaving force of highway tunnels in cold regions. Mod. Tunn. Technol. 2016, 53, 63–70. [Google Scholar] [CrossRef]
- Xia, C.; Huang, J.; Han, C.; Tang, Z. Methods of frost-heave ratio evaluation and classification of frost-heave susceptibility of tunnel surrounding rocks in cold regions. Chin. J. Rock Mech. Eng. 2013, 32, 1876–1885. [Google Scholar]
- Yuan, Y.; Lai, Y. The Identification and Classification of Freezing-Thawing and Frozen Environments for the Surrounding Rocks of Tunnels in Cold Regions. Mod. Tunn. Technol. 2016, 53, 19–25. [Google Scholar] [CrossRef]
- Zhang, G.; Xia, C.; Sun, M.; Zou, Y.; Xiao, S. A new model and analytical solution for the heat conduction of tunnel lining ground heat exchangers. Cold Reg. Sci. Technol. 2013, 88, 59–66. [Google Scholar] [CrossRef]
- Zeng, Y.; Liu, K.; Zhou, X.; Fan, L. Tunnel temperature fields analysis under the couple effect of convection-conduction in cold regions. Appl. Therm. Eng. 2017, 120, 378–392. [Google Scholar] [CrossRef]
- Yu, W.; Lu, Y.; Han, F.; Liu, Y.; Zhang, X. Dynamic process of the thermal regime of a permafrost tunnel on Tibetan Plateau. Tunn. Undergr. Space Technol. 2018, 71, 159–165. [Google Scholar] [CrossRef]
- Fan, D.; Xia, C.; Han, C. Option of laying position of insulation layer for tunnel in frost region. Chin. J. Undergr. Space Eng. 2014, 10, 391. [Google Scholar]
- Hao, F.; Sun, Q.S. Research on the Temperature Fields and Insulating Layers of Highway Tunnels in a Cold Region. Mod. Tunn. Technol. 2012, 49, 39–43. [Google Scholar] [CrossRef]
- Ma, Q.; Luo, X.; Lai, Y.; Niu, F.; Gao, J. Numerical investigation on thermal insulation layer of a tunnel in seasonally frozen regions. Appl. Therm. Eng. 2018, 138, 280–291. [Google Scholar] [CrossRef]
- Wang, Z.H.; Zhang, Y.N.; She, X.K.; Dong, F.R.; Wang, S.H. Surrounding Rock Insulation Measures for Construction of Four-season Cross-country Skiing Tunnel. J. Water Resour. Archit. Eng. 2019, 17, 177–180+198. [Google Scholar]
- Yuan, J.X.; Wang, D.Y.; Ma, H.L. Study on Thermal Insulation Technology of Insulation Layer of Tunnels in Seasonal Frozen Soil Area. Railw. Stand. Des. 2018, 62, 100–105. [Google Scholar] [CrossRef]
- Chen, J.X.; Luo, Y.B. Calculation method of antifreezing layer thickness in cold region tunnel. J. Traffic Transp. Eng. 2007, 7, 76–79. [Google Scholar]
- Fan, H. Computational Optimization of the Insulation Parameter of Freeze-proof Separate Lining in Cold-region Tunnel. J. Inf. Comput. Sci. 2015, 12, 6201–6208. [Google Scholar] [CrossRef]
- Lu, T.; Zhang, G.; Liu, S.; Zheng, B.; Zhang, X. Numerical investigation of the temperature field and thermal insulation design of cold-region tunnels considering airflow effect. Appl. Therm. Eng. 2021, 191, 116923. [Google Scholar] [CrossRef]
- Yu, L.; Sun, Y.; Wang, M.N. Research on the calculation method for frost-resistance fortification lengths of tunnels in cold regions. Mod. Tunn. Technol. 2021, 58, 21–28. [Google Scholar] [CrossRef]
- Ministry of Transport of the People’s Republic of China. Technical Specifications for Design and Construction of Highway in Seasonal Frozen Soil Region: JTG/T D31-06-2017; China Communication Press: Beijing, China, 2018.
- Li, Y.; Sun, Y.; Zhuang, Y.; Duan, L.; Xie, K. Thermal Conductivity Characteristics of Thermal Insulation Materials Immersed in Water for Cold-Region Tunnels. Adv. Mater. Sci. Eng. 2020, 2020, 9345615. [Google Scholar] [CrossRef]
- Amin, S.; Heweidak, M. Phenolic Foams: The Insulating Materials to Reduce the Frost Penetration, Skidding, and Flooding Risk of Road and Airfield Pavements. In Phenolic Based Foams: Preparation, Characterization, and Applications; Springer Nature: Singapore, 2022; pp. 359–369. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, S.; Guo, C.; Lin, C.; Zhao, C. Analyses of non-aqueous reactive polymer insulation layer in high geothermal tunnel. J. Rock Mech. Geotech. Eng. 2022, 15, 169–178. [Google Scholar] [CrossRef]
- Chen, J.X.; Zan, Y.J. Field test and analysis of antifreezing thermal protective layer effect of the highway tunnel in cold area. China J. Highw. Transp. 2001, 14, 75–79. [Google Scholar] [CrossRef]
- Son, H.S.; Jun, K.J.; Yune, C.Y. Analysis on Freezing Reduction of Road Tunnels with Heat Insulation Method during Winter. J. Korean Geotech. Soc. 2017, 33, 17–27. [Google Scholar] [CrossRef]
- Yan, Q.; Li, B.; Zhang, Y.; Yan, J.; Zhang, C. Numerical Investigation of Heat-Insulating Layers in a Cold Region Tunnel, Taking into Account Airflow and Heat Transfer. Appl. Sci. 2017, 7, 679. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Zhang, X.; Deng, J. A mathematical optimization model of insulation layer’s parameters in seasonally frozen tunnel engineering. Cold Reg. Sci. Technol. 2014, 101, 73–80. [Google Scholar] [CrossRef]
- Xie, H.Q.; He, C.; Li, Y.L. Study on insulating layer thickness by phase-change temperature field of highway tunnel in cold region. Chin. J. Rock Mech. Eng. 2007, 26, 4395–4401. [Google Scholar]
- Li, Y.; Sun, Y.; Qiu, J.; Liu, T.; Yang, L.; She, H. Moisture absorption characteristics and thermal insulation performance of thermal insulation materials for cold region tunnels. Constr. Build. Mater. 2020, 237, 117765. [Google Scholar] [CrossRef]
- Broch, E.; Grøv, E.; Davik, K.I. The inner lining system in Norwegian traffic tunnels. Tunn. Undergr. Space Technol. 2002, 17, 305–314. [Google Scholar] [CrossRef]
- Yan, Q.X.; Chuan, H.; Zeng, D.Y. Study of temperature field and heat preservation and insulation layer for tunnel in cold area. Adv. Eng. Sci. 2005, 37, 24–27. [Google Scholar]
- Lai, J.; Qiu, J.; Chen, J.; Fan, H.; Wang, K. New Technology and Experimental Study on Snow-Melting Heated Pavement System in Tunnel Portal. Adv. Mater. Sci. Eng. 2015, 2015, 706536. [Google Scholar] [CrossRef]
- Feng, Q.; Jiang, B.-S.; Zhang, Q.; Wang, G. Reliability research on the 5-cm-thick insulation layer used in the Yuximolegai tunnel based on a physical model test. Cold Reg. Sci. Technol. 2016, 124, 54–66. [Google Scholar] [CrossRef]
- Wang, T.; Zhou, G.; Wang, J.; Yin, L. Stochastic analysis of uncertainty mechanical characteristics for surrounding rock and lining in cold region tunnels. Cold Reg. Sci. Technol. 2018, 145, 160–168. [Google Scholar] [CrossRef]
- Zhang, G.Z.; Xia, C.C.; Ma, X.G.; Li, P.; Wei, Q. Rock-soil thermal response test of tunnel heating system using heat pump in cold region. Chin. J. Rock Mech. Eng. 2012, 31, 99–105. [Google Scholar]
- Zhang, G.; Guo, Y.; Zhou, Y.; Ye, M.; Chen, R.; Zhang, H.; Yang, J.; Chen, J.; Zhang, M.; Lian, Y.; et al. Experimental study on the thermal performance of tunnel lining GHE under groundwater flow. Appl. Therm. Eng. 2016, 106, 784–795. [Google Scholar] [CrossRef]
- Zhang, H.M.; Cao, H.B.; Zhang, M.J. Analysis of Temperature Field of the Tunnel Surrounding Rock in Cold Regions. Adv. Mater. Res. 2013, 753–755, 745–749. [Google Scholar] [CrossRef]
- Lai, J.; Qiu, J.; Fan, H.; Chen, J.; Xie, Y. Freeze-proof method and test verification of a cold region tunnel employing electric heat tracing. Tunn. Undergr. Space Technol. 2016, 60, 56–65. [Google Scholar] [CrossRef]
- Wu, Y.M.; Li, W.B.; Fu, H.L.; Wang, B.S.; Liu, B. Frost protection system of heating from back of lining for tunnel in cold region and its control model. Electron. J. Geotech. Eng. 2013, 18, 5479–5490. [Google Scholar]
- Lai, Y.M.; Wu, Z.W.; Zhang, S.J.; Yu, W.B.; Den, Y.S. In-situ observed study for the effect of heat preservation in cold regions tunnels. J. China Railw. Soc. 2003, 25, 81–86. [Google Scholar]
- Wu, Z.; Zhang, S.; Yu, W.; Deng, Y. Study of Methods to Control Frost Action in Cold Regions Tunnels. J. Cold Reg. Eng. 2003, 17, 144–152. [Google Scholar] [CrossRef]
- Zhang, X.; Lai, Y.; Yu, W.; Zhang, S. Non-linear analysis for the freezing–thawing situation of the rock surrounding the tunnel in cold regions under the conditions of different construction seasons, initial temperatures and insulations. Tunn. Undergr. Space Technol. 2002, 17, 315–325. [Google Scholar] [CrossRef]
- Zhang, X.F.; Yu, W.B. Forecast analysis for the re-frozen of Kunlunshan Tunnel on Qing-Tibet railway. China J. High-Way Transp. 2005, 18, 67–71+82. [Google Scholar] [CrossRef]
- Zhang, X.F.; Zhang, M.X.; Yang, F.C. Nonlinear analysis on temperature characteristics of Fenghuo Mountain tunnel. Chin. J. Geotech. Eng. 2009, 31, 1680–1685. [Google Scholar]
- Zhang, Y.; Lai, Y.M.; Zhang, X.F. A practical method for calculating the design parameters of the heat insulation layer in cold region tunnel. China Railw. Sci. 2009, 30, 66–70. [Google Scholar] [CrossRef]
- Xia, C.C.; Fa, D.F.; Li, Z.H.; He, J. Discussion on analytical calculation for thermal-insulation layer thickness of tunnel in perma-frost area. China Civ. Eng. J. 2015, 48, 118–124. [Google Scholar] [CrossRef]
- Li, S.; Niu, F.; Lai, Y.; Pei, W.; Yu, W. Optimal design of thermal insulation layer of a tunnel in permafrost regions based on coupled heat-water simulation. Appl. Therm. Eng. 2017, 110, 1264–1273. [Google Scholar] [CrossRef]
- Liu, K.; Cai, H.C.; Li, F. Application of Thermal Probe Group in Protection of Shallow Section of Tunnel in Permafrost Area. J. Railw. Eng. Soc. 2013, 30, 60–64. [Google Scholar]
- Mainali, G.; Dineva, S.; Nordlund, E. Experimental study on debonding of shotcrete with acoustic emission during freezing and thawing cycle. Cold Reg. Sci. Technol. 2015, 111, 1–12. [Google Scholar] [CrossRef]
- Wang, F.; Li, G.; Alexander, F.; Ma, W.; Chen, D.; Wu, G.; Mu, Y.; Wang, X.; Jing, H.; Zhang, Z. Applicability analysis of thermosyphon for thermally stabilizing pipeline foundation perma-frost and its layout optimization. Cold Reg. Sci. Technol. 2023, 208, 103769. [Google Scholar] [CrossRef]
- Xia, C.C.; He, J.; Fan, D.F. Roles and structures of cold-proof drainage tunnels for different permafrost tunnels. Mod. Tunn. Technol. 2017, 54, 1–8. [Google Scholar] [CrossRef]
- Lv, K.C.; Ma, C.C.; Ji, Z.; Xu, P. Analysis on stripe insulating layer for ring drain pipe of tunnel in cold region and its temperature field. Chin. J. Undergr. Space Eng. 2013, 9, 304–308. [Google Scholar]
- Tattersall, C.; Mitchells, R.; Gallion, E.; Weller, R. Water and Ice Control in the Anton Anderson Memorial Tunnel. In Cold Regions Engineering: Cold Regions Impacts on Transportation and Infrastructure; American Society of Civil Engineers: Anchorage, AK, USA, 2002; pp. 219–229. [Google Scholar]
- Zhang, X.; Zhang, Y. Study on a new-styled measure for treating water leakage of the permafrost tunnels. Tunn. Undergr. Space Technol. 2006, 21, 656–667. [Google Scholar] [CrossRef]
- Zhang, Y.; Xia, C.; Zhou, S.; Hu, Y.; Zhang, J. A new sustainable energy based freeze proof method for drainage system in cold-region tunnels: A case study of Tianshan Shengli Tunnel. Case Stud. Therm. Eng. 2022, 34, 102020. [Google Scholar] [CrossRef]
- Huang, S.L.; Aughenbaugh, N.B.; Wu, M. Stability Study of Crrel Permafrost Tunnel. J. Geotech. Eng. 1986, 112, 777–790. [Google Scholar] [CrossRef]
- Jia, X.Y.; Zhu, Y.Q.; Li, W.J. Study of the temperature field of the surrounding rock during the tunnel construction in permafrost regions. Traffic Eng. Technol. Natl. Def. 2003, 4, 42–45. [Google Scholar] [CrossRef]
- Zhang, D.H.; Wang, M.S.; Ren, S.Q. Experimental study on temperature and response of seasonal active layer of tunnels sur-rounding rock in permafrost region on Qinghai-Tibet plateau. Chin. J. Rock Mech. Eng. 2007, 26, 614–619. [Google Scholar]
- Jia, X.Y.; Li, W.J.; Zhu, Y.Q. Analysis of stability for surrounding rock caused by depth of thawing range during plateau perma-frost tunnel construction. Chin. J. Rock Mech. Eng. 2005, 24, 5693–5697. [Google Scholar]
- Chu, H.B.; Yang, X.L.; Liang, W.M.; Yu, Y.Q.; Huang, X.G. Choose of Liquid Medium for Compound Non-coupling Charging for Frozen Soil Tunnel. Min. Metall. Eng. 2007, 27, 5–8. [Google Scholar]
- Tan, Z.S.; Kuang, C.M.; Yang, X.L.; Wang, M.S. Research on Blasting Technology for Construction of Fenghuoshan Tunnel in Permafrost. Chin. J. Rock Mech. Eng. 2006, 25, 1056–1061. [Google Scholar]
- Zhou, J.Z. Constructing technology research on water-proof/drainage and heat insulation lining in kunlunshan tunnel of qinghai-tibet railway, tibetan plateau. J. Glaciol. Geocryol. 2003, 25, 106–111. [Google Scholar]
- Liu, G.Y. Tunnel construction technology for the high altitude and the high and cold area. China Railw. Sci. 2001, 4, 50–55. [Google Scholar]
- Chen, J.X. Technique of preventing frost damage in highway tunnel. J. Chang. Univ. (Nat. Sci. Ed.) 2006, 26, 68–70. [Google Scholar] [CrossRef]
- Li, C.F.; Mei, Z.R. Research on leakage prevention techniques for tunnels embedded in frozen ground and located in bitter cold plateau. Mod. Tunn. Technol. 2005, 4, 44–49. [Google Scholar] [CrossRef]







| Name | Formulas | Parameters | Reference |
|---|---|---|---|
| Physical model | λf, λu refer to thermal conductivity under frozen and unfrozen states; n is the initial porosity of pore media; Sr is saturation degree; θu is volumetric unfrozen water; the subscript u and f refer to the unfrozen and frozen states, respectively; ρ is density, and subscript s and w refer to soil-rock particle and water, respectively; ρd is dry density; W is water content. | [20] | |
| CK model | λf, λu refer to thermal conductivity under frozen and unfrozen states; λsat(f), λsat(u) refer to thermal conductivity of saturated soil under frozen and unfrozen states; λdry is thermal conductivity of dry soil; λrf, λru are thermal conductivity of frozen and unfrozen states for unsaturated soil which relate to the saturation degree. | [21] | |
| Multiple linear regression model | λf, λu refer to thermal conductivity under frozen and unfrozen states; ρd is dry density; w is water content; Sr is saturation degree; n is the initial porosity of pore media; | [19] |
| No. | Formulas | Parameters | Reference |
|---|---|---|---|
| 1 | The subscripts and superscripts f, u represent the frozen and the unfrozen states, respectively; T, C, λ are the temperature, volumetric heat capacity and thermal conductivity of surrounding rock, respectively; H, S, K are water head, water-supply degree, hydraulic conductivities, respectively; x, y refer to directions; ρ is density of water; s(t) is the phase front position; L is the latent heat per unit volume; n is the normal direction of phase front position; the phase change occurs in a range of temperatures T ± ΔT; W and Wu are the moisture content and the unfrozen water content; β is a constant, determined by experiments; Tm is frozen temperature of surrounding rocks; V is water filtration velocity; t is time. | [27,28] | |
| 2 | T, C, λ are the temperature, volumetric heat capacity and thermal conductivity of surrounding rock, respectively; x, y, z refer to directions; t is time. | [29,30] | |
| 3 | u, v and w are flow velocities in the direction of x, y, z, respectively; p is effective pressure of air; T is air temperature; ν is kinematic viscosity coefficient for air; ca and λa are volumetric heat capacity and thermal conductivity for air, respectively; x, y and z are three directions in a rectangular coordinate system, respectively; t is time. | [31] | |
| 4 | T is temperature; t is time; x, z are two directions in a rectangular coordinate system, respectively; C and λ are heat capacity and thermal conductivity of soft rock, respectively; L is the latent heat; ρw is density of water; K* is comprehensive hydraulic conductivity; Tk is absolute temperature; θw is volume content of liquid water. | [32] | |
| 5 | T is temperature; t is time; qi is heat flux density, i = 1, 2, 3; qv is volume heat source of rock and soil; c and λ are heat capacity and thermal conductivity; ρ is density. | [33] | |
| 6 | T is temperature; t is time; c and λ are heat capacity and thermal conductivity; subscripts 1, 2, refer to frozen zone and unfrozen zone; Q is the volumetric heat production generated (consumed) heat by heating (heat release) in unit body; ρw is the density of water; and Lf is the heat latent; νw is the seepage velocity of water; θw is volume content of liquid water; θi is volumetric ice content; ρi is the density of ice; μw is dynamic viscosity of water; kw is the permeability; pw is the water pressure; g is the gravity acceleration; SP0 is segregation potential; DT is heat diffusion rate under the action of temperature gradient; q is per unit volume. | [34] | |
| 7 | T is temperature; t is time; ρw is the density of water; QTi, ki and Ci are the heat source, the thermal conductivity and the volumetric specific heat in the ith zone; subscripts 1, 2, 3 refer to frozen zone, freezing zone and unfrozen zone; Lf is the latent heat of water; χ is the unfrozen water volumetric content, χ* is the residual unfrozen water volumetric content at some lower reference temperature; a is a parameter to describe the rate of decay; Tc is the freezing point of water; n is the porosity; ρi and ρs are the densities of ice and skeleton, respectively; λw, λi and λs are the thermal conductivities of water, ice and skeleton, respectively; cw, ci and cs are the specific heats of water, ice and skeleton, respectively; | [35] | |
| 8 | u is the velocity of the airflow in the tunnel; ρ is the density of the airflow; p is the pressure; μ is the viscosity coefficient; I is the unit matrix; μt is the eddy viscosity coefficient; X is the body force along with coordinate axis orientation; μ’ is the second viscosity coefficient; Ta is the temperature of the airflow; cp is the specific heat of the airflow; λg is the conductivity of the airflow; PrT is the turbulence Prandtl number; QT is the heat source; where σk, σε, Cε1, Cε2 and Cμ are empirical constants, and their values areσk = 1.00, σε = 1.30, Cε1 = 1.44, Cε2 = 1.92 and Cμ = 0.07. | [36,37] | |
| 9 | T is the temperature of the tunnel lining and surrounding rock; Tf is the wind temperature; r is the radial distance; a is the thermal diffusion coefficient; t is time; ρ is the density of the tunnel lining and surrounding rock; h is the convective heat transfer rate; Tb is the temperature of the tunnel wall; U is the perimeter of the cross section; qs is the equipment heating effect in the tunnel; cp is the constant-pressure specific heat capacity of the surrounding rock; A is the area of cross section. | [38] |
| No. | Formulas | Parameters | Reference |
|---|---|---|---|
| 1 | W and Wu are the water content and the unfrozen water content of the surrounding rock, respectively; α is the volumetric expansion per unit volume when water is frozen to ice. The subscripts 1, 2, 3 refer to the lining, the frozen surrounding rock and the unfrozen surrounding rock, respectively; E and μ are the elastic modulus and Poisson’s ratio, respectively; Pb is frost heave force; P0 is the initial geostress; a is the inner diameter of circle lining; b, c are the inner diameter and outer diameter of frozen surrounding rock. | [40] | |
| 2 | P is frost heave force; α is frost heaving ratio of water, α = 0.09; t is the depth of water body; Δ is the average displacement of each point of lining when 1 MPa frost heaving force acts on it; δ is the average displacement of each point of surrounding rock when 1 MPa frost heaving force acts on it. | [46] | |
| 3 | P is the frost heave force; α is the frost heaving ratio of ice; t is the depth of water body; Krm is the average of elastic resistance coefficient of surrounding rock; Klm is the average of elastic equivalent coefficient of lining; Kim is the average of elastic equivalent coefficient of ice. | [47] | |
| 4 | mi is the quality of ice; mw is the quality of unfrozen water; u is frozen water ratio; n is porosity; Sr is saturation degree; β is volume expansion coefficient when water is changed into ice; Ki, Ks are the bulk modulus of ice and rock skeleton, respectively. | [48] | |
| 5 | a is the inner diameter of circle lining; b, c are the inner diameter and outer diameter of frozen surrounding rock; Ⅰ, Ⅱ, Ⅲ refer to lining, frozen surrounding rock, unfrozen surrounding rock, respectively; E is elastic modulus; μ is Poisson’s ratio. | [26,50] | |
| 6 | B1, B2, B3, B4 are the parameters of frost heave force distribution; Pb is frost heave force of equivalent circle tunnel; h is the buried depth of tunnel; qmax is the load acting on arch foot. | [51] |
| Frost-Heave Susceptibility of Rock Mass | Grades of Surrounding Rock | Porosity | Supply Condition of Groundwater | Frost Heaving Ratio | Frost Heave Characteristic | |
|---|---|---|---|---|---|---|
| Rock | Fissure Filler | |||||
| No frost-heave susceptibility | No frost-heave susceptibility (or no Fissure filler) | I~V | <5 | Open condition | <0.13 | No |
| 5~20.5 | 0.13~0.47 | Weak | ||||
| 20.5~37 | 0.47~0.80 | Less strong | ||||
| >37 | 0.80~1.60 | Strong | ||||
| No frost-heave susceptibility | Frost-heave susceptibility | IV | <7.5 | Open condition | 0.13~0.47 | Weak |
| 7.5~23.5 | 0.47~0.80 | Less strong | ||||
| >23.5 | 0.80~1.60 | Strong | ||||
| V | <9 | 0.47~0.80 | Medium | |||
| 9~49.5 | 0.80~1.60 | Less strong | ||||
| >49.5 | >1.60 | Strong | ||||
| Frost-heave susceptibility | Frost-heave susceptibility | IV | <4.5 | Open condition | 0.13~0.47 | Weak |
| 4.5~15 | 0.47~0.80 | Less strong | ||||
| 15~39 | 0.80~1.60 | Strong | ||||
| >39 | >1.60 | Severe | ||||
| V | <5.5 | 0.47~0.80 | Less strong | |||
| 5.5~31 | 0.80~1.60 | Strong | ||||
| >31 | >1.60 | Severe | ||||
| State of Water Content | Freezing Index /°C·d | Freeze-Thaw Sensitivity | Classification | Subclassification | Phenomenon |
|---|---|---|---|---|---|
| Watery | 200~2000 | Sensitive | Freeze-thaw surrounding rock | Sensitive freeze-thaw surrounding rock | The freeze–thaws happen with the seasons in surrounding rock. The frost heaving, relaxation and thermal collapse act on lining. The freezing and thermal erosion of the mix of water and particles act on back of lining. |
| Insensitivity | Insensitive freeze–thaw surrounding rock | There is no seasonal frost heaving in surrounding rock. There are no frost heaving materials behind lining. But there is only freeze–thaw of fissure water and collection water of it. | |||
| >2000 | Sensitive | Permafrost surrounding rock | Sensitive permafrost surrounding rock | Although the surrounding rock is sensitive to freezing and thawing, it is always freezing. The thickness of frozen circle would be changed with seasons. Most of the frost heaving force is borne by the frozen circle itself. | |
| Insensitivity | Insensitive permafrost surrounding rock | The surrounding rock is not sensitive to freezing and thawing. The surrounding rock is always freezing. The fissure water is changed to ice in surrounding rock. The tunnel structure is not affected by the frost heaving force | |||
| No water | — | — | — | — | — |
| Zone ID | Average Temperature in the Coldest Month/°C | Frost Depth/m | Characteristics of Frost Problems |
|---|---|---|---|
| Ⅰ | −5~0 | 0.15~0.5 | No frost problems |
| Ⅱ | −5~−10 | 0.5~1.0 | There is a small amount of water seepage and icing in some parts of the tunnel, which will not affect the traffic. |
| Ⅲ | −10~−15 | 1.0~1.5 | There is ice on the wall and pavement of tunnel, which affects driving speed. |
| Ⅳ | −15~−25 | 1.5~2.5 | There is a lot of ice on the wall and pavement of the tunnel, which affects driving safety. Human or mechanical de-icing is required to ensure access and safety. |
| Ⅴ | ≥−25 | >2.5 | There is a large amount of ice on wall and pavement of the tunnel; the drainage ditch is completely frozen. Traffic is interrupted. |
| Performance | Phenolic | Polyurethane | Polystyrene | High Pressure Polyethylene | Rubber–Plastic | Rock Wool |
|---|---|---|---|---|---|---|
| Cold tolerance (°C) | −180 | −110 | −80 | / | −40 | −60 |
| Thermal conductivity W/(m·K) | 0.02~0.033 | 0.022~0.036 | 0.033~0.04 | 0.029~0.035 | 0.031~0.036 | 0.033~0.064 |
| Water absorption (kg/m3) | 0.02 | 0.03 | 0.2 | 0.02 | 0.3 | <2 |
| Compressive strength (MPa) | 0.216 | 0.127 | 0.107 | 0.033 | 0.03 | 0.107 |
| No. | Tunnel Name | Material | Thermal ConductivityW/(m.k) | Thickness (cm) | Preference | Remarks | The Minimum Temperature |
|---|---|---|---|---|---|---|---|
| 1 | - | Air & polyurethane foam | / | / | [76] | Reasonable | / |
| 2 | - | Hard polyurethane board | 0.0207 | 3 | [77] | Reasonable | / |
| 3 | Galongla tunnel | Flolic | 0.025 | 6 | [34,37] | Reasonable | −30.1 °C |
| 4 | - | PU rigid polyurethane foam board | 0.02 | 4 | [58] | Unreasonable | / |
| 5 | - | Air, phenolic foam | 0.0259, 0.021 | 5 | [63] | Reasonable | / |
| 6 | - | Air & polyurethane foam board | / | / | [78] | Reasonable | / |
| 7 | Yuximolegai tunnel | Hard polyurethane board | 0.024 | 5 | [79] | Reasonable | −29.5 °C |
| 8 | Huapiling Tunnel | Hard polyurethane board | 0.024 | 5 | [61] | Reasonable | −34.1 °C |
| 9 | - | FLOLIC | 0.025 | 5 | [80] | Reasonable | / |
| 10 | Four-season cross-country skiing tunnel | Polyurethane | 0.03 | 5 | [60] | Reasonable | −6 °C |
| Techniques | Advantages | Disadvantages | Ways to Improve | |
|---|---|---|---|---|
| Heating | Geothermal energy | Highly effective, sustainable developmental strategy, low-carbon green, cheap | Efficiency gradually decreases. It is not universal, and some places do not have the conditions to utilize geothermal heat. | Heat compensation, improve heat conversion efficiency |
| Electric heating | Extremely effective | Expensive, energy consumption. There is no power transmission line in remote areas, and only wind or solar energy can be used. It is inconvenient to repair the damaged heating circuit. | Improve the durability of circuit materials and laying methods. | |
| Hot water | Extremely effective | Expensive, energy consumption. Water pipes are easy to crystallize and block. It is inconvenient to repair the damaged hot water circuit. | Improve the durability of circuit materials and laying methods. Use auxiliary technology to eliminate pipeline crystallization. | |
| Thermal insulation doors | Highly effective, cheap, low-carbon green | Inconvenient, limited warming. | Automatic sensing, automatic opening or closing of the door | |
| Snow shelters | Effective, cheap, low-carbon green | Poor durability. Low heating efficiency. | Improve durability of materials | |
| Thermosyphon | Low carbon green, strong heat transfer ability, safety and economy | Expensive, poor durability | Improve durability of materials | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Liu, M.; Zhang, X.; Suo, X.; Li, M. Frost Mitigation Techniques for Tunnels in Cold Regions: The State of the Art and Perspectives. Atmosphere 2023, 14, 369. https://doi.org/10.3390/atmos14020369
Zhou Y, Liu M, Zhang X, Suo X, Li M. Frost Mitigation Techniques for Tunnels in Cold Regions: The State of the Art and Perspectives. Atmosphere. 2023; 14(2):369. https://doi.org/10.3390/atmos14020369
Chicago/Turabian StyleZhou, Yuanfu, Min Liu, Xuefu Zhang, Xiaoqing Suo, and Mingyong Li. 2023. "Frost Mitigation Techniques for Tunnels in Cold Regions: The State of the Art and Perspectives" Atmosphere 14, no. 2: 369. https://doi.org/10.3390/atmos14020369
APA StyleZhou, Y., Liu, M., Zhang, X., Suo, X., & Li, M. (2023). Frost Mitigation Techniques for Tunnels in Cold Regions: The State of the Art and Perspectives. Atmosphere, 14(2), 369. https://doi.org/10.3390/atmos14020369






