Extreme Temperature and Rainfall Events and Future Climate Change Projections in the Coastal Savannah Agroecological Zone of Ghana
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
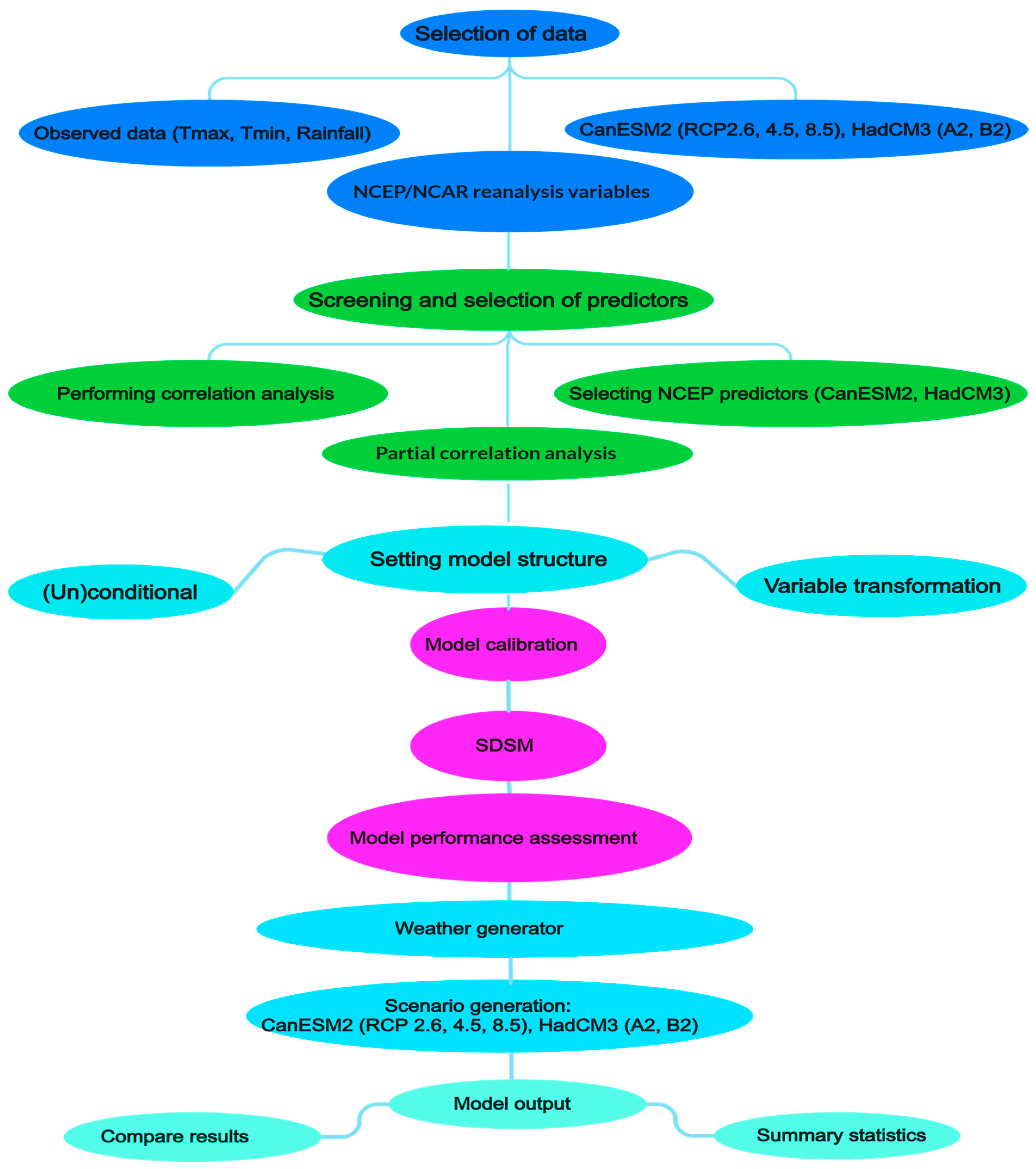
2.2. Data Sources and Methods of Analysis
2.2.1. Observed Data
2.2.2. Homogeneity Test and Homogenization
2.2.3. Calculation of Extreme Climate Indices
2.2.4. Trend Analysis
2.3. General Circulation Models (GCMs) Data
2.3.1. Statistical Downscaling Model (SDSM)
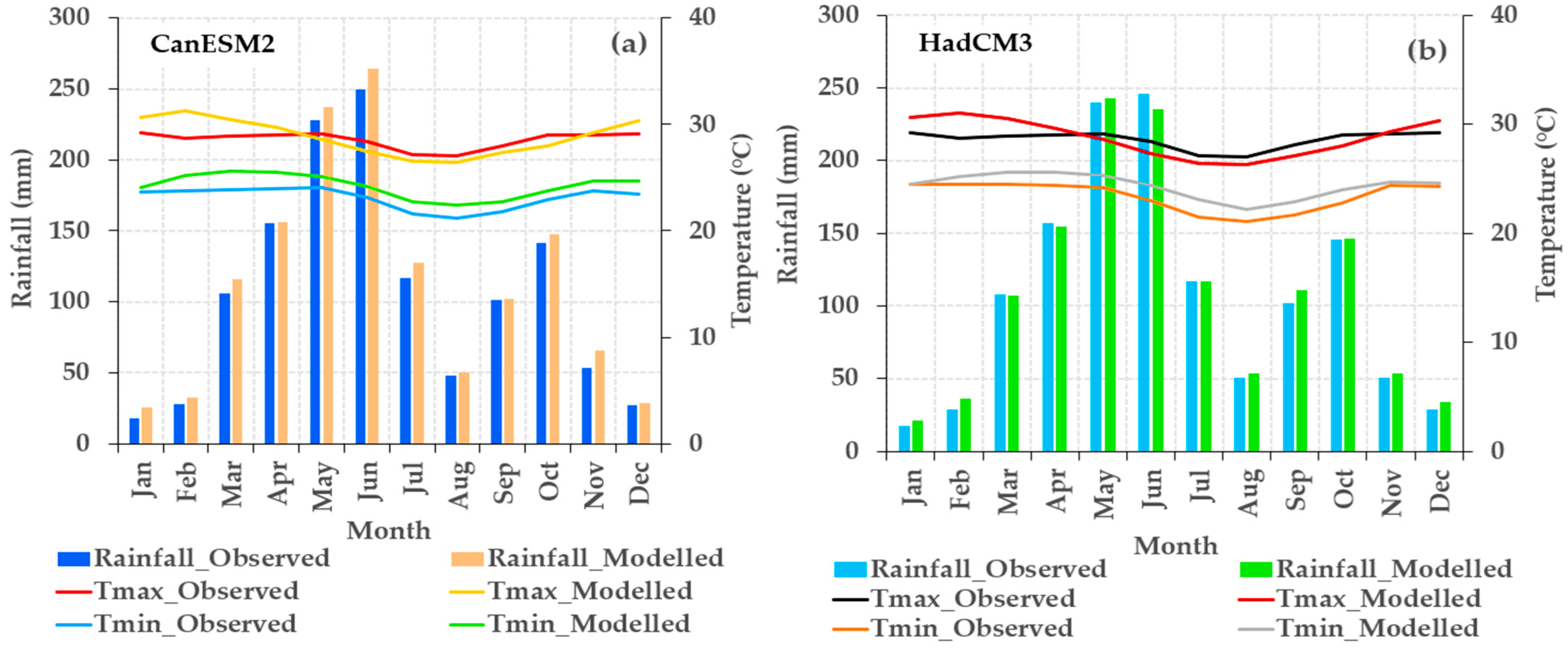
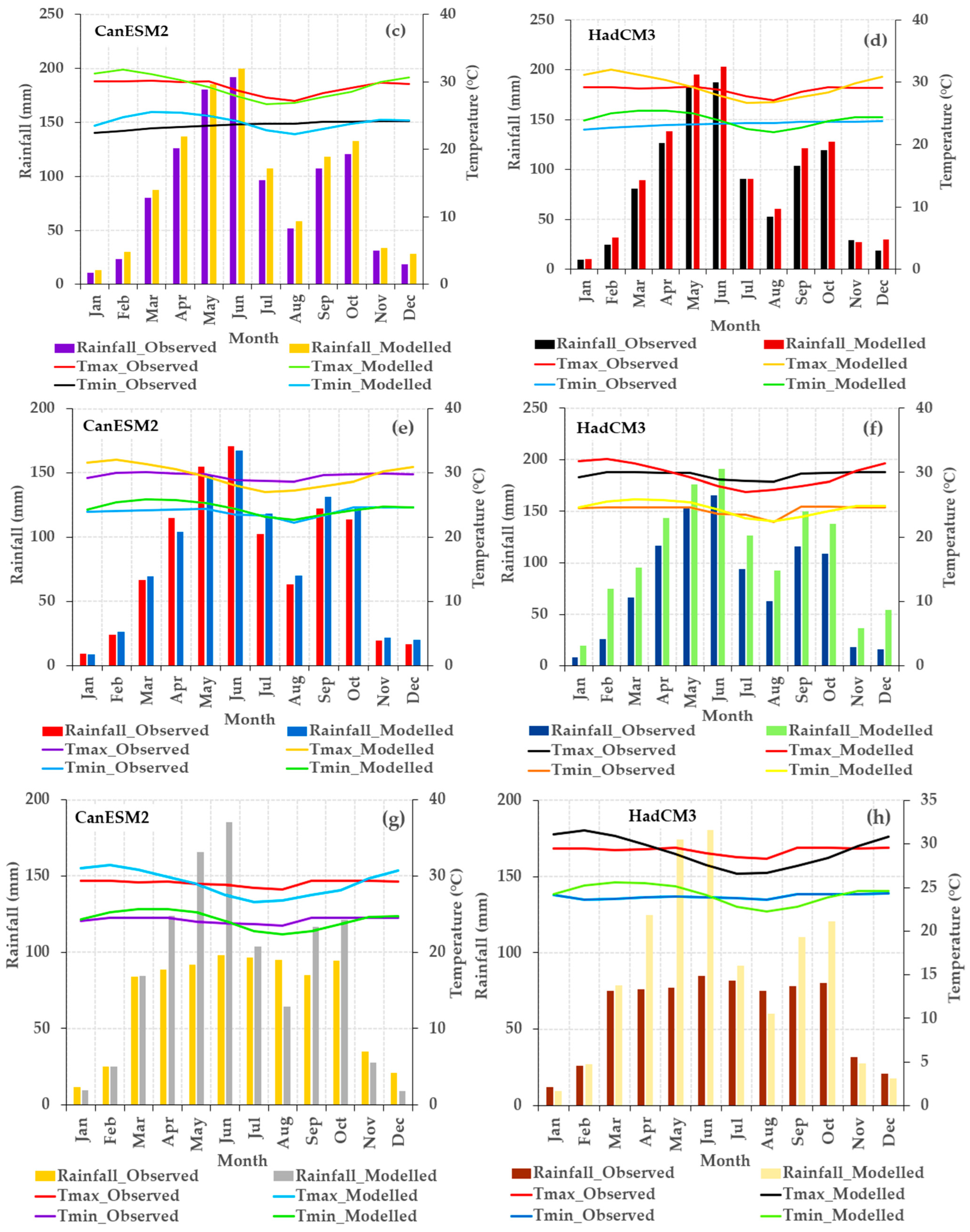
2.3.2. Model Performance Assessment
3. Results
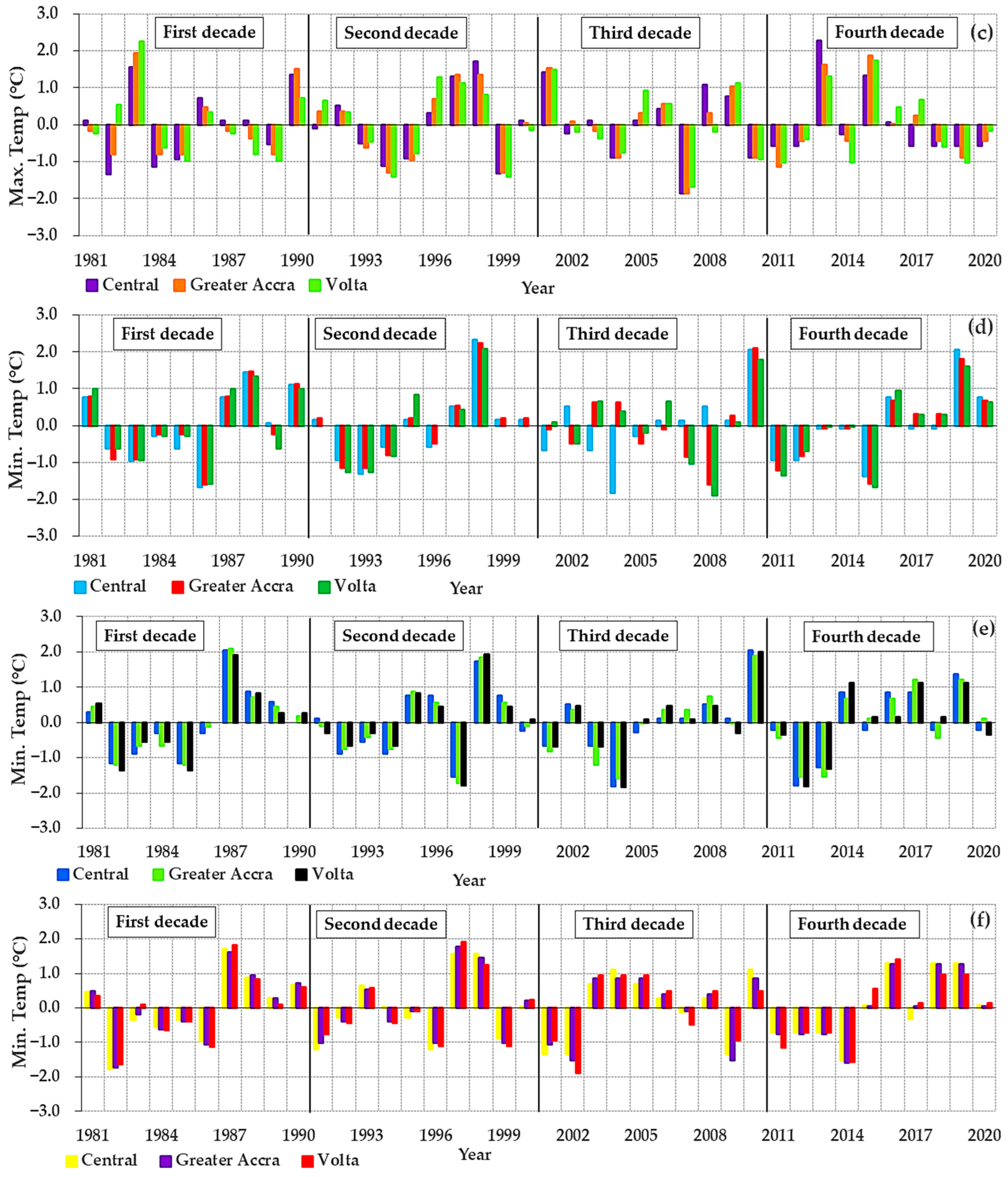
3.1. Results from Extreme Temperature and Rainfall Indices
3.1.1. Changepoints and Homogenization of Temperature and Rainfall
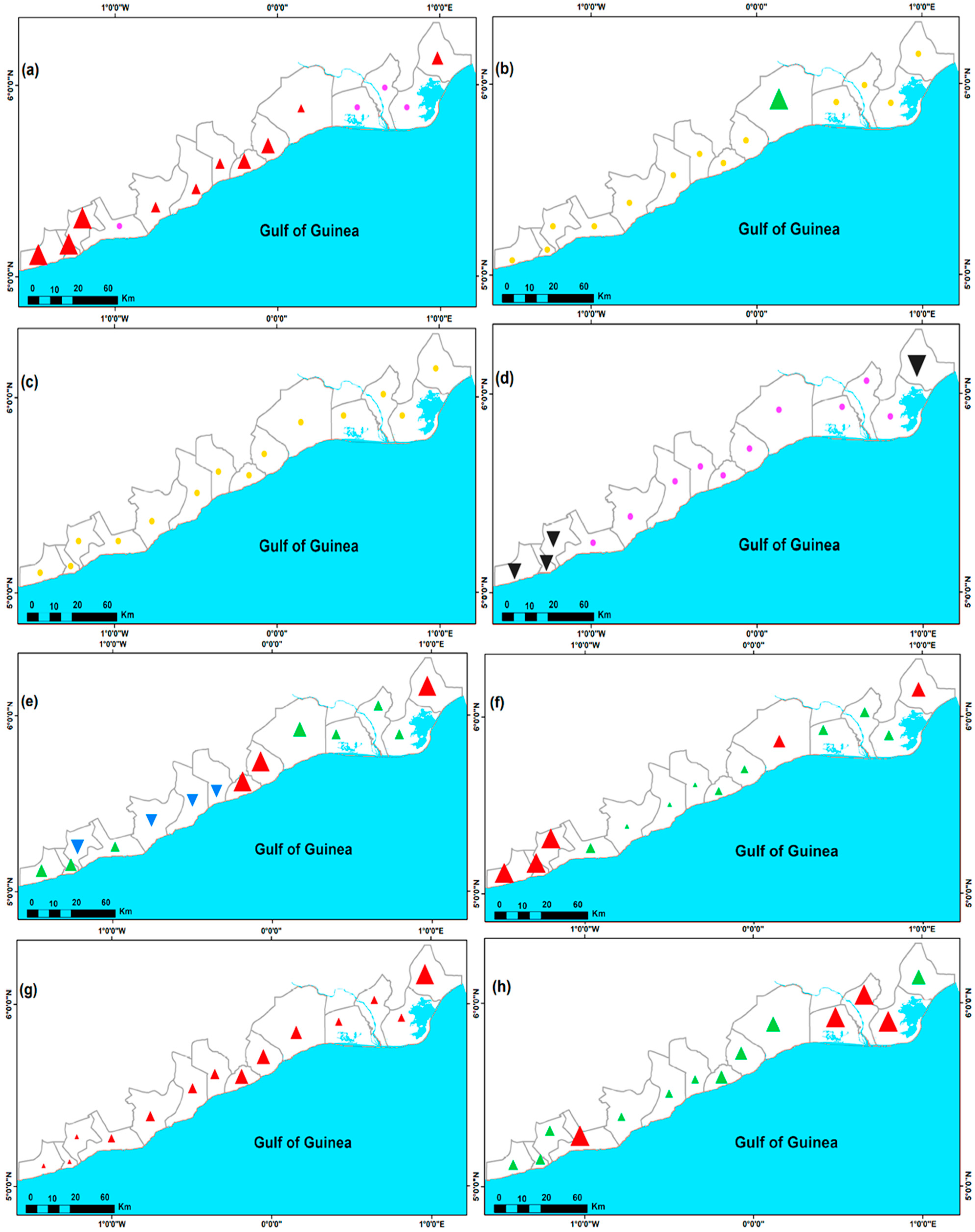
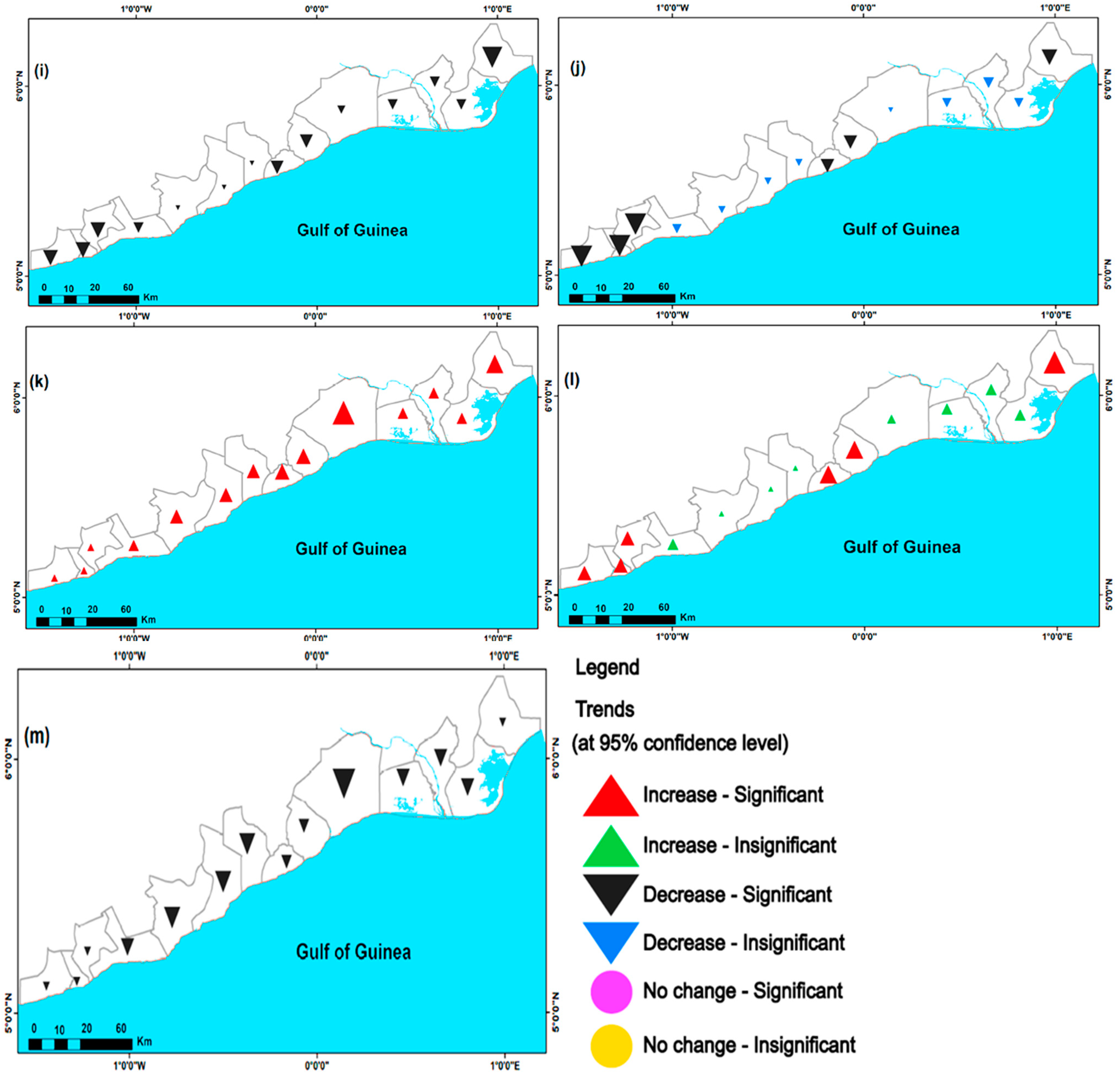
3.1.2. Extreme Temperature Indices
3.1.3. Extreme Rainfall Indices
3.1.4. Decadal Variations in Temperature and Rainfall
3.2. Results for Future Climate Change Projection
3.2.1. Predictor Variables Selection
3.2.2. Model Performance Assessment during Calibration and Validation
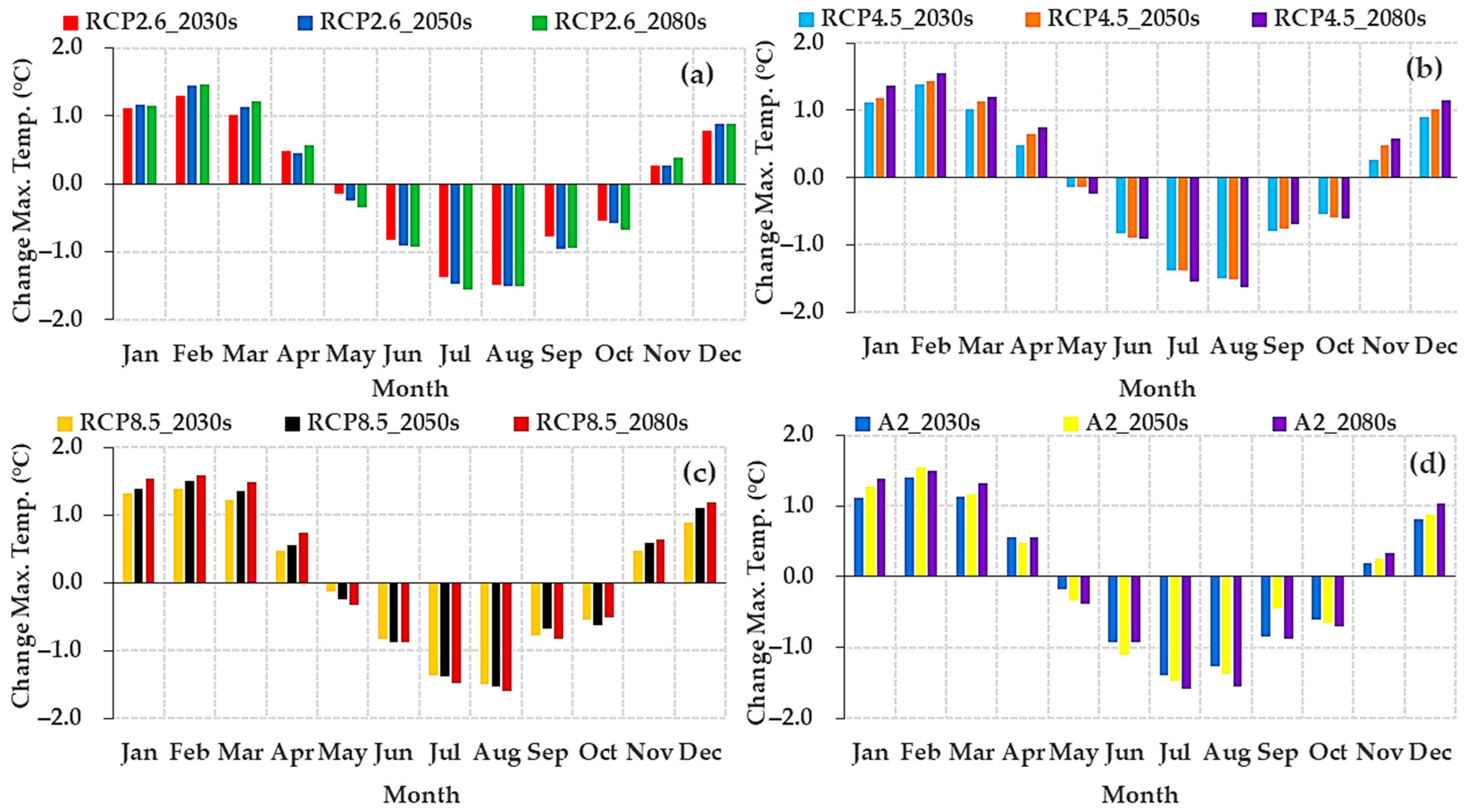
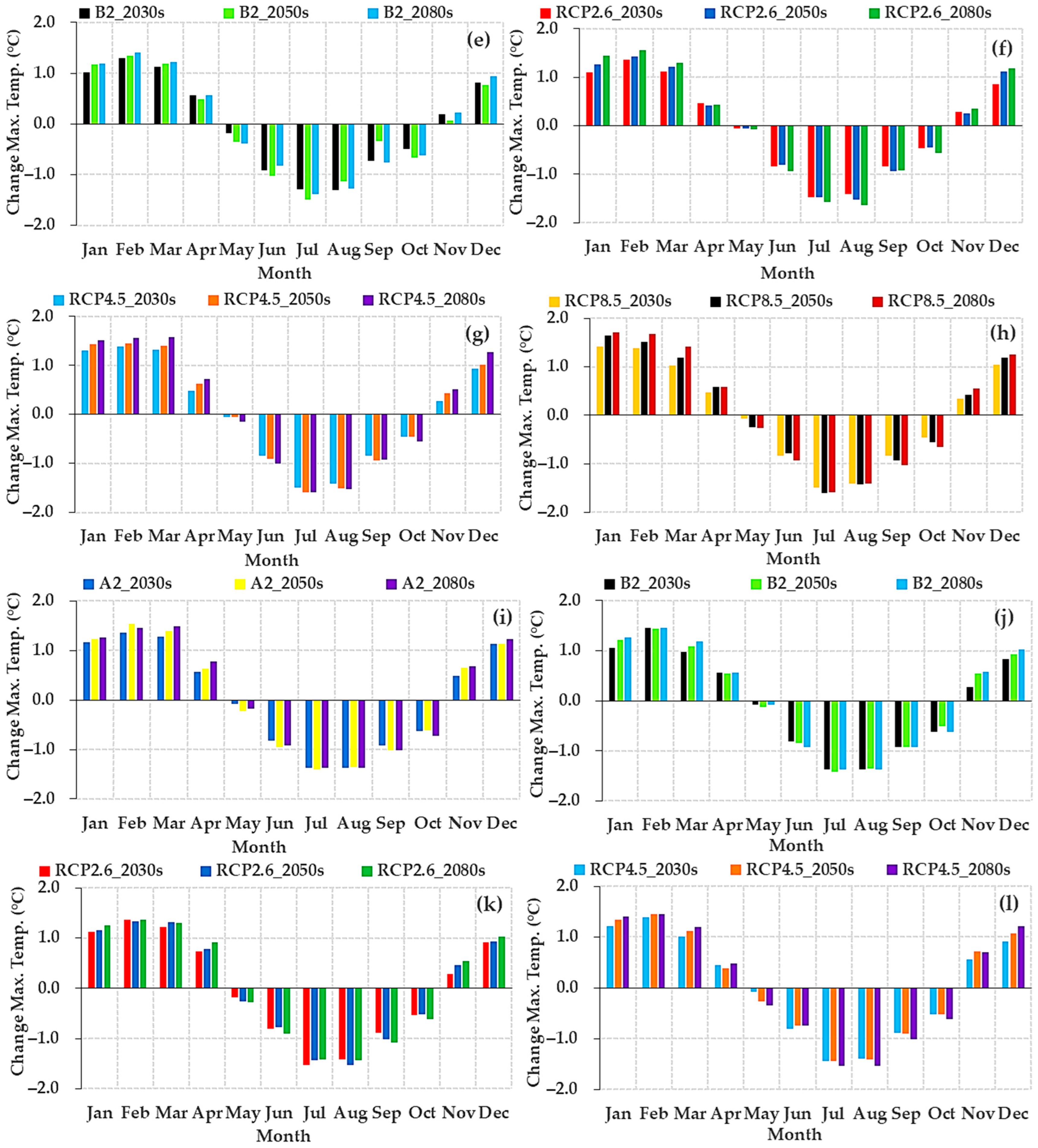
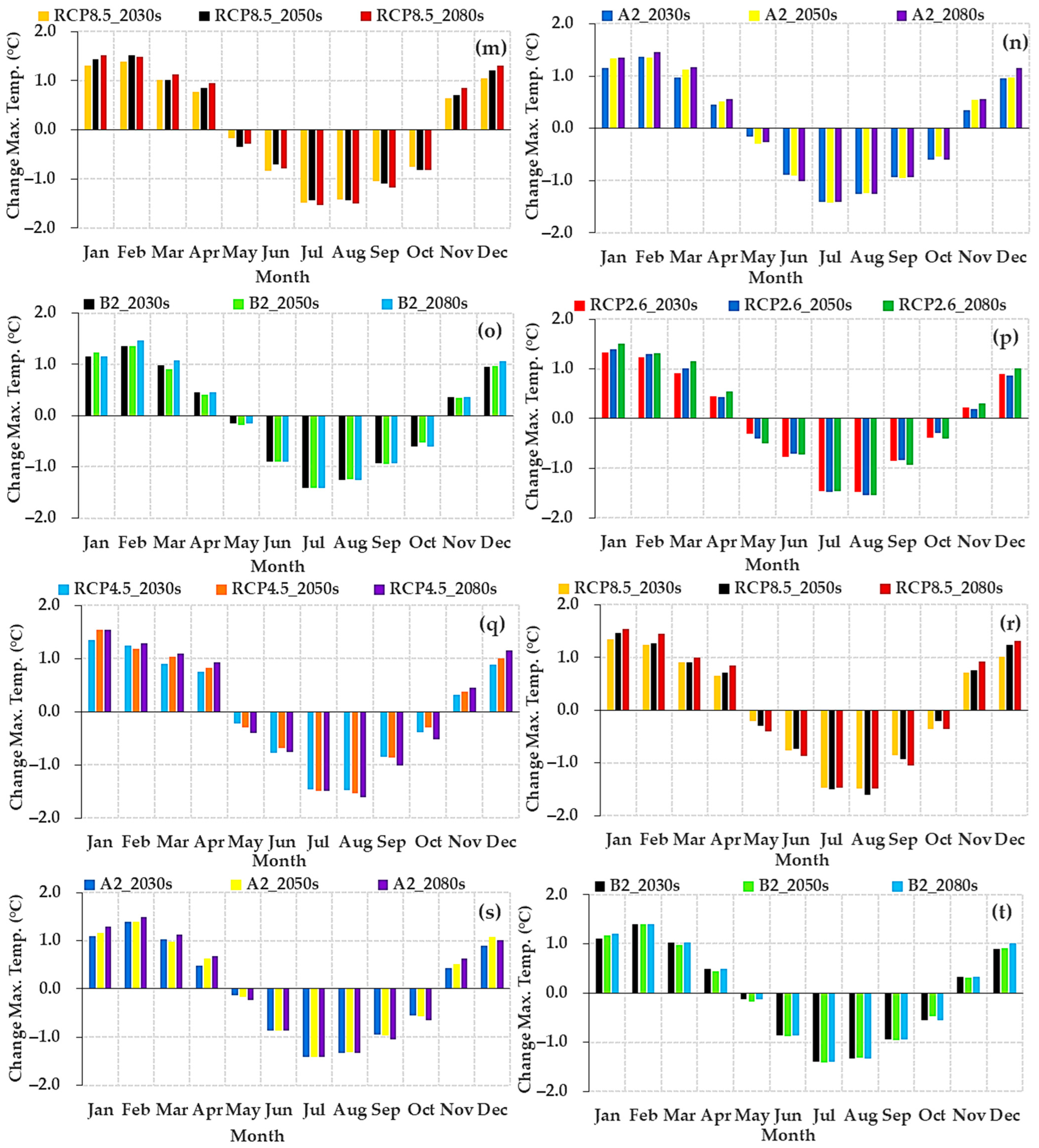
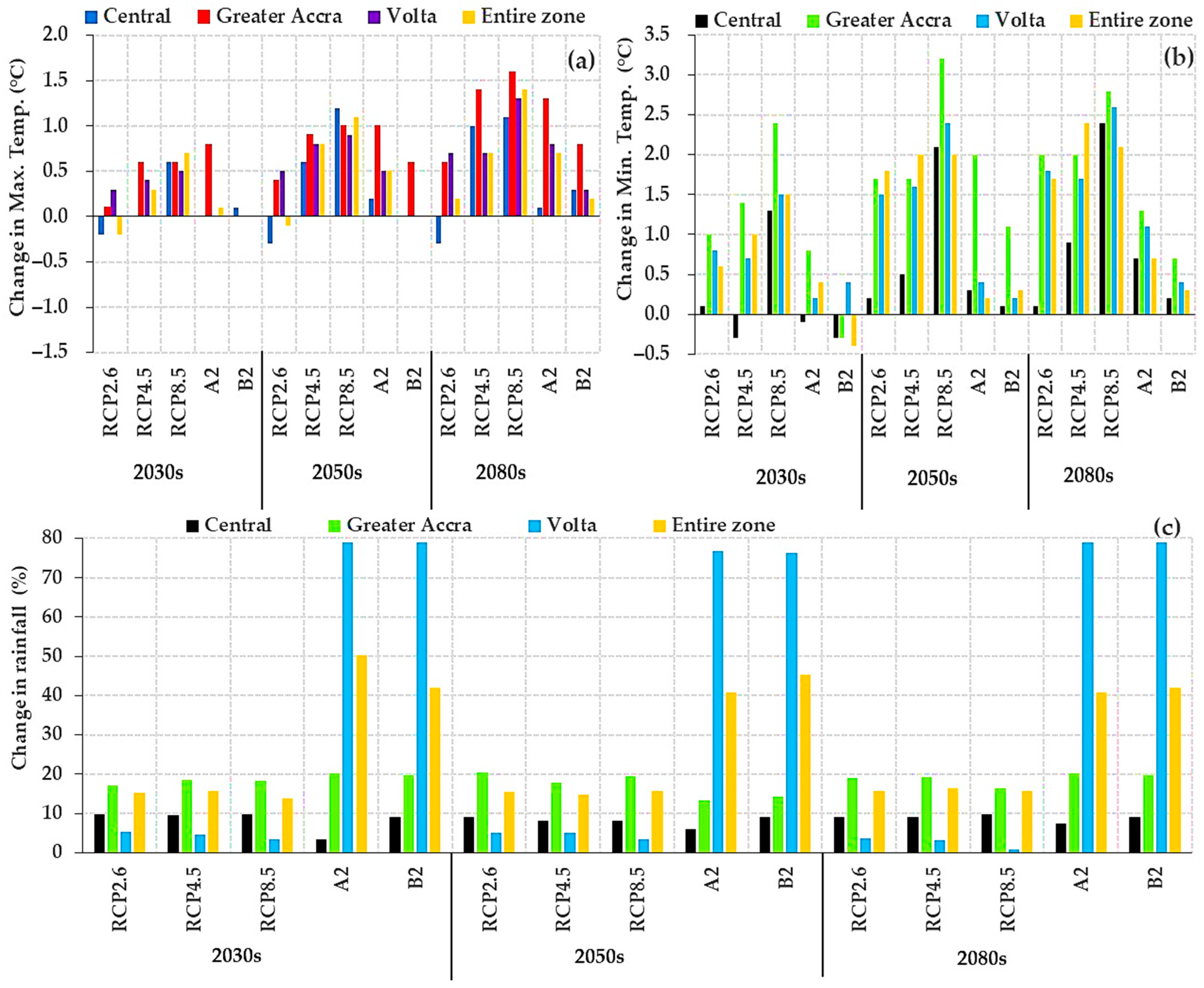
3.2.3. Change in Projected Future Monthly Maximum Temperature (Tmax)
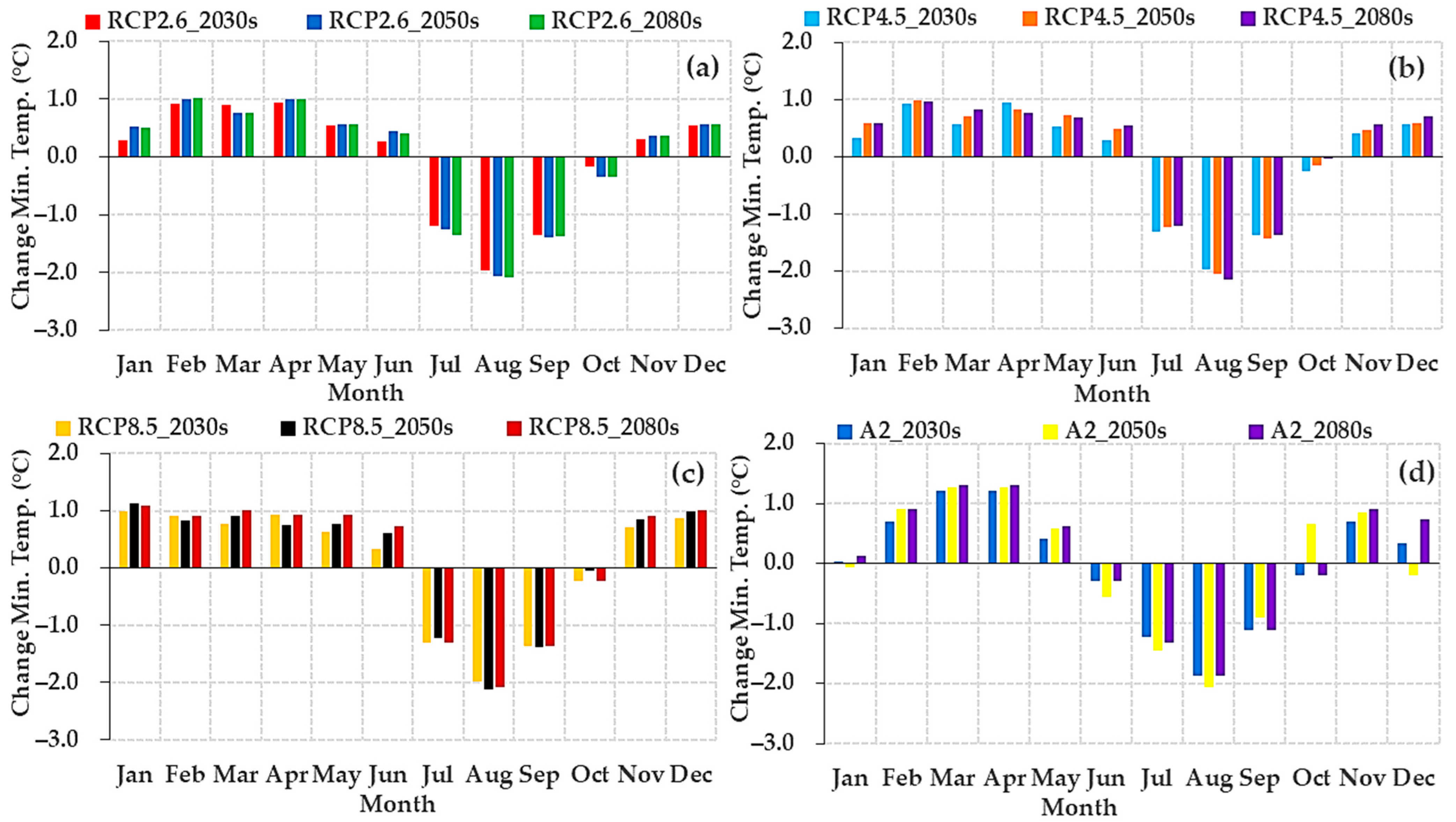
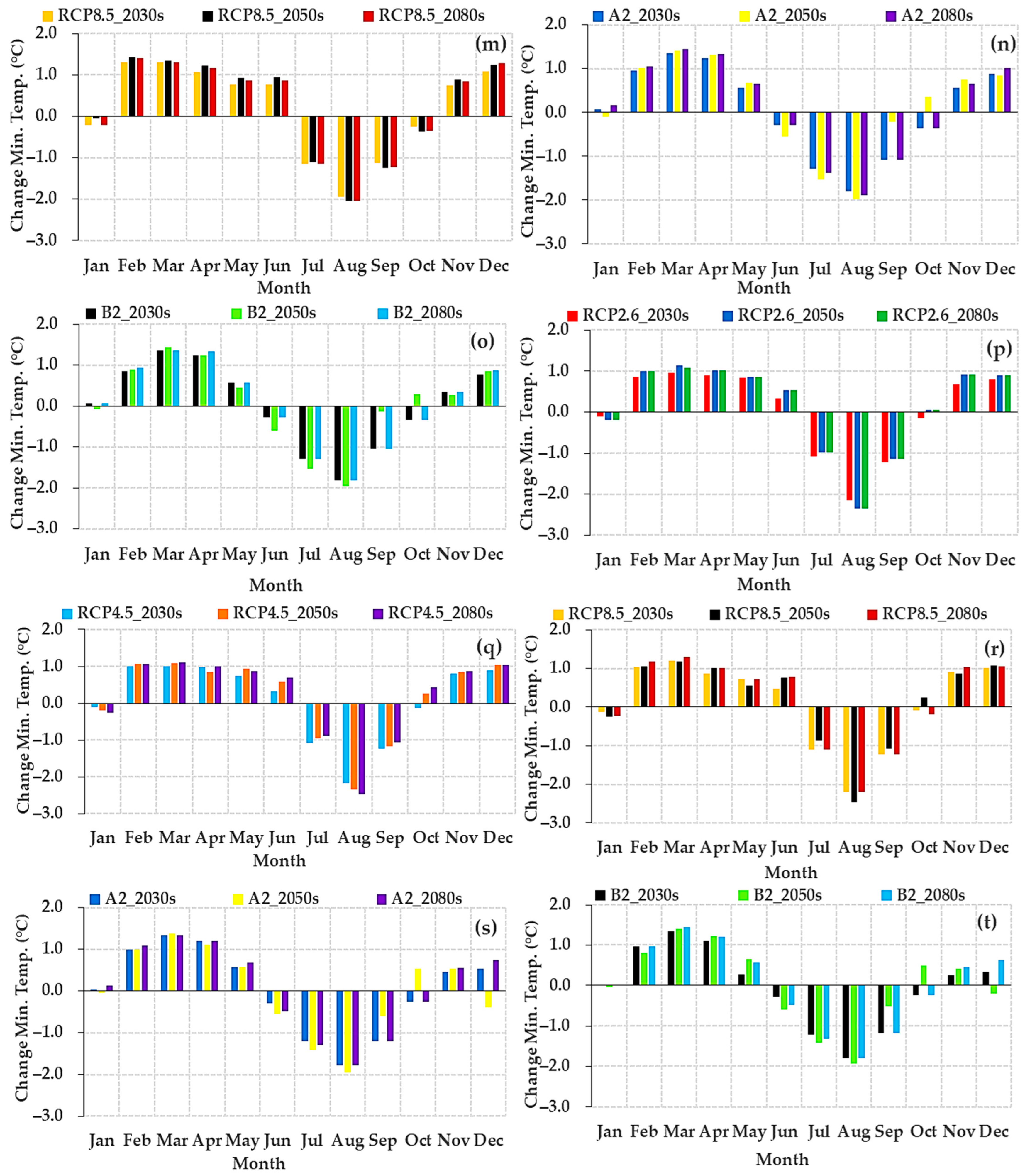
3.2.4. Change in Projected Future Monthly Minimum Temperature (Tmin)
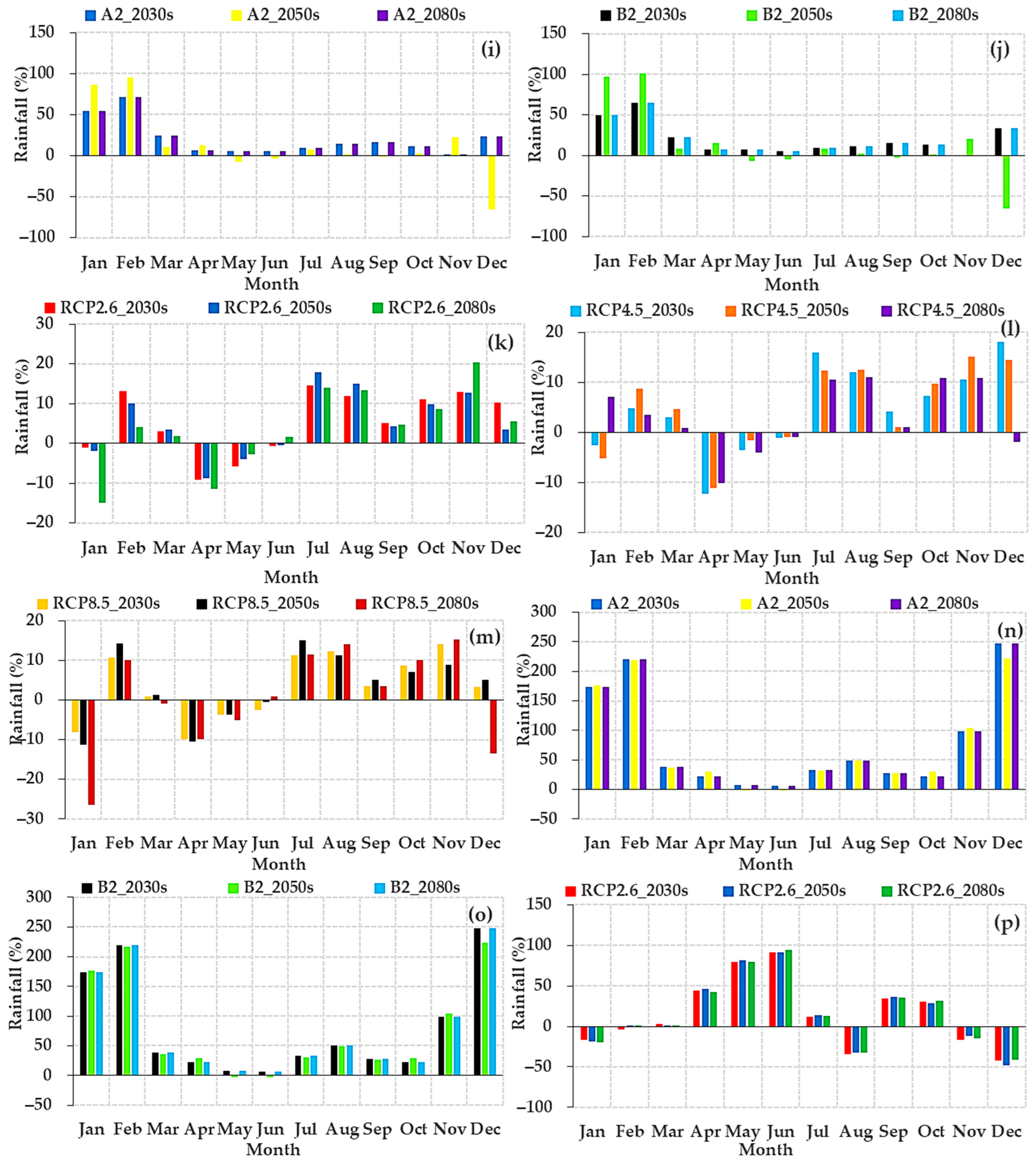
3.2.5. Change in Projected Future Monthly Rainfall
3.2.6. Projected Future Annual Change in Maximum (Tmax) and Minimum (Tmin) and Rainfall
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1535. [Google Scholar]
- Folland, C.K.; Karl, T.R.; Jim Salinger, M. Observed climate variability and change. Weather 2002, 57, 269–278. [Google Scholar] [CrossRef]
- Alexander, L.V.; Zhang, X.; Peterson, T.C.; Caesar, J.; Gleason, B.; Klein Tank, A.M.G.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F.; et al. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. Atmos. 2006, 111, 1–22. [Google Scholar] [CrossRef]
- Maidment, R.I.; Allan, R.P.; Black, E. Recent observed and simulated changes in precipitation over Africa. Geophys. Res. Lett. 2015, 42, 1–10. [Google Scholar] [CrossRef]
- Klein Tank, A.M.G.; Peterson, T.C.; Quadir, D.A.; Dorji, S.; Zou, X.; Tang, H.; Santhosh, K.; Joshi, U.R.; Jaswal, A.K.; Kolli, R.K.; et al. Changes in daily temperature and precipitation extremes in central and south Asia. J. Geophys. Res. Atmos. 2006, 111, 1–8. [Google Scholar] [CrossRef]
- Worku, G.; Teferi, E.; Bantider, A.; Dile, Y.T. Observed changes in extremes of daily rainfall and temperature in Jemma sub-basin, upper blue Nile basin, Ethiopia. Theor. Appl. Climatol. 2019, 135, 839–854. [Google Scholar] [CrossRef]
- da Silva, P.E.; Santos e Silva, C.M.; Spyrides, M.H.C.; Andrade, L.D.M.B. Precipitation and air temperature extremes in the Amazon and northeast Brazil. Int. J. Climatol. 2019, 39, 579–595. [Google Scholar] [CrossRef]
- Easterling, D.R.; Evans, J.L.; Groisman, P.Y.; Karl, T.R.; Kunkel, K.E.; Ambenje, P. Observed variability and trends in extreme climate events: A brief review. Bull. Am. Meteorol. Soc. 2000, 81, 417–425. [Google Scholar] [CrossRef]
- Sharma, D.; Babel, M.S. Trends in extreme rainfall and temperature indices in the western Thailand. Int. J. Climatol. 2014, 34, 2393–2407. [Google Scholar] [CrossRef]
- Peterson, T.C.; Manton, M.J. Monitoring changes in climate extremes: A tale of international collaboration. Bull. Am. Meteorol. Soc. 2008, 89, 1266–1271. [Google Scholar] [CrossRef]
- Tierney, J.E.; Smerdon, J.E.; Anchukaitis, K.J.; Seager, R. Multidecadal variability in East African hydroclimate controlled by the Indian Ocean. Nature 2013, 493, 389–392. [Google Scholar] [CrossRef]
- IPCC. Managing The Risks of Extreme Events and Disasters to Advance Climate Change Adaptation; A special report of working groups I and II of the intergovernmental panel on climate change (IPCC); Field, C.B., Barros, V., Stocker, T., Qin, D., Dokken, D., Ebi, K., Mastrandrea, M., Mach, K., Plattner, G.-K., Allen, S., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2012; pp. 555–564. [Google Scholar]
- Frich, P.; Alexander, L.V.; Della-Marta, P.; Gleason, B.; Haylock, M.; Tank Klein, A.M.G.; Peterson, T. Observed coherent changes in climatic extremes during the second half of the twentieth century. Clim. Res. 2002, 19, 193–212. [Google Scholar] [CrossRef]
- Manton, M.; Della-Marta, P.; Haylock, M.; Hennessy, K.; Nicholls, N.; Chambers, L.; Collins, D.; Daw, G.; Finet, A.; Gunawan, D.; et al. Trends in extreme daily rainfall and temperature in southeast Asia and the south Pacific: 1961–1998. Int. J. Climatol. 2001, 21, 269–284. [Google Scholar] [CrossRef]
- Peterson, T.C.; Taylor, M.A.; Demeritte, R.; Duncombe, D.L.; Burton, S.; Thompson, F.; Porter, A.; Mercedes, M.; Villegas, E.; Fils, R.S.; et al. Recent changes in climate extremes in the Caribbean region. J. Geophys. Res. Atmos. 2002, 107, 1–9. [Google Scholar] [CrossRef]
- Karl, T.R.; Knight, R.W.; Easterling, D.R.; Quayle, R.G. Indices of climate change for the United States. Bull. Am. Meteorol. Soc. 1996, 77, 279–292. [Google Scholar] [CrossRef]
- Vincent, L.A.; Mekis, É. Changes in daily and extreme temperature and precipitation indices for Canada over the twentieth century. Atmos.Ocean 2006, 44, 177–193. [Google Scholar] [CrossRef]
- Klein Tank, A.M.G.; Können, G.P. Trends in indices of daily temperature and precipitation extremes in Europe, 1946–1999. J. Clim. 2003, 16, 3665–3680. [Google Scholar] [CrossRef]
- You, Q.; Kang, S.; Aguilar, E.; Yan, Y. Changes in daily climate extremes in the eastern and central Tibetan plateau during 1961–2005. J. Geophys. Res. Atmos. 2008, 113, 1–17. [Google Scholar] [CrossRef]
- Haylock, M.R.; Peterson, T.C.; Alves, L.M.; Ambrizzi, T.; Anunciação, Y.M.T.; Baez, J.; Barros, V.R.; Berlato, M.A.; Bidegain, M.; Coronel, G.; et al. Trends in total and extreme South American rainfall in 1960–2000 and links with sea surface temperature. J. Clim. 2006, 19, 1490–1512. [Google Scholar] [CrossRef]
- Vincent, L.A.; Peterson, T.C.; Barros, V.R.; Marino, M.B.; Rusticucci, M.; Carrasco, G.; Ramirez, E.; Alves, L.M.; Ambrizzi, T.; Berlato, M.A.; et al. Observed trends in indices of daily temperature extremes in South America 1960–2000. J. Clim. 2005, 18, 5011–5023. [Google Scholar] [CrossRef]
- Alexander, L.V.; Hope, P.; Collins, D.; Trewin, B.; Lynch, A.; Nicholls, N. Trends in Australia’s climate means and extremes: A global context. Aust. Meteorol. Mag. 2007, 56, 1–18. [Google Scholar]
- Guerreiro, S.B.; Fowler, H.J.; Barbero, R.; Westra, S.; Lenderink, G.; Blenkinsop, S.; Lewis, E.; Li, X.F. Detection of continental-scale intensification of hourly rainfall extremes. Nat. Clim. Chang. 2018, 8, 803–807. [Google Scholar] [CrossRef]
- New, M.; Hewitson, B.; Stephenson, D.B.; Tsiga, A.; Kruger, A.; Manhique, A.; Gomez, B.; Coelho, C.A.S.; Masisi, D.N.; Kululanga, E.; et al. Evidence of trends in daily climate extremes over Southern and West Africa. J. Geophys. Res. Atmos. 2006, 111, 1–11. [Google Scholar] [CrossRef]
- Omondi, P.A.; Awange, J.L.; Forootan, E.; Ogallo, L.A.; Barakiza, R.; Girmaw, G.B.; Fesseha, I.; Kululetera, V.; Kilembe, C.; Mbati, M.M.; et al. Changes in temperature and precipitation extremes over the Greater Horn of Africa region from 1961 to 2010. Int. J. Climatol. 2014, 34, 1262–1277. [Google Scholar] [CrossRef]
- Barry, A.A.; Caesar, J.; Klein Tank, A.M.G.; Aguilar, E.; McSweeney, C.; Cyrille, A.M.; Nikiema, M.P.; Narcisse, K.B.; Sima, F.; Stafford, G.; et al. West Africa climate extremes and climate change indices. Int. J. Climatol. 2018, 38, e921–e938. [Google Scholar] [CrossRef]
- Sylla, M.B.; Giorgi, F.; Coppola, E.; Mariotti, L. Uncertainties in daily rainfall over Africa: Assessment of gridded observation products and evaluation of a regional climate model simulation. Int. J. Climatol. 2013, 33, 1805–1817. [Google Scholar] [CrossRef]
- Ben Mohamed, A. Climate change risks in Sahelian Africa. Reg. Environ. Chang. 2011, 11 (Suppl. S1), 109–117. [Google Scholar] [CrossRef]
- Panthou, G.; Vischel, T.; Lebel, T. Recent trends in the regime of extreme rainfall in the Central Sahel. Int. J. Climatol. 2014, 34, 3998–4006. [Google Scholar] [CrossRef]
- Monerie, P.-A.; Fontaine, B.; Roucou, P. Expected future changes in the African monsoon between 2030 and 2070 using some CMIP3 and CMIP5 models under a medium-low RCP scenario. J. Geophys. Res. 2012, 117, D16111. [Google Scholar] [CrossRef]
- De Longueville, F.; Hountondji, Y.C.; Kindo, I.; Gemenne, F.; Ozer, P. Long-term analysis of rainfall and temperature data in Burkina Faso (1950–2013). Int. J. Climatol. 2016, 36, 4393–4405. [Google Scholar] [CrossRef]
- Hountondji, Y.-C.; De Longueville, F.; Ozer, P. Trends in extreme rainfall events in Benin (West Africa), 1960–2000. In Proceedings of the 1st International Conference on Energy, Environment and Climate Change, Ho Chi Minh City, Vietnam, 26–27 August 2011. [Google Scholar]
- Obada, E.; Alamou, E.A.; Biao, E.I.; Zandagba, E.B.J. Interannual variability and trends of extreme rainfall indices over Benin. Climate 2021, 9, 160. [Google Scholar] [CrossRef]
- Mouhamed, L.; Traore, S.B.; Alhassane, A.; Sarr, B. Evolution of some observed climate extremes in the West African Sahel. Weather Clim. Extrem. 2013, 1, 19–25. [Google Scholar] [CrossRef]
- Larbi, I.; Hountondji, F.C.C.; Annor, T.; Agyare, W.A.; Gathenya, J.M.; Amuzu, J. Spatio-temporal trend analysis of rainfall and temperature extremes in the Vea Catchment, Ghana. Climate 2018, 6, 87. [Google Scholar] [CrossRef]
- Atiah, W.A.; Muthoni, F.K.; Kotu, B.; Kizito, F.; Amekudzi, L.K. Trends of rainfall onset, cessation, and length of growing season in northern Ghana: Comparing the rain gauge, satellite, and farmer’s perceptions. Atmosphere 2021, 12, 1674. [Google Scholar] [CrossRef]
- Braimah, M.; Asante, V.A.; Ahiataku, M.A.; Ansah, S.O.; Otu-Larbi, F.; Yahaya, B.; Ayabilah, J.B.; Nkrumah, F. Variability of the minor season rainfall over southern Ghana (1981–2018). Adv. Meteorol. 2022, 2022, 1861130. [Google Scholar] [CrossRef]
- Cooper, P.J.M.; Dimes, J.; Rao, K.P.C.; Shapiro, B.; Shiferaw, B.; Twomlow, S. Coping better with current climatic variability in the rain-fed farming systems of Sub-Saharan Africa: An essential first step in adapting to future climate change? Agric. Ecosyst. Environ. 2008, 126, 24–35. [Google Scholar] [CrossRef]
- Sultan, B.; Gaetani, M. Agriculture in West Africa in the twenty-first century: Climate change and impacts scenarios, and potential for adaptation. Front. Plant Sci. 2016, 7, 1–20. [Google Scholar] [CrossRef]
- Antwi-Agyei, P.; Fraser, E.D.G.; Dougill, A.J.; Stringer, L.C.; Simelton, E. Mapping the vulnerability of crop production to drought in Ghana using rainfall, yield and socioeconomic data. Appl. Geogr. 2012, 32, 324–334. [Google Scholar] [CrossRef]
- Owusu, K.; Waylen, P.R. The changing rainy season climatology of mid-Ghana. Theor. Appl. Climatol. 2013, 112, 419–430. [Google Scholar] [CrossRef]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 851–870. [Google Scholar] [CrossRef]
- IPCC. Summary for Policymakers. In Global Warming of 1.5 °C. An IPCC Special Report on the Impacts of Global Warming of 1.5 °C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; Masson-Delmotte, V., Zhai, P., Pörtner, H.-O., Roberts, D., Skea, J., Shukla, P., Pirani, A., Moufouma-Okia, W., Péan, C., Pidcock, R., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2018; pp. 3–24. [Google Scholar] [CrossRef]
- Siabi, E.K.; Kabobah, A.T.; Akpoti, K.; Anornu, G.K.; Amo-boateng, M.; Nyantakyi, E.K. Statistical downscaling of global circulation models to assess future climate changes in the Black Volta basin of Ghana. Environ. Challenges 2021, 5, 100299. [Google Scholar] [CrossRef]
- Phuong, D.N.D.; Duong, T.Q.; Liem, N.D.; Tram, V.N.Q.; Cuong, D.K.; Loi, N.K. Projections of future climate change in the Vu Gia Thu Bon River Basin, Vietnam by using statistical downscaling model (SDSM). Water 2020, 12, 755. [Google Scholar] [CrossRef]
- Arnell, N.W.; Lowe, J.A.; Bernie, D.; Nicholls, R.J.; Brown, S.; Challinor, A.J.; Osborn, T.J. The global and regional impacts of climate change under representative concentration pathway forcings and shared socioeconomic pathway socioeconomic scenarios. Environ. Res. Lett. 2019, 14, 084046. [Google Scholar] [CrossRef]
- James, R.; Washington, R.; Rowell, D.P. African climate change uncertainty in perturbed physics ensembles: Implications of global warming to 4 °C and beyond. J. Clim. 2014, 27, 4677–4692. [Google Scholar] [CrossRef]
- Diedhiou, A.; Bichet, A.; Wartenburger, R.; Seneviratne, S.I.; Rowell, D.P. Changes in climate extremes over West and Central Africa at 1.5 °C and 2 °C global warming. Environ. Res. Lett. 2018, 13, 065020. [Google Scholar] [CrossRef]
- Endris, H.S.; Omondi, P.; Jain, S.; Lennard, C.; Hewitson, B.; Chang’a, L.; Awange, J.L.; Dosio, A.; Ketiem, P.; Nikulin, G.; et al. Assessment of the performance of CORDEX regional climate models in simulating East African rainfall. J. Clim. 2013, 26, 8453–8475. [Google Scholar] [CrossRef]
- Shongwe, M.E.; van Oldenborgh, G.J.; van den Hurk, B.J.J.M.; de Boer, B.; Coelho, C.A.S.; van Aalst, M.K. Projected changes in mean and extreme precipitation in Africa under global warming. Part I: Southern Africa. J. Clim. 2009, 22, 3819–3837. [Google Scholar] [CrossRef]
- Wilby, R.L.; Wigley, T.M.L. Downscaling general circulation model output: A review of methods and limitations. Prog. Phys. Geogr. Earth Environ. 1997, 21, 530–548. [Google Scholar] [CrossRef]
- Benestad, R.E. Empirical-statistical downscaling in climate modeling. EOS Trans. Am. Geophys. Union 2004, 85, 417–422. [Google Scholar] [CrossRef]
- Wilby, R.L.; Dawson, C.W. Using SDSM Version 3.1—A Decision Support Tool for the Assessment of Regional Climate Change Impacts. User Man. 2004, 8, 1–7. Available online: https://unfccc.int/resource/cd_roms/na1/v_and_a/Resoursce_materials/Climate/SDSM/SDSM.Manual.pdf (accessed on 28 August 2022).
- Semenov, M.A.; Barrow, E.M. A Stochastic Weather Generator for Use in Climate Impact Studies; User Manual: Hertfordshire, UK, 2002; pp. 1–27. Available online: http://resources.rothamsted.ac.uk/sites/default/files/groups/mas-models/download/LARS-WG-Manual.pdf (accessed on 28 August 2022).
- Akbari, H.; Rakhshandehroo, G.R.; Afrooz, A.H.; Pourtouiserkani, A. Climate change impact on intensity-duration-frequency curves in Chenar-Rahdar river basin. Watershed Manag. 2015, 5, 48–61. [Google Scholar] [CrossRef]
- Birara, H.; Mishra, R.P.P.S.K. Projections of future rainfall and temperature using statistical downscaling techniques in Tana Basin, Ethiopia. Sustain. Water Resour. Manag. 2020, 6, 1–17. [Google Scholar] [CrossRef]
- Daksiya, V.; Mandapaka, P.; Lo, E.Y.M. A comparative frequency analysis of maximum daily rainfall for a SE Asian region under current and future climate conditions. Adv. Meteorol. 2017, 2017, 2620798. [Google Scholar] [CrossRef]
- Gebrechorkos, S.H.; Hülsmann, S.; Bernhofer, C. Statistically downscaled climate dataset for East Africa. Sci. Data 2019, 6, 31. [Google Scholar] [CrossRef] [PubMed]
- Iwadra, M.; Odirile, P.T.; Parida, B.P.; Moalafhi, D.B. Evaluation of future climate using SDSM and secondary data (TRMM and NCEP) for poorly gauged catchments of Uganda: The case of Aswa catchment. Theor. Appl. Climatol. 2019, 137, 2029–2048. [Google Scholar] [CrossRef]
- Fenta Mekonnen, D.; Disse, M. Analyzing the future climate change of upper blue Nile River basin using statistical downscaling techniques. Hydrol. Earth Syst. Sci. 2018, 22, 2391–2408. [Google Scholar] [CrossRef]
- Vallam, P.; Qin, X.S. Projecting future precipitation and temperature at sites with diverse climate through multiple statistical downscaling schemes. Theor. Appl. Climatol. 2018, 134, 669–688. [Google Scholar] [CrossRef]
- Campozano, L.; Tenelanda, D.; Sanchez, E.; Samaniego, E.; Feyen, J. Comparison of statistical downscaling methods for monthly total precipitation: Case study for the Paute River basin in southern Ecuador. Adv. Meteorol. 2016, 2016, 6526341. [Google Scholar] [CrossRef]
- Etemadi, H.; Samadi, S.; Sharifikia, M. Uncertainty analysis of statistical downscaling models using general circulation model over an international wetland. Clim. Dyn. 2014, 42, 2899–2920. [Google Scholar] [CrossRef]
- Hashmi, M.Z.; Shamseldin, A.Y.; Melville, B.W. Comparison of SDSM and LARS-WG for simulation and downscaling of extreme precipitation events in a watershed. Stoch. Environ. Res. Risk Assess. 2011, 25, 475–484. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, Z.; Charles, S.P.; Fu, G.; Liu, L. Evaluation of two statistical downscaling models for daily precipitation over an arid basin in China. Int. J. Climatol. 2011, 31, 2006–2020. [Google Scholar] [CrossRef]
- Najafi, R.; Hessami Kermani, M. Uncertainty modeling of statistical downscaling to assess climate change impacts on temperature and precipitation. Water Resour. Manag. 2017, 31, 1843–1858. [Google Scholar] [CrossRef]
- Khan, M.S.; Coulibaly, P.; Dibike, Y. Uncertainty analysis of statistical downscaling methods. J. Hydrol. 2006, 319, 357–382. [Google Scholar] [CrossRef]
- Khan, M.S.; Coulibaly, P.; Dibike, Y. Uncertainty analysis of statistical downscaling methods using Canadian Global Climate Model predictors. Hydrol. Process. 2006, 20, 3085–3104. [Google Scholar] [CrossRef]
- Bessah, E.; Boakye, E.A.; Agodzo, S.K.; Nyadzi, E.; Larbi, I.; Awotwi, A. Increased seasonal rainfall in the twenty-first century over Ghana and its potential implications for agriculture productivity. Environ. Dev. Sustain. 2021, 23, 12342–12365. [Google Scholar] [CrossRef]
- Bessah, E.; Raji, A.O.; Taiwo, O.J.; Agodzo, S.K.; Ololade, O.O. Variable resolution modeling of near future mean temperature changes in the dry sub-humid region of Ghana. Model. Earth Syst. Environ. 2018, 4, 919–933. [Google Scholar] [CrossRef]
- Larbi, I.; Hountondji, F.C.C.; Dotse, S.; Mama, D.; Nyamekye, C.; Adeyeri, O.E.; Djan, H.; Rock, P.; Odoom, E.; Mensah, Y. Local climate change projections and impact on the surface hydrology in the Vea Catchment, West Africa. Hydrol. Res. 2021, 52, 1200–1215. [Google Scholar] [CrossRef]
- Addi, M.; Asare, K.; Fosuhene, S.K.; Ansah-Narh, T.; Aidoo, K.; Botchway, C.G. Impact of large-scale climate indices on meteorological drought of coastal Ghana. Adv. Meteorol. 2021, 2021, 8899645. [Google Scholar] [CrossRef]
- Ghana Statistical Service. 2010 Population and Housing Census. National Analytical Report. 2013. Available online: https://statsghana.gov.gh/gssmain/fileUpload/pressrelease/2010_PHC_National_Analytical_Report.pdf (accessed on 27 August 2022).
- Dickson, K.B.; Benneh, G. A New Geography of Ghana; Revised edition; Longman Group Ltd.: Essex, UK, 1995; pp. 17–40. [Google Scholar]
- Wilby, R.L.; Dawson, C.W.; Murphy, C.; O’Connor, P.; Hawkins, E. The Statistical downscaling model-decision centric (SDSM-DC): Conceptual basis and applications. Clim. Res. 2014, 61, 259–276. [Google Scholar] [CrossRef]
- Graham, J.W. Missing data analysis: Making it work in the real world. Annu. Rev. Psychol. 2009, 60, 549–576. [Google Scholar] [CrossRef]
- Schafer, J.L.; Graham, J.W. Missing data: Our view of the state of the art. Psychol. Methods 2002, 7, 147–177. [Google Scholar] [CrossRef]
- Zhang, Z. Multiple imputation with multivariate imputation by chained equation (MICE) package. Ann. Transl. Med. 2016, 4, 30. [Google Scholar] [CrossRef] [PubMed]
- Abdullah, A.Y.M.; Bhuian, M.H.; Kiselev, G.; Dewan, A.; Hassan, Q.K.; Rafiuddin, M. Extreme temperature and rainfall events in Bangladesh: A comparison between coastal and inland areas. Int. J. Climatol. 2022, 42, 3253–3273. [Google Scholar] [CrossRef]
- Azur, M.J.; Stuart, E.A.; Frangakis, C.; Leaf, P.J. Multiple imputation by chained equations: What is it and how does it work? Int. J. Methods Psychiatr. Res. 2011, 20, 40–49. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Yang, F. RClimDex (1.0) User Manual. Climate Research Branch Environment Canada. 2004. Available online: http://www.acmad.net/rcc/procedure/RClimDexUserManual.pdf (accessed on 27 August 2022).
- Wang, X.; Feng, Y. RHTestV4 User Manual; Climate Research Division, Atmospheric Science and Technology Directorate, Science and Technology Branch, Environment Canada: Toronto, ON, Canada, 2013; Available online: http://cccma.seos.uvic.ca/ETCCDMI/RHTest/RHTestUserManual.doc (accessed on 27 August 2022).
- Wang, X.L. Accounting for autocorrelation in detecting mean shifts in climate data series using the penalized maximal t or F test. J. Appl. Meteorol. Climatol. 2008, 47, 2423–2444. [Google Scholar] [CrossRef]
- Wang, X.L. Penalized maximal F test for detecting undocumented mean shift without trend change. J. Atmos. Ocean. Technol. 2008, 25, 368–384. [Google Scholar] [CrossRef]
- Wang, X.L.; Feng, Y. RHtests_dlyPrcp User Manual; Climate Research Division, Atmospheric Science and Technology Directorate, Science and Technology Branch, Environment Canada: Toronto, ON, Canada, 2013; Available online: http://etccdi.pacificclimate.org/software.shtml. (accessed on 27 August 2022).
- Ruml, M.; Gregorić, E.; Vujadinović, M.; Radovanović, S.; Matović, G.; Vuković, A.; Počuča, V.; Stojičić, D. Observed changes of temperature extremes in Serbia over the period 1961−2010. Atmos. Res. 2017, 183, 26–41. [Google Scholar] [CrossRef]
- Sein, K.K.; Chidthaisong, A.; Oo, K.L. Observed trends and changes in temperature and precipitation extreme indices over Myanmar. Atmosphere 2018, 9, 477. [Google Scholar] [CrossRef]
- Wang, X.L.; Chen, H.; Wu, Y.; Feng, Y.; Pu, Q. New techniques for the detection and adjustment of shifts in daily precipitation data series. J. Appl. Meteorol. Climatol. 2010, 49, 2416–2436. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1975. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- da Silva, R.M.; Santos, C.A.G.; Moreira, M.; Corte-Real, J.; Silva, V.C.L.; Medeiros, I.C. Rainfall and river flow trends using Mann–Kendall and Sen’s slope estimator statistical tests in the Cobres River basin. Nat. Hazards 2015, 77, 1205–1221. [Google Scholar] [CrossRef]
- Derrick, B.; Toher, D.; White, P. Why Welch’s test is Type I error robust. Quant. Methods Psychol. 2016, 12, 30–38. [Google Scholar] [CrossRef]
- Wilby, R.L.; Dawson, C.W.; Barrow, E.M. SDSM—a decision support tool for the assessment of regional climate change impacts. Environ. Model. Softw. 2002, 17, 145–157. [Google Scholar] [CrossRef]
- Wilby, R.L.; Charles, S.; Mearns, L.O.; Whetton, P.; Zorito, E.; Timbal, B. Guidelines for use of climate scenarios developed from statistical downscaling methods. IPCC Task Group on Scenarios for Climate Impact Assessment (TGCIA). 2004. Available online: http://www.ipccdata.org/guidelines/dgmno2v1092004.pd (accessed on 27 August 2022).
- Wilby, R.L.; Dawson, C.W. SDSM 4.2-A Decision Support Tool for the Assessment of Regional Climate Change Impacts; User Manual; Lancaster University: Lancaster, UK; Environment Agency England: Wales, UK, 2007; Volume 94, pp. 1–94. [Google Scholar]
- Wilby, R.L.; Dawson, C.W. The statistical downscaling model: Insights from one decade of application. Int. J. Climatol. 2013, 33, 1707–1719. [Google Scholar] [CrossRef]
- Mahmood, R.; Babel, M.S. Future changes in extreme temperature events using the statistical downscaling model (SDSM) in the trans-boundary region of the Jhelum river basin. Weather. Clim. Extrem. 2014, 5, 56–66. [Google Scholar] [CrossRef]
- Fan, X.; Jiang, L.; Gou, J. Statistical downscaling and projection of future temperatures across the Loess Plateau, China. Weather Clim. Extrem. 2021, 32, 100328. [Google Scholar] [CrossRef]
- Cao, L.; Zhu, Y.; Tang, G.; Yuan, F.; Yan, Z. Climatic warming in China according to a homogenized data set from 2419 stations. Int. J. Climatol. 2016, 36, 4384–4392. [Google Scholar] [CrossRef]
- Li, Q.; Dong, W. Detection and adjustment of undocumented discontinuities in Chinese temperature series using a composite approach. Adv. Atmos. Sci. 2009, 26, 143–153. [Google Scholar] [CrossRef]
- Jaiswal, R.K.; Lohani, A.K.; Tiwari, H.L. Statistical analysis for change detection and trend assessment in climatological parameters. Environ. Process. 2015, 2, 729–749. [Google Scholar] [CrossRef]
- Sarangi, C.; Qian, Y.; Li, J.; Leung, L.R.; Chakraborty, T.C.; Liu, Y. Urbanization amplifies nighttime heat stress on warmer days over the US. Geophys. Res. Lett. 2021, 48, 1–12. [Google Scholar] [CrossRef]
- Yu, M.; Ruggieri, E. Change point analysis of global temperature records. Int. J. Climatol. 2019, 39, 3679–3688. [Google Scholar] [CrossRef]
- Ajjur, S.B.; Al-Ghamdi, S.G. Global hotspots for future absolute temperature extremes from CMIP6 Models. Earth Space Sci. 2021, 8, e2021EA001817. [Google Scholar] [CrossRef]
- Donat, M.G.; Alexander, L.V.; Yang, H.; Durre, I.; Vose, R.; Dunn, R.J.H.; Willett, K.M.; Aguilar, E.; Brunet, M.; Caesar, J.; et al. Updated analyses of temperature and precipitation extreme indices since the beginning of the twentieth century: The HadEX2 Dataset. J. Geophys. Res. Atmos. 2013, 118, 2098–2118. [Google Scholar] [CrossRef]
- Shrestha, A.B.; Bajracharya, S.R.; Sharma, A.R.; Duo, C.; Kulkarni, A. Observed trends and changes in daily temperature and precipitation extremes over the Koshi River basin 1975–2010. Int. J. Climatol. 2017, 37, 1066–1083. [Google Scholar] [CrossRef]
- Zhou, B.; Xu, Y.; Wu, J.; Dong, S.; Shi, Y. Changes in temperature and precipitation extreme indices over China: Analysis of a high-resolution grid dataset. Int. J. Climatol. 2016, 36, 1051–1066. [Google Scholar] [CrossRef]
- Dashkhuu, D.; Kim, J.P.; Chun, J.A.; Lee, W.S. Long-term trends in daily temperature extremes over Mongolia. Weather Clim. Extrem. 2015, 8, 26–33. [Google Scholar] [CrossRef]
- Ullah, S.; You, Q.; Ullah, W.; Ali, A.; Xie, W.; Xie, X. Observed changes in temperature extremes over China–Pakistan economic corridor during 1980–2016. Int. J. Climatol. 2019, 39, 1457–1475. [Google Scholar] [CrossRef]
- Saddique, N.; Khaliq, A.; Bernhofer, C. Trends in temperature and precipitation extremes in historical (1961–1990) and projected (2061–2090) periods in a data scarce mountain basin, Northern Pakistan. Stoch. Environ. Res. Risk Assess. 2020, 34, 1441–1455. [Google Scholar] [CrossRef]
- Viceto, C.; Cardoso Pereira, S.; Rocha, A. Climate change projections of extreme temperatures for the Iberian Peninsula. Atmosphere 2019, 10, 229. [Google Scholar] [CrossRef]
- Teshome, A.; Zhang, J. Increase of extreme drought over Ethiopia under climate warming. Adv. Meteorol. 2019, 2019, 5235429. [Google Scholar] [CrossRef]
- van der Walt, A.J.; Fitchett, J.M. Exploring extreme warm temperature trends in South Africa: 1960–2016. Theor. Appl. Climatol. 2021, 143, 1341–1360. [Google Scholar] [CrossRef]
- Iyakaremye, V.; Zeng, G.; Ullah, I.; Gahigi, A.; Mumo, R.; Ayugi, B. Recent observed changes in extreme high-temperature events and associated meteorological conditions over Africa. Int. J. Climatol. 2022, 42, 4522–4537. [Google Scholar] [CrossRef]
- Moberg, A.; Jones, P.D.; Lister, D.; Walther, A.; Brunet, M.; Jacobeit, J.; Alexander, L.V.; Della-Marta, P.M.; Luterbacher, J.; Yiou, P.; et al. Indices for daily temperature and precipitation extremes in Europe analyzed for the period 1901–2000. J. Geophys. Res. Atmos. 2006, 111, D22106. [Google Scholar] [CrossRef]
- Quenum, G.M.L.D.; Nkrumah, F.; Klutse, N.A.B.; Sylla, M.B. Spatiotemporal changes in temperature and precipitation in West Africa. Part i: Analysis with the CMIP6 historical dataset. Water 2021, 13, 3506. [Google Scholar] [CrossRef]
- Wazneh, H.; Arain, M.A.; Coulibaly, P. Climate indices to characterize climatic changes across Southern Canada. Meteorol. Appl. 2020, 27, 1–19. [Google Scholar] [CrossRef]
- Ji, F.; Wu, Z.; Huang, J.; Chassignet, E.P. Evolution of land surface air temperature trend. Nat. Clim. Chang. 2014, 4, 462–466. [Google Scholar] [CrossRef]
- Tong, S.; Li, X.; Zhang, J.; Bao, Y.; Bao, Y.; Na, L.; Si, A. Spatial and temporal variability in extreme temperature and precipitation events in Inner Mongolia (China) during 1960–2017. Sci. Total Environ. 2019, 649, 75–89. [Google Scholar] [CrossRef]
- Stephenson, T.S.; Vincent, L.A.; Allen, T.; Van Meerbeeck, C.J.; Mclean, N.; Peterson, T.C.; Taylor, M.A.; Aaron-Morrison, A.P.; Auguste, T.; Bernard, D.; et al. Changes in extreme temperature and precipitation in the Caribbean Region, 1961–2010. Int. J. Climatol. 2014, 34, 2957–2971. [Google Scholar] [CrossRef]
- Rahimzadeh, F.; Asgari, A.; Fattahi, E. Variability of extreme temperature and precipitation in Iran during recent decades. Int. J. Climatol. 2009, 29, 329–343. [Google Scholar] [CrossRef]
- Braganza, K.; Karoly, D.J.; Arblaster, J.M. Diurnal temperature range as an index of global climate change during the twentieth century. Geophys. Res. Lett. 2004, 31, 2–5. [Google Scholar] [CrossRef]
- Mall, R.K.; Chaturvedi, M.; Singh, N.; Bhatla, R.; Singh, R.S.; Gupta, A.; Niyogi, D. Evidence of asymmetric change in diurnal temperature range in recent decades over different agro-climatic zones of India. Int. J. Climatol. 2021, 41, 2597–2610. [Google Scholar] [CrossRef]
- Bartolini, G.; Morabito, M.; Crisci, A.; Grifoni, D.; Torrigiani, T.; Petralli, M.; Maracchi, G.; Orlandini, S. Recent trends in Tuscany (Italy) summer temperature and indices of extremes. Int. J. Climatol. 2008, 28, 1751–1760. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E.; Sirangelo, B. Trend analysis of monthly mean values and extreme indices of daily temperature in a region of southern Italy. Int. J. Climatol. 2017, 37, 284–297. [Google Scholar] [CrossRef]
- Rahman, M.A.; Kang, S.C.; Nagabhatla, N.; Macnee, R. Impacts of temperature and rainfall variation on rice productivity in major ecosystems of Bangladesh. Agric. Food Secur. 2017, 6, 1–11. [Google Scholar] [CrossRef]
- dos Santos, C.A.C.; Neale, C.M.U.; Rao, T.V.R.; da Silva, B.B. Trends in indices for extremes in daily temperature and precipitation over Utah, USA. Int. J. Climatol. 2011, 31, 1813–1822. [Google Scholar] [CrossRef]
- You, Q.; Kang, S.; Aguilar, E.; Pepin, N.; Flügel, W.-A.; Yan, Y.; Xu, Y.; Zhang, Y.; Huang, J. Changes in daily climate extremes in China and their connection to the large scale atmospheric circulation during 1961–2003. Clim. Dyn. 2011, 36, 2399–2417. [Google Scholar] [CrossRef]
- Felix, M.L.; Kim, Y.K.; Choi, M.; Kim, J.C.; Do, X.K.; Nguyen, T.H.; Jung, K. Detailed trend analysis of extreme climate indices in the upper Geum River basin. Water 2021, 13, 3171. [Google Scholar] [CrossRef]
- Randriamarolaza, L.Y.A.; Aguilar, E.; Skrynyk, O.; Vicente-Serrano, S.M.; Domínguez-Castro, F. Indices for daily temperature and precipitation in Madagascar, based on quality-controlled and homogenized data, 1950–2018. Int. J. Climatol. 2022, 42, 265–288. [Google Scholar] [CrossRef]
- Easterling, D.R.; Horton, B.; Jones, P.D.; Peterson, T.C.; Karl, T.R.; Parker, D.E.; Salinger, M.J.; Razuvayev, V.; Plummer, N.; Jamason, P.; et al. Maximum and minimum temperature trends for the globe. Science 1997, 277, 364–367. [Google Scholar] [CrossRef]
- Vose, R.S.; Easterling, D.R.; Gleason, B. Maximum and minimum temperature trends for the globe: An update through 2004. Geophys. Res. Lett. 2005, 32, 1–5. [Google Scholar] [CrossRef]
- Kalnay, E.; Cai, M. Impact of urbanization and land-use. Nature 2003, 425, 528–531. [Google Scholar] [CrossRef]
- Mohan, M.; Kandya, A. Impact of urbanization and land-use/land-cover change on diurnal temperature range: A case study of tropical urban airshed of India using remote sensing data. Sci. Total Environ. 2015, 506–507, 453–465. [Google Scholar] [CrossRef]
- Wei, W.; Shi, Z.; Yang, X.; Wei, Z.; Liu, Y.; Zhang, Z.; Ge, G.; Zhang, X.; Guo, H.; Zhang, K.; et al. Recent trends of extreme precipitation and their teleconnection with atmospheric circulation in the Beijing-Tianjin sand source region, China, 1960–2014. Atmosphere 2017, 8, 83. [Google Scholar] [CrossRef]
- Ortiz-Gómez, R.; Muro-Hernández, L.J.; Flowers-Cano, R.S. Assessment of extreme precipitation through climate change indices in Zacatecas, Mexico. Theor. Appl. Climatol. 2020, 141, 1541–1557. [Google Scholar] [CrossRef]
- Liang, K. Spatio-Temporal Variations in precipitation extremes in the endorheic Hongjian lake basin in the Ordos Plateau, China. Water 2019, 11, 1981. [Google Scholar] [CrossRef]
- Alavinia, S.H.; Zarei, M. Analysis of spatial changes of extreme precipitation and temperature in Iran over a 50-Year Period. Int. J. Climatol. 2021, 41, E2269–E2289. [Google Scholar] [CrossRef]
- Subba, S.; Ma, Y.; Ma, W. Spatial and temporal analysis of precipitation extremities of eastern Nepal in the last two decades (1997–2016). J. Geophys. Res. Atmos. 2019, 124, 7523–7539. [Google Scholar] [CrossRef]
- Vondou, D.A.; Guenang, G.M.; Djiotang, T.L.A.; Kamsu-Tamo, P.H. Article trends and interannual variability of extreme rainfall indices over Cameroon. Sustainability. 2021, 13, 6803. [Google Scholar] [CrossRef]
- Santos, M.; Fonseca, A.; Fragoso, M.; Santos, J.A. Recent and future changes of precipitation extremes in mainland Portugal. Theor. Appl. Climatol. 2019, 137, 1305–1319. [Google Scholar] [CrossRef]
- Diatta, S.; Diedhiou, C.W.; Dione, D.M.; Sambou, S. Spatial variation and trend of extreme precipitation in West Africa and teleconnections with remote indices. Atmosphere 2020, 11, 999. [Google Scholar] [CrossRef]
- Sanogo, S.; Fink, A.H.; Omotosho, J.A.; Ba, A.; Redl, R.; Ermert, V. Spatio-temporal characteristics of the recent rainfall recovery in West Africa. Int. J. Climatol. 2015, 35, 4589–4605. [Google Scholar] [CrossRef]
- Nicholson, S.E. The nature of rainfall variability over Africa on time scales of decades to millenia. Glob. Planet. Chang. 2000, 26, 137–158. [Google Scholar] [CrossRef]
- Roudier, P.; Sultan, B.; Quirion, P.; Berg, A. The impact of future climate change on West African crop yields: What does the recent literature say? Glob. Environ. Chang. 2011, 21, 1073–1083. [Google Scholar] [CrossRef]
- Biasutti, M. Forced Sahel rainfall trends in the CMIP5 archive. J. Geophys. Res. Atmos. 2013, 118, 1613–1623. [Google Scholar] [CrossRef]
- Dong, B.; Sutton, R. Dominant role of greenhouse-gas forcing in the recovery of Sahel rainfall. Nat. Clim. Chang. 2015, 5, 757–760. [Google Scholar] [CrossRef]
- Skinner, C.B.; Ashfaq, M.; Diffenbaugh, N.S. Influence of twenty-first-century atmospheric and sea surface temperature forcing on West African climate. J. Clim. 2012, 25, 527–542. [Google Scholar] [CrossRef]
- Meenu, R.; Rehana, S.; Mujumdar, P.P. Assessment of hydrologic impacts of climate change in Tunga-Bhadra River basin, India with HEC-HMS and SDSM. Hydrol. Process. 2013, 27, 1572–1589. [Google Scholar] [CrossRef]
- Gulacha, M.M.; Mulungu, D.M.M. Generation of climate change scenarios for precipitation and temperature at local scales using SDSM in Wami-Ruvu River basin Tanzania. Phys. Chem. Earth 2017, 100, 62–72. [Google Scholar] [CrossRef]
- Shahriar, S.A.; Siddique, M.A.M.; Rahman, S.M.A. Climate change projection using statistical downscaling model over Chittagong Division, Bangladesh. Meteorol. Atmos. Phys. 2021, 133, 1409–1427. [Google Scholar] [CrossRef]
- Hassan, W.H.; Nile, B.K. Climate change and predicting future temperature in Iraq using CanESM2 and HadCM3 modeling. Model. Earth Syst. Environ. 2021, 7, 737–748. [Google Scholar] [CrossRef]
- Koukidis, E.N.; Berg, A.A. Sensitivity of the statistical downscaling model (SDSM) to reanalysis products. Atmos. -Ocean. 2009, 47, 1–18. [Google Scholar] [CrossRef]
- Ding, Y.; Hayes, M.J.; Widhalm, M. Measuring economic impacts of drought: A review and discussion. Disaster Prev. Manag. 2011, 20, 434–446. [Google Scholar] [CrossRef]
- Armah, F.A.; Yawson, D.O.; Yengoh, G.T.; Odoi, J.O.; Afrifa, E.K.A. Impact of floods on livelihoods and vulnerability of natural resource dependent communities in Northern Ghana. Water 2010, 2, 120. [Google Scholar] [CrossRef]
- Bosello, F.; Roson, R.; Tol, R.S.J. Economy-wide estimates of the implications of climate change: Human health. Ecol. Econ. 2006, 58, 579–591. [Google Scholar] [CrossRef]
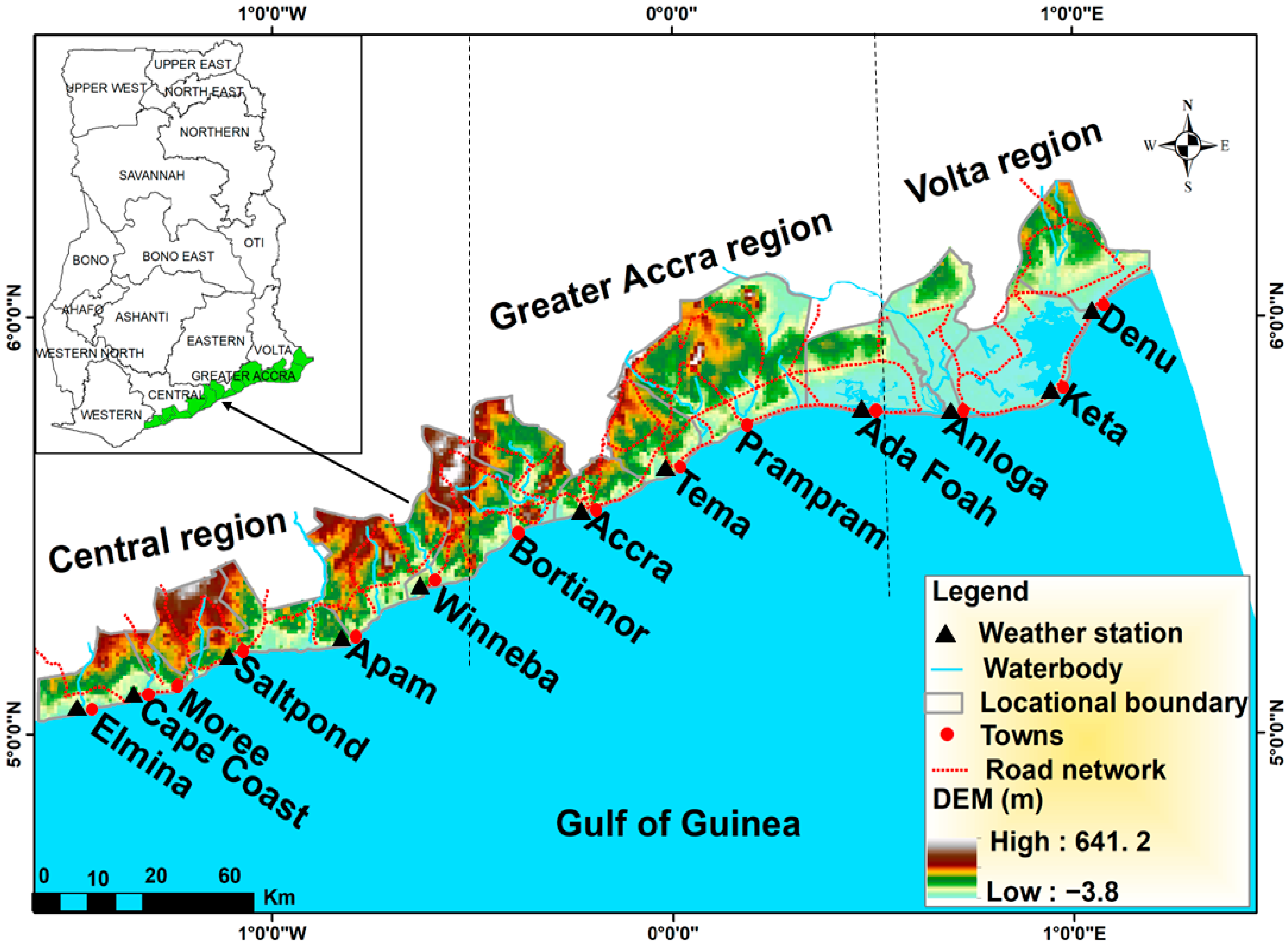
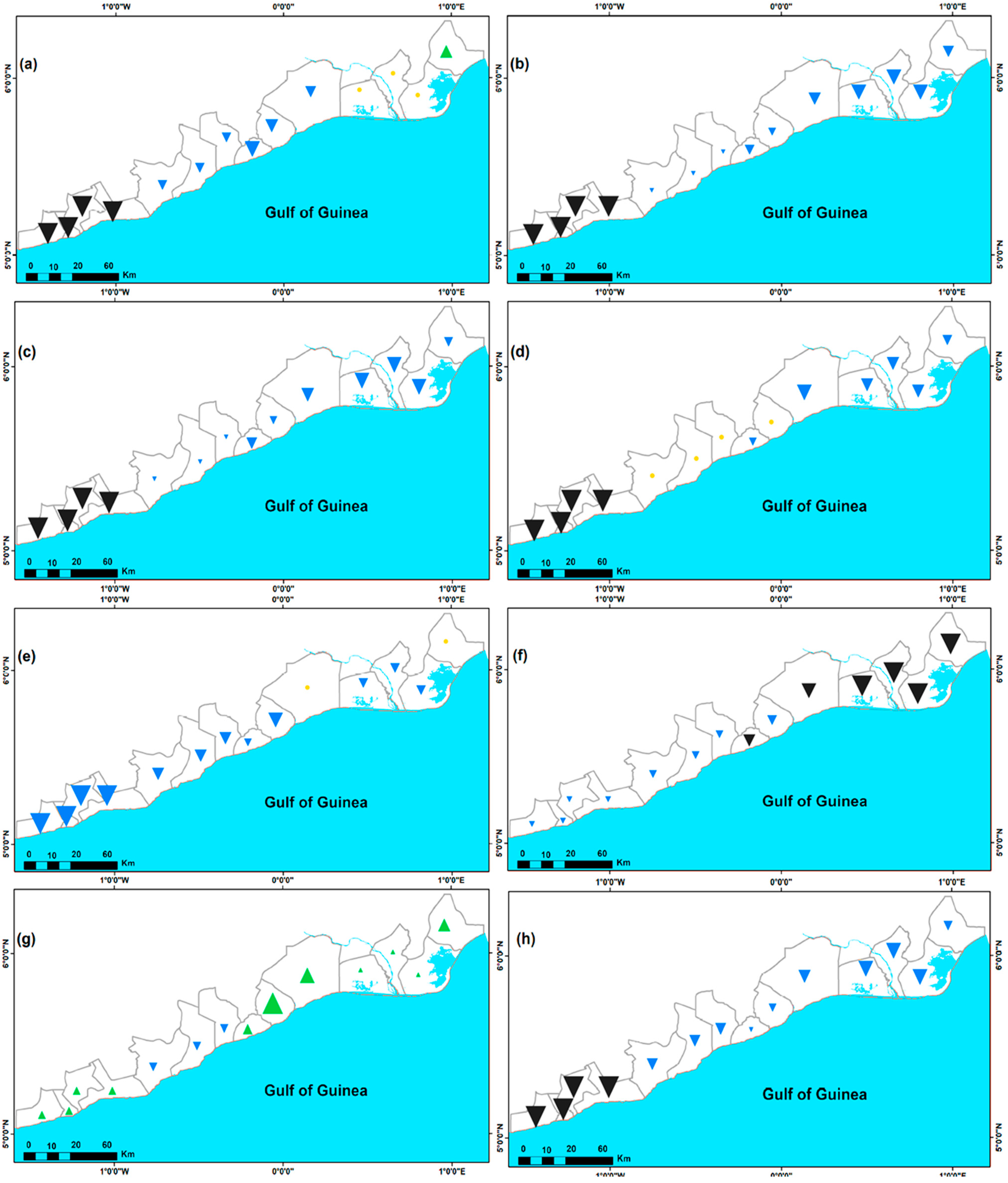

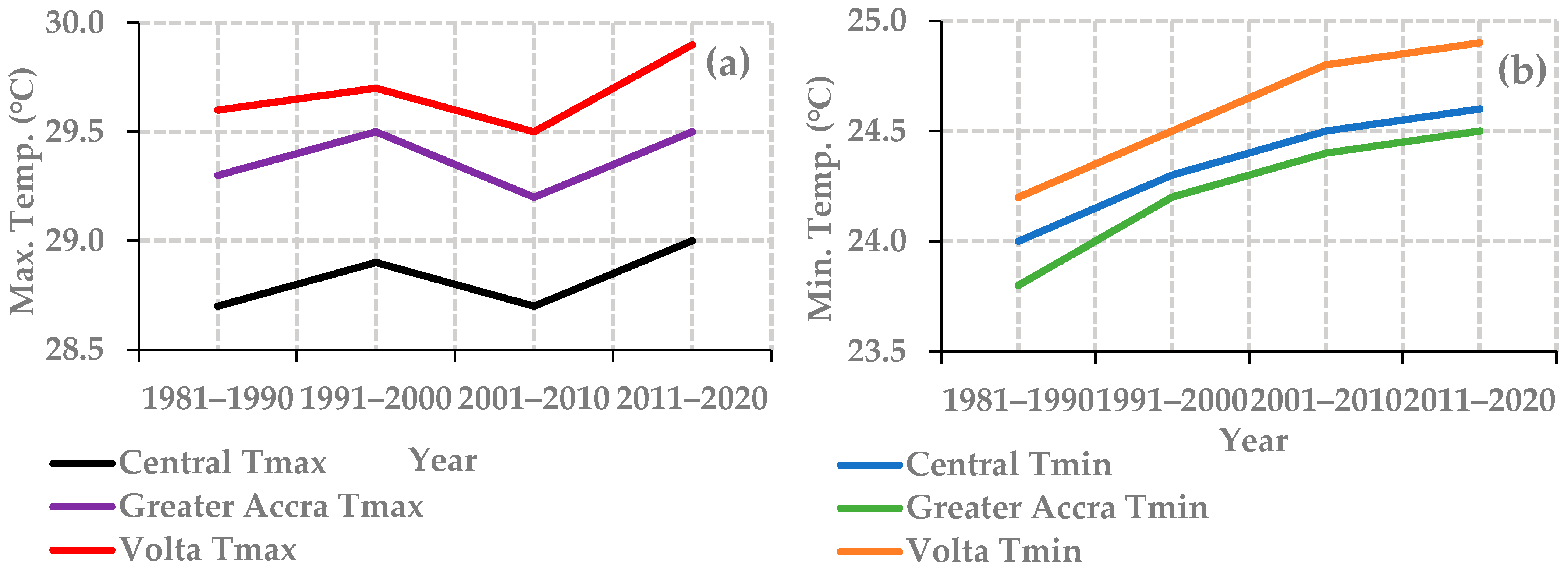
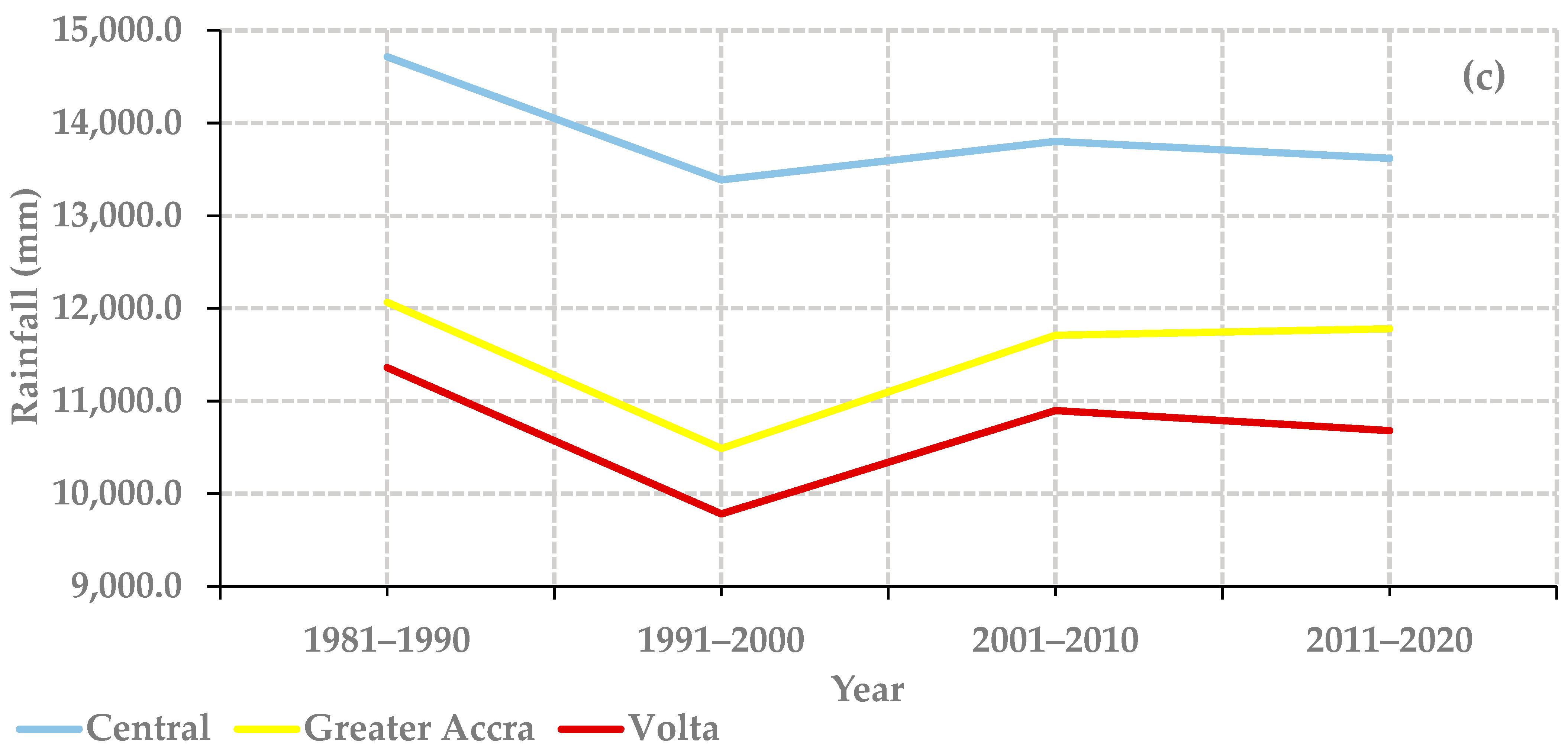
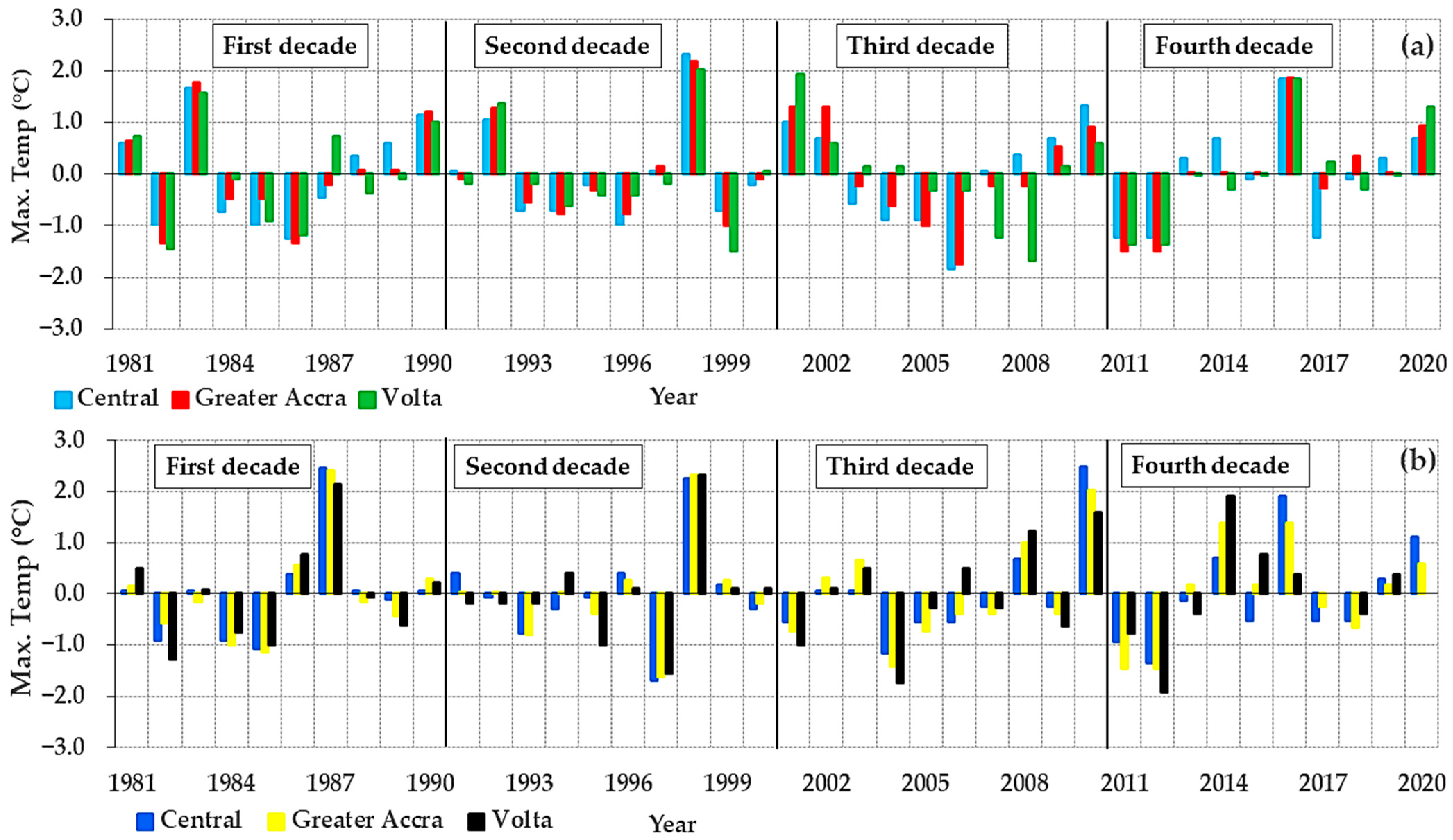





| S/N | Location | Latitude | Longitude | Population |
|---|---|---|---|---|
| 1 | Accra | 5° 60′ N | 0° 18′ W | 1,665,086 |
| 2 | Ada Foah | 5° 46′ N | 0° 37′ E | 71,671 |
| 3 | Anloga | 5° 47′ N | 0° 53′ E | 22,722 |
| 4 | Apam | 5° 17′ N | 0° 44′ W | 135,189 |
| 5 | Bortianor | 5° 30′ N | 0° 20′ W | 32,485 |
| 6 | Cape Coast | 5° 06′ N | 1° 15′ W | 169,894 |
| 7 | Denu | 6° 03′ N | 1° 11′ E | 160,756 |
| 8 | Elmina | 5° 05′ N | 1° 20′ W | 144,705 |
| 9 | Keta | 5° 45′ N | 0° 30′ E | 147,618 |
| 10 | Moree | 5° 07′ N | 1° 12′ W | 117,185 |
| 11 | Prampram | 5° 43′ N | 0° 07′ E | 14,897 |
| 12 | Saltpond | 5° 20′ N | 1° 05′ W | 144,332 |
| 13 | Tema | 5° 44′ N | 0° 01′ E | 402,637 |
| 14 | Winneba | 5° 21′ N | 0° 37′ W | 68,597 |
| Type | Indices | Description | Definition | Units |
|---|---|---|---|---|
| Temperature indices | TR20 | Tropical nights | The annual count of days when daily minimum temperature is greater than 20 °C | Days |
| CSDI | Cold spell duration index | A sequence of 6 or more days where daily minimum temperature is below the 10th percentile | Days | |
| WSDI | Warm spell duration index | A sequence of 6 or more days where daily maximum temperature is exceeds the 90th percentile | Days | |
| SU25 | Summer days | The annual count of days where daily maximum temperature exceeds 25 °C | Days | |
| TNx | Max Tmin | Computes monthly or annual maximum of daily minimum temperature | °C | |
| TNn | Min Tmin | Computes monthly or annual minimum of daily minimum temperature | °C | |
| TN10p | Cool nights | Computes monthly or annual proportion of minimum temperature below 10th percentile | Days | |
| TN90p | Warm nights | Computes monthly or annual proportion of minimum temperature above 90th percentile | Days | |
| TXx | Max Tmax | Computes monthly or annual maximum of daily maximum temperature | °C | |
| TXn | Min Tmax | Computes monthly or annual minimum of daily maximum temperature | °C | |
| TX10p | Cool days | Computes monthly or annual proportion of maximum temperature below 10th percentile | Days | |
| TX90p | Warm days | Computes monthly or annual proportion of maximum temperature above 90th percentile | Days | |
| DTR | Diurnal temperature range | Computes the mean daily diurnal temperature range. The frequency of observation can either be monthly or annual | °C | |
| Precipitation indices | R10 | Number of heavy precipitation days | Computes the annual count of days where daily precipitation is more than 10 mm per day | Days |
| R20 | Number of very heavy precipitation days | Computes the annual count of days where daily precipitation is more than 20 mm per day | Days | |
| SDII | Simple precipitation index | Computes the annual sum of precipitation in wet days (days with precipitation over 1 mm) during the year divided by the number of wet days in the years | mm | |
| CDD | Consecutive dry days | Maximum number of days when precipitation is less than 1 mm | Days | |
| CWD | Consecutive wet days | Maximum number of days when precipitation is more than 1 mm | Days | |
| RX1day | Max 1-day precipitation amount | Computes monthly maximum 1-day precipitation | mm | |
| RX5day | Max 5-day precipitation amount | Computes monthly maximum consecutive 5-day precipitation | mm | |
| R95p | Very wet days | Computes the annual sum of precipitation in days where daily precipitation exceeds the 95th percentile | mm | |
| R99p | Extremely wet days | Computes the annual sum of precipitation in days where daily precipitation exceeds the 99th percentile | mm | |
| PRCPTOT | Annual total wet-day precipitation | Computes the annual sum of precipitation in wet days (days where precipitation is at least 1 mm) | mm |
| CanESM2 | HadCM3 | |||
|---|---|---|---|---|
| No. | Variable | Description | Variable | Description |
| 1 | mslp | Mean sea level pressure | mslp | Mean sea level pressure |
| 2 | p1_f | Surface airflow strength | p_f | Surface airflow strength |
| 3 | p1_u | Surface zonal velocity | p_u | Surface zonal velocity |
| 4 | p1_v | Surface meridional velocity | p_v | Surface meridional velocity |
| 5 | p1_z | Surface velocity | p_z | Surface velocity |
| 6 | p1th | Surface wind direction | p_th | Surface wind direction |
| 7 | p1zh | Surface divergence | p_zh | Surface divergence |
| 8 | p5_f | 500 hPa airflow strength | p5_f | 500 hPa airflow strength |
| 9 | p5_u | 500 hPa zonal velocity | p5_u | 500 hPa velocity |
| 10 | p5_v | 500 hPa meridional velocity | p5_v | 500 hPa meridional velocity |
| 11 | p5_z | 500 hPa vorticity | p5_z | 500 hPa vorticity |
| 12 | p500 | 500 hPa geopotential height | p500 | 500 hPa geopotential height |
| 13 | p5th | 500 hPa wind direction | p5th | Mean sea level pressure |
| 14 | p5zh | 500 hPa divergence | p5_zh | 500 hPa divergence |
| 15 | p8_f | 850 hPa airflow strength | p8_f | 850 hPa airflow strength |
| 16 | p8_u | 850 hPa zonal velocity | p8_u | 850 hPa zonal velocity |
| 17 | p8_v | 850 hPa meridional velocity | p8_v | 850 hPa meridional velocity |
| 18 | p8_z | 850 hPa vorticity | p8_z | 850 hPa vorticity |
| 19 | p850 | 850 hPa geopotential height | p850 | 850 hPa geopotential height |
| 20 | p8th | 850 hPa wind direction | p8th | 850 hPa wind speed |
| 21 | p8zh | 850 hPa divergence | p8zh | 850 hPa divergence |
| 22 | prcp | Precipitation | r500 | Relative humidity at 500 hPa |
| 23 | s500 | Specific humidity at 500 hPa height | r850 | Relative humidity at 850 hPa |
| 24 | s850 | Specific humidity at 850 hPa height | rhum | Near surface relative humidity |
| 25 | shum | Surface specific humidity | Shum | 850 hPa geopotential height |
| 26 | temp | Mean temperature at 2m | temp | Mean temperature |
| Location | Tmax | Changepoints a | Tmin | Changepoints a | Rainfall | Changepoints b |
|---|---|---|---|---|---|---|
| Accra | 0 | − | 3 | 31 December 1981, 31 November 1986, 31 January 1988 | 0 | − |
| Ada Foah | Reference station | |||||
| Anloga | 0 | − | 0 | − | 0 | − |
| Apam | 1 | 31 September 2003 | 1 | 31 November 1986 | 0 | − |
| Bortianor | 1 | 31 September 2003 | 1 | 31 November 1986 | 0 | − |
| Cape Coast | 0 | − | 2 | 31 November 1981, 31 November 1986 | 0 | − |
| Denu | 0 | − | 0 | − | 0 | − |
| Elmina | 0 | − | 2 | 31 November 1981, 31 November 1986 | 0 | − |
| Keta | 0 | − | 0 | − | 0 | − |
| Moree | 0 | − | 2 | 31 November 1981, 31 November 1986 | 0 | − |
| Prampram | 0 | − | 3 | 31 December 1981, 31 November 1986, 31 January 1998 | 0 | − |
| Saltpond | 0 | − | 2 | 31 November 1981, 31 November 1986 | 0 | − |
| Tema | 0 | − | 3 | 31 December 1981, 31 November 1986, 31 January 1988 | 0 | − |
| Winneba | 1 | 31 September 2003 | 1 | 31 November 1986 | 0 | − |
| Locations | SU25 | TR20 | WSDI | CSDI | TXx | TNx | TXn | TNn | TN10p | TX10p | TN90p | TX90p | DTR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Accra | 0.231 | 0.000 | 0.000 | 0.000 | 0.014 | 0.008 | 0.033 | 0.016 | −0.400 | −0.220 | 0.383 | 0.217 | −0.015 |
| Ada Foah | 0.000 | 0.000 | 0.000 | 0.000 | 0.003 | 0.010 | 0.026 | 0.026 | −0.299 | −0.113 | 0.376 | 0.104 | −0.017 |
| Anloga | 0.000 | 0.000 | 0.000 | 0.000 | 0.003 | 0.010 | 0.026 | 0.026 | −0.299 | −0.116 | 0.376 | 0.104 | −0.017 |
| Apam | 0.059 | 0.000 | 0.000 | 0.000 | −0.004 | 0.007 | 0.030 | 0.008 | −0.272 | −0.041 | 0.378 | 0.020 | −0.022 |
| Bortianor | 0.059 | 0.000 | 0.000 | 0.000 | −0.004 | 0.007 | 0.030 | 0.008 | −0.272 | −0.041 | 0.378 | 0.020 | −0.022 |
| Cape Coast | 0.571 | 0.000 | 0.000 | −0.029 | 0.004 | 0.015 | 0.024 | 0.013 | −0.409 | −0.239 | 0.358 | 0.174 | −0.012 |
| Denu | 0.167 | 0.000 | 0.000 | −0.375 | 0.014 | 0.014 | 0.035 | 0.022 | −0.432 | −0.223 | 0.387 | 0.260 | −0.012 |
| Elmina | 0.571 | 0.000 | 0.000 | −0.029 | 0.004 | 0.015 | 0.024 | 0.013 | −0.409 | −0.239 | 0.358 | 0.174 | −0.012 |
| Keta | 0.000 | 0.000 | 0.000 | 0.000 | 0.003 | 0.010 | 0.026 | 0.026 | −0.299 | −0.113 | 0.376 | 0.104 | −0.017 |
| Moree | 0.571 | 0.000 | 0.000 | −0.029 | −0.008 | 0.015 | 0.024 | 0.013 | −0.409 | −0.239 | 0.358 | 0.174 | −0.012 |
| Prampram | 0.053 | 0.056 | 0.000 | 0.000 | 0.008 | 0.013 | 0.032 | 0.022 | −0.284 | −0.037 | 0.399 | 0.058 | −0.023 |
| Saltpond | 0.000 | 0.000 | 0.000 | 0.000 | 0.003 | 0.010 | 0.026 | 0.026 | −0.299 | −0.113 | 0.376 | 0.104 | −0.017 |
| Tema | 0.231 | 0.000 | 0.000 | 0.000 | 0.014 | 0.008 | 0.033 | 0.016 | −0.400 | −0.220 | 0.383 | 0.217 | −0.015 |
| Winneba | 0.059 | 0.000 | 0.000 | 0.000 | −0.004 | 0.007 | 0.030 | 0.008 | −0.272 | −0.041 | 0.378 | 0.020 | −0.022 |
| Central region | 0.290 | 0.000 | 0.000 | −0.167 | 0.003 | 0.011 | 0.030 | 0.014 | −0.335 | −0.146 | 0.383 | 0.117 | −0.016 |
| Greater Accra region | 0.000 | 0.016 | 0.000 | −0.197 | 0.006 | 0.009 | 0.033 | 0.019 | −0.332 | −0.140 | 0.393 | 0.116 | −0.019 |
| Volta region | 0.073 | 0.000 | 0.000 | −0.233 | 0.007 | 0.012 | 0.029 | 0.024 | −0.354 | −0.142 | 0.393 | 0.156 | −0.016 |
| Entire zone (all locations) | 0.176 | 0.006 | 0.000 | −0.195 | 0.005 | 0.011 | 0.032 | 0.018 | −0.346 | −0.169 | 0.388 | 0.127 | −0.018 |
| Locations | RX1day | RX5day | SDII | R10 | R20 | CDD | CWD | R95p | R99p | PRCPTOT |
|---|---|---|---|---|---|---|---|---|---|---|
| Accra | −0.105 | −0.228 | −0.011 | −0.060 | −0.029 | −0.364 | 0.258 | −1.086 | −0.552 | 2.994 |
| Ada Foah | 0.000 | −0.375 | −0.016 | −0.128 | −0.030 | −0.500 | 0.070 | −2.099 | −0.619 | 0.396 |
| Anloga | 0.000 | −0.375 | −0.016 | −0.128 | −0.030 | −0.500 | 0.070 | −2.099 | −0.619 | 0.396 |
| Apam | −0.058 | −0.111 | −0.002 | 0.000 | −0.031 | −0.123 | −0.082 | −1.649 | −0.343 | 2.892 |
| Bortianor | −0.058 | −0.111 | −0.002 | 0.000 | −0.031 | −0.123 | −0.082 | −1.649 | −0.343 | 2.892 |
| Cape Coast | −0.333 | −0.895 | −0.018 | −0.279 | −0.078 | 0.067 | 0.101 | −4.500 | −1.892 | −3.694 |
| Denu | 0.016 | −0.244 | −0.010 | −0.087 | 0.000 | −0.500 | 0.282 | −1.600 | 0.000 | 1.852 |
| Elmina | −0.333 | −0.895 | −0.018 | −0.279 | −0.078 | 0.067 | 0.101 | −4.500 | −1.892 | −3.694 |
| Keta | 0.000 | −0.375 | −0.016 | −0.128 | −0.030 | −0.500 | 0.070 | −2.099 | −0.619 | 0.396 |
| Moree | −0.333 | −0.895 | −0.018 | −0.279 | −0.078 | 0.067 | 0.101 | −4.500 | −1.892 | −3.694 |
| Prampram | −0.086 | −0.250 | −0.014 | −0.164 | 0.000 | −0.378 | 0.308 | −2.000 | −0.679 | 0.542 |
| Saltpond | −0.333 | −0.895 | −0.018 | −0.279 | −0.078 | 0.067 | 0.101 | −4.500 | −1.892 | −3.694 |
| Tema | −0.098 | −0.209 | −0.004 | 0.000 | −0.039 | −0.143 | 0.449 | −1.091 | −1.225 | 2.496 |
| Winneba | −0.058 | −0.111 | −0.002 | 0.000 | −0.031 | −0.123 | −0.082 | −1.649 | −0.343 | 2.892 |
| Central region | −0.248 | −0.724 | −0.013 | −0.222 | −0.082 | 0.000 | −0.044 | −3.967 | −1.521 | −2.049 |
| Greater Accra region | −0.096 | −0.199 | −0.010 | −0.083 | −0.043 | −0.294 | 0.218 | −1.319 | −1.000 | 1.654 |
| Volta region | 0.022 | −0.272 | −0.014 | −0.102 | −0.032 | −0.500 | 0.195 | −1.850 | −1.850 | 1.161 |
| Entire zone (all locations) | −0.127 | −0.496 | −0.026 | −0.163 | −0.077 | −0.214 | 0.104 | −2.759 | −1.439 | −0.758 |
| Central | Greater Accra | Volta | |||||||
|---|---|---|---|---|---|---|---|---|---|
| T Stat | p-Value | Sig. | T Stat | p-Value | Sig. | T Stat | p-Value | Sig. | |
| First- and second-decades Tmax | −3.128 | 0.002 | * | −3.306 | 0.000 | * | −2.328 | 0.002 | * |
| Second- and third-decades Tmax | 4.216 | 2.518 | − | 6.372 | 1.972 | − | 5.055 | 4.404 | − |
| Third- and fourth-decades Tmax | −6.572 | 5.286 | − | −7.966 | 1.890 | − | −9.244 | 3.063 | − |
| First- and second-decades Tmin | −10.176 | 3.662 | − | −10.706 | 1.497 | − | −9.572 | 1.404 | − |
| Second- and third-decades Tmin | −8.544 | 1.554 | − | −7.436 | 1.155 | − | −7.565 | 4.346 | − |
| Third- and fourth-decades Tmin | −2.177 | 0.029 | * | −3.130 | 0.002 | * | −4.111 | 3.976 | − |
| First- and second-decades rainfall | 2.896 | 0.004 | * | 4.189 | 2.835 | − | 0.727 | 0.467 | − |
| Second- and third-decades rainfall | 2.896 | 0.004 | * | −3.713 | 0.000 | * | −3.713 | 0.000 | * |
| Third- and fourth-decades rainfall | 0.471 | 0.638 | − | −0.190 | 0.849 | − | 4.135 | 3.594 | − |
| Predictand | Area | CanESM2 | HadCM3 | |||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | PBIAS | R2 | RMSE | PBIAS | |||
| Tmax | Central region | Calibration | 0.95 | 0.01 | −0.22 | 0.79 | 0.10 | 0.01 |
| Validation | 0.82 | 0.20 | 0.34 | 0.68 | 0.32 | −0.42 | ||
| Greater Accra region | Calibration | 0.99 | 0.22 | 0.11 | 0.99 | 0.33 | 0.23 | |
| Validation | 0.91 | 0.41 | −0.23 | 0.98 | 0.56 | −0.32 | ||
| Volta region | Calibration | 0.99 | 0.02 | 0.02 | 0.99 | 0.11 | 0.01 | |
| Validation | 0.79 | 0.31 | 0.34 | 0.77 | 0.21 | 0.23 | ||
| Entire zone | Calibration | 0.99 | 0.20 | 0.11 | 0.96 | 0.10 | 0.11 | |
| Validation | 0.87 | 0.31 | 0.23 | 0.86 | 0.32 | 0.31 | ||
| Tmin | Central region | Calibration | 0.99 | 0.01 | 0.02 | 0.98 | 0.02 | 0.01 |
| Validation | 0.91 | 0.32 | 0.11 | 0.88 | 0.52 | 0.40 | ||
| Greater Accra region | Calibration | 0.99 | 0.21 | 0.23 | 0.99 | 0.12 | 0.21 | |
| Validation | 0.87 | 0.44 | 1.13 | 0.89 | 0.91 | 0.52 | ||
| Volta region | Calibration | 0.99 | 0.03 | 0.02 | 0.99 | 0.13 | 0.02 | |
| Validation | 0.94 | 0.52 | 0.31 | 0.79 | 0.31 | 0.70 | ||
| Entire zone | Calibration | 0.99 | 0.21 | 0.22 | 0.99 | 0.05 | 0.20 | |
| Validation | 0.91 | 0.42 | 0.31 | 0.89 | 0.23 | 0.61 | ||
| Rainfall | Central region | Calibration | 0.99 | 0.54 | 5.44 | 0.89 | 0.61 | 6.02 |
| Validation | 0.76 | 0.63 | 6.03 | 0.77 | 0.80 | 7.22 | ||
| Greater Accra region | Calibration | 0.95 | 0.82 | 4.01 | 0.89 | 0.81 | 4.41 | |
| Validation | 0.91 | 1.02 | 7.11 | 0.79 | 0.90 | 6.32 | ||
| Volta region | Calibration | 0.92 | 0.42 | 4.12 | 0.88 | 0.40 | 7.01 | |
| Validation | 0.79 | 0.55 | 6.23 | 0.58 | 0.61 | 9.15 | ||
| Entire zone | Calibration | 0.99 | 0.54 | 7.34 | 0.99 | 0.90 | 7.89 | |
| Validation | 0.76 | 0.63 | 10.01 | 0.89 | 0.81 | 11.79 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ankrah, J.; Monteiro, A.; Madureira, H. Extreme Temperature and Rainfall Events and Future Climate Change Projections in the Coastal Savannah Agroecological Zone of Ghana. Atmosphere 2023, 14, 386. https://doi.org/10.3390/atmos14020386
Ankrah J, Monteiro A, Madureira H. Extreme Temperature and Rainfall Events and Future Climate Change Projections in the Coastal Savannah Agroecological Zone of Ghana. Atmosphere. 2023; 14(2):386. https://doi.org/10.3390/atmos14020386
Chicago/Turabian StyleAnkrah, Johnson, Ana Monteiro, and Helena Madureira. 2023. "Extreme Temperature and Rainfall Events and Future Climate Change Projections in the Coastal Savannah Agroecological Zone of Ghana" Atmosphere 14, no. 2: 386. https://doi.org/10.3390/atmos14020386
APA StyleAnkrah, J., Monteiro, A., & Madureira, H. (2023). Extreme Temperature and Rainfall Events and Future Climate Change Projections in the Coastal Savannah Agroecological Zone of Ghana. Atmosphere, 14(2), 386. https://doi.org/10.3390/atmos14020386










