Medium- and Long-Term Wind-Power Forecasts, Considering Regional Similarities
Abstract
:1. Introduction
2. Research Methods
2.1. Data Preprocessing
2.2. Forecast Method
2.2.1. Wind-Power Trend Fitting
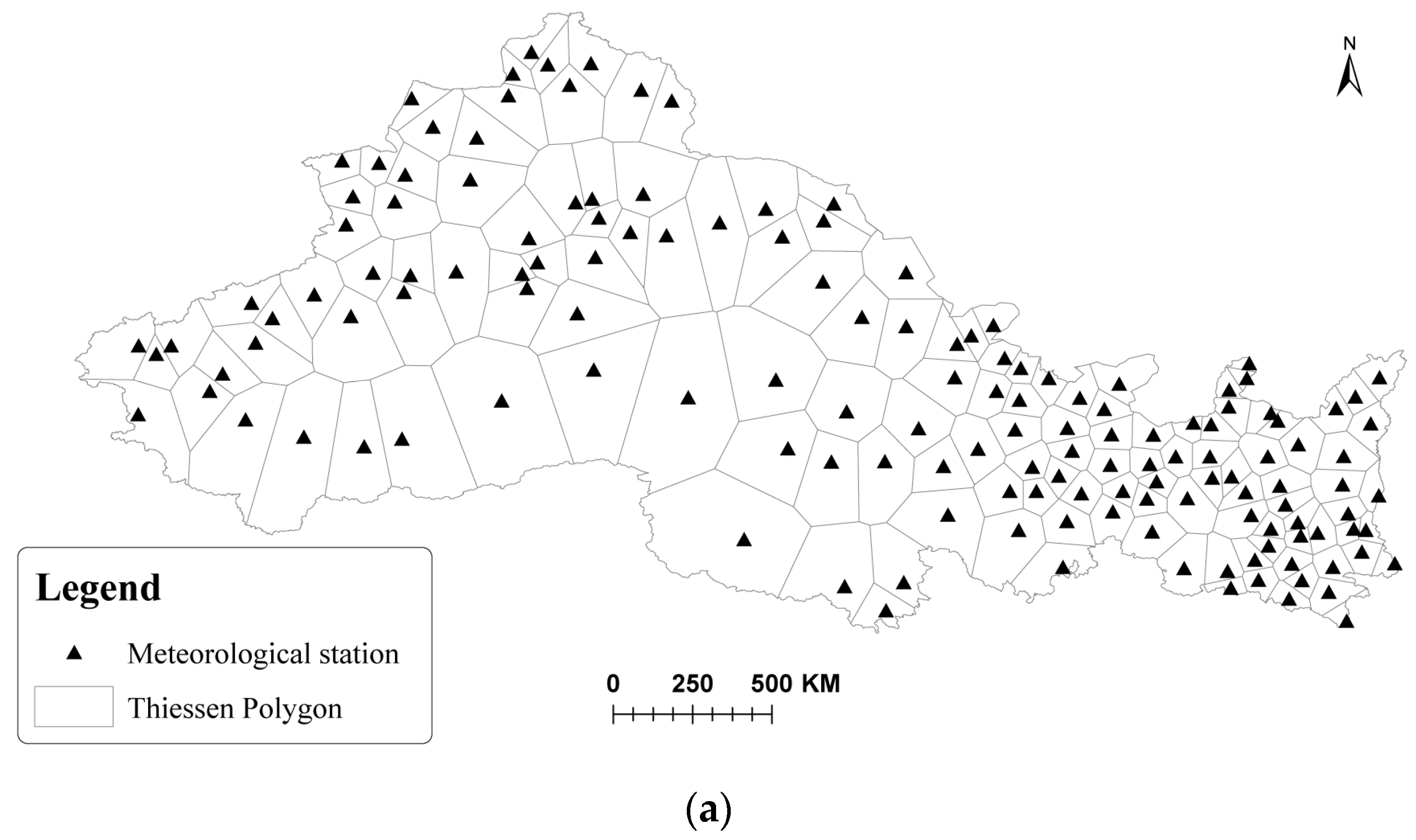
2.2.2. Region-Division Method Based on Regional Similarities
- Analysis of the wind-power process line.
- 2.
- Segmentation of the wind-power process line.
- 3.
- Calculation of the area of trapezoidal column, , and the coordinates of its centroid.
- 4.
- Calculation of the line centroid coordinates of the wind-power process.
- 5.
- Process-line centroid relative-position calculation.
- 6.
- Calculation of the wind-power process-line similar distance.
2.2.3. Long- and Short-Term-Memory Neural Network
3. Results and Analysis
3.1. Effectiveness of Regional Forecasting
3.2. Large-Area Division and Forecasts
3.3. Small-Area Classification and Forecasting
4. Conclusions
- The proposed method was effective. Compared with the single-station forecast, the forecast error was significantly reduced, and the mean value of RMSE was reduced by 20%, on average. The forecast accuracy is improved.
- The approach of area division had a certain impact on the accuracy of the regional forecast, which will be studied in the future.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Han, Z.; Jing, Q.; Zhang, Y.; Bai, R.Q.; Guo, K.M.; Zhang, Y. Review of wind power forecasting methods and new trends. Power Syst. Prot. Control 2019, 47, 178–187. [Google Scholar]
- Zhang, H.Y.; Ding, Y.G.; Liu, M.; Yang, H.Q.; Zhang, B. Numerical simulation of wind energy resources distribution in Hubei province. Meteorol. Environ. Sci. 2008, 138, 35–38. [Google Scholar]
- Peijun, S.; Gangfeng, Z.; Feng, K.; Qian, Y. Wind speed change regionalization in China in 1961–2012. Progress. Inquisitiones Mutat. Clim. 2015, 11, 387–394. [Google Scholar]
- Ding, C.X.; Yan, J.P.; Li, M.M. Climate change and response characteristics to wind speed in northwestern China. Bull. Soil Water Conserv. 2014, 34, 134–137. [Google Scholar]
- Luo, W.; Cui, N.; Zhang, Q.; Feng, Y.; Gong, D.; LV, M. The spatial and temporal characteristics and causes of meteorological factors in Northwest China in recent 50 years. China Rural Water Hydropower 2018, 431, 12–19. [Google Scholar]
- Sun, S.; Dong, C.; Wang, Z.; Jiang, J.; Zhang, Y. Medium- and long-term quantity of electricity forecasting method in wind power considering different wind energy characteristics. High Volt. Eng. 2021, 47, 1224–1233. [Google Scholar]
- Xu, Y. Research of the Methods of Medium- and Long-Term Wind Power Forecasting; Shenyang Institute of Engineering: Shenyang, China, 2017. [Google Scholar]
- Dang, R.; Zhang, J. Wind Power Prediction Based on Auto-regressive and Moving Average Model. J. Anhui Univ. Technol. (Nat. Sci.) 2015, 32, 273–277. [Google Scholar]
- Kusiak, A.; Zhang, Z. Short-horizon prediction of wind power: A data-driven approach. IEEE Trans. Energy Convers. 2010, 25, 1112–1122. [Google Scholar] [CrossRef]
- Abdel-Karim, N.; Small, M.; Ilic, M. Short term wind speed prediction by finite and infinite impulse response filters a state space model representation using discrete markov process. IEEE Buchar. Power Tech. Conf. 2009, 13, 1–8. [Google Scholar]
- Bessa, R.J.; Miranda, V.; Gama, J. Entropy and correntropy against minimum square error in offline and online three-day ahead wind power forecasting. IEEE Trans. Power Syst. 2009, 24, 1657–1666. [Google Scholar] [CrossRef]
- Gao, S.; Dong, L.; Gao, Y.; Liao, X. Medium- and long-term wind speed prediction based on rough set theory. Proc. CSEE 2012, 32, 32–37. [Google Scholar]
- Wang, W.; Liu, H.; Chen, Y.; Zheng, N.; Li, Z.; Ji, X.; Yu, G.; Kang, J. Wind power forecast based on LSTM cyclic neural network. Renew. Energy Resour. 2020, 38, 1187–1191. [Google Scholar]
- Preeti, R.B.; Singh, R.P. Financial and Non-Stationary Time Series Forecasting using LSTM Recurrent Neural Network for Short and Long Horizon. In Proceedings of the 2019 10th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Kanpur, India, 6–8 July 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, Q.; Zhang, S.; Liu, E.; Huang, Y. An Ultra-short-term Wind Power Prediction Method Based on LSTM-XGboost Combination. Sci. Technol. Eng. 2022, 22, 5629–5635. [Google Scholar]
- Han, S.; Qiao, Y.H.; Yan, J.; Liu, Y.Q.; Li, L.; Wang, Z. Mid-to-long term wind and photovoltaic power generation prediction based on copula function and long short term memory network. Appl. Energy 2019, 239, 181–191. [Google Scholar] [CrossRef]
- Zhang, H. Research on Spatial-Temporal Uncertainty Prediction Method of Wind Power; North China Electric Power University: Beijing, China, 2021. [Google Scholar]
- Lu, J.; Wang, Y.; Yang, Y.; He, Z.; Xiang, L.; Li, X. Wind Power Short-term Prediction Based on the Long-term Memory Model the Time Series Analysis Method. Sci. Technol. Eng. 2015, 15, 50–55. [Google Scholar]
- Shan, B.; Li, H.; Gu, R.; Li, L. Short-term Wind Power Combination Prediction Based on Beetle Antennae Search Algorithm. Sci. Technol. Eng. 2022, 22, 540–546. [Google Scholar]
- Li, H. Analysis of the Temporal and Spatial Variation of Wind Shear Index in China; Lanzhou University: Lanzhou, China, 2016. [Google Scholar]
- GB/T 18710-2002; Wind Energy Resource Assessment Method for Wind Farms. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2002.
- DL/T 5240-2010; Technical Regulations for Design and Calculation of Thermal Power Plant Combustion System. GB Electric Standards: Beijing, China, 2010.
- Cao, Y.; Yan, S.; Liu, H.; Guo, L. Short-term wind power forecasting method based on noise-reduction time-series deep learning network. Proc. CSU-EPSA 2020, 32, 145–150. [Google Scholar]
- John, F.E.; Ric, W. Fractal dimension as a market mode sensor. Tech. Anal. Stock. Commod. 2010, 28, 16–20. [Google Scholar]
- Gurrib, I.; Elshareif, E. Optimizing the performance of the fractal adaptive moving average strategy: The case of EUR/USD. Int. J. Econ. Financ. 2016, 8, 171–178. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Mei, Y. Flood Process Similarity Analysis Method and System Based on Centroid Process Line. CN Patent CN201410284732.8, 3 September 2014. [Google Scholar]




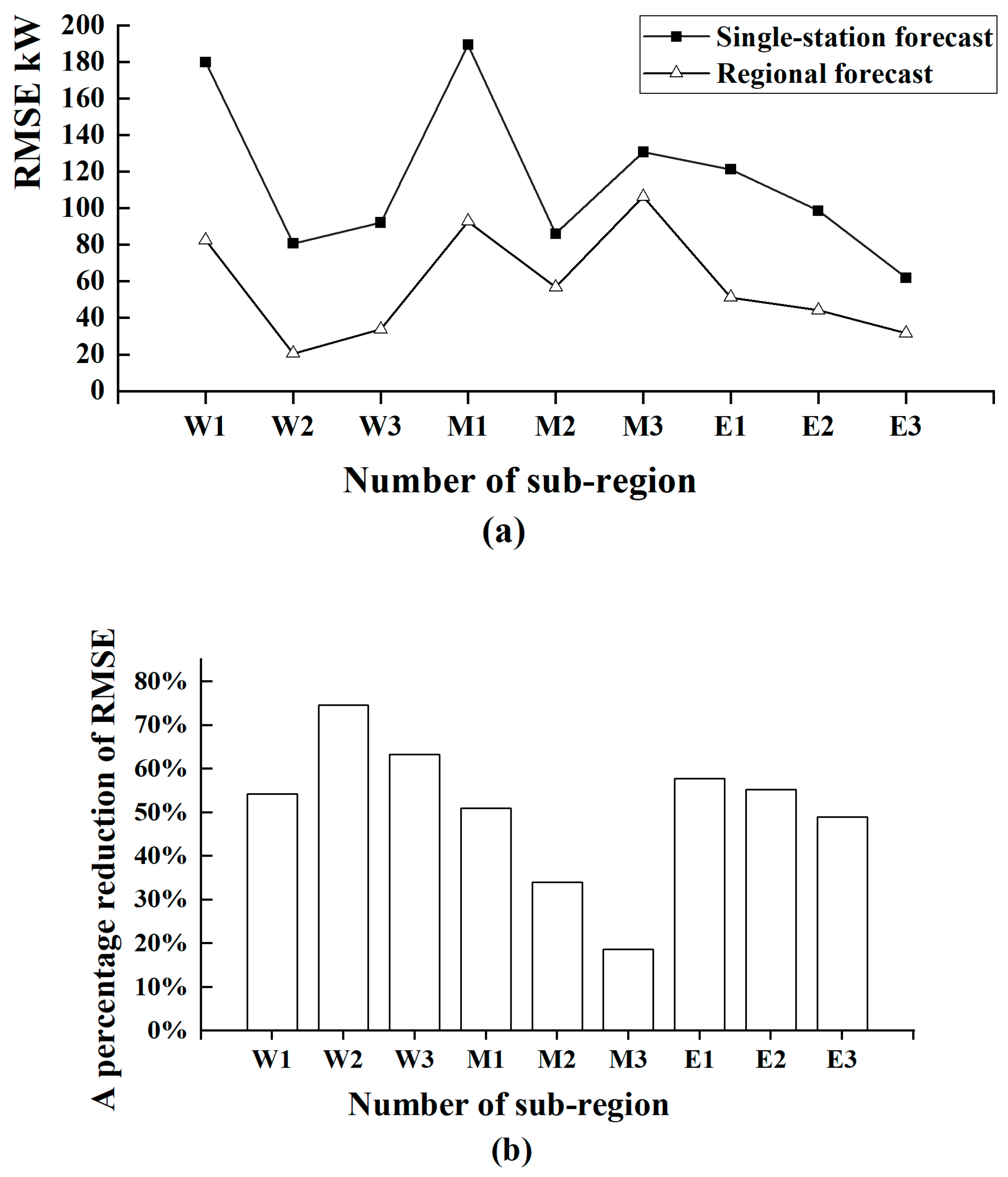

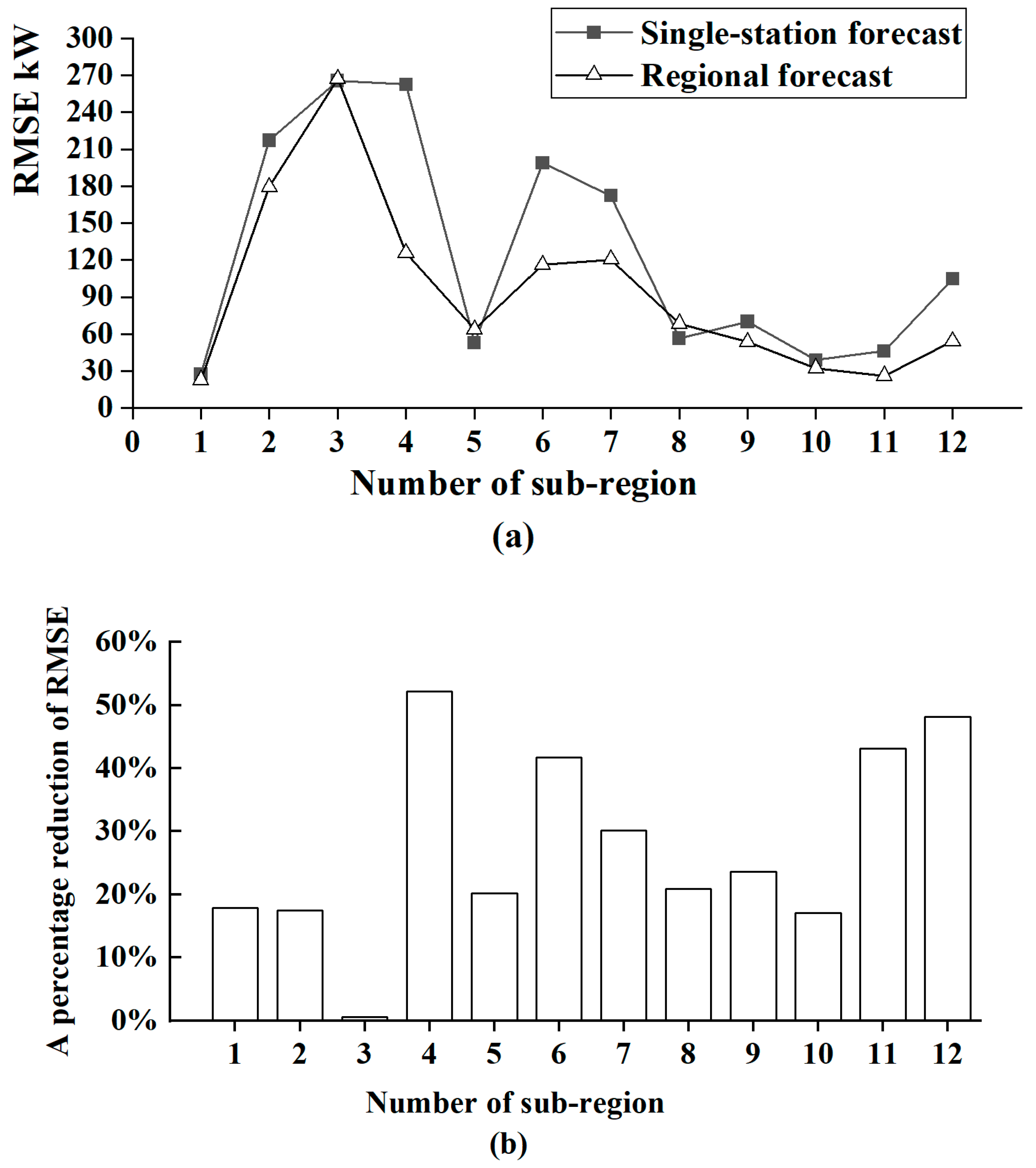
| Station Position | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | Average Value |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Single-station forecast error (kW) | 255 | 314 | 126 | 217 | 073 | 245 | 147 | 362 | 27 | 104 | 110 | 180 |
| Regional forecast error (kW) | 82 | |||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Liu, Y.; Hou, J.; Wang, S.; Yao, H. Medium- and Long-Term Wind-Power Forecasts, Considering Regional Similarities. Atmosphere 2023, 14, 430. https://doi.org/10.3390/atmos14030430
Wang X, Liu Y, Hou J, Wang S, Yao H. Medium- and Long-Term Wind-Power Forecasts, Considering Regional Similarities. Atmosphere. 2023; 14(3):430. https://doi.org/10.3390/atmos14030430
Chicago/Turabian StyleWang, Xianxun, Yaru Liu, Jiachen Hou, Suoping Wang, and Huaming Yao. 2023. "Medium- and Long-Term Wind-Power Forecasts, Considering Regional Similarities" Atmosphere 14, no. 3: 430. https://doi.org/10.3390/atmos14030430
APA StyleWang, X., Liu, Y., Hou, J., Wang, S., & Yao, H. (2023). Medium- and Long-Term Wind-Power Forecasts, Considering Regional Similarities. Atmosphere, 14(3), 430. https://doi.org/10.3390/atmos14030430






