Characteristic Features of the Antarctic Surface Air Temperature with Different Reanalyses and In Situ Observations and Their Uncertainties
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. The CMCA Method
2.3. Spatial Pattern Correlation
2.4. Ratio of Root Mean Square Deviation
2.5. The PCA Method
2.6. Correlation and Regression
3. Results
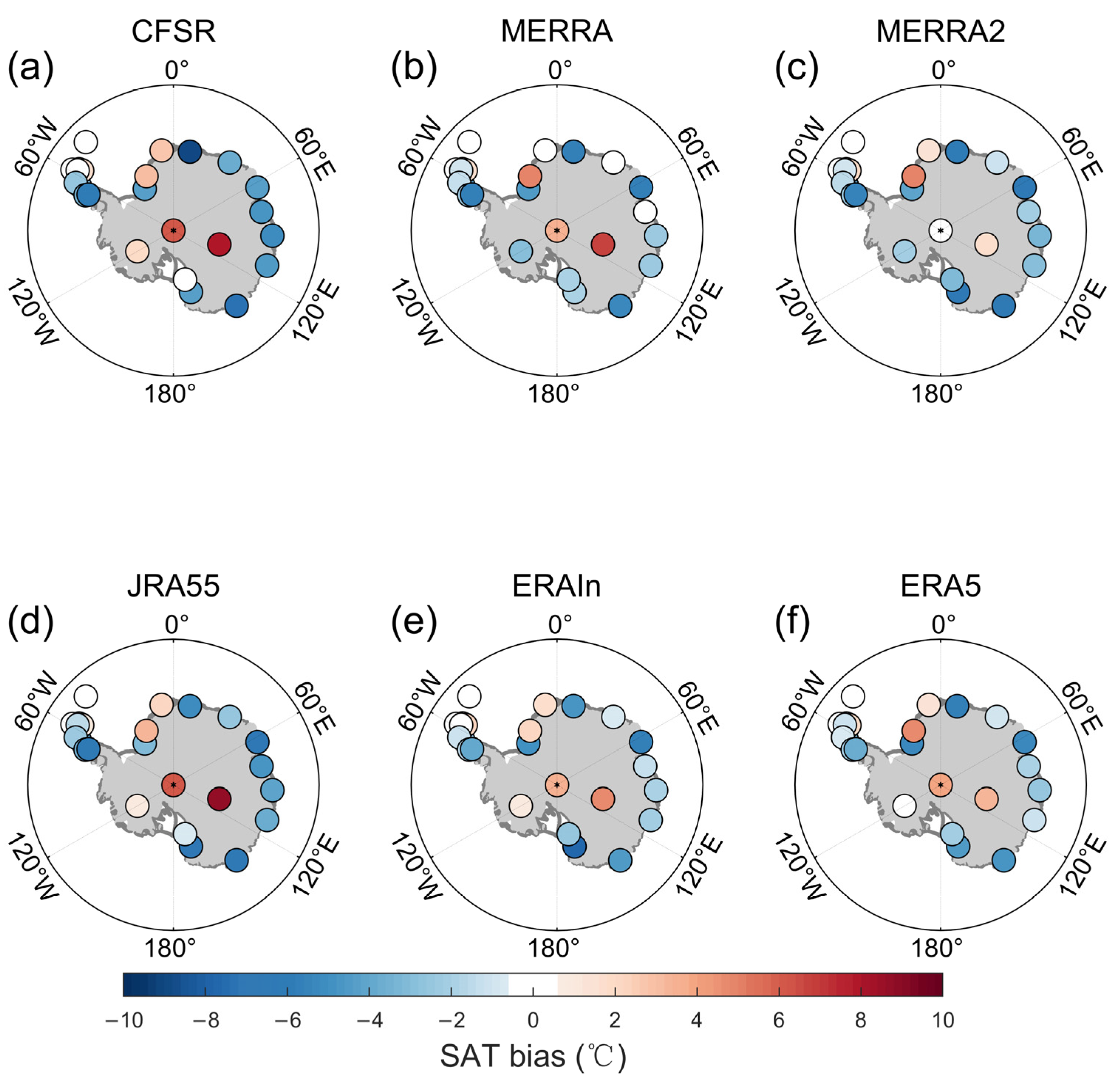
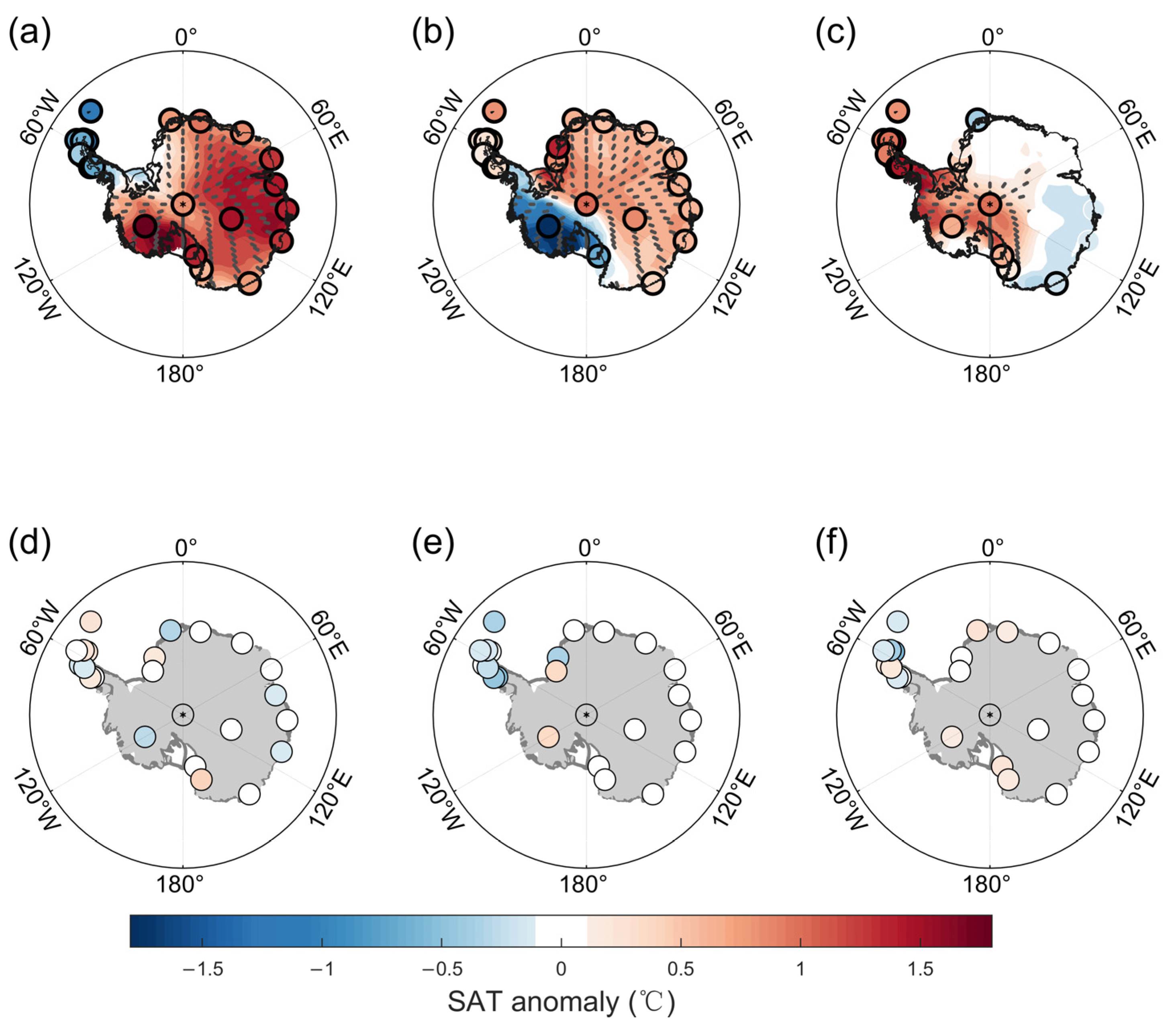
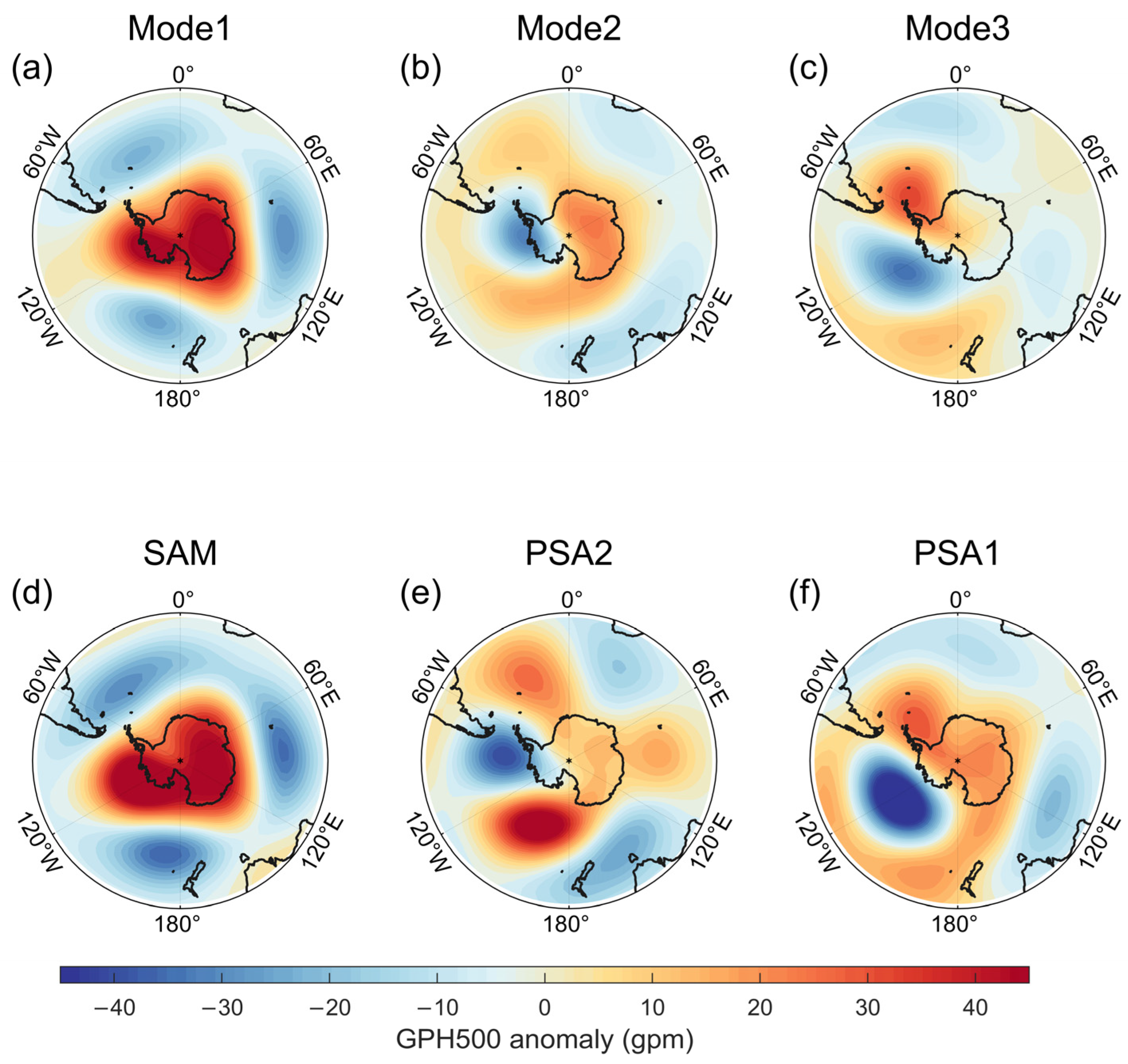
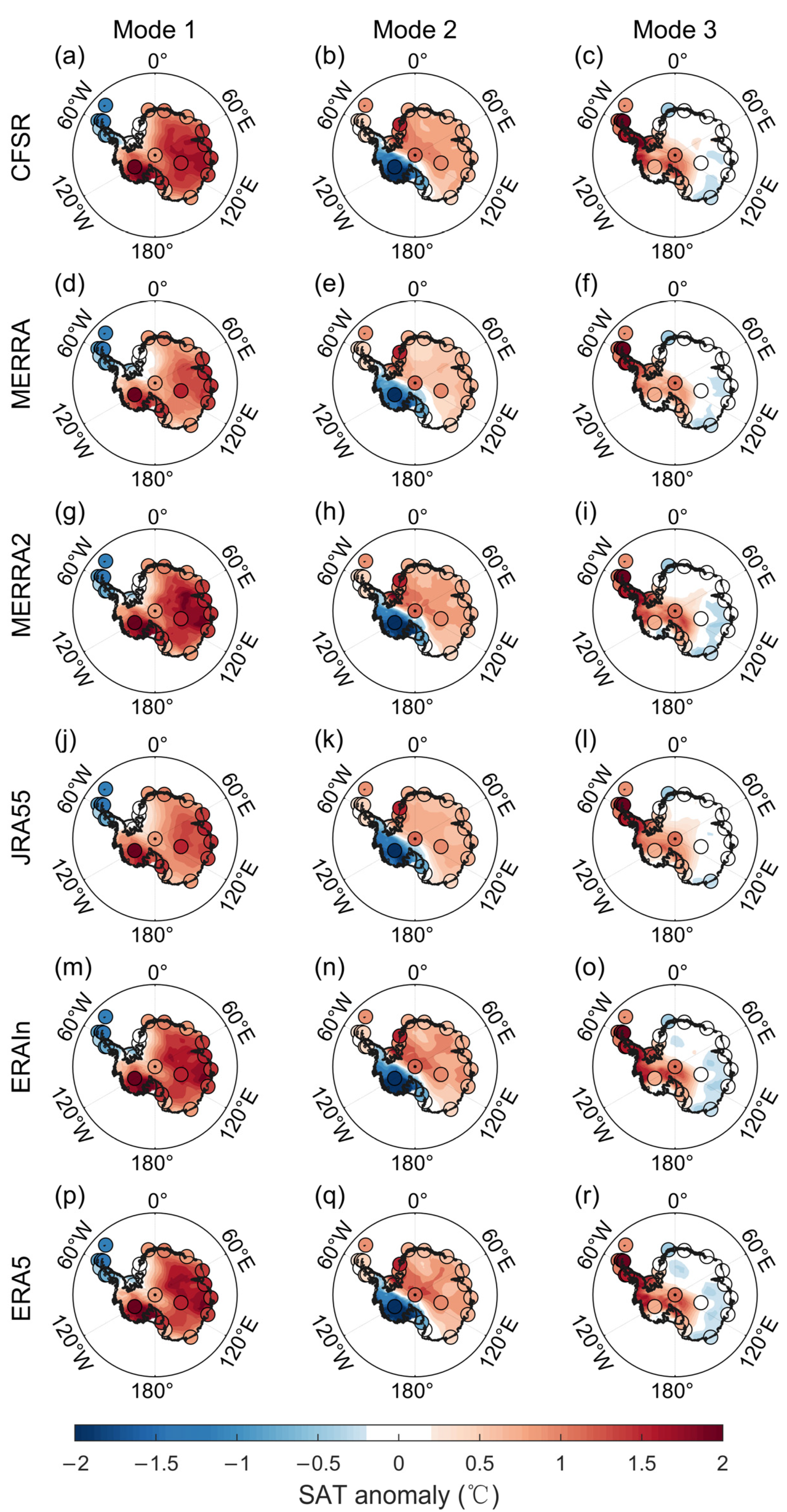
3.1. Coherent SAT Modes in the Reanalyses and In Situ Observations
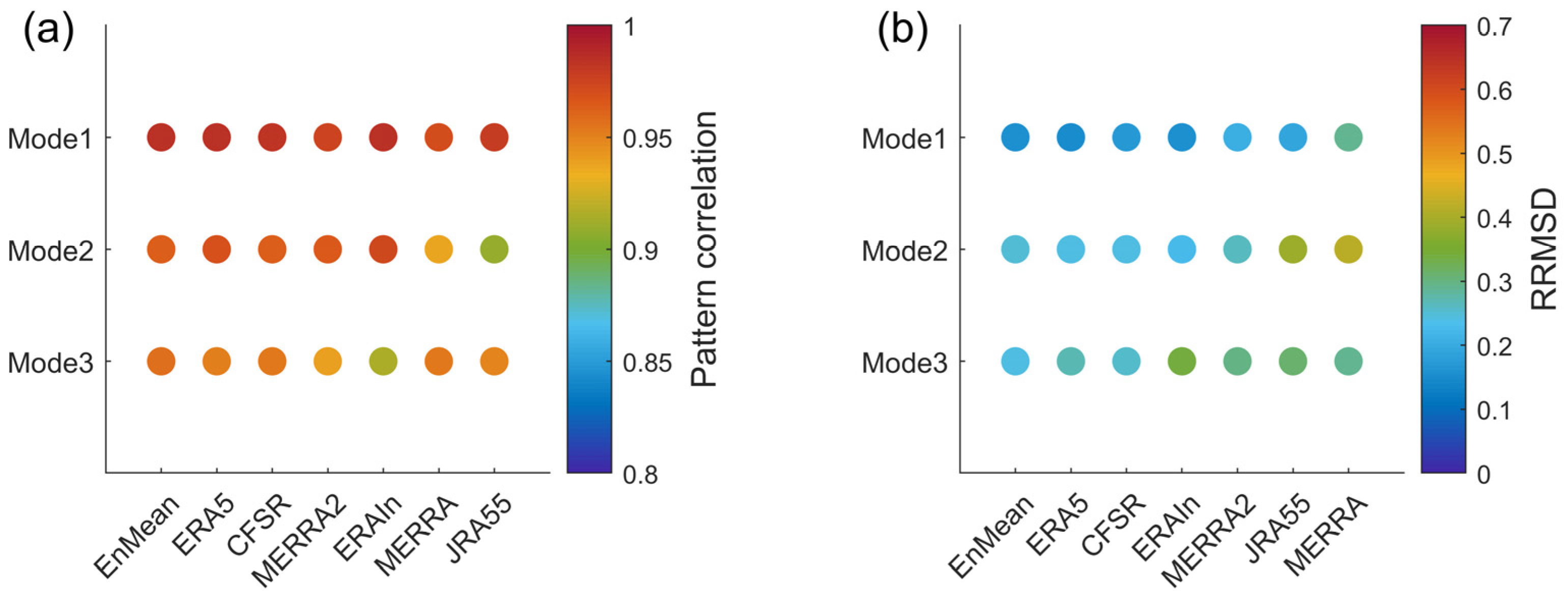
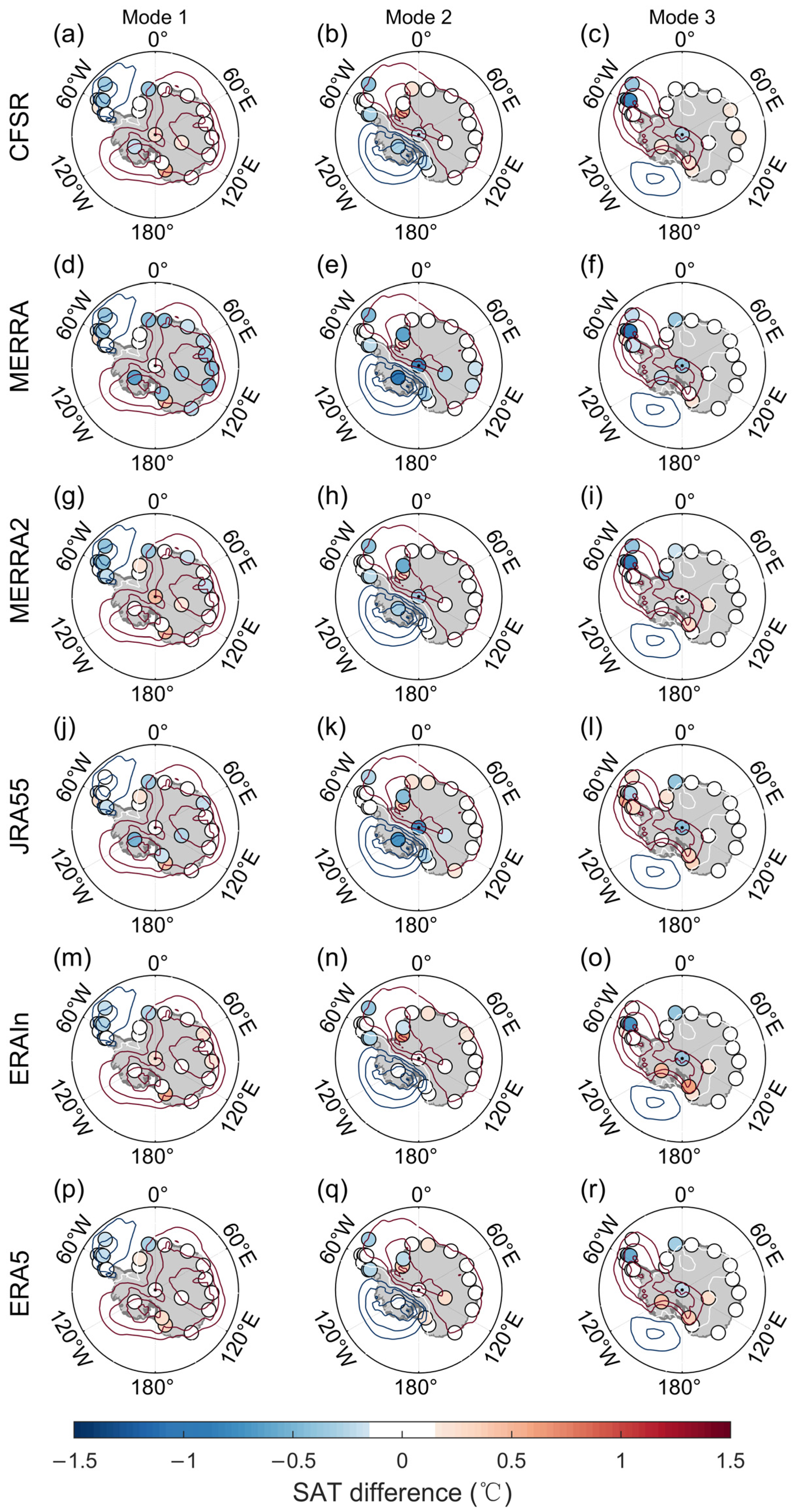
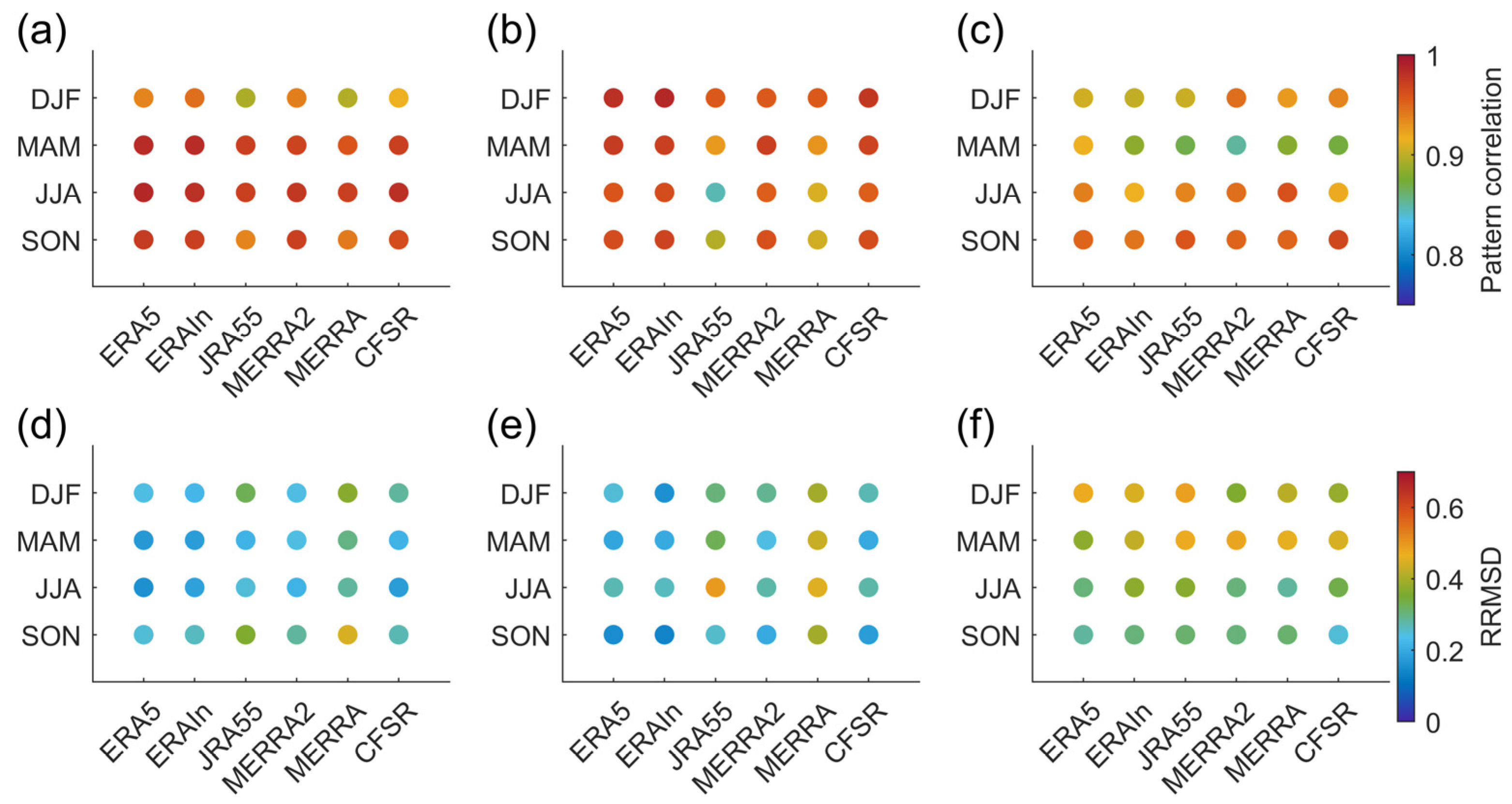
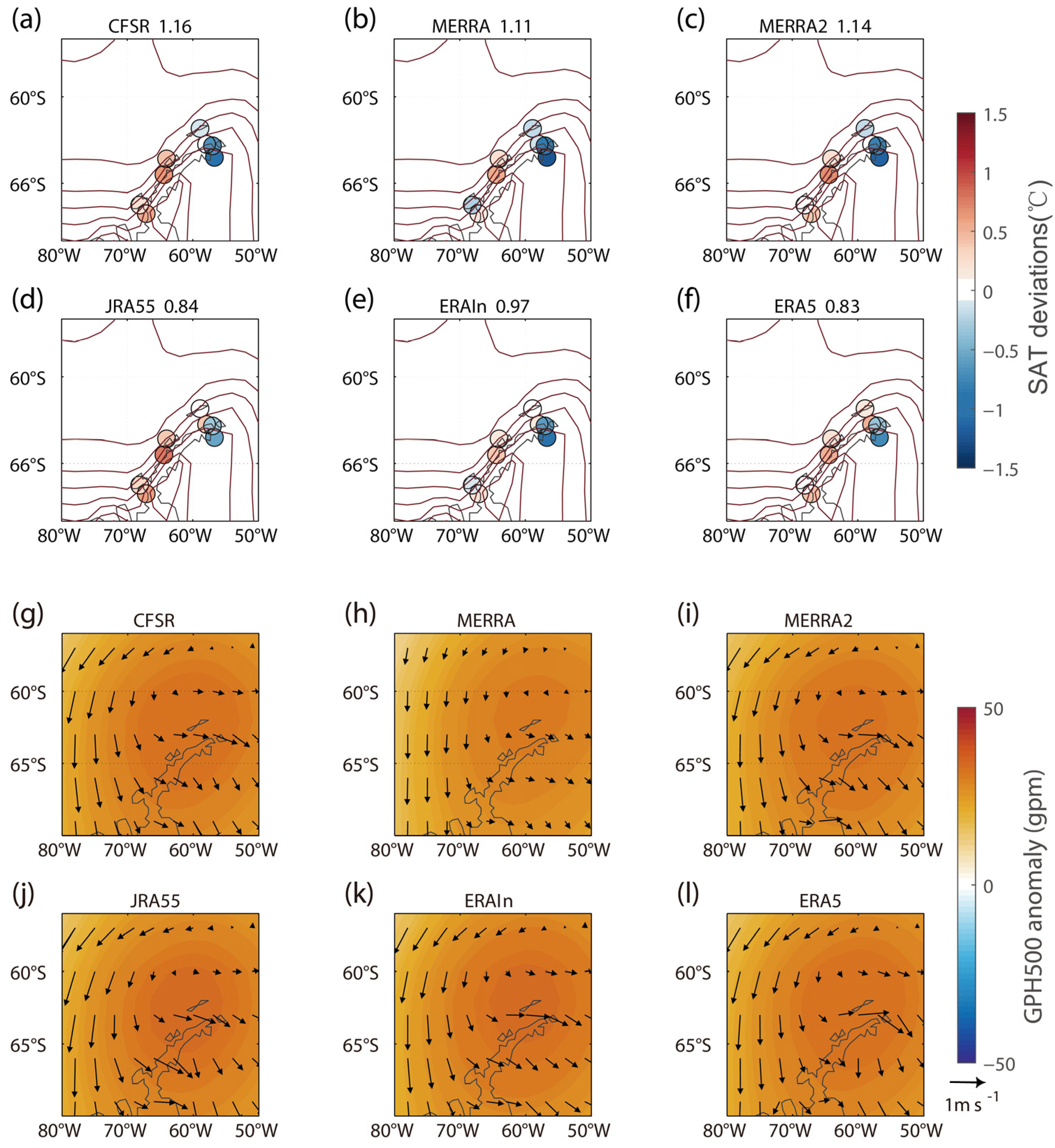
3.2. Diversity of Different Reanalyses According to the Leading CMCA Modes
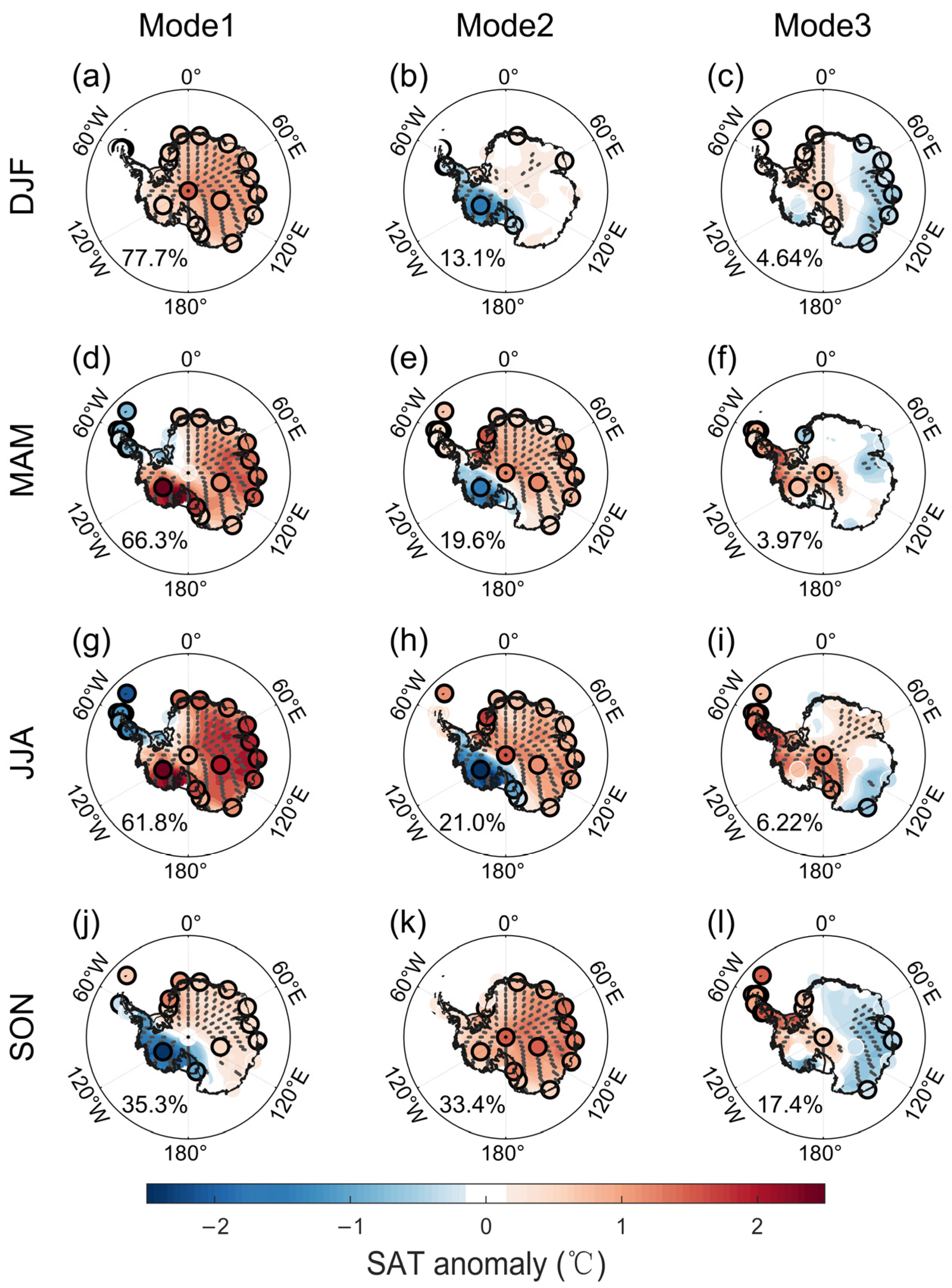
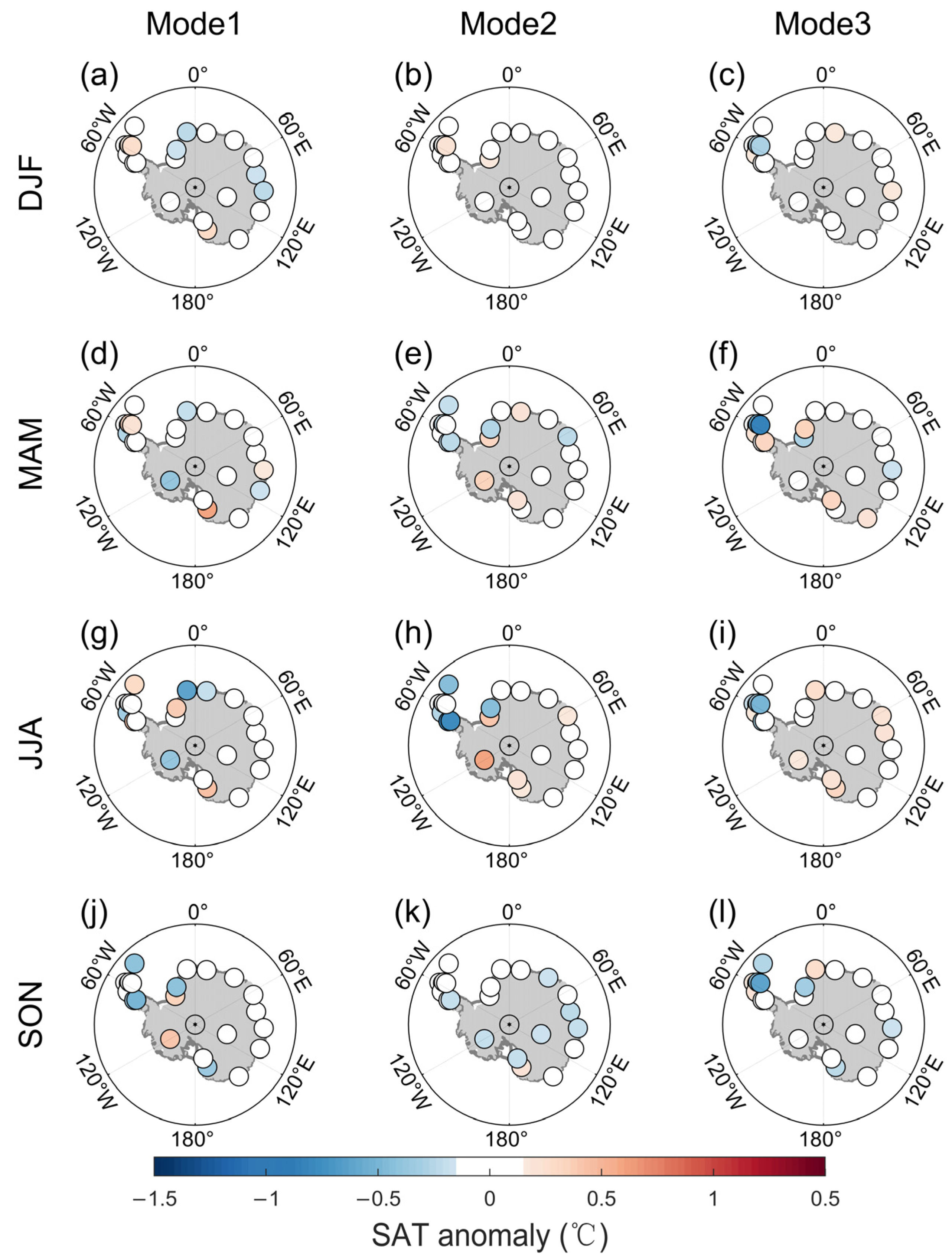
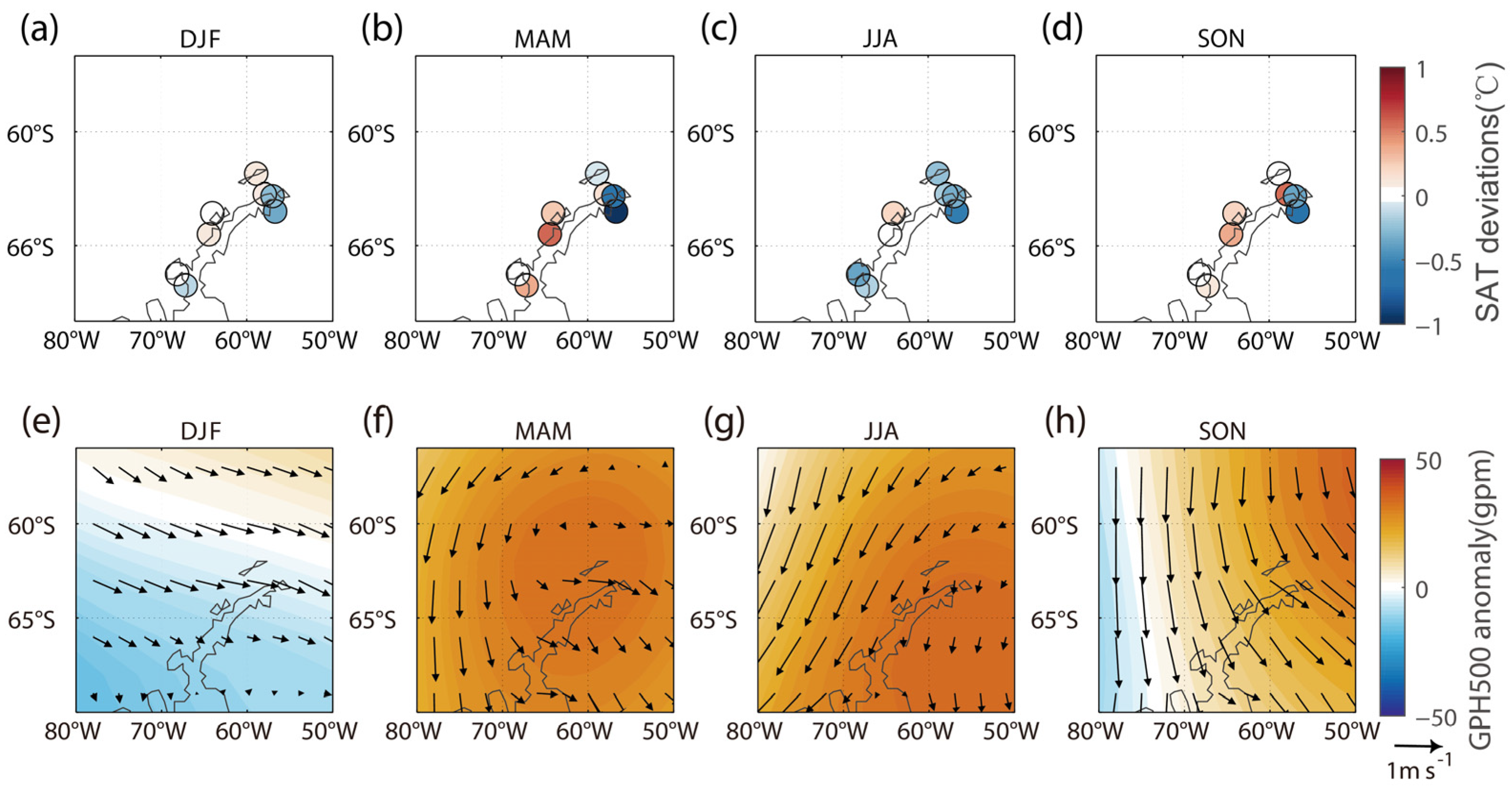
3.3. Seasonality of the CMCA Modes
3.4. The Deviation over the Antarctic Peninsula
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bromwich, D.H.; Nicolas, J.P.; Monaghan, A.J.; Lazzara, M.A.; Keller, L.M.; Weidner, G.A.; Wilson, A.B. Central West Antarctica among the most rapidly warming regions on Earth. Nat. Geosci. 2013, 6, 139–145. [Google Scholar] [CrossRef] [Green Version]
- Clem, K.R.; Fogt, R.L.; Turner, J.; Lintner, B.R.; Marshall, G.J.; Miller, J.R.; Renwick, J.A. Record warming at the South Pole during the past three decades. Nat. Clim. Chang. 2020, 10, 762–770. [Google Scholar] [CrossRef]
- Ding, Q.; Steig, E.J.; Battisti, D.S.; Küttel, M. Winter warming in West Antarctica caused by central tropical Pacific warming. Nat. Geosci. 2011, 4, 398–403. [Google Scholar] [CrossRef] [Green Version]
- Turner, J.; Colwell, S.R.; Marshall, G.J.; Lachlan-Cope, T.A.; Carleton, A.M.; Jones, P.D.; Lagun, V.; Reid, P.A.; Iagovkina, S. Antarctic climate change during the last 50 years. Int. J. Climatol. 2005, 25, 279–294. [Google Scholar] [CrossRef]
- Turner, J.; Lu, H.; White, I.; King, J.C.; Phillips, T.; Hosking, J.S.; Bracegirdle, T.J.; Marshall, G.J.; Mulvaney, R.; Deb, P. Absence of 21st century warming on Antarctic Peninsula consistent with natural variability. Nature 2016, 535, 411–415. [Google Scholar] [CrossRef] [Green Version]
- Nicolas, J.P.; Bromwich, D.H. New reconstruction of Antarctic near-surface temperatures: Multidecadal trends and reliability of global reanalyses. J. Clim. 2014, 27, 8070–8093. [Google Scholar] [CrossRef]
- Stammerjohn, S.E.; Scambos, T.A. Warming reaches the South pole. Nat. Clim. Chang. 2020, 10, 710–711. [Google Scholar] [CrossRef]
- King, J.C.; Bannister, D.; Hosking, J.S.; Colwell, S.R. Causes of the Antarctic region record high temperature at Signy Island, 30th January 1982. Atmos. Sci. Lett. 2017, 18, 491–496. [Google Scholar] [CrossRef] [Green Version]
- Xu, M.; Yu, L.; Liang, K.; Vihma, T.; Bozkurt, D.; Hu, X.; Yang, Q. Dominant role of vertical air flows in the unprecedented warming on the Antarctic Peninsula in February 2020. Commun. Earth Environ. 2021, 2, 133. [Google Scholar] [CrossRef]
- Turner, J.; Marshall, G.J.; Clem, K.; Colwell, S.; Phillips, T.; Lu, H. Antarctic temperature variability and change from station data. Int. J. Climatol. 2019, 40, 2986–3007. [Google Scholar] [CrossRef] [Green Version]
- Bracegirdle, T.J.; Marshall, G.J. The reliability of Antarctic tropospheric pressure and temperature in the latest global reanalyses. J. Clim. 2012, 25, 7138–7146. [Google Scholar] [CrossRef] [Green Version]
- Marshall, G.J. Trends in the Southern Annular Mode from observations and reanalyses. J. Clim. 2003, 16, 4134–4143. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Huai, B.; Ding, M.; Sun, W. Skill of the two 20th century reanalyses in representing Antarctic near-surface air temperature. Int. J. Climatol. 2018, 38, 4225–4238. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, D.; Bunde, A.; Havlin, S. Testing reanalysis data sets in Antarctica: Trends, persistence properties, and trend significance. J. Geophys. Res. Atmos. 2016, 121, 12839–12855. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wang, M.; Zhao, J. A comparison of MODIS LST retrievals with in situ observations from AWS over the Lambert Glacier Basin, East Antarctica. Int. J. Geosci. 2013, 4, 611–617. [Google Scholar] [CrossRef] [Green Version]
- Mo, K.C. Relationships between low-frequency variability in the Southern Hemisphere and sea surface temperature anomalies. J. Clim. 2000, 13, 3599–3610. [Google Scholar] [CrossRef]
- Arblaster, J.M.; Meehl, G.A. Contributions of external forcings to southern annular mode trends. J. Clim. 2006, 19, 2896–2905. [Google Scholar] [CrossRef]
- Hahn, L.C.; Armour, K.C.; Battisti, D.S.; Donohoe, A.; Pauling, A.; Bitz, C. Antarctic elevation drives hemispheric asymmetry in polar lapse rate climatology and feedback. Geophys. Res. Lett. 2020, 47, e2020GL088965. [Google Scholar] [CrossRef]
- Li, X.; Cai, W.; Meehl, G.A.; Chen, D.; Yuan, X.; Raphael, M.; Holland, D.M.; Ding, Q.; Fogt, R.L.; Markle, B.R. Tropical teleconnection impacts on Antarctic climate changes. Nat. Rev. Earth Environ. 2021, 2, 680–698. [Google Scholar] [CrossRef]
- Li, X.; Xie, S.-P.; Gille, S.T.; Yoo, C. Atlantic-induced pan-tropical climate change over the past three decades. Nat. Clim. Chang. 2016, 6, 275–279. [Google Scholar] [CrossRef] [Green Version]
- Goosse, H.; Zunz, V. Decadal trends in the Antarctic sea ice extent ultimately controlled by ice-ocean feedback. Cryosphere 2014, 8, 453–470. [Google Scholar] [CrossRef] [Green Version]
- Meehl, G.A.; Arblaster, J.M.; Chung, C.T.; Holland, M.M.; DuVivier, A.; Thompson, L.; Yang, D.; Bitz, C.M. Sustained ocean changes contributed to sudden Antarctic sea ice retreat in late 2016. Nat. Commun. 2019, 10, 14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thompson, D.W.; Solomon, S. Interpretation of recent Southern Hemisphere climate change. Science 2002, 296, 895–899. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thompson, D.W.; Solomon, S.; Kushner, P.J.; England, M.H.; Grise, K.M.; Karoly, D.J. Signatures of the Antarctic ozone hole in Southern Hemisphere surface climate change. Nat. Geosci. 2011, 4, 741–749. [Google Scholar] [CrossRef]
- Ding, Q.; Steig, E.J. Temperature change on the Antarctic Peninsula linked to the tropical Pacific. J. Clim. 2013, 26, 7570–7585. [Google Scholar] [CrossRef]
- Li, X.; Holland, D.M.; Gerber, E.P.; Yoo, C. Impacts of the north and tropical Atlantic Ocean on the Antarctic Peninsula and sea ice. Nature 2014, 505, 538–542. [Google Scholar] [CrossRef]
- Simpkins, G.R.; McGregor, S.; Taschetto, A.S.; Ciasto, L.M.; England, M.H. Tropical connections to climatic change in the extratropical Southern Hemisphere: The role of Atlantic SST trends. J. Clim. 2014, 27, 4923–4936. [Google Scholar] [CrossRef] [Green Version]
- Clem, K.R.; Fogt, R.L. Varying roles of ENSO and SAM on the Antarctic Peninsula climate in austral spring. J. Geophys. Res. Atmos. 2013, 118, 11481–11492. [Google Scholar] [CrossRef]
- Li, X.; Gerber, E.P.; Holland, D.M.; Yoo, C. A Rossby wave bridge from the tropical Atlantic to West Antarctica. J. Clim. 2015, 28, 2256–2273. [Google Scholar] [CrossRef]
- Yuan, X.; Martinson, D.G. The Antarctic dipole and its predictability. Geophys. Res. Lett. 2001, 28, 3609–3612. [Google Scholar] [CrossRef] [Green Version]
- Jun, S.-Y.; Kim, J.-H.; Choi, J.; Kim, S.-J.; Kim, B.-M.; An, S.-I. The internal origin of the west-east asymmetry of Antarctic climate change. Sci. Adv. 2020, 6, eaaz1490. [Google Scholar] [CrossRef]
- Li, J.; Carlson, B.; Lacis, A. Application of spectral analysis techniques to the intercomparison of aerosol data–Part 4: Synthesized analysis of multisensor satellite and ground-based AOD measurements using combined maximum covariance analysis. Atmos. Meas. Tech. 2014, 7, 2531–2549. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Pan, H.-L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D. The NCEP climate forecast system reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1058. [Google Scholar] [CrossRef] [Green Version]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.-T.; Chuang, H.-y.; Iredell, M. The NCEP climate forecast system version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.-K. MERRA: NASA’s modern-era retrospective analysis for research and applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R. The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H. The JRA-55 reanalysis: General specifications and basic characteristics. J. Meteorol. Soc. Jpn. Ser. II 2015, 93, 5–48. [Google Scholar] [CrossRef] [Green Version]
- Dee, D.P.; Uppala, S.M.; Simmons, A.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.; Balsamo, G.; Bauer, d.P. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Turner, J.; Colwell, S.R.; Marshall, G.J.; Lachlan-Cope, T.A.; Carleton, A.M.; Jones, P.D.; Lagun, V.; Reid, P.A.; Iagovkina, S. The SCAR READER project: Toward a high-quality database of mean Antarctic meteorological observations. J. Clim. 2004, 17, 2890–2898. [Google Scholar] [CrossRef]
- Ding, H.; Greatbatch, R.J.; Gollan, G. Tropical influence independent of ENSO on the austral summer Southern Annular Mode. Geophys. Res. Lett. 2014, 41, 3643–3648. [Google Scholar] [CrossRef] [Green Version]
- O’Kane, T.J.; Monselesan, D.P.; Risbey, J.S. A multiscale reexamination of the Pacific–South American pattern. Mon. Weather Rev. 2017, 145, 379–402. [Google Scholar] [CrossRef]
- Clem, K.R.; Renwick, J.A.; McGregor, J. Large-scale forcing of the Amundsen Sea Low and its influence on sea ice and West Antarctic temperature. J. Clim. 2017, 30, 8405–8424. [Google Scholar] [CrossRef]
- Gossart, A.; Helsen, S.; Lenaerts, J.; Broucke, S.V.; Van Lipzig, N.; Souverijns, N. An evaluation of surface climatology in state-of-the-art reanalyses over the Antarctic Ice Sheet. J. Clim. 2019, 32, 6899–6915. [Google Scholar] [CrossRef]
- Cape, M.; Vernet, M.; Skvarca, P.; Marinsek, S.; Scambos, T.; Domack, E. Foehn winds link climate-driven warming to ice shelf evolution in Antarctica. J. Geophys. Res. Atmos. 2015, 120, 11037–11057. [Google Scholar] [CrossRef] [Green Version]
- Grosvenor, D.; King, J.; Choularton, T.; Lachlan-Cope, T. Downslope föhn winds over the Antarctic Peninsula and their effect on the Larsen ice shelves. Atmos. Chem. Phys. 2014, 14, 9481–9509. [Google Scholar] [CrossRef] [Green Version]
- Kirchgaessner, A.; King, J.C.; Anderson, P.S. The impact of Föhn conditions across the Antarctic Peninsula on local meteorology based on AWS measurements. J. Geophys. Res. Atmos. 2021, 126, e2020JD033748. [Google Scholar] [CrossRef]
| Number | Name | Latitude | Longitude | Elevation (m) | Period |
|---|---|---|---|---|---|
| 1 | Amundsen–Scott | −90 | 0 | 2835 | 1979–2020 |
| 2 | Belgrano II | −77.9 | 325.4 | 256 | 1980–2001, 2005, 2007, 2009–2020 |
| 3 | Bellingshausen | −62.2 | 301.1 | 16 | 1979–2020 |
| 4 | Byrd | −80 | 240 | 1515 | 1979–2020 |
| 5 | Casey | −66.3 | 110.5 | 42 | 1979–2020 |
| 6 | Davis | −68.6 | 78 | 13 | 1979–2020 |
| 7 | Dumont D’Urville | −66.7 | 140 | 43 | 1979–2020 |
| 8 | Esperanza | −63.4 | 303 | 13 | 1979–2020 |
| 9 | Faraday Vernadsky | −65.4 | 295.6 | 11 | 1979–2020 |
| 10 | Halley | −75.5 | 333.6 | 30 | 1979–2020 |
| 11 | Marambio | −64.2 | 303.3 | 198 | 1979–2020 |
| 12 | Mario Zucchelli | −74.7 | 164.1 | 92 | 1988–2005, 2008–2019 |
| 13 | Marsh | −62.2 | 301.1 | 10 | 1979–2020 |
| 14 | Mawson | −67.6 | 62.9 | 16 | 1979–2020 |
| 15 | McMurdo | −77.9 | 166.7 | 24 | 1979–2020 |
| 16 | Mirny | −66.5 | 93 | 30 | 1979–2020 |
| 17 | Neumayer | −70.7 | 351.6 | 50 | 1982–2020 |
| 18 | Novolazarevskaya | −70.8 | 11.8 | 119 | 1979–2020 |
| 19 | O’Higgins | −63.3 | 302.1 | 10 | 1979–2020 |
| 20 | Orcadas | −60.7 | 315.3 | 6 | 1979–2002,2004–2020 |
| 21 | Palmer | −64.3 | 296 | 8 | 1981–2020 |
| 22 | Rothera | −67.5 | 291.9 | 32 | 1979–2020 |
| 23 | San Martin | −68.1 | 292.9 | 4 | 1979–2002, 2005–2020 |
| 24 | Scott Base | −77.9 | 166.7 | 16 | 1979–2018 |
| 25 | Syowa | −69 | 39.6 | 21 | 1979–2020 |
| 26 | Vostok | −78.5 | 106.9 | 3490 | 1979–1995, 1997–2020 |
| SAM | PSA1 | PSA2 | |
|---|---|---|---|
| Mode1 (58.0%) | 0.80 | 0.19 | −0.16 |
| Mode2 (24.5%) | −0.02 | 0.20 | 0.55 |
| Mode3 (7.8%) | −0.25 | 0.62 | −0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, M.; Li, X.; Zhu, J.; Song, C.; Zhou, Y.; Wang, W.; Hou, Y. Characteristic Features of the Antarctic Surface Air Temperature with Different Reanalyses and In Situ Observations and Their Uncertainties. Atmosphere 2023, 14, 464. https://doi.org/10.3390/atmos14030464
Xin M, Li X, Zhu J, Song C, Zhou Y, Wang W, Hou Y. Characteristic Features of the Antarctic Surface Air Temperature with Different Reanalyses and In Situ Observations and Their Uncertainties. Atmosphere. 2023; 14(3):464. https://doi.org/10.3390/atmos14030464
Chicago/Turabian StyleXin, Meijiao, Xichen Li, Jiang Zhu, Chentao Song, Yi Zhou, Wenzhu Wang, and Yurong Hou. 2023. "Characteristic Features of the Antarctic Surface Air Temperature with Different Reanalyses and In Situ Observations and Their Uncertainties" Atmosphere 14, no. 3: 464. https://doi.org/10.3390/atmos14030464




