Possible Pre-Seismic Indications Prior to Strong Earthquakes That Occurred in Southeastern Mediterranean as Observed Simultaneously by Three VLF/LF Stations Installed in Athens (Greece)
Abstract
1. Introduction
2. Sub-Ionospheric Propagation Data, Studied EQs, and Other Non-Examined Extreme Events
3. Methods
3.1. Nighttime Fluctuation Method (NFM)
3.2. Terminator Time Method (TTM)
3.3. Natural Time (NT) Method
3.4. Wavelet Analysis
3.5. Long Wavelength Propagation Capability
4. Analysis of the Lower Ionosphere Prior to “2021 Crete EQs” and “2022 Cyprus EQ”
4.1. NFM Analysis Results
4.2. Diurnal Variation and TTM Analysis Results
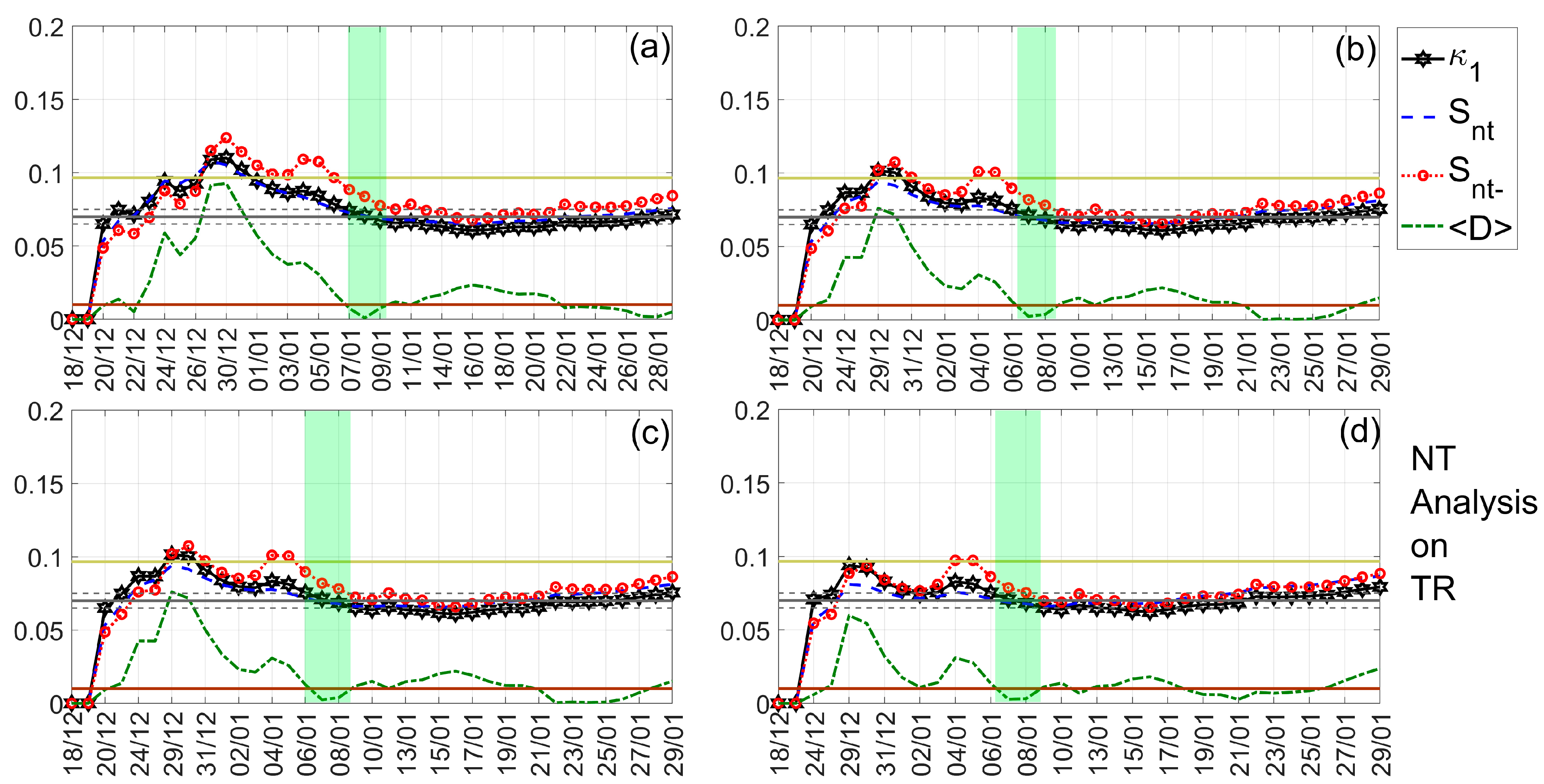
4.3. NT Analysis Results
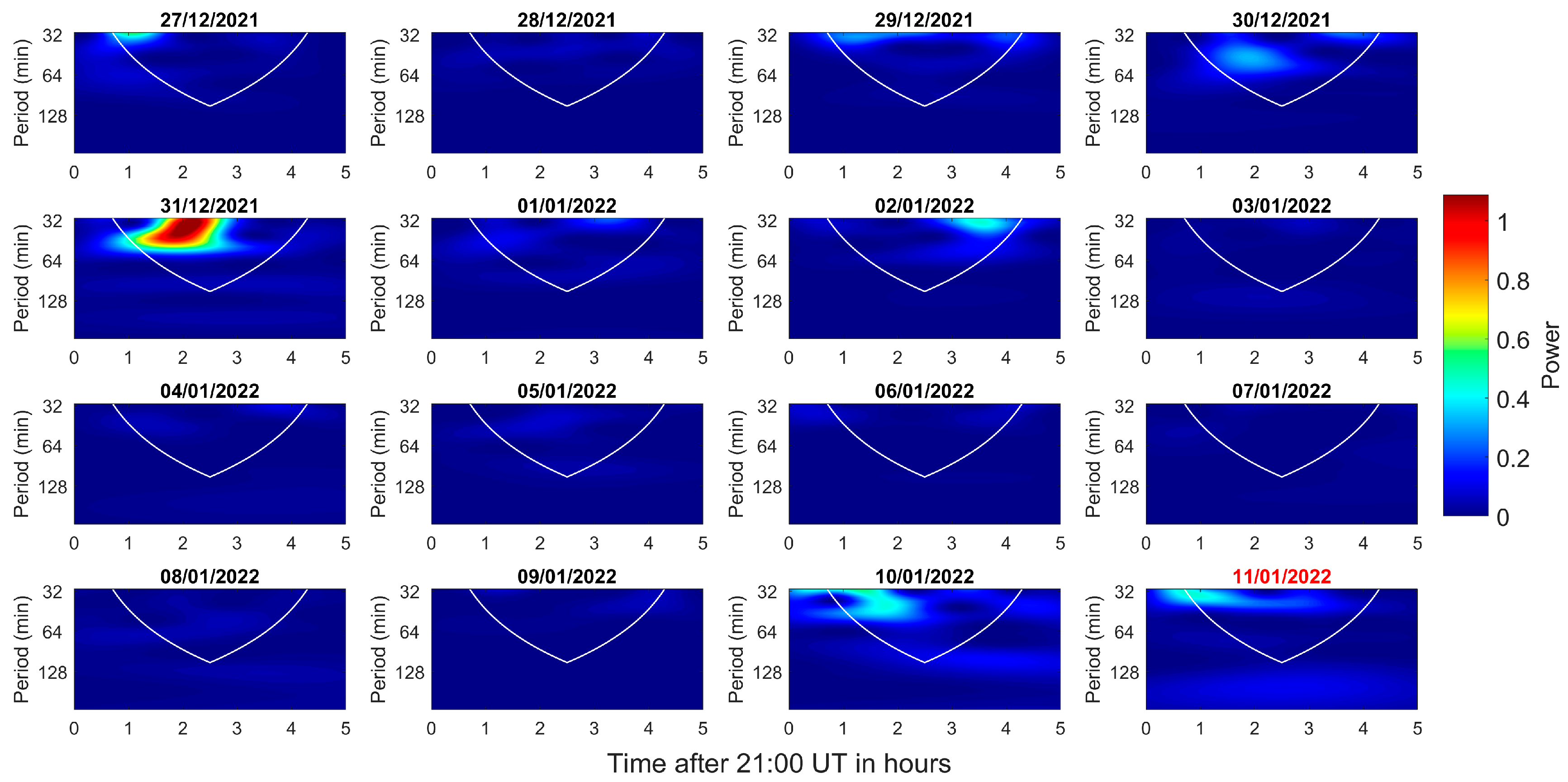
4.4. Wavelet Analysis Results
4.5. Simulation Results form Long Wavelength Propagation Capability Code
4.6. Summary of Analysis Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hayakawa, M. Probing the lower ionospheric perturbations associated with earthquakes by means of subionospheric VLF/LF propagation. Earthq. Sci. 2011, 24, 609–637. [Google Scholar] [CrossRef]
- Malkotsis, F.; Politis, D.Z.; Dimakos, D.; Potirakis, S.M. An amateur-radio-based open-source (HW/SW) VLF/LF receiver for lower ionosphere monitoring, examples of identified perturbations. Foundations 2022, 2, 639–663. [Google Scholar] [CrossRef]
- Rozhnoi, A.; Hayakawa, M.; Solovieva, M.; Hobara, Y.; Fedun, V. Ionospheric effects of the Mt. Kirishima volcanic eruption as seen from Subionospheric VLF Observations. J. Atmos. Sol. Terr. Phys. 2014, 107, 54–59. [Google Scholar] [CrossRef]
- Rodger, C.J. Subionospheric VLF perturbations associated with lightning discharges. J. Atmos. Sol. Terr. Phys. 2003, 65, 591–606. [Google Scholar] [CrossRef]
- Biagi, P.F.; Maggipinto, T.; Righetti, F.; Loiacono, D.; Schiavulli, L.; Ligonzo, T.; Ermini, A.; Moldovan, I.A.; Moldovan, A.S.; Buyuksarac, A.; et al. The European VLF/LF Radio Network to search for earthquake precursors: Setting up and natural/man-made disturbances. Nat. Hazards Earth Syst. Sci. 2011, 11, 333–341. [Google Scholar] [CrossRef]
- Chakrabarti, S.K.; Mondal, S.K.; Sasmal, S.; Pal, S.; Basak, T.; Chakrabarti, S.; Bhowmick, D.; Ray, S.; Maji, S.K.; Nandi, A.; et al. VLF signals in summer and winter in the Indian sub-continent using multi-station campaigns. Indian J. Phys. 2012, 86, 323–334. [Google Scholar] [CrossRef]
- Raulin, J.-P.; Bertoni, F.C.; Gavilán, H.R.; Guevara-Day, W.; Rodriguez, R.; Fernandez, G.; Correia, E.; Kaufmann, P.; Pacini, A.; Stekel, T.R.; et al. Solar flare detection sensitivity using the South America VLF Network (SAVNET). J. Geophys. Res. Space Phys. 2010, 115, A7. [Google Scholar] [CrossRef]
- Politis, D.Z.; Potirakis, S.M.; Contoyiannis, Y.F.; Biswas, S.; Sasmal, S.; Hayakawa, M. Statistical and criticality analysis of the lower ionosphere prior to the 30 October 2020 Samos (Greece) earthquake (M6.9), based on VLF electromagnetic propagation data as recorded by a new VLF/LF receiver installed in Athens (Greece). Entropy 2021, 23, 676. [Google Scholar] [CrossRef] [PubMed]
- Freund, F.T.; Kulahci, I.G.; Cyr, G.; Ling, J.; Winnick, M.; Tregloan-Reed, J.; Freund, M.M. Air ionization at rock surfaces and pre-earthquake signals. J. Atmos. Sol.-Terr. Phys. 2009, 71, 1824–1834. [Google Scholar] [CrossRef]
- Eftaxias, K.; Potirakis, S.M.; Contoyiannis, Y. 13-Four-stage model of earthquake generation in terms of fracture-induced electromagnetic emissions. In Complexity of Seismic Time Series, 1st ed.; Chelidze, T., Vallianatos, F., Telesca, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 437–502. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Natural Time Analysis: The New View of Time Precursory Seismic Electric Signals, Earthquakes and Other Complex Time Series, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Contoyiannis, Y.; Potirakis, S.M.; Eftaxias, K.; Hayakawa, M.; Schekotov, A. Intermittent criticality revealed in ULF Magnetic Fields prior to the 11 March 2011 Tohoku earthquake (Mw = 9). Phys. A Stat. Mech. Appl. 2016, 452, 19–28. [Google Scholar] [CrossRef]
- Hayakawa, M.; Schekotov, A.; Potirakis, S.M.; Eftaxias, K.; Li, Q.; Asano, T. An integrated study of ULF magnetic field variations in association with the 2008 Sichuan earthquake, on the basis of statistical and critical analyses. Open J. Earthq. Res. 2015, 04, 85–93. [Google Scholar] [CrossRef]
- Potirakis, S.M.; Contoyiannis, Y.; Asano, T.; Hayakawa, M. Intermittency-induced criticality in the lower ionosphere prior to the 2016 Kumamoto earthquakes as embedded in the VLF propagation data observed at multiple stations. Tectonophysics 2018, 722, 422–431. [Google Scholar] [CrossRef]
- Potirakis, S.; Asano, T.; Hayakawa, M. Criticality analysis of the lower ionosphere perturbations prior to the 2016 Kumamoto (Japan) earthquakes as based on VLF electromagnetic wave propagation data observed at multiple stations. Entropy 2018, 20, 199. [Google Scholar] [CrossRef]
- Hayakawa, M.; Molchanov, O.A.; Ondoh, T.; Kawai, E. Anomalies in the sub-ionospheric VLF signals for the 1995 Hyogo-Ken Nanbu earthquake. J. Phys. Earth 1996, 44, 413–418. [Google Scholar] [CrossRef]
- Biswas, S.; Chowdhury, S.; Sasmal, S.; Politis, D.Z.; Potirakis, S.M.; Hayakawa, M. Numerical modelling of sub-ionospheric very low frequency radio signal anomalies during the Samos (Greece) earthquake (M = 6.9) on October 30, 2020. Adv. Space Res. 2022, 70, 1453–1471. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Biswas, S.; Kundu, S.; Ghosh, S.; Chowdhury, S.; Yang, S.-S.; Hayakawa, M.; Chakraborty, S.; Chakrabarti, S.K.; Sasmal, S. Contaminated effect of geomagnetic storms on pre-seismic atmospheric and ionospheric anomalies during Imphal earthquake. Open J. Earthq. Res. 2020, 09, 383–402. [Google Scholar] [CrossRef]
- Biswas, S.; Kundu, S.; Sasmal, S.; Politis, D.Z.; Potirakis, S.M.; Hayakawa, M. Preseismic perturbations and their inhomogeneity as computed from ground- and space-based investigation during the 2016 Fukushima earthquake. J. Sens. 2023, 2023, 7159204. [Google Scholar] [CrossRef]
- Righetti, F.; Biagi, P.F.; Maggipinto, T.; Schiavulli, L.; Ligonzo, T.; Ermini, A.; Moldovan, I.A.; Moldovan, A.S.; Buyuksarac, A.; Silva, H.G.; et al. Wavelet analysis of the LF radio signals collected by the European VLF/LF network from July 2009 to April 2011. Ann. Geophys. 2012, 55, 171–180. [Google Scholar] [CrossRef]
- Ferguson, J.A. Computer Programmes for Assessment of Long Wavelength Radio Communications; Version 2.0, Tech. doc. 3030; Space and Naval Warfare Systems Center: San Diego, CA, USA, 1998. [Google Scholar]
- Grubor, D.P.; Šulić, D.M.; Žigman, V. Classification of X-ray solar flares regarding their effects on the lower ionosphere electron density profile. Ann. Geophys. 2008, 26, 1731–1740. [Google Scholar] [CrossRef]
- Maurya, A.K.; Venkatesham, K.; Kumar, S.; Singh, R.; Tiwari, P.; Singh, A.K. Effects of St. Patrick’s day geomagnetic storm of March 2015 and of June 2015 on low-equatorial D region ionosphere. J. Geophys. Res. Space Phys. 2018, 123, 6836–6850. [Google Scholar] [CrossRef]
- Ghosh, S.; Chakraborty, S.; Sasmal, S.; Basak, T.; Chakrabarti, S.K.; Samanta, A. Comparative study of the possible lower ionospheric anomalies in very low frequency (VLF) signal during Honshu, 2011 and Nepal, 2015 earthquakes. Geomat. Nat. Hazards Risk 2019, 10, 1596–1612. [Google Scholar] [CrossRef]
- Cummer, S.A.; Inan, U.S.; Bell, T.F. Ionospheric D region remote sensing using VLF radio atmospherics. Radio Sci. 1998, 33, 1781–1792. [Google Scholar] [CrossRef]
- Wait, J.R.; Spies, K.P. Characteristics of the Earth–Ionosphere Waveguide for VLF Radio Waves; NBS Technical Note 300; US Department of Commerce, National Bureau of Standards: Washington, DC, USA, 1964. [Google Scholar]
- Tatsuta, K.; Hobara, Y.; Pal, S.; Balikhin, M. Sub-ionospheric VLF signal anomaly due to geomagnetic storms: A statistical study. Ann. Geophys. 2015, 33, 1457–1467. [Google Scholar] [CrossRef]
- Rozhnoi, A.; Solovieva, M.S.; Molchanov, O.A.; Hayakawa, M. Middle latitude LF (40 kHz) phase variations associated with earthquakes for quiet and disturbed geomagnetic conditions. Phys. Chem. Earth 2004, 29, 589–598. [Google Scholar] [CrossRef]
- Maekawa, S.; Horie, T.; Yamauchi, T.; Sawaya, T.; Ishikawa, M.; Hayakawa, M.; Sasaki, H. A statistical study on the effect of earthquakes on the ionosphere, based on the subionospheric LF propagation data in Japan. Ann. Geophs. 2006, 24, 2219–2225. [Google Scholar] [CrossRef]
- Kasahara, Y.; Muto, F.; Horie, T.; Yoshida, M.; Hayakawa, M.; Ohta, K.; Rozhnoi, A.; Solovieva, M.; Molchanov, O.A. On the statistical correlation between the ionospheric perturbations as detected by subionospheric VLF/LF propagation anomalies and earthquakes. Nat. Hazards Earth Syst. Sci. 2008, 8, 653–656. [Google Scholar] [CrossRef]
- Yoshida, M.; Yamauchi, T.; Horie, T.; Hayakawa, M. On the generation mechanism of terminator times in subionospheric VLF/LF propagation and its possible application to seismogenic effects. Nat. Hazards Earth Syst. Sci. 2008, 8, 129–134. [Google Scholar] [CrossRef]
- Molchanov, O.A.; Hayakawa, M. Subionospheric VLF signal perturbations possibly related to earthquakes. J. Geophys. Res. Space Phys. 1998, 103, 17489–17504. [Google Scholar] [CrossRef]
- Ray, S.; Chakrabarti, S.K. A Study of the Behavior of the Terminator Time Shifts Using Multiple VLF Propagation Paths During the Pakistan Earthquake (M = 7.2) of 18 January 2011. Nat. Hazards Earth Syst. Sci. 2013, 13, 1501–1506. [Google Scholar] [CrossRef]
- Sasmal, S.; Chakrabarti, S.K. Ionosperic Anomaly Due to Seismic Activities—Part 1: Calibration of the VLF Signal of VTX 18.2 Khz Station from Kolkata and Deviation During Seismic Events. Nat. Hazards Earth Syst. Sci. 2009, 9, 1403–1408. [Google Scholar] [CrossRef]
- Sasmal, S.; Chakrabarti, S.K.; Chakrabarti, S. Studies of the correlation between ionospheric anomalies and seismic activities in the Indian subcontinent. AIP Conf. Proc. 2010, 1286, 270. [Google Scholar] [CrossRef]
- Chakraborty, S.; Sasmal, S.; Basak, T.; Ghosh, S.; Palit, S.; Chakrabarti, S.K.; Ray, S. Numerical Modeling of Possible Lower Ionospheric Anomalies Associated with Nepal Earthquake in May, 2015. Adv. Space Res. 2017, 60, 1787–1796. [Google Scholar] [CrossRef]
- Chakrabarti, S.K.; Saha, M.; Khan, R.; Mandal, S.; Acharyya, K.; Saha, R. Possible Detection of Ionospheric Disturbances During the Sumatra-Andaman Islands Earthquakes of December, 2004. Indian J. Radio Sp. Phys. 2005, 34, 314–317. [Google Scholar]
- Chakrabarti, S.; Sasmal, S.; Saha, M.; Khan, R.; Bhoumik, D.; Chakrabarti, S.K. Unusual Behavior of D-Region Ionization Time at 18.2kHz During Seismically Active Days. Indian J. Phys. 2007, 81, 531–538. [Google Scholar]
- Chakrabarti, S.K.; Sasmal, S.; Chakrabarti, S. Ionospheric Anomaly Due to Seismic Activities—Part 2: Evidence from D-Layer Preparation and Disappearance Times. Nat. Haz. Earth Syst. Sci. 2010, 10, 1751–1757. [Google Scholar] [CrossRef]
- Ray, S.; Chakrabarti, S.K.; Sasmal, S.; Choudhury, A.K.; Chakrabarti, S.K. Correlations between the anomalous behavior of the ionosphere and the seismic events for VTX-MALDA VLF propagation. AIP Conf. Proc. 2010, 1286, 298. [Google Scholar] [CrossRef]
- Ray, S.; Chakrabarti, S.K.; Mondal, S.K.; Sasmal, S. Ionospheric Anomaly Due to Seismic Activities-III: Correlation Between Night Time VLF Amplitude Fluctuations and Effective Magnitudes of Earthquakes in Indian Sub-Continent. Nat. Hazards Earth Syst. Sci. 2011, 11, 2699–2704. [Google Scholar] [CrossRef]
- Ray, S.; Chakrabarti, S.K.; Sasmal, S. Precursory Effects in the Nighttime VLF Signal Amplitude for the 18th January, 2011 Pakistan Earthquake. Indian J. Phys. 2012, 86, 85–88. [Google Scholar] [CrossRef]
- Sasmal, S.; Chakrabarti, S.K.; Ray, S. Unusual Behavior of Very Low Frequency Signal During the Earthquake at Honshu/Japan on 11 March, 2011. Indian J. Phys. 2014, 88, 1013–1019. [Google Scholar] [CrossRef]
- Pal, P.; Sasmal, S.; Chakrabarti, S.K. Studies of Seismo-Ionospheric Correlations Using Anomalies in Phase of Very Low Frequency Signal. Geomat. Nat. Haz. Risk 2017, 8, 167–176. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Long-Range Correlations in the Electric Signals that Precede Rupture. Phys. Rev. E 2002, 66, 011902. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.A.; Sarlis, N.V.; Tanaka, H.K.; Skordas, E.S. Similarity of Fluctuations in Correlated Systems: The Case of Seismicity. Phys. Rev. E 2005, 72, 041103. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Spatio-Temporal Complexity Aspects on the Interrelation Between Seismic Electric Signals and Seismicity. Pract. Athens Acad. 2001, 76, 294–321. [Google Scholar]
- Abe, S.; Sarlis, N.V.; Skordas, E.S.; Tanaka, H.K.; Varotsos, P.A. Origin of the Usefulness of the Natural-Time Representation of Complex Time Series. Phys. Rev. Lett. 2005, 94, 170601. [Google Scholar] [CrossRef] [PubMed]
- Potirakis, S.M.; Contoyiannis, Y.; Schekotov, A.; Eftaxias, K.; Hayakawa, M. Evidence of critical dynamics in various electromagnetic precursors. Eur. Phys. J. Spec. Top. 2021, 230, 151–177. [Google Scholar] [CrossRef]
- Ghosh, S.; Chowdhury, S.; Kundu, S.; Sasmal, S.; Politis, D.Z.; Potirakis, S.M.; Hayakawa, M.; Chakraborty, S.; Chakrabarti, S.K. Unusual surface latent heat flux variations and their critical dynamics revealed before strong earthquakes. Entropy 2021, 24, 23. [Google Scholar] [CrossRef]
- Yang, S.-S.; Potirakis, S.M.; Sasmal, S.; Hayakawa, M. Natural Time Analysis of global navigation satellite system surface deformation: The case of the 2016 Κumamoto earthquakes. Entropy 2020, 22, 674. [Google Scholar] [CrossRef]
- Politis, D.Z.; Potirakis, S.M.; Kundu, S.; Chowdhury, S.; Sasmal, S.; Hayakawa, M. Critical Dynamics in stratospheric potential energy variations prior to significant (M > 6.7) earthquakes. Symmetry 2022, 14, 1939. [Google Scholar] [CrossRef]
- Potirakis, S.M.; Karadimitrakis, A.; Eftaxias, K. Natural time analysis of critical phenomena: The case of pre-fracture electromagnetic emissions. Chaos 2013, 23, 023117. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Tanaka, H.K.; Lazaridou, M.S. Entropy of Seismic Electric Signals: Analysis in the Natural Time Under Time Reversal. Phys. Rev. E 2006, 73, 031114. [Google Scholar] [CrossRef] [PubMed]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A. Similarity of Fluctuations in Systems Exhibiting Self-Organized Criticality. Europhys. Lett. 2011, 96, 28006. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S.; Varotsos, P.A. Investigation of Seismicity After the Initiation of a Seismic Electric Signal Activity Until the Mainshock. Proc. Jpn. Acad. Ser. B 2008, 84, 331–343. [Google Scholar] [CrossRef]
- Sasmal, S.; Pal, S.; Chakrabarti, S.K. Study of long path VLF signal propagation characteristics as Observed from Indian Antarctic station, Maitri. Adv. Space Res. 2014, 54, 1619–1628. [Google Scholar] [CrossRef]
- Sasmal, S.; Palit, S.; Chakrabarti, S.K. Modeling of long path propagation characteristics of Very Low Frequency (VLF) radio waves as observed from Indian Antarctic station. J. Geophys. Res. Space Phys. 2015, 120, 8872–8883. [Google Scholar] [CrossRef]
- Sasmal, S.; Basak, T.; Chakraborty, S.; Palit, S.; Chakrabarti, S.K. Modeling of temporal variation of Very Low Frequency (VLF) radio waves over long paths as observed from Indian Antarctic stations. J. Geophys. Res. Space Phys. 2017, 122, 7698–7712. [Google Scholar] [CrossRef]
- Chowdhury, S.; Kundu, S.; Ghosh, S.; Basak, T.; Hayakawa, M.; Chakraborty, S.; Chakrabarti, S.K.; Sasmal, S. Numerical simulation of lower ionospheric reflection parameters by using International Reference Ionosphere (IRI) model and validation with Very Low Frequency (VLF) radio signal characteristics. Adv. Space Res. 2021, 67, 1599–1611. [Google Scholar] [CrossRef]

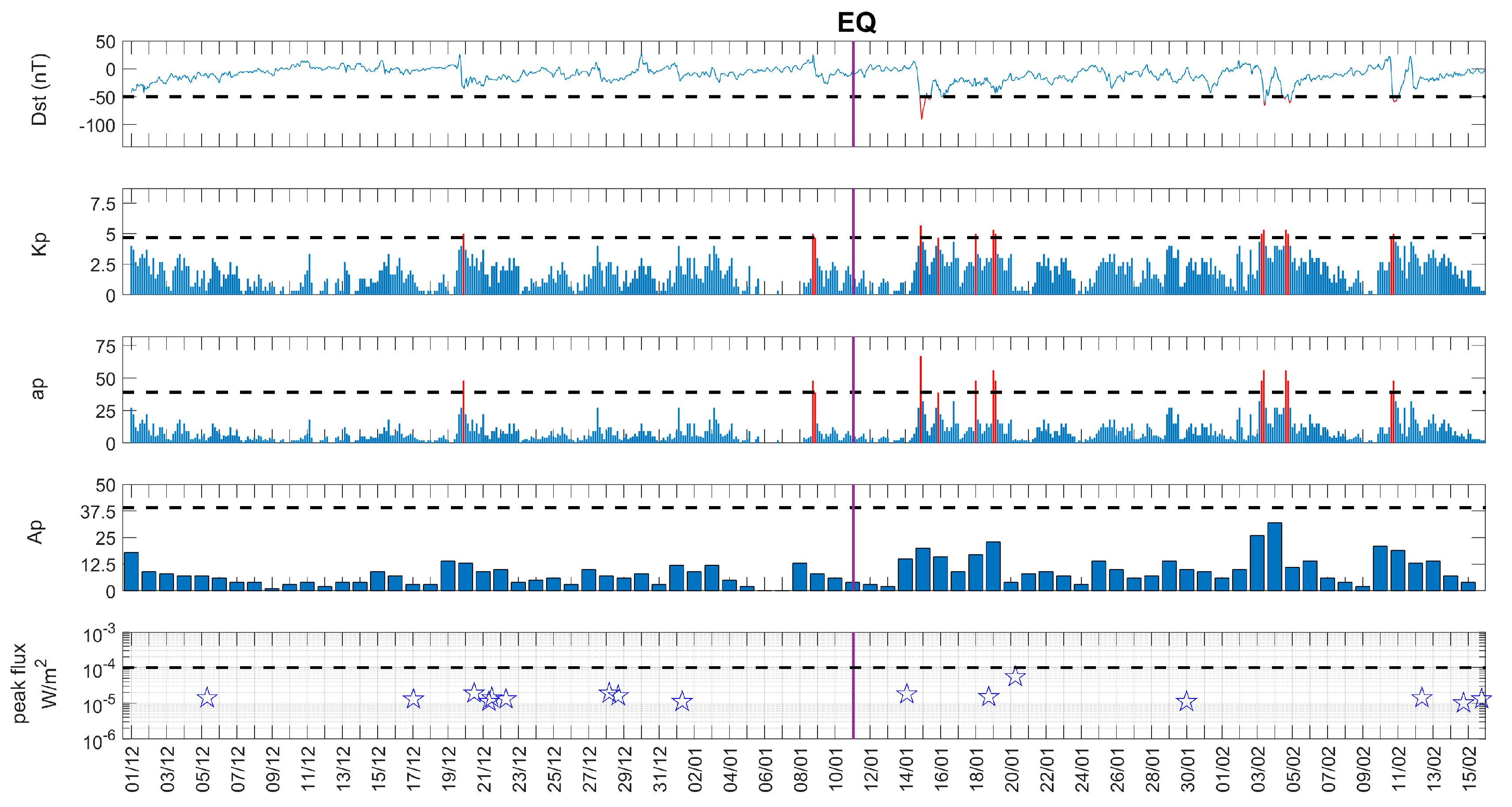





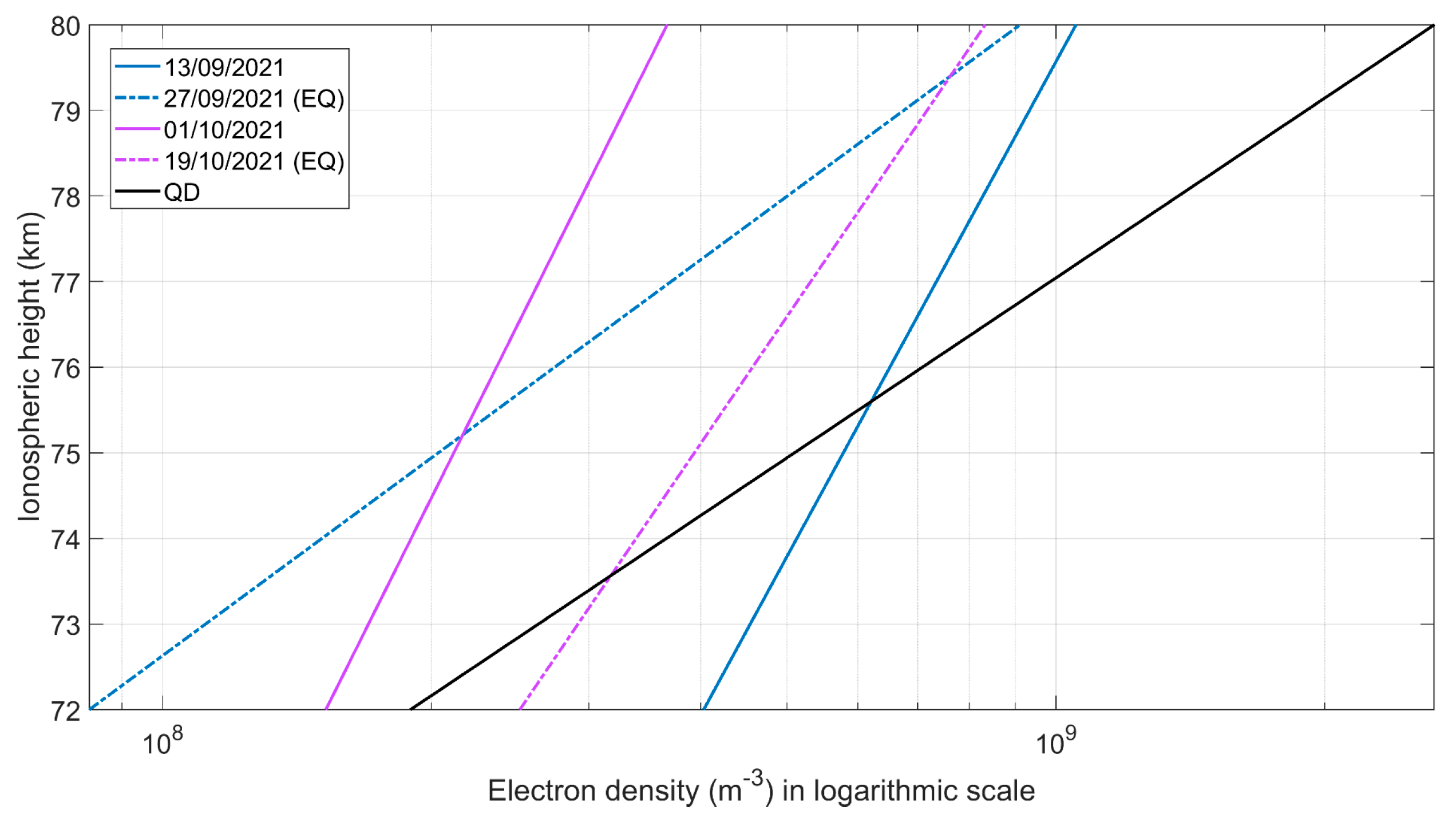



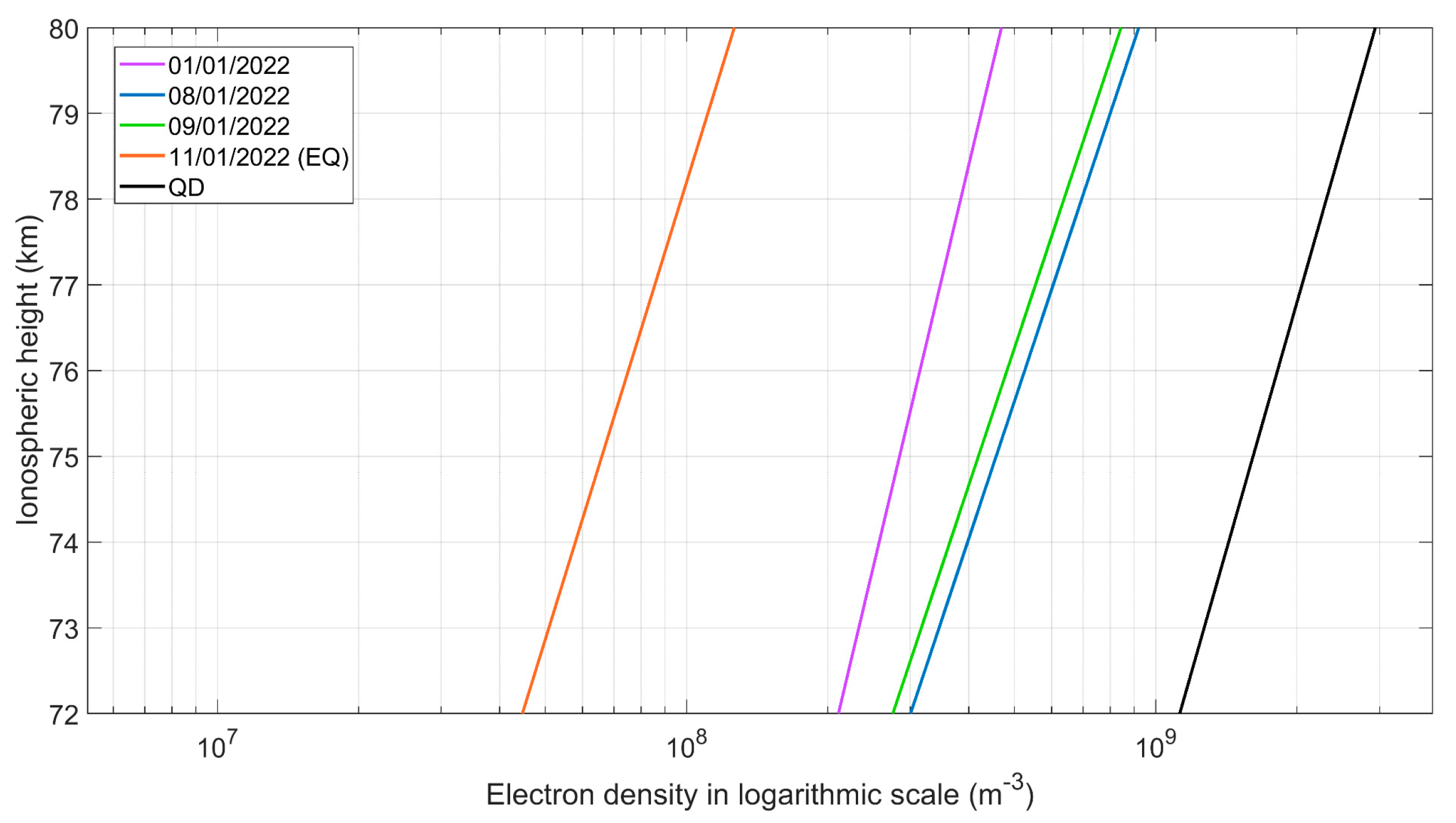

| “EQ Group” Based on the Time Occurrence and the Location of the Epicenter of the Studied EQ | Date and Time of Occurrence (UT) | Depth (km) | Latitude | Longitude | |
|---|---|---|---|---|---|
| 2021 Crete EQs | 27 September 2021 06:17:21 | 5.8 | 9.6 | 35.1521° N | 25.2736° E |
| 2021 Crete EQs | 12 October 2021 09:24:02 | 6.3 | 10.4 | 34.8944° N | 26.4716° E |
| 2021 Crete EQs | 19 October 2021 05:32:35 | 6.1 | 58.5 | 34.7131° N | 28.2532° E |
| 2022 Cyprus EQ | 11 January 2022 01:07:49 | 6.4 | 34.7 | 35.1398° N | 31.9537° E |
| Date of Appearance of the Anomaly (UT) | TR* | DP* | NF* | Possibly Associated Extreme Event(s) |
|---|---|---|---|---|
| 2 December 2021 | GER | GER | UWA, GER | - |
| 11 December 2021 | GER | b | ||
| 21 December 2021 | UWA | b, c | ||
| 4 January 2022 | ACH | ACH, GER | ACH | a |
| 5 January 2022 | UWA, ACH, GER | ACH | UWA, ACH, GER | a |
| 27 January 2022 | ACH | - |
| Date of Appearance of the Anomaly (UT) | TR* | DP* | NF* | Possibly Associated Extreme Event(s) |
|---|---|---|---|---|
| 5 September 2021 | UWA | UWA, GER | UWA, GER | - |
| 9 September 2021 | GER | GER | GER | a |
| 19 September 2021 | UWA, GER | a | ||
| 28 September 2021 | GER | b | ||
| 4 October 2021 | UWA | b, c | ||
| 7 October 2021 | UWA, GER | UWA, GER | b, c | |
| 9 October 2021 | GER | b, c | ||
| 11 October 2021 | UWA | UWA, GER | c | |
| 12 October 2021 | UWA | c | ||
| 27 October 2021 | UWA | GER | - |
| Date of Appearance of the Anomaly (UT) | Shift in | Shift in | Possibly Associated Extreme Event(s) |
|---|---|---|---|
| 28 December 2021 | UWA, GER, ACH | a, b | |
| 1 January 2022 | UWA, GER, ACH | b | |
| 2 January 2022 | GER, ACH | GER, ACH | b |
| 3 January 2022 | GER, ACH | b | |
| 4 January 2022 | GER, ACH | b | |
| 5 January 2022 | UWA, GER, ACH | b | |
| 6 January 2022 | UWA, GER, ACH | b | |
| 7 January 2022 | UWA | b | |
| 8 January 2022 | UWA, GER, ACH | b | |
| 9 January 2022 | UWA, GER, ACH | UWA, GER, ACH | b |
| Date of Appearance of the Anomaly (UT) | Shift in | Shift in | Shift in | Shift in | Possibly Associated Extreme Event(s) |
|---|---|---|---|---|---|
| 13 September 2021 | UWA, GER | a | |||
| 15 September 2021 | UWA | GER | a | ||
| 17 September 2021 | GER | a | |||
| 18 September 2021 | UWA, GER | a | |||
| 19 September 2021 | UWA, GER | UWA | a | ||
| 20 Septemebr 2021 | UWA, GER | a | |||
| 21 September 2021 | UWA | a | |||
| 22 September 2021 | UWA | a | |||
| 24 September 2021 | UWA, GER | UWA | a | ||
| 25 September 2021 | UWA | UWA | a | ||
| 26 September 2021 | UWA | a | |||
| 27 September 2021 | UWA | a, b | |||
| 28 September 2021 | GER | UWA | UWA | b | |
| 2 October 2021 | GER | GER | b | ||
| 3 October 2021 | GER | b | |||
| 4 October 2021 | GER | b, c | |||
| 6 October 2021 | b, c | ||||
| 7 October 2021 | UWA, GER | UWA | b, c | ||
| 8 October 2021 | UWA | b, c | |||
| 9 October 2021 | UWA | b, c | |||
| 10 October 2021 | UWA | b, c | |||
| 11 October 2021 | GER | UWA, GER | b, c | ||
| 14 October 2021 | GER | c | |||
| 15 October 2021 | GER | c | |||
| 16 October 2021 | UWA | c | |||
| 17 October 2021 | UWA | UWA | c |
| Date of Appearance of the Anomaly (UT) | Excess of | Excess of | Excess of | Excess of | Possibly Associated Extreme Event(s) |
|---|---|---|---|---|---|
| 7 December 2021 | ACH (shifted −12.1 min) | - | |||
| 8 December 2021 | UWA (shifted −19.6 min), GER (shifted −12.2 min) | - | |||
| 21 December 2021 | UWA (shifted −50.1 min) | b, c | |||
| 28 December 2021 | GER (shifted 26.9 min) | a, c | |||
| 1 January 2021 | UWA (shifted −34.7 min) | a | |||
| 6 January 2021 | ACH (shifted 29.8 min) | a | |||
| 8 January 2021 | UWA (shifted −33.2 min), ACH (shifted −34.5 min), GER (shifted −40.6 min) | a | |||
| 9 January 2021 | UWA (shifted 43.4 min), ACH (shifted 51.3 min), GER (shifted 53.9 min) | a | |||
| 24 January 2021 | UWA (shifted 34 min) | - |
| Date of Appearance of the Anomaly (UT) | for | for | for | for | for | for | for | for | Possibly Associated Extreme Event(s) |
|---|---|---|---|---|---|---|---|---|---|
| 4 September 2021 | UWA (shifted 34.5 min) | UWA (shifted 35 min) | UWA (shifted 35.83 min) | - | |||||
| 6 September 2021 | GER (shifted 52.5 min) | GER (shifted 57 min) | GER (shifted 47.75 min) | a | |||||
| 19 September 2021 | UWA (shifted 28.4 min) | a | |||||||
| 20 September 2021 | UWA (shifted −13.7 min), GER (shifted −20.1 min) | a | |||||||
| 28 September 2021 | UWA (shifted 26 min) | UWA (shifted 26.3 min) | b | ||||||
| 1 October 2021 | GER (shifted −18.75 min) | UWA (shifted 36.9 min) | UWA (shifted 32.5 min) | UWA (shifted 39.1 min) | b | ||||
| 2 October 2021 | GER (shifted −35.66 min) | GER (shifted 44.16 min) | GER (shifted 38 min) | b | |||||
| 7 October 2021 | UWA (shifted −45 min), GER (shifted −43.8 min) | UWA (shifted 57.6 min) | b, c | ||||||
| 11 October 2021 | GER (shifted −32 min) | UWA (shifted 26 min) | GER (shifted 48.7 min) | b, c | |||||
| 12 October 2021 | UWA (shifted −10.87 min) | b, c |
| Date of Appearance of the Criticality Signature (UT) | NT Analysis on TR | NT Analysis on DP | NT Analysis on NF | Possibly Associated Extreme Event(s) |
|---|---|---|---|---|
| 29 December 2021 | UWA | a | ||
| 30 December 2021 | GER | ACH | a | |
| 4 January 2022 | ACH | a | ||
| 7 January 2022 | UWA, GER | a | ||
| 8 January 2022 | ACH | UWA | a | |
| 10 January 2022 | ACH | a | ||
| 15 January 2022 | UWA, GER | b, c, d, e | ||
| 20 January 2022 | GER | GER | f, g | |
| 22 January 2022 | ACH | GER | f, g | |
| 23 January 2022 | GER, ACH | GER | f, g | |
| 24 January 2022 | ACH | f, g | ||
| 25 January 2022 | GER, ACH | UWA | f, g |
| Date of Appearance of the Criticality Signature (UT) | NT Analysis on TR | NT Analysis on DP | NT Analysis on NF | Possibly Associated Extreme Event(s) |
|---|---|---|---|---|
| 9 September 2021 | GER | a | ||
| 10 September 2021 | UWA, GER | a | ||
| 11 September 2021 | UWA | a | ||
| 12 September 2021 | UWA | UWA | a | |
| 19 September 2021 | GER | a |
| Receiver Call Name | Date of Appearance of the Anomaly (UT) | Time of Appearance of the Anomaly (UT) | Range of Periodic Structures (min.) | Intensity of the Wave-Like Structures | Possibly Associated Extreme Event(s) |
|---|---|---|---|---|---|
| UWA | 27 December 2021 | 21:45:57–22:24:00 | 31–36 | moderate | a, b |
| 31 December 2021 | 22:10:48–23:21:00 | 31–54 | high | a | |
| 2 January 2021 | 00:07:48–00:54:00 | 31–38 | moderate | a | |
| 10 January 2021 | 21:43:48–23:07:48 | 31–50 | moderate | a | |
| 11 January 2021 | 21:45:36–22:27:00 | 31–38 | moderate | a | |
| GER | 5 January 2022 | 21:37:48–22:12:36 | 31–38 | high | a |
| ACH | 9 January 2022 | 23:48:00–00:25:48 | 31–36 | moderate | a |
| 10 January 2022 | 00:24:36–01:12:00 | 31–41 | high | a |
| Receiver Call Name | Date of Appearance of the Anomaly | Time of Appearance of the Anomaly (UT) | Range of Periodic Structures (min.) | Intensity of the Wave-Like Structures | Possibly Associated Extreme Event(s) |
|---|---|---|---|---|---|
| UWA | 13 September 2021 | 22:48:36–00:22:48 | 31–47 | moderate | a |
| 17 September 2021 | 22:52:48–00:43:48 | 31–36 | high | a | |
| 17 September 2021 | 23:21:00–00:36:00 | 47–71 | moderate | a | |
| 4 October 2021 | 22:07:48–00:31:48 | 31–38 | high | b, c | |
| 8 October 2021 | 23:21:36–00:27:00 | 31–36 | high | b, c | |
| 8 October 2021 | 22:54:36–00:01:48 | 71–94 | high | b, c | |
| 9 October 2021 | 23:45:36–00:57:00 | 31–50 | moderate | b, c | |
| 10 October 2021 | 21:58:48–00:55:48 | 41–47 | moderate | b, c | |
| 11 October 2021 | 23:46:48–01:09:00 | 36–54 | high | b, c | |
| 12 October 2021 | 23:04:48–00:21:00 | 41–62 | moderate | b, c | |
| 13 October 2021 | 23:46:48–01:49:48 | 54–66 | moderate | c | |
| 16 October 2021 | 22:09:36–23:18:36 | 31–33 | moderate | c | |
| GER | 12 September 2021 | 00:00:00–00:45:36 | 31–36 | high | a |
| 28 September 2021 | 22:43:48–00:09:36 | 31–50 | high | b | |
| 28 September 2021 | 22:58:48–00:22:48 | 57–87 | moderate | b | |
| 4 October 2021 | 23:03:36–00:24:36 | 35–43 | high | b, c | |
| 9 October 2021 | 23:36:36–01:00:00 | 43–66 | high | b, c | |
| 10 October 2021 | 00:03:00–01:09:36 | 33–46 | moderate | b, c | |
| 12 October 2021 | 23:33:36–00:18:00 | 33–44 | moderate | b, c | |
| 13 October 2021 | 22:36:00–23:54:36 | 31–41 | moderate | c | |
| 16 October 2021 | 21:42:36–00:09:00 | 31–35 | high | c | |
| 19 October 2021 | 21:43:48–00:33:36 | 31–38 | high | c |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Politis, D.Z.; Potirakis, S.M.; Sasmal, S.; Malkotsis, F.; Dimakos, D.; Hayakawa, M. Possible Pre-Seismic Indications Prior to Strong Earthquakes That Occurred in Southeastern Mediterranean as Observed Simultaneously by Three VLF/LF Stations Installed in Athens (Greece). Atmosphere 2023, 14, 673. https://doi.org/10.3390/atmos14040673
Politis DZ, Potirakis SM, Sasmal S, Malkotsis F, Dimakos D, Hayakawa M. Possible Pre-Seismic Indications Prior to Strong Earthquakes That Occurred in Southeastern Mediterranean as Observed Simultaneously by Three VLF/LF Stations Installed in Athens (Greece). Atmosphere. 2023; 14(4):673. https://doi.org/10.3390/atmos14040673
Chicago/Turabian StylePolitis, Dimitrios Z., Stelios M. Potirakis, Sudipta Sasmal, Filopimin Malkotsis, Dionisis Dimakos, and Masashi Hayakawa. 2023. "Possible Pre-Seismic Indications Prior to Strong Earthquakes That Occurred in Southeastern Mediterranean as Observed Simultaneously by Three VLF/LF Stations Installed in Athens (Greece)" Atmosphere 14, no. 4: 673. https://doi.org/10.3390/atmos14040673
APA StylePolitis, D. Z., Potirakis, S. M., Sasmal, S., Malkotsis, F., Dimakos, D., & Hayakawa, M. (2023). Possible Pre-Seismic Indications Prior to Strong Earthquakes That Occurred in Southeastern Mediterranean as Observed Simultaneously by Three VLF/LF Stations Installed in Athens (Greece). Atmosphere, 14(4), 673. https://doi.org/10.3390/atmos14040673












