Glaciers Variation at ‘Shocking’ Pace in the Northeastern Margin of Tibetan Plateau from 1957 to 21st Century: A Case Study of Qiyi Glacier
Abstract
:1. Introduction
2. Study Area
3. Data and Methods
3.1. Data Collection and Organization
3.1.1. Qiyi Glacier Observations and Geometry
3.1.2. Climate Data Collection and Reconstruction
3.1.3. Future Climate Forcing and Downscaling
3.1.4. Digital Elevation Models
3.2. Methods
3.2.1. Glacier Mass Balance Model Description
3.2.2. Modified V-A Scaling Method
- (1)
- Area and Volume calculation
- (2)
- Terminus elevation change
4. Results
4.1. Glacier SMB Model Calibrations and Validation
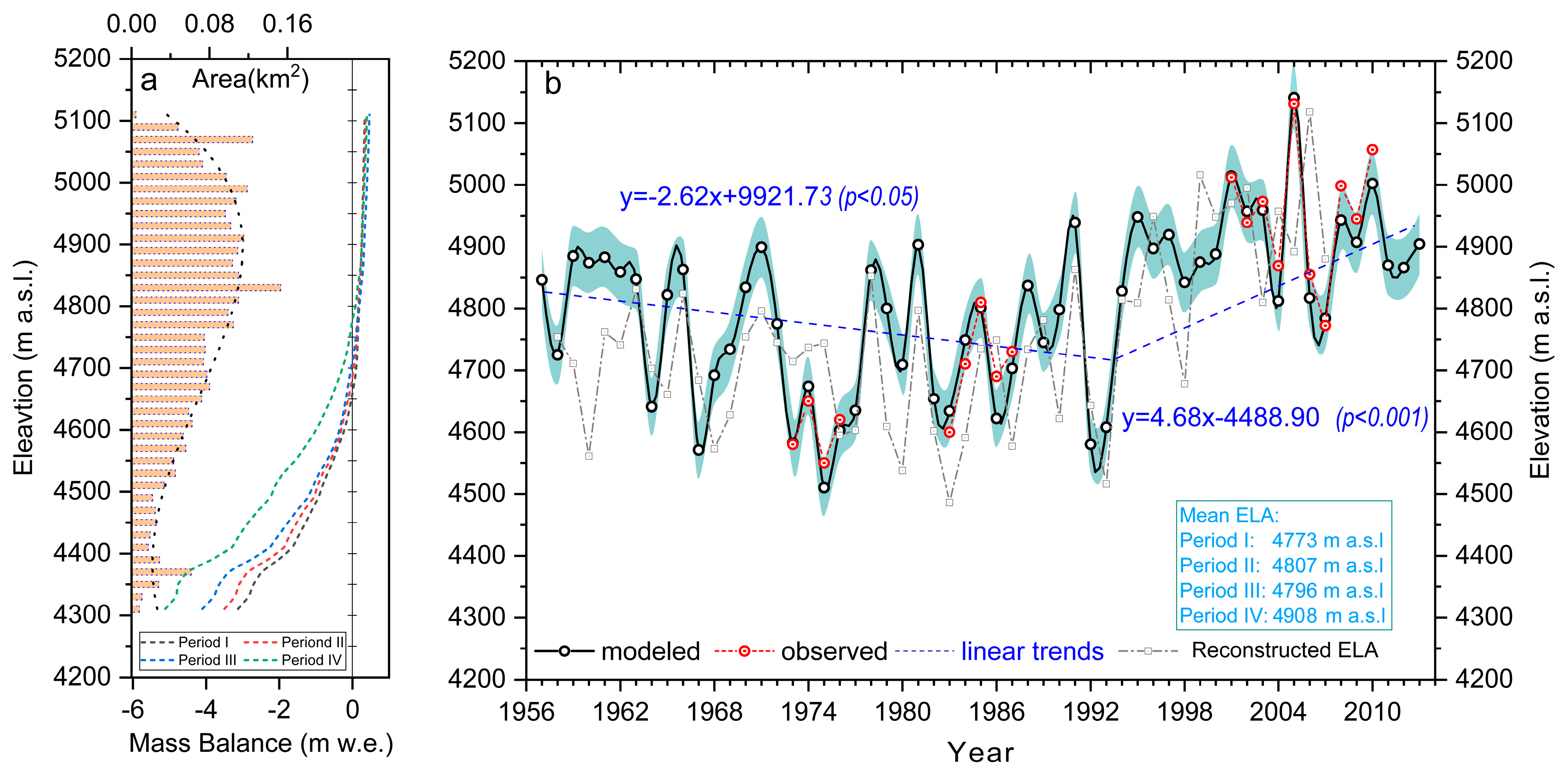
4.2. The Temporal Variation of Reconstructed Mass Balance during 1957–2013
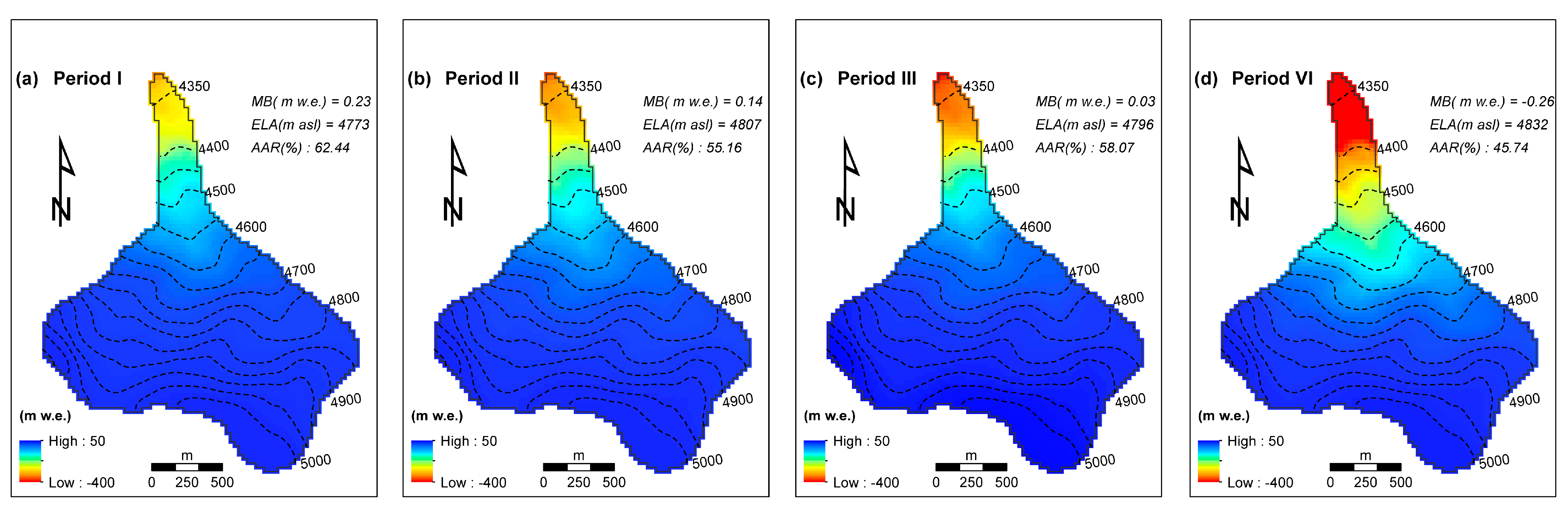
4.3. The Mass Balance Distribution and ELA Variation during 1957–2013
4.3.1. Mass Balance Distribution of Qiyi Glacier
4.3.2. Variations of ELA on Qiyi Glacier
5. Discussions
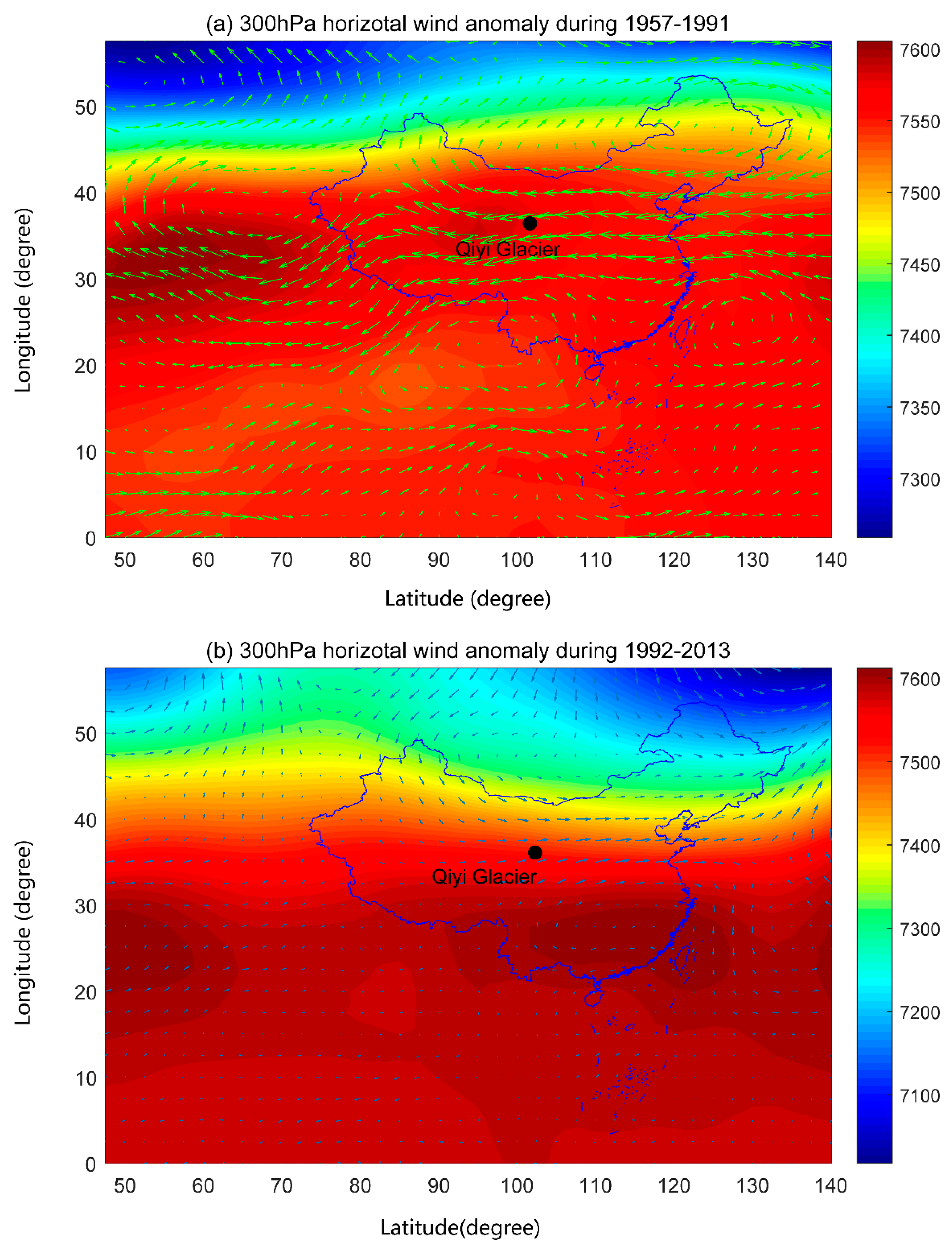
5.1. Qiyi Glacier SMB Response to Climate Change
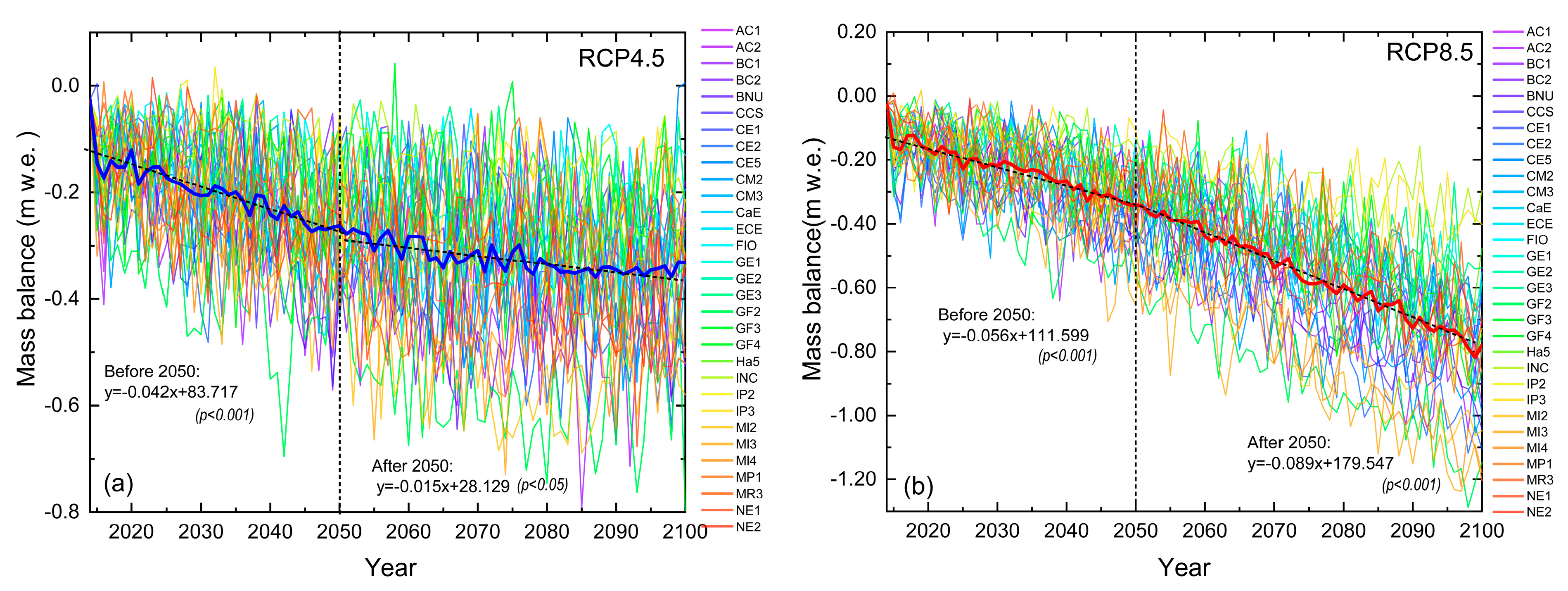
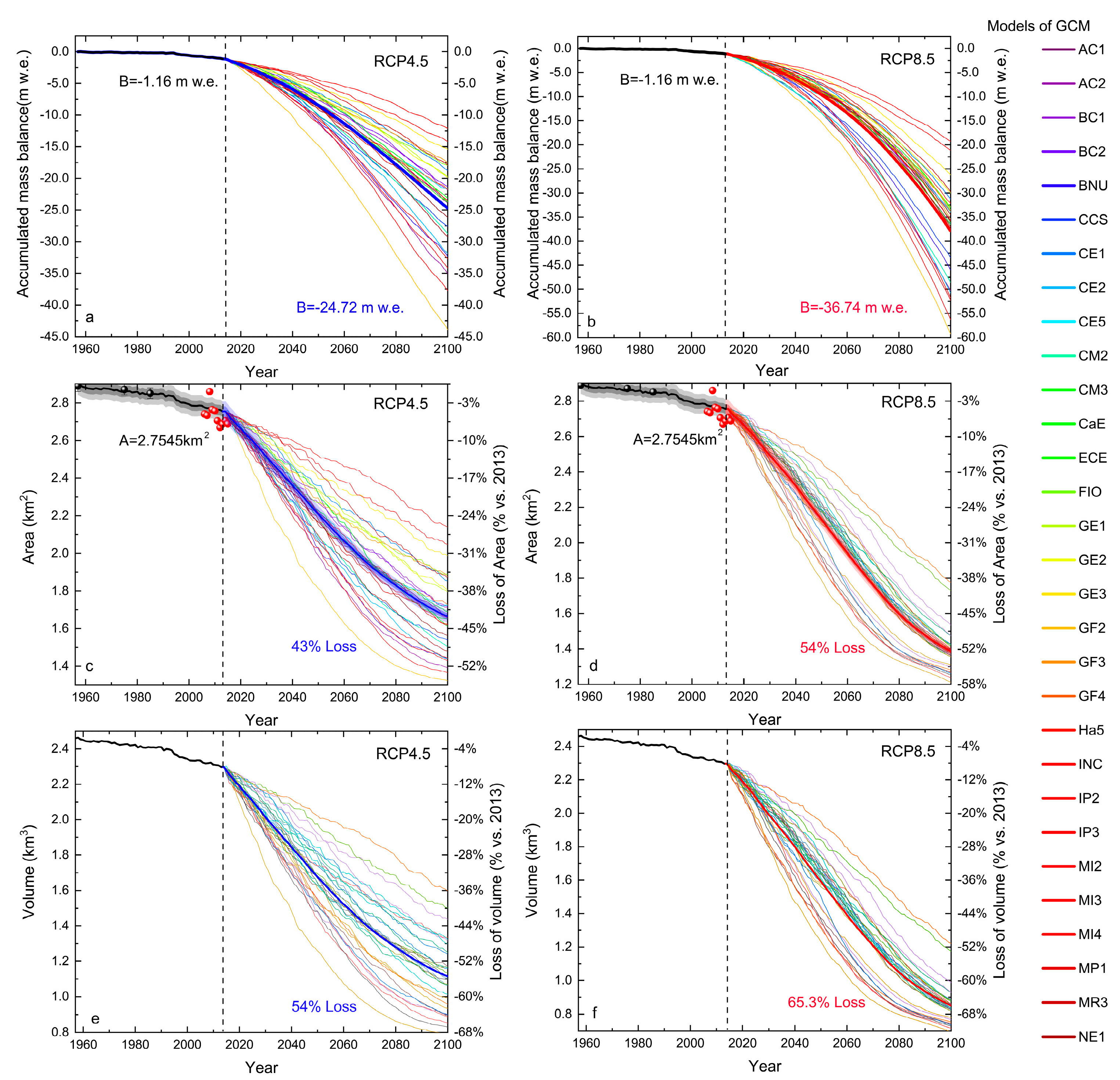
5.2. Surface Mass Balance Projections
5.3. Glacier Area, Volume, and Terminus Elevation Projections
5.3.1. Area and Volume Evolution
5.3.2. Terminus Elevation and ELA Evolution
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Immerzeel, W.W.; Van Beek, L.P.; Bierkens, M.F. Climate change will affect the Asian water towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef]
- Bolch, T.; Kulkarni, A.; Kääb, A.; Huggel, C.; Paul, F.; Cogley, J.G.; Frey, H.; Kargel, J.S.; Fujita, K.; Scheel, M.; et al. The state and fate of Himalayan glaciers. Science 2012, 336, 310–314. [Google Scholar] [CrossRef]
- Marzeion, B.; Jarosch, A.H.; Hofer, M. Past and future sea-level change from the surface mass balance of glaciers. Cryosphere 2012, 6, 1295–1322. [Google Scholar] [CrossRef]
- Shiyin, L.; Wenxin, S.; Yongping, S.; Gang, L. Glacier changes since the Little Ice Age maximum in the western Qilian Shan, northwest China, and consequences of glacier runoff for water supply. J. Glaciol. 2003, 49, 117–124. [Google Scholar] [CrossRef]
- Yao, T.; Bolch, T.; Chen, D.; Gao, J.; Immerzeel, W.; Piao, S.; Su, F.; Thompson, L.; Wada, Y.; Wang, L.; et al. The imbalance of the Asian water tower. Nat. Rev. Earth Environ. 2022, 3, 618–632. [Google Scholar] [CrossRef]
- Huss, M.; Fischer, M. Sensitivity of Very Small Glaciers in the Swiss Alps to Future Climate Change. Front. Earth Sci. 2016, 4, 34. [Google Scholar] [CrossRef]
- Zemp, M.; Huss, M.; Thibert, E.; Eckert, N.; McNabb, R.; Huber, J.; Barandun, M.; Machguth, H.; Nussbaumer, S.U.; Gärtner-Roer, I.; et al. Global glacier mass changes and their contributions to sea-level rise from 1961 to 2016. Nature 2019, 568, 382–386. [Google Scholar] [CrossRef]
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.L.; Péan, C.; Chen, Y.; Goldfarb, L.; Gomis, M.I.; Matthews, J.B.R.; Berger, S.; et al. Climate Change 2021: The Physical Science Basis. In Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Tian, H.; Yang, T.; Liu, Q. Climate change and glacier area shrinkage in the Qilian mountains, China, from 1956 to 2010. Ann. Glaciol. 2014, 55, 187–197. [Google Scholar] [CrossRef]
- Sun, M.; Liu, S.; Yao, X.; Guo, W.; Xu, J. Glacier changes in the Qilian Mountains in the past half-century: Based on the revised First and Second Chinese Glacier Inventory. Acta Geogr. Sin. 2018, 28, 206–220. [Google Scholar] [CrossRef]
- He, J.; Wang, N.; Chen, A.A.; Yang, X.; Hua, T. Glacier Changes in the Qilian Mountains, Northwest China, between the 1960s and 2015. Water 2019, 11, 623. [Google Scholar] [CrossRef]
- Wang, S.; Yao, T.; Tian, L.; Pu, J. Glacier mass variation and its effect on surface runoff in the Beida River catchment during 1957–2013. J. Glaciol. 2017, 63, 523–534. [Google Scholar] [CrossRef]
- Wang, N.; He, J.; Pu, J.; Jiang, X.; Jing, Z. Variations in equilibrium line altitude of the Qiyi Glacier, Qilian Mountains, over the past 50 years. Chin. Sci. Bull. 2010, 55, 3810–3817. [Google Scholar] [CrossRef]
- Wang, Z.T.; Liu, C.; You, G.; Pu, J.; Yang, H.; Tian, P. Glacier Inventory of China, I, Qilian Mountain; Lanzhou Institute of Glaciology and Geocryology, Chinese Academy of Sciences: Lanzhou China, 1981; pp. 1–35. (In Chinese) [Google Scholar]
- Pu, J.C.; Yao, T.D.; Duan, K.Q.; Sakai, A.; Fujita, K.; Matsuda, Y. Mass Balance of the Qiyi Glacier in the Qilian Mountains: A New Observation. J. Glaciol. Geocryol. 2005, 27, 199–204. (In Chinese) [Google Scholar]
- Duan, K.; Yao, T.; Wang, N.; Shi, P.; Meng, Y. Changes in equilibrium-line altitude and implications for glacier evolution in the Asian high mountains in the 21st century. Sci. China Earth Sci. 2022, 65, 1308–1316. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, N.; He, J.; Jiang, X. Estimating Mountain glacier surface temperatures from Landsat-ETM+ thermal infrared data: A case study of Qiyi glacier, China. Remote Sens. Environ. 2015, 163, 286–295. [Google Scholar] [CrossRef]
- Wang, S.; Wang, J.; Pu, J. Application of a distributed degree-day model of glaciers in the upper reaches of the Beida River Basin. Environ. Earth Sci. 2016, 75, 1–14. [Google Scholar] [CrossRef]
- Marzeion, B.; Jarosch, A.H.; Gregory, J.M. Feedbacks and mechanisms affecting the global sensitivity of glaciers to climate change. Cryosphere 2014, 8, 59–71. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, N.; He, J.; Wu, X.; Song, G. A distributed surface energy and mass balance model and its application to a mountain glacier in China. Chin. Sci. Bull. 2010, 55, 2079–2087. [Google Scholar] [CrossRef]
- Wu, X.; He, J.; Jiang, X.; Wang, N. Analysis of surface energy and mass balance in the accumulation zone of Qiyi Glacier, Tibetan Plateau in an ablation season. Environ. Earth Sci. 2016, 75, 1–13. [Google Scholar] [CrossRef]
- Hock, R.; Radić, V.; De Woul, M. Climate sensitivity of Storglaciären, Sweden: An intercomparison of mass-balance models using ERA-40 re-analysis and regional climate model data. Ann. Glaciol. 2007, 46, 342–348. [Google Scholar] [CrossRef]
- Radić, V.; Bliss, A.; Beedlow, A.C.; Hock, R.; Miles, E.; Cogley, J.G. Regional and global projections of twenty-first century glacier mass changes in response to climate scenarios from global climate models. Clim. Dyn. 2014, 42, 37–58. [Google Scholar] [CrossRef]
- Cogley, J.G. The future of Asia’s glaciers. Nature 2017, 549, 166–167. [Google Scholar] [CrossRef] [PubMed]
- Liang, L.; Cuo, L.; Liu, Q. Mass Balance Variation and Associative Climate Drivers for the Dongkemadi Glacier in the Central Tibetan Plateau. J. Geophys. Res. Atmos. 2019, 124, 10814–10825. [Google Scholar] [CrossRef]
- Duan, K. Simulation and prediction of equilibrium line altitude of glaciers in the eastern Tibetan plateau. In Proceedings of the EGU General Assembly Conference, Vienna, Austria, 23–28 April 2017; pp. 104–113. [Google Scholar]
- Hock, R. Glacier melt: A review of processes and their modelling. Prog. Phys. Geogr. 2005, 29, 362–391. [Google Scholar] [CrossRef]
- Huss, M.; Bauder, A.; Funk, M.; Hock, R. Determination of the seasonal mass balance of four Alpine glaciers since 1865. J. Geophys. Res. Earth Surf. 2008, 113, F01015. [Google Scholar] [CrossRef]
- Ohmura, A. Physical Basis for the Temperature-Based Melt-Index Method. J. Appl. Meteorol. 2001, 40, 753–761. [Google Scholar] [CrossRef]
- Gabbi, J.; Carenzo, M.; Pellicciotti, F.; Bauder, A.; Funk, M. A comparison of empirical and physically based glacier surface melt models for long-term simulations of glacier response. J. Glaciol. 2014, 60, 1140–1154. [Google Scholar] [CrossRef]
- Réveillet, M.; Six, D.; Vincent, C.; Rabatel, A.; Dumont, M.; Lafaysse, M.; Morin, S.; Vionnet, V.; Litt, M. Relative performance of empirical and physical models in assessing the seasonal and annual glacier surface mass balance of Saint-Sorlin Glacier (French Alps). Cryosphere 2018, 12, 1367–1386. [Google Scholar] [CrossRef]
- Sorg, A.; Huss, M.; Rohrer, M.; Stoffel, M. The days of plenty might soon be over in glacierized Central Asian catchments. Environ. Res. Lett. 2014, 9, 104018. [Google Scholar] [CrossRef]
- Kienholz, C.; Hock, R.; Truffer, M.; Bieniek, P.; Lader, R. Mass Balance Evolution of Black Rapids Glacier, Alaska, 1980–2100, and Its Implications for Surge Recurrence. Front. Earth Sci. 2017, 5, 56. [Google Scholar] [CrossRef]
- IPCC. Climate change 2013: The physical science basis. In Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Watanabe, M.; Yanagawa, A.; Watanabe, S.; Hirabayashi, Y.; Kanae, S. Quantifying the range of future glacier mass change projections caused by differences among observed past-climate datasets. Clim. Dyn. 2019, 53, 2425–2435. [Google Scholar] [CrossRef]
- Wang, S.; Pu, J.; Wang, N. Study on mass balance and sensitivity to climate change in summer on the Qiyi Glacier, Qilian Mountains. Sci. Cold Arid Reg. 2012, 4, 281–287. [Google Scholar]
- Guo, Z.; Wang, N.; Wu, H.; Wu, Y.; Wu, X.; Li, Q. Variations in Firn Line Altitude and Firn Zone Area on Qiyi Glacier, Qilian Mountains, Over the Period of 1990 to 2011. Arct. Antarct. Alp. Res. 2015, 47, 293–300. [Google Scholar] [CrossRef]
- Wang, D.; Liu, J.; Wang, H.; Shao, W.; Mei, C.; Ding, X. Performance evaluations of CMIP6 and CMIP5 models for precipitation simulation over the Hanjiang River Basin, China. J. Water Clim. Chang. 2022, 13, 2089–2106. [Google Scholar] [CrossRef]
- Salathé, E.P. Downscaling simulations of future global climate with application to hydrologic modelling. Int. J. Climatol. 2005, 25, 419–436. [Google Scholar] [CrossRef]
- Shi, P.-H.; Duan, K.-Q.; Liu, H.-C.; Yang, J.-H.; Zhang, X.; Sun, J.-Y. Response of Xiao Dongkemadi Glacier in the central Tibetan Plateau to the current climate change and future scenarios by 2050. J. Mt. Sci. 2016, 13, 13–28. [Google Scholar] [CrossRef]
- Fujita, K.; Suzuki, R.; Nuimura, T.; Sakai, A. Performance of ASTER and SRTM DEMs, and their potential for assessing glacial lakes in the Lunana region, Bhutan Himalaya. J. Glaciol. 2008, 54, 220–228. [Google Scholar] [CrossRef]
- Oerlemans, J.; Fortuin, J.P.F. Sensitivity of Glaciers and Small Ice Caps to Greenhouse Warming. Science 1992, 258, 115–117. [Google Scholar] [CrossRef]
- Fujita, K.; Ohta, T.; Ageta, Y. Characteristics and climatic sensitivities of runoff from a cold-type glacier on the Tibetan Plateau. Hydrol. Process. 2007, 21, 2882–2891. [Google Scholar] [CrossRef]
- Young, J.C.; Arendt, A.; Hock, R.; Pettit, E. The challenge of monitoring glaciers with extreme altitudinal range: Mass-balance reconstruction for Kahiltna Glacier, Alaska. J. Glaciol. 2018, 64, 75–88. [Google Scholar] [CrossRef]
- Mosier, T.M.; Hill, D.F.; Sharp, K.V. How much cryosphere model complexity is just right? Exploration using the conceptual cryosphere hydrology framework. Cryosphere 2016, 10, 2147–2171. [Google Scholar] [CrossRef]
- Kang, E.; Cheng, G.; Lan, Y.; Jin, H. A model for simulating the response of runoff from the mountainous watersheds of inland river basins in the arid area of northwest China to climatic changes. Sci. China Ser. D Earth Sci. 1999, 42 (Suppl. 1), 52–63. [Google Scholar] [CrossRef]
- Oerlemans, J. Extracting a Climate Signal from 169 Glacier Records. Science 2005, 308, 675–677. [Google Scholar] [CrossRef]
- Radić, V.; Hock, R. Regional and global volumes of glaciers derived from statistical upscaling of glacier inventory data. J. Geophys. Res. Earth Surf. 2010, 115, F01010. [Google Scholar] [CrossRef]
- Grinsted, A. An estimate of global glacier volume. Cryosphere 2013, 7, 141–151. [Google Scholar] [CrossRef]
- Zhao, Q.; Ding, Y.; Wang, J.; Gao, H.; Zhang, S.; Zhao, C.; Xu, J.; Han, H.; Shangguan, D. Projecting climate change impacts on hydrological processes on the Tibetan Plateau with model calibration against the glacier inventory data and observed streamflow. J. Hydrol. 2019, 573, 60–81. [Google Scholar] [CrossRef]
- Berthier, E.; Arnaud, Y.; Kumar, R.; Ahmad, S.; Wagnon, P.; Chevallier, P. Remote sensing estimates of glacier mass balances in the Himachal Pradesh (Western Himalaya, India). Remote Sens. Environ. 2007, 108, 327–338. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, Y.; Cheng, W.; Ji, D.; Moore, J.C. Glacier evolution in high-mountain Asia under stratospheric sulfate aerosol injection geoengineering. Atmos. Chem. Phys. 2017, 17, 6547–6564. [Google Scholar] [CrossRef]
- Che, Y.; Zhang, M.; Li, Z.; Li, H.; Wang, S.; Sun, M.; Zha, S. Glacier mass-balance and length variation observed in China during the periods 1959–2015 and 1930–2014. Quat. Int. 2017, 454, 68–84. [Google Scholar] [CrossRef]
- Rupper, S.; Roe, G. Glacier Changes and Regional Climate: A Mass and Energy Balance Approach. J. Clim. 2008, 21, 5384–5401. [Google Scholar] [CrossRef]
- Yao, T.; Thompson, L.; Yang, W.; Yu, W.; Gao, Y.; Guo, X.; Yang, X.; Duan, K.; Zhao, H.; Xu, B.; et al. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Cao, B.; Pan, B.-T.; Cai, M.-Y.; Wang, J. An investigation on changes in glacier mass balance and hypsometry for a small mountainous glacier in the northeastern Tibetan Plateau. J. Mt. Sci. 2017, 14, 1624–1632. [Google Scholar] [CrossRef]
- Ji, Q.; Yang, T.B.; Dong, J.; He, Y. Glacier variations in response to climate change in the eastern Nyainqêntanglha Range, Tibetan Plateau from 1999 to 2015. Arct. Antarct. Alp. Res. 2018, 50, e1435844. [Google Scholar] [CrossRef]
- Zhu, M.; Yao, T.; Yang, W.; Xu, B.; Wu, G.; Wang, X.; Xie, Y. Reconstruction of the mass balance of Muztag Ata No. 15 glacier, eastern Pamir, and its climatic drivers. J. Glaciol. 2018, 64, 259–274. [Google Scholar] [CrossRef]
- Ke, L.; Ding, X.; Song, C. Estimation of mass balance of Dongkemadi glaciers with multiple methods based on multi-mission satellite data. Quat. Int. 2015, 371, 58–66. [Google Scholar] [CrossRef]
- Mölg, T.; Maussion, F.; Scherer, D. Mid-latitude westerlies as a driver of glacier variability in monsoonal High Asia. Nat. Clim. Chang. 2014, 4, 68–73. [Google Scholar] [CrossRef]
- Zhao, L.; Ding, R.; Moore, J.C. Glacier volume and area change by 2050 in high mountain Asia. Glob. Planet. Chang. 2014, 122, 197–207. [Google Scholar] [CrossRef]
- Zhang, Y.; Enomoto, H.; Ohata, T.; Kitabata, H.; Kadota, T.; Hirabayashi, Y. Projections of glacier change in the Altai Mountains under twenty-first century climate scenarios. Clim. Dyn. 2016, 47, 2935–2953. [Google Scholar] [CrossRef]
- Xie, Z.-C.; Wang, X.; Feng, Q.-H.; Kang, E.; Liu, C.-H.; Li, Q.-Y. Modeling the response of glacier systems to climate warming in China. Ann. Glaciol. 2006, 43, 313–316. [Google Scholar] [CrossRef]
- Shi, Y.; Liu, S. Estimation on the response of glaciers in China to the global warming in the 21st century. Chin. Sci. Bull. 2000, 45, 668–672. [Google Scholar] [CrossRef]
- Li, L.; Shen, M.; Hou, Y.; Xu, C.-Y.; Lutz, A.F.; Chen, J.; Jain, S.K.; Li, J.; Chen, H. Twenty-first-century glacio-hydrological changes in the Himalayan headwater Beas River basin. Hydrol. Earth Syst. Sci. 2019, 23, 1483–1503. [Google Scholar] [CrossRef]
- Li, Y.; Tian, L.; Yi, Y.; Moore, J.C.; Sun, S.; Zhao, L. Simulating the Evolution of Qiangtang No. 1 Glacier in the Central Tibetan Plateau to 2050. Arct. Antarct. Alp. Res. 2017, 49, 1–12. [Google Scholar] [CrossRef]

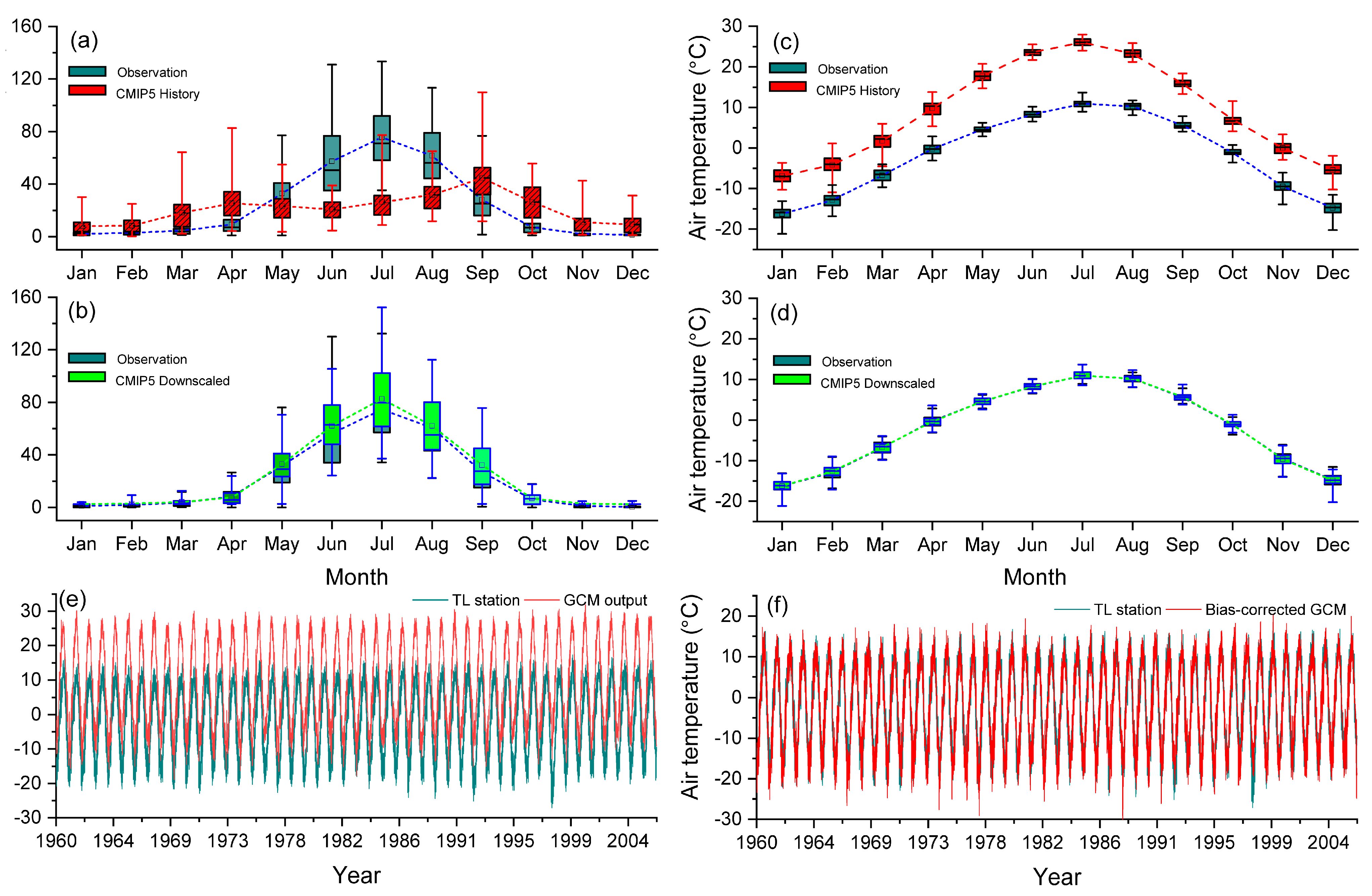

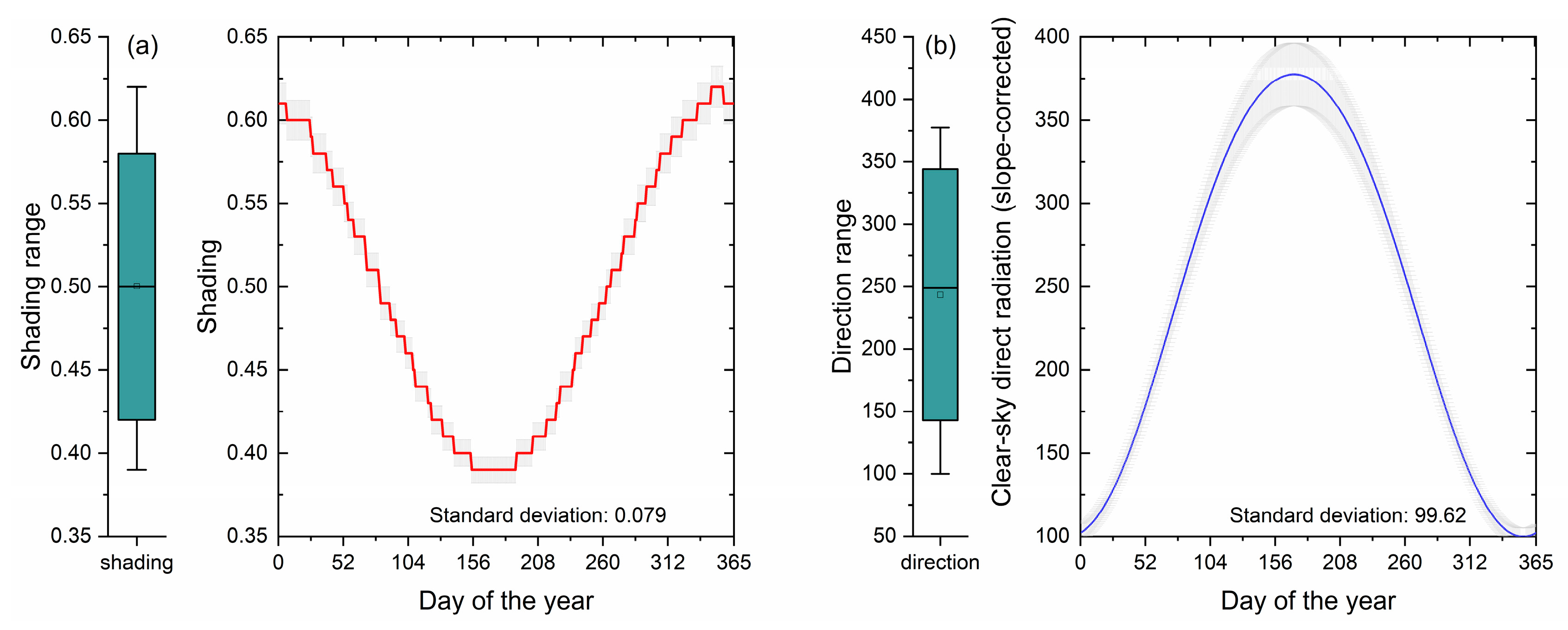
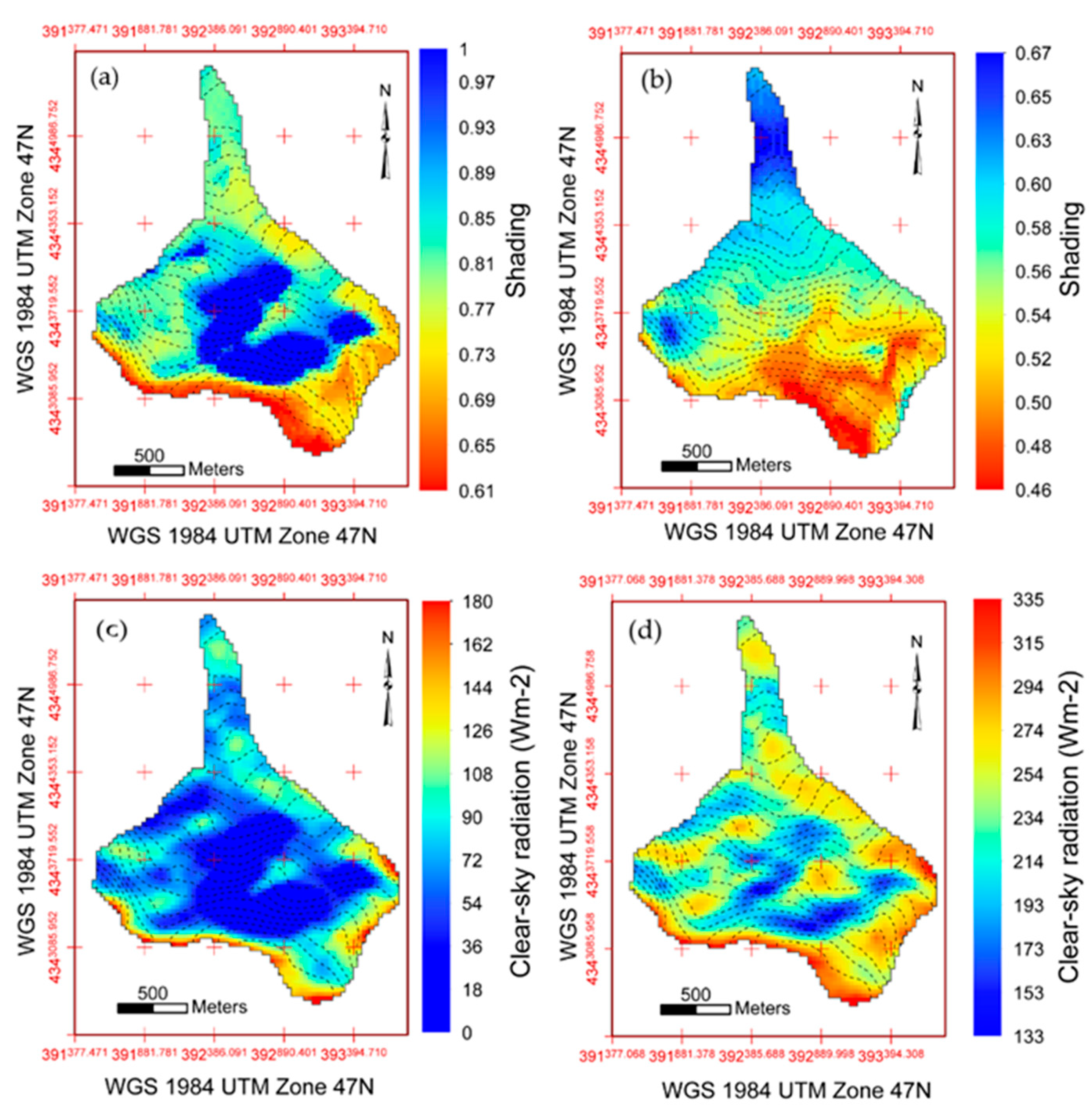
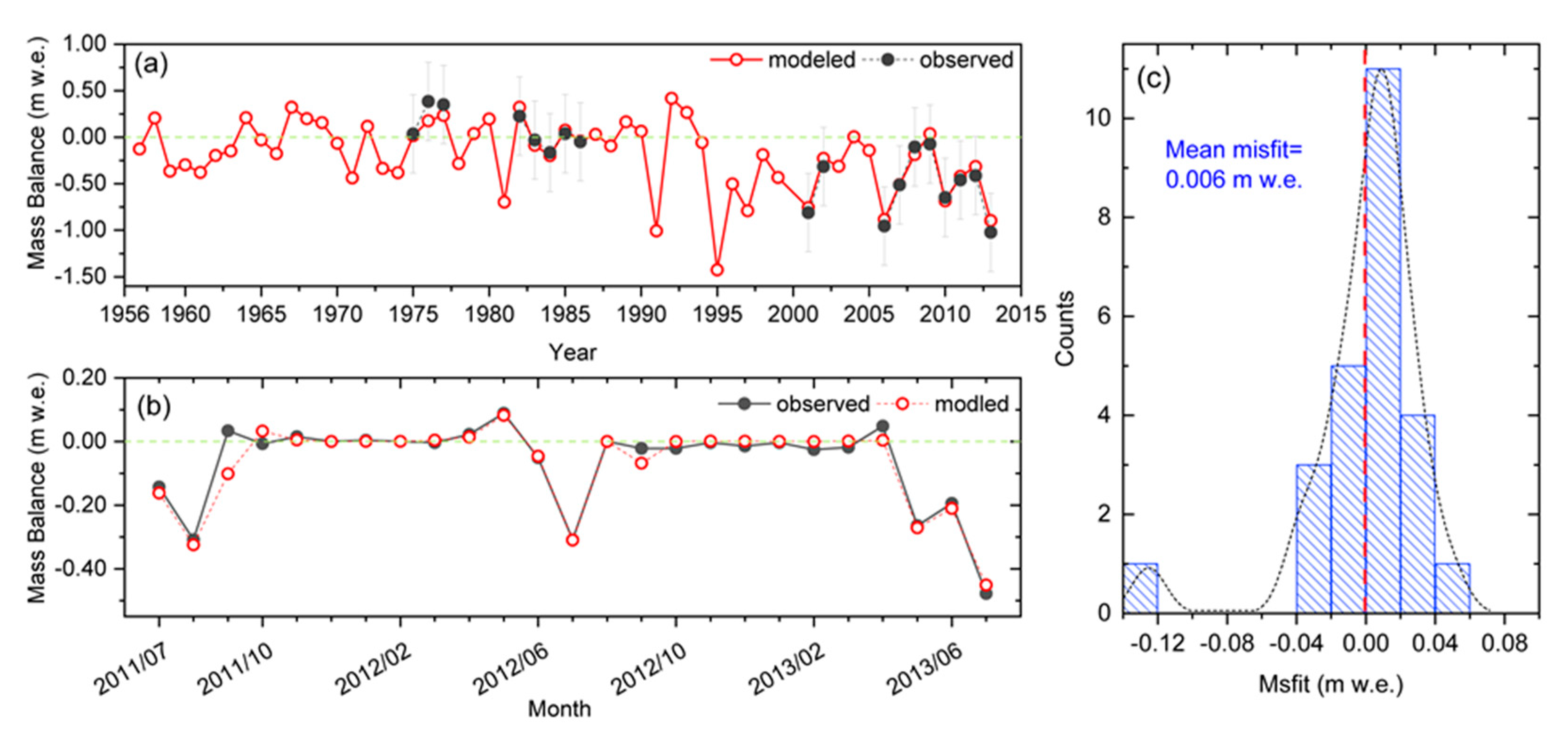



| Station | Periods | Latitude /°N | Longitude /°E | Altitude /m | Summer T/°C | Winter T/°C | Summer P/mm | Winter P/mm |
|---|---|---|---|---|---|---|---|---|
| Tuole | 1957–2013 | 38.48 | 98.25 | 3820 | 8.34 | −8.06 | 1.74 | 0.15 |
| Yeniugou | 1960–2013 | 38.25 | 99.35 | 4429 | 7.38 | −8.03 | 2.52 | 0.24 |
| Qilian | 1957–2013 | 38.11 | 100.15 | 3597 | 11.11 | −3.93 | 2.58 | 0.26 |
| Wuwei | 1953–2013 | 37.55 | 102.40 | 3772 | 20.67 | 2.17 | 0.70 | 0.10 |
| No. | Abbreviation | Model Name | Organization | Resolution (Lon. × Lat., No. Levels) | Nationality |
|---|---|---|---|---|---|
| 1 | AC1 | ACCESS1-0 | CSIRO and BoM | 192 × 145, L38 | Australia |
| 2 | AC2 | ACCESS1-3 | CSIRO and BoM | 192 × 145, L38 | Australia |
| 3 | BC1 | BCC-CSM1-1 | BCC | 128 × 64, L26 (T42) | China |
| 4 | BC2 | BCC-CSM1-1-m | BCC | 128 × 64, L26 (T42) | China |
| 5 | BNU | BNU-ESM | GCESS | 128 × 64, L26 (T42) | China |
| 6 | CaE | CanESM2 | CCCMA | 128 × 64, L35 (T63) | Canada |
| 7 | CCS | CCSM4 | NCAR | 288 × 192, L26 | USA |
| 8 | CE1 | CESM1-BGC | NSF-DOE-NCAR | 288 × 192, L26 | USA |
| 9 | CE2 | CESM1-CAM5 | NSF-DOE-NCAR | 288 × 192, L26 | USA |
| 10 | CE5 | CESM1-WACCM | NSF-DOE-NCAR | 288 × 192, L26 | USA |
| 11 | CM2 | CMCC-CM | CMCC | 480 × 240, L31 (T159) | Europe |
| 12 | CM3 | CMCC-CMS | CMCC | 480 × 240, L31 (T159) | Europe |
| 13 | ECE | EC-EARTH | EC-EARTH | 320 × 160, L62 (T159) | Europe |
| 14 | FIO | FIO-ESM | FIO | 128 × 64, | China |
| 15 | GE1 | GISS-E2-H | NASA GISS | 144 × 90, | USA |
| 16 | GE2 | GISS-E2-H-CC | NASA GISS | 144 × 90, | USA |
| 17 | GE3 | GISS-E2-R | NASA GISS | 144 × 90, | USA |
| 18 | GF2 | GFDL-CM3 | NOAA GFDL | 144 × 90, L24 | USA |
| 19 | GF3 | GFDL-ESM2G | NOAA GFDL | 144 × 90, L24 | USA |
| 20 | GF4 | GFDL-ESM2M | NOAA GFDL | 144 × 90, L24 | USA |
| 21 | Ha5 | HadGEM2-AO | NIMR/KMA | 192 × 145, | Korea |
| 22 | INC | INM-CM4 | INM | 180 × 120, L21 | Russia |
| 23 | IP2 | IPSL-CM5A-MR | IPSL | 144 × 143, L39 | France |
| 24 | IP3 | IPSL-CM5B-LR | IPSL | 96 × 96, L39 | France |
| 25 | MI2 | MIROC5 | MIROC | 256 × 128, L40 (T85) | Japan |
| 26 | MI3 | MIROC-ESM | MIROC | 128 × 64, L80 (T42) | Japan |
| 27 | MI4 | MIROC-ESM-CHEM | MIROC | 128 × 64, L80 (T42) | Japan |
| 28 | MP1 | MPI-ESM-LR | MPI-M | 192 × 96, L47 (T63) | Germany |
| 29 | MR3 | MRI-CGCM3 | MRI | 320 × 160, L48 (T159) | Japan |
| 30 | NE1 | NorESM1-M | NCC | 144 × 96, L26 | Norway |
| 31 | NE2 | NorESM1-ME | NCC | 144 × 96, L26 | Norway |
| References | Volume-Area Scaling Laws | Comments |
|---|---|---|
| Radić and Hock [48] | V = 0.0365A1.375 | Based on earlier studies |
| Grinsted et al. [49] | V = 0.0433A1.290 | Obtained from minimizing the absolute volume deviation from glacier inventory |
| Huss et al. [28] | V = 0.0259A1.275 | Relationship for Central Asia |
| Liu et al. [4] | V = 0.0395A1.350 | From the observation of Qilian and Tien Shan |
| Parameters | January | February | March | April | May | June | July | August | September | October | November | December |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Temperature | 0.53 | 0.55 | 0.52 | 0.67 | 0.71 | 0.58 | 0.63 | 0.62 | 0.61 | 0.49 | 0.51 | 0.46 |
| Precipitation | 0.39 | 0.49 | 0.29 | 0.43 | 0.40 | 0.24 | 0.23 | 0.16 | 0.21 | 1.25 | 0.93 | 1.89 |
| Parameters | Values | Units |
|---|---|---|
| Melt factor, fm | 2 | mm day−1 °C−1 |
| Radiation coefficient for snow, αsnow | 6 | mm day−1W−1m2 °C−1 |
| Radiation coefficient for ice, αice | 1.5 | mm day−1W−1m2 °C−1 |
| Precipitation correction factor, S | 25 | % |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, P.; Han, B.; Duan, K.; Cao, L.; Chen, A.; Wu, Y. Glaciers Variation at ‘Shocking’ Pace in the Northeastern Margin of Tibetan Plateau from 1957 to 21st Century: A Case Study of Qiyi Glacier. Atmosphere 2023, 14, 723. https://doi.org/10.3390/atmos14040723
Shi P, Han B, Duan K, Cao L, Chen A, Wu Y. Glaciers Variation at ‘Shocking’ Pace in the Northeastern Margin of Tibetan Plateau from 1957 to 21st Century: A Case Study of Qiyi Glacier. Atmosphere. 2023; 14(4):723. https://doi.org/10.3390/atmos14040723
Chicago/Turabian StyleShi, Peihong, Bangshuai Han, Keqin Duan, Liguo Cao, Anan Chen, and Yuwei Wu. 2023. "Glaciers Variation at ‘Shocking’ Pace in the Northeastern Margin of Tibetan Plateau from 1957 to 21st Century: A Case Study of Qiyi Glacier" Atmosphere 14, no. 4: 723. https://doi.org/10.3390/atmos14040723
APA StyleShi, P., Han, B., Duan, K., Cao, L., Chen, A., & Wu, Y. (2023). Glaciers Variation at ‘Shocking’ Pace in the Northeastern Margin of Tibetan Plateau from 1957 to 21st Century: A Case Study of Qiyi Glacier. Atmosphere, 14(4), 723. https://doi.org/10.3390/atmos14040723








