Uncertainty in the Mobile Observation of Wind
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
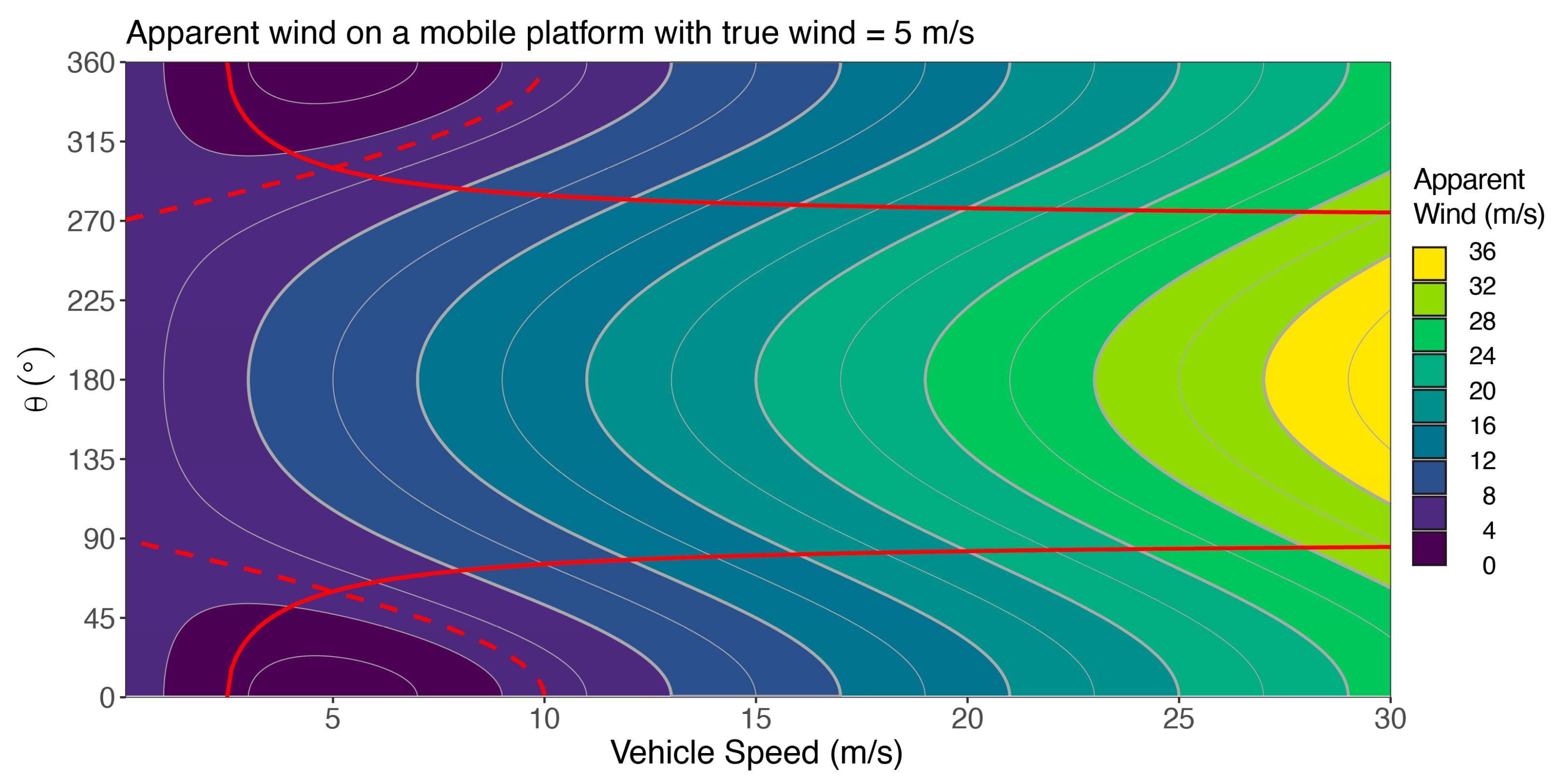
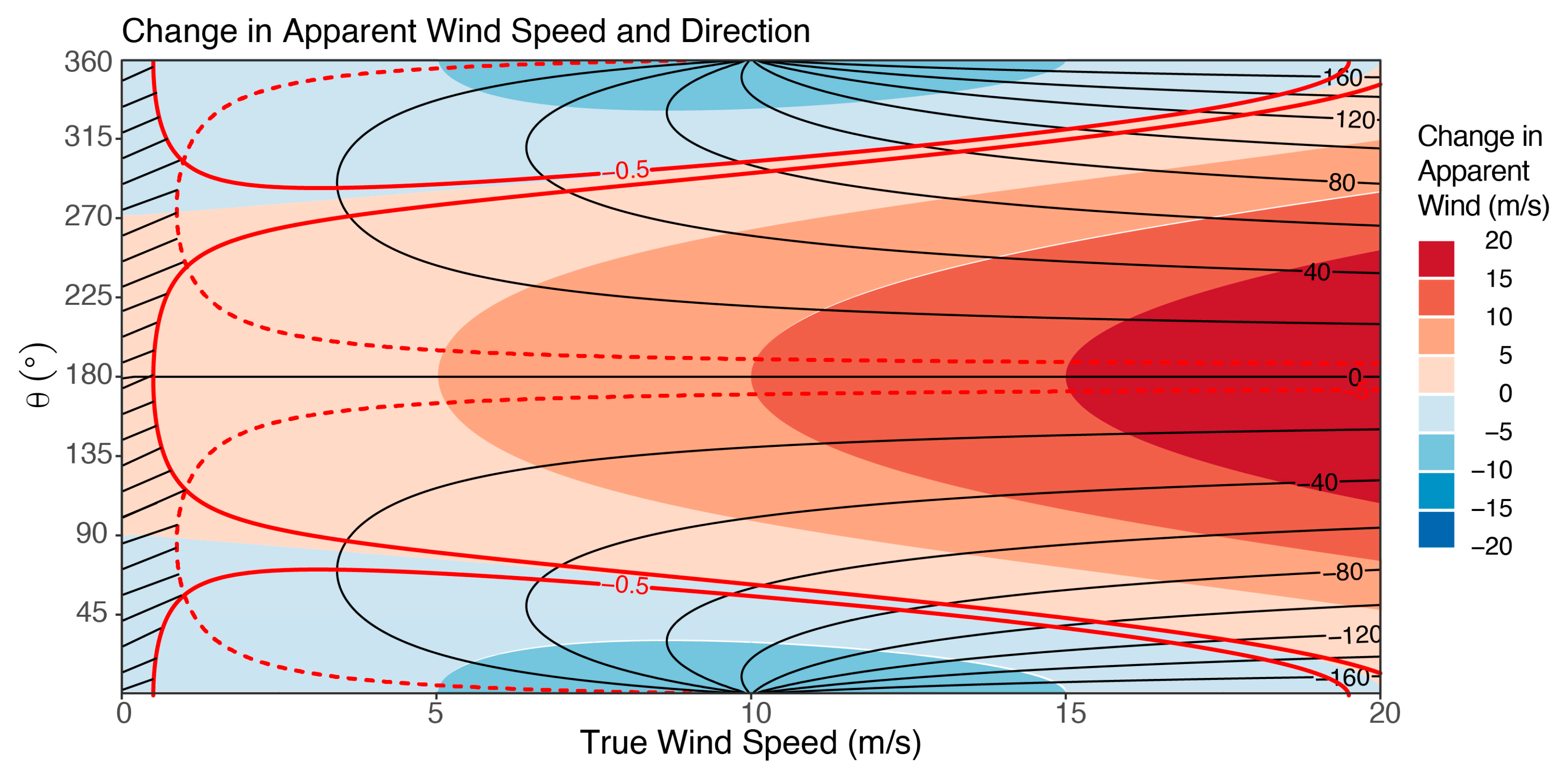
3.1. Distinguishing True Wind from Apparent Wind
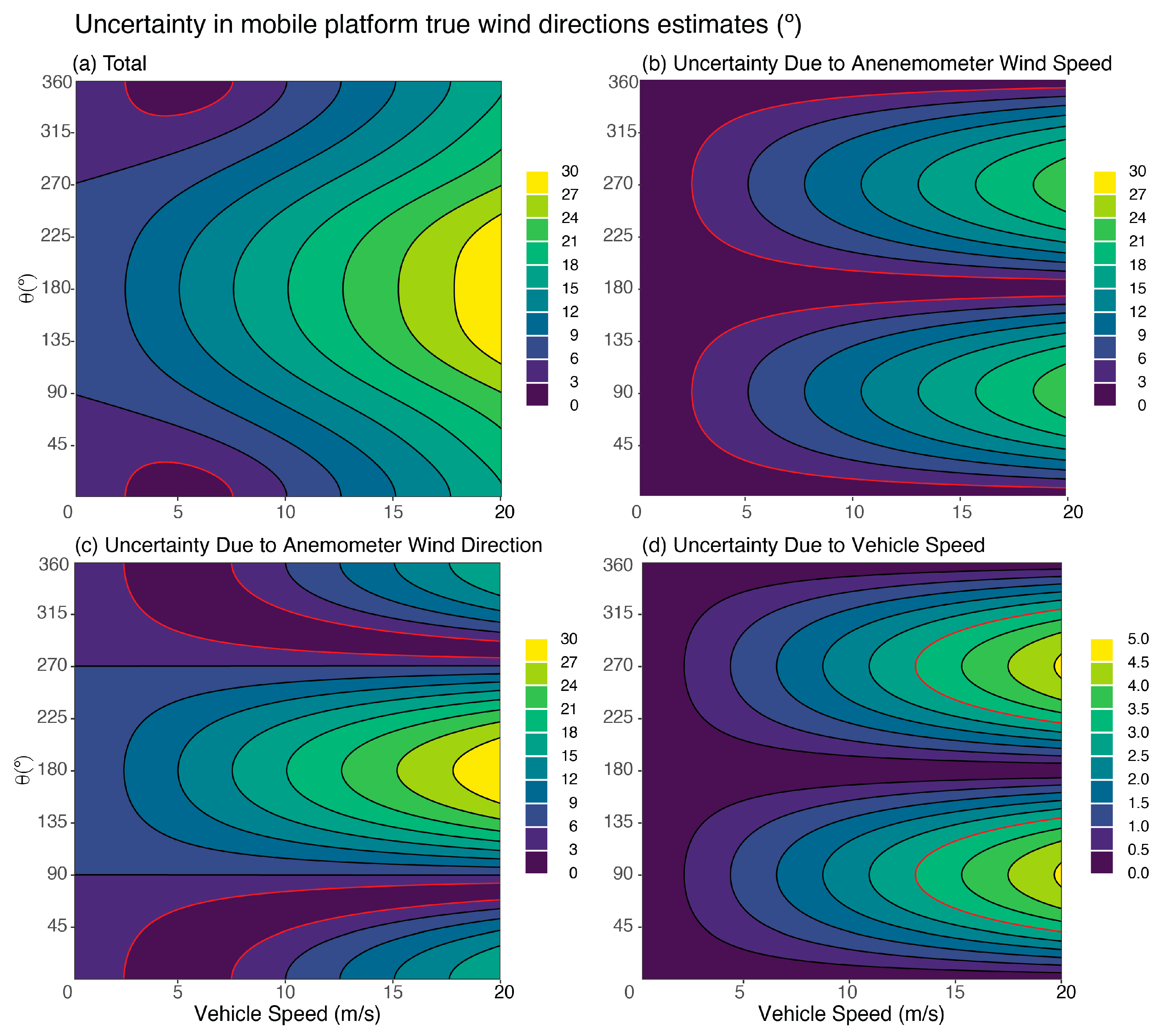
3.2. Uncertainty in True Wind Estimation
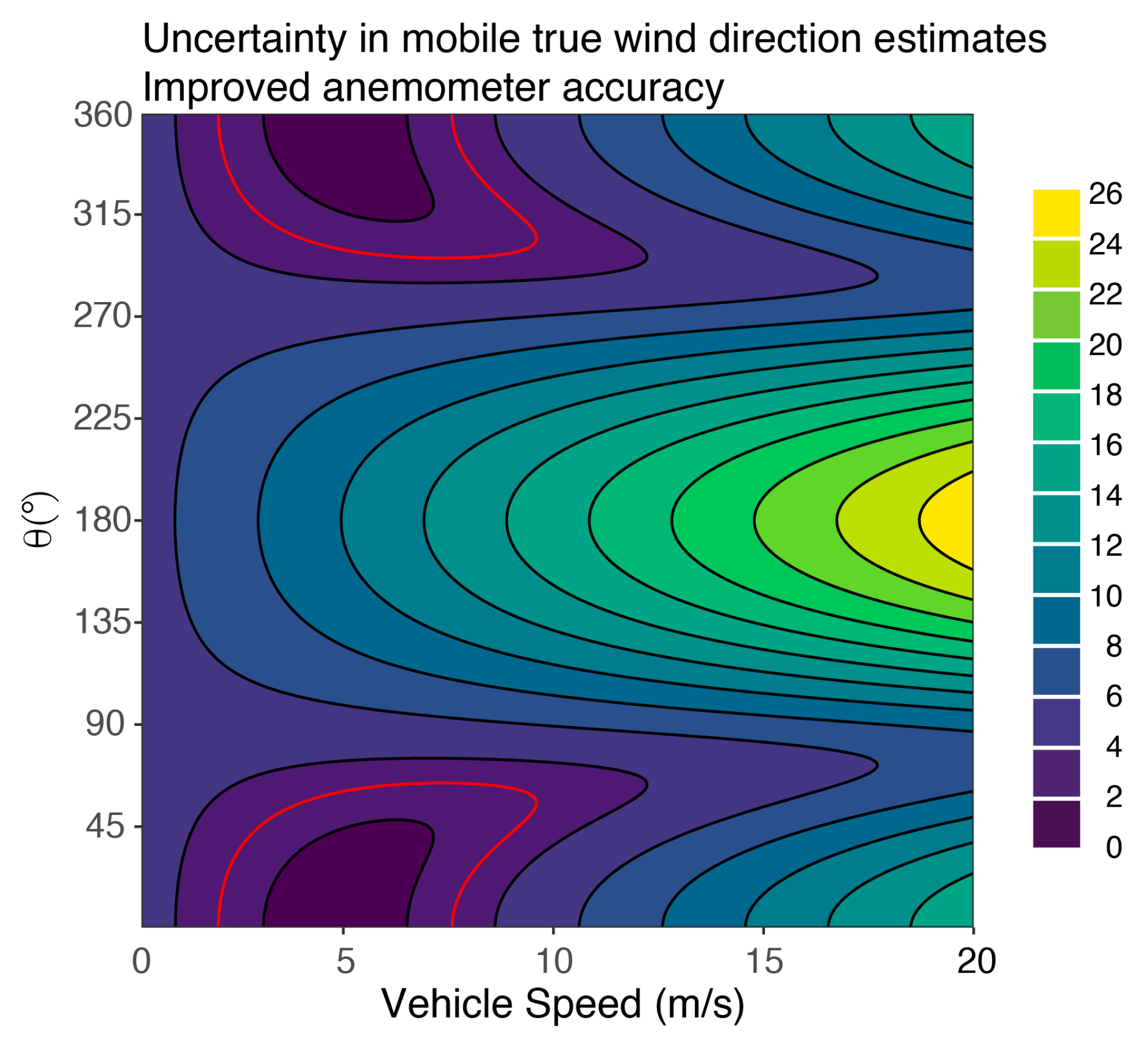
3.3. Additional Sources of Uncertainty
3.4. Example—Transect across a Plume
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Belušić, D.; Lenschow, D.H.; Tapper, N.J. Performance of a mobile car platform for mean wind and turbulence measurements. Atmos. Meas. Tech. 2014, 7, 1825–1837. [Google Scholar] [CrossRef]
- Miller, S.J.; Gordon, M.; Staebler, R.M.; Taylor, P.A. A Study of the Spatial Variation of Vehicle-Induced Turbulence on Highways Using Measurements from a Mobile Platform. Boundary-Layer Meteorol. 2019, 171, 1–29. [Google Scholar] [CrossRef]
- De Boer, G.; Waugh, S.; Erwin, A.; Borenstein, S.; Dixon, C.; Shanti, W.; Houston, A.; Argrow, B. Measurements from mobile surface vehicles during the Lower Atmospheric Profiling Studies at Elevation—A Remotely-piloted Aircraft Team Experiment (LAPSE-RATE). Earth Syst. Sci. Data 2021, 13, 155–169. [Google Scholar] [CrossRef]
- Miller, S.J.; Gordon, M. The measurement of mean wind, variances, and covariances from an instrumented mobile car in a rural environment. Atmos. Meas. Tech. 2022, 15, 6563–6584. [Google Scholar] [CrossRef]
- Caulton, D.R.; Li, Q.; Bou-Zeid, E.; Fitts, J.P.; Golston, L.M.; Pan, D.; Lu, J.; Lane, H.M.; Buchholz, B.; Guo, X.; et al. Quantifying uncertainties from mobile-laboratory-derived emissions of well pads using inverse Gaussian methods. Atmos. Chem. Phys. 2018, 18, 15145–15168. [Google Scholar] [CrossRef]
- Zhang, J.; Ninneman, M.; Joseph, E.; Schwab, M.J.; Shrestha, B.; Schwab, J.J. Mobile laboratory measurements of high surface ozone levels and spatial heterogeneity during LISTOS 2018: Evidence for sea breeze influence. J. Geophys. Res.-Atmos. 2019, 124, e2019JD031961. [Google Scholar] [CrossRef]
- Catena, A.M.; Zhang, J.; Commane, R.; Murray, L.T.; Schwab, M.J.; Leibensperger, E.M.; Marto, J.; Smith, M.L.; Schwab, J.J. Hydrogen Sulfide Emission Properties from Two Large Landfills in New York State. Atmosphere 2022, 13, 1251. [Google Scholar] [CrossRef]
- Boanini, C.; Mecca, D.; Pognant, F.; Bo, M.; Clerico, M. Integrated Mobile Laboratory for Air Pollution Assessment: Literature Review and cc-TrAIRer Design. Atmosphere 2021, 12, 1004. [Google Scholar] [CrossRef]
- Majluf, F.Y.; Krechmer, J.E.; Daube, C.; Knighton, W.B.; Dyroff, C.; Lambe, A.T.; Fortner, E.C.; Yacovitch, T.I.; Roscioli, J.R.; Herndon, S.C.; et al. Mobile Near-Field Measurements of Biomass Burning Volatile Organic Compounds: Emission Ratios and Factor Analysis. Environ. Sci. Technol. Lett. 2022, 9, 383–390. [Google Scholar] [CrossRef]
- Shah, A.; Allen, G.; Pitt, J.R.; Ricketts, H.; Williams, P.I.; Helmore, J.; Finlayson, A.; Robinson, R.; Kabbabe, K.; Hollingsworth, P.; et al. A Near-Field Gaussian Plume Inversion Flux Quantification Method, Applied to Unmanned Aerial Vehicle Sampling. Atmosphere 2019, 10, 396. [Google Scholar] [CrossRef]
- Viatte, C.; Lauvaux, T.; Hedelius, J.K.; Parker, H.; Chen, J.; Jones, T.; Franklin, J.E.; Deng, A.J.; Gaudet, B.; Verhulst, K.; et al. Methane emissions from dairies in the Los Angeles Basin. Atmos. Chem. Phys. 2017, 17, 7509–7528. [Google Scholar] [CrossRef]
- Golston, L.M.; Pan, D.; Sun, K.; Tao, L.; Zondlo, M.A.; Eilerman, S.J.; Peischl, J.; Neuman, J.A.; Floerchinger, C. Variability of Ammonia and Methane Emissions from Animal Feeding Operations in Northeastern Colorado. Environ. Sci. Technol. 2020, 54, 11015–11024. [Google Scholar] [CrossRef]
- Atherton, E.; Risk, D.; Fougère, C.; Lavoie, M.; Marshall, A.; Werring, J.; Williams, J.P.; Minions, C. Mobile Measurement of Methane Emissions from Natural Gas Developments in Northeastern British Columbia, Canada. Atmos. Chem. Phys. 2017, 17, 12405–12420. [Google Scholar] [CrossRef]
- Hoesly, R.M.; Smith, S.J.; Feng, L.; Klimont, Z.; Janssens-Maenhout, G.; Pitkanen, T.; Seibert, J.J.; Vu, L.; Andres, R.J.; Bolt, R.M.; et al. Historical (1750–2014) anthropogenic emissions of reactive gases and aerosols from the Community Emissions Data System (CEDS). Geosci. Model Dev. 2018, 11, 369–408. [Google Scholar] [CrossRef]
- Jacob, D.J.; Turner, A.J.; Maasakkers, J.D.; Sheng, J.; Sun, K.; Liu, X.; Chance, K.; Aben, I.; McKeever, J.; Frankenberg, C. Satellite observations of atmospheric methane and their value for quantifying methane emissions. Atmos. Chem. Phys. 2016, 16, 14371–14396. [Google Scholar] [CrossRef]
- Palmer, P.I.; Feng, L.; Lunt, M.F.; Parker, R.J.; Bösch, H.; Lan, X.; Lorente, A.; Borsdorff, T. The added value of satellite observations of methane for understanding the contemporary methane budget. Phil. Trans. R. Soc. A 2021, 379, 20210106. [Google Scholar] [CrossRef]
- Montzka, S.A.; Dutton, G.S.; Portmann, R.W.; Chipperfield, M.P.; Davis, S.; Feng, W.; Manning, A.J.; Ray, E.; Rigby, M.; Hall, B.D.; et al. A decline in global CFC-11 emissions during 2018–2019. Nature 2021, 590, 428–432. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Jia, H.; Qiu, Q.; Lu, Y.; Zhang, J.; Mao, J.; Fan, W.; Huang, M. Typhoon-Induced Fragility Analysis of Transmission Tower in Ningbo Area Considering the Effect of Long-Term Corrosion. Appl. Sci. 2022, 12, 4774. [Google Scholar] [CrossRef]
- Conley, S.; Faloona, I.; Mehrotra, S.; Suard, M.; Suard, M.; Lenschow, D.H.; Sweeney, C.; Herndon, S.; Schwietzke, S.; Pétron, G.; et al. Application of Gauss’s theorem to quantify localized surface emissions from airborne measurements of wind and trace gases. Atmos. Meas. Tech. 2017, 10, 2245–2258. [Google Scholar] [CrossRef]
- Hanlon, T.; Risk, D. Using Computational Fluid Dynamics and Field Experiments to Improve Vehicle-Based Wind Measurements for Environmental Monitoring. Atmos. Meas. Tech. 2020, 13, 191–203. [Google Scholar] [CrossRef]
- Yahaya, S.; Frangi, J.P. Cup Anemometer Response to the Wind Turbulence-Measurement of the Horizontal Wind Variance. Ann. Geophys. 2004, 22, 3363–3374. [Google Scholar] [CrossRef]
- Barbieri, L.; Kral, S.T.; Bailey, S.C.C.; Frazier, A.E.; Jacob, J.D.; Reuder, J.; Brus, D.; Chilson, P.B.; Crick, C.; Detweiler, C.; et al. Intercomparison of Small Unmanned Aircraft System (sUAS) Measurements for Atmospheric Science during the LAPSE-RATE Campaign. Sensors 2019, 19, 2179. [Google Scholar] [CrossRef]
- Thielicke, W.; Hübert, W.; Müller, U.; Eggert, M.; Wilhelm, P. Towards Accurate and Practical Drone-Based Wind Measurements with an Ultrasonic Anemometer. Atmos. Meas. Tech. 2021, 14, 1303–1318. [Google Scholar] [CrossRef]
- Anemoment TriSonica Features. Available online: https://anemoment.com/features/ (accessed on 8 April 2023).
- Airmar 200WX WeatherStation® Instrument Specifications. Available online: https://www.airmar.com/weather-description.html?id=154 (accessed on 7 March 2023).
- Young, R.M. ResponseONE Ultrasonic Anemometer. Available online: https://www.youngusa.com/product/responseone-ultrasonic-anemometer/ (accessed on 7 March 2023).
- Campbell Scientific Wind Speed and Direction. Available online: https://www.campbellsci.com/wind-speed-direction (accessed on 7 March 2023).
- Smith, S.R.; Bourassa, M.A.; Sharp, R.J. Establishing More Truth in True Winds. J. Atmos. Ocean Technol. 1999, 16, 939–952. [Google Scholar] [CrossRef]
- Moore, D.P.; Li, N.P.; Wendt, L.P.; Castañeda, S.R.; Falinski, M.M.; Zhu, J.-J.; Song, C.; Ren, Z.J.; Zondlo, M.A. Underestimation of Sector-Wide Methane Emissions from United States Wastewater Treatment. Environ. Sci. Technol. 2023, 57, 4082–4090. [Google Scholar] [CrossRef] [PubMed]
- Taylor, J.R. An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements; University Science Books: Herndon, VA, USA, 1996. [Google Scholar]
- Automated Surface Observation Systems. Available online: https://www.weather.gov/asos/ (accessed on 7 March 2023).
- The High-Resolution Rapid Refresh Model. Available online: https://rapidrefresh.noaa.gov/hrrr/ (accessed on 7 March 2023).
- Stull, R. Atmospheric Boundary Layer in: Meteorology: An Algebra-Based Survey of Atmospheric Science; University of British Columbia: Vancouver, BC, Canada, 2023. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leibensperger, E.M.; Konieczny, M.; Weil, M.D. Uncertainty in the Mobile Observation of Wind. Atmosphere 2023, 14, 765. https://doi.org/10.3390/atmos14050765
Leibensperger EM, Konieczny M, Weil MD. Uncertainty in the Mobile Observation of Wind. Atmosphere. 2023; 14(5):765. https://doi.org/10.3390/atmos14050765
Chicago/Turabian StyleLeibensperger, Eric M., Mikolaj Konieczny, and Matthew D. Weil. 2023. "Uncertainty in the Mobile Observation of Wind" Atmosphere 14, no. 5: 765. https://doi.org/10.3390/atmos14050765
APA StyleLeibensperger, E. M., Konieczny, M., & Weil, M. D. (2023). Uncertainty in the Mobile Observation of Wind. Atmosphere, 14(5), 765. https://doi.org/10.3390/atmos14050765




