Assessment of GPM Satellite Precipitation Performance after Bias Correction, for Hydrological Modeling in a Semi-Arid Watershed (High Atlas Mountain, Morocco)
Abstract
:1. Introduction
2. Research Location and Used Data
2.1. Study Area
2.2. Gauge Precipitation Data
2.3. Earth Observation of Precipitation Data
2.4. Discharge Data
2.5. HEC-HMS Software
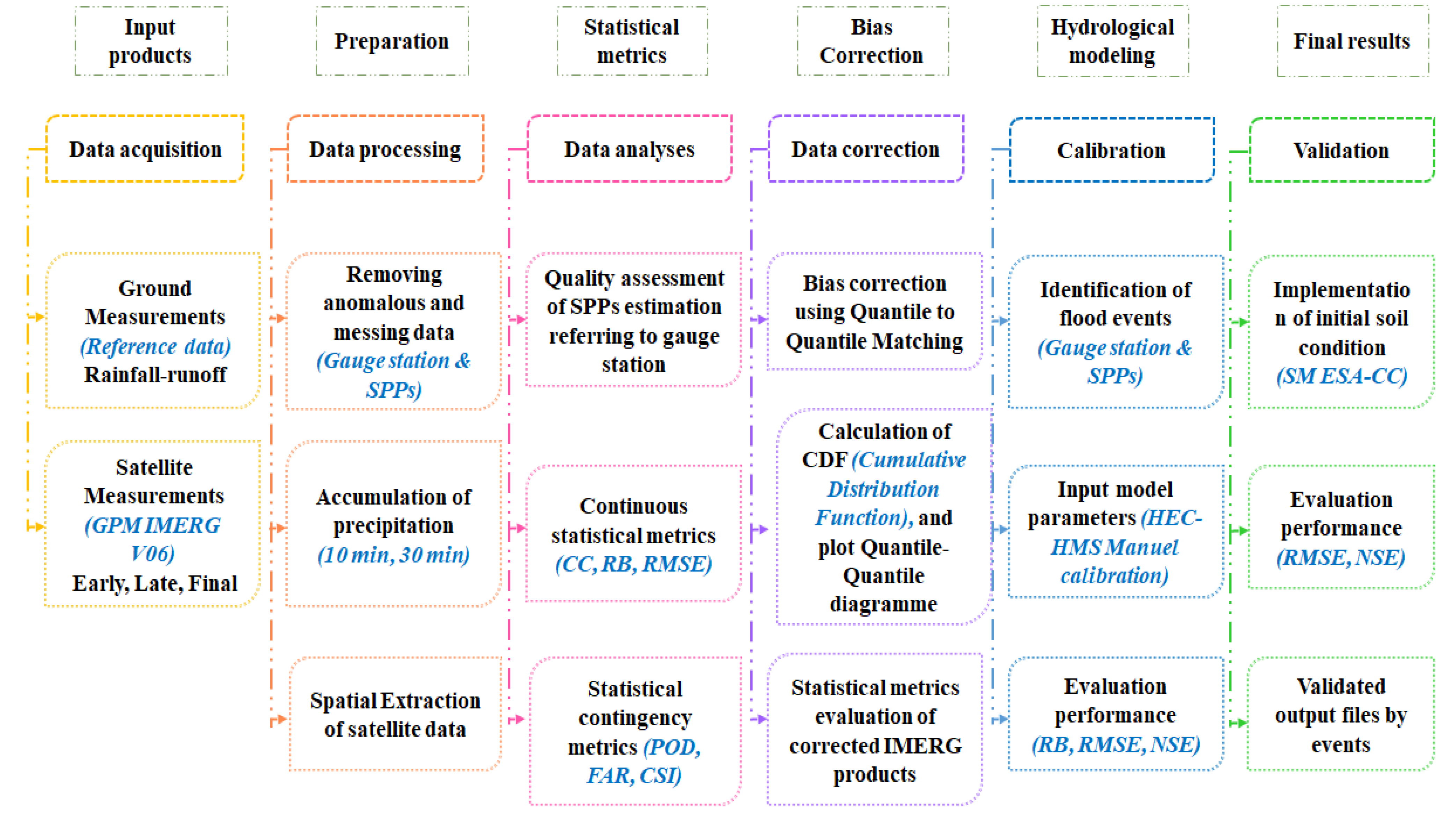
3. Methods
3.1. Processing Data
3.2. Satellite Monitoring of Precipitation Products
3.3. Metrics Assessment
3.4. Quantile Mapping Method
3.5. Hydrological Process
3.6. DEM
4. Results
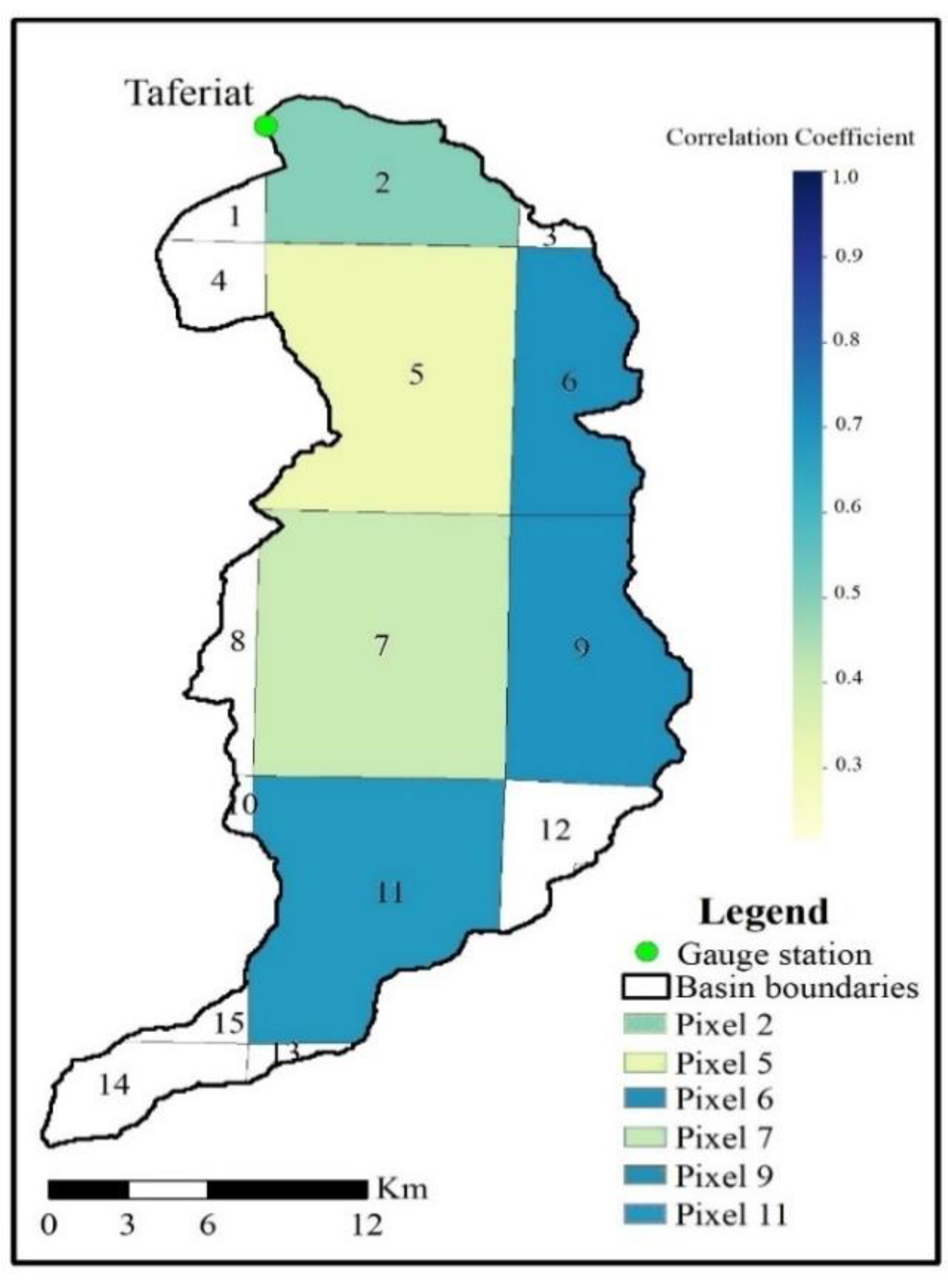
4.1. Rainfall Spatialization and Runoff Assessment
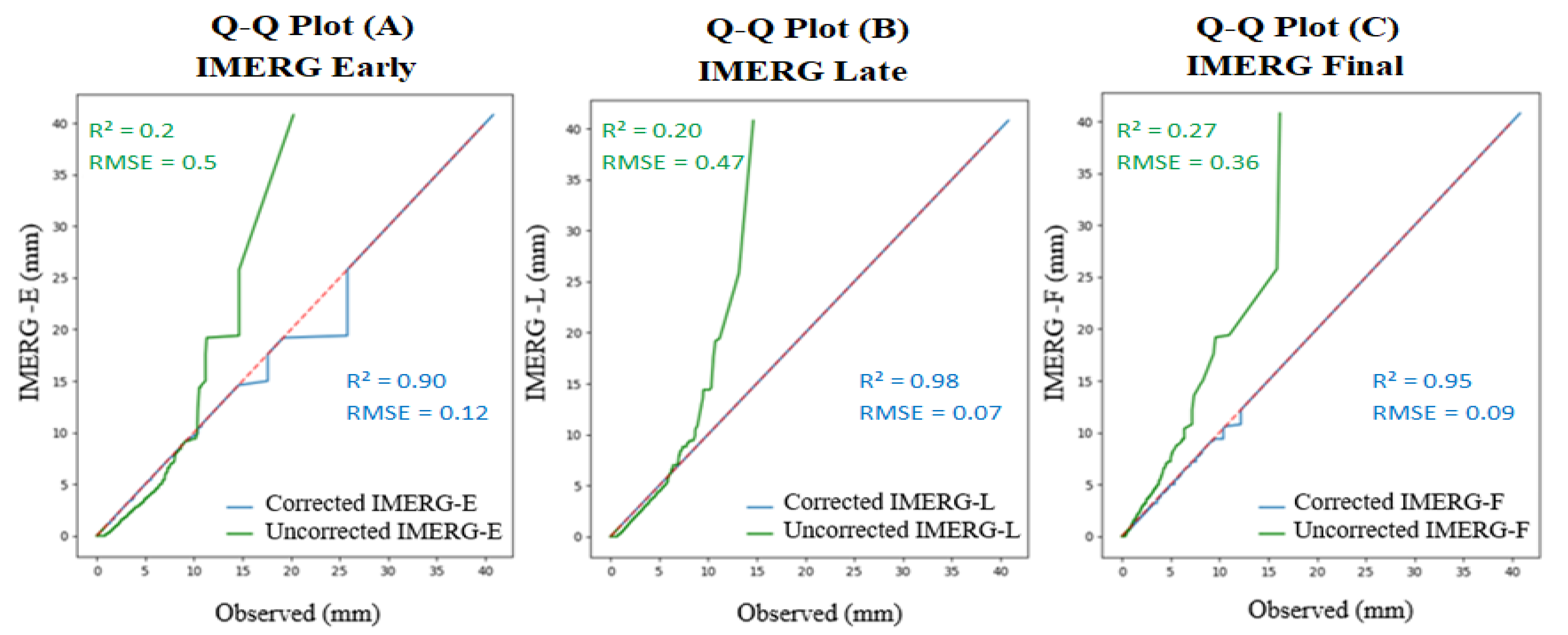
4.2. Performance of CDF Matching Method
4.3. Statistical Indices Assessment
4.4. Hydrological Calibration and Validation
4.4.1. Calibration and Validation of IMERG Early Events
4.4.2. Calibration and Validation of IMERG Late Events
4.4.3. Calibration and Validation of IMERG Final Events
5. Conclusions
- (1)
- The QM is an effective process for correcting the bias of satellite precipitation estimates when ground precipitation is not available. The statistical evaluation findings of the QM method indicated that IMERG_L showed a moderate improvement and performed slightly superior to IMERG_E and IMERG_F. Overall, the lack of rain-gauge stations prevents the correct evaluation of earth observation products and leads to an underestimation of the product’s performance, which is our case.
- (2)
- Regarding the effectiveness of the three SPPs, IMERG Late surpassed the remaining two SPPs in the majority of statistical metrics. However, IMERG Final ranked second to IMERG Early which slightly overestimated total precipitation.
- (3)
- The results of the hydrological model indicate that the IMERG Early, Late, and Final products achieved satisfactory hydrological performance with mean evaluation criteria (NSE) of 0.77, 0.82, and 0.82 respectively. However, during the validation of the flood events, by considering the initial soil conditions, IMERG_F and IMERG_E showed a significant overestimation of the discharge of 13%, and 10% respectively, while IMERG_L performed satisfactorily in the validation part with an avg. value of NSE = 0.69.
- (4)
- In synthesis, we can report that IMERG Early is quite reliable for capturing short-term extreme rainfall events of high intensity, and less suitable for precipitation events of medium and long duration and low intensity. Due to its 4-h latency, this product is not sensitive to the initial soil moisture conditions applied during the validation, which explains the decrease in these evaluation criteria, especially the NSE of 10%.
- (5)
- Furthermore, the IMERG Late precipitation product has the aptitude to estimate the precipitation time series at different flood intensities and durations, better than the IMERG Early and Final products. However, due to its time latency of about 14 h, it allows for some data adjustments, e.g., to take into account the initial soil moisture condition which clearly improved its validation results.
- (6)
- Nevertheless, the IMERG Finale product is not well adapted to short duration flash flood simulations in mountainous regions, which explains further the decrease in validation performance criteria by 13%. This may be due to the rugged topography of the region, which is characterized by mainly high-altitude areas.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Bollasina, M.A.; Ming, Y.; Ramaswamy, V. Anthropogenic Aerosols and the Weakening of the South Asian Summer Monsoon. Science 2011, 334, 502–505. [Google Scholar] [CrossRef] [PubMed]
- Pińskwar, I.; Choryński, A.; Graczyk, D.; Kundzewicz, Z.W. Observed Changes in Extreme Precipitation in Poland: 1991–2015 versus 1961–1990. Theor. Appl. Climatol. 2019, 135, 773–787. [Google Scholar] [CrossRef]
- Bonsal, B.; Peters, D.; Seglenieks, F.; Rivera, A.; Berg, A. Changes in Freshwater Availability across Canada. Canada’s Chang. Clim. Rep. 2019, pp. 261–342. Available online: https://natural-resources.canada.ca/sites/www.nrcan.gc.ca/files/energy/Climate-change/pdf/CCCR-Chapter6-ChangesInFreshwaterAvailabilityAcrossCanada.pdf (accessed on 2 February 2023).
- AghaKouchak, A.; Farahmand, A.; Melton, F.S.; Teixeira, J.; Anderson, M.C.; Wardlow, B.D.; Hain, C.R. Remote Sensing of Drought: Progress, Challenges and Opportunities. Rev. Geophys. 2015, 53, 452–480. [Google Scholar] [CrossRef]
- El Fels, A.E.A. Rainfall Regionalization and Variability of Extreme Precipitation Using Artificial Neural Networks: A Case Study from Western Central Morocco. J. Water Clim. Chang. 2021, 12, 1107. [Google Scholar] [CrossRef]
- Benkirane, M.; Laftouhi, N.E.; El Mansouri, B.; Salik, I.; Snineh, M.; El Ghazali, F.E.; Kamal, S.; Zamrane, Z. An Approach for Flood Assessment by Numerical Modeling of Extreme Hydrological Events in the Zat Watershed (High Atlas, Morocco). Urban Water J. 2020, 17, 381–389. [Google Scholar] [CrossRef]
- Kizza, M.; Rodhe, A.; Xu, C.-Y.; Ntale, H.K.; Halldin, S. Temporal Rainfall Variability in the Lake Victoria Basin in East Africa during the Twentieth Century. Theor. Appl. Climatol. 2009, 98, 119–135. [Google Scholar] [CrossRef]
- Dinku, T.; Funk, C.; Peterson, P.; Maidment, R.; Tadesse, T.; Gadain, H.; Ceccato, P. Validation of the CHIRPS Satellite Rainfall Estimates over Eastern Africa. Q. J. R. Meteorol. Soc. 2018, 144, 292–312. [Google Scholar] [CrossRef]
- Ageet, S.; Fink, A.H.; Maranan, M.; Diem, J.E.; Hartter, J.; Ssali, A.L.; Ayabagabo, P. Validation of Satellite Rainfall Estimates over Equatorial East Africa. J. Hydrometeorol. 2022, 23, 129–151. [Google Scholar] [CrossRef]
- Monsieurs, E.; Kirschbaum, D.B.; Tan, J.; Maki Mateso, J.-C.; Jacobs, L.; Plisnier, P.-D.; Thiery, W.; Umutoni, A.; Musoni, D.; Bibentyo, T.M.; et al. Evaluating TMPA Rainfall over the Sparsely Gauged East African Rift. J. Hydrometeorol. 2018, 19, 1507–1528. [Google Scholar] [CrossRef]
- Ouaba, M.; El Khalki, E.M.; Saidi, M.E.; Alam, M.J. Bin Estimation of Flood Discharge in Ungauged Basin Using GPM-IMERG Satellite-Based Precipitation Dataset in a Moroccan Arid Zone. Earth Syst. Environ. 2022, 6, 541–556. [Google Scholar] [CrossRef]
- Panegrossi, G.; Casella, D.; Dietrich, S.; Marra, A.C.; Sano, P.; Mugnai, A.; Baldini, L.; Roberto, N.; Adirosi, E.; Cremonini, R.; et al. Use of the GPM Constellation for Monitoring Heavy Precipitation Events Over the Mediterranean Region. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2733–2753. [Google Scholar] [CrossRef]
- Panegrossi, G.; Marra, A.C.; Sanò, P.; Baldini, L.; Casella, D.; Porcù, F. Heavy Precipitation Systems in the Mediterranean Area: The Role of GPM. In Satellite Precipitation Measurement; Springer: Cham, Switzerland, 2020; pp. 819–841. [Google Scholar]
- Benkirane, M.; Laftouhi, N.-E.; Khabba, S.; Hera-Portillo, Á. de la Hydro Statistical Assessment of TRMM and GPM Precipitation Products against Ground Precipitation over a Mediterranean Mountainous Watershed (in the Moroccan High Atlas). Appl. Sci. 2022, 12, 8309. [Google Scholar] [CrossRef]
- Saouabe, T.; Naceur, K.A.; El Khalki, E.M.; Hadri, A.; Saidi, M.E. GPM-IMERG Product: A New Way to Assess the Climate Change Impact on Water Resources in a Moroccan Semi-Arid Basin. J. Water Clim. Chang. 2022, 13, 2559–2576. [Google Scholar] [CrossRef]
- Li, Z.; Yang, D.; Hong, Y. Multi-Scale Evaluation of High-Resolution Multi-Sensor Blended Global Precipitation Products over the Yangtze River. J. Hydrol. 2013, 500, 157–169. [Google Scholar] [CrossRef]
- Massari, C.; Brocca, L.; Pellarin, T.; Abramowitz, G.; Filippucci, P.; Ciabatta, L.; Maggioni, V.; Kerr, Y.; Fernandez Prieto, D. A Daily/25 Km Short-Latency Rainfall Product for Data Scarce Regions Based on the Integration of the GPM IMERG Early Run with Multiple Satellite Soil Moisture Products. Hydrol. Earth Syst. Sci. Discuss. 2020, 24, 2687–2710. [Google Scholar] [CrossRef]
- Einfalt, T.; Arnbjerg-nielsen, K.; Golz, C.; Jensen, N.; Quirmbach, M.; Vaes, G.; Vieux, B. Towards a Roadmap for Use of Radar Rainfall Data in Urban Drainage. J. Hydrol. 2004, 299, 186–202. [Google Scholar] [CrossRef]
- Xu, R.; Tian, F.; Yang, L.; Hu, H.; Lu, H.; Hou, A. Ground Validation of GPM IMERG and Trmm 3B42V7 Rainfall Products over Southern Tibetan Plateau Based on a High-Density Rain Gauge Network. J. Geophys. Res. 2017, 122, 910–924. [Google Scholar] [CrossRef]
- Tang, G.; Zeng, Z.; Long, D.; Guo, X.; Yong, B.; Zhang, W.; Hong, Y. Statistical and Hydrological Comparisons between TRMM and GPM Level-3 Products over a Midlatitude Basin: Is Day-1 IMERG a Good Successor for TMPA 3B42V7? J. Hydrometeorol. 2016, 17, 121–137. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Yi, L.; Zhang, W.; Wang, K. Evaluation of Heavy Precipitation Simulated by the WRF Model Using 4D-Var Data Assimilation with TRMM 3B42 and GPM IMERG over the Huaihe River Basin, China. Remote Sens. 2018, 10, 646. [Google Scholar] [CrossRef]
- Scheel, M.L.M.; Rohrer, M.; Huggel, C.; Santos Villar, D.; Silvestre, E.; Huffman, G.J. Evaluation of TRMM Multi-Satellite Precipitation Analysis (TMPA) Performance in the Central Andes Region and Its Dependency on Spatial and Temporal Resolution. Hydrol. Earth Syst. Sci. 2011, 15, 2649–2663. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Navarro, A.; García-Ortega, E.; Merino, A.; Sánchez, J.L.; Marcos, C.; Kummerow, C. The Contribution of Rain Gauges in the Calibration of the IMERG Product: Results from the First Validation over Spain. J. Hydrometeorol. 2020, 21, 161–182. [Google Scholar] [CrossRef]
- Yong, B.; Liu, D.; Gourley, J.J.; Tian, Y.; Huffman, G.J.; Ren, L.; Hong, Y. Global View of Real-Time TRMM Multisatellite Precipitation Analysis: Implications for Its Successor Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2015, 96, 283–296. [Google Scholar] [CrossRef]
- Gebregiorgis, A.S.; Kirstetter, P.; Hong, Y.E.; Gourley, J.J.; Huffman, G.J.; Petersen, W.A.; Xue, X.; Schwaller, M.R. To What Extent Is the Day 1 GPM IMERG Satellite Precipitation Estimate Improved as Compared to TRMM TMPA-RT? J. Geophys. Res. Atmos. 2018, 123, 1694–1707. [Google Scholar] [CrossRef]
- Ammar, H. Elsheikh Applications of Machine Learning in Friction Stir Welding: Prediction of Joint Properties, Real-Time Control and Tool Failure Diagnosis. Eng. Appl. Artif. Intell. 2023, 121, 105961. [Google Scholar] [CrossRef]
- Gaona, M.F.R.; Overeem, A.; Leijnse, H.; Uijlenhoet, R. First-Year Evaluation of GPM Rainfall over the Netherlands: IMERG Day 1 Final Run (V03D). J. Hydrometeorol. 2016, 17, 2799–2814. [Google Scholar] [CrossRef]
- Gao, Y.; Wu, T.; Wang, J.; Tang, S. Evaluation of GPM Dual-Frequency Precipitation Radar (DPR) Rainfall Products Using the Rain Gauge Network over China. J. Hydrometeorol. 2021, 22, 547–559. [Google Scholar] [CrossRef]
- Liu, Z. Comparison of Integrated Multisatellite Retrievals for GPM (IMERG) and TRMM Multisatellite Precipitation Analysis (TMPA) Monthly Precipitation Products: Initial Results. J. Hydrometeorol. 2016, 17, 777–790. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; AghaKouchak, A.; Liu, Z.; Norouzi, H.; Pai, D.S. A Preliminary Assessment of GPM-Based Multi-Satellite Precipitation Estimates over a Monsoon Dominated Region. J. Hydrol. 2018, 556, 865–876. [Google Scholar] [CrossRef]
- Sharifi, E.; Steinacker, R.; Saghafian, B. Assessment of GPM-IMERG and Other Precipitation Products against Gauge Data under Different Topographic and Climatic Conditions in Iran: Preliminary Results. Remote Sens. 2016, 8, 135. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Long, D.; Zhong, L.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA Version-7 Legacy Products over Mainland China at Multiple Spatiotemporal Scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, Z.; Huang, Y.; Jin, Q.; Chen, X.; Chang, J. Evaluation of the GPM IMERG v5 and TRMM 3B42 v7 Precipitation Products in the Yangtze River Basin, China. Water 2019, 11, 1459. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Mehran, A.; Norouzi, H.; Behrangi, A. Systematic and Random Error Components in Satellite Precipitation Data Sets. Geophys. Res. Lett. 2012, 39, e1–e7. [Google Scholar] [CrossRef]
- Kimani, M.; Hoedjes, J.; Su, Z. An Assessment of Satellite-Derived Rainfall Products Relative to Ground Observations over East Africa. Remote Sens. 2017, 9, 430. [Google Scholar] [CrossRef]
- Tang, L.; Tian, Y.; Yan, F.; Habib, E. An Improved Procedure for the Validation of Satellite-Based Precipitation Estimates. Atmos. Res. 2015, 163, 61–73. [Google Scholar] [CrossRef]
- Sadeghi, M.; Asanjan, A.A.; Faridzad, M.; Nguyen, P.; Hsu, K.; Sorooshian, S.; Braithwaite, D. PERSIANN-CNN: Precipitation Estimation from Remotely Sensed Information Using Artificial Neural Networks–Convolutional Neural Networks. J. Hydrometeorol. 2019, 20, 2273–2289. [Google Scholar] [CrossRef]
- Alsaiari, A.O.; Moustafa, E.B.; Alhumade, H.; Abulkhair, H.; Elsheikh, A. A Coupled Artificial Neural Network with Artificial Rabbits Optimizer for Predicting Water Productivity of Different Designs of Solar Stills. Adv. Eng. Softw 2023, 175, 103315. [Google Scholar] [CrossRef]
- Fang, G.H.; Yang, J.; Chen, Y.N.; Zammit, C. Comparing Bias Correction Methods in Downscaling Meteorological Variables for a Hydrologic Impact Study in an Arid Area in China. Hydrol. Earth Syst. Sci. 2015, 19, 2547–2559. [Google Scholar] [CrossRef]
- Serrat-Capdevila, A.; Merino, M.; Valdes, J.; Durcik, M. Evaluation of the Performance of Three Satellite Precipitation Products over Africa. Remote Sens. 2016, 8, 836. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Xie, P.; Xiong, A.-Y. A Conceptual Model for Constructing High-Resolution Gauge-Satellite Merged Precipitation Analyses. J. Geophys. Res. Atmos. 2011, 116, 47–64. [Google Scholar] [CrossRef]
- Katiraie-Boroujerdy, P.; Akbari Asanjan, A.; Chavoshian, A.; Hsu, K.; Sorooshian, S. Assessment of Seven CMIP5 Model Precipitation Extremes over Iran Based on a Satellite-based Climate Data Set. Int. J. Climatol. 2019, 39, 3505–3522. [Google Scholar] [CrossRef]
- Piani, C.; Haerter, J.O.; Coppola, E. Statistical Bias Correction for Daily Precipitation in Regional Climate Models over Europe. Theor. Appl. Climatol. 2010, 99, 187–192. [Google Scholar] [CrossRef]
- Le Coz, C.; van de Giesen, N. Comparison of Rainfall Products over Sub-Saharan Africa. J. Hydrometeorol. 2020, 21, 553–596. [Google Scholar] [CrossRef]
- Boudhar, A.; Hanich, L.; Boulet, G.; Duchemin, B.; Berjamy, B.; Chehbouni, A. Evaluation of the Snowmelt Runoff Model in the Moroccan High Atlas Mountains Using Two Snow-Cover Estimates. Hydrol. Sci. J. 2009, 54, 1094–1113. [Google Scholar] [CrossRef]
- Hanich, L.; Chehbouni, A.; Gascoin, S.; Boudhar, A.; Jarlan, L.; Tramblay, Y.; Boulet, G.; Marchane, A.; Baba, M.W.; Kinnard, C.; et al. Snow Hydrology in the Moroccan Atlas Mountains. J. Hydrol. Reg. Stud. 2022, 42, 101101. [Google Scholar] [CrossRef]
- Baba, M.W.; Gascoin, S.; Kinnard, C.; Marchane, A.; Hanich, L. Effect of Digital Elevation Model Resolution on the Simulation of the Snow Cover Evolution in the High Atlas. Water Resour. Res. 2019, 55, 5360–5378. [Google Scholar] [CrossRef]
- El Arabi, E.H.; Diez, J.B.; Broutin, J.; Essamoud, R. Première Caractérisation Palynologique Du Trias Moyen Dans Le Haut Atlas; Implications Pour l’initiation Du Rifting Téthysien Au Maroc. Comptes Rendus Geosci. 2006, 338, 641–649. [Google Scholar] [CrossRef]
- Chaponnière, A.; Boulet, G.; Chehbouni, A.; Aresmouk, M. Understanding Hydrological Processes with Scarce Data in a Mountain Environment. Hydrol. Process. 2008, 22, 1908–1921. [Google Scholar] [CrossRef]
- Rudolf, B.; Beck, C.; Grieser, J.; Schneider, U. Global Precipitation climatology center of the GPCC. Glob. Precip. Climatol. Cent. Rep. 2005, 1–8. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Tan, J. Algorithm Theoretical Basis Document (ATBD) Version 06. NASA Global Precipitation Measurement (GPM) Integrated Multi-satellitE Retrievals for GPM (IMERG). 2019. Available online: Https://Gpm.Nasa.Gov/Sites/Default/Files/Document_files/IMERG_ATBD_V06_0.Pdf (accessed on 2 February 2023).
- U.S. Army Corps of Engineers Hydrologic Modeling System. In Application Guide; U.S. Army Corps of Engineers: Davis, CA, USA, 2017; p. 158.
- Lashkari, A.; Salehnia, N.; Asadi, S.; Paymard, P.; Zare, H.; Bannayan, M. Evaluation of Different Gridded Rainfall Datasets for Rainfed Wheat Yield Prediction in an Arid Environment. Int. J. Biometeorol. 2018, 62, 1543–1556. [Google Scholar] [CrossRef] [PubMed]
- Condom, T.; Rau, P.; Espinoza, J.C. Correction of TRMM 3B43 Monthly Precipitation Data over the Mountainous Areas of Peru during the Period 1998-2007. Hydrol. Process. 2011, 25, 1924–1933. [Google Scholar] [CrossRef]
- Katiraie-Boroujerdy, P.-S.; Rahnamay Naeini, M.; Akbari Asanjan, A.; Chavoshian, A.; Hsu, K.; Sorooshian, S. Bias Correction of Satellite-Based Precipitation Estimations Using Quantile Mapping Approach in Different Climate Regions of Iran. Remote Sens. 2020, 12, 2102. [Google Scholar] [CrossRef]
- Brocca, L.; Hasenauer, S.; Lacava, T.; Melone, F.; Moramarco, T.; Wagner, W.; Dorigo, W.; Matgen, P.; Martínez-Fernández, J.; Llorens, P.; et al. Soil Moisture Estimation through ASCAT and AMSR-E Sensors: An Intercomparison and Validation Study across Europe. Remote Sens. Environ. 2011, 115, 3390–3408. [Google Scholar] [CrossRef]
- Fang, L.; Hain, C.R.; Zhan, X.; Anderson, M.C. An Inter-Comparison of Soil Moisture Data Products from Satellite Remote Sensing and a Land Surface Model. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 37–50. [Google Scholar] [CrossRef]
- Reichle, R.H. Bias Reduction in Short Records of Satellite Soil Moisture. Geophys. Res. Lett. 2004, 31, L19501. [Google Scholar] [CrossRef]
- Daniel, S.W. Wilks Statistical Methods in the Atmospheric Sciences. Academic Press: Cambridge, MA, USA, 2011; ISBN 0123850223. [Google Scholar]
- Themeßl, M.J.; Gobiet, A.; Heinrich, G. Empirical-Statistical Downscaling and Error Correction of Regional Climate Models and Its Impact on the Climate Change Signal. Clim. Chang. 2012, 112, 449–468. [Google Scholar] [CrossRef]
- USACE Hydrologic Modeling System (HEC-HMS) User’s Manual: Version 4.3.0; Hydrologic Engineering Center: Davis, CA, USA, 2018.
- Arlen, D. Feldman Hydrologic Modeling System HEC-HMS: Technical Reference Manual; US Army Corps of Engineers, Hydrologic Engineering Center: Davis, CA, USA.
- El Khalki, E.M.; Tramblay, Y.; El Mehdi Saidi, M.; Bouvier, C.; Hanich, L.; Benrhanem, M.; Alaouri, M. Comparison of Modeling Approaches for Flood Forecasting in the High Atlas Mountains of Morocco. Arab. J. Geosci. 2018, 11, 410. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Veith Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Valdés-Pineda, R.; Demaría, E.M.C.; Valdés, J.B.; Wi, S.; Serrat-Capdevilla, A. Bias Correction of Daily Satellite-Based Rainfall Estimates for Hydrologic Forecasting in the Upper Zambezi, Africa. Hydrol. Earth Syst. Sci. Discuss. 2016, 1–28. [Google Scholar] [CrossRef]
- Ramesh, V. Application of the HEC-HMS Model for Runoff Simulation in the Krishna Basin. Master’s Thesis, National Institute of Technology Karnataka, Surathkal, India, 2017. [Google Scholar] [CrossRef]
- Tramblay, Y.; Bouaicha, R.; Brocca, L.; Dorigo, W.; Bouvier, C.; Camici, S.; Servat, E. Estimation of Antecedent Wetness Conditions for Flood Modelling in Northern Morocco. Hydrol. Earth Syst. Sci. 2012, 16, 4375–4386. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Gourley, J.J.; Huffman, G.J.; Tian, Y.; Cao, Q.; Yong, B.; Kirstetter, P.E.; Hu, J.; Hardy, J.; et al. Evaluation of the Successive V6 and V7 TRMM Multisatellite Precipitation Analysis over the Continental United States. Water Resour. Res. 2013, 49, 8174–8186. [Google Scholar] [CrossRef]


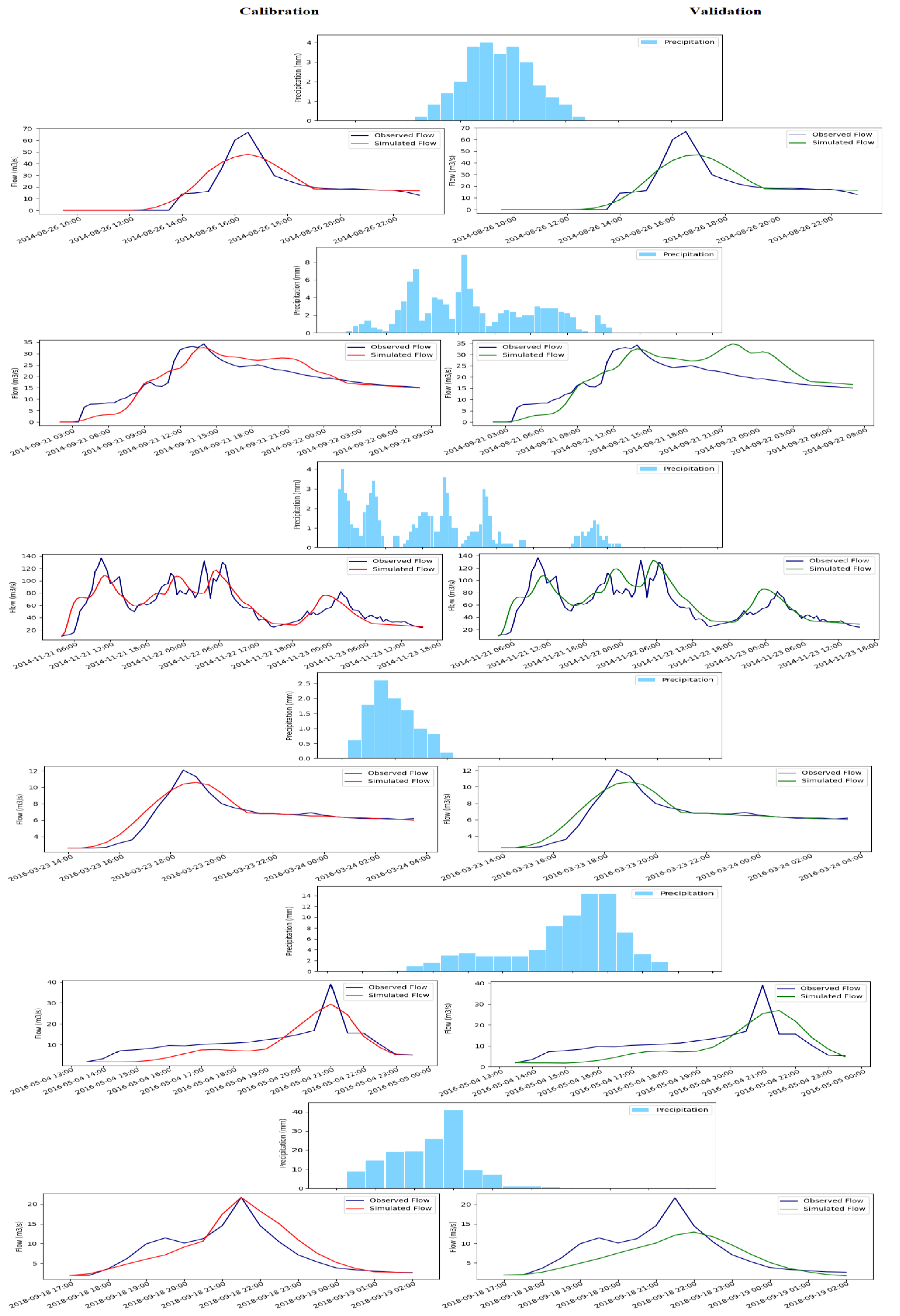
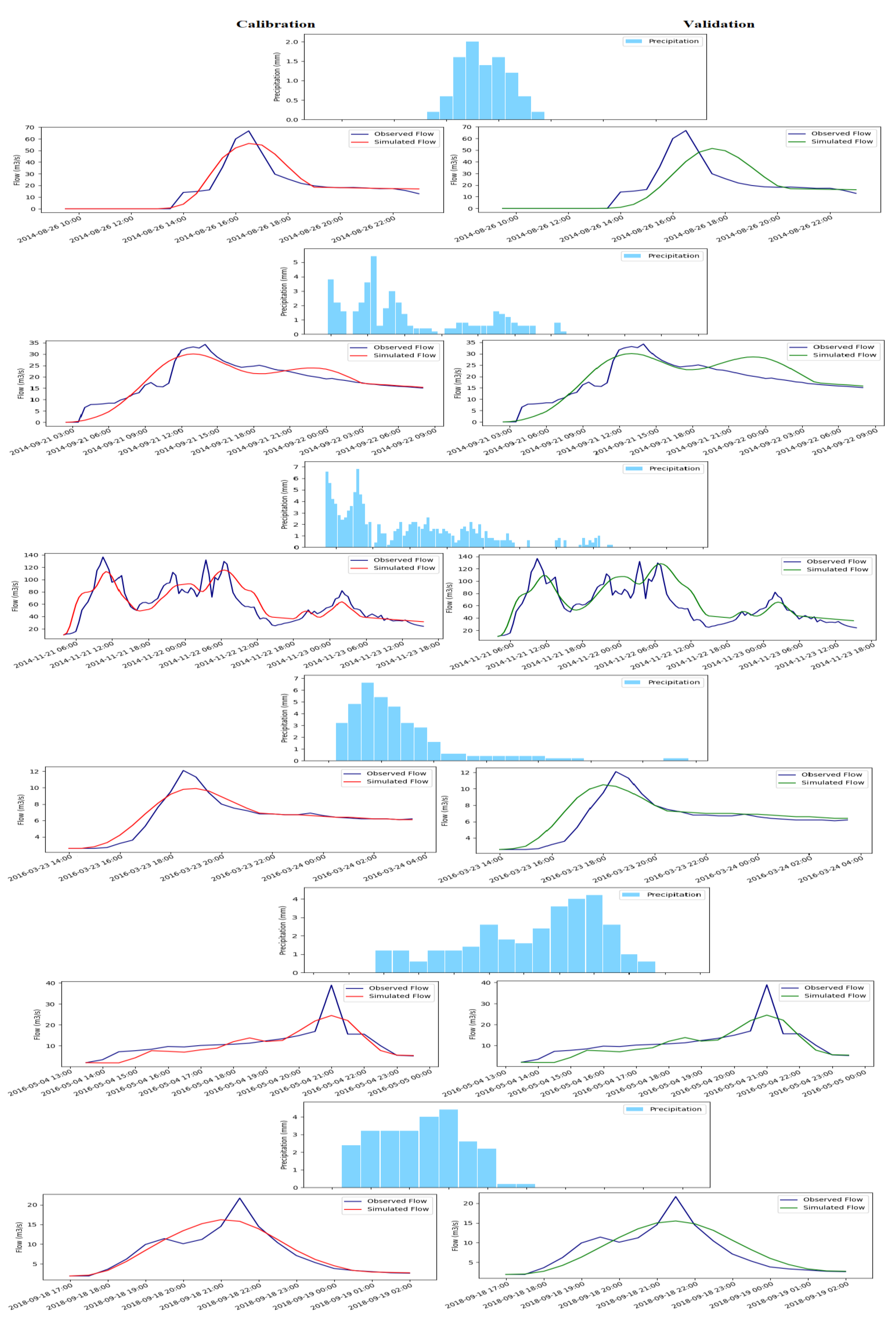
| Events | Begin | End | Peak Flood (m3/s) | Peak Flood Occurrence Time | Total Flood Volume (mm) |
|---|---|---|---|---|---|
| Event 1 | 26/08/2014 (09:30) | 26/08/2014 (23:00) | 66.82 | 26/08/2014 (16:30) | 1.66 |
| Event 2 | 21/09/2014 (02:00) | 21/09/2014 (08:00) | 34.3 | 21/09/2014 (14:00) | 3.81 |
| Event 3 | 21/11/2014 (04:00) | 21/11/2014 (15:30) | 136.61 | 21/11/2014 (10:30) | 25.22 |
| Event 4 | 23/03/2016 (14:00) | 24/03/2016 (03:30) | 12.13 | 23/03/2016 (18:30) | 0.6 |
| Event 5 | 04/05/2016 (13:30) | 04/05/2016 (23:30) | 38.86 | 04/05/2016 (21:00) | 0.81 |
| Event 6 | 18/09/2018 (17:00) | 19/09/2018 (02:00) | 21.74 | 18/09/2018 (21:30) | 0.49 |
| Basin Model | Meteorological Model | ||
|---|---|---|---|
| Parameter Method | Selected Method | Parameter Method | Selected Method |
| Loss | SCS-CN | Precipitation | Inverse distance |
| Transform | Clark U-H | Specified Hyetograph | |
| Baseflow | Recession | ||
| No Corrected Data | Corrected Data | Optimum Values | Unit | |||||
|---|---|---|---|---|---|---|---|---|
| IMERG Early | IMERG Late | IMERG Finale | IMERG Early | IMERG Late | IMERG Finale | |||
| R2 | 0.2 | 0.2 | 0.27 | 0.29 | 0.42 | 0.56 | 1 | Ratio |
| Bias | 2.94 | 3.11 | 1.57 | 1.12 | 1.08 | 1.07 | 0 | mm |
| RMSE | 0.5 | 0.47 | 0.36 | 0.43 | 0.45 | 0.42 | 0 | mm |
| MSE | 0.23 | 0.22 | 0.17 | 0.19 | 0.18 | 0.13 | 0 | mm |
| MAE | 0.50 | 0.60 | 0.40 | 0.05 | 0.04 | 0.06 | 0 | mm |
| POD | 0.28 | 0.28 | 0.18 | 0.19 | 0.16 | 0.18 | 1 | Ratio |
| FAR | 0.9 | 0.91 | 0.84 | 0.88 | 0.9 | 0.84 | 0 | Ratio |
| CSI | 0.07 | 0.06 | 0.09 | 0.07 | 0.06 | 0.09 | 1 | Ratio |
| Calibration | Precipitation Products | Date | Curve Number | Time of Concentration | Recession Constant | P BIAS | RMSE | Nash-Sutcliffe |
| Gauge Precipitation | 26/08/2014 | - | - | - | - | - | - | |
| 21/09/2014 | 60 | 0.5 | 0.6 | 1.02 | 0.4 | 0.85 | ||
| 21/11/2014 | 46 | 0.3 | 0.2 | 0.44 | 5 | 0.71 | ||
| 23/03/2016 | 66 | 0.3 | 0.5 | −7.51 | 0.5 | 0.78 | ||
| 04/05/2016 | 70 | 0.4 | 0.4 | −5.37 | 0.6 | 0.61 | ||
| 18/09/2018 | 65 | 0.5 | 0.3 | −8.75 | 0.4 | 0.84 | ||
| IMERG Early | 26/08/2014 | 63 | 2 | 0.2 | 5.52 | 0.3 | 0.91 | |
| 21/09/2014 | 36 | 1.5 | 0.6 | −0.25 | 0.3 | 0.90 | ||
| 21/11/2014 | 58 | 0.9 | 0.6 | 11.93 | 0.6 | 0.61 | ||
| 23/03/2016 | 67 | 0.4 | 0.6 | 1.2 | 0.4 | 0.83 | ||
| 04/05/2016 | 43 | 0.7 | 0.56 | −6.76 | 0.6 | 0.60 | ||
| 18/09/2018 | 25.4 | 0.4 | 0.1 | −7.61 | 0.5 | 0.78 | ||
| IMERG Late | 26/08/2014 | 64 | 0.6 | 0.6 | 4.93 | 0.4 | 0.87 | |
| 21/09/2014 | 30 | 1 | 0.6 | 1.01 | 0.4 | 0.83 | ||
| 21/11/2014 | 52 | 0.8 | 0.6 | 0.51 | 0.5 | 0.76 | ||
| 23/03/2016 | 57 | 4.9 | 0.6 | 3.17 | 0.3 | 0.90 | ||
| 04/05/2016 | 39 | 0.1 | 0.2 | −15.77 | 0.6 | 0.59 | ||
| 18/09/2018 | 27.5 | 0.5 | 0.1 | 5.16 | 0.4 | 0.81 | ||
| IMERG Final | 26/08/2014 | 69 | 1 | 0.6 | 6.79 | 0.3 | 0.88 | |
| 21/09/2014 | 60 | 8 | 0.6 | −0.07 | 0.4 | 0.84 | ||
| 21/11/2014 | 43 | 1.8 | 0.6 | 2.28 | 0.5 | 0.74 | ||
| 23/03/2016 | 61 | 3.9 | 0.6 | 2.19 | 0.3 | 0.90 | ||
| 04/05/2016 | 51 | 0.7 | 0.3 | −8.65 | 0.6 | 0.68 | ||
| 18/09/2018 | 56 | 2.1 | 0.3 | 2.44 | 0.4 | 0.87 |
| Validation | Precipitation Products | Date | Calculated CN (from ‘SM’) | RMSE | Nash-Sutcliffe |
| Gauge Precipitation | 26/08/2014 | - | - | - | |
| 21/09/2014 | 60.65 | 0.40 | 0.82 | ||
| 21/11/2014 | 48 | 0.60 | 0.60 | ||
| 23/03/2016 | 52.55 | 0.50 | 0.78 | ||
| 04/05/2016 | 58.09 | 0.60 | 0.61 | ||
| 18/09/2018 | 59.32 | 0.40 | 0.84 | ||
| IMERG Early | 26/08/2014 | 41.02 | 0.40 | 0.84 | |
| 21/09/2014 | 38 | 0.60 | 0.65 | ||
| 21/11/2014 | 53.64 | 0.50 | 0.74 | ||
| 23/03/2016 | 60.29 | 0.50 | 0.75 | ||
| 04/05/2016 | 69.86 | 0.70 | 0.57 | ||
| 18/09/2018 | 45.58 | 0.70 | 0.47 | ||
| IMERG Late | 26/08/2014 | 37.41 | 0.40 | 0.85 | |
| 21/09/2014 | 37.8 | 0.70 | 0.55 | ||
| 21/11/2014 | 55.51 | 0.60 | 0.70 | ||
| 23/03/2016 | 60 | 0.30 | 0.90 | ||
| 04/05/2016 | 50 | 0.70 | 0.54 | ||
| 18/09/2018 | 36 | 0.60 | 0.62 | ||
| IMERG Final | 26/08/2014 | 51.98 | 0.70 | 0.51 | |
| 21/09/2014 | 62.68 | 0.50 | 0.71 | ||
| 21/11/2014 | 57.35 | 0.60 | 0.63 | ||
| 23/03/2016 | 64.92 | 0.50 | 0.70 | ||
| 04/05/2016 | 60.2 | 0.60 | 0.68 | ||
| 18/09/2018 | 61.87 | 0.40 | 0.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benkirane, M.; Amazirh, A.; Laftouhi, N.-E.; Khabba, S.; Chehbouni, A. Assessment of GPM Satellite Precipitation Performance after Bias Correction, for Hydrological Modeling in a Semi-Arid Watershed (High Atlas Mountain, Morocco). Atmosphere 2023, 14, 794. https://doi.org/10.3390/atmos14050794
Benkirane M, Amazirh A, Laftouhi N-E, Khabba S, Chehbouni A. Assessment of GPM Satellite Precipitation Performance after Bias Correction, for Hydrological Modeling in a Semi-Arid Watershed (High Atlas Mountain, Morocco). Atmosphere. 2023; 14(5):794. https://doi.org/10.3390/atmos14050794
Chicago/Turabian StyleBenkirane, Myriam, Abdelhakim Amazirh, Nour-Eddine Laftouhi, Saïd Khabba, and Abdelghani Chehbouni. 2023. "Assessment of GPM Satellite Precipitation Performance after Bias Correction, for Hydrological Modeling in a Semi-Arid Watershed (High Atlas Mountain, Morocco)" Atmosphere 14, no. 5: 794. https://doi.org/10.3390/atmos14050794
APA StyleBenkirane, M., Amazirh, A., Laftouhi, N.-E., Khabba, S., & Chehbouni, A. (2023). Assessment of GPM Satellite Precipitation Performance after Bias Correction, for Hydrological Modeling in a Semi-Arid Watershed (High Atlas Mountain, Morocco). Atmosphere, 14(5), 794. https://doi.org/10.3390/atmos14050794









