Next Article in Journal
Thermal Hazards Evaluation Based on Weight of Evidence Method in the Resource Area of Datong River in Qinghai-Tibetan Plateau
Next Article in Special Issue
Study of the Sea Temperature Backgrounds to Tropical Cyclones Affecting Hainan Province in the Dry Season
Previous Article in Journal
Two Case Studies of the Northwestern Argentinean Low: With and without a Coupled Transient Trough
Previous Article in Special Issue
A Hurricane Initialization Scheme with 4DEnVAR Satellite Ozone and Bogus Data Assimilation (SOBDA) and Its Application: Case Study
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 14
Issue 5
10.3390/atmos14050884
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Dynamical Analyses of a Supercell Tornado in Eastern China Based on a Real-Data Simulation

by
Shiqi Wang
1,2 and
Jinzhong Min
1,2,*
1
Key Laboratory of Meteorological Disaster of Ministry of Education, Nanjing University of Information Science and Technology, Nanjing 210044, China
2
Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters, Nanjing University of Information Science and Technology, Nanjing 210044, China
*
Author to whom correspondence should be addressed.
Atmosphere 2023, 14(5), 884; https://doi.org/10.3390/atmos14050884
Submission received: 26 April 2023 / Revised: 13 May 2023 / Accepted: 16 May 2023 / Published: 18 May 2023
(This article belongs to the Special Issue Data Assimilation for Predicting Hurricane, Typhoon and Storm)
Browse Figures
Versions Notes

Abstract

:
Tornadoes are extremely destructive natural disasters, and East China has become a high-incidence area for tornadoes in China in recent years. On 7 July 2013, an EF2-intensity tornado occurred in Gaoyou County, Jiangsu Province in eastern China, within a supercell storm near a Meiyu frontal system. To investigate the dynamical process of the tornado, a numerical simulation was performed using four one-way nested grids within the Advanced Regional Prediction System (ARPS). Data from a nearby operational S-band Doppler radar are assimilated using a 4D ensemble Kalman filter (4DEnKF) at 5 min intervals. Forecasts are run with a nested 50 m grid, capturing the tornado embedded within the supercell storm with a reasonable agreement with observations. The tornadogenesis processes within the simulation results are analyzed in detail, including the three-dimensional evolution of the tornado vortex. It is found that a cold surge within the rear flank downdraft region plays a key role in instigating tornadogenesis when the leading edge of the cold surge approaches a near-ground convergence center located underneath the main updraft, and the enhancement of the convergence center caused by the descending of the low-level mesocyclone is the direct cause of the rapid increase in tornado vorticity. Backward trajectories are calculated based on model output, and the origins of the parcels feeding the intensifying tornado vortex are identified. It is found that parcels from the mid-level of the rear flank downdraft region follow the cold surge, descending to the ground under the influence of the downdraft in the cold surge, and then entering the convergence center, merging into the core of the tornado and being lifted up. Vertical profiles of the mass and vorticity fluxes into the core of the tornado vortex are examined, and it is found that the near-ground airflow contributes significantly to the growth of the tornado vorticity, with the contribution increasing as it gets closer to the ground.

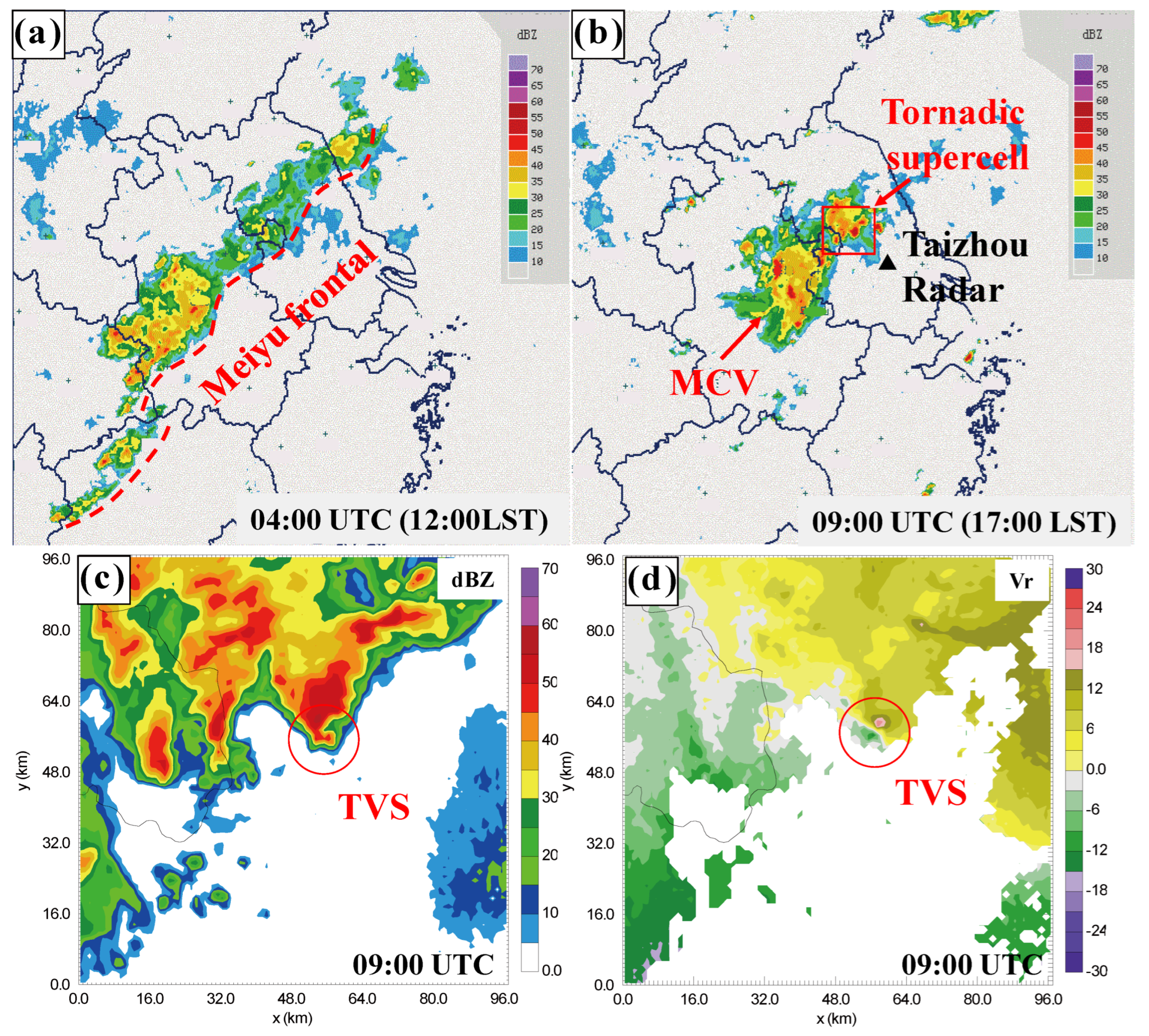
1. Introduction

Tornadoes are an extremely hazardous and violent weather phenomenon in the atmosphere. They appear as narrow columns of rotating air with a small scale, typically 1–2 km in diameter, and only a few hundred meters at their minimum. These powerful events have a short duration, lasting from only a few minutes to half an hour [1]. Near the center of a tornado, the wind speed can reach up to 140 m s−1, accompanied by severe convective weather, including hail and heavy rainfall, resulting in casualties and property damage wherever they pass through [2]. The American meteorological community has proposed the Enhanced Fujita Scale (EF Scale), ranging from EF0 to EF5. This scale considers the degree of damage to buildings, storm-generated wind speed, and tornado path width. Tornadoes rated EF2 or higher, with wind speeds exceeding 50 m s−1, are considered strong tornadoes as a convention.
There are mainly two types of tornadoes: supercell tornadoes and nonsupercell tornadoes. The supercell tornado forms in supercell thunderstorms with obvious rotation and containing mid-level mesocyclones [2], and the most destructive tornadoes are usually supercell tornadoes. It has been more than 50 years since Browning [3] introduced the term “supercell” to describe the large thunderstorm cells generated by rotating updrafts. Since then, significant progress has been made in the study of supercells and tornadoes with the understanding of relevant atmospheric dynamical processes and environmental conditions. However, a thorough understanding of the complete process of tornado formation and evolution is still lacking [4].
The foundation of current research on supercell dynamics can be traced back to the numerical and theoretical studies in the late 1970s and early 1980s [5,6,7,8,9,10,11,12,13]. These studies explained many observation features of supercells, including storm splitting, mid-level rotation, convergent downdrafts, and low-level horizontal rotation in the forward flank region [11,13]. Davies-Jones and Brooks [14] explained that the development of vertical vorticity in supercells is caused by the growth and tilting of streamwise horizontal vorticity due to the horizontal pressure gradient force during the downdraft process. With the advances in computing ability, Wicker and Wilhelmson [15] and Klemp and Rotunno [11] conducted higher-resolution numerical simulations of tornadic supercells in idealized experiments. According to their research, the mid-level downdrafts increase the upward pressure gradient force, producing strong low-level updrafts. This low-level updraft tilts the horizontally generated vorticity vertically and, through stretching, results in tornado formation. However, their studies are unable to explain how the generation of near-surface vorticity.
Over the past few decades, most of the idealized numerical studies conducted in the 1980s and 1990s have been verified by observations. In particular, the VORTEX (Verification of the Origins of Rotation in Tornadoes Experiment) large-scale experiment, led by the National Oceanic and Atmospheric Administration (NOAA) in collaboration with multiple research institutions and universities, has achieved numerous important scientific achievements in tornado formation and evolution mechanisms. However, the relationship between baroclinic and tornadogenesis in supercells observed during the VORTEX experiment remains unexplained [16]. These observations suggest that both tornadic and nontornadic supercells have mid-level mesocyclones, indicating that the physical mechanism behind mid-level mesocyclone formation may not be sufficient to explain tornado formation [17,18,19,20,21,22].
Although valuable results have been obtained through observation studies and idealized experiments, these researches often neglect factors such as horizontal heterogeneity and land surface processes in realistic environments, which may be crucial for tornadogenesis.
Tornadoes have a short lifespan and small spatial scale, making them difficult to capture using conventional observation methods [4]. Furthermore, observational data have many limitations in terms of temporal and spatial resolution and coverage. As a result, a combination of observational data with numerical models is the primary research method for tornadoes nowadays. In recent years, there has been significant progress in numerical simulation and forecasting of extreme weather, particularly for small-scale tornadoes [23]. With the progress of computing resources, high-resolution numerical models can more accurately simulate the physical processes in the tornado-scale [24]. Primary, 3Dvar and EnKF data assimilation methods have been well-developed and effectively applied to assimilate convective-scale radar data [24,25,26,27,28]. Hu et al. [29] successfully simulated an F4-level supercell tornado for the first time using high-resolution radar data assimilation with a 50 m grid spacing. Xue et al. [30] further validated the forecast results.
Based on high-resolution numerical simulations of real tornadic supercells, the near-surface dynamical progress during tornadogenesis has been revealed. Mashiko et al. [31] and Schenkman et al. [32], respectively, investigated tornadoes generated in microcells within typhoon rain-band and quasi-linear convective systems (QLCSs). They found that the secondary strengthening of the rear-flank gust front and surface frictional effects were crucial for tornado formation in high-resolution simulations. Subsequently, Schenkman et al. [33] proposed a new theory that surface-friction-generated vorticity is an important source of vorticity for tornado formation, based on a detailed diagnostic analysis of a simulated F4 tornado-producing supercell using real data. The generation of frictional vorticity, particularly its role in tornadogenesis in the early stages of a supercell’s lifecycle, has been further confirmed by idealized tornado simulations [34,35].
Recent research has shown that the majority of parcels that enter the tornado vortex come from the rear flank downdraft (RFD) of the supercell. Radar observations have also shown that tornado formation is often accompanied by strong echoes sinking to the ground in the early stages [36], and the strengthening of the “cold surge” originating from the rear cold pool has been observed [37]. The cause of the cold surge and its role in tornadogenesis, as well as the thermodynamic and dynamic characteristics of parcels entering the tornado, are issues of concern to scientists in recent times. Schenkman et al. [38] analyzed the cause of cold surges using tornado simulation results based on real data. The analysis reveals that the cold internal outflow surge is forced by the dynamic part of the vertical pressure gradient, which is the result of a high-pressure perturbation in an area of stagnating flow on the west and northwest sides of the low-level mesocyclone. Dawson et al. [39,40] found through numerical simulations of actual tornado cases that changes in the hail and raindrop spectrum distribution in the microphysical parameterization scheme can alter the intensity of cold pools and the thermodynamic characteristics of inflow, thus determining whether a tornado can form. Dawson et al. [41] further analyzed the dynamic mechanism of vertical acceleration of airflow and vortex stretching after entering the tornado vortex. These works represent the forefront of international research on numerical simulation and dynamical analysis of real tornado cases.
The frequency of tornado occurrences is closely related to the geographical distribution and environmental conditions of tornado formation in each region. Despite being located in the mid-latitudes of the Northern Hemisphere, China has recorded much fewer tornadoes compared to the United States. Over the past 50 years, the average number of tornadoes with EF1 intensity or higher in China was 21 per year [42], compared to 495 in the United States [43]. However, tornadoes in China often occur in densely populated inland plains and coastal areas, resulting in significant impacts and casualties due to the lack of awareness of disaster prevention. Incomplete statistics show that tornadoes have caused at least 1772 deaths in China from 1961 to the present [42]. Recently, the frequency and intensity of tornadoes in China have been increasing, particularly in eastern China. About 81% of tornadoes in China occurred in eastern China from 1960 to 2009, with the highest number and strongest intensity occurring in Jiangsu Province according to Yao et al. [44] This is likely due to the favorable conditions for tornado formation in the East China Plain, particularly in northern Jiangsu, where the flat terrain is influenced by strong low-level southerly winds and northern weather systems.
Since the increasing frequency of tornado occurrence in eastern China, in-depth research on the dynamical characteristics of tornadoes in this region is extremely necessary. Moreover, the tornadogenesis and numerical simulation of tornadoes are also cutting-edge scientific issues that have not been resolved internationally. This study focuses on a supercell tornado that occurred in eastern China. Based on real observation data, numerical simulations were performed and radar data were assimilated to improve the simulation accuracy and credibility. The simulation results are used to analyze the formation process of the tornado and to identify the key factors that affect the tornadogenesis and the source of the tornado vortex. The study aims to enhance our understanding of the dynamical process and formation mechanism of tornadoes in eastern China and contribute to improving forecasting and warning capabilities for tornado disasters in this region.
The Section 2 of this paper introduces the actual situation of the selected tornado process based on radar observation data, and the experimental design and parameter selection for numerical simulation and data assimilation. The Section 3 analyzes the life history of the tornado process through simulation results, explores the key factors that affect the formation of the tornado, and quantitatively calculates the initial source of the tornado vortex using backward trajectory analysis. Additionally, the mass and vorticity flux of the tornado are quantitatively calculated. The Section 4 concludes this study, discussing existing problems and shortcomings and outlining plans for future research.

2. Case Overview and Experimental Design

2.1. Case Overview

From 7 to 8 July 2013, heavy rainfall occurred in central Jiangsu in eastern China, accompanied by strong convective weather, such as thunderstorm gusts and short-term heavy precipitation. According to other research [45], the accumulated precipitation in 24 h at 00:00 UTC on 8 July is over 100 mm in Gaoyou County, and the maximum precipitation per hour is over 50 mm during the tornado period. In the afternoon of 7 July, a tornado was reported in Gaoyou City, at the border of Anhui and Jiangsu Province. According to media reports, the tornado was reported to hit Gaoyou around 0840 UTC (1640 LST) and then tracked through at least six villages near Gaoyou County between 08:50 and 09:10 UTC. The destructive wind near the ground was over 20 m s−1 and lasted for about 20 min, with a damage path of 10 km long and 400 m wide [46]. The damage to factories, power and communication poles and lines, trees, crops, and other infrastructure was severe. Cars were overturned, 600 houses were damaged, including 4 houses flattened. The tornado caused injuries to over 50 people, with more than 570 households affected and over 1100 houses damaged. Large trees were uprooted, and crops suffered significant damage. According to statistics, the direct economic losses from the disaster were approximately 45 million RMB yuan (http://www.globaltimes.cn/content/794507.shtml, accessed on 26 April 2023). Based on the degree of damage to houses and trees and eyewitness descriptions, the tornado intensity can be determined as an EF2 tornado.
According to the combined radar echoes in East China (Figure 1a,b), the tornadic supercell was formed in the unstable environment on the northeast of a mesoscale convective vortex (hereinafter referred to as MCV) system, which is near a Meiyu frontal system. On 7 July 2013 at 04:00 UTC (Figure 1a), a clear Meiyu frontal system (red dotted line in Figure 1a) appeared in the Anhui and Jiangsu Province of eastern China, with the rain belt distributed southwest–northeast. As the Meiyu frontal system developed, an MCV system appeared at the boundary between Anhui and central Jiangsu and moved northeast at 08:50 UTC (Figure 1b). The supercell storm, where the tornado occurred, formed in the unstable environment in the northeast part of the MCV system (highlighted in the red box in Figure 1b).
A tornado vortex signature (hereinafter referred to as TVS) is a rotational feature on the radar reflectivity image which is indicative of a strong cyclonic rotation and is often a precursor to the formation of a tornado. TVS is typically represented by a curved or hook-shaped reflectivity echo, which implies the possible presence of a tornado. Based on the Doppler radar data from the Taizhou S-band radar, located about 50 km from Gaoyou, the TVS was evident in the vicinity of Gaoyou between 08:55 and 09:12 UTC, with a hook-shaped reflectivity echo on the radar reflectivity image (Figure 1c, in red circle), and adjacent centers of maximum and minimum values on the radial velocity image (Figure 1d, in red circle), which indicated the presence of a strong near-surface cyclonic circulation or a meso-cyclonic shear. According to online sounding data provided by the University of Wyoming, the maximum convective available potential energy (CAPE) in the vicinity of Nanjing (about 100 km south of Gaoyou) reached 1689 J/kg at 12:00 UTC on 7 July 2013, which was highly favorable for the development and intensification of the tornadic supercell.

2.2. Experimental Design

The simulation of the 7 July 2013 Gaoyou tornado is performed using the Advanced Regional Prediction System (ARPS) [47,48] model using four one-way nested grids in order to capture the evolution of the tornado outbreak on a variety of scales (Figure 2a). The outermost grid has 5 km grid spacing and contains 300 × 200 grids. The Global Forecast System (GFS) reanalysis data are used to provide the initial condition (IC) and the lateral boundary conditions. A deterministic simulation is performed from 00:00 to 09:30 UTC for the outermost domain.
A 1 km grid-spacing domain is nested within the 5 km domain, containing 100 × 100 grids, including Gaoyou County where the tornado occurred and its surrounding areas (Figure 2b). The outermost 5 km grid simulation result at 08:00 UTC is interpolated to the inner domain. Based on this IC, perturbations are added to form the initial ensemble for the inner domain. A total of 40 members are generated with random-smoothed perturbations. Five-minute data assimilation cycles are performed over a 90 min period beginning at 08:00 UTC. Radial velocity data from the Doppler radar at Taizhou city (approximately 50 km southeast of Gaoyou, marked in Figure 2b) are assimilated within these cycles using the 4D ensemble Kalman filter (4DEnKF) while the reflectivity data are assimilated using a complex cloud analysis package [49]. Due to the outstanding advantages of 4DEnKF in convective-scale radar data assimilation in recent studies, especially tornado-scale simulation, this study adopts this method for radar data assimilation of the tornado simulation [50,51,52,53,54,55,56,57,58,59,60].
Two very-high-resolution domains are nested within the 1 km domain to contain the supercell and tornado region (indicated by the red dotted box) as in Figure 2b. The outer domain has 200 m grid spacing and contains 300 × 250 grids. One of the analysis fields at 08:40 UTC from the 1 km domain is used to initialize the 50 min long simulation on a 200 m grid. We note here that the choice of the analysis field is based on the simulation test from all 40 ensemble members. The deterministic forecast till the tornado time of each member is evaluated and the member with the best forecast result is selected, where the evaluation criteria are mainly the organization of the supercell and the maximum velocity and vertical vorticity at the first grid level (about 10 m) above the surface. A 50 m grid-spacing domain is further nested within the 200 m domain, contains 900 × 800 grids, and begins at 09:00 UTC and lasts 30 min. No additional data assimilation is performed on the 200 or 50 m grid. In the vertical direction, the 5 km and 1 km domain uses a stretching grid with 53 vertical levels and 400 m average vertical grid spacing, while the 200 m and 50 m domain have 100 levels and 200 m average vertical grid spacing in order to contain more information in low levels. For all four domains, the lowest vector and scalar model grid point is about 10 m AGL. The simulation uses about 60 cores for parallel computing and takes several hours to complete.
Model configurations for all four domains are summarized as follows. The Lin 3 ice scheme [61] is used for parameterizing microphysics. Default values of the intercept parameters are used for the outer domains. The default values are 8 × 106, 3 × 106, and 4 × 104 m−4 for rain, snow, and hail, respectively. Only the innermost 50 m domain uses smaller rain and hail intercept parameters. The values are 2 × 106 and 4 × 103 m−4. Fourth-order computational mixing is used to suppress spurious shortwaves; the default value coefficient of this filter in ARPS is used. Surface fluxes are calculated using stability-dependent drag coefficients [62], while surface roughness length is dependent on vegetation properties. For radiation parameterization, radiative processes are calculated from the National Aeronautics and Space Administration (NASA) Goddard Space Flight Center long- and short-wave radiation package. The planetary boundary layer scheme proposed by Sun and Chang [63] was used. The subgrid-scale turbulence is parameterized by a 1.5-order turbulence kinetic energy (TKE) scheme [64]. A two-layer soil model based on Noilhan and Planton [65] is used. More details on the parameterizations within the ARPS can be found in [47,48].

3. Simulation Results

In this section, the simulated tornado is first inspected based on the simulation results. Because the focus of this paper is on the dynamical processes responsible for tornadogenesis in the supercell, the remainder of this section is focused on the 50 m grid-spacing simulation. We then provide an overview of the evolution of tornadogenesis processes, including the three-dimensional evolution of the tornado vortex. This discussion is followed by a backward trajectory analysis of the origins of the parcels feeding the tornado vortex. The mass and vorticity fluxes into the core of the tornado vortex are then examined. In this study, a simulated vortex is considered a tornado if it has vertical vorticity greater than 1.0 s−1 and winds greater than 30 m s−1 (F1 intensity) at the first grid level (about 10 m) above the surface.
The innermost 50 m grid reproduces the tornado embedded within the supercell storm. Figure 3a shows the simulated radar reflectivity and horizontal wind field at 20 m above ground level (hereinafter referred to as AGL) at 09:16 UTC, while the concentrated vertical vorticity contours indicate the location of the tornado. Figure 3b shows the reflectivity distribution at a 1.45 PPI elevation angle from the Taizhou radar at 09:12 UTC. We note here that the X and Y axes in Figure 3 and the remaining figures in this paper represent the distance in the 50 m grid-spacing simulation domain to the southeast corner, and both the X and Y axes have their origin at the lower-left corner of the domain in each figure. The coordinate of the origin at the southeast corner of the domain is (32.67° N, 119.28° E), which is also (0 km, 0 km) of the X and Y axes.
Both the simulation and the radar observation exhibit a clear “hook” echo feature in Figure 3. The simulation reproduces the characteristics of the mature stage of the tornado within the supercell reasonably well and shows a good agreement with the observed reflectivity pattern. The maximum value of the vertical vorticity in Figure 3a is found at the center of the “hook” echo, exceeding 1.0 s−1. The wind field around the maximum vorticity center has a cyclonic distribution, with a maximum near-surface wind speed of over 30 m s−1. These results indicate the occurrence of a relatively strong tornado at this location, with an estimated intensity of EF1 to EF2 according to the maximum near-ground wind speed. It is noteworthy that the simulated tornado supercell is located about 2 km west and 4 km south of the observed hook echo position, and the appearance of the hook echo is delayed by about 5 min. The overall intensity is also relatively weak, possibly due to unavoidable biases in the simulation process. Nevertheless, the simulation reproduces the tornadic supercell well and captures the tornado embedded within the supercell storm with a reasonable agreement with observations in the mature stage of tornado.

3.1. Life Stage of Tornado

According to the classic theory of tornadogenesis, tornadoes often generate after the descending of the low-level mesocyclone, which is manifested as a rapid increase in the near-surface vertical vorticity accompanied by strong updrafts [12]. In order to further determine the accurate time and intensity of the tornadoes in the simulation results, maximum vertical velocity and maximum vertical vorticity were calculated at different heights within the supercell area at different times based on the position and area of the supercell at each moment. Then, a time–height diagram of the maximum vertical velocity and maximum vertical vorticity was constructed in Figure 4. The core of the low-level mesocyclone in a supercell is usually accompanied by strong updrafts, and the maximum vertical velocity often exceeds 15 m s−1. Therefore, the specific location and temporal evolution of the mesocyclone in the area can be determined by the distribution of the maximum vertical velocity in height and position [14].
According to the time–height diagram of the maximum vertical velocity in the supercell region (Figure 4a), it can be seen that the core of the low-level mesocyclone first appeared around 09:10 UTC, at an altitude of about 500 m AGL, and then rapidly descended to around 200 m AGL (red arrow), while its intensity continued to increase and reached its maximum at 09:16 UTC (black solid line), influenced by the strong suction caused by the mesocyclone’s intense low-pressure center. At this time, the maximum vertical velocity near the ground at around 30 m AGL (green solid line) also reached 10 m s−1. The descending of the low-level mesocyclone is closely related to the triggering of tornadoes. The strong low-pressure center of the mesocyclone will form a strong suction effect near the ground, forming a convergence center near the ground. At this time, the internal airflow with preexisting positive vertical vorticity near the surface will be stretched in the convergence center, leading to a rapid increase in vertical vorticity and triggering the tornadogenesis [11,13].
According to the time–height diagram of the maximum vertical vorticity in the supercell region during the same period (Figure 4b), the growth of vorticity near the ground (vorticity greater than 0.15 s−1) began at 09:13 UTC (black solid line), then continued to strengthen and extend upward, rapidly increased at 09:16 UTC (exceeding 1.0 s−1) and extend to an altitude of 400 m AGL. This is well coordinated with the descending of the low-level mesocyclone core (red arrow), indicating that the near-ground convergence center created by the descending of the low-level mesocyclone causes the internal airflow with preexisting positive vertical vorticity near the surface to undergo stretching and lead to a rapid increase in vertical vorticity. Based on the above analysis, both wind speed and vertical vorticity reached the tornado intensity at 09:16 UTC, so this time is defined as the trigger time of the tornadogenesis. Before the trigger time, the growth of vertical vorticity had already begun at 09:13 UTC. Although the vorticity and speed were not as strong as those of a tornado, the growth of vorticity during this period is particularly important for studying the source of tornado vorticity. It is usually referred to as a tornado-like vortex (hereinafter referred to as TLV) before the trigger time of the tornadogenesis, so 09:13 UTC is defined as the time of TLV formation.
The equivalent potential temperature (hereinafter referred to as θe) is used to describe the stability of air parcels in the atmosphere. It refers to the temperature that an air parcel would have if all its water vapor condensed and released its latent heat during adiabatic compression or expansion as it descends or rises to a reference pressure level. θe is conserved during a saturated adiabatic process, and it is often used to study the vertical motion of airflow in small-scale convective processes. Therefore, in this study, the distribution of θe will be used to analyze the effects of different environmental factors on the tornadogenesis process.
Figure 5 shows the distribution of θe, perturbation pressure, and wind field at 20 m AGL at 09:00 UTC (Figure 5a) and 09:05 UTC (Figure 5b), 16 min and 11 min before tornadogenesis time, respectively. The location of the gust front is indicated by the red dashed line. At 09:00 UTC, which is the initialization time of the 50 m simulation, the rear flank downdraft (RFD) is approaching the low-pressure center behind the gust front, and a near-ground convergence center (indicated by the red arrow) has formed ahead of the gust front, corresponding to the low-level mesocyclone core above. According to the previous analysis, the low-level mesocyclone core has not yet begun to descend, so the intensity of the surface convergence center is relatively weak. As the supercell evolves (Figure 5b), the downdraft motion of the RFD intensifies and creates a strong cold surge that rapidly moves towards the near-ground convergence center, causing a distinct bow echo to form on the gust front (indicated by the blue arrow). At the same time, the low-level mesocyclone is also descending, causing the near-ground convergence center to further strengthen. In recent years, numerous studies have revealed that the cold surge originating from the RFD plays a crucial role in tornadogenesis [36,37,39,40]. Schenkman et al. [38] found that in a numerical simulation study based on real data of a supercell tornado in the United States, the cold surge from the RFD caused the near-surface internal out-flow to develop streamwise vorticity due to surface friction, which was then lifted and stretched by the convergence center, ultimately resulting in the tilting and rapid intensification of the tornado vortex.
In order to further investigate the role of the cold surge in the tornadogenesis process, we analyzed in detail the evaluation of the tornado vortex in the 5 min’ prior tornadogenesis (Figure 6). It can be seen that as the cold surge moves towards the convergence center (indicated by the red arrow), the gust front further bends and splits into the front flank gust front (FFGF) and the rear flank gust front (RFGF) with the convergence center as the boundary (Figure 6a). At this time, a vertical vorticity maximum center appears on the rear side of the gust front at the leading edge of the cold surge, and it continuously moves towards the convergence center as the cold surge is approaching. At this time, the vertical vorticity is still relatively small and no vortex wind field is formed, so we refer to it as the pre-tornado vortex (hereinafter referred to as PTV; Figure 6a,b). Then, as the cold surge further approaches, the PTV also approaches the convergence center. Under the influence of stretching in the convergence center, the vertical vorticity begins to rapidly increase and a vortex wind field is formed, which indicates the tornado vortex entering the TLV stage (Figure 6c–e). According to the previous analysis, at this time, the core of the low-level mesocyclone is also continuously descending and strengthening, causing the near-ground convergence center also strengthen. This leads to further stretching of the TLV in the convergence center and rapid strengthening, resulting in clear cyclonic features in the wind field, which causes the gust front to completely split and the near-surface wind speed to continuously increase, ultimately reaching tornado intensity (Figure 6f).
Based on the above analysis, it can be concluded that the cold surge from the RFD plays a crucial role in the formation of tornadoes. The cold surge approaches towards the near-ground convergence center ahead of the gust front, and the sinking airflow ahead of the cold surge generates vertical vorticity at the leading edge of the cold surge. As the cold surge approaches the convergence center, the descending of the low-level mesocyclone further strengthens the convergence center. Subsequently, the vortex is stretched by the convergence center, causing the vertical vorticity to rapidly increase and eventually form a tornado.
By analyzing the position and intensity changes of the tornado vortex at various times during its life stage (Figure 7a), it can be seen that after the tornado vortex is generated along the leading edge of the cold surge, it advances continuously along with the cold surge and slowly enlarges, then starts to intensify rapidly and reaches the tornado intensity after entering the near-ground convergence center. The tornado vortex then maintains its position near the convergence center, gradually weakens, and eventually disappears around 09:23 UTC. Figure 7b shows the horizontal wind field and perturbation pressure during the mature stage of the tornado. It can be seen that the tornado vortex core produces a violent low-pressure center, which is the product of the coincidence of the tornado vortex with the near-ground convergence center. The intense low-pressure center continuously sucks in the surrounding airflow into the tornado vortex core, forming a distinct cyclonic wind field structure around the tornado, which increases the wind speed continuously. Meanwhile, the stretching effect of the low-pressure center also further strengthens the tornado vortex. Observing the vertical cross-section passing through the tornado core at this moment (Figure 7c), it can be seen that the tornado vortex column has extended to a height of 400 m AGL and sloped northwestward due to the influence of the low-level mesocyclone. The closer the tornado vortex is to the ground, the stronger the vortex is, indicating that the source of the tornado vortex is the near-surface airflow. The downdraft of the cold surge enters the convergence center, undergoes a stretching effect in the convergence center, and the vertical vorticity rapidly increases near the ground, extending to the upper layer, which is consistent with the research results of Schenkman et al. [33].
To further investigate the three-dimensional structure evolution of the tornado vortex, the three-dimensional vertical vorticity iso-surface at different times during its formation process was plotted (Figure 8), with the viewing angle from northwest to southeast. It can be observed that during the tornadogenesis process, the vorticity maximum core corresponding to the low-level mesocyclone continuously descends and intensifies (red arrow), with a near-ground convergence center directly underneath it. Meanwhile, the cold surge (blue arrow) approaches the convergence center from right to left, pushing the PTV (black arrow) at the leading edge of the cold surge closer to the convergence center (Figure 8a). Later, the PTV moves under the low-level mesocyclone, and their vorticity “merges” from the bottom (Figure 8b), indicating that the PTV enters the near-ground convergence center and begins to intensify. As the low-level mesocyclone continues to descend, the convergence center constantly strengthens, causing violent stretching of the tornado vortex and a rapid increase in the vertical vorticity, entering the TLV stage (Figure 8c). Subsequently, the tornado vorticity intensifies and eventually becomes a tornado (Figure 8d). The three-dimensional evolution of the tornado vortex further confirms the analysis presented above: The cold surge from the RFD moves towards the near-ground convergence center, and the downdraft at the leading edge of the cold surge produces vertical vorticity maxima, forming the PTV, which continuously approaches the convergence center with the cold surge. Meanwhile, the descending of the low-level mesocyclone further strengthens the convergence center. Subsequently, the PTV is stretched after entering the convergence center, and the vertical vorticity rapidly increases and ultimately causes tornadogenesis.

3.2. Backward Trajectory Analysis

Backward trajectory analysis is a common method in tornado-related research, which can visually reveal the parcels’ origin and movement process before entering the tornado vortex core. The backward interpolation and integration of each term along the trajectories can reveal the changes in the dynamic and thermodynamic states of parcels during the movement process and play an important role in studying the origination of the tornado vortex [39]. In early tornado research, accurate calculations of parcels’ backward trajectories could not be performed due to incomplete observation data and a lack of near-surface data. With the development of numerical models, gridded tornado process simulation data have made backward trajectory analysis possible and greatly promoted the development of tornado theory. In particular, the abundant computing resources in recent years have increased the credibility of parcels’ trajectory calculations for high-resolution near-surface process simulations. Some studies using high-resolution numerical simulation results and backward trajectory analysis methods have made breakthroughs in exploring the tornadogenesis mechanism of real tornadoes [33,34,35,38]. Therefore, in this study, a backward trajectory will be calculated to analyze the specific sources and development of the tornado vortex.
According to the analysis above, the approaching of the RFD cold surge to the near-ground convergence center, along with the descending of the low-level mesocyclone which strengthens the convergence center, subsequently rapidly intensifying the preexisted PTV at the leading edge of the cold surge by the large stretching as the cold surge merged into the convergence center, is the direct cause of tornadogenesis. The initial vertical vorticity of PTV obtained by the downdraft at the leading edge of the cold surge during its movement is the fundamental origin of the tornado vortex. Therefore, this study selected the moment of 09:13:20 UTC (Figure 8c) as the initial time for the backward trajectory. At this time, the PTV at the leading edge of the cold surge had already entered the near-ground convergence center. Under the influence of the descending of the low-level mesocyclone, the convergence center continued to strengthen, causing the PTV column to experience intense stretching and the extending upward, forming a TLV from the surface with maximum vertical vorticity exceeding 0.2 s−1. Selecting this moment as the initial time for backward trajectory can ensure that the parcels’ trajectory includes the above movement processes, including the approaching of the cold surge, the downdraft of the mesocyclone, and the stretching and lifting in the convergence center, so that the backward trajectory analysis can fully reflect the entire process of the tornadogenesis. Besides that, at the same time, the selected moment, which before the vortex rapidly intensifies further, can avoid the intense stretching effect of the vorticity in later moments, which would lead to the stretching effect occupying too much of the vorticity increment in the backward trajectory analysis and affecting the determination of the origin of the parcel’s vorticity.
In summary, 896 parcels were selected at the moment when the vertical vorticity was greater than 0.15 s−1 (Figure 9) as the initial parcels for backward trajectory analysis. To ensure that the parcels’ trajectory reflects the contributions of different effects to the growth of the tornado vortex reasonably, the initial parcels were uniformly distributed in space, with a spacing of 10 m between each parcel in both the horizontal and vertical directions. The height of the bottom parcel is 10 m AGL, which is the lowest level of the model. It can be seen that the distribution of parcels in space is more concentrated near the ground than at higher levels because the growth of vertical vorticity starts from near the ground and extends upward. This can reflect the movement process of parcels near the ground as accurately as possible, and the parcels at upper levels can also reflect the process of stretching and lifting under the influence of the convergence center comprehensively. In order to accurately and comprehensively record the movement process of parcels, the time step for calculating the backward trajectory was set to 0.2 s, which is one-tenth of the output time interval of the model. This can ensure that the calculated trajectory reflects the actual movement process of the parcels as much as possible. At the same time, the backward trajectory calculation was continued backward to the initial time of the innermost grid of the simulation, which is 09:00 UTC, so that the trajectory results can comprehensively rebuild the entire life of the parcels and their origin.
Figure 10 displays the horizontal trajectory map of all parcels initialized in the tornado vortex column, from the model start time (09:00 UTC) to the moment when they converge into the tornado vortex (09:13:20 UTC). The color of the trajectory indicates the parcel’s height at that moment. The starting time of each trajectory is marked in the figure, and the red dot denotes the position of the tornado vortex and the endpoint of all trajectories. It can be seen that most of the parcels come from the near-surface environment surrounding the tornado vortex, and they move near the ground for most of the time, with their positions distributed around the near-ground convergence center. After the convergence center increases due to the descending of the low-level mesocyclone, these parcels are influenced by the suction effect of the convergence center and are “sucked” into the convergence center, converging into the tornado vortex core and being lifted up by the influence of the convergence center. The movement process of these parcels is relatively simple, without experiencing large-scale upward and downward motion.
At the same time, about 100 parcels were initiated in the RFD region and followed the cold surge to the northeast direction (blue arrow). During this process, they experienced upward and downward motion and then merged into the near-ground convergence center with the cold surge. Before converging into the tornado vortex core and being lifted up, they experienced significant near-ground motion. The trajectories of these parcels are consistent with the analysis presented above: The parcels originating from the RFD followed the cold surge to approach the convergence center, and influenced by the downdraft in the cold surge, these parcels were forced to descend to the ground, where the initial vorticity was generated because of the frictional effect near surface. Then, they followed the leading edge of the cold surge into the convergence center, where the vertical vorticity rapidly increased by the stretching effect in the convergence center, and lifted by the updraft, forming a tornado vortex. Therefore, it can be inferred that these parcels play an important role in the initial vorticity generation process of the tornado. In the following part, we will extract these parcels separately and further analyze and verify the hypothesis above.
By separately plotting the trajectories of the parcels following the cold surge (the parcels in black and the trajectories in gray) and superimposing them onto the θe field (in color) and wind field (in arrow) at the average altitude of the parcels at the corresponding time (Figure 11), it can be seen that the parcels originating from the RFD were initially located at an altitude of approximately 200 m AGL. As the cold surge approached towards the convergence center, these parcels followed and converged at the leading edge of the cold surge (Figure 11a). Meanwhile, under the influence of the downdraft within the cold surge, the average altitude of these parcels continued to decrease. At 09:05:00 UTC, the mean altitude of the parcels was 180 m AGL (Figure 11a) and subsequently decreased to 60 m AGL by 09:07:30 UTC (Figure 11b) as they descended with the downdraft. After that, the parcels quickly descended towards the near-surface layer by 09:10:50 UTC, and their average altitude was only 10 m AGL (Figure 11c). It should be noted that the bottom layer of the simulation model was set at 10 m AGL, indicating that the parcels were horizontally moving at ground level at this time. During this period, the parcels remained at the leading edge of the cold surge and constantly approached towards the near-ground convergence center. Based on the time–height plot of the parcels, it was estimated that the parcels moved near the surface for approximately 6 min. Subsequently, the parcels followed the cold surge into the convergence center and were lifted upwards due to the stretching effect within the convergence center (Figure 11d). The rapid increase in vertical vorticity within the convergence center led to the formation of a tornado. The black solid line in the figure represents the average trajectory of the parcels. Previous studies have shown that the near-surface movement of parcels usually causes the frictional generation of vorticity, which is considered to be the source of the initial vorticity of tornadogenesis [33,34,35,38]. This phenomenon was also observed in this study.
Along the vertical profile of the average trajectory shown by the black solid line in Figure 11d, the vertical distribution of θe field (in colors), vertical velocity field (contour lines), and the parcels’ position (black dots) were further observed (Figure 12). At the beginning stage, the parcels were uniformly distributed at 100–200 m AGL (Figure 12a), located on the leading edge of the cold surge (blue arrow). In front of the cold surge, the updraft core corresponding to the low-level mesocyclone (black arrow) extended to the ground and was located at about 600 m AGL, below which a near-ground convergence center (red arrow) was formed. With the movement of the cold surge (Figure 12b), the parcels were influenced by the downdraft within the cold surge and moved downwards to below 100 m AGL. At the same time, the low-level mesocyclone also kept descending, leading to further strengthening of the convergence center. Subsequently, all the parcels sank to the ground level (Figure 12c), approaching the convergence center continuously with the cold surge. Meanwhile, the mesocyclone descended further to 300 m AGL, causing the convergence center to continue to grow. Finally, the parcels quickly lifted after entering the convergence center (Figure 12d), leading to the strengthening of the tornado vortex. This further confirms the previous hypothesis and demonstrates the crucial role of the cold surge in tornadogenesis, which is consistent with recent studies [33,38].

3.3. Flux Analysis of Tornado

To study the mass distribution of the airflow entering the core of the tornado vortex during its formation, as well as the contribution of airflow at different levels to the growth of the vorticity of the tornado vortex column, the vertical distribution of mass flux and vorticity flux of the airflow entering the tornado vortex was investigated. Figure 13a shows a schematic diagram of a three-dimensional tornado vortex column at the moment of tornado formation (09:13:20 UTC, also the initial time of trajectory analysis), with the red iso-surface representing the 0.1 s−1 vertical vorticity. Using the tornado vortex column as the core, a blue cylindrical surface encompassing the tornado core was established. The upper and lower boundaries of the cylinder are located at 10 m AGL and 410 m AGL, respectively. The diameter of the lower circle is 200 m, with the center at the vortex core near the ground, while the diameter of the upper circle is 400 m, with the center at the corresponding height of the vortex core. The cylinder completely encloses the tornado core with the upper and lower circles as boundaries and is uniformly distributed linearly in the vertical direction. Note that the diameter of the lower circle is smaller than that of the upper circle, taking into account that the tornado vortex is mainly developed from near the ground, where the parcels are stretched and lifted to the upper level by the near-ground convergence center. Therefore, the parcels at the upper levels enter the tornado core earlier than those at the lower levels, and the vorticity of the parcels at the upper levels decreases during the stretching and lifting process due to the decrease in velocity with increasing height. This leads to the “thick bottom and thin top” structure of the tornado vortex. Therefore, to eliminate the difference between the upper and lower layers within the tornado vortex, the diameter of the upper circle is designed to be larger than that of the lower circle.
Figure 13b,c show the vertical profiles of the mass and vorticity fluxes of the airflow at different altitudes on the blue cylindrical surface in Figure 13a, with the airflow entering the tornado vortex as positive flux and the outflow as negative flux. From the vertical profile of mass flux (Figure 13b), it can be seen that most of the airflow entering the tornado vortex comes from the lower atmosphere below 300 m AGL, and the mass flux increases with decreasing height, reaching a maximum near the ground. The negative flux at heights above 300 m AGL represents the outflow of the upper-level airflow from the tornado vortex. The same phenomenon can also be observed in the vertical profile of vorticity flux (Figure 13c): The vorticity flux is positive in the lower atmosphere below 200 m AGL and increases quickly with decreasing height, reaching the maximum in the ground level, while the upper layers are dominated by negative vorticity flux. The analysis above indicates that the airflow entering the core of the tornado mainly comes from levels below 300 m AGL, with a larger inflow at lower altitudes. Moreover, the low-level inflow contributes positively to the growth of the tornado vortex, indicating that the airflow contributing to the growth of the tornado vortex mainly comes from the levels below 200 m AGL, and is mainly concentrated near the ground.
This conclusion is consistent with the results of trajectory analysis in the previous section: Parcels entering the tornado vortex experience vorticity generation due to surface friction during near-ground motion. As it enters the near-ground convergence center, it undergoes stretching and uplift, resulting in rapid intensification of vertical vorticity and the formation of a tornado.

4. Discussion and Conclusions

In this study, a typical supercell tornado event in eastern China is selected for numerical simulation, and its formation mechanism is analyzed in depth. On the afternoon of 7 July 2013, an EF2 tornado occurred in Gaoyou County, Jiangsu Province. The tornado formed in a supercell thunderstorm near the Meiyu front system and lasted for about 20 min. The ARPS numerical model is used in this study, and the 4DEnKF is applied to assimilate Taizhou S-band Doppler radar data located near the tornado. A four-layer one-way nested grid with the inner-most horizontal grid spacing of 50 m is used. The simulation results reproduce the tornado embedded within the supercell with a reasonable agreement with observations. Based on the 50 m grid simulation results, the following conclusions are disclosed:
(1) The cold surge from the RFD plays a key role in tornadogenesis. The cold surge approaches towards the near-ground convergence center ahead of the gust front. The downdraft within the cold surge generates vertical vorticity as descending to the ground, forming a vertical vorticity maximum which is defined as PTV, which approaches the convergence center as the cold surge moves forward. Meanwhile, the descending of the low-level mesocyclone further strengthens the convergence center. The vortex is stretched in the convergence center, causing a rapid increase in vertical vorticity, ultimately forming a tornado.
(2) The backward trajectory analysis indicates that parcels originating from the RFD move towards the convergence center following the cold surge. During the process, the parcels are influenced by the downdraft within the cold surge and move near the surface, and vertical vorticity is generated during the movement near the ground. Subsequently, they merge into the convergence center following the cold surge, then being stretched and lifted with the pregenerated vertical vorticity rapidly increasing, and forming the tornado vortex eventually.
(3) Analysis of the mass and vorticity flux of the tornado vortex column indicates that the airflow entering the tornado core comes mainly from the levels below 300 m AGL, and the closer to the ground, the larger the inflow flux is. Furthermore, the low-level inflow also contributes positively to the tornado vorticity flux, which mainly comes from the level below 200 m AGL and is concentrated near the ground. This indicates that the near-surface airflow contributes significantly to the growth of the tornado vorticity and the closer to the ground, the greater the contribution has.
The results of this study further reveal the key importance of near-surface processes in the formation of tornadoes and are first demonstrated in the real data simulation of tornadoes in eastern China, which is consistent with cutting-edge theoretical advances in this field in recent years, making a significant contribution to the investigation of the dynamical process and formation mechanism of real tornadoes.
In addition, quantitative analysis of different vorticity equation terms on tornadogenesis, especially the contribution of surface friction to tornado vorticity generation, still needs further investigation.

Author Contributions

Conceptualization, S.W.; methodology, S.W.; software, S.W.; validation, S.W.; formal analysis, S.W.; investigation, S.W.; resources, J.M.; data curation, S.W.; writing—original draft preparation, S.W.; writing—review and editing, J.M.; visualization, S.W.; supervision, J.M.; project administration, J.M.; funding acquisition, J.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by a grant from the National Natural Science Foundation of China, grant number 42192553.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All observed and reanalysis datasets used in this study are freely available to the public. NCEP GFS 0.25 Degree Global Forecast Grids: https://rda.ucar.edu/datasets/ds084-1/, accessed on 26 April 2023.

Acknowledgments

Simulations were performed using the Advanced Regional Prediction System (ARPS) developed by the Center for Analysis and Prediction of Storms, University of Oklahoma.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Wurman, J.; Straka, J.M.; Rasmussen, E.N. Fine-scale Doppler radar observations of tornadoes. Science 1996, 272, 1774–1777. [Google Scholar] [CrossRef] [PubMed]
  2. Davies-Jones, R.; Trapp, R.J.; Bluestein, H.B. Tornadoes and tornadic storms. In Severe Convective Storms; American Meteorological Society: Boston, MA, USA, 2001; pp. 167–221. [Google Scholar]
  3. Browning, K.A.; Ludlam, F.H. Airflow in convective storms. Q. J. R. Meteorol. Soc. 1962, 88, 117–135. [Google Scholar] [CrossRef]
  4. Wurman, J.; Dowell, D.; Richardson, Y.; Markowski, P.; Rasmussen, E.; Burgess, D.; Wicker, L.; Bluestein, H.B. The second verification of the origins of rotation in tornadoes experiment: VOR-TEX2. Bull. Am. Meteorol. Soc. 2012, 93, 1147–1170. [Google Scholar] [CrossRef]
  5. Klemp, J.B.; Wilhelmson, R.B. The simulation of three-dimensional convective storm dynamics. J. Atmos. Sci. 1978, 35, 1070–1096. [Google Scholar] [CrossRef]
  6. Klemp, J.B.; Wilhelmson, R.B. Simulations of right-and left-moving storms produced through storm splitting. J. Atmos. Sci. 1978, 35, 1097–1110. [Google Scholar]
  7. Schlesinger, R.E. A three-dimensional numerical model of an isolated thunderstorm: Part I. Comparative experiments for variable ambient wind shear. J. Atmos. Sci. 1978, 35, 690–713. [Google Scholar] [CrossRef]
  8. Wilhelmson, R.B.; Klemp, J.B. A numerical study of storm splitting that leads to long-lived storms. J. Atmos. Sci. 1978, 35, 1974–1986. [Google Scholar] [CrossRef]
  9. Schlesinger, R.E. A three-dimensional numerical model of an isolated thunderstorm. Part II: Dynamics of updraft splitting and mesovortex couplet evolution. J. Atmos. Sci. 1980, 37, 395–420. [Google Scholar] [CrossRef]
  10. Klemp, J.B.; Wilhelmson, R.B.; Ray, P.S. Observed and numerically simulated structure of a mature supercell thunder-storm. J. Atmos. Sci. 1981, 38, 1558–1580. [Google Scholar] [CrossRef]
  11. Klemp, J.B.; Rotunno, R. A study of the tornadic region within a supercell thunderstorm. J. Atmos. Sci. 1983, 40, 359–377. [Google Scholar] [CrossRef]
  12. Davies-Jones, R. Streamwise vorticity: The origin of updraft rotation in supercell storms. J. Atmos. Sci. 1984, 41, 2991–3006. [Google Scholar] [CrossRef]
  13. Rotunno, R.; Klemp, J. On the rotation and propagation of simulated supercell thunderstorms. J. Atmos. Sci. 1985, 42, 271–292. [Google Scholar] [CrossRef]
  14. Davies-Jones, R.; Brooks, H. Mesocyclogenesis from a theoretical perspective. Am. Geophys. Union Geophys. Monogr. Ser. 1993, 79, 105–114. [Google Scholar]
  15. Wicker, L.J.; Wilhelmson, R.B. Simulation and analysis of tornado development and decay within a three-dimensional supercell thunderstorm. J. Atmos. Sci. 1995, 52, 2675–2703. [Google Scholar] [CrossRef]
  16. Rasmussen, E.N.; Straka, J.M.; Davies-Jones, R.; Doswell, C.A.; Carr, F.H.; Eilts, M.D.; MacGorman, D.R. Verification of the origins of rotation in tornadoes experiment: VORTEX. Bull. Am. Meteorol. Soc. 1994, 75, 995–1006. [Google Scholar] [CrossRef]
  17. Trapp, R.J.; Mitchell, E.D.; Tipton, G.A.; Effertz, D.W.; Watson, A.I.; Andra, D.L.; Magsig, M.A. Descending and nondescending tornadic vortex signatures detected by WSR-88Ds. Weather Forecast. 1999, 14, 625–639. [Google Scholar] [CrossRef]
  18. Wakimoto, R.M.; Cai, H. Analysis of a nontornadic storm during VORTEX 95. Mon. Weather Rev. 2000, 128, 565–592. [Google Scholar] [CrossRef]
  19. Markowski, P.M.; Straka, J.M.; Rasmussen, E.N. Direct surface thermodynamic observations within the rear-flank downdrafts of nontornadic and tornadic supercells. Mon. Weather Rev. 2002, 130, 1692–1721. [Google Scholar] [CrossRef]
  20. Grzych, M.L.; Lee, B.D.; Finley, C.A. Thermodynamic analysis of supercell rear-flank downdrafts from Project ANSWERS. Mon. Weather Rev. 2007, 135, 240–246. [Google Scholar] [CrossRef]
  21. Hirth, B.D.; Schroeder, J.L.; Weiss, C.C. Surface analysis of the rear-flank downdraft outflow in two tornadic supercells. Mon. Weather Rev. 2008, 136, 2344–2363. [Google Scholar] [CrossRef]
  22. Markowski, P.; Richardson, Y. Mesoscale Meteorology in Midlatitudes; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
  23. Markowski, P.M.; Richardson, Y.P. Tornadogenesis: Our current understanding, forecasting considerations, and questions to guide future research. Atmos. Res. 2009, 93, 3–10. [Google Scholar] [CrossRef]
  24. Sun, J.; Xue, M.; Wilson, J.W.; Zawadzki, I.; Ballard, S.P.; Onvlee-Hooimeyer, J.; Joe, P.; Barker, D.; Li, P.-W.; Golding, B.; et al. Use of NWP for nowcasting convective precipitation: Recent progress and challenges. Bull. Am. Meteorol. Soc. 2014, 95, 409–426. [Google Scholar] [CrossRef]
  25. Snyder, C.; Zhang, F. Assimilation of simulated Doppler radar observations with an ensemble Kalman filter. Mon. Weather Rev. 2003, 131, 1663–1677. [Google Scholar] [CrossRef]
  26. Tong, M.; Xue, M. Ensemble Kalman filter assimilation of Doppler radar data with a compressible nonhydrostatic model: OSS experiments. Mon. Weather Rev. 2005, 133, 1789–1807. [Google Scholar] [CrossRef]
  27. Snook, N.; Xue, M.; Jung, Y. Ensemble probabilistic forecasts of a tornadic mesoscale convective system from ensemble Kalman filter analyses using WSR-88D and CASA radar data. Mon. Weather Rev. 2012, 140, 2126–2146. [Google Scholar] [CrossRef]
  28. Stensrud, D.J.; Wicker, L.J.; Xue, M.; Dawson, D.T.; Yussouf, N.; Wheatley, D.M.; Thompson, T.E.; Snook, N.A.; Smith, T.M.; Schenkman, A.D.; et al. Progress and challenges with Warn-on-Forecast. Atmos. Res. 2013, 123, 2–16. [Google Scholar] [CrossRef]
  29. Hu, M.; Xue, M. Impact of configurations of rapid intermittent assimilation of WSR-88D radar data for the 8 May 2003 Oklahoma City tornadic thunderstorm case. Mon. Weather Rev. 2007, 135, 507–525. [Google Scholar] [CrossRef]
  30. Xue, M.; Hu, M.; Schenkman, A.D. Numerical prediction of the 8 May 2003 Oklahoma City tornadic supercell and embedded tornado using ARPS with the assimilation of WSR-88D data. Weather Forecast. 2014, 29, 39–62. [Google Scholar] [CrossRef]
  31. Mashiko, W.; Niino, H.; Kato, T. Numerical simulation of tornadogenesis in an outer-rainband minisupercell of Typhoon Shanshan on 17 September 2006. Mon. Weather Rev. 2009, 137, 4238–4260. [Google Scholar] [CrossRef]
  32. Schenkman, A.D.; Xue, M.; Shapiro, A. Tornadogenesis in a simulated mesovortex within a mesoscale convective system. J. Atmos. Sci. 2012, 69, 3372–3390. [Google Scholar] [CrossRef]
  33. Schenkman, A.D.; Xue, M.; Hu, M. Tornadogenesis in a high-resolution simulation of the 8 May 2003 Oklahoma City supercell. J. Atmos. Sci. 2014, 71, 130–154. [Google Scholar] [CrossRef]
  34. Roberts, B.; Xue, M.; Schenkman, A.D.; Dawson, D.T. The role of surface drag in tornadogenesis within an idealized supercell simulation. J. Atmos. Sci. 2016, 73, 3371–3395. [Google Scholar] [CrossRef]
  35. Roberts, B.; Xue, M. The Role of Surface Drag in Mesocyclone Intensification Leading to Tornadogenesis within an Idealized Supercell Simulation. J. Atmos. Sci. 2017, 74, 3055–3077. [Google Scholar] [CrossRef]
  36. Rasmussen, E.N.; Straka, J.M.; Gilmore, M.S.; Davies-Jones, R. A preliminary survey of rear-flank descending reflectivity cores in supercell storms. Weather Forecast. 2006, 21, 923–938. [Google Scholar] [CrossRef]
  37. Skinner, P.S.; Weiss, C.C.; French, M.M.; Bluestein, H.B.; Markowski, P.M.; Richardson, Y.P. VORTEX2 observations of a low-level mesocyclone with multiple internal rear-flank downdraft momentum surges in the 18 May 2010 Dumas, Texas, supercell. Mon. Weather Rev. 2014, 142, 2935–2960. [Google Scholar] [CrossRef]
  38. Schenkman, A.D.; Xue, M.; Dawson, D.T. The cause of internal outflow surges in a high-resolution simulation of the 8 May 2003 Oklahoma City tornadic supercell. J. Atmos. Sci. 2016, 73, 353–370. [Google Scholar] [CrossRef]
  39. Dawson, D.T.; Xue, M.; Milbrandt, J.A.; Yau, M.K. Comparison of evaporation and cold pool development between single-moment and multimoment bulk microphysics schemes in idealized simulations of tornadic thunderstorms. Mon. Weather Rev. 2010, 138, 1152–1171. [Google Scholar] [CrossRef]
  40. Dawson, D.T.; Xue, M.; Milbrandt, J.A.; Shapiro, A. Sensitivity of real-data simulations of the 3 May 1999 Oklahoma City tornadic supercell and associated tornadoes to multimoment microphysics. Part I: Storm-and tornado-scale numerical forecasts. Mon. Weather Rev. 2015, 143, 2241–2265. [Google Scholar] [CrossRef]
  41. Dawson, D.T.; Xue, M.; Shapiro, A.; Milbrandt, J.A.; Schenkman, A.D. Sensitivity of real-data simulations of the 3 May 1999 Oklahoma City tornadic supercell and associated tornadoes to multimoment microphysics. Part II: Analysis of buoyancy and dynamic pressure forces in simulated tornado-like vortices. J. Atmos. Sci. 2016, 73, 1039–1061. [Google Scholar] [CrossRef]
  42. Fan, W.; Yu, X. Characteristics of Spatial Temporal Distribution of Tornadoes in China. Meteorol. Mon. 2015, 41, 793–805. [Google Scholar]
  43. Brooks, H.E.; Carbin, G.W.; Marsh, P.T. Increased variability of tornado occurrence in the United States. Science 2014, 346, 349–352. [Google Scholar] [CrossRef] [PubMed]
  44. Yao, Y.; Yu, X.; Zhang, Y.; Zhou, Z.; Xie, W.; Lu, Y.; Yu, J.; Wei, L. Climate analysis of tornadoes in China. J. Meteorol. Res. 2015, 29, 359–369. [Google Scholar] [CrossRef]
  45. Zeng, M.; Wu, H.; Wang, X.; Jiang, Y. Analysis on Environmental Conditions and Structural Features of Typical Convective Tornado Storm in Meiyu Period. Meteorol. Mon. 2016, 42, 280–293. [Google Scholar]
  46. Zhou, H.; Diao, X.; Xia, W.; Wang, D.; Xiang, Y. Analysis of the tornado supercell storm and its environmental parameters in the Yangtze-Huaihe region. Acta Meteorol. Sin. 2014, 72, 306–317. [Google Scholar]
  47. Xue, M.; Droegemeier, K.K.; Wong, V.; Shapiro, A.; Brewster, K.; Carr, F.; Weber, D.; Liu, Y.; Wang, D. The Advanced Regional Prediction System (ARPS)–A multiscale nonhydrostatic atmospheric simulation and prediction tool. Part II: Model physics and applications. Meteor. Atmos. Phys. 2001, 76, 143–165. [Google Scholar] [CrossRef]
  48. Xue, M.; Wang, D.; Gao, J.; Brewster, K.; Droegemeier, K.K. The Advanced Regional Prediction System (ARPS), storm-scale numerical weather prediction and data assimilation. Meteor. Atmos. Phys. 2003, 82, 139–170. [Google Scholar] [CrossRef]
  49. Hu, M.; Xue, M.; Brewster, K. 3DVAR and cloud analysis with WSR-88D level-II data for the prediction of the Fort Worth, Texas, tornadic thunderstorms. Part I: Cloud analysis and its impact. Mon. Weather Rev. 2006, 134, 675–698. [Google Scholar] [CrossRef]
  50. Shen, F.; Min, J.; Xu, D.; Dai, Z.; Zhang, B.; Chen, Y. Application of assimilating dual Doppler radar data in forecast of hurricane Ike. Haiyang Xuebao 2016, 38, 60–72. [Google Scholar]
  51. Shen, F.; Min, J.; Xu, D. Assimilation of radar radial velocity data with the WRF Hybrid ETKF-3DVAR system for the prediction of Hurricane Ike (2008). Atmos. Res. 2016, 169, 127–138. [Google Scholar] [CrossRef]
  52. Shen, F.; Xue, M.; Min, J. A comparison of limited-area 3DVAR and ETKF-En3DVAR data assimilation using radar observations at convective scale for the prediction of Typhoon Saomai (2006). Meteorol. Appl. 2017, 24, 628–641. [Google Scholar] [CrossRef]
  53. Shen, F.; Xu, D.; Xue, M.; Min, J. A comparison between EDA-EnVar and ETKF-EnVar data assimilation techniques using radar observations at convective scales through a case study of Hurricane Ike (2008). Meteorol. Atmos. Phys. 2018, 130, 649–666. [Google Scholar] [CrossRef]
  54. Shen, F.; Xu, D.; Min, J. Effect of momentum control variables on assimilating radar observations for the analysis and forecast for Typhoon Chanthu (2010). Atmos. Res. 2019, 230, 104622. [Google Scholar] [CrossRef]
  55. Xu, D.; Shen, F.; Min, J. Effect of background error tuning on assimilating radar radial velocity observations for the forecast of hurricane tracks and intensities. Meteorol. Appl. 2020, 27, e1820. [Google Scholar] [CrossRef]
  56. Shen, F.; Song, L.; Li, H.; He, Z.; Xu, D. Effects of different momentum control variables in radar data assimilation on the analysis and forecast of strong convective systems under the background of northeast cold vortex. Atmos. Res. 2022, 280, 106415. [Google Scholar] [CrossRef]
  57. Xu, D.; Shen, F.; Min, J. Effect of Adding Hydrometeor Mixing Ratios Control Variables on Assimilating Radar Observations for the Analysis and Forecast of a Typhoon. Atmosphere 2019, 10, 415. [Google Scholar] [CrossRef]
  58. Xu, D.; Shu, A.; Shen, F.; Min, J.; Li, H.; Xia, X. Impacts of Multiple Radiance Data Assimilation on the Simulation of Typhoon Chan-Hom. Atmosphere 2020, 11, 957. [Google Scholar] [CrossRef]
  59. Xu, D.; Shu, A.; Li, H.; Shen, F.; Li, Q.; Su, H. Effects of Assimilating Clear-Sky FY-3D MWHS2 Radiance on the Numerical Simulation of Tropical Storm Ampil. Remote Sens. 2021, 13, 2873. [Google Scholar] [CrossRef]
  60. Xu, D.; Zhang, X.; Li, H.; Wu, H.; Shen, F.; Shu, A.; Wang, Y.; Zhuang, X. Evaluation of the Simulation of Typhoon Lekima (2019) Based on Different Physical Parameterization Schemes and FY-3D Satellite’s MWHS-2 Data Assimilation. Remote Sens. 2021, 13, 4556. [Google Scholar] [CrossRef]
  61. Lin, Y.L.; Farley, R.D.; Orville, H.D. Bulk parameterization of the snow field in a cloud model. J. Appl. Meteorol. Climatol. 1983, 22, 1065–1092. [Google Scholar] [CrossRef]
  62. Byun, D.W. On the analytical solutions of flux-profile relationships for the atmospheric surface layer. J. Appl. Meteorol. 1990, 29, 652–657. [Google Scholar] [CrossRef]
  63. Sun, W.Y.; Chang, C.Z. Diffusion model for a convective layer. Part I: Numerical simulation of convective boundary layer. J. Appl. Meteorol. Climatol. 1986, 25, 1445–1453. [Google Scholar] [CrossRef]
  64. Moeng, C.H. A large-eddy-simulation model for the study of planetary boundary-layer turbulence. J. Atmos. Sci. 1984, 41, 2052–2062. [Google Scholar] [CrossRef]
  65. Noilhan, J.; Planton, S. A simple parameterization of land surface processes for meteorological models. Mon. Weather Rev. 1989, 117, 536–549. [Google Scholar] [CrossRef]
Atmosphere 14 00884 g001 550
Figure 1. (a,b) The combined radar echoes (dBZ) in the East China region at 04:00 UTC and 08:50 UTC on 7 July 2013, respectively. (c,d) The reflectivity (dBZ) and radial wind (m s−1) of the Taizhou radar at 09:00 UTC on 7 July 2013. The elevation angle of the radar in (c) is 1.45PPI, and the elevation angle of the radar in (d) is 2.42PPI.
Figure 1. (a,b) The combined radar echoes (dBZ) in the East China region at 04:00 UTC and 08:50 UTC on 7 July 2013, respectively. (c,d) The reflectivity (dBZ) and radial wind (m s−1) of the Taizhou radar at 09:00 UTC on 7 July 2013. The elevation angle of the radar in (c) is 1.45PPI, and the elevation angle of the radar in (d) is 2.42PPI.
Atmosphere 14 00884 g001
Atmosphere 14 00884 g002 550
Figure 2. (a) The four-layer grid design process in this study, and (b) a schematic diagram of the 1 km, 200 m, and 50 m grid areas in the experiment. The gray area in the figure represents the water surface, and the asterisk indicates the location of the Taizhou radar.
Figure 2. (a) The four-layer grid design process in this study, and (b) a schematic diagram of the 1 km, 200 m, and 50 m grid areas in the experiment. The gray area in the figure represents the water surface, and the asterisk indicates the location of the Taizhou radar.
Atmosphere 14 00884 g002
Atmosphere 14 00884 g003 550
Figure 3. (a) The model output of the 20 m AGL radar reflectivity (shaded, dBZ) and wind arrow (m s−1) of the 50 m simulation domain (the X and Y axes have their origin at the lower-left corner of the domain) at 09:16 UTC on 7 July 2013. The contours represent the vertical vorticity (s−1), starting at 0.05 s−1 with an interval of 0.05 s−1. (b) The Taizhou radar reflectivity (shaded, dBZ) at 09:12 UTC on 7 July 2013, with a radar elevation angle of 1.45PPI.
Figure 3. (a) The model output of the 20 m AGL radar reflectivity (shaded, dBZ) and wind arrow (m s−1) of the 50 m simulation domain (the X and Y axes have their origin at the lower-left corner of the domain) at 09:16 UTC on 7 July 2013. The contours represent the vertical vorticity (s−1), starting at 0.05 s−1 with an interval of 0.05 s−1. (b) The Taizhou radar reflectivity (shaded, dBZ) at 09:12 UTC on 7 July 2013, with a radar elevation angle of 1.45PPI.
Atmosphere 14 00884 g003
Atmosphere 14 00884 g004 550
Figure 4. The time–height diagrams of the maximum vertical velocity (m s−1) (a) and maximum vertical vorticity (s−1) (b) in the supercell region. The black vertical lines indicate the time of TLV formation (left) and tornado formation (right), and the green horizontal line represents 30 m AGL.
Figure 4. The time–height diagrams of the maximum vertical velocity (m s−1) (a) and maximum vertical vorticity (s−1) (b) in the supercell region. The black vertical lines indicate the time of TLV formation (left) and tornado formation (right), and the green horizontal line represents 30 m AGL.
Atmosphere 14 00884 g004
Atmosphere 14 00884 g005 550
Figure 5. The equivalent potential temperature (shaded, K), perturbation pressure (contour, Pa), and wind arrow (m s−1) at 20 m AGL at 09:00 UTC (a) and 09:05 UTC (b) on 7 July 2013. The red dashed line represents the gust front, the blue arrow represents the cold surge, and the red arrow represents the center of low-level convergence.
Figure 5. The equivalent potential temperature (shaded, K), perturbation pressure (contour, Pa), and wind arrow (m s−1) at 20 m AGL at 09:00 UTC (a) and 09:05 UTC (b) on 7 July 2013. The red dashed line represents the gust front, the blue arrow represents the cold surge, and the red arrow represents the center of low-level convergence.
Atmosphere 14 00884 g005
Atmosphere 14 00884 g006 550
Figure 6. The equivalent potential temperature (shaded, K), vertical vorticity (contour, s−1), and wind arrow (m s−1) at 20 m AGL at (a) 09:11 UTC, (b) 09:12 UTC, (c) 09:13 UTC, (d) 09:14 UTC, (e) 09:15 UTC, and (f) 09:16 UTC on 7 July 2013. The red dashed line represents the gust front, the red arrow represents the center of low-level convergence, and the black arrow indicates the tornado vortex. The contour levels start at 0.05 s−1 with an interval of 0.05 s−1.
Figure 6. The equivalent potential temperature (shaded, K), vertical vorticity (contour, s−1), and wind arrow (m s−1) at 20 m AGL at (a) 09:11 UTC, (b) 09:12 UTC, (c) 09:13 UTC, (d) 09:14 UTC, (e) 09:15 UTC, and (f) 09:16 UTC on 7 July 2013. The red dashed line represents the gust front, the red arrow represents the center of low-level convergence, and the black arrow indicates the tornado vortex. The contour levels start at 0.05 s−1 with an interval of 0.05 s−1.
Atmosphere 14 00884 g006
Atmosphere 14 00884 g007 550
Figure 7. (a) The positions of tornado vortices at different times on 7 July 2013, with the shading and contour representing vertical vorticity (s−1), starting at 0.1 s−1 with an interval of 0.05 s−1. (b) The perturbation pressure (shaded, Pa) and vertical vorticity (contour, m s−1) at 20 m AGL at 09:16 UTC on 7 July 2013, with contour levels starting at 0.1 s−1 with an interval of 0.05 s−1. The black solid line AB represents the position of the vertical cross-section, and (c) the vertical cross-section along AB in (b), with the same legend as above.
Figure 7. (a) The positions of tornado vortices at different times on 7 July 2013, with the shading and contour representing vertical vorticity (s−1), starting at 0.1 s−1 with an interval of 0.05 s−1. (b) The perturbation pressure (shaded, Pa) and vertical vorticity (contour, m s−1) at 20 m AGL at 09:16 UTC on 7 July 2013, with contour levels starting at 0.1 s−1 with an interval of 0.05 s−1. The black solid line AB represents the position of the vertical cross-section, and (c) the vertical cross-section along AB in (b), with the same legend as above.
Atmosphere 14 00884 g007
Atmosphere 14 00884 g008 550
Figure 8. Isopleths of vertical vorticity (s−1) at (a) 09:11:00 UTC, (b) 09:12:20 UTC, (c) 09:13:20 UTC, and (d) 09:16:00 UTC on 7 July 2013. The viewpoint is from northwest to southeast. The colors of the isopleths correspond to the following values: 0.05 s−1 (red), 0.1 s−1 (green), 0.15 s−1 (blue), and 0.2 s−1 (black). The red arrow represents a near-surface mesocyclone, the blue arrow represents the cold air surge direction, and the black arrow represents the tornado vortex.
Figure 8. Isopleths of vertical vorticity (s−1) at (a) 09:11:00 UTC, (b) 09:12:20 UTC, (c) 09:13:20 UTC, and (d) 09:16:00 UTC on 7 July 2013. The viewpoint is from northwest to southeast. The colors of the isopleths correspond to the following values: 0.05 s−1 (red), 0.1 s−1 (green), 0.15 s−1 (blue), and 0.2 s−1 (black). The red arrow represents a near-surface mesocyclone, the blue arrow represents the cold air surge direction, and the black arrow represents the tornado vortex.
Atmosphere 14 00884 g008
Atmosphere 14 00884 g009 550
Figure 9. Distribution of initial positions of the trajectories. The red contour represents the vertical vorticity of 0.15 s−1 at 09:13:20 UTC on 7 July 2013.
Figure 9. Distribution of initial positions of the trajectories. The red contour represents the vertical vorticity of 0.15 s−1 at 09:13:20 UTC on 7 July 2013.
Atmosphere 14 00884 g009
Atmosphere 14 00884 g010 550
Figure 10. The trajectory plot of the parcels, where the color of the trajectories represents the height (m) of the parcels. The red dots indicate the location of the tornado vortex. The blue arrows represent the direction of the cold front.
Figure 10. The trajectory plot of the parcels, where the color of the trajectories represents the height (m) of the parcels. The red dots indicate the location of the tornado vortex. The blue arrows represent the direction of the cold front.
Atmosphere 14 00884 g010
Atmosphere 14 00884 g011 550
Figure 11. The 20 m AGL equivalent potential temperature (shaded, K) and wind arrows (m s−1) at (a) 09:05:00 UTC, (b) 09:07:30 UTC, (c) 09:10:50 UTC, and (d) 09:13:20 UTC on 7 July 2013. The trajectories of parcels from the cold surge are superimposed on the plot (in gray), with the average trajectory shown in black.
Figure 11. The 20 m AGL equivalent potential temperature (shaded, K) and wind arrows (m s−1) at (a) 09:05:00 UTC, (b) 09:07:30 UTC, (c) 09:10:50 UTC, and (d) 09:13:20 UTC on 7 July 2013. The trajectories of parcels from the cold surge are superimposed on the plot (in gray), with the average trajectory shown in black.
Atmosphere 14 00884 g011
Atmosphere 14 00884 g012 550
Figure 12. Vertical cross-sections of equivalent potential temperature (shaded, K) and vertical velocity (contours, m s−1) along the mean track shown by the black line in Figure 11a at (a) 09:05:00 UTC, (b) 09:07:30 UTC, (c) 09:10:50 UTC, and (d) 09:13:20 UTC on 7 July 2013. The position of the parcels at the corresponding time is indicated by a black dot. The red arrow denotes the center of the low-level convergence, the blue arrow indicates the direction of the cold surge, and the black arrow represents the near-surface cyclone.
Figure 12. Vertical cross-sections of equivalent potential temperature (shaded, K) and vertical velocity (contours, m s−1) along the mean track shown by the black line in Figure 11a at (a) 09:05:00 UTC, (b) 09:07:30 UTC, (c) 09:10:50 UTC, and (d) 09:13:20 UTC on 7 July 2013. The position of the parcels at the corresponding time is indicated by a black dot. The red arrow denotes the center of the low-level convergence, the blue arrow indicates the direction of the cold surge, and the black arrow represents the near-surface cyclone.
Atmosphere 14 00884 g012
Atmosphere 14 00884 g013 550
Figure 13. (a) The 0.1 s−1 vertical vorticity contour surface of the tornado at 09:13:20 UTC on 7 July 2013, viewed from northeast to southwest. (b,c) The vertical profiles of mass flux (g m−2 s−1) and vorticity fluxes (m−2) calculated with respect to the blue cylindrical surface in (a), where the direction of the inflow to the cylinder is defined as positive.
Figure 13. (a) The 0.1 s−1 vertical vorticity contour surface of the tornado at 09:13:20 UTC on 7 July 2013, viewed from northeast to southwest. (b,c) The vertical profiles of mass flux (g m−2 s−1) and vorticity fluxes (m−2) calculated with respect to the blue cylindrical surface in (a), where the direction of the inflow to the cylinder is defined as positive.
Atmosphere 14 00884 g013
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Wang, S.; Min, J. Dynamical Analyses of a Supercell Tornado in Eastern China Based on a Real-Data Simulation. Atmosphere 2023, 14, 884. https://doi.org/10.3390/atmos14050884

AMA Style

Wang S, Min J. Dynamical Analyses of a Supercell Tornado in Eastern China Based on a Real-Data Simulation. Atmosphere. 2023; 14(5):884. https://doi.org/10.3390/atmos14050884

Chicago/Turabian Style

Wang, Shiqi, and Jinzhong Min. 2023. "Dynamical Analyses of a Supercell Tornado in Eastern China Based on a Real-Data Simulation" Atmosphere 14, no. 5: 884. https://doi.org/10.3390/atmos14050884

APA Style

Wang, S., & Min, J. (2023). Dynamical Analyses of a Supercell Tornado in Eastern China Based on a Real-Data Simulation. Atmosphere, 14(5), 884. https://doi.org/10.3390/atmos14050884

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop