Extreme Heat Events over Southeast Europe Based on NEX-GDDP Ensemble: Present Climate Evaluation and Future Projections
Abstract
:1. Introduction
2. Material and Methods
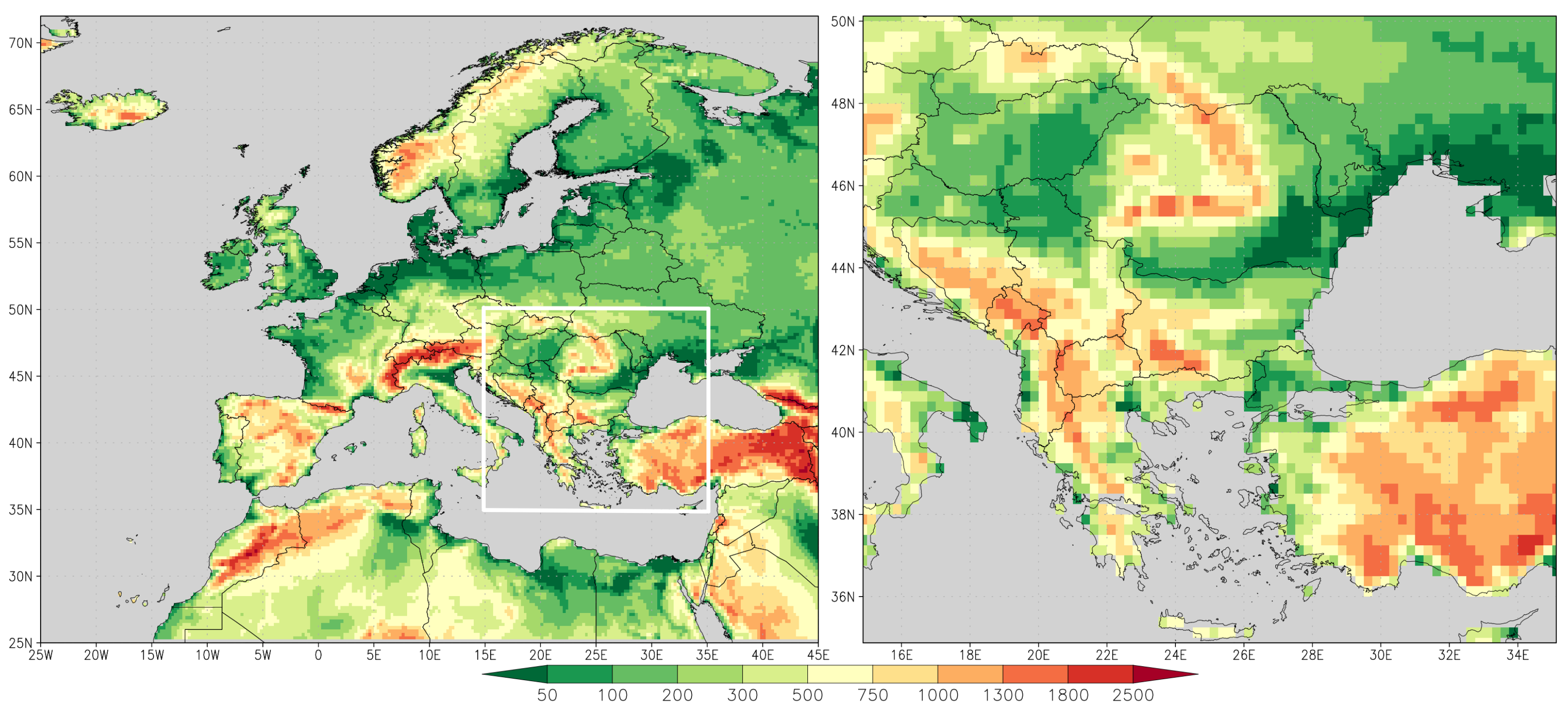
2.1. Study Area
2.2. Data
2.3. Methodology
- 1.
- Annual number of hot days (nhd), i.e., the annual count of days when °C;
- 2.
- Maximum number of consecutive hot days (chd), i.e., the longest continuous calendar period in the year when °C;
- 3.
- Hot spells duration at different thresholds (hsd32/34/36/38/40), i.e., the annual count of days when , 34, 36, 38 and 40 °C for at least 6, 5, 4, 3 and 2 consecutive days, respectively.
3. Results and Discussion
3.1. Present Climate Evaluation
3.2. Future Projections of EHEs
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. NEX-GDDP GCMs
| GCM | Institution, Country | Resolution (Lon × Lat Levels) |
|---|---|---|
| ACCESSl-0 | Commonwealth Scientific and Industrial Research Organization and Bureau of Meteorology, Australia | 92 × 145 L38 |
| BCC-CSMl-1 | Beijing Climate Center, China Meteorological Administration, China | 128 × 64 L26 (T42) |
| BNU-ESM | Beijing Normal University, China | 128 × 64 L26 (T42) |
| CanESM2 | Canadian Centre for Climate Modelling and Analysis, Canada | 128 × 64 L35 (T63) |
| CCSM4 | National Center for Atmospheric Research (NCAR), USA | 288 × 192 L26 |
| CESMl-BGC | National Science Foundation/Department of Energy NCAR, USA | 288 × 192 L26 |
| CNRM-CM5 | Centre National de Recherches Meteorologiques, Meteo-France, France | 256 × 128 L31 (T127) |
| CSIRO-MK3-6-0 | Australian Commonwealth Scientific and Industrial Research Organization, Australia | 192 × 96 L18 (T63) |
| GFDL-CM3 | Geophysical Fluid Dynamics Laboratory, USA | 144 × 90 L48 |
| GFDL-ESM2G | Geophysical Fluid Dynamics Laboratory, USA | 144 × 90 L24 |
| GFDL-ESM2M | Geophysical Fluid Dynamics Laboratory, USA | 144 × 90 L24 |
| INM-CM4 | Institute for Numerical Mathematics, Russia | 180 × 120 L21 |
| IPSL-CM5A-LR | Institute Pierre-Simon Laplace, France | 96 × 96 L39 |
| IPSL-CM5A-MR | Institute Pierre-Simon Laplace, France | 144 × 143 L39 |
| MIROC-ESM | AORI, NIES, JAMSTEC, Japan | 128 × 64 L80 (T42) |
| MIROC-ESM-CHEM | AORI, NIES, JAMSTEC, Japan | 128 × 64 L80 (T42) |
| MIROC5 | AORI, NIES, JAMSTEC, Japan | 256 × 128 L40 (T85) |
| MPI-ESM-LR | Max Planck Institute for Meteorology, Germany | 192 × 96 L47 (T63) |
| MPI-ESM-MR | Max Planck Institute for Meteorology, Germany | 192 × 96 L95 (T63) |
| MRl-CGCM3 | Meteorological Research Institute, Japan | 320 × 160 L48 (T159) |
| NorESMl-M | Norwegian Climate Centre, Norway | 144 × 96 L26 |
References
- Horton, R.M.; Mankin, J.S.; Lesk, C.; Coffel, E.; Raymond, C. A Review of Recent Advances in Research on Extreme Heat Events. Curr. Clim. Change Rep. 2016, 2, 242–259. [Google Scholar] [CrossRef] [Green Version]
- Sun, Q.; Miao, C.; Hanel, M.; Borthwick, A.G.L.; Duan, Q.; Ji, D.; Li, H. Global Heat Stress on Health, Wildfires, and Agricultural Crops under Different Levels of Climate Warming. Environ. Int. 2019, 128, 125–136. [Google Scholar] [CrossRef] [PubMed]
- Harkness, C.; Semenov, M.A.; Areal, F.; Senapati, N.; Trnka, M.; Balek, J.; Bishop, J. Adverse Weather Conditions for UK Wheat Production under Climate Change. Agric. For. Meteorol. 2020, 282–283, 107862. [Google Scholar] [CrossRef]
- Hatfield, J.L.; Prueger, J.H. Temperature Extremes: Effect on Plant Growth and Development. Weather. Clim. Extrem. 2015, 10, 4–10. [Google Scholar] [CrossRef] [Green Version]
- WMO. The Global Climate 2001–2010, a Decade of Climate Extremes; WMO-No. 1103; WMO: Geneva, Switzerland, 2013; p. 119. [Google Scholar]
- Schoetter, R.; Cattiaux, J.; Douville, H. Changes of Western European Heat Wave Characteristics Projected by the CMIP5 Ensemble. Clim. Dyn. 2015, 45, 1601–1616. [Google Scholar] [CrossRef]
- Spinoni, J.; Vogt, J.V.; Barbosa, P.; Dosio, A.; McCormick, N.; Bigano, A.; Füssel, H.-M. Changes of Heating and Cooling Degree-Days in Europe from 1981 to 2100: HDD and CDD in Europe from 1981 to 2100. Int. J. Climatol. 2018, 38, e191–e208. [Google Scholar] [CrossRef] [Green Version]
- Coccolo, S.; Kämpf, J.; Scartezzini, J.; Pearlmutter, D. Outdoor human comfort and thermal stress: A comprehensive review on models and standards. Urban Clim. 2016, 18, 33–57. [Google Scholar] [CrossRef]
- Vandentorren, S.; Bretin, P.; Zeghnoun, A.; Mandereau-Bruno, L.; Croisier, A.; Cochet, C.; Ribéron, J.; Siberan, I.; Declercq, B.; Ledrans, M. August 2003 Heat Wave in France: Risk Factors for Death of Elderly People Living at Home. Eur. J. Public Health 2006, 16, 583–591. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, M.; Yang, J.; Gong, D.; Shi, P.; Han, Z.; Kim, S.-J. Footprints of Atlantic Multidecadal Oscillation in the Low-Frequency Variation of Extreme High Temperature in the Northern Hemisphere. J. Clim. 2019, 32, 791–802. [Google Scholar] [CrossRef]
- Perkins, S.E.; Alexander, L.V.; Nairn, J.R. Increasing Frequency, Intensity and Duration of Observed Global Heatwaves and Warm Spells. Geophys. Res. Lett. 2012, 39, 2012GL053361. [Google Scholar] [CrossRef]
- Vautard, R.; van Aalst, M.; Boucher, O.; Drouin, A.; Haustein, K.; Kreienkamp, F.; van Oldenborgh, G.J.; Otto, F.E.L.; Ribes, A.; Robin, Y.; et al. Human contribution to the record-breaking June and July 2019 heatwaves in Western Europe. Environ. Res. Lett. 2020, 15, 094077. [Google Scholar] [CrossRef]
- Becker, F.N.; Fink, A.H.; Bissolli, P.; Pinto, J.G. Towards a More Comprehensive Assessment of the Intensity of Historical European Heat Waves (1979–2019). Atmos. Sci. Lett. 2022, 23, e1120. [Google Scholar] [CrossRef]
- Morabito, M.; Crisci, A.; Messeri, A.; Messeri, G.; Betti, G.; Orlandini, S.; Raschi, A.; Maracchi, G. Increasing Heatwave Hazards in the Southeastern European Union Capitals. Atmosphere 2017, 8, 115. [Google Scholar] [CrossRef] [Green Version]
- Russo, S.; Sillmann, J.; Fischer, E.M. Top ten European heatwaves since 1950 and their occurrence in the coming decades. Environ. Res. Lett. 2015, 10, 124003. [Google Scholar] [CrossRef]
- Beniston, M. The 2003 heatwave in Europe: A shape of things to come? An analysis based on Swiss climatological data and model simulations: The 2003 heat wave in Europe. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Barriopedro, D.; Fischer, E.M.; Luterbacher, J.; Trigo, R.M.; García-Herrera, R. The Hot Summer of 2010: Redrawing the Temperature Record Map of Europe. Science 2011, 332, 220–224. [Google Scholar] [CrossRef] [Green Version]
- Sánchez-Benítez, A.; García-Herera, R.; Barriopedro, D.; Sousa, P.M.; Trigo, R.M. June 2017: The Earliest European Summer Megaheatwave of Reanalysis Period. Geophys. Res. Lett. 2018, 45, 1955–1962. [Google Scholar] [CrossRef]
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.; Péan, C.; Berger, S.; Caud, N.; Chen, Y.; Goldfarb, L.; Gomis, M.; et al. Climate Change 2021: The Physical Science Basis. In Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Technical Report; IPCC: Geneva, Switzerland, 2021. [Google Scholar]
- Kostopoulou, E.; Jones, P.D. Assessment of climate extremes in the Eastern Mediterranean. Meteorol. Atmos. Phys. 2005, 89, 69–85. [Google Scholar] [CrossRef]
- Alexandrov, V.; Schneider, M.; Koleva, E.; Moisselin, J.M. Climate variability and change in Bulgaria during the 20th century. Theor. Appl. Climatol. 2004, 79, 133–149. [Google Scholar] [CrossRef]
- Philandras, C.M.; Nastos, P.T.; Repapis, C.C. Air temperature variability and trends over Greece. Glob. Nest J. 2008, 10, 273–285. [Google Scholar]
- Toreti, A.; Desiato, F.; Fioravanti, G.; Perconti, W. Seasonal temperatures over Italy and their relationship with low-frequency atmospheric circulation patterns. Clim. Change 2008, 99, 211–227. [Google Scholar] [CrossRef]
- Bartolini, G.; di Stefano, V.; Maracchi, G.; Orlandini, S. Mediterranean warming is especially due to summer season - evidences from Tuscany (central Italy). Theor. Appl. Climatol. 2012, 107, 279–295. [Google Scholar] [CrossRef]
- Xoplaki, E.; González-Rouco, J.; Gyalistras, D.; Luterbacher, J.; Rickli, R.; Wanner, H. Interannual summer air temperature variability over Greece and its connection to the large-scale atmospheric circulation and Mediterranean SSTs 1950–1999. Clim. Dyn. 2003, 20, 537–554. [Google Scholar] [CrossRef]
- Lhotka, O.; Kyselý, J. The 2021 European Heat Wave in the Context of Past Major Heat Waves. Earth Space Sci. 2022, 9, e2022EA002567. [Google Scholar] [CrossRef]
- Xoplaki, E.; Trigo, R.M.; García-Herrera, R.; Barriopedro, D.; D’Andrea, F.; Fischer, E.M.; Gimeno, L.; Gouveia, C.; Hernández, E.; Kuglitsch, F.G.; et al. Large-Scale Atmospheric Circulation Driving Extreme Climate Events in the Mediterranean and Its Related Impacts. In The Climate of the Mediterranean Region; Elsevier: Amsterdam, The Netherlands, 2012; pp. 347–417. ISBN 9780124160422. [Google Scholar] [CrossRef]
- Lelieveld, J.; Hadjinicolaou, P.; Kostopoulou, E.; Chenoweth, J.; El Maayar, M.; Giannakopoulos, C.; Hannides, C.; Lange, M.A.; Tanarhte, M.; Tyrlis, E.; et al. Climate change and impacts in the Eastern Mediterranean and the Middle East. Clim. Chang. 2012, 114, 667–687. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Molina, M.O.; Sánchez, E.; Gutiérrez, C. Future heat waves over the Mediterranean from an Euro-CORDEX regional climate model ensemble. Sci Rep. 2020, 10, 8801. [Google Scholar] [CrossRef]
- Giorgi, F. Climate change hot-spots. Geophys. Res. Lett. 2006, 33, L08707. [Google Scholar] [CrossRef]
- Diffenbaugh, N.S.; Pal, J.S.; Giorgi, F.; Gao, X. Heat stress intensification in the Mediterranean climate change hotspot. Geophys. Res. Lett. 2007, 34, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Seneviratne, S.I.; Zhang, X.; Adnan, M.; Badi, W.; Dereczynski, C.; Di Luca, A.; Vicente-Serrano, S.M.; Wehner, M.; Zhou, B. Weather and Climate. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2021; pp. 1513–1766. [Google Scholar] [CrossRef]
- Cramer, W.; Guiot, J.; Fader, M.; Garrabou, J.; Gattuso, J.-P.; Iglesias, A.; Lange, M.A.; Lionello, P.; Llasat, M.C.; Paz, S.; et al. Climate Change and Interconnected Risks to Sustainable Development in the Mediterranean. Nat. Clim Chang. 2018, 8, 972–980. [Google Scholar] [CrossRef] [Green Version]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef] [Green Version]
- Raghavan, S.V.; Hur, J.; Liong, S.-Y. Evaluations of NASA NEX-GDDP Data over Southeast Asia: Present and Future Climates. Clim. Chang. 2018, 148, 503–518. [Google Scholar] [CrossRef]
- Sillmann, J.; Kharin, V.V.; Zwiers, F.W.; Zhang, X.; Bronaugh, D. Climate Extremes Indices in the CMIP5 Multimodel Ensemble: Part 2. Future Climate Projections. J. Geophys. Res. Atmos. 2013, 118, 2473–2493. [Google Scholar] [CrossRef]
- Meehl, G.A.; Tebaldi, C. More Intense, More Frequent, and Longer Lasting Heat Waves in the 21st Century. Science 2004, 305, 994–997. [Google Scholar] [CrossRef] [Green Version]
- Wobus, C.; Zarakas, C.; Malek, P.; Sanderson, B.; Crimmins, A.; Kolian, M.; Sarofim, M.; Weaver, C.P. Reframing Future Risks of Extreme Heat in the United States. Earth’s Future 2018, 6, 1323–1335. [Google Scholar] [CrossRef] [PubMed]
- Jacob, D.; Petersen, J.; Eggert, B.; Alias, A.; Christensen, O.B.; Bouwer, L.M.; Braun, A.; Colette, A.; Déqué, M.; Georgievski, G.; et al. EURO-CORDEX: New High-Resolution Climate Change Projections for European Impact Research. Reg. Environ. Change 2014, 14, 563–578. [Google Scholar] [CrossRef]
- Parker, W.S. Ensemble Modeling, Uncertainty and Robust Predictions. WIREs Clim. Change 2013, 4, 213–223. [Google Scholar] [CrossRef]
- Jain, S.; Salunke, P.; Mishra, S.K.; Sahany, S.; Choudhary, N. Advantage of NEX-GDDP over CMIP5 and CORDEX Data: Indian Summer Monsoon. Atmos. Res. 2019, 228, 152–160. [Google Scholar] [CrossRef]
- Merrifield, A.L.; Brunner, L.; Lorenz, R.; Medhaug, I.; Knutti, R. An Investigation of Weighting Schemes Suitable for Incorporating Large Ensembles into Multi-Model Ensembles. Earth Syst. Dynam. 2020, 11, 807–834. [Google Scholar] [CrossRef]
- Herger, N.; Abramowitz, G.; Knutti, R.; Angélil, O.; Lehmann, K.; Sanderson, B.M. Selecting a Climate Model Subset to Optimise Key Ensemble Properties. Earth Syst. Dynam. 2018, 9, 135–151. [Google Scholar] [CrossRef] [Green Version]
- Ali, J.; Syed, K.H.; Gabriel, H.F.; Saeed, F.; Ahmad, B.; Bukhari, S.A.A. Centennial Heat Wave Projections Over Pakistan Using Ensemble NEX GDDP Data Set. Earth Syst. Environ. 2018, 2, 437–454. [Google Scholar] [CrossRef]
- Cao, N.; Li, G.; Rong, M.; Yang, J.; Xu, F. Large Future Increase in Exposure Risks of Extreme Heat Within Southern China Under Warming Scenario. Front. Earth Sci. 2021, 9, 686865. [Google Scholar] [CrossRef]
- Luo, Z.; Yang, J.; Gao, M.; Chen, D. Extreme Hot Days over Three Global Mega-regions: Historical Fidelity and Future Projection. Atmos. Sci. Lett. 2020, 21, e1003. [Google Scholar] [CrossRef]
- Chervenkov, H.; Slavov, K. NEX-GDDP Multimodel Ensemble vs. E-OBS—Evaluation of the Extreme Temperatures and Precipitation over Southeast Europe: Historical Comparison. Atmosphere 2022, 13, 581. [Google Scholar] [CrossRef]
- Malcheva, K.; Bocheva, L.; Chervenkov, H. Spatio-Temporal Variation of Extreme Heat Events in Southeastern Europe. Atmosphere 2022, 13, 1186. [Google Scholar] [CrossRef]
- Malcheva, K.; Bocheva, L.; Chervenkov, H. Climatology of extremely hot spells in bulgaria (1961–2019). In Proceedings of the 21st International Multidisciplinary Scientific GeoConference SGEM (2021), SPA Albena Complex, Bulgaria, 26 June–5 July 2021; pp. 311–318. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef] [PubMed]
- Lionello, P.; Abrantes, F.; Congedi, L.; Dulac, F.; Gacic, M.; Gomis, D.; Goodess, C.; Hoff, H.; Kutiel, H.; Luterbacher, J.; et al. Introduction: Mediterranean Climate-Background Information. In The Climate of the Mediterranean Region; Elsevier: Amsterdam, The Netherlands, 2012; p. xxxv–xc. [Google Scholar] [CrossRef] [Green Version]
- Cornes, R.C.; Van Der Schrier, G.; Van Den Besselaar, E.J.M.; Jones, P.D. An Ensemble Version of the E-OBS Temperature and Precipitation Data Sets. J. Geophys. Res. Atmos. 2018, 123, 9391–9409. [Google Scholar] [CrossRef] [Green Version]
- Kotlarski, S.; Keuler, K.; Christensen, O.B.; Colette, A.; Déqué, M.; Gobiet, A.; Goergen, K.; Jacob, D.; Lüthi, D.; Van Meijgaard, E.; et al. Regional Climate Modeling on European Scales: A Joint Standard Evaluation of the EURO-CORDEX RCM Ensemble. Geosci. Model Dev. 2014, 7, 1297–1333. [Google Scholar] [CrossRef] [Green Version]
- Thrasher, B.; Maurer, E.P.; McKellar, C.; Duffy, P.B. Technical Note: Bias Correcting Climate Model Simulated Daily Temperature Extremes with Quantile Mapping. Hydrol. Earth Syst. Sci. 2012, 16, 3309–3314. [Google Scholar] [CrossRef] [Green Version]
- Meinshausen, M.; Smith, S.J.; Calvin, K.; Daniel, J.S.; Kainuma, M.L.T.; Lamarque, J.-F.; Matsumoto, K.; Montzka, S.A.; Raper, S.C.B.; Riahi, K.; et al. The RCP Greenhouse Gas Concentrations and Their Extensions from 1765 to 2300. Clim. Change 2011, 109, 213–241. [Google Scholar] [CrossRef] [Green Version]
- Thomson, A.M.; Calvin, K.V.; Smith, S.J.; Kyle, G.P.; Volke, A.; Patel, P.; Delgado-Arias, S.; Bond-Lamberty, B.; Wise, M.A.; Clarke, L.E.; et al. RCP4.5: A pathway for stabilization of radiative forcing by 2100. Clim. Change 2011, 109, 77–94. [Google Scholar] [CrossRef] [Green Version]
- Riahi, K.; Rao, S.; Krey, V.; Cho, C.; Chirkov, V.; Fischer, G.; Kindermann, G.; Nakicenovic, N.; Rafaj, P. RCP 8.5—A scenario of comparatively high greenhouse gas emissions. Clim. Change 2011, 109, 33–57. [Google Scholar] [CrossRef] [Green Version]
- Maurer, E.P.; Hidalgo, H.G. Utility of daily vs. monthly large-scale climate data: An intercomparison of two statistical downscaling methods. Hydrol. Earth Syst. Sci. 2008, 12, 551–563. [Google Scholar] [CrossRef] [Green Version]
- Chadalavada, K.; Gummadi, S.; Kundeti, K.R.; Kadiyala, D.M.; Deevi, K.C.; Dakhore, K.K.; Bollipo Diana, R.K.; Thiruppathi, S.K. Simulating Potential Impacts of Future Climate Change on Post-Rainy Season Sorghum Yields in India. Sustainability 2021, 14, 334. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, S.; Barat, A.; Sarthi, P.P.; Sinha, A.K. Evaluation of NASA’s NEX-GDDP-Simulated Summer Monsoon Rainfall over Homogeneous Monsoon Regions of India. Theor. Appl. Climatol. 2020, 141, 525–536. [Google Scholar] [CrossRef]
- Bao, Y.; Wen, X. Projection of China’s near- and Long-Term Climate in a New High-Resolution Daily Downscaled Dataset NEX-GDDP. J. Meteorol. Res. 2017, 31, 236–249. [Google Scholar] [CrossRef]
- Perkins, S.E.; Alexander, L.V. On the Measurement of Heat Waves. J. Clim. 2013, 26, 4500–4517. [Google Scholar] [CrossRef]
- Nairn, J.; Fawcett, R. The Excess Heat Factor: A Metric for Heatwave Intensity and Its Use in Classifying Heatwave Severity. Int. J. Environ. Res. Public Health 2014, 12, 227–253. [Google Scholar] [CrossRef] [Green Version]
- WMO. Guidelines on the Definition and Characterization of Extreme Weather and Climate Events; WMO-No. 1310; WMO: Geneva, Switzerland, 2023; ISBN 978-92-63-11310-8. [Google Scholar]
- Schulzweida, U. CDO User Guide. 2020. [Google Scholar] [CrossRef]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; Legates, D.R.; O’Donnell, J.; Rowe, C.M. Statistics for the Evaluation and Comparison of Models. J. Geophys. Res. 1985, 90, 8995. [Google Scholar] [CrossRef] [Green Version]
- Jose, D.M.; Vincent, A.M.; Dwarakish, G.S. Improving Multiple Model Ensemble Predictions of Daily Precipitation and Temperature through Machine Learning Techniques. Sci. Rep. 2022, 12, 4678. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of Different Efficiency Criteria for Hydrological Model Assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef] [Green Version]
- Prado, R.C.D.; Blain, G.C.; Picoli, M.C.A. Rainfall Data from the European Center for Medium-Range Weather Forecast for Monitoring Meteorological Drought in the State of São Paulo. Acta Sci. Technol. 2018, 40, 34947. [Google Scholar] [CrossRef] [Green Version]
- Chervenkov, H.; Slavov, K. Theil-Sen Estimator vs. Ordinary Least Squares—Trend Analysis for Selected ETCCDI Climate Indices. Comptes Rendus Acad. Bulg. Sci. 2019, 72, 47–54. [Google Scholar] [CrossRef]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B. and Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. WIREs Clim Change 2011, 2, 851–870. [Google Scholar] [CrossRef]
- Chervenkov, H.; Ivanov, V.; Gadzhev, G.; Ganev, K. Assessment of the Future Climate over Southeast Europe Based on CMIP5 Ensemble of Climate Indices—Part Two: Results and Discussion. In Proceedings of the 1st International Conference on Environmental Protection and Disaster Risks, Sofia, Bulgaria, 29–30 September 2020. [Google Scholar] [CrossRef]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis. I, II, III. Nederl. Akad. Wetensch. Proc. 1950, 53, 386–392, 521–525, 1397–1412. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. A New Measure of Rank Correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]











Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chervenkov, H.; Malcheva, K. Extreme Heat Events over Southeast Europe Based on NEX-GDDP Ensemble: Present Climate Evaluation and Future Projections. Atmosphere 2023, 14, 1000. https://doi.org/10.3390/atmos14061000
Chervenkov H, Malcheva K. Extreme Heat Events over Southeast Europe Based on NEX-GDDP Ensemble: Present Climate Evaluation and Future Projections. Atmosphere. 2023; 14(6):1000. https://doi.org/10.3390/atmos14061000
Chicago/Turabian StyleChervenkov, Hristo, and Krastina Malcheva. 2023. "Extreme Heat Events over Southeast Europe Based on NEX-GDDP Ensemble: Present Climate Evaluation and Future Projections" Atmosphere 14, no. 6: 1000. https://doi.org/10.3390/atmos14061000






