Study of Time-Frequency Domain Characteristics of the Total Column Ozone in China Based on Wavelet Analysis
Abstract
:1. Introduction
2. Data Sources and Methods
2.1. Data Introduction
2.2. Introduction of Research Methods
2.2.1. Linear Regression
2.2.2. Pearson Correlation Coefficient
2.2.3. Coefficient of Variation
2.2.4. Mann-Kendall Mutation Test
2.2.5. Wavelet Analysis
2.2.6. EOF (Empirical Orthogonal Function Decomposition) Analysis
2.2.7. Time Series Forecasting Algorithm SARIMA Model
- (1)
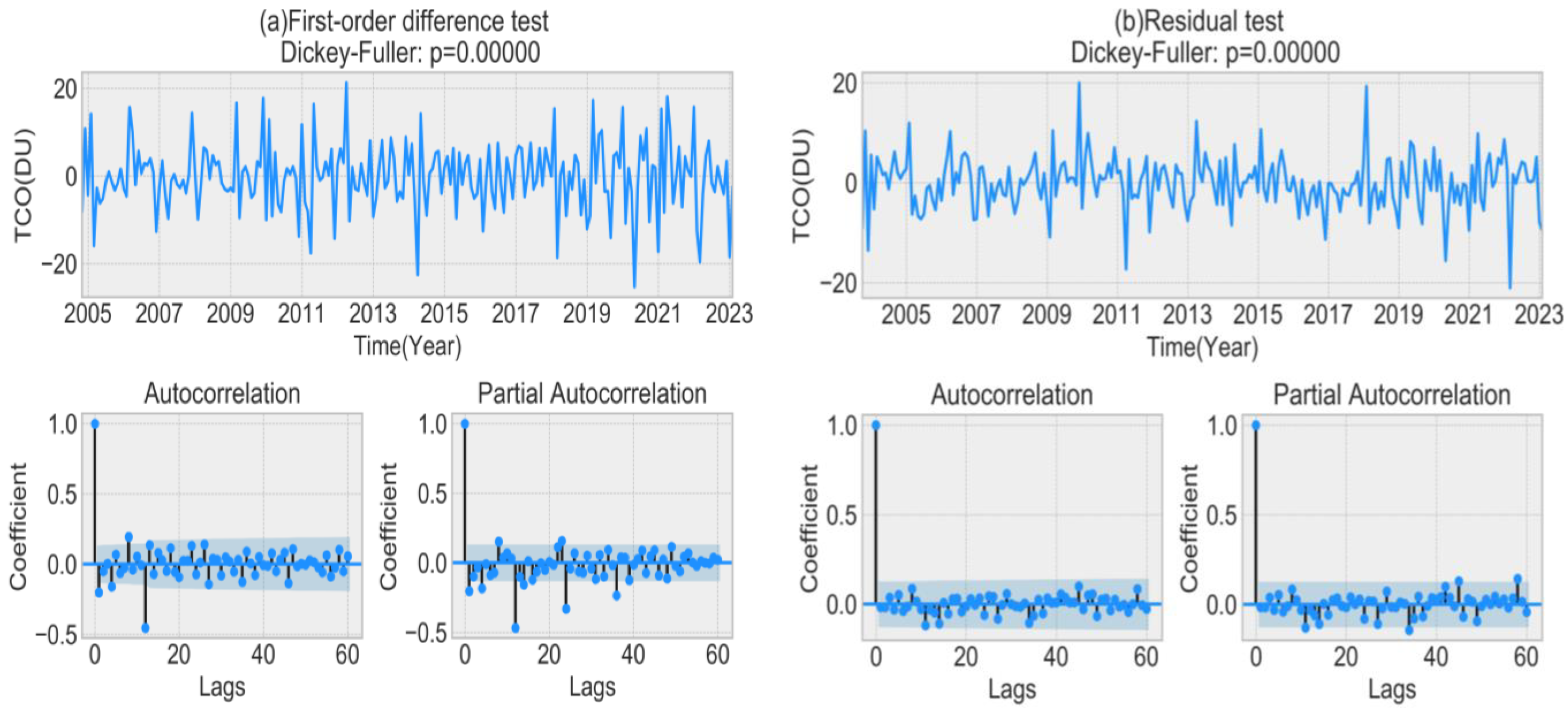
- Test the data for smoothness by the augmented Dickey–Fuller (ADF) test to determine whether the data meet the smoothness requirement. (The ADF test can be used to test whether the current series is smooth. P-value is one of the parameters used to determine whether the data are smooth or not. If the p-value is less than 0.05, the original hypothesis can be rejected [24], the data do not have a unit root, and the series is smooth; if it is greater than or equal to 0.05, the original hypothesis cannot be significantly rejected and the next step of judgment is required.)
- (2)
- Plot the data time series, observe its seasonal characteristics, determine the seasonal characteristic period s of the data, and eliminate the seasonal characteristics of the data by seasonal differencing (s-order differencing).
- (3)
- Draw auto- and bias correlation diagrams and determine the approximate parameter value range by observing these two diagrams.
- (4)
- Use the iterative method and Akaike information criterion (AIC) to determine the optimal parameters and use the optimal parameters to train the model to complete the modeling (for a detailed explanation of the AIC, see [25]).
- (5)
- Perform a residual test on the established model to test the model fit.
- (6)
- Perform forecasting by using the model and conducting error rate analysis using the MAPE index.
2.3. Data Validation
3. Results
3.1. Analysis of the Time-Frequency Domain Variation of Regional TCO in China
3.1.1. Analysis of the Interannual Variation of Regional TCO in China
3.1.2. Analysis of Monthly Variation of TCO in China
3.1.3. Seasonal Variation Analysis of TCO in China
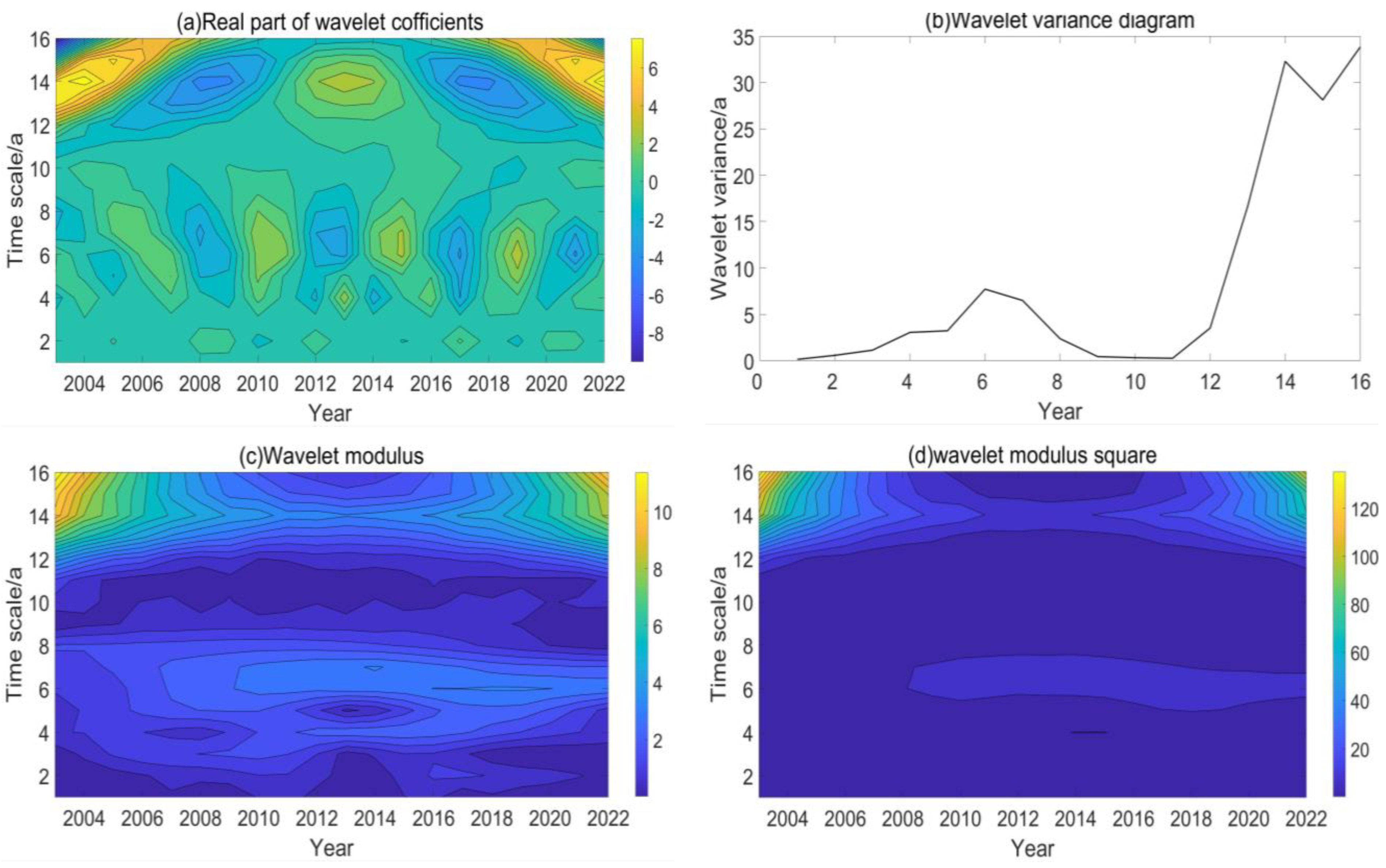
3.1.4. Frequency Domain Analysis of TCO in China
3.2. Spatial Distribution of TCO in China
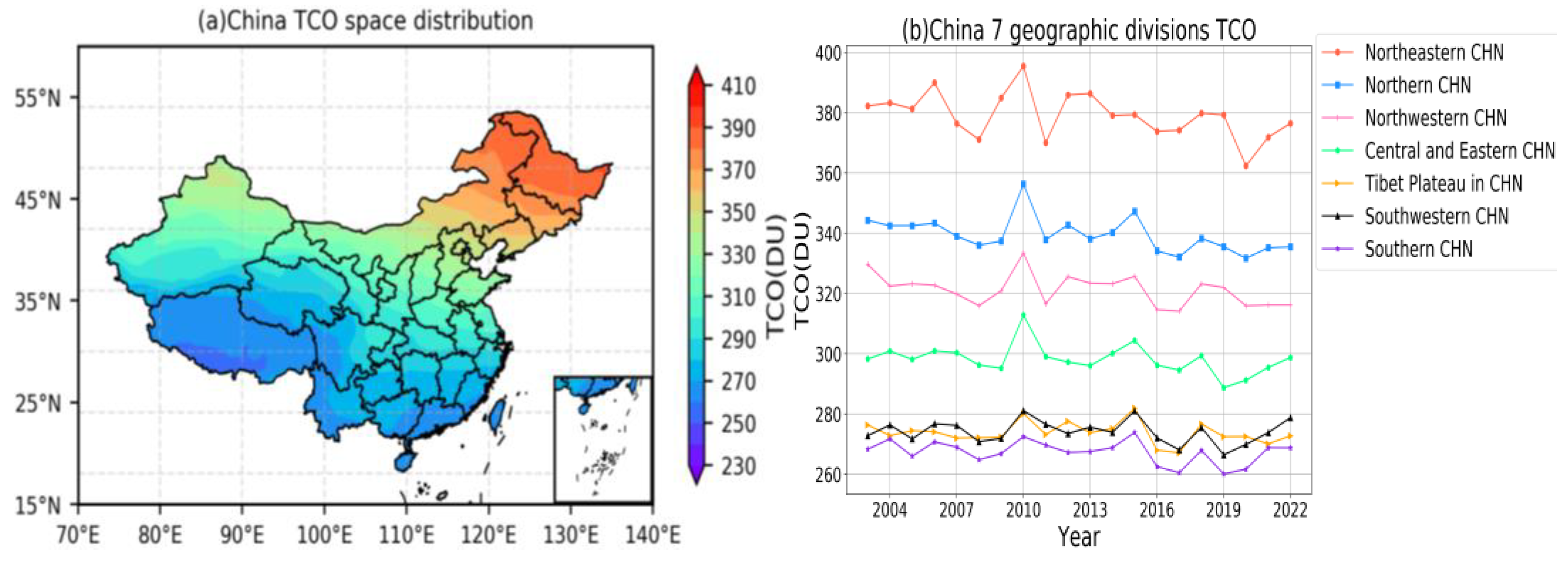
3.2.1. Spatial Distribution Characteristics of Annual Mean TCO in China
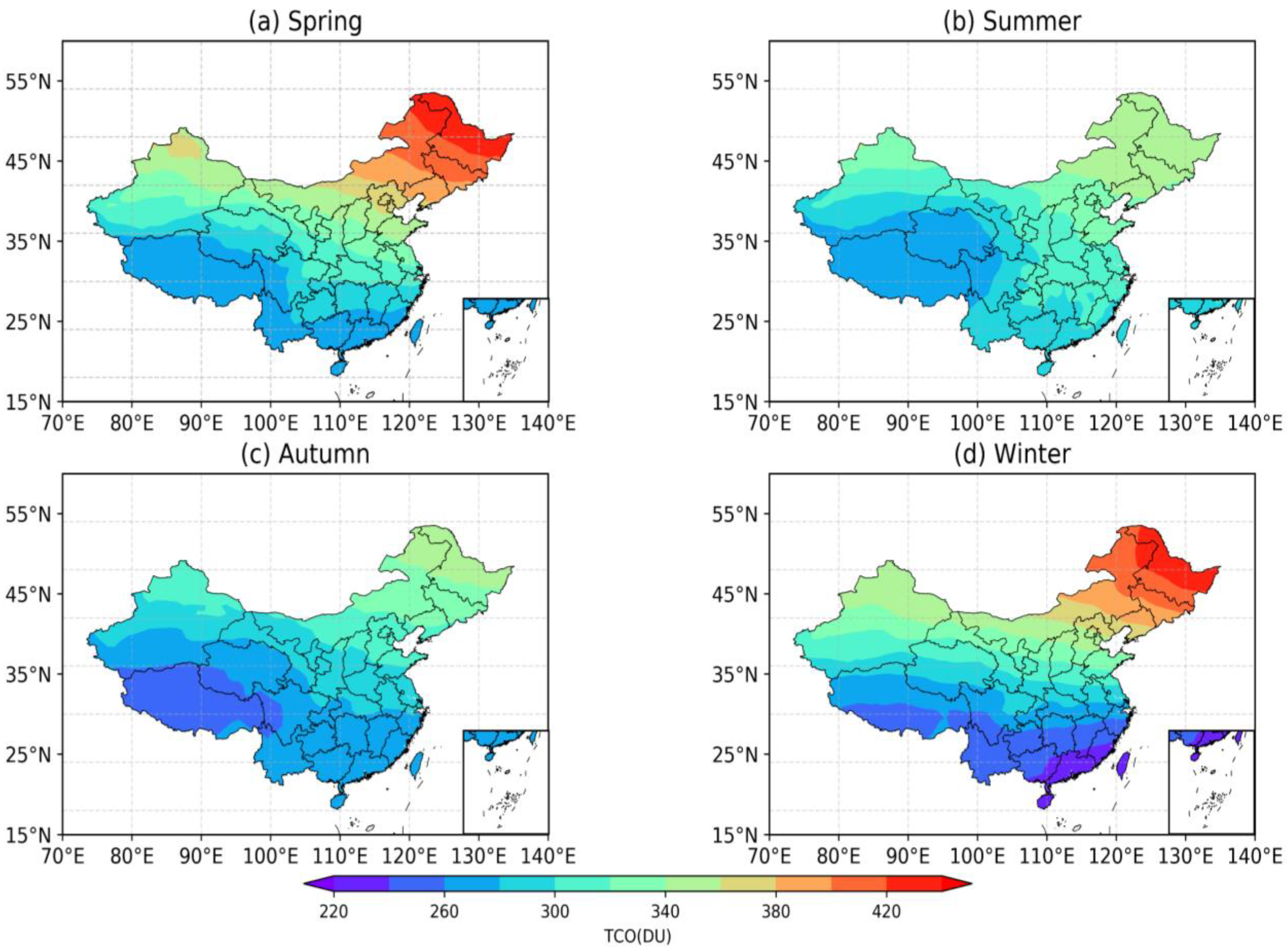
3.2.2. Seasonal Spatial Distribution Characteristics of TCO in China
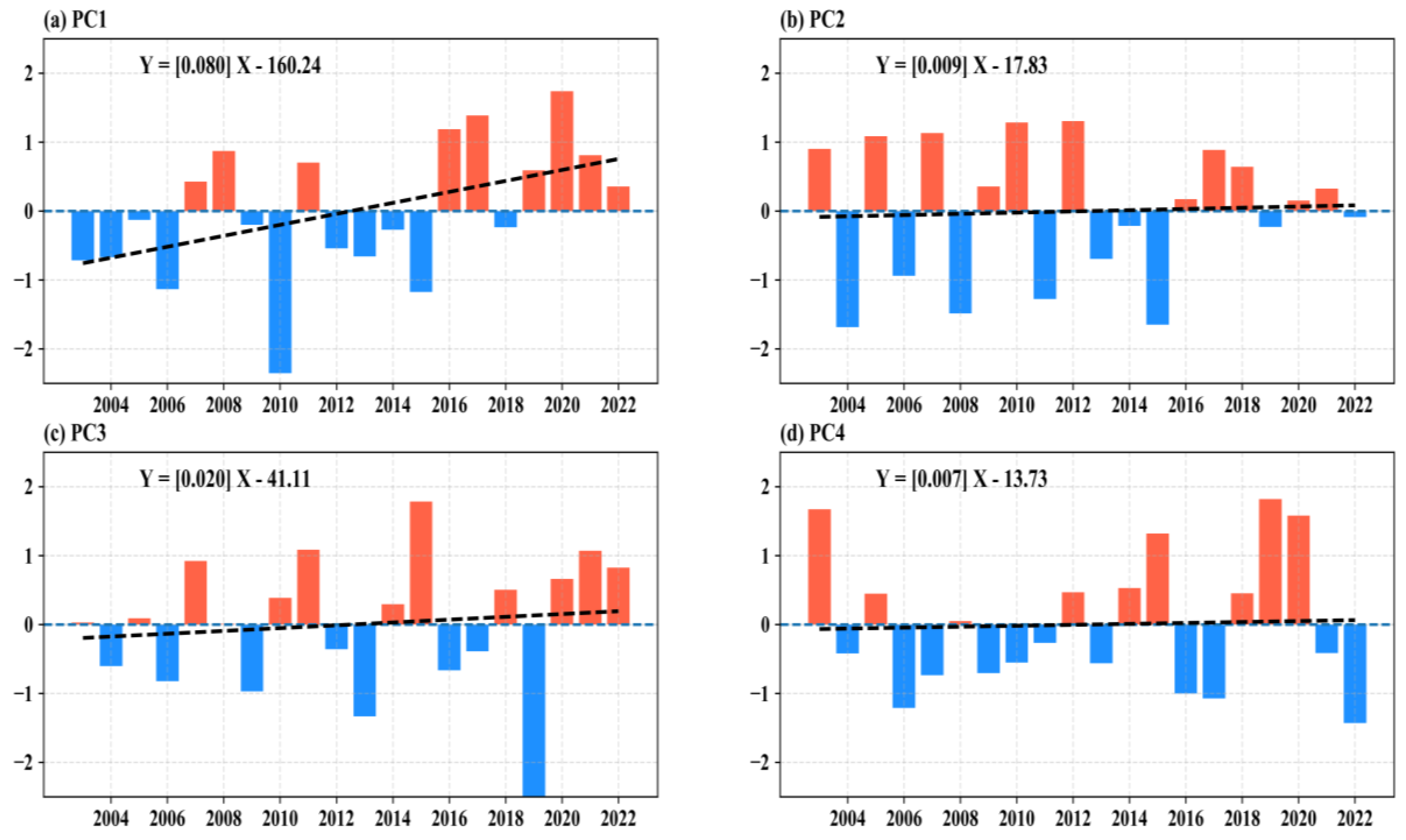
3.2.3. EOF Analysis of Temporal and Spatial Characteristics of TCO in China
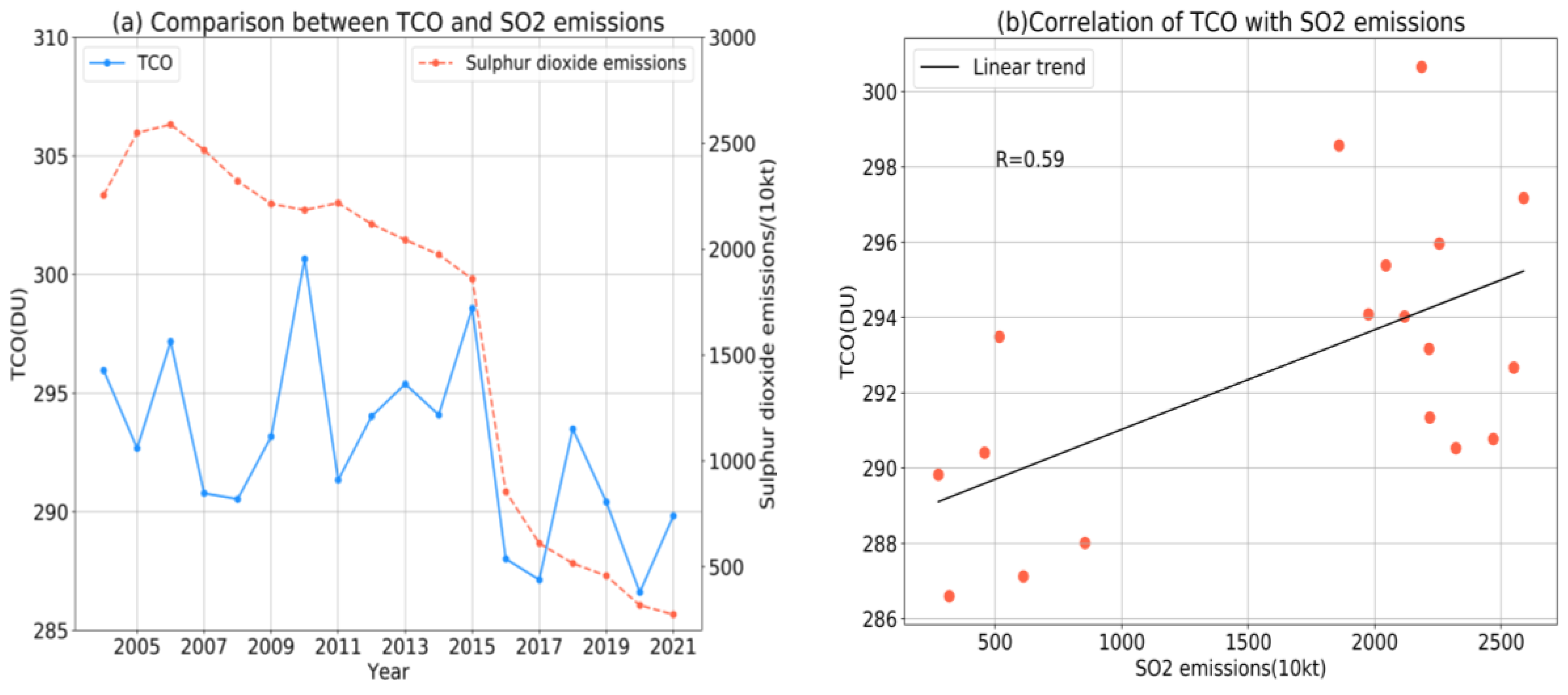
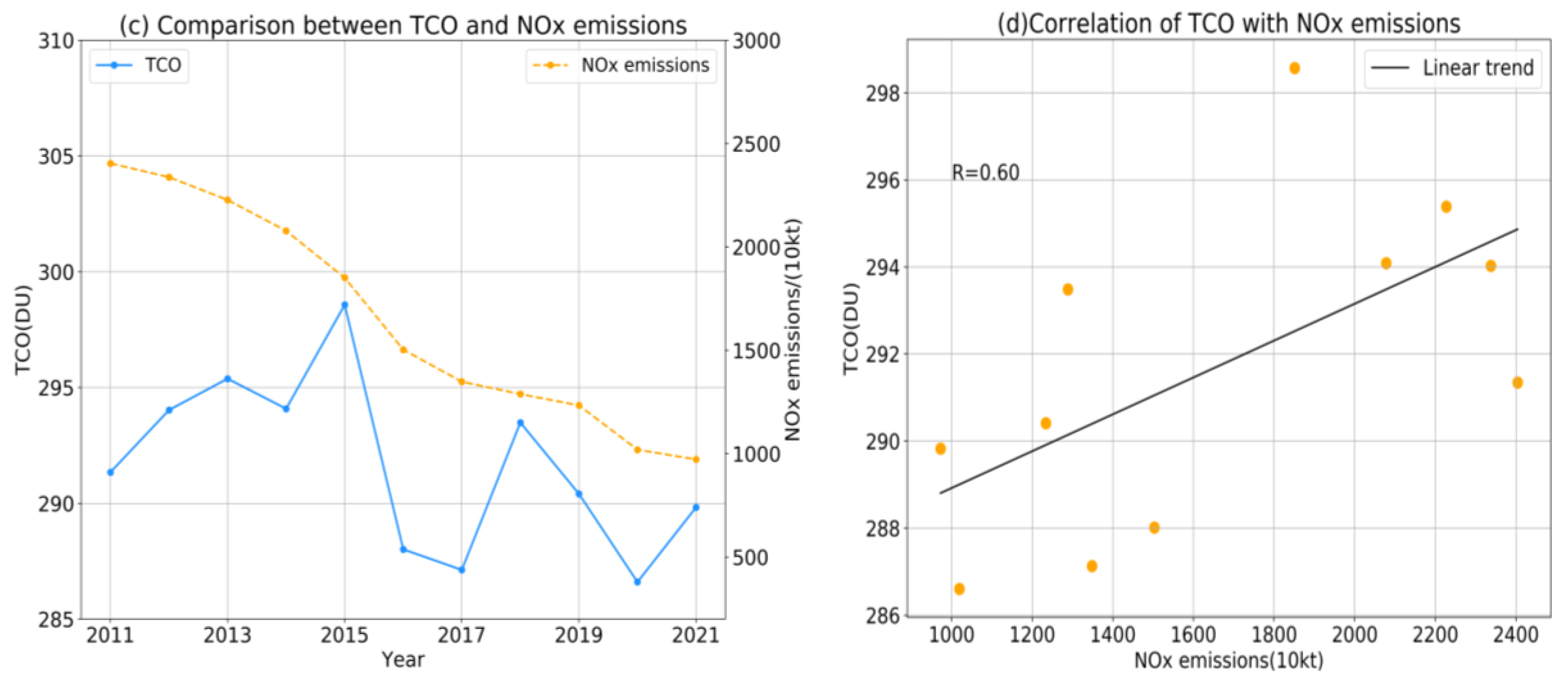
3.3. Analysis of Factors Influencing the Change in TCO in China
3.4. Prediction of TCO in China Based on the SARIMA Model
4. Discussion
5. Conclusions
- (1)
- Firstly, the monthly average data of AIRS were selected for correlation analysis with the data of the BLD, BRW, and OHP stations in the same period, and the Pearson correlation coefficients were 0.9509, 0.9771, and 0.9403, respectively. The above verification showed that the AIRS data used in this study were reliable.
- (2)
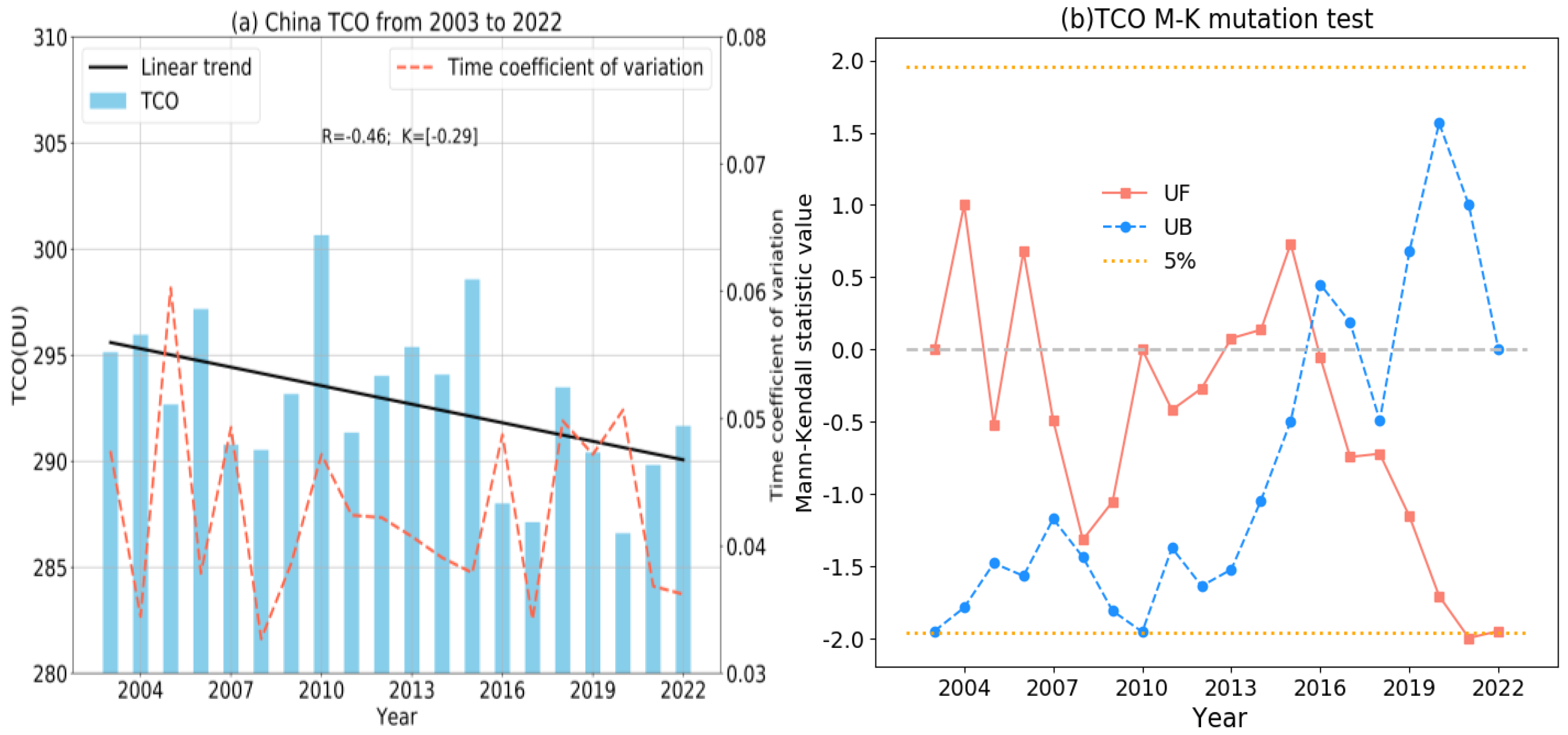
- The annual mean data of the TCO in China from 2003 to 2022 were analyzed. The TCO in 2010 was the highest of that in the past 20 years, reaching 300.7 DU. In 2020, the TCO reached 286.6 DU, the lowest level in nearly 20 years. The overall trend from 2003 to 2022 was found to be a slow decline by linear regression analysis, with a change rate of K = −0.29 DU/a. From the results of the coefficient of variation, the annual fluctuation of the TCO in 2005 was the greatest and that in 2008 was the smallest. Analysis using an M-K mutation test found that TCO experienced a mutation around 2016.
- (3)
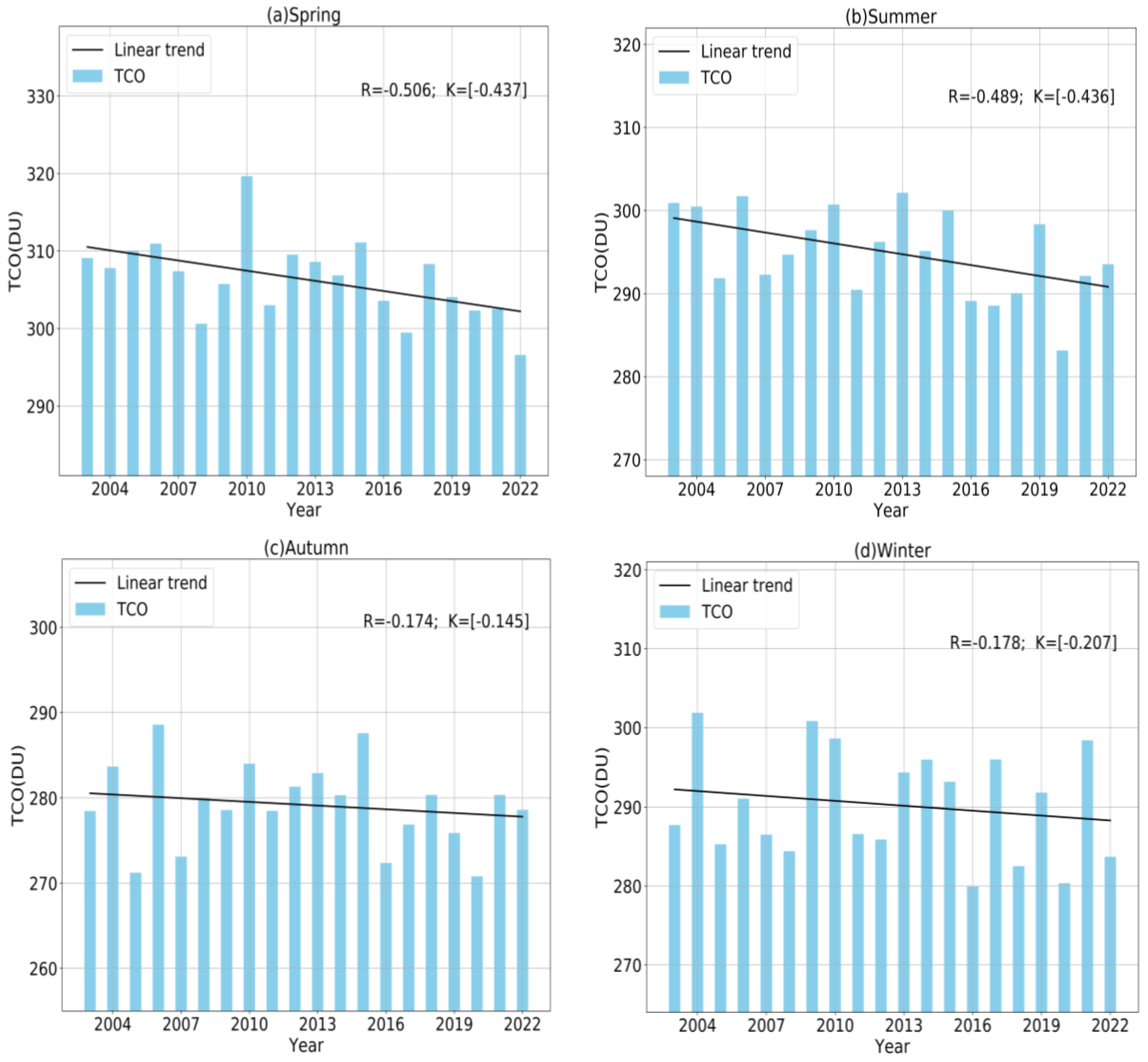
- The multi-year monthly mean TCO from 2003 to 2022 was analyzed. In these 20 years, the average TCO was highest in April and lowest in November each year. At the same time, using the coefficient of variation to analyze the fluctuation of the multi-year monthly mean TCO, it was found that the month with the largest fluctuation in the total ozone column was February and the most stable month was July. From a seasonal perspective, the fluctuation in TCO change was the smallest in autumn and the largest in winter. The order of the fluctuation degree of TCO change in the four seasons was winter > spring > summer > autumn.
- (4)
- The multi-annual mean value of the four seasons in 2003 to 2022 was analyzed. In terms of quantity, TCO levels in spring were the highest, while TCO levels in autumn were the lowest. The order of total column ozone size in the four seasons was spring > summer > winter > autumn. From the perspective of change rate, the decline rate was the fastest in summer and the slowest in winter. The order of decline rate in the four seasons was spring > summer > winter > autumn.
- (5)
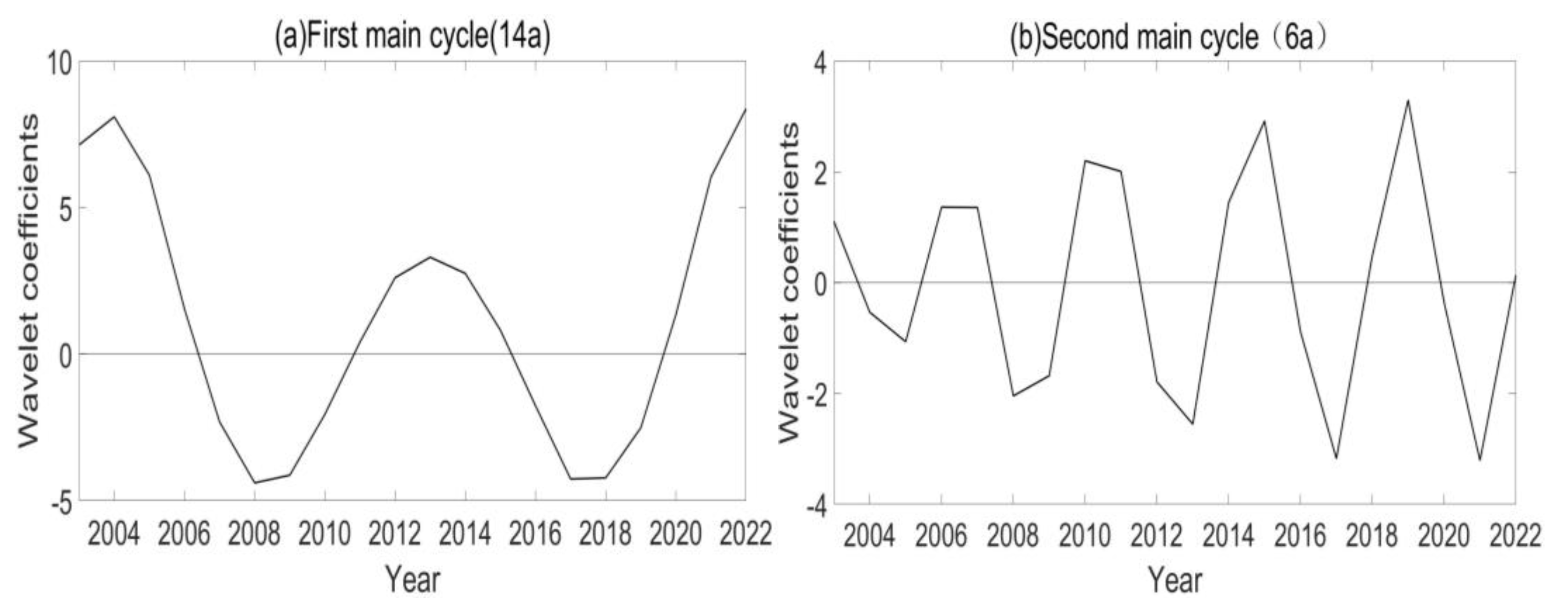
- Wavelet transform was used to analyze the frequency domain characteristics of TCO over China from 2003 to 2022. The study revealed that there were two major time scales, known as major cycles. Among them, 14 years was the first main cycle corresponding to the change cycle of the TCO in China for approximately 10 years, with 2003~2022 experiencing two cycles; 6 years was the change cycle corresponding to the second main cycle for approximately 4 years, with 2003~2022 experiencing approximately five cycles. The above analysis results fully demonstrate that the cyclical characteristics of the TCO in China are very complex and various.
- (6)
- The spatial distribution characteristics of China’s TCO are extremely clear, with clear latitude and longitude distribution characteristics. First, as the latitude increased, the TCO also increased. Generally speaking, the TCO in Northeast China and Northern China was relatively high; the TCO in Southwestern China, Qinghai-Tibet Plateau, and Southern China was relatively low. The multi-year average time series comparison of the TCO in China divided into seven major regions found that in the 20 years from 2003 to 2022, their order of size was as follows: Northeastern China > Northern China > Northwestern China > Central and Eastern China > Qinghai-Tibet Plateau > Southwestern China > Southern China. Using EOF analysis to decompose the space–time mode of the TCO in China, the variance contribution rate of the first mode was as high as 52.85%, which had the highest reference value among many modes. The cumulative contribution rate of the first four modes reached 85.54%. Among them, the spatial distribution of the first mode presented “-”, indicating that the changes in the TCO in the entire Chinese region in the past 20 years had a very high consistency.
- (7)
- Using the correlation analysis of the TCO and SO2 emissions and NOx emissions, it was found that changes in the total amount of ozone are related to these factors. The correlation coefficient for the TCO and sulfur dioxide emissions reached 0.59 and the correlation coefficient for nitrogen oxide emission reached 0.60.
- (8)
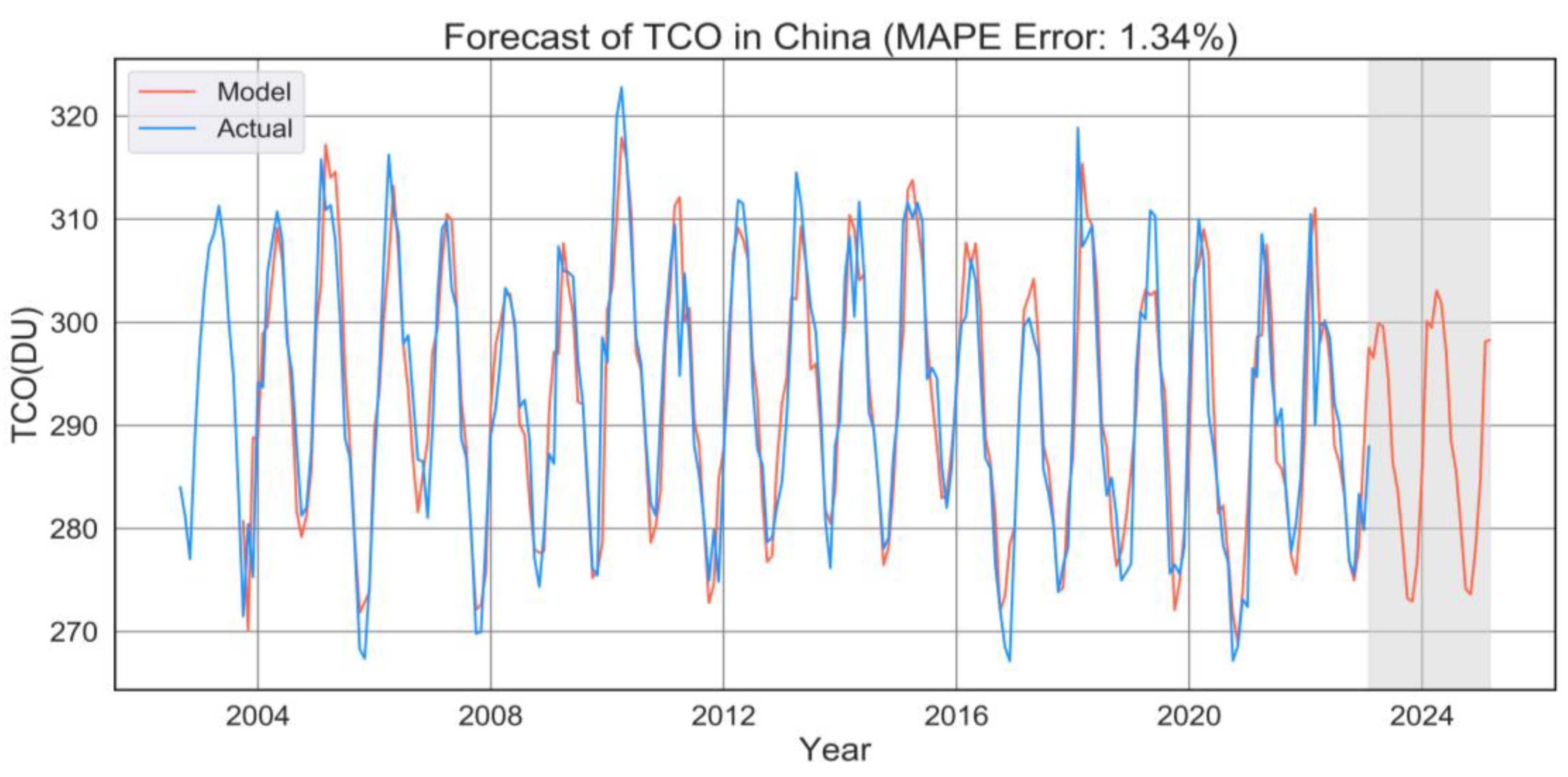
- This study used the SARIMA model to predict the TCO of China. Considering the seasonality and other characteristics of the data, the data were pre-processed and then trained with the AIC information criterion to find the best model parameters. The best prediction model of monthly average TCO in China was determined to be SARIMA (1, 1, 2) × (0, 1, 2, 12); we used this model to forecast the TCO over China for the next 24 months. In order to objectively measure the accuracy of the prediction results, MAPE was introduced to calculate the error rate, and the error rate of the model prediction was as low as 1.34%, which shows that the model fitted in this study had good accuracy. This result indicates that the predicted TCO trend of China was also relatively accurate.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, L.; Yu, B.; Chen, Z.; Li, B.; Wu, J. Investigating the temporal and spatial variability of total ozone column in the Yangtze River Delta using satellite data: 1978–2013. Remote. Sens. 2014, 6, 12527–12543. [Google Scholar] [CrossRef]
- Midya, S.K.; Goswami, S. Seasonal variation of daily total column ozone (TCO) and its depletion and formation role on surface temperature over Ahmedabad (23°01′ N, 72°39′ E). Indian J. Phys. 2013, 87, 953–961. [Google Scholar] [CrossRef]
- Staehelin, J.; Harris, N.R.P.; Appenzeller, C.; Eberhard, J. Ozone trends: A review. Rev. Geophys. 2001, 39, 231–290. [Google Scholar] [CrossRef]
- Jana, P.K.; Bhattacharyya, S.; Banerjee, A. Effect of some climatic parameters on tropospheric and total ozone column over Alipore (22.52° N, 88.33° E), India. J. Earth Syst. Sci. 2014, 123, 1653–1669. [Google Scholar] [CrossRef]
- Shin, D.; Oh, Y.-S.; Seo, W.; Chung, C.-Y.; Koo, J.-H. Total Ozone Trends in East Asia from Long-Term Satellite and Ground Observations. Atmosphere 2021, 12, 982. [Google Scholar] [CrossRef]
- Wang, W.; Cheng, T.; van der A, R.J.; de Laat, J.; Williams, J.E. Verification of the Atmospheric Infrared Sounder (AIRS) and the Microwave Limb Sounder (MLS) ozone algorithms based on retrieved daytime and night-time ozone. Atmos. Meas. Tech. 2021, 14, 1673–1687. [Google Scholar] [CrossRef]
- Zhang, J.; Li, D.; Bian, J.; Xuan, Y.; Chen, H.; Bai, Z.; Wan, X.; Zheng, X.; Xia, X.; Lü, D. Long-term ozone variability in the vertical structure and integrated column over the North China Plain: Results based on ozonesonde and Dobson measurements during 2001–2019. Environ. Res. Lett. 2021, 16, 074053. [Google Scholar] [CrossRef]
- Zhou, P.; Wen, Y.; Yang, J.; Yang, L.; Liang, M.; Wen, T.; Cai, S. Spatiotemporal Variation, Driving Mechanism and Predictive Study of Total Column Ozone: A Case Study in the Yangtze River Delta Urban Agglomerations. Remote. Sens. 2022, 14, 4576. [Google Scholar] [CrossRef]
- Bian, J.; Yan, R.; Chen, H.; Lu, D.; Massie, S.T. Formation of the summertime ozone valley over the Tibetan Plateau: The Asian summer monsoon and air column variations. Adv. Atmos. Sci. 2011, 28, 1318–1325. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, W.; Xie, F.; Tian, H.; Luo, J.; Zhang, J.; Liu, W.; Dhomse, S. Climate warming and decreasing total column ozone over the Tibetan Plateau during winter and spring. Tellus B Chem. Phys. Meteorol. 2014, 66, 23415. [Google Scholar] [CrossRef]
- Chidinma, O.E.; Yan, Y.-H.; Yin, Z.; Kingsley, O.U.; Nneka, O.F. Impact of solar and geomagnetic activities on total column ozone in China. J. Atmospheric Solar-Terrestrial Phys. 2021, 223, 105738. [Google Scholar] [CrossRef]
- Okoro, E.C.; Yan, Y.-H.; Bisoi, S.K.; Zhang, Y. Response and periodic variation of total atmospheric ozone to solar activity over Mountain Waliguan. Adv. Space Res. 2021, 68, 2257–2271. [Google Scholar] [CrossRef]
- Wang, S.; Huo, Y.; Mu, X.; Jiang, P.; Xun, S.; He, B.; Wu, W.; Liu, L.; Wang, Y. A High-Performance Convolutional Neural Network for Ground-Level Ozone Estimation in Eastern China. Remote. Sens. 2022, 14, 1640. [Google Scholar] [CrossRef]
- Zou, M.; Xiong, X.; Wu, Z.; Yu, C. Ozone Trends during 1979–2019 over Tibetan Plateau Derived from Satellite Observations. Front. Earth Sci. 2020, 8, 579624. [Google Scholar] [CrossRef]
- Valipour, M. Long-term runoff study using SARIMA and ARIMA models in the United States. Meteorol. Appl. 2015, 22, 592–598. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Y.; Cai, K.; Zhu, S.; Zhang, X.; Chen, L. Evaluating the Performance of Ozone Products Derived from CrIS/NOAA20, AIRS/Aqua and ERA5 Reanalysis in the Polar Regions in 2020 Using Ground-Based Observations. Remote. Sens. 2021, 13, 4375. [Google Scholar] [CrossRef]
- Liu, J.; Hagan, D.F.T.; Liu, Y. Global Land Surface Temperature Change (2003–2017) and Its Relationship with Climate Drivers: AIRS, MODIS, and ERA5-Land Based Analysis. Remote. Sens. 2020, 13, 44. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.; Chang, T.-J. Correlations between hydrological drought and climate indices with respect to the impact of a large reservoir. Theor. Appl. Clim. 2019, 139, 727–739. [Google Scholar] [CrossRef]
- Kamau-Muthoni, F.; Omondi-Odongo, V.; Ochieng, J.; Mugalavai, E.M.; Kjumula-Mourice, S.; Hoesche-Zeledon, I.; Mwila, M.; Bekunda, M. Long-term spatial-temporal trends and variability of rainfall over eastern and Southern Africa. Theor. Appl. Climatol. 2019, 137, 1869–1882. [Google Scholar] [CrossRef]
- Gargour, C.; Gabrea, M.; Ramachandran, V.; Lina, J.-M. A short introduction to wavelets and their applications. IEEE Circuits Syst. Mag. 2009, 9, 57–68. [Google Scholar] [CrossRef]
- Tuo, W.; Zhang, X.; Song, C.; Hu, D.; Liang, T. Annual precipitation analysis and Forecasting—Taking Zhengzhou as an example. Water Supply 2020, 20, 1604–1616. [Google Scholar] [CrossRef]
- Zhang, M.-L.; Liu, C.; Wan, W.; Liu, L.; Ning, B. A global model of the ionospheric F2 peak height based on EOF analysis. Ann. Geophys. 2009, 27, 3203–3212. [Google Scholar] [CrossRef]
- Yu, Y.; Wan, W.; Xiong, B.; Ren, Z.; Zhao, B.; Zhang, Y.; Ning, B.; Liu, L. Modeling Chinese ionospheric layer parameters based on EOF analysis. Space Weather. 2015, 13, 339–355. [Google Scholar] [CrossRef]
- Mushtaq, R. Augmented dickey fuller test. SSRN J. 2011. [CrossRef]
- Portet, S. A primer on model selection using the Akaike Information Criterion. Infect. Dis. Model. 2020, 5, 111–128. [Google Scholar] [CrossRef] [PubMed]
- Butchart, N. The Brewer-Dobson circulation. Rev. Geophys. 2014, 52, 157–184. [Google Scholar] [CrossRef]
- Chen, D.; Nunez, M. Temporal and spatial variability of total ozone in Southwest Sweden revealed by two ground-based instruments. Int. J. Climatol. A J. R. Meteorol. Soc. 1998, 18, 1237–1246. [Google Scholar] [CrossRef]
- Tung, K.K.; Yang, H. Dynamic variability of column ozone. J. Geophys. Res. Atmos. 1988, 93, 11123. [Google Scholar] [CrossRef]
- Antón, M.; Bortoli, D.; Costa, M.J.; Kulkarni, P.; Domingues, A.; Barriopedro, D.; Serrano, A.; Silva, A.M. Temporal and spatial variabilities of total ozone column over Portugal. Remote. Sens. Environ. 2011, 115, 855–863. [Google Scholar] [CrossRef]
- Aesawy, A.M.; Mayhoub, A.B.; Sharobim, W.M. Seasonal variation of photochemical and dynamical components of ozone in subtropical regions. Theor. Appl. Clim. 1994, 49, 241–247. [Google Scholar] [CrossRef]
- Tian, X.; Tang, C.; Wu, X.; Yang, J.; Zhao, F.; Liu, D. The global spatial-temporal distribution and EOF analysis of AOD based on MODIS data during 2003–2021. Atmos. Environ. 2023, 302, 119722. [Google Scholar] [CrossRef]
- Liu, J.; Strode, S.A.; Liang, Q.; Oman, L.D.; Colarco, P.R.; Fleming, E.L.; Manyin, M.E.; Douglass, A.R.; Ziemke, J.R.; Lamsal, L.N.; et al. Change in Tropospheric Ozone in the Recent Decades and Its Contribution to Global Total Ozone. J. Geophys. Res. Atmos. 2022, 127, e2022JD037170. [Google Scholar] [CrossRef]
- Szolgayova, E.; Parajka, J.; Blöschl, G.; Bucher, C. Long term variability of the Danube River flow and its relation to precipitation and air temperature. J. Hydrol. 2014, 519, 871–880. [Google Scholar] [CrossRef]
- Ma, L.H.; Han, Y.B.; Yin, Z.Q. Possible Influence of the 11-year Solar Cycle on Precipitation in Huashan Mountain of China over the Last 300 Years. Earth Moon Planets 2010, 107, 219–224. [Google Scholar] [CrossRef]
- Gao, W.; Yang, S.; Hu, X.; Wei, W.; Xiao, Y. Characteristics and Formation Mechanisms of Spring SST Anomalies in the South China Sea and Its Adjacent Regions. Atmosphere 2019, 10, 649. [Google Scholar] [CrossRef]
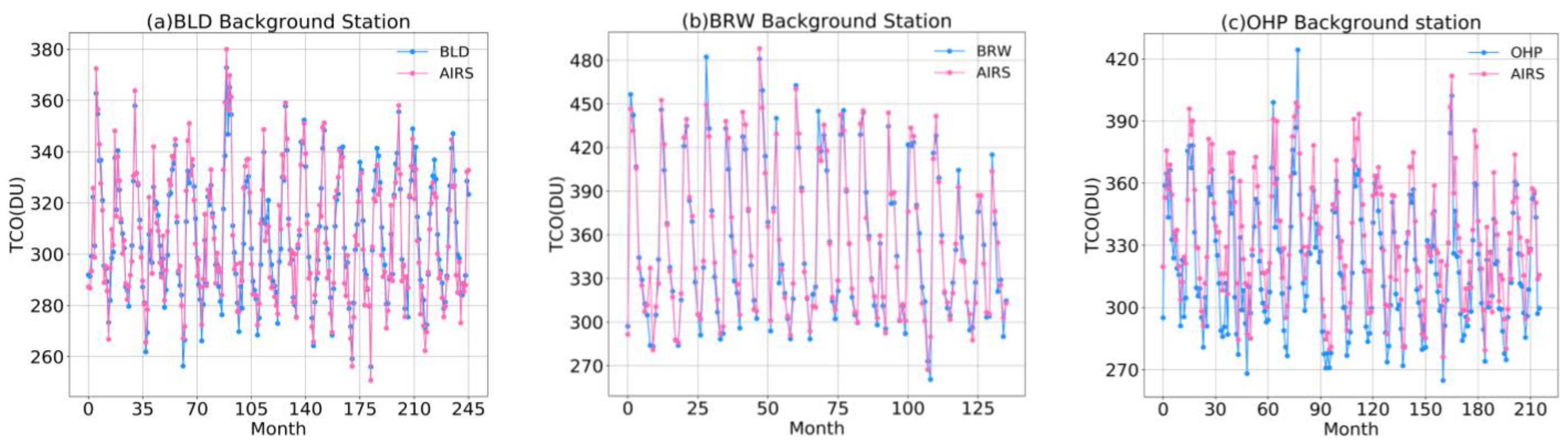
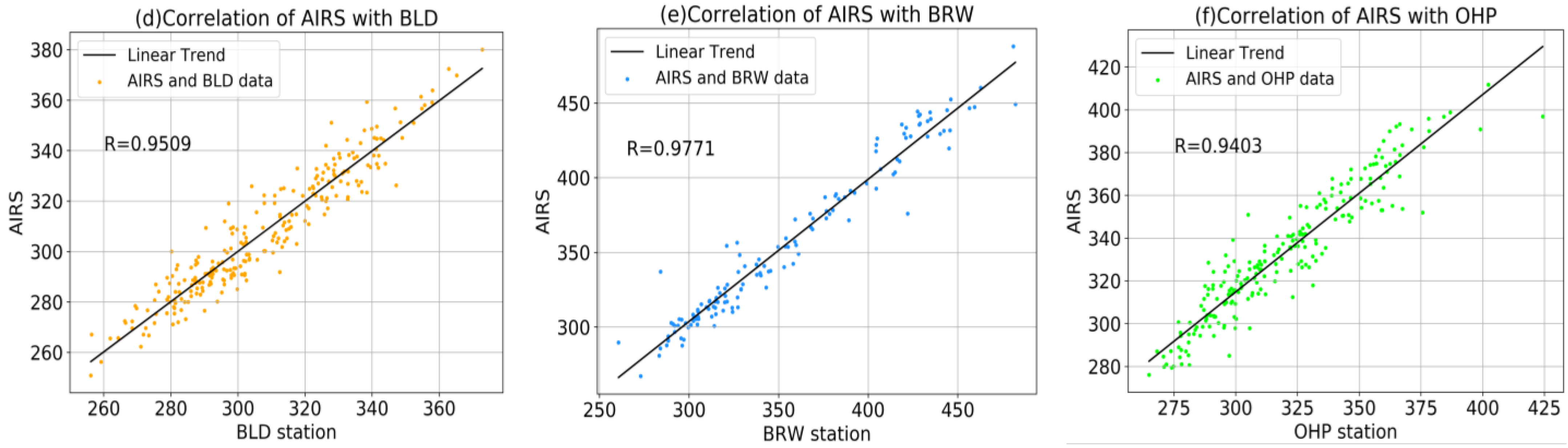




| Site | Nation | Latitude | Longitude |
|---|---|---|---|
| BLD | United States | 39.9° N | 105.3° W |
| BRW | United States | 71.3° N | 156.6° W |
| OHP | France | 43.9° N | 6.8° E |
| Mode | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Variance contribution rate | 52.85% | 15.93% | 10.71% | 6.05% |
| Cumulative variance contribution rate | 52.85% | 68.78% | 79.49% | 85.54% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, C.; Zhu, F.; Wei, Y.; Tian, X.; Yang, J.; Zhao, F. Study of Time-Frequency Domain Characteristics of the Total Column Ozone in China Based on Wavelet Analysis. Atmosphere 2023, 14, 941. https://doi.org/10.3390/atmos14060941
Tang C, Zhu F, Wei Y, Tian X, Yang J, Zhao F. Study of Time-Frequency Domain Characteristics of the Total Column Ozone in China Based on Wavelet Analysis. Atmosphere. 2023; 14(6):941. https://doi.org/10.3390/atmos14060941
Chicago/Turabian StyleTang, Chaoli, Fangzheng Zhu, Yuanyuan Wei, Xiaomin Tian, Jie Yang, and Fengmei Zhao. 2023. "Study of Time-Frequency Domain Characteristics of the Total Column Ozone in China Based on Wavelet Analysis" Atmosphere 14, no. 6: 941. https://doi.org/10.3390/atmos14060941
APA StyleTang, C., Zhu, F., Wei, Y., Tian, X., Yang, J., & Zhao, F. (2023). Study of Time-Frequency Domain Characteristics of the Total Column Ozone in China Based on Wavelet Analysis. Atmosphere, 14(6), 941. https://doi.org/10.3390/atmos14060941






