The Local Unscented Transform Kalman Filter for the Weather Research and Forecasting Model
Abstract
:1. Introduction
2. LUTKF Algorithm
2.1. Ensemble Sampling (Ensemble Member Selection) with UT
2.2. State Estimation with Spatial Localization
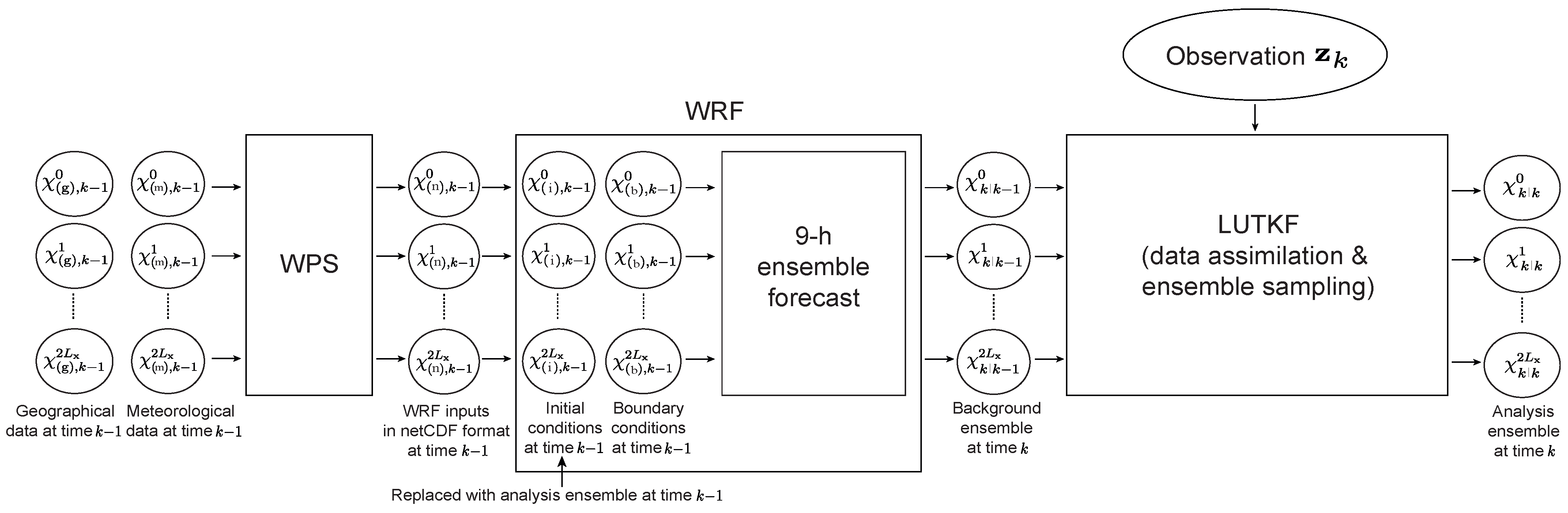
3. WRF-LUTKF System
4. Experiments with Real Observations
4.1. Experimental Setup
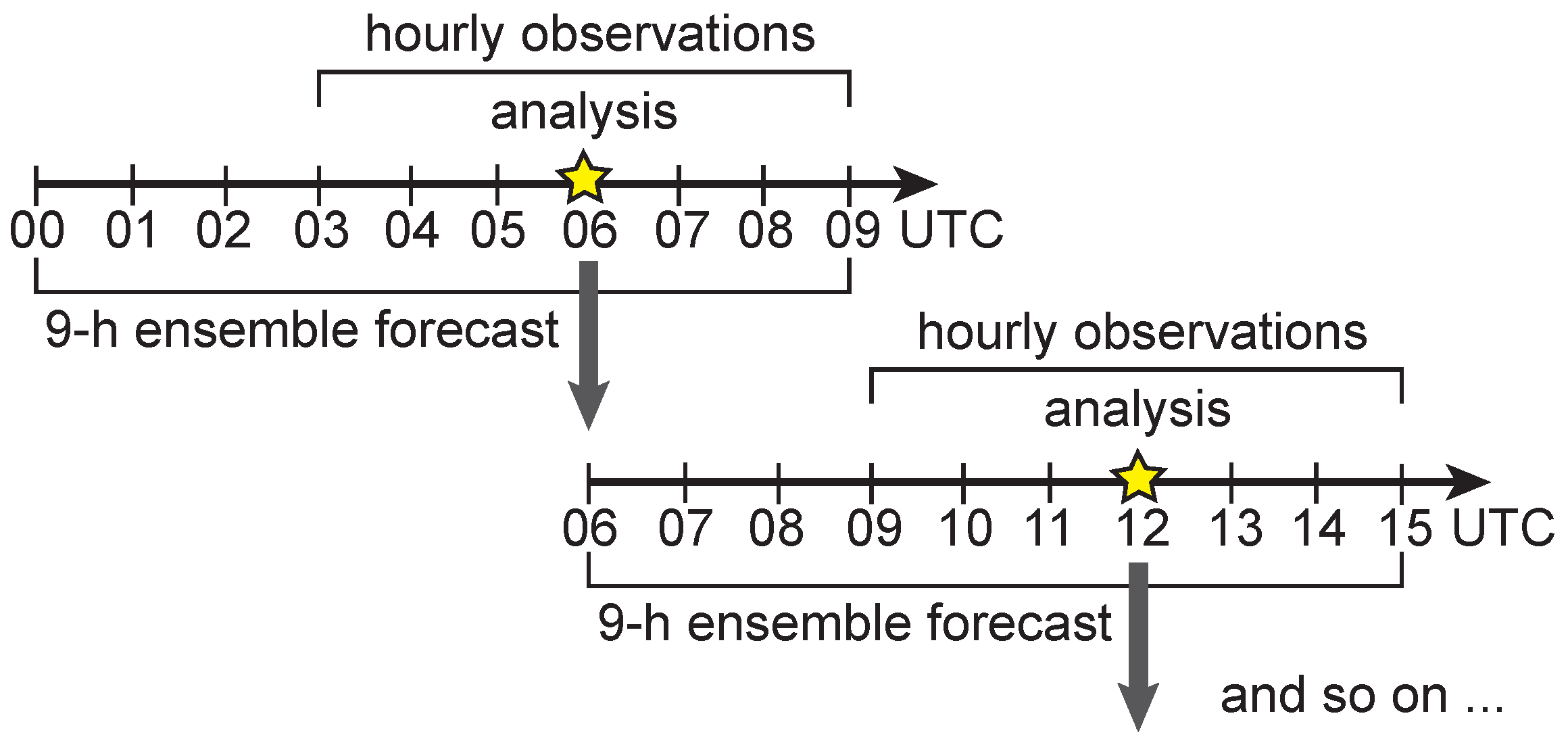
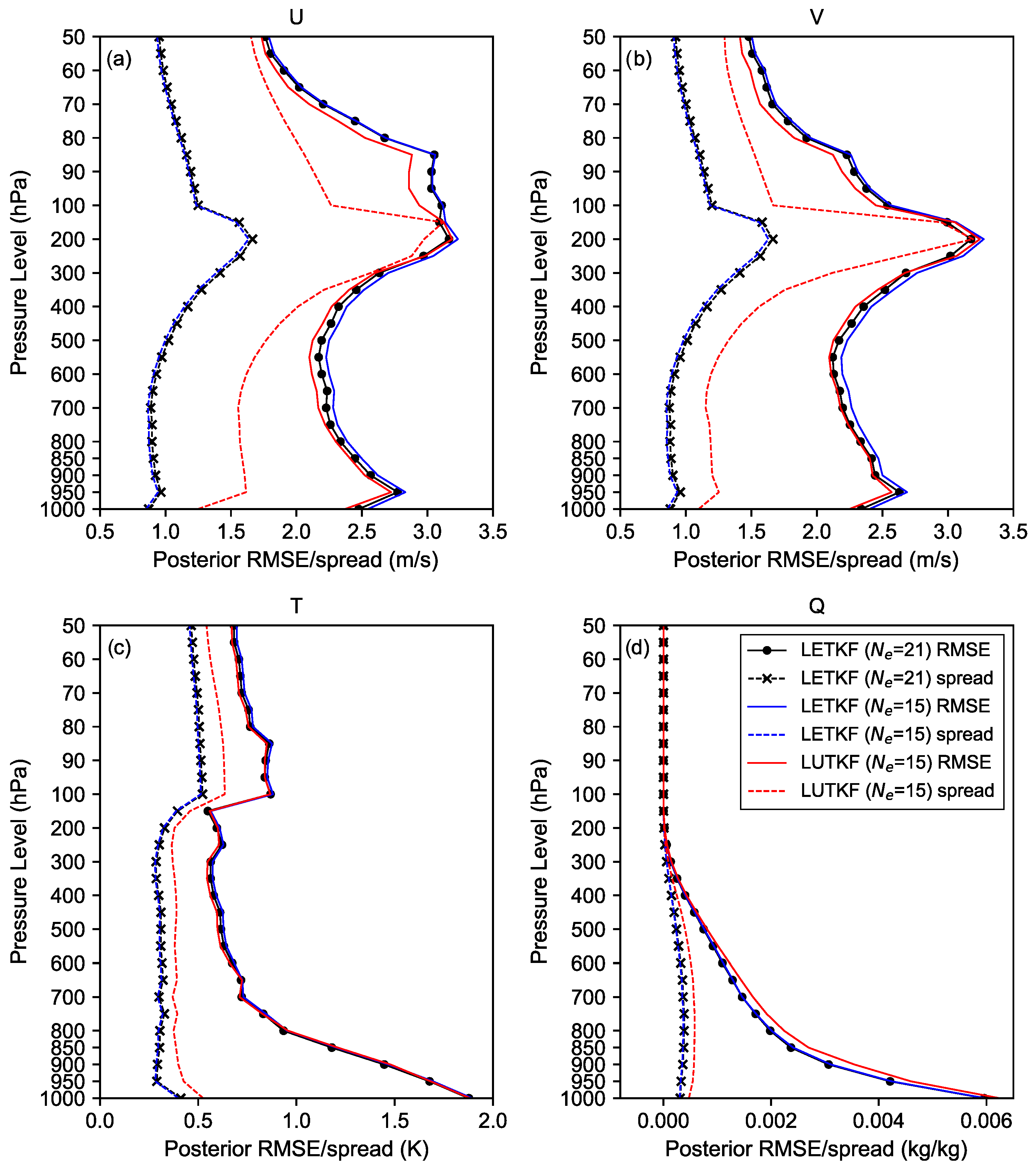
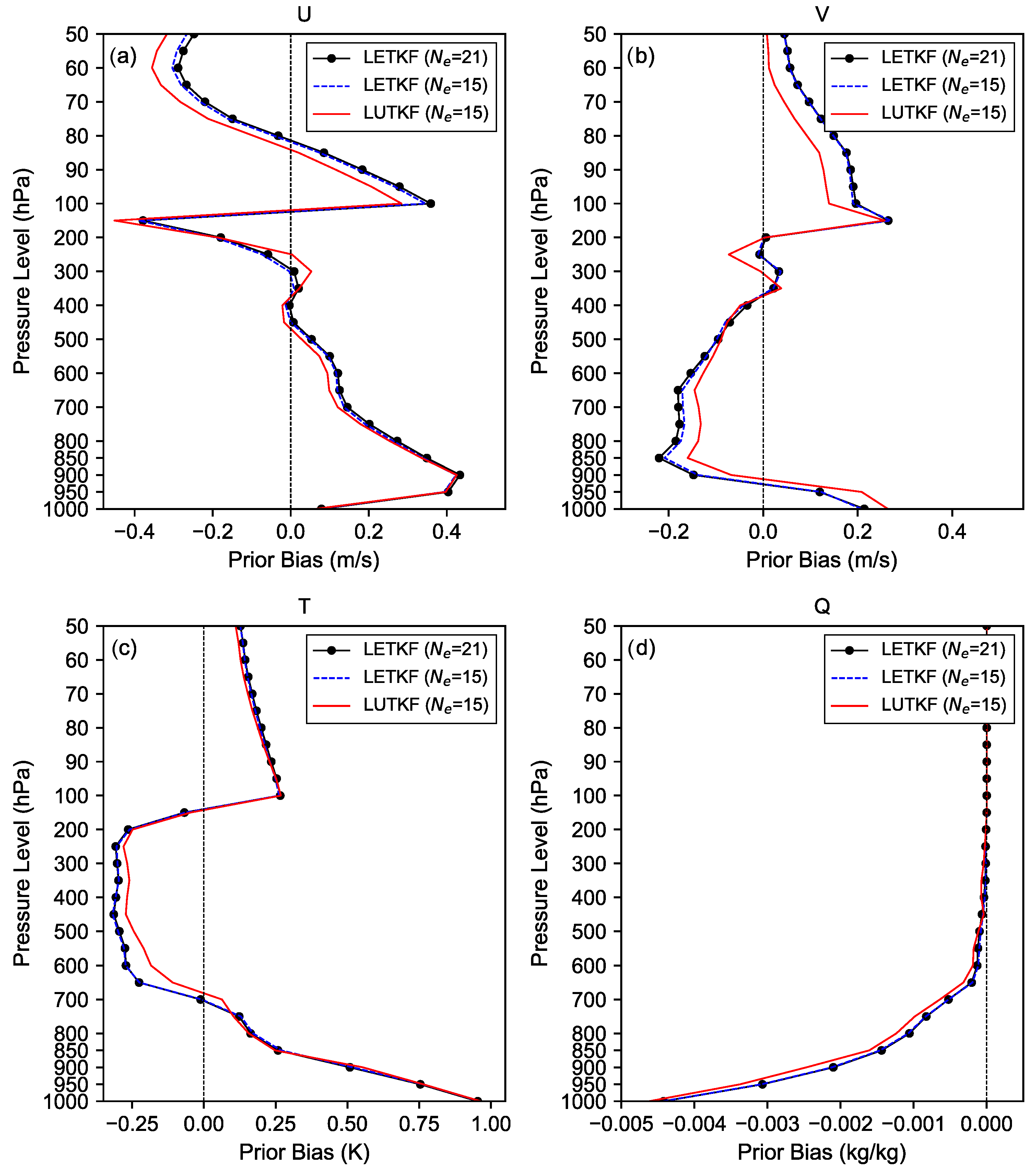
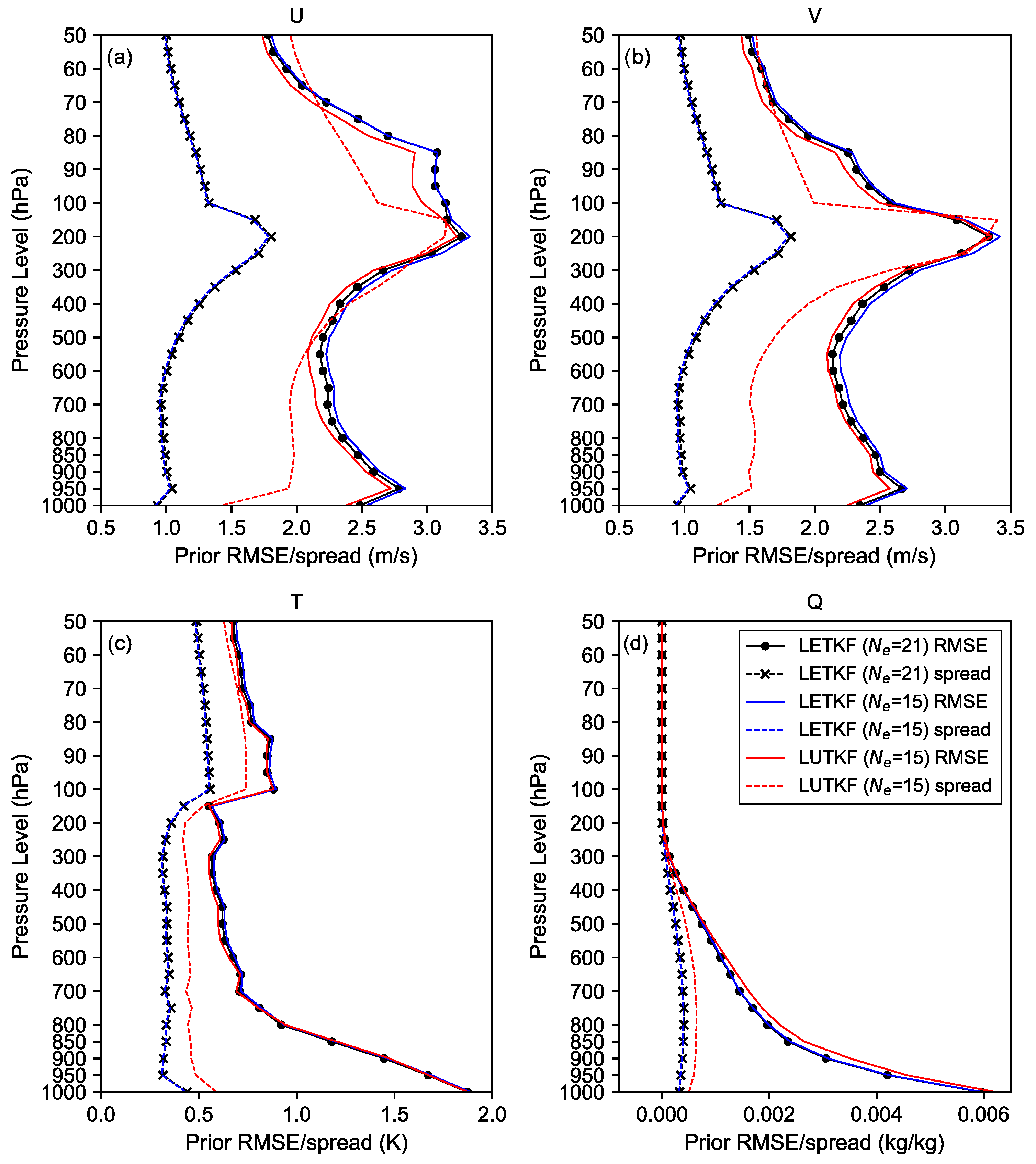
4.2. Cycling Data Assimilation Experiments
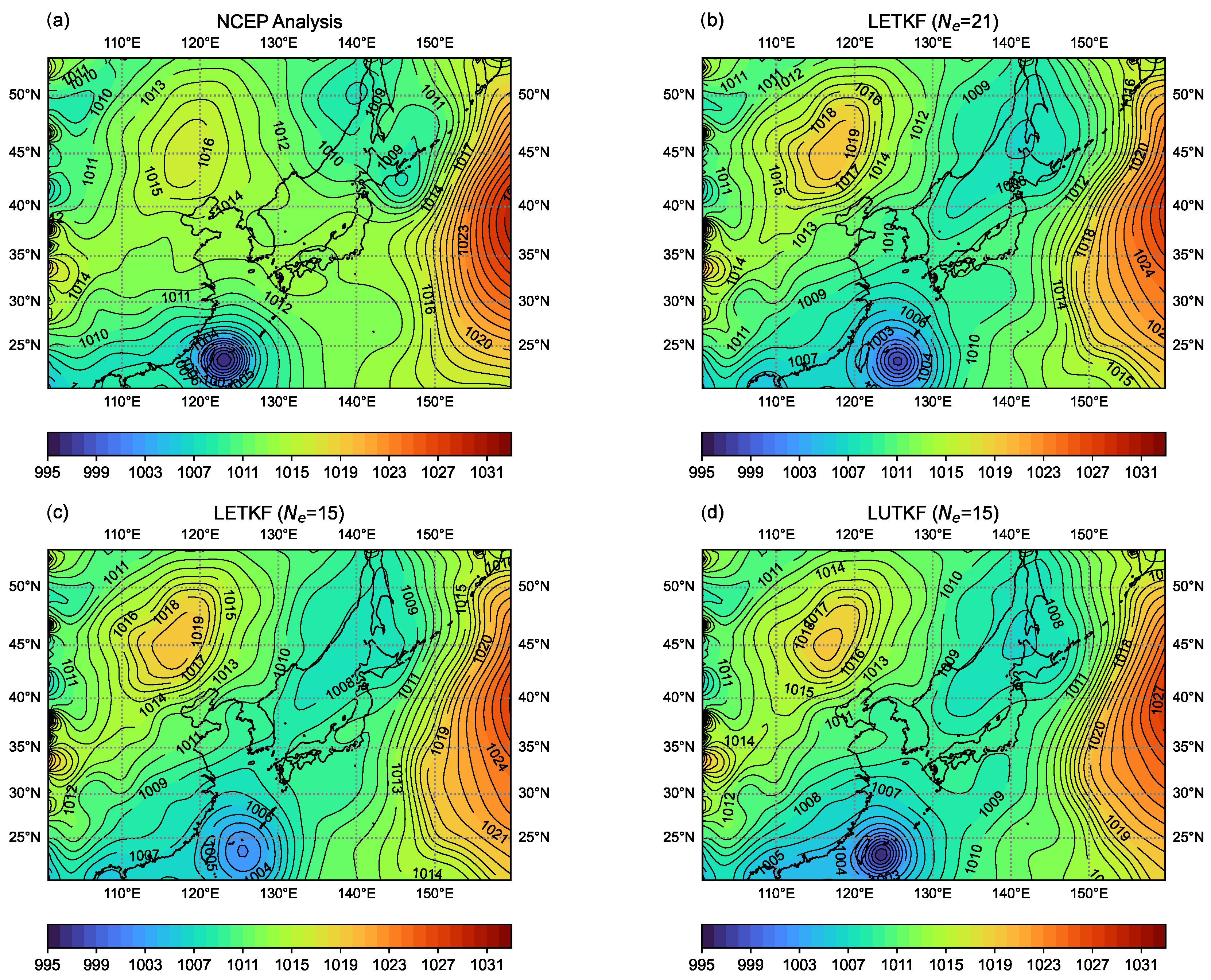
4.3. Evaluation with EBKF Analysis against NECP Analysis
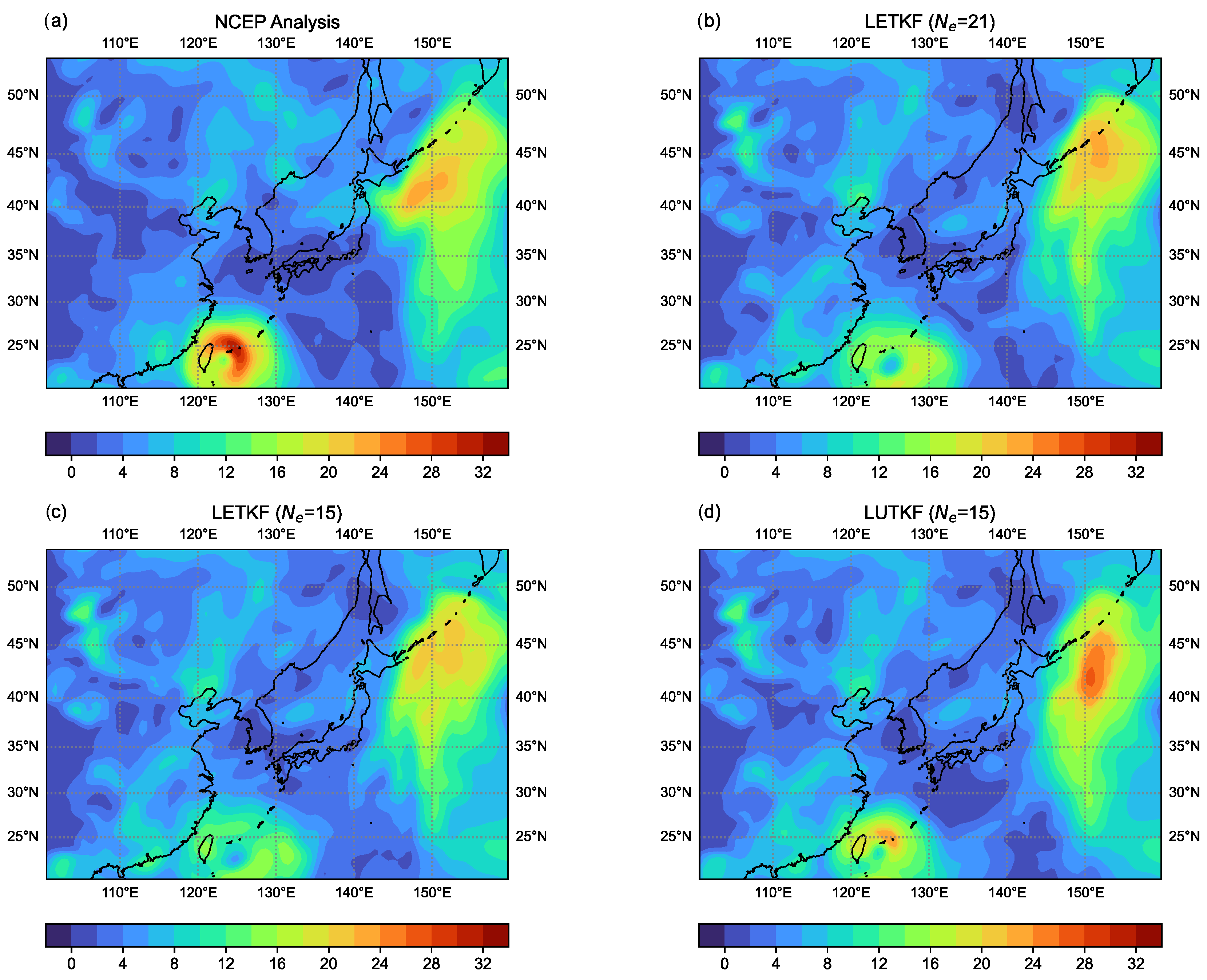
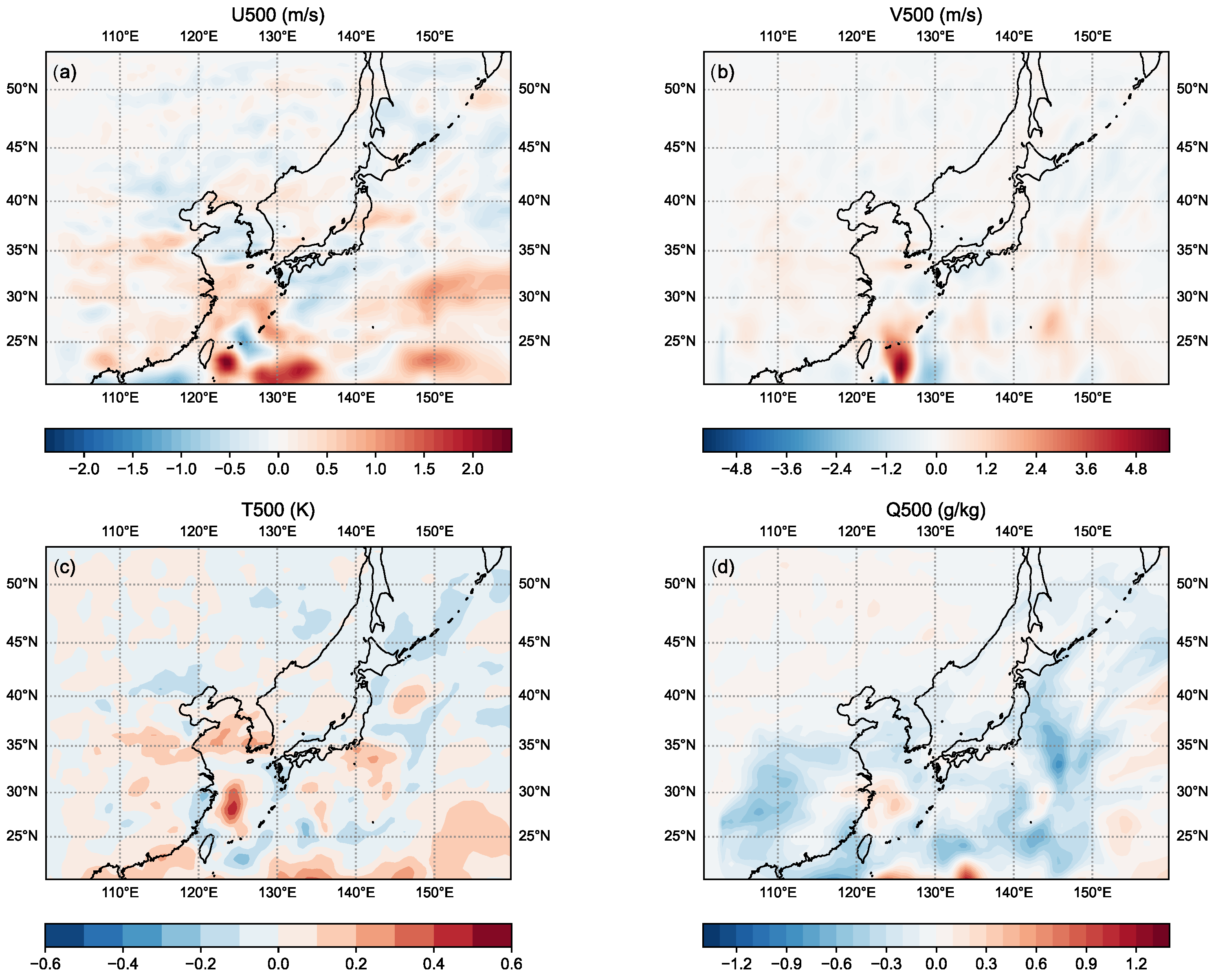
4.4. Evaluation with EBKF Short-Term Ensemble Forecast against NECP Analysis
4.5. Computational Time
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NWP | numerical weather prediction |
| NCEP | National Centers for Environmental Prediction |
| NCAR | National Center for Atmospheric Research |
| GFS | Global Forecast System |
| GEFS | Global Ensemble Forecast System |
| GDAS | Global Data Assimilation System |
| WRF | Weather Research and Forecasting |
| NMM | Non-hydrostatic Mesoscale Model |
| ARW | Advanced Research WRF |
| WPS | WRF Preprocessing System |
| PBL | planetary boundary layer |
| SPKF | sigma-point Kalman filter |
| UT | unscented transformation |
| LUTKF | local unscented transform Kalman filter |
| LETKF | local ensemble transform Kalman filter |
| EnKF | ensemble Kalman filter |
| EnSRF | ensemble square root filter |
| EBKF | ensemble-based Kalman filter |
| 3DVAR | three-dimensional variational |
| 4DVAR | four-dimensional variational |
| EnVAR | ensemble variational |
| PCA | principal component analysis |
| SVD | singular value decomposition |
| JMA | Japan Meteorological Agency |
| KMA | Korea Meteorological Administration |
| ECMWF | European Center for Medium-Range Weather Forecasts |
| DWD | Deutscher Wetterdienst |
| PREPBUFR | prepared or quality-controlled data in Binary Universal Form for the Representation of meteorological data |
| ASCAT | Advanced Scatterometer |
| GOES | Geostationary Operational Environmental Satellite |
| U | zonal wind |
| V | meridional wind |
| T | temperature |
| Q | specific humidity |
| U500 | 500 hPa zonal wind component |
| V500 | 500 hPa meridional wind component |
| T500 | 500 hPa temperature |
| Q500 | 500 hPa specific humidity |
| potential temperature perturbation | |
| pressure perturbation | |
| pressure base | |
| water vapor mixing ratio | |
| surface pressure | |
| 2-m temperature | |
| 2-m water vapor mixing ratio | |
| MPI | message passing interface |
| RTPP | relaxation to prior perturbation |
| RTPS | relaxation to prior spread |
| RMSE | root-mean-square error |
| ensemble size (the number of ensemble members) |
References
- Barker, D.M.; Huang, W.; Guo, Y.R.; Bourgeois, A.J.; Xiao, Q.N. A Three-Dimensional Variational Data Assimilation System for MM5: Implementation and Initial Results. Mon. Weather Rev. 2004, 132, 897–914. [Google Scholar] [CrossRef]
- Gao, J.; Xue, M.; Brewster, K.; Droegemeier, K.K. A Three-Dimensional Variational Data Analysis Method with Recursive Filter for Doppler Radars. J. Atmos. Oceanic Technol. 2004, 21, 457–469. [Google Scholar] [CrossRef]
- Gauthier, P.; Tanguay, M.; Laroche, S.; Pellerin, S.; Morneau, J. Extension of 3DVAR to 4DVAR: Implementation of 4DVAR at the Meteorological Service of Canada. Mon. Weather Rev. 2007, 135, 2339–2354. [Google Scholar] [CrossRef] [Green Version]
- Rawlins, F.; Ballard, S.P.; Bovis, K.J.; Clayton, A.M.; Li, D.; Inverarity, G.W.; Lorenc, A.C.; Payne, T.J. The Met Office global four-dimensional variational data assimilation scheme. Q. J. R. Meteorol. Soc. 2007, 133, 347–362. [Google Scholar] [CrossRef]
- Evensen, G.; van Leeuwen, P.J. An Ensemble Kalman Smoother for Nonlinear Dynamics. Mon. Weather Rev. 2000, 128, 1852–1867. [Google Scholar] [CrossRef]
- Whitaker, J.S.; Hamill, T.M. Ensemble Data Assimilation without Perturbed Observations. Mon. Weather Rev. 2002, 130, 1913–1924. [Google Scholar] [CrossRef]
- Hunt, B.R.; Kostelich, E.J.; Szunyogh, I. Efficient data assimilation for spatiotemporal chaos: A local ensemble transform Kalman filter. Physica D 2007, 230, 112–126. [Google Scholar] [CrossRef] [Green Version]
- Hamill, T.M.; Snyder, C. A Hybrid Ensemble Kalman Filter–3D Variational Analysis Scheme. Mon. Weather Rev. 2000, 128, 2905–2919. [Google Scholar] [CrossRef]
- Penny, S.G. The Hybrid Local Ensemble Transform Kalman Filter. Mon. Weather Rev. 2014, 142, 2139–2149. [Google Scholar] [CrossRef] [Green Version]
- Lorenc, A.C.; Bowler, N.E.; Clayton, A.M.; Pring, S.R.; Fairbairn, D. Comparison of Hybrid-4DEnVar and Hybrid-4DVar Data Assimilation Methods for Global NWP. Mon. Weather Rev. 2015, 143, 212–229. [Google Scholar] [CrossRef]
- Luo, X.; Moroz, I. Ensemble Kalman filter with the unscented transform. Physica D 2009, 238, 549–562. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.; Deng, Z.; Manoj, K.K.; Chen, D. A practical scheme of the sigma-point Kalman filter for high-dimensional systems. J. Adv. Model. Earth Syst. 2014, 6, 21–37. [Google Scholar] [CrossRef]
- Sung, K.; Song, H.J.; Kwon, I.H. A Local Unscented Transform Kalman Filter for Nonlinear Systems. Mon. Weather Rev. 2020, 148, 3243–3266. [Google Scholar] [CrossRef]
- Julier, S.; Uhlmann, J. Reduced sigma point filters for the propagation of means and covariances through nonlinear transformations. In Proceedings of the IEEE American Control Conference (ACC’02), Anchorage, AK, USA, 8–10 May 2002; Volume 2, pp. 887–892. [Google Scholar] [CrossRef] [Green Version]
- Ambadan, J.T.; Tang, Y. Sigma-Point Kalman Filter Data Assimilation Methods for Strongly Nonlinear Systems. J. Atmos. Sci. 2009, 66, 261–285. [Google Scholar] [CrossRef]
- Yang, Q.; Wu, X.; Luo, T.; Qing, C.; Yuan, R.; Su, C.; Xu, C.; Wu, Y.; Ma, X.; Wang, Z. Forecasting surface-layer optical turbulence above the Tibetan Plateau using the WRF model. Opt. Laser Technol. 2022, 153, 108217. [Google Scholar] [CrossRef]
- Skamarock, W.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Liu, Z.; Berner, J.; Wang, W.; Powers, J.G.; Duda, M.G.; Barker, D.M. A Description of the Advanced Research WRF Model Version 4.3; National Center for Atmospheric Research: Boulder, CO, USA, 2021. [Google Scholar] [CrossRef]
- Powers, J.G.; Klemp, J.B.; Skamarock, W.C.; Davis, C.A.; Dudhia, J.; Gill, D.O.; Coen, J.L.; Gochis, D.J.; Ahmadov, R.; Peckham, S.E.; et al. The Weather Research and Forecasting Model: Overview, System Efforts, and Future Directions. Bull. Am. Meteor. Soc. 2017, 98, 1717–1737. [Google Scholar] [CrossRef]
- Hsiao, L.F.; Chen, D.S.; Kuo, Y.H.; Guo, Y.R.; Yeh, T.C.; Hong, J.S.; Fong, C.T.; Lee, C.S. Application of WRF 3DVAR to Operational Typhoon Prediction in Taiwan: Impact of Outer Loop and Partial Cycling Approaches. Weather Forecast. 2012, 27, 1249–1263. [Google Scholar] [CrossRef]
- Huang, X.Y.; Xiao, Q.; Barker, D.M.; Zhang, X.; Michalakes, J.; Huang, W.; Henderson, T.; Bray, J.; Chen, Y.; Ma, Z.; et al. Four-Dimensional Variational Data Assimilation for WRF: Formulation and Preliminary Results. Mon. Weather Rev. 2009, 137, 299–314. [Google Scholar] [CrossRef] [Green Version]
- Miyoshi, T.; Kunii, M. The Local Ensemble Transform Kalman Filter with the Weather Research and Forecasting Model: Experiments with Real Observations. Pure Appl. Geophys. 2012, 169, 321–333. [Google Scholar] [CrossRef]
- Maldonado, P.; Ruiz, J.; Saulo, C. Parameter Sensitivity of the WRF–LETKF System for Assimilation of Radar Observations: Imperfect-Model Observing System Simulation Experiments. Weather Forecast. 2020, 35, 1345–1362. [Google Scholar] [CrossRef]
- Houtekamer, P.L.; Zhang, F. Review of the Ensemble Kalman Filter for Atmospheric Data Assimilation. Mon. Weather Rev. 2016, 144, 4489–4532. [Google Scholar] [CrossRef]
- Dillon, M.E.; Skabar, Y.G.; Ruiz, J.; Kalnay, E.; Collini, E.A.; Echevarría, P.; Saucedo, M.; Miyoshi, T.; Kunii, M. Application of the WRF-LETKF Data Assimilation System over Southern South America: Sensitivity to Model Physics. Weather Forecast. 2016, 31, 217–236. [Google Scholar] [CrossRef]
- Miyoshi, T.; Sato, Y.; Kadowaki, T. Ensemble Kalman Filter and 4D-Var Intercomparison with the Japanese Operational Global Analysis and Prediction System. Mon. Weather Rev. 2010, 138, 2846–2866. [Google Scholar] [CrossRef]
- Hamrud, M.; Bonavita, M.; Isaksen, L. EnKF and Hybrid Gain Ensemble Data Assimilation. Part I: EnKF Implementation. Mon. Weather Rev. 2015, 143, 4847–4864. [Google Scholar] [CrossRef]
- Schraff, C.; Reich, H.; Rhodin, A.; Schomburg, A.; Stephan, K.; Periáñez, A.; Potthast, R. Kilometre-scale ensemble data assimilation for the COSMO model (KENDA). Q. J. R. Meteorol. Soc. 2016, 142, 1453–1472. [Google Scholar] [CrossRef]
- Julier, S.; Uhlmann, J. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef]
- Wan, E.; Van Der Merwe, R. The unscented Kalman filter for nonlinear estimation. In Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium (ASSPCCS’00), Lake Louise, AB, Canada, 1–4 October 2000; pp. 153–158. [Google Scholar] [CrossRef]
- van der Merwe, R. Sigma-Point Kalman Filters for Probabilistic Inference in Dynamic State-Space Models. Ph.D. Thesis, The Faculty of the OGI School of Science & Engineering at Oregon Health & Science University, Portland, OR, USA, 2004. [Google Scholar]
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Gaspari, G.; Cohn, S.E. Construction of correlation functions in two and three dimensions. Q. J. R. Meteorol. Soc. 1999, 125, 723–757. [Google Scholar] [CrossRef]
- Keyser, D. PREPBUFR Processing at NCEP. NOAA/NWS/NCEP/EMC. Available online: http://www.emc.ncep.noaa.gov/mmb/data_processing/prepbufr.doc/document.htm (accessed on 9 April 2023).
- Lorenz, E.N. Energy and Numerical Weather Prediction. Tellus 1960, 12, 364–373. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Snyder, C.; Sun, J. Impacts of Initial Estimate and Observation Availability on Convective-Scale Data Assimilation with an Ensemble Kalman Filter. Mon. Weather Rev. 2004, 132, 1238–1253. [Google Scholar] [CrossRef]
- Whitaker, J.S.; Hamill, T.M. Evaluating Methods to Account for System Errors in Ensemble Data Assimilation. Mon. Weather Rev. 2012, 140, 3078–3089. [Google Scholar] [CrossRef]
- Hodyss, D.; Campbell, W.F.; Whitaker, J.S. Observation-Dependent Posterior Inflation for the Ensemble Kalman Filter. Mon. Weather Rev. 2016, 144, 2667–2684. [Google Scholar] [CrossRef]
- Bishop, C.H.; Whitaker, J.S.; Lei, L. Gain Form of the Ensemble Transform Kalman Filter and Its Relevance to Satellite Data Assimilation with Model Space Ensemble Covariance Localization. Mon. Weather Rev. 2017, 145, 4575–4592. [Google Scholar] [CrossRef]
- Lei, L.; Whitaker, J.S.; Bishop, C. Improving Assimilation of Radiance Observations by Implementing Model Space Localization in an Ensemble Kalman Filter. J. Adv. Model. Earth Syst. 2018, 10, 3221–3232. [Google Scholar] [CrossRef] [Green Version]



| Assimilation Method | U (m/s) | V (m/s) | T (K) | Q (kg/kg) |
|---|---|---|---|---|
| LETKF () | 3.86 | 3.86 | 1.95 | 174.56 |
| LETKF () | 3.91 | 3.93 | 1.99 | 179.47 |
| LUTKF () | 3.84 | 3.88 | 1.89 | 180.94 |
| Assimilation Method | U (m/s) | V (m/s) | T (K) | Q (kg/kg) |
|---|---|---|---|---|
| LETKF () | 3.38 | 3.34 | 1.75 | 124.03 |
| LETKF () | 3.48 | 3.45 | 1.80 | 129.19 |
| LUTKF () | 3.38 | 3.33 | 1.69 | 130.24 |
| Assimilation Method | 9 h Ensemble Forecast for the First Guess | Data Assimilation | Total |
|---|---|---|---|
| LETKF () | 148.45 | 17.36 | 165.81 |
| LETKF () | 75.68 | 14.58 | 90.26 |
| LUTKF () | 77.81 | 46.47 | 124.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sung, K. The Local Unscented Transform Kalman Filter for the Weather Research and Forecasting Model. Atmosphere 2023, 14, 1143. https://doi.org/10.3390/atmos14071143
Sung K. The Local Unscented Transform Kalman Filter for the Weather Research and Forecasting Model. Atmosphere. 2023; 14(7):1143. https://doi.org/10.3390/atmos14071143
Chicago/Turabian StyleSung, Kwangjae. 2023. "The Local Unscented Transform Kalman Filter for the Weather Research and Forecasting Model" Atmosphere 14, no. 7: 1143. https://doi.org/10.3390/atmos14071143
APA StyleSung, K. (2023). The Local Unscented Transform Kalman Filter for the Weather Research and Forecasting Model. Atmosphere, 14(7), 1143. https://doi.org/10.3390/atmos14071143






