Contribution of Climate Change and Human Activities to Runoff and Sediment Discharge Changes Based on Budyko Theory and Water–Sediment Relationships during 1960–2019 in the Taohe River Basin, China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.3. Methodology
2.3.1. Calculation of Rainfall Erosivity
2.3.2. Calculation of Potential Evapotranspiration
2.3.3. Contribution to Runoff Change Based on Water Balance and the Budyko Hypothesis
2.3.4. Contribution to Sediment Discharge Change Based on the Budyko Hypothesis and Water–Sediment Relationships
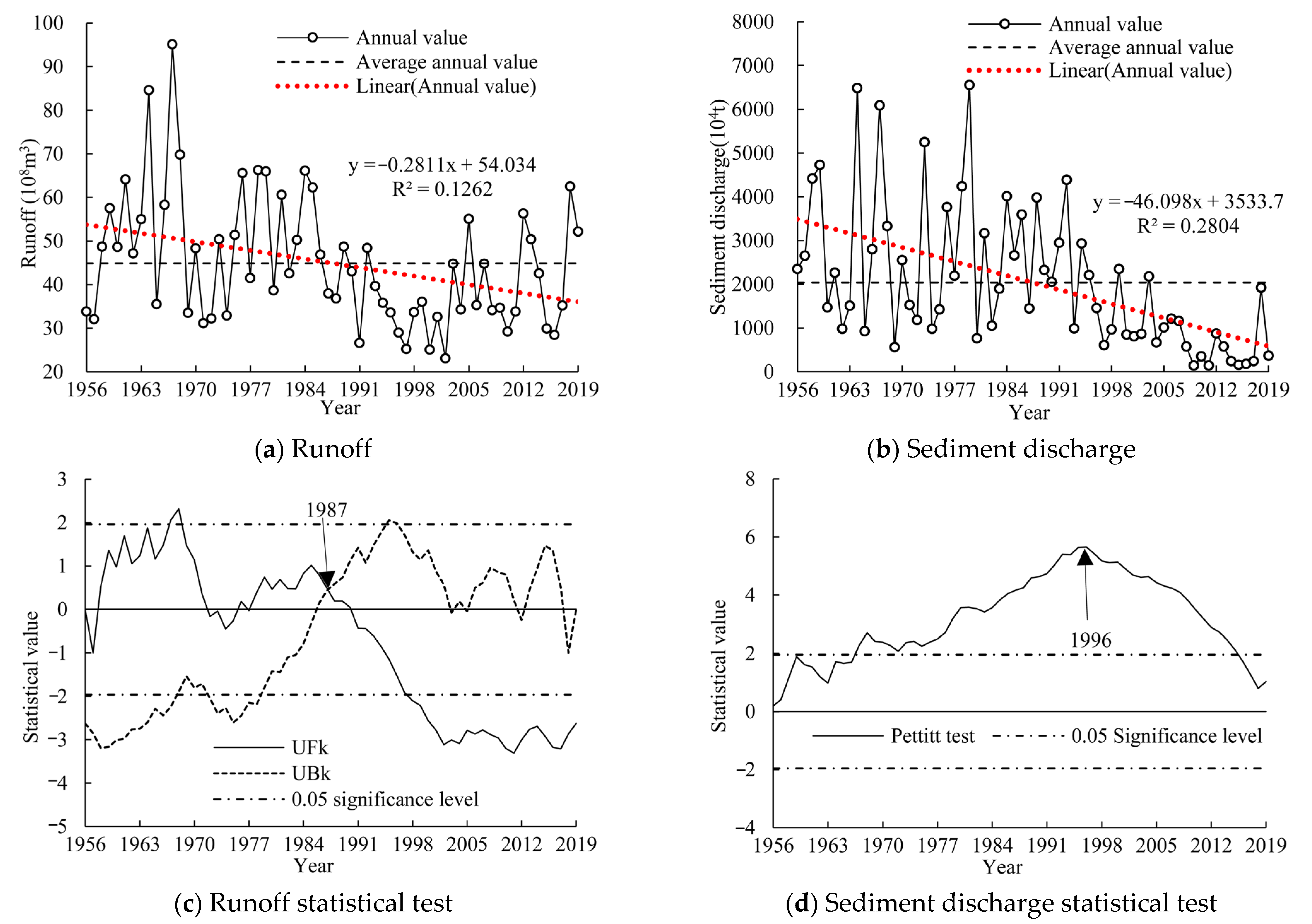
2.3.5. Trend and Change Point Analysis
3. Results
3.1. Interannual Variation of Runoff and Sediment Discharge
3.2. Spatiotemporal Variation of Driving Variables
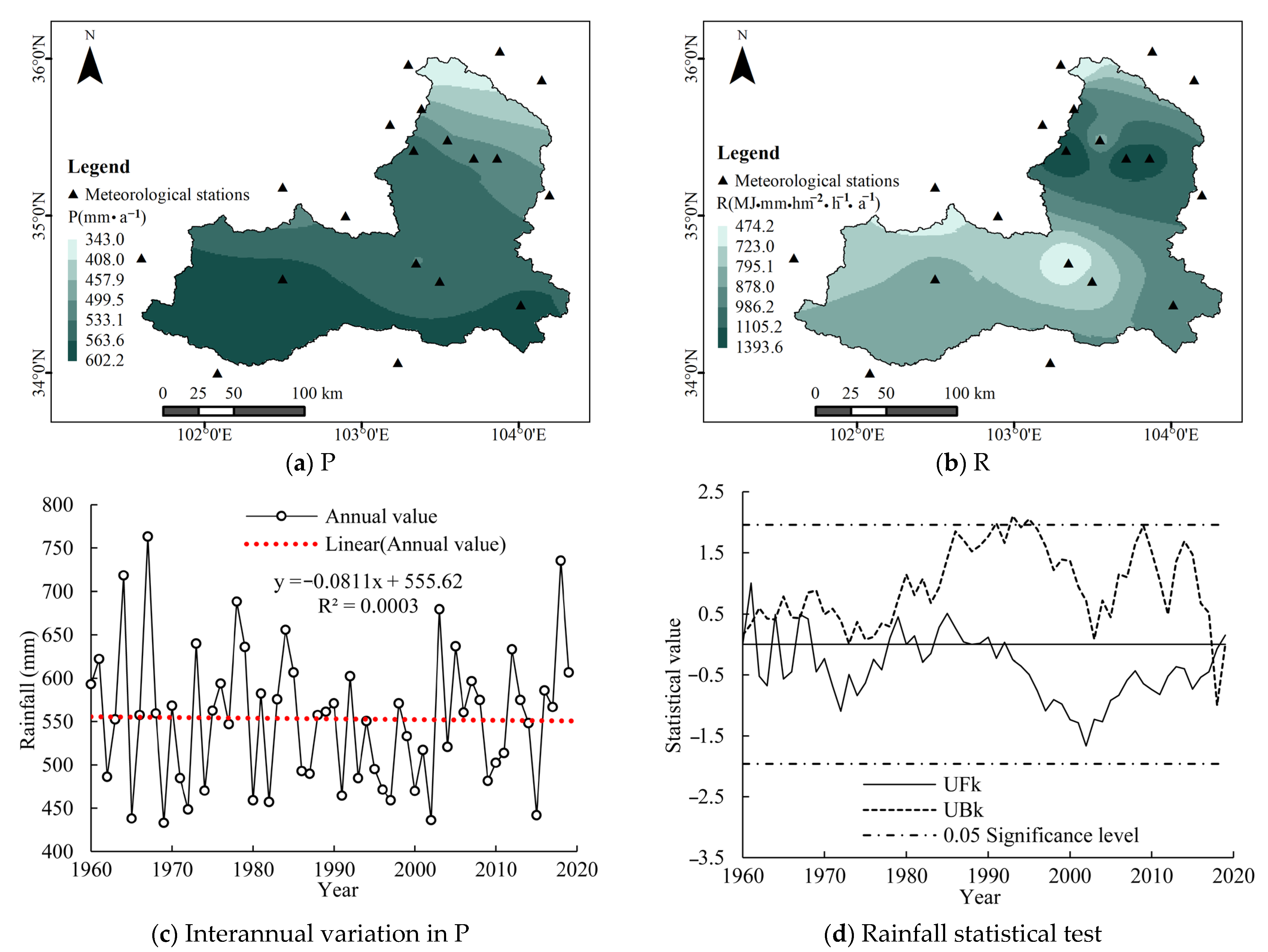
3.2.1. Temporal and Spatial Variations of Rainfall and Rainfall Erosivity
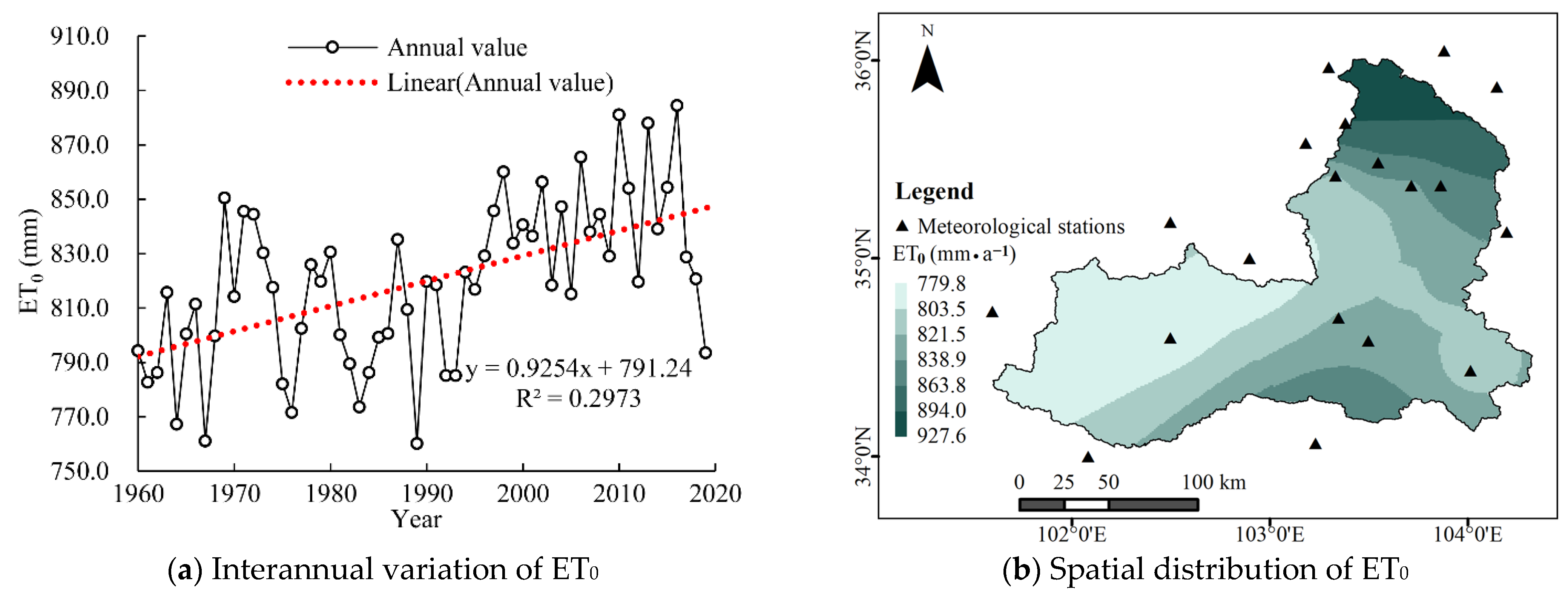
3.2.2. Temporal and Spatial Variations in Potential Evapotranspiration
3.2.3. Interannual Variation of Sediment Concentration
3.3. Qualitative Analysis of Driving Variables
3.3.1. Correlation Coefficient between Runoff and Driving Variables
3.3.2. Correlation Coefficient between Sediment Discharge and Driving Variables
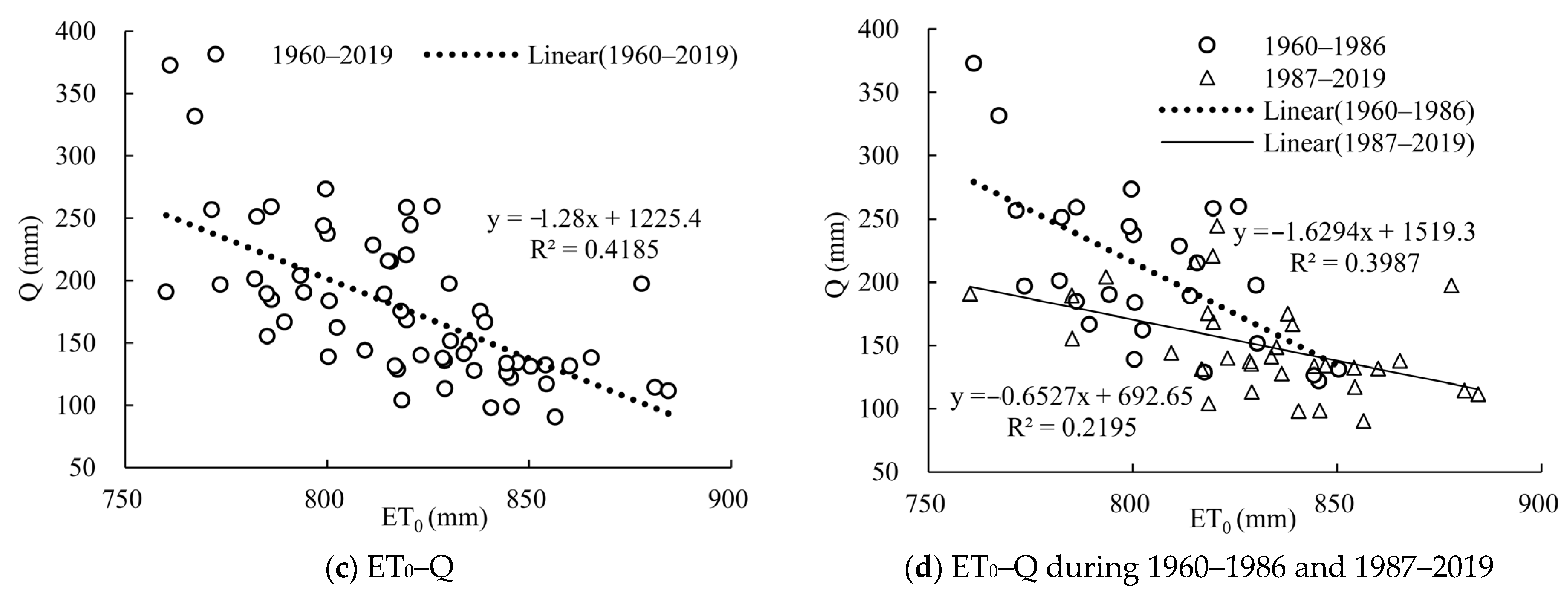
3.3.3. Regression Relationship between Runoff and Driving Variables
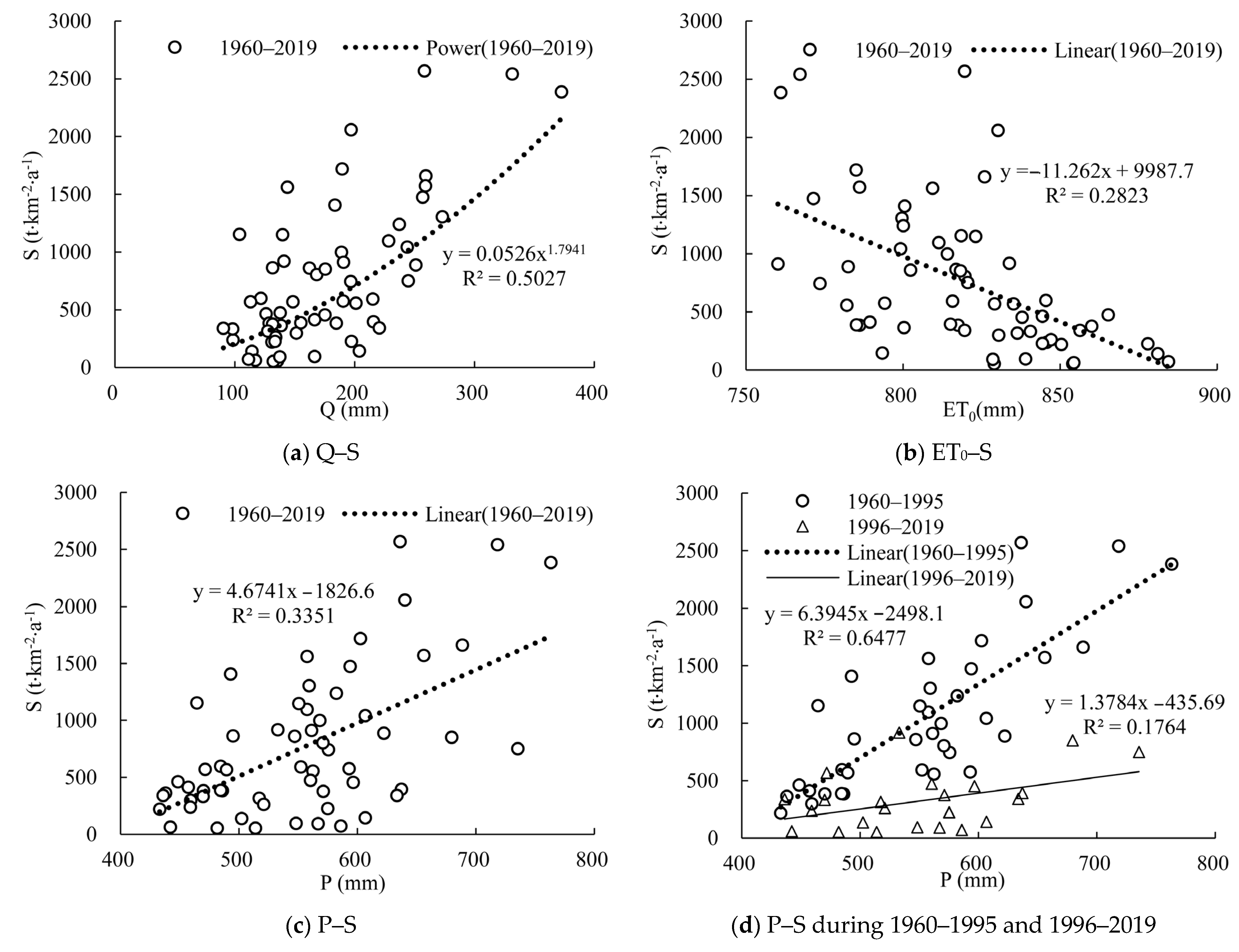
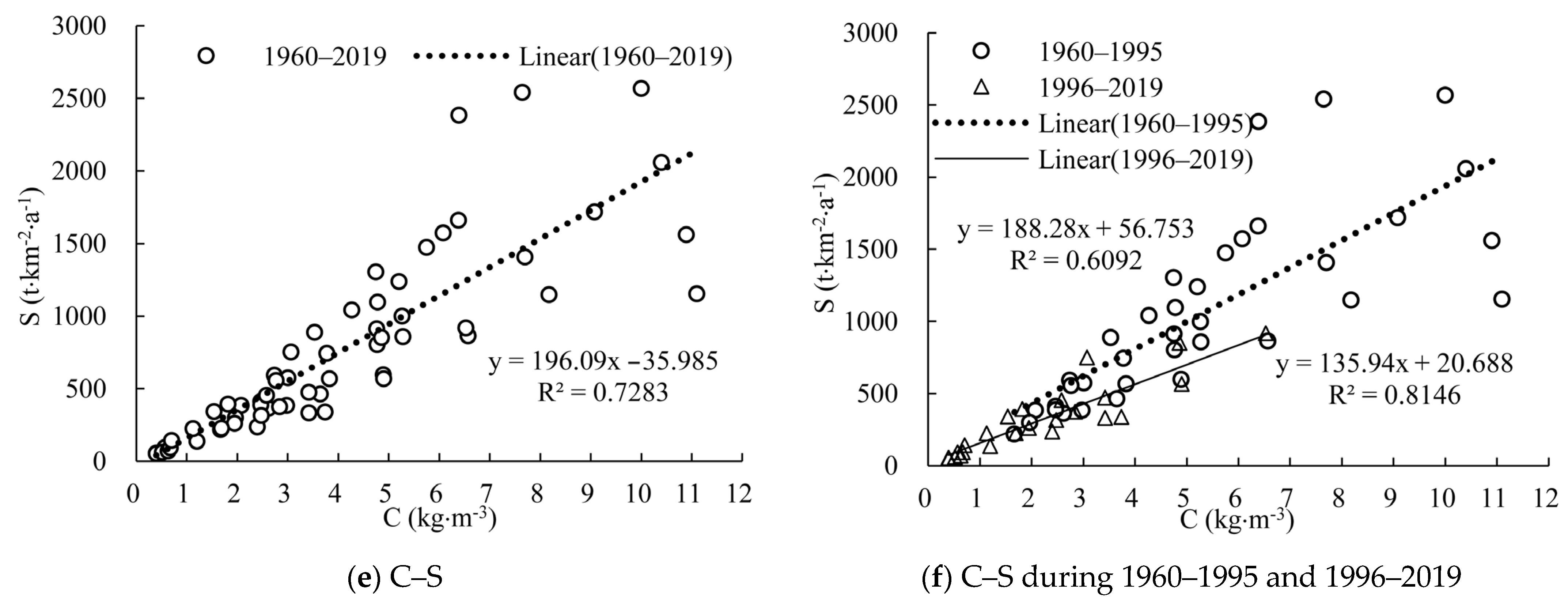
3.3.4. Regression Relationship between Sediment Discharge and Driving Variables
3.4. Quantitative Analysis of driving Variables
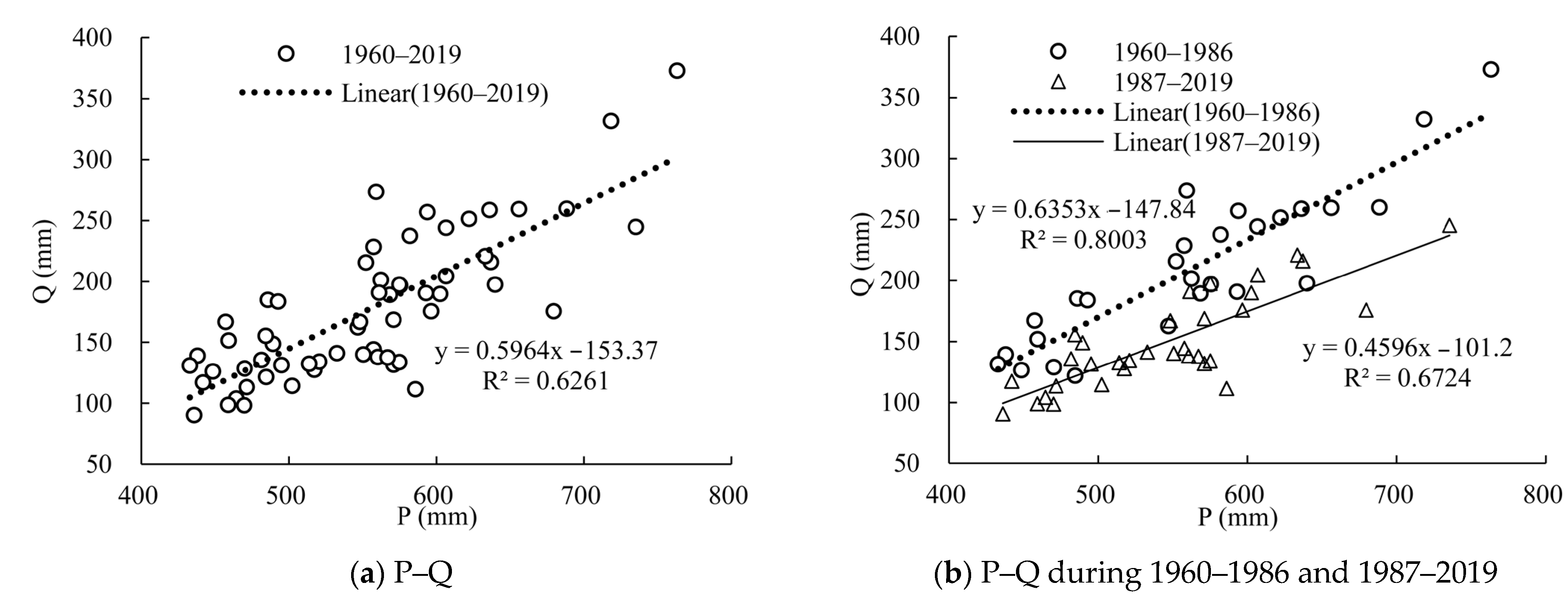
3.4.1. Quantitative Analysis of the Attribution of Runoff Change
3.4.2. Quantitative Analysis of the Attribution of Sediment Discharge Changes
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feng, X.; Cheng, W.; Fu, B.; Lü, Y. The role of climatic and anthropogenic stresses on long-term runoff reduction from the Loess Plateau, China. Sci. Total Environ. 2016, 571, 688–698. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Yang, Q.; Chen, S.; Luo, Z.; Yuan, F.; Wang, R. Temporal and spatial variability of sediment flux into the sea from the three largest rivers in China. J. Asian Earth Sci. 2014, 87, 102–115. [Google Scholar] [CrossRef]
- Wang, S.; Fu, B.; Piao, S.; Lü, Y.; Ciais, P.; Feng, X.; Wang, Y. Reduced sediment transport in the Yellow River due to anthropogenic changes. Nat. Geosci. 2016, 9, 38–41. [Google Scholar] [CrossRef]
- Xu, K.; Milliman, J.D.; Xu, H. Temporal trend of precipitation and runoff in major Chinese Rivers since 1951. Glob. Planet. Change 2010, 73, 219–232. [Google Scholar] [CrossRef]
- Wang, S.; Fu, B.; Liang, W. Developing policy for the Yellow River sediment sustainable control. Natl. Sci. Rev. 2016, 3, 162–164. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Fu, B.; Liang, W.; Liu, Y.; Wang, Y. Driving forces of changes in the water and sediment relationship in the Yellow River. Sci. Total Environ. 2017, 576, 453–461. [Google Scholar] [CrossRef]
- Xu, J.; Jiang, X.; Sun, H.; Xu, H.; Zhong, X.; Liu, B.; Li, L. Driving forces of nature and human activities on water and sediment changes in the middle reaches of the Yellow River in the past 100 years. J. Soil Sediment 2021, 21, 2450–2464. [Google Scholar] [CrossRef]
- Chu, H.; Wei, J.; Qiu, J.; Li, Q.; Wang, G. Identification of the impact of climate change and human activities on rainfall-runoff relationship variation in the Three-River Headwaters region. Ecol. Indic. 2019, 106, 105516. [Google Scholar] [CrossRef]
- Huntington, T.G. Evidence for intensification of the global water cycle: Review and synthesis. J. Hydrol. 2006, 319, 83–95. [Google Scholar] [CrossRef]
- Chang, J.; Zhang, H.; Wang, Y.; Zhu, Y. Assessing the impact of climate variability and human activities on streamflow variation. Hydrol. Earth Syst. Sci. 2016, 20, 1547–1560. [Google Scholar] [CrossRef] [Green Version]
- Zhao, G.; Tian, P.; Mu, X.; Jiao, J.; Wang, F.; Gao, P. Quantifying the impact of climate variability and human activities on streamflow in the middle reaches of the Yellow River basin, China. J. Hydrol. 2014, 519, 387–398. [Google Scholar] [CrossRef]
- Zhao, Y.; Zou, X.; Gao, J.; Xu, X.; Wang, C.; Tang, D.; Wang, T.; Wu, X. Quantifying the anthropogenic and climatic contributions to changes in water discharge and sediment load into the sea: A case study of the Yangtze River, China. Sci. Total Environ. 2015, 536, 803–812. [Google Scholar] [CrossRef]
- Chen, T.; Ao, T.; Zhang, X.; Li, X.; Yang, K. Climate Change Characteristics of Extreme Temperature in the Minjiang River Basin. Adv. Meteorol. 2019, 2019, 1935719. [Google Scholar] [CrossRef] [Green Version]
- Zhao, G.; Gao, P.; Tian, P.; Sun, W.; Hu, J.; Mu, X. Assessing sediment connectivity and soil erosion by water in a representative catchment on the Loess Plateau, China. Catena 2020, 185, 104284. [Google Scholar] [CrossRef]
- Kong, D.; Miao, C.; Wu, J.; Duan, Q. Impact assessment of climate change and human activities on net runoff in the Yellow River Basin from 1951 to 2012. Ecol. Eng. 2016, 91, 566–573. [Google Scholar] [CrossRef]
- Wu, L.; Wang, S.; Bai, X.; Luo, W.; Tian, Y.; Zeng, C.; Luo, G.; He, S. Quantitative assessment of the impacts of climate change and human activities on runoff change in a typical karst watershed, SW China. Sci. Total Environ. 2017, 601–602, 1449–1465. [Google Scholar] [CrossRef] [PubMed]
- Jia, L.; Yu, K.; Li, Z.; Li, P.; Zhang, J.; Wang, A.; Ma, L.; Xu, G.; Zhang, X. Temporal and spatial variation of rainfall erosivity in the Loess Plateau of China and its impact on sediment load. Catena 2022, 210, 105931. [Google Scholar] [CrossRef]
- Dang, S.; Liu, X.; Yin, H.; Guo, X. Prediction of sediment yield in the middle reaches of the Yellow River Basin under extreme precipitation. Front. Earth Sci. 2020, 8, 542686. [Google Scholar] [CrossRef]
- Li, T.; Wang, S.; Liu, Y.; Fu, B.; Zhao, W. Driving forces and their contribution to the recent decrease in sediment flux to ocean of major rivers in China. Sci. Total Environ. 2018, 634, 534–541. [Google Scholar] [CrossRef]
- Soksamnang, K.; He, H.M.; Zhao, H.F.; Jing, Z.W. Analysis of rainfall erosivity change and its impacts on soil erosion on the Loess Plateau over more than 50 years. Res. Soil Water Conserv. 2018, 25, 1–7. (In Chinese) [Google Scholar]
- Wu, J.; Miao, C.; Wang, Y.; Duan, Q.; Zhang, X. Contribution analysis of the long-term changes in seasonal runoff on the Loess Plateau, China, using eight Budyko-based methods. J. Hydrol. 2017, 545, 263–275. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, G.; Tian, P.; Mu, X.; Tian, X.; Feng, J.; Bai, Y. Runoff changes in the major river basins of China and their responses to potential driving forces. J. Hydrol. 2022, 607, 127536. [Google Scholar] [CrossRef]
- Xu, R.; Qiu, D.; Wu, C.; Mu, X.; Zhao, G.; Sun, W.; Gao, P. Quantifying climate and anthropogenic impacts on runoff using the SWAT model, a Budyko-based approach and empirical methods. Hydrol. Sci. J. 2023, 68, 1–14. [Google Scholar] [CrossRef]
- Song, X.; Sun, W.; Zhang, Y.; Song, S.; Li, J.; Gao, Y. Using hydrological modelling and data-driven approaches to quantify mining activities impacts on centennial streamflow. J. Hydrol. 2020, 585, 124764. [Google Scholar] [CrossRef]
- Hu, Y.; Duan, W.; Chen, Y.; Zou, S.; Kayumba, P.M.; Sahu, N. An integrated assessment of runoff dynamics in the Amu Darya River Basin: Confronting climate change and multiple human activities, 1960–2017. J. Hydrol. 2021, 603, 126905. [Google Scholar] [CrossRef]
- Li, C.; Hao, J.; Zhang, G.; Fang, H.; Wang, Y.; Lu, H. Runoff variations affected by climate change and human activities in Yarlung Zangbo River, southeastern Tibetan Plateau. Catena 2023, 230, 107184. [Google Scholar] [CrossRef]
- Sun, X.; Wang, J.; Ma, M.; Han, X. Attribution of Extreme Drought Events and Associated Physical Drivers across Southwest China Using the Budyko Framework. Remote Sens. 2023, 15, 2702. [Google Scholar] [CrossRef]
- Sun, L.; Wang, Y.; Zhang, J.; Yang, Q.; Bao, Z.; Guan, X.; Guan, T.; Chen, X.; Wang, G. Impact of environmental change on runoff in a transitional basin: Tao River Basin from the Tibetan Plateau to the Loess Plateau, China. Adv. Clim. Change Res. 2019, 10, 214–224. [Google Scholar] [CrossRef]
- Yang, L.; Feng, Q.; Li, C.; Si, J.; Wen, X.; Yin, Z. Detecting climate variability impacts on reference and actual evapotranspiration in the Taohe River Basin, NW China. Hydrol. Res. 2016, 48, 596–612. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.B.; Xie, Y.; Liu, B.Y. Rainfall erosivity estimation using daily rainfall amounts. Sci. Geogr. Sin. 2002, 22, 705–711. (In Chinese) [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D5109. [Google Scholar]
- Wu, L.; Liu, X.; Ma, X. Spatiotemporal distribution of rainfall erosivity in the Yanhe River watershed of hilly and gully region, Chinese Loess Plateau. Environ. Earth Sci. 2016, 75, 315. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, P.; Lai, C.; Chen, X.; Wu, X.; Zeng, Z.; Li, J. Spatiotemporal variability of reference evapotranspiration and contributing climatic factors in China during 1961–2013. J. Hydrol. 2017, 544, 97–108. [Google Scholar] [CrossRef]
- Yin, Y.; Wu, S.; Chen, G.; Dai, E. Attribution analyses of potential evapotranspiration changes in China since the 1960s. Theor. Appl. Climatol. 2010, 101, 19–28. [Google Scholar] [CrossRef]
- Sposito, G. Understanding the Budyko Equation. Water 2017, 9, 236. [Google Scholar] [CrossRef] [Green Version]
- Budyko, M.I. Climate and Life; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Hankey, A.; Stanley, H.E. An alternate formulation of the static scaling hypothesis. Int. J. Quantum. Chem. 1971, 5, 593–604. [Google Scholar] [CrossRef]
- Choudhury, B. Evaluation of an empirical equation for annual evaporation using field observations and results from a biophysical model. J. Hydrol. 1999, 216, 99–110. [Google Scholar] [CrossRef]
- Yang, H.; Yang, D.; Lei, Z.; Sun, F. New analytical derivation of the mean annual water-energy balance equation. Water Resour. Res. 2008, 44, W3410. [Google Scholar] [CrossRef]
- Schaake, J.C. From climate to flow. In Climate Change and US Water Resources; John Wiley: New York, NY, USA, 1990; pp. 177–206. [Google Scholar]
- Zheng, H.; Miao, C.; Wu, J.; Lei, X.; Liao, W.; Li, H. Temporal and spatial variations in water discharge and sediment load on the Loess Plateau, China: A high-density study. Sci. Total Environ. 2019, 666, 875–886. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1948. [Google Scholar]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Hamed, K.H.; Ramachandra Rao, A. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Pettitt, A.N. A Non-Parametric Approach to the Change-Point Problem. Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Sung, J.H.; Chung, E.; Kim, Y.; Lee, B. Meteorological hazard assessment based on trends and abrupt changes in rainfall characteristics on the Korean peninsula. Theor. Appl. Climatol. 2017, 127, 305–326. [Google Scholar] [CrossRef]
- Cheng, L.; Ma, L.; Yang, M.; Wan, G.; Wang, X. Changes of temperature and precipitation and their impacts on runoff in the upper Taohe River in northwest China from 1956 to 2014. Environ. Earth Sci. 2019, 78, 423. [Google Scholar] [CrossRef]
- Zhang, X.; Dong, Q.; Cheng, L.; Xia, J. A Budyko-based framework for quantifying the impacts of aridity index and other factors on annual runoff. J. Hydrol. 2019, 579, 124224. [Google Scholar] [CrossRef]
- Gao, G.; Fu, B.; Wang, S.; Liang, W.; Jiang, X. Determining the hydrological responses to climate variability and land use/cover change in the Loess Plateau with the Budyko framework. Sci. Total Environ. 2016, 557–558, 331–342. [Google Scholar] [CrossRef]
- Li, Y.; Liu, C.; Yu, W.; Tian, D.; Bai, P. Response of streamflow to environmental changes: A Budyko-type analysis based on 144 river basins over China. Sci. Total Environ. 2019, 664, 824–833. [Google Scholar] [CrossRef] [PubMed]
- Gan, G.; Liu, Y.; Sun, G. Understanding interactions among climate, water, and vegetation with the Budyko framework. Earth-Sci. Rev. 2021, 212, 103451. [Google Scholar] [CrossRef]
- Tan, X.; Liu, B.; Tan, X.; Chen, X. Long-Term Water Imbalances of Watersheds Resulting from Biases in Hydroclimatic Data Sets for Water Budget Analyses. Water Resour. Res. 2022, 58, e2021WR031209W. [Google Scholar] [CrossRef]


| Correlation Coefficient | P | ET0 | ||
|---|---|---|---|---|
| Pearson | Kendall | Pearson | Kendall | |
| Q | 0.698 ** | 0.520 ** | 0.325 ** | 0.302 ** |
| P | 0.752 ** | 0.584 ** | ||
| Correlation Coefficient | C | P | R | ET0 | ||||
|---|---|---|---|---|---|---|---|---|
| Pearson | Kendall | Pearson | Kendall | Pearson | Kendall | Pearson | Kendall | |
| S | 0.810 ** | 0.858 ** | 0.625 ** | 0.672 ** | 0.714 ** | 0.693 ** | 0.354 ** | 0.519 ** |
| C | 0.629 ** | 0.646 ** | 0.650 ** | 0.666 ** | 0.507 ** | 0.560 ** | ||
| P | 0.903 ** | 0.830 ** | 0.752 ** | 0.584 ** | ||||
| R | 0.601 ** | 0.606 ** | ||||||
| Period | Q/mm | P/mm | ET0/mm | εP | εET0 | εn | ∆Q/mm | ∆P/mm | ∆ET0/mm | ∆n/mm | δp/% | δET0/% | δn/% |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1960–1986 | 209.62 | 562.72 | 803.77 | 1.59 | −0.70 | −0.97 | . | ||||||
| 1987–2019 | 149.40 | 545.31 | 832.30 | 2.07 | −0.93 | −1.33 | 60.22 | 9.87 | 4.78 | 45.57 | 16.40 | 7.94 | 75.67 |
| 1987–1989 | 161.23 | 536.11 | 801.58 | 1.91 | −0.86 | −1.21 | 48.39 | 15.29 | −0.38 | 33.48 | 31.59 | −0.78 | 69.19 |
| 1990–1999 | 137.42 | 520.26 | 821.73 | 2.10 | −0.95 | −1.39 | 72.20 | 23.56 | 2.87 | 45.78 | 32.63 | 3.97 | 63.40 |
| 2000–2009 | 142.51 | 547.44 | 839.06 | 2.17 | −0.98 | −1.40 | 67.11 | 8.64 | 5.88 | 52.59 | 12.88 | 8.76 | 78.36 |
| 2010–2019 | 164.72 | 570.99 | 845.33 | 2.00 | −0.90 | −1.26 | 44.90 | −4.79 | 7.27 | 42.42 | −10.66 | 16.19 | 94.47 |
| Period | S /t/km2 | C /kg/m3 | P /mm | ET0 /mm | ηmc | ηP | ηET0 | ηn | ∆S /t/km2 | ∆P /mm | ∆ET0 /mm | ∆n /mm | ∆mc /kg/m3 | δ′P /% | δ′ET0 /% | δ′n /% | δ′mc /% |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1960–1995 | 1049.03 | 5.27 | 554.72 | 804.31 | 0.96 | 1.68 | −0.72 | −1.04 | |||||||||
| 1996–2019 | 323.49 | 2.23 | 550.78 | 842.20 | 1.26 | 2.21 | −0.96 | −1.43 | 725.54 | 5.11 | 13.95 | 151.79 | 554.68 | 0.70 | 1.92 | 20.92 | 76.45 |
| 1996–1999 | 524.59 | 4.17 | 508.63 | 842.19 | 1.26 | 2.25 | −0.99 | −1.54 | 524.44 | 106.82 | 23.37 | 219.81 | 174.43 | 20.37 | 4.46 | 41.91 | 33.26 |
| 2000–2009 | 369.90 | 2.64 | 547.44 | 839.06 | 1.29 | 2.28 | −0.99 | −1.47 | 679.13 | 11.19 | 15.10 | 176.03 | 476.81 | 1.65 | 2.22 | 25.92 | 70.21 |
| 2010–2019 | 196.64 | 1.04 | 570.99 | 845.33 | 1.02 | 1.79 | −0.77 | −1.13 | 852.39 | −10.06 | 7.36 | 40.19 | 814.90 | −1.18 | 0.86 | 4.71 | 95.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Sun, D.; Niu, Z.; Wang, X. Contribution of Climate Change and Human Activities to Runoff and Sediment Discharge Changes Based on Budyko Theory and Water–Sediment Relationships during 1960–2019 in the Taohe River Basin, China. Atmosphere 2023, 14, 1144. https://doi.org/10.3390/atmos14071144
Ma Y, Sun D, Niu Z, Wang X. Contribution of Climate Change and Human Activities to Runoff and Sediment Discharge Changes Based on Budyko Theory and Water–Sediment Relationships during 1960–2019 in the Taohe River Basin, China. Atmosphere. 2023; 14(7):1144. https://doi.org/10.3390/atmos14071144
Chicago/Turabian StyleMa, Yali, Dongyuan Sun, Zuirong Niu, and Xingfan Wang. 2023. "Contribution of Climate Change and Human Activities to Runoff and Sediment Discharge Changes Based on Budyko Theory and Water–Sediment Relationships during 1960–2019 in the Taohe River Basin, China" Atmosphere 14, no. 7: 1144. https://doi.org/10.3390/atmos14071144
APA StyleMa, Y., Sun, D., Niu, Z., & Wang, X. (2023). Contribution of Climate Change and Human Activities to Runoff and Sediment Discharge Changes Based on Budyko Theory and Water–Sediment Relationships during 1960–2019 in the Taohe River Basin, China. Atmosphere, 14(7), 1144. https://doi.org/10.3390/atmos14071144





