Critical Review on Radiative Forcing and Climate Models for Global Climate Change since 1970

Abstract

This review identifies a critical problem in the fundamental physics of current climate models. The large greenhouse effect of rising CO₂ assumed in climate models is assessed by six key observations from ground- and satellite-based measurements. This assessment is enhanced by statistical analyses and model calculations of global or regional mean surface temperature changes by conventional climate models and by a conceptual quantum physical model of global warming due to halogen-containing greenhouse gases (halo-GHGs). The postulated large radiative forcing of CO₂ in conventional climate models does not agree with satellite observations. Satellite-observed warming pattern resembles closely the atmospheric distribution of chlorofluorocarbons (CFCs). This review helps understand recent remarkable observations of reversals from cooling to warming in the lower stratosphere over most continents and in the upper stratosphere at high latitudes, surface warming cessations in the Antarctic, North America, UK, and Northern-Hemisphere (NH) extratropics, and the stabilization in NH or North America snow cover, since the turn of the century. The complementary observation of surface temperature changes in 3 representative regions (Central England, the Antarctic, and the Arctic) sheds new light on the primary mechanism of global warming. These observations agree well with not CO₂-based climate models but the CFC-warming quantum physical model. The latter offers parameter-free analytical calculations of surface temperature changes, exhibiting remarkable agreement with observations. These observations overwhelmingly support an emerging picture that halo-GHGs made the dominant contribution to global warming in the late 20th century and that a gradual reversal in warming has occurred since ~2005 due to the phasing out of halo-GHGs. Advances and insights from this review may help humans make rational policies to reverse the past warming and maintain a healthy economy and ecosystem.

1. Introduction

There was a rise of about 0.6 °C in measured global mean surface temperature (GMST) between 1970 and 2000 [1,2,3,4] and a global warming pause for the period 2000–2015 [2,3,5,6,7,8,9,10,11,12]. The GMST appears to have risen again in the past few years [13]. In CO₂-based climate models (e.g., general circulation models—GCMs), which were built primarily on the greenhouse effect of CO₂ as the major culprit of global warming, the re-rise in GMST after 2015 is attributed to increasing CO₂ [13]. In a recent study, however, this author [14] showed strong evidence that the post-2015 warming is mainly caused by Arctic amplification of surface warming due to sea-ice loss, without which a global reversal in warming would have occurred since ~2005. This conclusion is drawn from comprehensive observed datasets and statistical analyses of troposphere–stratosphere temperature (T) climatology, global lower-stratospheric T (GLST), global surface air T, sea-ice extent (SIE) and snow-cover extent (SCE), combined with analytical, parameter-free calculations of GMSTs by a quantum physical model of climate change caused by halogen-containing greenhouse gases (GHGs) (hereafter halo-GHGs) [3] and of GLSTs by the cosmic-ray-driven electron-induced reaction (CRE) model of stratospheric O₃ depletion conspired by anthropogenic chlorofluorocarbons (CFCs) and natural cosmic rays (CRs) [3,5,7,15]. The CRE model has now been developed into a complete quantitative model of global ozone depletion [16]. These observed and calculated results have reached a surprizing conclusion that global climate change is human-made but dominantly caused by halo-GHGs [14].

The above conclusion appears quite odd, especially when the 2021 Nobel Prize in Physics was just awarded to some pioneers of GCMs. However, it is not inconsistent with the conclusions reached in a significant body of literature [3,5,6,7,8,17,18,19,20,21,22,23,24,25,26], which do not agree with CO₂ climate models. In fact, there are long debates on the mechanisms and perspectives of climate change, as documented in the publications or lectures by renowned physicists (e.g., Ivar Giaever [27]—a 1973 Nobel laureate in physics, Freeman Dyson [28], William Happer [8], Steven Koonin [29], and most recently John Clauser—a 2022 Nobel laureate in Physics, according to his keynote lecture at Quantum Korea 2023) and climate scientists (e.g., Richard Lindzen [22,30], Reginald Newell [20], Sherwood Idso [21,23], and John Christy [24,25]). These previous investigations by others [8,17,18,19,20,21,22,23,24,25,26,27,28,29,30] and this author [3,5,6,7,14] have presented a compelling argument that the assumptions made in CO₂ climate models have to undergo close scrutiny. Notably, the former MIT professor Reginald Newell [20] wrote in 1979: “The fact that water vapor dominates CO₂ in the radiation budget has been known and discussed for many years (see, e.g., Kondratiev and Niilisk [17]; Moller [18]; Zdunkowski et al. [19]) but it seems important to reemphasize when so much attention is being paid to CO₂”. Given with substantial observations found and reviewed [3,14], this author feels that such a statement seems not out of date. This paper has the main purpose of using a series of key observations to assess the CO₂-based GCMs and the CFC-warming physical model [3,14].

GCMs are a class of ‘quasi-realistic’ climate models. GCMs not only include unresolved terms represented in equations with tunable parameters but also have major limitations such as the structural error and uncertainty across models with different representations of unresolved scales and the requirement of tuning the models to match certain aspects of observations [31]. Despite these weaknesses, GCMs have been a mainstay of climate research for several decades, and the awarding of the 2021 Nobel Prize in Physics to GCM-based work was just praised by the climate community [32]. As stated in a Perspective published in PNAS in 2022 by Balaji et al. [31], however, there is current debate on the obsolescence of GCMs, and considerable literature argues that the limitations of GCMs require a major overhaul for their continuing role in climate modeling. The bounds of uncertainties on equilibrium climate sensitivity (ECS) (the equilibrium change in GMST that would result from a doubling of CO₂ concentration) given by GCMs are known to be very large and have not significantly diminished since the late 1970s [26,33,34]. Satellite observations are unable to constrain GCMs adequately, and other indirect means (e.g., paleoclimate data) are often used to place limits on ECS. The most recent IPCC AR6 concluded that many GCMs were providing ECS outside the “very likely” range, and used emulators where ECS is a tunable parameter, to refine the consensus projections and their uncertainty bounds [31]. These facts imply a diminishing or limited role of GCMs in the past decades (from phase 3 to 6 of the Coupled Model Intercomparison Project, CMIP3 in the IPCC AR4 [1] to CMIP6 in the AR6 [13]).

In contrast to GCMs, the author has developed a conceptual quantum physical model of climate change, which evolved from the findings in studies of stratospheric ozone depletion by the CRE model [3,5,7,15,16,35,36,37,38]. First, it was robustly demonstrated that the variations in both ozone and lower-stratospheric temperature (LST) are dominantly governed by both (halogen-containing) ozone-depleting substances (ODSs) and CR intensity only [3,5,7,15,16,38]. This has in fact revealed no sign of the GCM-predicted greenhouse effect of increasing CO₂ on the stratospheric climate. Second, the author made the first prediction in 2008–2009 that the long-term change in GMST since 1950 was mainly caused by halo-GHGs (mainly CFCs). This prediction was first based on the found correlation between observed GMST and total concentration of atmospheric CFCs [5] and then on the calculations of changes in GMST due to anthropogenic emission of halo-GHGs [6] for the period from 1950 to 2009. The subsequent analysis of substantial observed datasets showed strong evidence of the warming ‘hiatus’ associated with declining halo-GHGs regulated by the Montreal Protocol [3,7]. Third, a simple quantum physical model of climate change caused by halo-GHGs was finally developed on the basis of the quantum physics of the Earth’s blackbody radiation [3]. Of special note is that this physical model includes no tunable parameter and directly gives analytical calculations of GMST, while exhibiting excellent agreement with observations [3], particularly after the removal of natural El Niño southern oscillation (ENSO) and volcanic effects [14]. These results have provided compelling evidence for the dominant warming mechanism of halo-GHGs (mainly CFCS) in the late 20th century [3,14]. This CFC-warming physical model has well explained the ‘hiatus’ in global warming and has predicted a long-term cooling trend starting around the turn of the century, corresponding to the changing trend of atmospheric halo-GHGs.

The ‘hiatus’ in warming since the turn of the century has widely been reported and there exist large discrepancies between observed and GCM-simulated GMST trends in 1998–2015 [2,3,5,6,7,8,9,10,11,12,39]. All historical simulations by GCMs did not reproduce the ‘hiatus’ in global warming over the period 2000–2015 [2,3,9,39,40]. Various mechanisms (mainly natural climate variability) have been proposed for the warming ‘hiatus’ [2,8,9,10,11,12,40], but natural climate variability has its limits. In fact, model simulations gave a duration of an observed 15-year absence of warming as an indication of a significant discrepancy with the prediction of CO₂ climate models and thus predicted in 2009 that “no sort of natural variability could hold off greenhouse warming much longer” and “(rapid) warming will resume in the next few years” [40].

The change in stratospheric T mirrors the change in surface T. Radiosonde- and satellite-measured data showed that the troposphere had warmed and the stratosphere had cooled from the mid-1970s to the turn of the century [2,4]. In CO₂ climate models, the observed cooling of the middle and upper stratosphere was primarily attributed to rising concentrations of well-mixed GHGs (WMGHGs) (mainly non-halogen GHGs) [41,42], whereas the changes in LST are attributed to WMGHGs and stratospheric ozone depletion [2,4,43]. CO₂ climate models have also made an iconic prediction that tropospheric warming and stratospheric cooling would continue due to continued WMGHG increases over the coming decades [2,13]. In contrast to this prediction and the reported post-2015 rise in surface-measured GMST, however, most satellite measurements have shown that stratospheric Ts steadily decreased to the end of the 20th century, but since then the GLST has stabilized [14,43], as widely stated in the 2018 WMO report [4] and the 2021 IPCC AR6 [13]. In fact, it is generally agreed that the GLST has dominantly been controlled by ODSs [3,4,5,7,14,15]. Interestingly, a recent analysis of upper-air radiosonde T profiles from 1976 to 2015 by a large international team (Philipona et al. [43]) has provided remarkable evidence that after decades of cooling, the lower stratosphere at altitudes between 15 and 30 km and over most continents has now been warming since the turn of the century. They also presented NOAA’s MSU/AMSU satellite data from 1979 to 2015 at the radiosonde locations, showing minor warming in the early 21st century. This reversal in LST from cooling in the late 20th century to current warming has been confirmed in our recent study [14], using the high-quality EUMETSAT’s ROM SAF satellite datasets of the troposphere-stratosphere T climatology. Furthermore, this author [14] also discovered that such a reversal has also occurred in the upper stratosphere at altitudes above 30 km over the past decade, especially at high latitudes. This critical observation provides a striking fingerprint that the radiative (greenhouse) effect of anthropogenic GHGs has been decreasing since the turn of the century.

In this review, the author will first briefly review the fundamental physics of global warming theory in Section 2. Then, brief reviews of CO₂ climate models and their applications for early calculations of warming caused by halo-GHGs will be given in Section 3 and Section 4, respectively. Section 5 will present a review of six key observations providing the fingerprints of the contribution of the greenhouse effect of halo-GHGs versus non-halogen GHGs (mainly CO₂) to climate change. A refined quantum physical model of climate change and parameter-free analytical calculations of GMST changes through the CFC-warming mechanism will be reviewed in Section 6, which is followed by Section 7 to give remarks and perspectives on global climate change. It will finally address the potential ramifications of this study on the recent proposals of “geoengineering” (stratospheric aerosol injection) to reduce global warming [44] and of a future generation of GCMs to “match them better to observations, theory, and process models” [31].

2. Fundamental Physics of Global Warming Theory

The thermal radiation from the Earth or the Sun can approximately be treated as blackbody radiation at temperature T. The radiation intensity spectrum I(λ) is obtained by integrating the radiation energy flux per unit wavelength given by Planck’s formula in quantum physics over a certain wavelength interval

$$B_{\lambda }\left(T\right)d\lambda =\frac{2h{c}^2}{{\lambda }^5\left(e^{\frac{hc}{\lambda kT}}-1\right)}d\lambda .$$

(1)

Here, the theoretical radiation intensity I(λ) spectrum, the satellite-measured outgoing long-wave radiation (OLR) transmittance (Γ) spectrum at the top of atmosphere (TOA) [45], and the atmospheric transmittance spectrum measured at the ground with the Sun as a blackbody source on Mount Miron at 30° ground-to-space slant path and simulated by Modtran4 [46] are plotted in Figure 1 [3,6,7]. The spectral region of 8–13 μm is called the ‘atmospheric window’ as the unpolluted atmosphere in this spectral region is quite transparent, except for absorption by ozone in the 9.6 μm band. Moreover, over 80% of the total radiation energy from Earth’s surface and clouds is emitted into space through this window. As a result, any polluting molecule that strongly absorbs radiation in the atmospheric window is highly effective GHGs. Unfortunately, many halogenated gases such as CFCs and HCFCs have strong absorption bands in this atmospheric window and are therefore not only ODSs but highly effective GHGs. So far, measured halo-GHGs have included CFCs, hydrochlorofluorocarbons (HCFCs), hydrofluorocarbons (HFCs), perfluorocarbons (PFCs), and SF6. CFCs and HCFCs are both ODSs and GHGs, whereas HFCs, PFCs, and SF6 are non-ODSs but GHGs. The major anthropogenic halo-GHGs were CFCs up to the 2000s, while since then the contributions of HCFCs, HFCs, and PFCs to the greenhouse effect have been increasing [2,4,13].

As also shown in Figure 1, CO₂ contributes to the strong infrared (IR) absorption bands at 4–5 μm and 13–17 μm, while CH₄ and N₂O also have strong absorption bands at 7.6 μm and 7.8 μm, respectively. However, H₂O (water vapor) is the primary absorber in the entire IR spectral range [2,20,47], with two major absorption bands at 5–8.3 μm and 11–17 μm. The IR flux dominated by CO₂ is well known to be only approximately 10% of that controlled by water vapor [20]. Therefore, H₂O, together with CO₂, CH₄, N₂O, and halo-GHGs, is the most important GHG, rendering the Earth a unique living environment. However, the atmospheric concentrations of CO₂, CH₄, and N₂O are so high that the atmosphere is completely opaque in the spectral regions of their IR absorption bands. This is clearly seen in the measured and simulated transmittance Γ(λ) spectrum on the ground using the Sun as a radiation source, showing Γ = 0 in their absorption spectral regions. The OLR transmittance spectrum measured at the TOA by a satellite appears to give a transmittance Γ = ~0.4 in their absorption spectral regions. However, this non-zero transmittance is due to the re-emission of these molecules in the tropopause or stratosphere, as evidenced by the measured OLR flux in the CO₂ absorption band at 14–16 µm corresponding to a blackbody T = ~220 K [3,8].

The current debate lies on the question as to whether the absorption at the wings of the IR bands of non-halogen WMGHGs (CO₂, CH₄, and N₂O) would continue to increase with rising gas concentrations and contribute considerably to the observed climate change. For a resolution to this critical question, it is required to have a deep and correct understanding of the basic physics of CO₂ in the atmosphere, as discussed by William Happer [8]. This key issue is closely related to water vapor, which has the largest greenhouse effect in the Earth’s atmosphere [2,20,47] and is most likely to be responsible for the largest uncertainties in CO₂ climate models [2,17,20,22,47]. As shown in Figure 1, water has strong and extensive absorption bands overlapping with the extended wings of CO₂, CH₄, and N₂O absorption bands. Interestingly, Kondratiev and Niilisk [17] made a study of the radiation budget by investigating the absorption and transmission functions of CO₂ and H₂O in the atmosphere in the spectral region of 12–18 μm, showing that the change in the terrestrial radiation with an increased or decreased CO₂ concentration is sharply diminished when the absorption of water vapor is taken into account and that the heat radiation of the atmosphere is almost independent of the variation in CO₂ in the atmosphere. They estimated the ECS to be ≤0.50 K. Similarly Newell and Dopplick [20] estimated with a static radiative flux model that at low latitudes (the tropics) the increase in surface air temperature due to CO₂ doubling is less than 0.25 K. ECS values of 0.3–0.5 K and 0.26–0.4 K were also observationally determined by Lindzen [22] and Idso [21,23] respectively. These researches showed that the far larger radiative forcings of rising CO₂ and resultant surface T changes computed by GCMs (e.g., the models of Manabe–Wetherald [48] and Augustsson–Ramanathan [49]) arise likely from the neglected account of water vapor in the atmosphere and not from the CO₂ itself. Thus, the theory that climatic change is caused primarily by rising CO₂ has been very questionable for decades.

The overlapping effect of water vapor in the spectral ranges of CO₂, CH₄, and N₂O adsorption bands can also potentially cause a negative feedback factor for the radiative forcings caused by these non-halogen GHGs if the forcings considerably exist. In contrast, water vapor obviously has almost no interference with the radiative forcings of halo-GHGs and ozone due to no or negligible overlapping between the absorptions of H₂O and halo-GHGs or O₃ in the atmospheric window at 8–13 μm. Furthermore, an increase in water vapor in the atmosphere due to surface warming caused by an increase in an effective GHG can lead to a positive feedback effect [2,20,47], particularly true for halo-GHGs and O₃. The critical overlapping effect of water vapor on the greenhouse effect of non-halogen WMGHGs (particularly CO₂) in the atmosphere must be examined carefully by observations.

3. Brief Review of CO₂-Based Climate Models

Climate models aim to estimate the surface T change in response to a change in the atmosphere. A central concept is radiative forcing, which is a radiative perturbation arising from an increase in a GHS, inducing an initial rise in surface T. This is followed by complex responses including enhanced evaporation of water vapor into the atmosphere, and changes in cloud cover and in the atmospheric or oceanic circulation. In various climate models from the global energy balance models to GCMs, the equilibrium GMST has a linear relationship with the radiative forcing [1,2,13,50]. Thus, the radiative forcing provides a useful metric to access and compare the impacts of various anthropogenic and natural variations on the Earth’s climate.

Considering the simple radiative balance model of the Earth, one can write the global mean net radiation flux F_z at the TOA as F_z = F₀ − F^↑, where F₀ is the incoming solar flux at the TOA, and F^↑ is the outgoing energy flux from the Earth. For the system to be at equilibrium, the net radiation flux F_z = 0. When the Earth’s climate system is imposed by a small energy perturbation, for example, by an increase in the atmospheric concentration of a GHG or in incoming solar radiation, this energy imbalance translates into an initial radiative flux perturbation ΔF at the TOA: ΔF = F₀ − F^↑, before the surface T changes. This energy flux imbalance is called the radiative forcing (ΔF). In climate models, however, radiative forcing (RF) is most commonly computed in terms of the radiative perturbation at the tropopause rather than at the TOA. That is, F₀ and F^↑ after the energy perturbation are retrieved from the model at the tropopause after stratospheric Ts have been allowed to readjust to radiative equilibrium while surface and tropospheric Ts and state variables such as water vapor and cloud cover are fixed at the initial unperturbed values. This definition of radiative forcing (RF, also called stratospherically-adjusted radiative forcing—SARF, as distinct from instantaneous radiative forcing) was adopted in the IPCC 2001 TAR [50], 2007 AR4 [1] and 2013 AR5 [2]. Moreover, another measure of radiative forcing, the so-called effective radiative forcing (ERF), was introduced in the IPCC AR5 [2]. ERF is defined as the change in net downward radiative flux at TOA after allowing for atmospheric Ts, water vapor, and clouds to adjust while keeping surface T or a portion of surface conditions unchanged. In GCMs such as CMIP5 and CMIP6, however, RF and ERF are practically equal for WMGHGs [2,13].

In fact, the calculations of radiative forcing are often simplified into an algebraic formulation specific to a GHG. Since the late 1990s, the IPCC Reports [1,2,50] have used simplified analytical expressions derived from atmospheric radiative transfer models to calculate the RFs for WMGHGs. Such simplified formulas of RF are the following [50,51]

$$RF=\chi \left(X-X_0\right)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left(\text{halo-GHGs}\right),$$

(2)

$$RF=5.35\times \ln \left(C/C_0\right)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left({\mathrm{CO}}_2\right),$$

(3)

where X is the concentration of a halo-GHG in ppb, χ in Wm⁻² ppb⁻¹ is the radiative efficiency of a specific halo-GHG, and C is the concentration of CO₂ in ppm. The subscript 0 denotes the unperturbed concentration (in 1750): C_o = 278 ppm, and X_o = 0. For CH₄ and N₂O, the radiative forcing is assumed to be approximately proportional to the square root of gas concentration [50,51]. Such RF calculations given by Myhre et al. [51] have shown excellent agreement (within 5%) with high spectral resolution radiative transfer calculations in GCMs [50]. Consistently, the author [3] indeed demonstrated that the RFs calculated by Equations (2) and (3) are exactly identical to the ERFs given in the 2013 IPCC AR5 [2]. 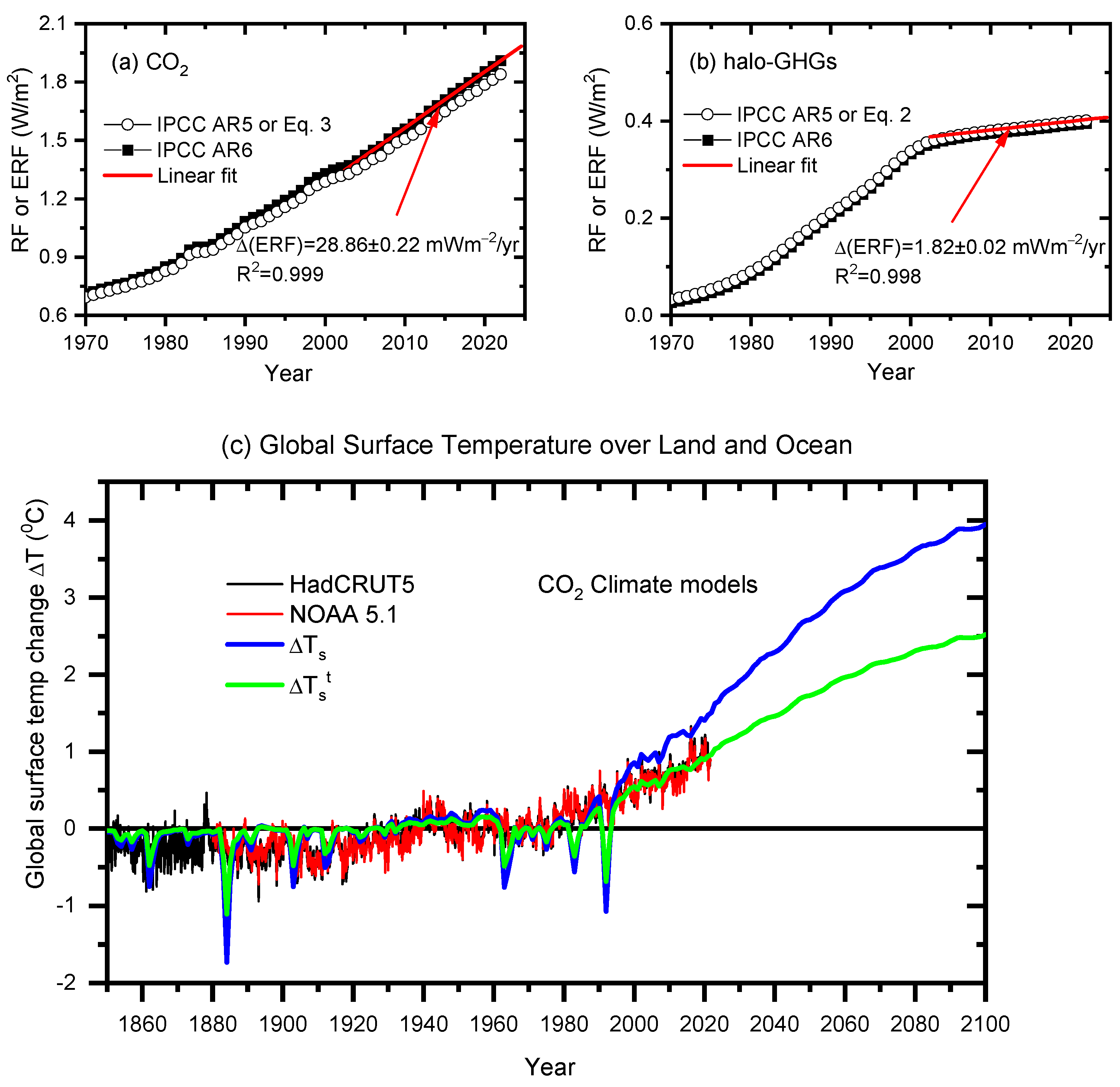As shown in Figure 2a,b, here we further note that for CO₂, there are small increases of 2–4% in ERFs computed by GCMs and given in the newest 2021 IPCC AR6 [13], compared with either ERFs given in the 2013 IPCC AR5 [2] or RFs calculated by Equation (3), whereas for halo-GHGs, there are no differences between RFs calculated by Equation (2) and ERFs given in the IPCC AR6 [13] or AR5 [2]. Therefore, for simplicity, one can use the simplified functional forms of RFs, instead of complex GCMs, to access and compare the potential climate effects of various WMGHGs [3].

Climate change occurs when the climate system responds to counteract the radiation flux changes, and all such responses are explicitly excluded from the definition of RF in GCMs [1,2,50]. The climate sensitivity factor (α_c) is defined as the ratio of the (Planck) responsive change in Earth’s surface T (ΔT_s) to a radiative forcing RF:

$${\alpha }_c\equiv \frac{∆T_s}{RF}.$$

(4)

α_c is also called the reference climate sensitivity or the Planck feedback factor, which is equal to ~0.30 K/(Wm⁻²). However, the change (ΔT_s) in Earth’s equilibrium GMST must also consider the climate feedback factors of water vapor, lapse rate, albedo, clouds, etc. that amplify the (Planck) response to a change in radiative forcing RF. The change in equilibrium GMST is then given by [2,50]

$$∆T_s=\beta {\alpha }_{c}RF={\lambda }_{c}RF,$$

(5)

where β is the total (feedback) amplification factor and λ_c = βα_c is called the equilibrium climate sensitivity factor. Note that in recent IPCC AR5 [2] and AR6 [13], there are no separate α_c and β terms; λ_c is instead expressed as the reciprocal of the ‘total feedback parameter’ η, i.e., λ_c = 1/η, where η is the sum of the Planck, water vapor, lapse-rate, cloud, and surface albedo feedback parameters [52]. Nevertheless, the IPCC AR6 also states that the climate feedbacks amplify the Planck T response by about (β = ) 2.8 [1.9 to 5.9] times, which was ~3.3 [1.7–5.0] in the AR5, and that cloud feedback contributes to the largest uncertainty of the total feedback. Comparing the observed global surface T rise ΔT_s = ~0.6 K during the period 1970–2000 with the computed total RF from all WMGHGs gives rise to a λ_c = ~0.8 K/(Wm⁻²) in IPCC’s TAR [50], which is virtually identical to λ_c = 0.79 K/(Wm⁻²) (= 1/η, where η = 1.27 K⁻¹Wm⁻²) obtained from the multi-model mean of GCMs (CMIP3 or IPCC AR4’s coupled atmosphere-ocean GCMs—AOGCMs) [52].

In CO₂ climate models, however, climate sensitivity is often expressed as the so-called equilibrium climate sensitivity (ECS), which is defined as the ΔT_s (ΔT_×2) that would result from a sustained doubling of atmospheric (equivalent) CO₂. In the IPCC AR6 [13], climate models have given the best estimate of the ECS to be 3 °C, with a likely range of 2.5–4 °C. This ECS value is identical to that in the IPCC AR4 [1] and is nearly the same as in the AR5 [2]. However, it is well-known that the ECS varies largely among climate models, is sensitive to model parameters, and is not well constrained by observations [26,33,34,53]. Estimates for modern climate conditions give ECS in the wide range of 0.1−10 °C, as reviewed previously [3,23,50]. For the 12 IPCC AR4’s AOGCMs reviewed by Dufresne and Bony [52], the multi-model mean values are: the net radiative forcing ΔF is 3.71 ± 0.2 W/m² for a doubling of CO₂, λ_c is 0.79 ± 0.19 K/(Wm⁻²), and ECS is 3.1 ± 0.7 K. It is noteworthy that these values are virtually equal to those calculated simply from RF = 5.35 × ln2 = 3.71 W/m² by Equation (3) and ΔT_s = λ_cRF = 3.0 K by Equation (5) with λ_c = 0.8 K/(Wm⁻²), which are also perfectly identical to the best estimate of ECS = 3 K given in the IPCC AR4 [1] or AR6 [13].

Figure 2. Time-series (effective) radiative forcings and observed and GCM-calculated global mean surface temperature changes. (a,b): Time-series (effective) radiative forcings (RFs/ERFs) of CO₂ and halo-GHGs, relative to the pre-industrial period in 1750, with RFs calculated by Equations (2) and (3) and ERFs obtained directly from the IPCC AR5 and AR6 (computed by GCMs), as indicated. Also shown are the linear fits to the ERFs after 2005 given in the IPCC AR6, with the produced annual rising rates in ERF indicated. (c) Observed and calculated global mean surface temperature changes ΔT_s for 1850–2100, with respect to the mean temperature in 1950–1970. ΔT_s are calculated by ΔT_s = λ_c × ERF (Equation (5)) with λ_c = 0.8 K/(Wm⁻²) (blue thick line) and transient temperature change ΔT_s^t = λ_c^t × ERF (Equation (6)) with λ_c^t = 0.51 K/(Wm⁻²) (green thick line) for all anthropogenic and natural ERFs given in the IPCC AR6 for the future projection SSP245. The observed annual GMST data were obtained from the UK Met Office’s HadCRUT5 dataset [54] (black thin line) and NOAA 5.1 [55] (red thin line). Updated from Lu [3] with ERFs from the IPCC AR6 [13].

Figure 2. Time-series (effective) radiative forcings and observed and GCM-calculated global mean surface temperature changes. (a,b): Time-series (effective) radiative forcings (RFs/ERFs) of CO₂ and halo-GHGs, relative to the pre-industrial period in 1750, with RFs calculated by Equations (2) and (3) and ERFs obtained directly from the IPCC AR5 and AR6 (computed by GCMs), as indicated. Also shown are the linear fits to the ERFs after 2005 given in the IPCC AR6, with the produced annual rising rates in ERF indicated. (c) Observed and calculated global mean surface temperature changes ΔT_s for 1850–2100, with respect to the mean temperature in 1950–1970. ΔT_s are calculated by ΔT_s = λ_c × ERF (Equation (5)) with λ_c = 0.8 K/(Wm⁻²) (blue thick line) and transient temperature change ΔT_s^t = λ_c^t × ERF (Equation (6)) with λ_c^t = 0.51 K/(Wm⁻²) (green thick line) for all anthropogenic and natural ERFs given in the IPCC AR6 for the future projection SSP245. The observed annual GMST data were obtained from the UK Met Office’s HadCRUT5 dataset [54] (black thin line) and NOAA 5.1 [55] (red thin line). Updated from Lu [3] with ERFs from the IPCC AR6 [13].

As shown in Figure 2c, the calculated ΔT_s values by Equation (5) arising from the computed total forcing of all anthropogenic and natural ERFs given by the IPCC AR6 are significantly larger than the observed ΔT_s since 1970. To fit the observed GMST rise during 1970–2002, AOGCMs introduced the so-called transient T change ΔT_s^t [also called the transient climate response (TCR), instead of equilibrium T change ΔT_s], in which an additional parameter, the ocean heat uptake efficiency κ (= 0.69 K⁻¹Wm⁻²) is added to the total feedback parameter η [see, e.g., Dufresne and Bony [52]]

$$\mathsf{\Delta }{T}_s^t={\lambda }_c^t\times RF,$$

(6)

where λ_c^t = 1/(η + κ) = 0.51 K/(Wm⁻²). The thus calculated ΔT_s^t results appear to show better agreement with the observed data, as shown in Figure 2c. Note also that a lag of 10 years for surface (lower-troposphere) measured anthropogenic GHG concentrations and resultant radiative forcings is applied in calculations of or comparisons with surface T changes throughout this paper [14,56,57], including this Section, Section 5 and Section 6. This lag also slightly improves the agreement with observations in Figure 2c.

At first glance, AOGCMs appear to show excellent agreement with observations, except for cooling magnitudes due to volcanic aerosol eruptions. The GCM-simulated volcanic ERFs given in the IPCC AR6 are likely largely overestimated when compared with the observed surface temperature record. For example, the well-known Pinatubo eruption produced global cooling of 0.2–0.3 K occurring primarily in 1992 and between 40° S and 70° N, deduced from a robust multivariate analysis of the observed surface temperature record from 1889 to 2006/2008 by Lean and Rind [56,57], which is also consistent with the author’s recent analysis of the temperature record from 1850 to 2021 [14]. In contrast, the volcanic ERF given in the IPCC AR6 leads to volcanic cooling of 1.43 and 0.91 K in 1992 when λ_c = 0.8 K/(Wm⁻²) and λ_c^t = 0.51 K/(Wm⁻²) are used respectively, as shown in Figure 2c. These magnitudes of volcanic cooling are approximately 5 and 3 times larger than the observed ones. Although the volcanic ERFs, to which the response in surface T occurs relatively rapidly (within months) [56,57], have no effect on the simulated long-term trend in GMST, this discrepancy implies that the aerosol ERFs presented in the IPCC Reports, which are generated from GCM-simulations rather than directly from historical observations, are likely largely overestimated, as further discussed below.

Here we must note that the IPCC-given total radiative forcing ERF includes large contributions from the ERF (RF) of tropospheric (and stratospheric) ozone (ERF_O3) and the aerosol ERF, which are based entirely and mainly on GCM model simulations, respectively, rather than observational determinations. In the AR6 [13], the 50% uncertainty (5–95% range) in ERF_O3 remains from AR5 which is largely due to the uncertainty in pre-industrial emissions (though observational ozone data are available since the late 1950s). The AR5 [2] assessed the total ozone RF to be +0.35 [0.15 to 0.55] Wm⁻² from 1750 to 2011, which could be split either to be 0.40 [0.20 to 0.60] Wm⁻² for tropospheric ozone and −0.05 ± 0.10 Wm⁻² for stratospheric ozone or to be 0.50 [0.30 to 0.70] Wm⁻² from ozone precursors and −0.15 [−0.3 to 0.0] Wm⁻² from the effect of ODSs. The AR6 gives with high confidence an assessed ERF_O3 of 0.41 and 0.47 [0.24 to 0.70] Wm⁻² over the 1850–2010 and 1750–2019 periods, respectively. These assessments of ERF_O3 are sensitive to the assumptions on precursor emissions used to drive the models. It is summarized in the AR6 [13] (p. 838): “The CMIP6 model ensemble shows a constant global (tropospheric ozone) increase since the mid-20th century whose rate is consistent with that derived from observations since the mid-1990s”. Thus, there is potentially a larger uncertainty in ERF_O3 for periods prior to the mid-1990s given in the IPCC Reports.

It is a robust fact that the large uncertainty in aerosol ERF is the dominant contributor to the uncertainty in total ERF since 1750, given by the IPCC. The estimates of aerosol ERF are based mainly on GCM model simulations, as reviewed in the IPCC AR5 and AR6. It must also be noted that there are very large changes in the given aerosol ERF from the AR5 to AR6 (see Table 7.8 of the AR6 [13]), namely the magnitude of the aerosol ERF (“ERFari”) due to aerosol-radiation interactions is reduced by about 50% compared to AR5, while the magnitude of the aerosol ERF due to aerosol-cloud interactions (“ERFaci”) is increased by about 85% compared to AR5, based on the so-called “observation-based and modeling-based evidence”. Although the AR6 assesses that the total aerosol ERF is virtually certainly negative, large uncertainty remains, particularly regarding the adjustment contribution of aerosol-cloud interactions to ERF, as well as missing processes in current Earth system models, notably aerosol effects on mixed-phase, ice, and convective clouds. Note also that observational constraints (e.g., by the observed temperature record) on the total aerosol ERF are made often by combination with GCMs, assuming that the historical evolution of the total forcing of GHGs would be well constrained [13]. If this assumption in GCMs, particularly a dominantly large ERF from CO₂, is seriously incorrect (as unfortunately demonstrated by observational fingerprints in Section 5), then all such estimates are invalid. Even so, the estimates based on energy balance considerations or other observational constrains are strongly model-dependent and give an extremely wide range of −2.0 to 0 Wm⁻² for the total aerosol ERF (see Figure 7.5 of the AR6 [13]). Thus, it is clear that there are very large uncertainties in ERF_O3 and aerosol ERF given by GCMs and IPCC Reports.

For an analysis, we show measured aerosol loadings (sulfate and black carbon—BC) from ice-core measurements, measured ozone climatology from the WOUDC’s TOST ozonesonde datasets, and GCM-simulated ERFs in Figure 3, all of which are used or presented in the IPCC AR6 [13]. As stated in the AR6, data from ice cores allow for the estimation of multi-centennial trends of aerosol deposition in mid- and high-latitudes, as plotted in Figure 3a,b. In these regions, sulfate or BC concentrations exhibited large increases by factors of 2–8 from the end of the 19th century to the 1970s, namely reaching their peak around 1950 in the Arctic and 1970 in Europe and Russia, and have declined by about a factor of about 2 thereafter. South America has kept a small positive trend in either sulfate or BC concentration since 1750. Of particular interest are the sulfate and BC concentrations in the Antarctic, which have exhibited extremely low levels and no increases since 1750, and in the Arctic, which have returned to their pre-industrial levels since around 2000. According to the AR6, these changes in aerosol concentration are also consistent with and are likely the main contributor to observed changes in Earth’s surface energy budget characterized by surface solar radiation, which exhibits that downward and upward thermal radiation has increased since the 1970s. Satellite- and ground-based data indicate that aerosol optical depth (AOD) exhibits predominantly negative trends since 2000 over Northern Hemisphere (NH) mid-latitudes and Southern Hemisphere (SH) continents while increasing over South Asia and East Africa. These lead to a globally deceasing aerosol abundance assessed with medium confidence.

As shown in Figure 3c, the observed TOST ozone data for the period 1960s–2000s [38] are practically consistent with the conclusion in the IPCC AR6 [13] (p. 307), which states that tropospheric ozone increased by 30–70% across the NH from the mid-20th century to the mid-1990s and that since then, free tropospheric ozone has increased by 2–7% per decade in most regions of NH mid-latitudes, 2–12% per decade in the sampled regions of the NH and SH tropics, and less than 5% per decade at SH mid-latitudes. Note that the TOST datasets used in Figure 3c are also used in the AR6.

As shown in Figure 3d,e, the above-measured data of aerosol loadings and ozone are somewhat reflected in ERFs simulated by GCMs (CMIP6) and given in the AR6, though there are large uncertainties in modeled ERF magnitude, especially for periods prior to the mid-1990s. For example, Figure 3e shows that the aerosol ERF changed largely and negatively from about zero in 1850 to −1.4 Wm⁻² in ~1975, became almost constant during 1975–2010, and has become less negative thereafter. Figure 3f interestingly shows that the sum of O₃ ERF and aerosol ERF exhibits a large negative net ERF of about −1.1 Wm⁻² from 1850 to ~1970, followed by a very small change (within 0.1 Wm⁻²) between 1970 and 2010. It is noteworthy that under the robust observational constrain of a very small rise in regional or global surface temperature of about 0.2 K after removal of natural effects from 1750 (1850) to 1970, this large negative net ERF (mainly aerosol ERF) for the period 1850(1750)–1970 is absolutely required to offset the large positive modeled ERF arising from CO₂ (CH₄ and N₂O) since the Industrial Revolution, which is +1.30 to +1.45 Wm⁻² in 1970–1975, in CO₂-based GCMs.

The AR6 concludes that the total ERF due to all anthropogenic and natural climate drivers is positive and has grown in magnitude since the late 19th century and that the change rate has likely increased in the last 3 decades due to the observed increasing growth rate of CO₂ and the changing to become less negative in aerosol ERF (Figure 3e). However, it is worth noting that Figure 3f also indicates that the net of ozone and aerosol ERFs made very little contribution to the observed rapid surface warming during 1975–2005 (the late 20th century), while both climate drivers (ozone and aerosols) are well known to cause a rather quick response in surface temperature (on timescales of months only), as well observed from the Antarctic ozone hole and past volcanic eruptions.

There are other contributors to the total ERF, including stratospheric water vapor, land use, surface albedo (black plus organic carbon aerosol on snow and ice), combined contrails, and aviation-induced cirrus [13]. However, these contributors are relatively minor, far smaller than the uncertainties of ERF_O3 and the aerosol ERF. Thus, they will not be considered in this study.

Note also that it is the calculated ΔT_s by Equation (5) with λ_c = 0.8 K/(Wm⁻²), rather than the calculated ΔT_s^t by Equation (6) with λ_c^t = 0.51 K/(Wm⁻²), for a doubling of CO₂ (RF = ~3.71 W/m²), that matches perfectly the best estimate of ECS = 3 K in the IPCC AR4 [1] or AR6 [13]. The calculated ΔT_s^t (=1.89 K) for a CO₂ doubling is obviously much lower than the best-estimated ECS. One may argue that ΔT_s^t in AOGCMs is not an equilibrium T change that might take a multi-century to millennial timescale to reach. However, the natural climate drivers such as 11-year solar cyclic variability, ENSO, volcanic eruptions, as well as sudden surface temperature changes in the Antarctic due to ozone depletion since the 1960s (to be shown in Section 5), have taught that the observed surface temperature response to natural radiative forcing occurs rather rapidly (within months) [3,14,56,57,58]. Thus, it seems quite reasonable to assume that the measured GMST with a lag of 10 years from anthropogenic RF (ERF) is approximately the equilibrium T [14,56,57]. In any case, a major aspect in introducing the ocean heat uptake efficiency as an additional parameter to GCMs is apparently to better match the models to the measured GMSTs, as shown in Figure 2c. One can see from Figure 2c that Equations (5) and (6) serve well to show the prediction capability of GCMs or AOGCMs and their calculated results of long-term GMST changes.

According to the IPCC AR5 [2] and AR6 [13], there are major differences in definition between RF and ERF. In contrast to RF, ERF is defined as the change in net downward radiative flux at TOA after allowing for atmospheric Ts, water vapor, and clouds to adjust in both the stratosphere and troposphere. If the modeled results on the overlapping effect of water vapor on the climate forcings of CO₂ in the literature [17,18,19,20] are correct, which will be tested with the key observations reviewed in Section 5, it will be quite surprising to see no significant differences between RF and ERF or even a small increase rather than decrease in ERF for CO₂ (the tropospheric water vapor is increased when the surface is warmer). This may imply that there exist severe problems in the fundamental assumption of no significant overlapping (nullifying) effect of water vapor on the CO₂-produced radiative forcing in CO₂ climate models.

4. Early Calculations of Global Warming Caused by Halo-GHGs

In 1975, Ramanathan [59] made the first calculations that the greenhouse effect by CFCs and chlorocarbons could lead to a rise of ~0.9 K in global surface T if each atmospheric concentration of these compounds would increase to 2000 ppt. This projected concentration is far larger than the observed values due to the successful Montreal Protocol. Subsequently, Ramanathan and co-workers [49,60,61,62] and Wang and Molnar [63] also studied the climatic effects of CO₂ and non-CO₂ GHGs (CFCs, CH₄, N₂O, O₃, and others), showing that CFCs, through their indirect O₃-depleting effect, would have a potentially large stratospheric cooling effect, as large as that due to the CO₂ increase. Fisher et al. [64] also calculated the greenhouse effect of HCFCs. Ramanathan [65] concluded that the non-CO₂ GHGs contributed to the radiative heating of the surface-atmosphere system as much as CO₂ during the middle to late 20th century.

Interestingly, Wang et al. [66,67] showed that the spatial distribution of atmospheric opacity which absorbs and emits the long-wave radiation for halo-GHGs (CFCs) is different from that for CO₂. Their simulations indicated that halo-GHGs provide an important radiative energy source for the Earth climate system and that different infrared opacities of CO₂ and halo-GHGs can lead to different climatic effects. They concluded that it is inappropriate to use an ‘effective’ CO₂ concentration to simulate the total greenhouse effect of CO₂, CFCs, and other GHGs. Forster and Joshi [68] used various climate models to examine the role of halo-GHGs on stratospheric and tropospheric Ts. They found that halo-GHGs (mainly CFC-12) would have contributed a significant warming of ~0.4 K at the tropical tropopause since 1950, dominating the effect of other WMGHGs. They also noted that the “disappearance” of such T increases would suggest that some other mechanism(s) such as stratospheric cooling due to O₃ loss are highly likely to be compensating for this, and as O₃ will likely recover in the next few decades, a slightly faster rate of warming would be expected from the net effect of halo-GHGs.

Since the 2000s, Ramanathan and co-workers [69,70,71,72] have turned to emphasize the importance of black carbon (BC) and atmospheric brown clouds in causing regional and global warming. They estimated that when globally averaged, the current BC radiative forcing at the TOA is as much as 60% of the current RF due to the greenhouse effect of CO₂, and therefore, concluded that BC is potentially the second major contributor to the observed 20th-century global warming, just next to CO₂. Thus, halo-GHGs would become the third contributor to the warming.

Today, it is well known that CFCs are much more potent GHGs than CO₂ on a molecule-by-molecule basis, and the radiative impacts of halo-GHGs on global climate change have received gradually increased attention [62,73,74,75]. However, the contribution of halo-GHGs has only been assessed under CO₂ climate models, and the newest IPCC AR6 [13] gives that CO₂ and halo-GHGs have currently accounted for ~65% and 12%, respectively, of the GCM-computed total ERF from all WMGHGs with respect to their pre-industrial concentrations in 1750 and for ~82% and ~4%, respectively, for the ERF increase in the past decade. All these studies unavoidably concluded that CO₂, rather than halo-GHGs, would make the primary contribution to climate change, and that the total ERF (GMST) rising rate has increased in the last 30 years due to the observed increasing growth rate of CO₂ and the changing to become less negative in aerosol ERF [2,4,13] (Figure 2 and Figure 3). However, the assumed large greenhouse (forcing) effect of non-halogen WMGHGs under CO₂ climate models (GCMs) is yet to be validated by a series of critical observations below.

5. Six Key Observations

5.1. Signature of No Climate Forcing of Rising CO₂ from Measured OLR Spectra in the Late 20th Century

Changes in the Earth’s greenhouse effect can be directly detected from variations in the radiance spectrum of OLR at the TOA. If a careful analysis of available satellite data is performed properly, the OLR spectrum can be a measure of how the Earth’s radiation emits to space and carries the signature of GHGs that cause the warming effect [76]. According to the atmospheric transmittance spectrum shown in Figure 1, CO₂ climate models would expect to observe a marked negative brightness temperature difference at the wing 600–800 cm⁻¹ of the main CO₂ absorption band centered at 667 cm⁻¹ between the OLR spectra in 1970 and around 2000. Whether this fingerprint of CO₂-caused global warming is present or absent in the observed OLR difference spectrum is a critical test of CO₂ climate models, as this climate forcing of rising CO₂ concentrations lies at the heart of the debate on the cause of global warming observed in the late half of the 20th century.

Brindley and Allan [77] in 2003 reported a careful analysis of the difference spectrum between the Earth’s OLR spectra as measured by the NASA IRIS instrument onboard the Nimbus 4 spacecraft in 1970 and the IMG instrument onboard the ADEOS satellite in 1997, over the 27-year period (1970–1997) of the most rapid global warming. As shown in Figure 4a, the GCM-simulated negative brightness temperature (T_B) band in the wing 600–800 cm⁻¹ of the CO₂ absorption is absent in the observed OLR difference spectrum averaged over the tropical oceans at 30° S–30° N. In the meantime, an independent analysis of the same satellite datasets by James Anderson et al. [78] at Harvard showed similar results to those of Brindley and Allan [77], as shown in Figure 4b. In particular, Anderson et al. [78] achieved a more reliable analysis of the radiance spectra in the entire tropical belt by increasing the data sample number to 2~3 × 10⁴ spectra and applying a new method averaging the spectra, largely reducing the random and system errors. In 2007, Griggs and Harries [79] re-analyzed the radiance spectra of IRIS and IMG and obtained essentially similar results, as shown in Figure 4c. Given the overall consistent observation by the three teams [77,78,79], we can convincingly conclude that the postulated warming forcing of increased levels of CO₂ over the most rapidly warming period 1970–1997 is absent in the observed OLR difference spectrum, as we discussed in detail previously [3,6,7]. This key observation has unraveled the marked contrast to CO₂-based climate models (GCMs), but is in good accord with the modeled results on the nullifying effect of water vapor in the spectral region of the absorption of CO₂ (CH₄ and N₂O) [17,18,19,20], leading to the absence in warming effect (mainly forcing) of the non-halogen GHG, as discussed in Section 2.

5.2. Temperature Climatology in the Troposphere and Stratosphere

The author [14] has recently investigated the zonal mean latitude-altitude distribution of the T climatology in the troposphere and stratosphere for the period of 2002–2020, obtained from the high-quality ROM SAF gridded monthly mean climate data sets provided by the EUMETSAT [80]. Interesting results were found from the global T trends at altitudes of 8–40 km in the 2010s with respect to the 2000s, as re-plotted in Figure 5a. First, we showed an interesting observation that the entire warming pattern (temperature difference) in the troposphere and lower stratosphere exhibits a close resemblance to the atmospheric distribution pattern of CFCs (Figure 5b). This observation provides direct and visual evidence of the CFC-dominating mechanism of global warming.

Second, the author [14] found that a significant reversal from upper-stratospheric cooling to warming has occurred at high latitudes of both SH and NH and has been more significant at NH than SH high latitudes over the past decade, as seen from the temperature difference between the 2010s and 2000s shown in Figure 5c; the upper-stratospheric T increase is as large as 2.8 K in the springtime Arctic, as shown previously [14]. This finding is particularly important since upper-stratospheric cooling is a direct fingerprint of the greenhouse effect of increasing GHGs and associated surface warming [41,42], as illustrated by the 2021 Nobel Prize Committee in Physics and here also shown in Figure 5d. The observed upper-stratospheric warming gives direct evidence that the greenhouse effect of GHGs is decreasing. Obviously and strongly this observation contradicts the prediction of upper-stratospheric cooling by CO₂ climate models, provided with well-measured increasing annual growth rates of atmospheric CO₂ in the past two decades [13]. Opposite to this prediction, the observed upper-stratospheric warming is in excellent agreement with the CFC warming model [3,5,6,7,14]. According to the latter physical model of global warming and the CRE mechanism of stratospheric ozone depletion [3,5,7,15,16], upper-stratospheric cooling (surface warming) should have been reversed first at high latitudes with decreased levels of atmospheric halogen-containing ODSs (mainly CFCs) because ODSs are more effectively destroyed by the stronger CRE reaction at higher latitudes due to stronger CR radiation (see also satellite data in Figure 5b). Note also that this upper-stratospheric warming is counteracted by the emerging recovery of lower-stratospheric O₃ depletion at high latitudes, as ozone itself is an effective GHG. Such an effect from O₃ recovery should be much smaller at NH than SH high latitudes because O₃ loss over the Arctic has been far less than over the Antarctic since the 1970s. Another effect is related to the change in tropospheric ozone. As shown in Figure 3c, there was a significant increase in tropospheric ozone at NH mid- and high-latitudes in the late half of the 20th century, while the tropospheric ozone in the Antarctic exhibited little change or a small decrease. With regulations and controls of air quality, it is expected to see a significant decrease in tropospheric ozone at NH mid- and high-latitudes from now to coming decades. All these effects will lead to more significant upper-stratospheric warming at NH than at SH high latitudes. These major features of the CFC warming model are exactly observed, as seen in Figure 5a–c.

Third, from Figure 5a, the author [14] also observed a reversal from lower-stratospheric cooling to warming in the tropics and mid-latitudes over the past decade. This is consistent with an earlier observation reported by an international team of Philipona et al. [43] in 2018, showing that after decades of cooling, the lower stratosphere has now been warming since the turn of the century. However, both the team and the present author consistently found that this reversal has not yet occurred over the polar regions. For the latter, lower-stratospheric cooling continues slightly over the Antarctic and is significantly enhanced over the Arctic. These results are also consistent with the observed map of GLST from MSU/AMSU satellite data, as shown in Figure S1 in SI, and are well explained by the measured trends of halo-GHGs (mainly CFCs) coupled with the Arctic amplification (AA) mechanism of surface warming due to sea-ice melting in the polar regions, especially at some Arctic and Antarctic coastal areas [14]. The mechanisms of AA are still under investigation [13], but there is a compelling mechanism of AA proposed by Dai et al. [81]. According to the latter, AA is closely related to the surface albedo feedback associated with sea-ice loss, leading to increased OLR and heat fluxes from newly opened waters; AA occurs primarily in the cold seasons (from October to April) due to the extra OLR radiation and sensible and latent heat release from the newly opened waters and only over areas with significant continued sea-ice loss. By showing the maps of global and NH land surface air T differences, the author [14] has shown that the observed trends in GLST and spatially-resolved global surface T are indeed caused by halo-GHGs and the AA mechanism. Particularly, the continued regional warmings at some coasts of the Arctic (particularly Russia and Alaska) are only observed in the cold seasons, as shown in Figure S2 in SI. These results are characteristic of the sea-ice-loss-caused AA mechanism and are drastically different from the expectation from CO₂-warming climate models.

5.3. Correlation of Global Mean Surface Temperature with CFCs but Not CO₂

Correlation as a statistical method is widely used as the basis for hypothesis tests for causality in research, though ‘correlation does not imply causation’. This author made the first analysis of the correlation between measured GMST and atmospheric CO₂ concentration for the period 1850–1930 [6]. Of particular interest is that in this pre-CFC period, the anthropogenic CO₂ level in the Earth’s atmosphere had increasingly enlarged due to the Industrial Revolution, while there was almost no use of halo-GHGs (CFCs) in industry before 1930 [82], and the atmospheric concentrations of CFCs became significant since the late 1960s (1970). Here measured time series surface temperature of the Antarctic and atmospheric concentration of CO₂ for the 100-year period from 1850 to 1950 and their correlation analysis are shown in Figure 6a,b, respectively. Figure 6a clearly shows that despite the continued increase in atmospheric CO₂ in the pre-CFC era, the Antarctic temperature exhibited nearly constant or even a slightly declining trend over the 100 years. When the temperature was plotted versus CO₂ concentration, a negative correlation coefficient (R = −0.60) was found (Figure 6b). In other words, the Antarctic temperature had a negative correlation with CO₂ from 285 ppm to 313 ppm over this pre-CFC era of 100 years from 1850 to 1950.

This author [3,6,7] also made an analysis of the observed data of GMST, CO₂, and halo-GHGs from 1970 to 2012 (the post-CFC era). The analysis was built on the fact that the data from direct measurements of CFCs have become available since the 1970s when observable atmospheric impact (particularly stratospheric O₃ depletion) of CFCs began. Thus, the significant anthropogenic greenhouse effect of CFCs on Earth’s climate is also reasonably expected to start around 1970. Here the results are updated and re-plotted in Figure 6c,d, which shows time-series measured data of GMST and the total concentration of all halo-GHGs over the past 52 years from 1970 to 2022 and their correlation analysis. Moreover, using the empirical model developed by Lean and Rind [56,57], we also removed the natural effects of ENSO and volcanic eruptions from observed GMST data with details given previously [14]. Here both original and thus processed GMST data are co-plotted in Figure 6c,d. Interestingly, in contrast to CO₂ which has kept rising with increasing annual growth rates [13], the total concentration of halo-GHGs has reached a plateau since the turn of the century. Correspondingly, it is clearly seen in Figure 6c that GMST had a linear rise from 1975 to ~2002 and its rising rate has largely declined since around 2002.

The results of correlation analyses in Figure 6b,d are particularly interesting. In striking contrast to Figure 6b for the pre-CFC era, Figure 6d shows that GMST has had a nearly perfectly linear dependence on the total amount of atmospheric halo-GHGs from 1970 to the present. Statistically, the linear fit to observed data of GMST and halo-GHG total concentration gives a statistical linear correlation coefficient R as high as 0.97 (close to unit) and p < 0.0001 for R = 0. This R-value is very close to R = 0.98 obtained in our previous analyses with measured data up to 2009 or 2013 [3,6,7]. Overall, the results in Figure 6a–d exhibit a nearly perfect correlation of GMST with halo-GHGs but not CO₂.

The results in Figure 6b,d deserve a more in-depth and quantitative analysis for causality [3,7]. Time-series calculated RFs or ERFs of atmospheric CO₂ and halo-GHGs are already shown in Figure 2a,b. RFs were calculated by Equations (2) and (3) with the gas abundances obtained from the IPCC AR5 [2] or AR6 [13], whereas the data of ERFs computed by GCMs were obtained directly from the IPCC AR5 and AR6 [2,13], as indicated in Figure 2a,b. Interestingly, the author [3,6,7] showed that an equal radiative forcing RF ≈ 0.72 W/m² was produced from the CO₂ concentration rises of 285 to 326 ppm in 1850–1970 and of 326 to 373 ppm in 1970–2002 (Figure 2a). As shown in Figure 2c, this radiative forcing would cause a GMST rise of about 0.6 °C, provided with λ_c = 0.8 K/(Wm⁻²) that is equivalent to the best-estimated ECS (3 K) in the IPCC AR4 [1] and AR6 [13]. This modeled result contradicts the observed GMST rise of about 0.25 °C only during 1850 (1750)–1970, of which a rise of about 0.05 °C was due to the increase in total solar irradiance (TSI), as shown in Figure S3 in SI, and the sharp rise of ~0.6 °C during 1970–2002, not to mention the observed slowing down or pausing in global warming with increasing CO₂ concentrations ≥373 ppm since ~2002. It must also be noted that when the modeled radiative forcings of CH₄ and N₂O are added to that of CO₂ under CO₂ climate models, an even larger discrepancy between the observed (0.2 °C) and the calculated GMST rise (0.93 °C) in 1850–1970 is seen (Figure 2c) [3]. In CO₂-based GCMs, this discrepancy is mainly attributed to the balance of the large positive modeled ERF arising from CO₂ (CH₄ and N₂O) by the large negative net ERF of ozone and aerosol ERFs for the period 1850–1970, as discussed in Section 3.

5.4. Observation of Global Warming Cessation at North America and NH Extratropics

All the observations in Figure 4, Figure 5 and Figure 6 point to the likely mechanism that human-made halo-GHGs have played a dominant role in global warming that occurred mainly in the late 20th century. If this is true, then the cessation or reversal of global warming should occur first at high-latitude regions if there were not the ice-loss-caused AA effect [3,7,14,15], as mentioned above. To test this hypothesis, time-series land surface air T at NH extratropics (latitudes 30–90° N) excluding Russia and Alaska since 1950 is shown in Figure 7a, in which the natural ENSO and volcanic effects are eliminated [14]. The results indeed show that the surface T has reached a plateau since around 2005. This is qualitatively consistent with the total RF or ERF trend of halo-GHGs [3,13] and is in sharp contrast to the rising trend for the computed ERFs of CO₂ given in CO₂ climate models [13], as displayed in Figure 2a,b. This slowing down or ceasing of surface warming has been further validated by the following observations: (i) The surface T changes in North America (Canada, contiguous USA, and Greenland) show a similar warming-ceasing behavior (Figure 7b). (ii) Consistently, time-series annual mean snow cover extent (SCE) data over NH and North America since 1967 [83,84] show that SCEs have clearly stabilized since ~1995 (Figure 7c,d), in excellent agreement with the observed trend in GLST [4,13,14]. (iii) A quite similar result with no T increase since 2000 has also been found from the central England temperature (HadCET) dataset for the period of 1659–2021 [14] (to be shown in Section 5.6). (iv) The Antarctic surface temperature has not increased significantly since 1980 (Section 5.6). (v) Surface T changes in NH high-latitude countries or regions including North Europe (Sweden, Norway, Finland, UK, Ireland and Iceland) and North Asia, including 11 countries plus 12 north and west provinces of China, show similar warming slowing down or stopping phenomena [14].

Furthermore, the results of statistical analyses by linear fits to the observed data after 2005 are also shown in Figure 7, in which the slope (changed amount per year) and the R² value for each fit are given. The fitted results show that the surface T at NH extratropics is nearly flat with ΔT = 5.1 ± 2.2 mK/year and R² = 0.03 (Figure 7a). Remarkably, the fit to the data of ERFs arising from atmospheric halo-GHGs gives a slope Δ(ERF) = 1.82 ± 0.02 mWm⁻²/year and R² = 0.998 (≈1.0), as indicated in Figure 2b. With the given equilibrium climate sensitivity factor λ_c^halo = 1.77 K/(Wm⁻²) specific for halo-GHGs obtained from the CFC-warming physical model [3] (to be detailed in Section 6), we can straightforwardly find the corresponding T-rising rate to be 3.2 ± 0.0 mK/year for the period 2005–2020, which is in good agreement with the observed rate 5.1 ± 2.2 mK/year (Figure 7a) [14]. In contrast, the fit to the modeled ERFs for CO₂ given in the IPCC AR6 [13] leads to a slope Δ(ERF) = 28.86 ± 0.22 mWm⁻²/year, as indicated in Figure 2a. As mentioned above, CO₂ climate models have given the best estimate of ECS = 3 °C in the IPCC’s AR6 [13]. Thus, the obtained slope for CO₂ ERFs in Figure 2a is equivalent to the best-estimated T-rising rate of 23.1 ± 0.3 mK/year, which is more than 4 times larger than the observed rate of 5.1 ± 2.2 mK/year in Figure 7a [14]. This discrepancy is much larger if the latitude effect of ECS, which is larger at a higher latitude (i.e., the AA effect), is taken into account.

Moreover, it is noteworthy that the fitted results in Figure 7b–d also show that, corresponding to the declining trend in North America’s surface T with ΔT = −8.1 ± 8.2 mK/year (Figure 7b), both North America and NH snow cover extents (SCEs) have exhibited similarly positive (increasing) trends with Δ(SCE) = 1.67 ± 0.74 × 10⁴ km²/year and 1.65 ± 2.06 × 10⁴ km²/year, respectively (Figure 7c,d). Similar fitted results are also obtained for the HadCET with ΔT = 4.1 ± 16.4 mK/year and the Antarctic surface T with ΔT = 1.1 ± 2.5 mK/year (see Section 5.6). Note that all fits to the observed surface T or SCE data after 2005 give an almost zero R² value (≤0.03), indicating no significant change trend in each of these measured variables since 2005, except for the Antarctic surface T that shows a declining trend since 2005 (see Section 5.6). All the above results confirm the important facts that a reversal in global warming would have emerged around 2005 if there were no ice-loss-caused warming AA at some polar regions and NH high-latitudes and that the change trends in surface T and SCE are consistent with the dominance by the change in total radiative forcing of halo-GHGs rather than CO₂.

5.5. No Effects of Non-Halogen GHGs on Stratospheric Ozone Depletion and Lower Stratospheric Temperature (LST)

First, this author [3,7,15] demonstrated that the 11-year cyclic variations in ozone loss and LST in the springtime Antarctic ozone hole are well reproduced by the CRE equation with the level of halogenated ODSs (mainly CFCs) and the CR intensity in the stratosphere as the only two variables. Second, this author [14,38] strikingly found that the decadal mean zonal mean latitude-altitude distribution of the T climatology for the 2000s or 2010s unravels clearly the three ‘temperature holes’, corresponding to the ozone holes over the Antarctic, tropics, and Arctic, respectively, as shown in Figure 8a. Like in the springtime Antarctic O₃ hole, the LST variation in the ‘temperature hole’ corresponding to the all-season tropical ozone hole is also well reproduced by the CRE equation [38]. This is also true for the GLST [14], as shown in Figure 8b. The latter shows that the GLST from multiple ground- and satellite-measured datasets [80,85,86,87] consistently exhibited a clear drop between the 1970s and 1995 and has become stabilized since ~1995, with no significant change over the past 28 years. This is consistent with the previous observations [2,15,38,88] and those in the 2018 WMO Report [4] and the IPCC AR6 [13]. As also shown in Figure 8b, the calculated results of the GLST by the CRE model agree with the observed data well [14]. These results clearly demonstrate that the GLST has well been controlled only by the level of halogenated ODSs and the CR intensity and that lower-stratospheric cooling has ceased since the mid-1990s, corresponding well to the measured trend in ODSs [3,4,5,7,15,38].

Furthermore, this author [16] has recently formulated the CRE as a universal mechanism to provide a completely quantitative understanding of global ozone depletion and derived an analytical equation with the stratospheric concentrations of ODSs and the CR intensity as only two variables to give atmospheric chlorine atom concentration. Using the equation with concentrations of ODSs as the sole variable, the author’s calculated results of time-series ozone depletion rates in global regions in the 1960s, 1980s, and 2000s show excellent agreement with observations [16].

All the above-reviewed key results strongly indicate no greenhouse effect of increasing non-halogen GHGs on stratospheric ozone depletion and associated stratospheric cooling in the past five decades [3,5,7,14,16,38]. The observed data have solidly shown that the changes in both ozone loss and LST are governed completely by the CRE equation that has the stratospheric levels of ODSs and CRs as the only two variables [3,5,7,14,16,38]. This is in striking contrast to the simulated results of CO₂ climate models, which predicted that the greenhouse effect of increasing non-halogen GHGs (CO₂, CH₄, and N₂O) would largely enhance stratospheric ozone loss and associated stratospheric cooling [61,62,89,90]. Based on those model predictions, the excellent agreement between observed data and the CRE equation with no input of non-halogen GHGs has in turn provided proof of almost no greenhouse effects from increasing non-halogen GHGs on global stratospheric climate.

5.6. Surface Temperature Changes in Three Representative Regions

Studying regional climate changes may be of particular significance in resolving the underlying mechanisms for global climate change. Here we start by reviewing the changes in surface temperature in three representative regions. The UK probably gained a bad reputation for air pollution, especially due to its pioneering position in the Industrial Revolution and the Great Smog of 1952 in London. By the 1600s, smoke pollution had shown considerable environmental effects in the UK. Through the 1800s, coal-burning for the Industrial Revolution particularly made the UK the world’s leading source of carbon-based air pollution (surpassed by the US in 1888 and Germany in 1913) and caused serious environmental and health effects. Although governmental efforts have made a substantial improvement to urban air quality after the Great London Smog, air pollution remains a major environmental issue in the UK. On the other hand, the UK Met Office’s Hadley Centre Central England Temperature (HadCET) dataset has provided a remarkable record of daily and monthly temperatures in central England representative of a roughly triangular area of the United Kingdom enclosed by Lancashire, London, and Bristol since 1659, which is the longest available instrumental record of temperature in the world [91]. Thus, the HadCET dataset may provide very precious information on the effect of anthropogenic climate drivers on surface temperature.

The other regions on Earth of a particular value are the polar regions, the Arctic (60–90° N) and the Antarctic (60–90° S), which are most sensitive to climate change. Unlike the Arctic which consists mainly of the Arctic Ocean, much of the Antarctic is encompassed by the Antarctic continent and surrounding ice cover. This region is also much more isolated from the influence of populated continental areas of the SH and therefore essentially pollution-free (and hence no associated enhancement in tropospheric ozone production and no aerosol forcing issue mentioned in Section 3) (see Figure 3a–c). The T change over the entire continent in Antarctica is inhomogeneous: west Antarctica is warming, while the inland regions are cooling. Additionally, changes in surface and stratospheric Ts may alter wind patterns, likely due to the Antarctic ozone hole since the late 1970s. Despite these complications, the whole Antarctic region can provide an ideal complementary testing region to the populated and once highly polluted central England. If the latter is considered as a positive control in testing the effect of air pollution (aerosols) on climate change, then the Antarctic is an ideal negative control. Moreover, in contrast to the Arctic which has exhibited significant decreases in sea ice area/extent (SIA/SIE) since the late 1970s, the overall SIE/SIA in the Antarctic was pretty stable or even showed a small increase in the late half of the 20th century up to 2016 and since then it is decreasing [13,14]. This also led to the associated absence of the so-called ‘Arctic Amplification’ (AA) phenomenon on surface warming in the Antarctic in the pre-2016 period. In contrast, such an AA mechanism has been a main contributor to the well-observed largely amplified warming over the Arctic region in the past 3–4 decades. As a result, climate change in the Antarctic should be predominantly due to the greenhouse effect of anthropogenic WMGHGs and ozone depletion in the lower stratosphere and upper troposphere. In addition, surface and atmospheric levels of ozone and temperature have been well recorded and intensely studied from ground-based measurements at multiple Antarctic stations (Halley, starting in the late 1950s; Syowa, starting in the mid-1960s; and South Pole, beginning in 1975) and satellite measurements since 1979. In contrast to other parts of the Earth, the surface ozone in the Antarctic exhibited a gradual decline from the beginning of the records into the mid-1990s and a gradual recovery thereafter [92]. Tropospheric and stratospheric ozone and the total ozone from ozonesonde and satellite measurements over the Antarctic follow this same pattern [13,15,92]. Moreover, the dataset of atmospheric CO₂ generated by analyzing the air enclosed in ice cores at Law Dome, Antarctica provided a unique record of global atmospheric CO₂ mixing ratios from 1006 A.D. to 1978 A.D. [93], prior to the more reproducibly accurate measurements from flask sample measurements at Mauna Loa, Hawaii, USA starting in 1958. In fact, there has been no significant difference between CO₂ measurements at the two very distant locations since 1958, as shown in Figure S4 in SI. Thus, the whole Antarctic provides an ideal, well-controlled laboratory to unravel the main underlying mechanism for global climate change if the data are analyzed and understood properly.

Although the Arctic had serious air pollution in most time of the 20th century with the observed aerosol loading peaking in 1950, the observed data in Figure 3a,b indicates that the aerosol level has returned to the pre-industrial level since around 2000. Moreover, spatially resolved observed data of remote-sensing (fine-mode) aerosol optical depth (AOD or AODf) also exhibit non-significant trends in most areas of the Arctic, similar to the Antarctic, in the period 2000–2019, as reviewed in the IPCC AR6 [13]. Therefore, aerosols should have no or little contribution to the total RF/ERF in the Arctic in the 21st century. In contrast, it has been widely reported that the strongest AA effect is still ongoing over the Arctic region [13,14], as shown in Figure S2 in SI and discussed in Section 5.2 and will further be shown and discussed later.

Based on the above-described observations, central England in the UK, the Arctic, and the Antarctic are selected as three representative regions for our ‘controlled experiment’ studying current climate change. The three regions respectively represent a typical non-polar and polluted region that has substantial contributors of GHGs, ozone, and aerosols but no significant sea-ice melting and particularly was the birthplace of the Industrial Revolution (England), a special polar region with contributors of GHGs, ozone, and severe sea-ice melting but virtually no longer aerosol climate forcing since 2000 (the Arctic), and a unique polar region with contributors of GHGs and severe ozone variations caused by ODSs but no historical anthropogenic air pollution (the Antarctic). With some similarities to the polar regions, England is also surrounded by oceans. Here the surface temperature changes in central England since 1659 (HadCET) [91], the Arctic and the Antarctic since 1850 (the newest NOAA 5.1 datasets [55]) are plotted in Figure 9a–c, together with our theoretical estimates of the main individual contributors to the observed sudden surface T rise in the Antarctic during 1960–1980. Particularly the latter will be analyzed in detail in Section 6, which plays an important role in validating the CFC-warming physical model and the equilibrium climate sensitivity factor λ_c determined from an observational approach [3].

As we observed recently [14] and it is shown in Figure 9a, there was almost no or very small change in CET over the about 300 years from the 1660s to 1970, and then a sudden rise in the period 1970–2000. Since around 2000, the CET has mostly stabilized with a very small rising rate of 4.1 ± 16.4 mK/year (with no significant trend) over the past two decades. In sharp contrast, Figure 9b shows that the Arctic has kept a steep rising in surface T at 78.0 ± 12.6 mK/year since the 1990s. As shown in Figure 9c, strikingly the surface T change in the Antarctic is similar to the CET but drastically different from that in the Arctic, namely, it remained constant from 1850 to ~1885, followed by a small decrease from 1885 to 1960, had a sharp rise by about 0.27 °C in 1960–1980, and has become stabilized with almost no trend (1.1 ± 2.5 mK/year) for 1980–2022. Most remarkably, the Antarctic surface T exhibits a significantly declining (cooling) trend at −10.2 ± 8.7 mK/year for the period 2005–2022, in good agreement with the observed upper-stratospheric warming shown in Figure 5c. Although this trend might be affected by the observed start of sea ice melting over the Antarctic since 2016 [13,14], it is of particular interest to observe it continuously for the coming decades to see whether the Antarctic surface T will return to the T in the 1960s with the expected decline in total ERF of halo-GHGs.

Given the above-mentioned observations on various climate drivers (GHGs, ozone, aerosol, sea-ice melting, and the associated AA) in the 3 representative regions, the robust combined observation of the surface T changes in Figure 9a–c is in striking contrast to the main conclusion of the IPCC AR6 mentioned in Section 3. However, this observation is actually consistent with the acknowledgment in the IPCC AR6 [13] (p. 987), which states that “Southern Ocean sea surface temperatures (SSTs) have been slow to warm over the instrumental period, with cooling since about 1980 …. This stands in contrast to the equilibrium warming pattern either inferred from the proxy record or simulated by Earth system models (ESMs) under CO₂ forcing”. It seems clear that in contrast to the main conclusion of the IPCC AR6, surface temperature change is not driven primarily by the observed increasing growth rate of CO₂ and the change in aerosol ERF but by the greenhouse effect of halo-GHGs (mainly) and the climate forcing of ozone variations (minorly), leading to the stabilization in surface T since 1980 in the Antarctic and since 2000 in Central England and even the declining trend in the Antarctic surface T since 2005. It is also clear that the continued sharp rise in surface T in the Arctic region is dominantly due to the AA effect, where there has been no incremental aerosol RF and ERF_O3 since 2000 (Figure 3a,b). These conclusions drawn from the observations in Figure 9 are consistent with the observations shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8.

6. Refined Physical Model of Global Climate Change and Parameter-Free Theoretical Calculations of GMST Changes through the CFC-Warming Model

Let us briefly revisit the fundamental concept of radiative forcing. A small concentration increment of a GHG initially increases the absorption of OLR in the atmosphere in the wavelength range of the GHG IR absorption, which leads to an initial decrease in OLR at the TOA. To compensate for this decrease in OLR at the TOA, the Earth’s surface must raise its T to make an increase (dF_g) in upward long-wave radiation energy flux F_g. That is, the increase in F_g from the warming must balance the reduction in OLR at TOA due to the increased absorption of the GHG. Finally, a new equilibrium is restored at TOA. This is the well-known basic mechanism underlying global warming. According to this classical mechanism and the quantum physics of the Earth’s blackbody radiation (Equation (1) and Figure 1), the radiative forcing due to a GHG rise can be written as

$$dF=d\left[{\int }_0^{\infty }[1-\mathsf{\Gamma }\left(\lambda \right)]B_{\lambda }\left(T_s\right)d\lambda \right],$$

(7)

where B_λ(T_s) is given by Planck’s formula (Equation (1)), and Γ(λ) is the wavelength-dependent transmittance of the atmosphere (Figure 1). As discussed in Section 2, a change in absorption in the atmospheric window sensitively influences the radiative process of the Earth. Since most of the Earth’s thermal radiation is emitted into space through the atmospheric window, Equation (7) can approximately be rewritten as

$$dF\approx \left(1-{\mathsf{\Gamma }}_{wd}\right)d{F}_g=\left(1-{\mathsf{\Gamma }}_{wd}\right)4\sigma T_s^{3}d{T}_s,$$

(8)

where Γ_wd is the (mean) transmittance in the atmospheric window at 8–13 µm, and σ is the Stefan-Boltzmann constant. Note that Γ_wd is significantly different from the average transmittance Γ over the entire blackbody radiation spectrum. Hence, the climate sensitivity factor α is now given by

$$\alpha \equiv \frac{d{T}_s}{dF}=\frac{1}{4\left(1-{\mathsf{\Gamma }}_{wd}\right)\sigma T_s^3}.$$

(9)

Here Γ_wd can be determined from the OLR spectrum at the TOA measured by a satellite. Various infrared opacities of GHGs in the atmosphere can lead to different climatic effects. Below we will discuss the greenhouse effects of anthropogenic GHGs in the two major categories: non-halogen GHGs and halo-GHGs.

Non-halogen GHGs (CO₂, CH₄ and N₂O). In view of the key observations revealing no warming effects (forcings) of these non-halogen GHGs (Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9), we may as well let the RF due to an increase in CO₂ (CH₄ or N₂O) since 1970 be zero (RF = 0). Alternatively, one might attribute the nullifying effect of water vapor on the IR absorptions of these non-halogen GHGs to the feedback amplification factor and let the latter be zero (β = 0). In either case, this leads to virtually no change (ΔT_s = 0) in GMST caused by a concentration rise of non-halogen GHGs (CO₂, CH₄, and N₂O) since 1970. This conclusion can also be deduced either from the modeled results of the nullifying (overlapping) effect of water vapor on the climate forcings of CO₂ or from the observational determinations of the ECS, both of which gave the ECS = 0.25–0.5 K [17,18,19,20,21,22,23,26]. Given the radiative forcing RF = 3.7 W/m² for a doubling of CO₂ by Equation (3) or given in the IPCC AR5/AR6, then the forcing RF = 0.7 W/m² arising from the CO₂ increase in the rapidly warming period 1970–2002 should lead to an increase of 0.05–0.1 K only in GMST. Note that if one argues for any delay in surface T response to CO₂ RF due to ocean heat uptake, then this temperature increase would even become smaller because the CO₂ rising rate has been increasing since 1750. This small surface T change is within the general uncertainty of measurements for GMST and is therefore negligible (ΔT_s ≈ 0).

Halo-GHGs such as CFCs and HCFCs. From the satellite-measured atmospheric transmittance Γ(λ) spectrum shown in Figure 1, we can directly obtain the mean transmittance Γ_wd = 0.84 in the window of 8–13 µm. Substituting this measured Γ_wd and T_s = 288 K into Equation (9), we obtain a climate sensitivity factor for halo-GHGs [3]

$${\alpha }^{halo}=1.16 \mathrm{K}/\left(\mathrm{W}{\mathrm{m}}^{-2}\right).$$

(10)

The total amplification factor β is well-known to have the largest uncertainty due to the feedback effects of water vapor and clouds in GCMs [2,13,47]. To determine the value of β more reliably, in contrast, we took an observational approach by a careful analysis of well-observed GMST variations arising from solar irradiance variability during 11-year solar cycles [3]. First, a solar radiative forcing ΔF₀ arising from a change in the incoming solar energy flux F₀ at the TOA in solar cycles can reliably be calculated from the measured change in solar constant (F_S) (also called total solar irradiance, TSI) by

$$∆F_0=\left(1-A\right)∆F_s/4,$$

(11)

where A is the albedo of the Earth-atmosphere system (A ≈ 0.3). Second, the direct (Planck) response in surface T to the solar radiative forcing is simply given by

$$\frac{∆T_S}{T_{\mathrm{s}}}=\frac{∆F_S}{4F_S}.$$

(12)

From Equations (11) and (12), we can write the solar climate sensitivity factor (α^S)

$${\alpha }^S\equiv \frac{d{T}_S}{d{F}_0}=\frac{T_S}{\left(1-A\right)F_S}.$$

(13)

With the observed values of T_S = ~288 K, ΔF_S/F_S = ~0.1% from solar minimum to solar maximum in solar cycles, and F_S = ~1361 Wm⁻², we obtain ΔT_S =~0.072 K and α_c = 0.30 K/(Wm⁻²). Since the variation of GMST in solar cycles is well observed to about 0.11 K with a rapid response time of only one month to solar forcing [56,94], we directly obtain the total feedback amplification factor β = 1.53 [3].

The thus determined solar equilibrium climate sensitivity factor is [3]

$${\lambda }_c^s\equiv {\alpha }^s\beta =0.46 \mathrm{K}/\left(\mathrm{W}{\mathrm{m}}^{-2}\right),$$

(14)

which is slightly smaller than λ_c^s = 0.63 K/(Wm⁻²) obtained by Douglass and Clader [58] with a similar approach. But they used a slightly larger temperature modulation of 0.15 K instead of 0.11 K during solar cycles. Thus, our λ_c^s value should be more realistic.

With α^halo = 1.16 K/(Wm⁻²) and β = 1.53, we explicitly obtained the equilibrium climate sensitivity factor for halo-GHGs [3]

$${\lambda }_c^{halo}\equiv {\alpha }^{halo}\beta =1.77 \mathrm{K}/\left(\mathrm{W}{\mathrm{m}}^{-2}\right).$$

(15)

Combining the greenhouse effect of halo-GHGs with the solar radiative effect, we obtained the change (ΔT_s) in GMST as a result of a rise in halo-GHG concentration and a change in solar radiative output [3]

$$∆T_s={\lambda }_c^{halo}\times R{F}^{halo}+{\lambda }_c^s\times R{F}^{solar},$$

(16)

where the RF^halo of halo-GHGs can be calculated by Equation (2), and RF^solar is calculated from the measured solar constant (F_S or TSI) by Equation (11) for historical data and a simplification λ_c^s × RF^solar ≈ 0.055 × cos [2π (i-2014)/11] (°C) is used for future projections, based on the observed temperature modulation during solar cycles [56,94] (for details, see ref. [3]).

Thus, our conceptual physical model of climate change, built on the key observations reviewed in Section 5, includes no tunable parameter. It needs only inputs of atmospheric concentrations of halo-GHGs, which are available from the IPCC AR5 [2] or AR6 [13]. Using this simplified physical climate model (Equation (16)), the author [3,14] has calculated GMSTs from 1950 to 2070 and compared them with the observed data with and without the the removal of natural ENSO and volcanic effects since 1950. As shown in Figure 10, the calculated results of GMST exhibit surprisingly good agreement with the observed GMST data since the 1950s [14]. Remarkably, the calculated results also match nearly perfectly with the observed GMST data since 2015 if the regions in Russia and Alaska are excluded [14]. These results strongly indicate that the change in GMST since 1950 has been dominantly caused by the greenhouse effect of halo-GHGs (mainly CFCs).

For comparison, the calculated ΔT_s^t results induced by all natural and anthropogenic ERFs using the GCM-computed ERFs given in the IPCC AR6 and Equation (6) with the λ_c^t value given in AOGCMs [1,2,50] are also shown in Figure 10. It is clearly shown that the fundamental assumption on the climate forcing of increasing non-halogen GHGs inevitably leads to a continued warming trend over the past two decades and in the rest of this century, which is inconsistent with the crucial observations reviewed in Section 5.

Now we utilize our CFC-warming physical model to analyze the surface temperature change in the Antarctic shown in Figure 9c, which is caused primarily by the greenhouse effect of halo-GHGs and ozone depletion caused by ODSs. Note that like halo-GHGs, the IR absorption of ozone at 9.6 μm lies in the atmospheric window (Figure 1). Thus, λ_c^halo is also valid for quantifying the greenhouse effect of O₃. First, the ERF arising from the increase in total halo-GHG concentration is 0.177 Wm⁻² from 1960 to 1980 and 0.171 Wm⁻² from 1980 to 2000. Since the observed Antarctic surface T is nearly constant in 1980–2000 (Figure 9c), the latter ERF value must be balanced by the negative ERF caused by ozone depletion in the Antarctic troposphere and stratosphere. As a result, we deduce that ERF_O3 = −0.171 W/m² for the period 1980–2000. The measured decrease in total ozone in the period 1960–1980 is about 30% of the decrease in 1980–2000, as shown in Figure S5 in SI. Thus, the ERF_O3 = γ × (−0.171) × 30% = −0.051γ (Wm⁻²) for the period 1960–1980, where γ = 0−1 taking into account the non-linearity of the radiative efficiency of ozone [95] (γ = 0 represents a complete saturation for the undisturbed O₃ concentration with no significant ODSs in the atmosphere, and γ = 1 means no saturation, i.e., a linear dependence of ERF_O3 on ozone concentration). Since the warming ΔT_S = 0.27 K is observed during 1960–1980, we obtain λ_c = 0.27/(ERF_halo + ERF_O3) = 0.27/(0.177−0.051γ) (K/Wm⁻²). Thus, we obtain λ_c(min) = 1.52 K/(Wm⁻²) for γ = 0 (very unlikely, as seen from Figure 1), and λ_c(max) = 2.14 K/(Wm⁻²) for γ = 1. The realistic γ value is known to be 0 < γ < 1 [95]. It turns out that λ_c^halo = 1.77 K/(Wm⁻²) in Equation (15), which was obtained previously by our observational determination from 11-year solar variability [3], perfectly centers at this λ_c range estimated from the observed surface T change in the Antarctic. The individual contributions of halo-GHGs and ozone depletion and the net change to the Antarctic surface T in 1960–1980, as calculated by our CFC-warming model, are shown in Figure 9d, exhibiting perfect agreement with the observation. This agreement additionally gives strong evidence of our CFC warming model and validates the value of λ_c^halo determined from our observational approach [3].

The good agreements between the observed and calculated results in Figure 9d and Figure 10 are the most compelling message delivered by the CFC-warming model. However, we have to discuss the uncertainty in our calculations of the change in GMST since 1950 (1970), arising potentially from the inclusion of only the greenhouse effect of halo-GHGs and the solar forcing in Equation (16). We have not included the RFs (ERFs) of ozone, aerosols, and other relatively minor climate drivers in our calculations of the GMST change in the late half of the 20th century, especially since 1970, for the following reasons. First, there have been much more abundant observation data available after 1970, which could potentially better constrain the modeled results of RFs (ERFs) than in pre-1970 periods. Second, the net ERF of O₃ and aerosol ERFs exhibits a very small change (within 0.1 Wm⁻²) between 1970 and 2000s (Figure 3f), while our main goal is to unravel the primary underlying mechanism for the rapid warming that occurred from around 1975 to 2000. For comparison, we note again that an ERF as large as 1.30–1.45 Wm⁻² from non-halogen WMGHGs alone or a large negative net of about −1.1 Wm⁻² of O₃ and aerosol ERFs from 1850 to ~1970 has been given by the IPCC AR6 (GCM simulations), whereas only a very small GMST rise of ~0.2 K excluding natural effects but including the AA effect was observed during this period. Thus, such a small net ERF of ≤0.1 Wm⁻² should lead to a negligible contribution to the GMST change. Third, we believe that there are very large uncertainties in simulated ERFs given in the IPCC AR6, and new research beyond our current efforts will be needed to calculate more reliable ERFs of aerosols, ozone, and other minor drivers. For an approximation, we estimate that the uncertainty in our calculated GMSTs from 1950 to the present is approximately 0.1 °C, which is about 20% of the temperature change. This uncertainty is larger than the estimated GMST rise due to the CO₂ increase in the most rapid warming period 1970–2000 either from the climate models taking into account the overlapping effect of water vapor or from the observational determinations of the ECS [17,18,19,20,21,22,23]. In other words, the GMST change due to the variations of non-halogen WMGHGs (CO₂), ozone, and aerosols in the late 20th century is negligibly small and is therefore not included in our CFC-warming model calculations via Equation (16). Note also that although the AA effect and polar ozone depletion obviously play an important or dominant role in changing the surface temperatures of the Arctic and the Antarctic, respectively (as seen in Figure 9b,c), each area of the Arctic and Antarctic regions only takes 6.7% of the global surface area and therefore the AA effect or polar ozone depletion makes only a small contribution to the change in GMST. Therefore, it is generally agreed that uncertainty in GMST change under GHG forcing is dominated by water vapor and cloud feedbacks only, rather than by the AA effect or polar ozone depletion [2,13]. Our calculated results clearly demonstrate that the greenhouse effect of halo-GHGs alone has well accounted for the observed GMST data since the 1950s, without the necessity of introducing the ocean heat uptake efficiency parameter κ as in AOGCMs. This indicates that the response in GMST to anthropogenic RF is relatively rapid (within 10 years, including the lag of mixing and transports of WMGHGs in air circulation on the global scale) [14,56,57]. In view of the key observations reviewed in Section 5, there is a strong rationale to predict that a long-term cooling trend will occur in the coming decades.

7. Remarks and Perspectives

This paper identifies and tests the critical assumption of a large climate forcing of rising CO₂ in traditional climate models by the six key observations from ground-based and satellite measurements. These observations provide fingerprints of the contribution of CFCs versus CO₂ to global warming in the late 20th century. It is clearly shown that CO₂-based climate models (GCMs) do not pass the validation by any of the key observations. The observations strongly indicate that global climate change has been primarily caused by halo-GHGs since ~1970, with some disguises by ozone recovery and Arctic amplification of surface warming due to continued (sea) ice loss in high-latitude (polar) regions. CO₂ climate models show large discrepancies with the six critical observations, arising likely from the neglecting of the overlapping effect of water vapor on the climate forcing of CO₂ (N₂O and CH₄). A critical review of the observed surface temperature changes in the three representative regions (central England, the Arctic, and the Antarctic) shows that the surface temperature changes are primarily caused by the greenhouse effect of halo-GHGs, rather than by the observed increasing growth rate of CO₂ and the change in aerosol ERF, though the climate forcing of Antarctic ozone depletion and the AA effect also make large contributions to the surface temperature changes in the Antarctic and Arctic, respectively. These observations agree well with the CFC-warming physical model, whereas they are in marked contrast to the main conclusion in the IPCC AR6. The observations also show that a reversal in global warming would have occurred since around 2005 if there were no Arctic (polar) amplification. Remarkably, the analytically calculated surface temperature changes by the warming physical model of halo-GHGs with no tunable parameter, built on the quantum physics of the Earth’s blackbody radiation and the observational determination of the (equilibrium) climate sensitivity factor, exhibit excellent or perfect agreement with the observations of GMST and particularly the surface temperature in the Antarctic. Overwhelmingly the observed and calculated results support an emerging picture that halo-GHGs have played a dominant role in causing global warming in the late 20th century.

Since GMST is still around the peak over the past 150 years, sea-ice melting in the Arctic unavoidably remains and, in the Antarctic, may start to increase significantly with the emerging recovery of the Antarctic ozone hole (due to the increased greenhouse effect of recovering ozone). Thus, the polar amplification of surface warming due to sea-ice loss at certain Arctic or Antarctic coastal regions may continue to be significant for some years, and therefore regional warming in those polar areas may last for one to two decades until sea ice is stabilized, even if GMST has been stabilized or reversed.

Ice melting on land (glaciers, small ice caps, and ice sheets) and ocean water expansion due to warming can contribute to global mean sea level (GMSL) rise [13,96,97]. However, this rise may be a complex of natural and anthropogenic drivers. The rise in GMSL began about 20,000 years ago when the last glacial phase of the Pleistocene ice age ended and the continental ice sheets began to melt and continued for the ensuing 12 millennia until reaching a GMSL level a few meters below the present level ~7000 years ago [98]. For the period 8000–1000 years ago, GMSL rose much more gradually. Changes in sea level have been dominated more by regional and global than by glacial melt in the past millennium [98]. At present, GMSL rises are caused largely by the thermal expansion of seawater and by the calving of Antarctic and Greenland ice sheets. The IPCC AR6 [13] concludes with high confidence that GMSL is rising, and the GMSL rise rate since the 20th century has been the largest over the previous three millennia. However, recent marine oxygen-isotope-based GMSL reconstructions reviewed in the AR6 also show that GMSL during the Holocene was among the highest (5–25 m higher than the present level), and was surpassed only during the LIG (5–10 m higher) and MIS 11 (−3.5 to +0.5 m different) over the past 800 kyr. A (US) National Academies of Sciences, Engineering, and Medicine Report on Climate Stabilization Targets in 2011 [96] stated that GMSL from satellite measurements was rising at 3.1 ± 0.4 mm y⁻¹ since the records began in 1993 to 2003, but this rate decreased somewhat in the period 2003–2008 to 2.5 ± 0.4 mm y⁻¹ due to a reduction in ocean thermal expansion, whereas contributions from glaciers, small ice caps, and ice sheets increased. Moreover, some analyses based on observed trends rather than model results showed that at the 95% confidence level, no consistent or substantial evidence exists that recent rates of rise are higher or abnormal in the context of the historical records available for the data-rich United States [98,99]. Because oceans respond slowly to global warming and hence GMSL rises lag from Earth T changes, the rise in GMSL is expected to continue for coming centuries as a response to the past warming (even if GMST is stabilized through the phasing out of GHGs) [96,97]. Thus, there seems no conclusive evidence from recent trends of GMSL that global warming is continuing or stopping or is even caused by a main anthropogenic or natural driver.

This study leads to an important perspective, which may be regarded as good news, that with the phasing out of halo-GHGs (CFCs, HCFCs, HFCs, and PFCs) by international Agreements, including the most successful and important Montreal Protocol and its Amendments, it is very likely to see a gradual reversal in GMST in the coming decades. Nevertheless, this expected reversal in global warming and the emerging shrinking of the ozone holes, including the recently discovered tropical ozone hole that affects approximately half of the world’s population [16,38,100], will come true only with continued international efforts in phasing out all halogenated ODSs and halo-GHGs. Therefore, this study highlights the importance of such efforts from international governments and the global community. However, it is equally important to emphasize that the relevant international policies and political agenda must be built on a solid scientific foundation that has a correct understanding of the underlying science of global climate change. The 2021 Nobel Prize Committee in Physics gave a correct attribution of the primary cause of warming to being anthropogenic, yet to identify a correct GHG species as the primary anthropogenic driver is of critical importance for humans not only to reverse the climate change but to maintain a healthy economy and ecosystem around the globe [29].

This study and the recent advance in quantitative understanding of global ozone depletion through the CRE theory [16] lead to the following implications. Geoengineering has been proposed as a potential method to reduce climate warming by increasing sunlight reflection through the intentional addition of aerosols into the stratosphere, known as ‘stratospheric aerosol injection’ [44]. In view of both the observed evidence of the reversal in climate change since ~2005 and the significant enhancement (harmful) effect of atmospheric cloud and/or aerosol particles on global ozone depletion [16], this study strongly recommends the proposed geoengineering project not be proceeded.

On GCMs, some literature reviewed by Balaji et al. [31] has argued that the entire project of parameterization, i.e., the discovery of parsimonious representation through insight or mathematical methods, may have no future for GCMs, and that large-scale computation may be needed. For a future generation of GCMs, Balaji et al. have proposed to overcome the shortcomings of current GCMs through substantially higher resolution and detail, or through the use of machine learning techniques to match them better to observations, theory, and process models. They anticipate that with the new methods, understanding of climate processes would lie in an entire hierarchy of models where GCMs would continue to play a central role for foreseeable future climate modeling. Here we argue that the assumptions in any climate model including GCMs must carefully be validated with observations, however. Given the six key observations reviewed in this study, the fundamental assumption in GCMs seems invalid. Thus, it is very likely for GCMs to fail in making a correct prediction for long-term climate change whatever how complex and sophisticated they are. In contrast, it may be optimistic to anticipate that the presented conceptual physical model of climate change and insights provided by this study will help to reach proper and right decisions for humans to solve the important climate problem.