Abstract
In 1960, R.E. Kalman published his famous paper describing a recursive solution, the Kalman filter, to the discrete-data linear filtering problem. In the following decades, thanks to the continuous progress of numerical computing, as well as the increasing demand for weather prediction, target tracking, and many other problems, the Kalman filter has gradually become one of the most important tools in science and engineering. With the continuous improvement of its theory, the Kalman filter and its derivative algorithms have become one of the core algorithms in optimal estimation. This paper attempts to systematically collect and sort out the basic principles of the Kalman filter and some of its important derivative algorithms (mainly including the Extended Kalman filter (EKF), the Unscented Kalman filter (UKF), the Ensemble Kalman filter (EnKF)), as well as the scope of their application, and also to compare their advantages and limitations. In addition, because there are a large number of applications based on the Kalman filter in data assimilation, this paper also provides examples and classifies the applications of both the Kalman filter and its derivative algorithms in the field of data assimilation.
1. Introduction
Data assimilation refers to the methods that integrate new observational data in the dynamic operation of a numerical model by considering the temporal and spatial distribution of data plus the errors of the observation field and background field. Within the dynamic framework of the model, it can automatically adjust the model by continuously fusing the direct or indirect observation information from different sources and resolutions in time and space so as to improve both the estimation accuracy of model states and the prediction ability of the model. Since the 1990s, data assimilation has been successfully applied to not only atmospheric science and marine science but also other disciplines (See Table 1).
Data assimilation algorithms can be divided into two categories, sequential data assimilation algorithms and variational data assimilation algorithms. As the earliest form of sequential data assimilation algorithms, the Kalman filter is also the theoretical basis of the algorithms. All later algorithms of sequential data assimilation were evolved from the Kalman filter. On the other hand, although variational data assimilation algorithms are not the focuses of this paper, Appendix A provides a brief description of them.

Table 1.
Typical applications of data assimilation in various disciplines.
Table 1.
Typical applications of data assimilation in various disciplines.
| Discipline | Typical Applications |
|---|---|
| Atmospheric Science | Weather Forecast [1] |
| Marine Science | Sea surface temperature prediction [2] Ocean current change prediction [3] |
| Terrestrial Science | Soil moisture prediction [4] Ecohydrology [5] |
| Agricultural Science | Crop Yield Estimation [6] |
| Artificial Intelligence | Autonomous Driving [7] Machine Learning [8] |
The Kalman filter (KF), developed by R.E. Kalman in 1960 [9], is an “optimal recursive data processing algorithm”. It has become one of the standard methods of optimal estimation. It uses a series of data observed over time to estimate unknown variables more accurately.
The paper published by R.E. Kalman and R.S. Bucy in 1961 [10] first introduced the Kalman filter in continuous time. This Kalman filter is used for state estimation and prediction for both system models and observation models in continuous time. Under continuous time, the evolution of state variables is described by differential equations, and the observed data are also continuous. The goal of the continuous-time Kalman filter is to estimate the optimal solution to the state variables by minimizing the error covariance between the predicted states and observed data of the system. On the other hand, the discrete-time Kalman filter is achieved by discretizing the continuous-time model, where its optimal estimation is obtained by minimizing its estimation error covariance matrix. In practical applications, many observations and measurements of realistic systems are often provided at discrete time-grids, such as sensor sampling data and periodic signal processing. The discrete-time Kalman filter provides an efficient method for the state estimation and prediction in these cases, and the discrete-time Kalman filter is more commonly used in numerical computations.
Therefore, all the Kalman filters and their corresponding algorithms presented in this paper are discrete-time Kalman filters. However, the continuous-time Kalman filter still has its unique applications in some specific situations. For example, in a control system, if the system is modelled in continuous time, and its measurements are also modeled as continuous time processes, then the continuous-time Kalman filter should be more applicable.
For solving most of the optimal estimation problems, it is the best, the most efficient, and even the most useful algorithm [11]. It has been widely used in many fields for many years, including navigation and control [12,13] and target tracking [8,14,15]. Recently, it has been applied to microeconomics, as well as computer image processing [16], such as face recognition, image segmentation, and image edge detection.
From R.E. Kalman’s original Kalman filter (only applicable to linear conditions) to the Extended Kalman filter (EKF, applicable to near-linear conditions), the Kalman filter’s family was later joined by the Unscented Kalman filter (UKF) and then the Ensemble Kalman filter (EnKF), both of which have a wider range of application and higher efficiency. Kalman filter algorithms have been progressing continuously, and more algorithms have been derived based on these four commonly used Kalman filter variants. The Kalman filter is always developing in the direction of less limitation and higher efficiency.
2. Kalman Filter and Its Application
This section mainly introduces the theories of the Kalman filter (KF), Extended Kalman filter (EKF), Unscented Kalman filter (UKF), and Ensemble Kalman filter (EnKF), as well as their common applications in data assimilation.
2.1. Kalman Filter
In practical applications, the operation process of a physical system can be regarded as a state transition process. The Kalman filter introduces state space into the mathematical modeling process of the physical system, and it assumes that the system state can be represented by a vector . For the convenience of description, there are a few assumptions:
- ①
- The state transition process of a physical system can be described as a discrete-time stochastic process.
- ②
- The system state is affected by input.
- ③
- The system state and observation process are affected by noise.
- ④
- The system state is not directly observable.
On the premise of the above assumptions, the state equations applicable to the Kalman filter are first introduced as
The first equation of Equation (1) is the prediction equation, which simulates the evolution of the system from time to . denotes the value of different physical quantities at , denotes the system state at , and denotes the state transformation operator acting on a system state.
We define as the predicted value of the system derived from the prediction equation at , and as the analysis value of the system after combining the observations at . With regard to observations, there are three points to be emphasized: (i) The purpose of measurement is to express the properties of an object in terms of physical quantity, and thus, the result of the measurement must always be a real value expressed in a recognized unit of measurement; (ii) the measurement is always performed using measuring instrument; and (iii) the measurement is always an experimental process [17]. On the other hand, f (i.e., forecast) is specified to denote the predicted value, which is the result of the a priori estimation of the unknown quantity, and a (i.e., analysis) denotes the analyzed value, which is the result of the a posteriori estimation of the unknown quantity (usually used as the optimal estimate for the next time integration). The prediction error and analysis error are defined as
The covariance matrix of prediction error and analysis error are defined as
denotes the expectation function. is the model error (i.e., the error between and the transformation process). is assumed unbiased and uncorrelated at different times, i.e., , are the model error covariance matrix, and = .
The second equation in Equation (1) is the observation equation, which describes the relationship between the observed value and the true value of the system at time . is the observation operator acting on at . For the state transition operator and the observation operator , bold indicates that the operator is a linear operator or a tangent linear operator of a nonlinear operator, that is,
If H is linear, i.e., H[x] = Hx, then H′ = H, and the tangent linear identifies with the original observation operator. Consequently, the tangent linear operator depends on x if and only if is nonlinear. In the KF model, the state transition operator , as well as the observation operator , is specified to be linear operators, written as and . is the observation error, which is also assumed to be unbiased and uncorrelated with each other at different time, i.e., . is the observation error covariance matrix. In addition, the model error and the observation error are assumed to be uncorrelated with each other, i.e., .
In this theoretical derivation process, ideal assumptions about physical quantities are made. But, in practical applications, the combination of the data from different sources involves a weighted propagation of all input uncertainties to the uncertainties in outputs. Hence, data evaluation is intertwined with uncertainty analysis, requiring the inferences from incomplete information. Reference [17] provides detailed theoretical and practical information about the treatment of missing data in data assimilation.
Two sets of important equations in the Kalman filter can then be derived: prediction equations and update equations. Prediction equations are
where and are the system states defined above, is the analysis error covariance matrix, and is the prediction error covariance matrix. The above two formulas complete the prediction of the system state from to and calculate the prediction error covariance matrix for the next time integration.
On the other hand, the updated equations are defined as
is called Kalman gain, and determining is the key to establish the Kalman filter. Please refer to Appendix B for detailed derivations. The above formulas use the observation to update and adjust the prior estimate so as to obtain the analysis and the analysis error covariance matrix , which provides the basis for the prediction process at the next time integration.
The KF algorithm is proposed with its unique advantages: ① Compared with traditional statistical optimal interpolation algorithms, some of the states in the KF model are dynamically updated with time; its iterative calculation makes the model always close to the truth, while the optimal interpolation model is deterministic and detached from the model state, resulting in its deviation from true state over time. ② Compared with the variational method that is another important algorithm in data assimilation, KF provides the state mean and its error covariance, so the estimated results can be further understood by studying the nature of the error covariance matrix, such as the size, stability, and other information to determine whether the assimilation results are credible [17]. ③ The Kalman filter does not need to create an accompanying model, making it easier to implement.
This standard Kalman filter is no longer in common use due to the emergence of more and more efficient Kalman filter derivatives, but in the early days of the algorithm’s proposal, The KF’s ideas were plausible and effective in solving the practical problems of data assimilation. The KF was successfully used in the Apollo moon landing project when it was first proposed. When a spacecraft flies to space, it keeps measuring its position with various sensors, hoping that it is on an intended orbit. However, due to the effect of sensor errors, the spacecraft may slowly deviate from its intended orbit despite continuous measurement and adjustment. Using the KF, the errors can be filtered out, and the correct position of the spacecraft can be estimated.
In the field of atmospheric science, the KF is applicable to unknown variables predicted as continuous variables, such as maximum and minimum temperature and humidity dew point, but not to discontinuous variables, such as precipitation and thunderstorm [18]. Taking the prediction of the minimum and maximum temperature in a certain region as an example, relevant prediction factors (such as 1000 hPa temperature, 850 hPa temperature, specific humidity, etc.) are usually selected to predict the unknown quantities combined with a relevant numerical atmospheric model and the KF. According to experiment results, the KF algorithm has good forecasting performance and is more practical and easier to be operationalized when compared with other methods. For example, it has good prediction effects for continuous temperature rise and drop, but it has a certain lag for sharp warming and cooling conditions [19]. Those performances are also in line with the characteristics of the KF itself.
Please refer to reference [20] for more details on meteorological data assimilation; it provides a review and some suggestions for further improvement in meteorological data assimilation methods. Furthermore, references [17,21,22] are also useful in learning meteorological data assimilation or data assimilation with special conditions.
Although the KF has its unique advantages over other algorithms, it requires storing and analyzing various covariance matrices that evolve over time in actual usages. It means that as the dimension of the state vector increases, its computational time will increase greatly. In addition, according to the assumptions of Kalman gain, the KF is only applicable to the premise that the system state equation is linear and with Gaussian distribution, which is a particularly harsh prerequisite for the practical problems that need to be solved. All these restrict the application of the KF in solving complicated practical problems.
2.2. Extended Kalman Filter
The limitations of the Kalman filter implies that the study of nonlinear filters is very important. Senne [23] extended the KF to an extended Kalman filter (EKF) to apply the KF to nonlinear systems. The Extended Kalman filter is one of the most classical algorithms in the field of the nonlinear filter. The basic idea of the EKF is to focus on the first order term of the Taylor expansion of the system’s nonlinear equation and then transform the nonlinear equation into a linear one. The EKF is very common in the nonlinear filter and easy to implement.
The EKF is very similar to the KF in that it is divided into two steps, prediction and analysis, with the core operation being the linearization of the nonlinear equations. The prediction step consists of two time-update equations, both of which have the same physical quantities as the KF definition:
Analysis steps mainly include three state-update equations:
It should be noted that Equation (8) is written with instead of . Please refer to reference [11] for detailed derivations.
Compared with the KF, the EKF is the most common method for solving nonlinear assimilation problems, as it resolves to some extent the linearity requirement of the system equation and observation equation. The EKF can play a better role in solving the data assimilation problem that some system models are nearly linear and continuous. It is often used in vehicle tracking, spacecraft orbit estimation and control, and greenhouse climate control [24]. Because nonlinear data assimilation problems have better algorithms than the EKF in many cases, the applications of data assimilation introduced for the EnKF and UKF in later sections can also be solved by using the EKF. Those applications will not be repeated here, and the application idea of the EKF in storm surge forecasting in the North Sea [25] is briefly introduced in the following.
The abnormal rise and fall of seawater due to violent atmospheric disturbances, such as strong winds and sudden changes in air pressure, which cause the tide level in the affected area to rise significantly above normal level, is called a storm surge. Storm surges are catastrophic natural phenomena, and their prediction is important for the lives and the economic security of people in coastal cities.
Storm surge models are usually based on shallow water flow models incorporating the momentum conservation and mass conservation equations, which mainly portray the very complex water patterns caused by irregular coastlines. The very deep ocean depth in the North Sea region leads to a strong linearity of the shallow water model in this region. Because the shallow water model has a time-invariant observation equation, this makes the weak nonlinear shallow-water flow model a good fit for the prerequisites for the EKF. Using the EKF algorithm, the potential inaccuracy of a deterministic system can be taken into account by correcting the shallow-water model for the introduction of observations, so that the information provided by the system dynamics can be combined with measurements that contain measurement errors to achieve a better prediction of a storm surge.
The Kalman filter theory is flourishing in meteorological data assimilation. In simple low-dimensional data assimilation problems, the KF and EKF play an important role and their algorithms are well established. For complex high-dimensional strongly non-linear problems, the EnKF will play a major role [1].
Although the EKF is often used for nonlinear assimilation problems, it has some significant limitations [26]:
① Since Taylor expansion is a linearization process, the EKF estimations can only be relatively close to the truth if the system state and the observed equations are locally linear and continuous. ② The performance of the EKF is dependent on both the system error and the observation error. If both error covariance matrices are not estimated accurately enough, the EKF’s errors will accumulate rapidly and lead to divergence. ③ The calculations on the Jacobian matrix are tedious and error-prone and may even make it difficult to draw conclusions due to excessive computations. ④ Since the higher-order terms of the Taylor expansion of nonlinear function are ignored, the linearization process of the system equation may cause large errors, leading to rapid divergences of the model. ⑤ The EKF requires derivatives, so the specific form of nonlinear function must be clearly understood and cannot be encapsulated, making it difficult to apply modularly.
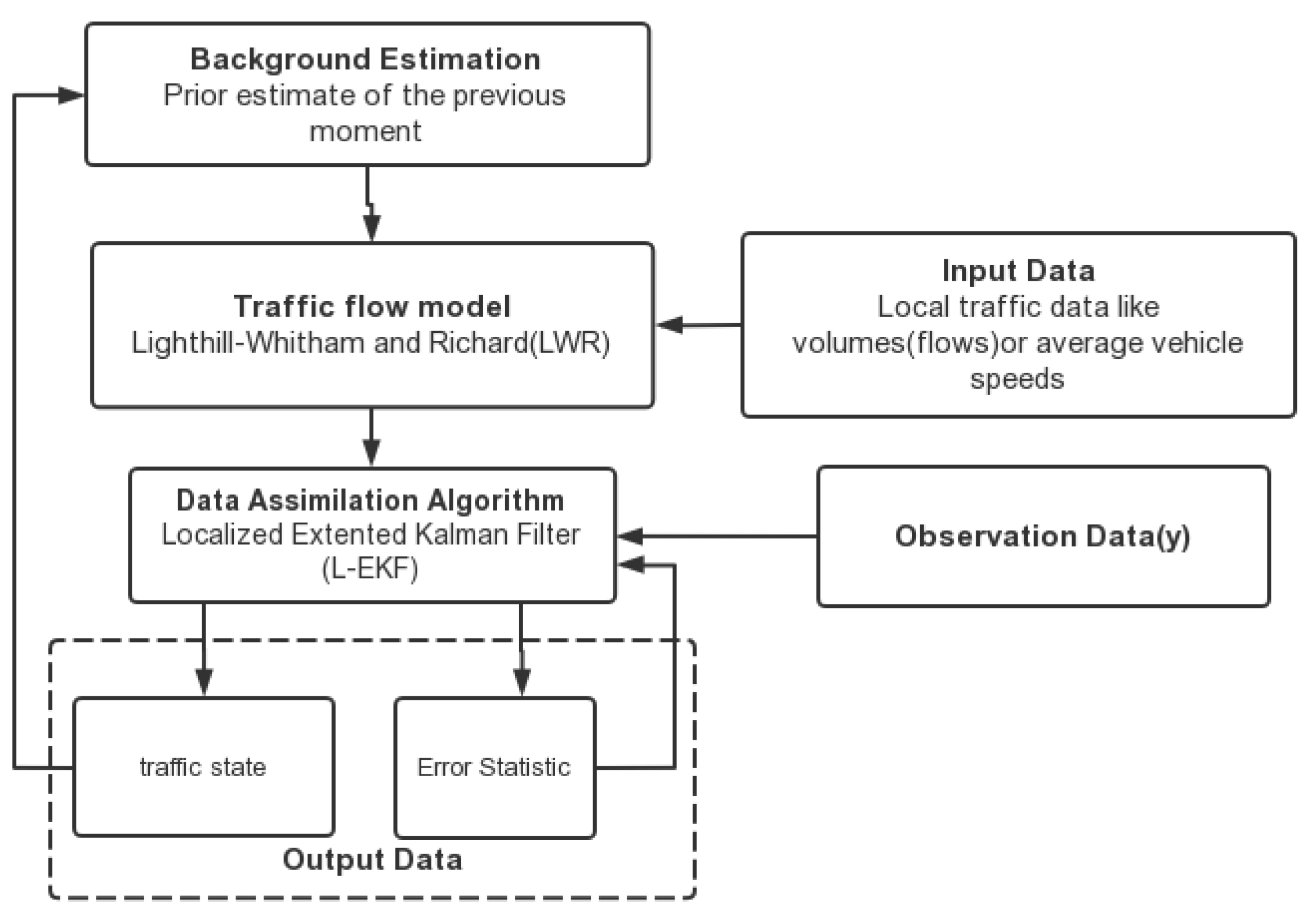
Another example of a modified version of the EKF was applied to a real-time traffic state estimation [27] Advanced traveler information systems (ATIS) and dynamic traffic management (DTM) require some estimate of the current traffic state as an input. Usually, the traffic state cannot be directly measured but needs to be estimated from incomplete, noisy, and local traffic data. One of the most widely applied estimation methods is the Lighthill–Whitham–Richards (LWR) model with an extended Kalman filter (EKF) [27]. Due to the above problems of the EKF, a modified version of a localized EKF (L-EKF) was proposed for the LWR application. The modified EKF is named as L-EKF to indicate the local nature of the corrections. In the L-EKF, many local EKFs are sequentially called for each cell containing measurements, instead of constructing one large EKF for the entire network. The basic process is depicted in Figure 1.
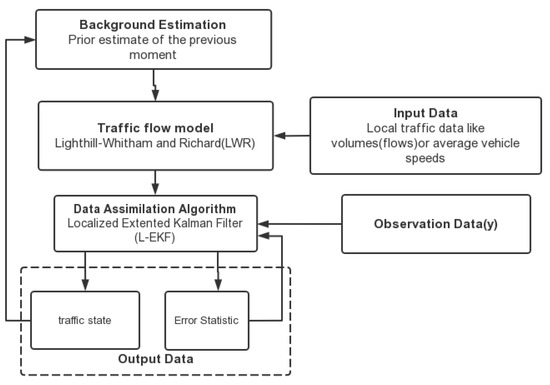
Figure 1.
The framework of Scalable Real-Time Traffic State Estimation [27].
The study in [27] found that the L-EKF clearly integrates the basic EKF with many advantages, and the predictions of the traffic state are similar to the EKF, which improves the computational speed under the premise of guaranteeing the feasibility and the accuracy of the results. This is a kind of improved approach to make the EKF applicable to large-scale calculations. Other issues in the EKF, EnKF, and UKF will be discussed next, and their solutions will be provided.
2.3. Ensemble Kalman Filter
The Ensemble Kalman filter (EnKF) algorithm is a combination of ensemble forecasting and Kalman filter methods from the mid-1990s [28,29]. It calculates the forecast error covariance matrix of states by the Monte Carlo method, solving the problem of difficultly estimating the forecast error covariance matrix in practical applications by using the idea of ensemble. It can be used for the data assimilation of non-linear systems, effectively reducing the computational effort of data assimilation [19].
The main idea of the EnKF is to use an ensemble of state vectors to represent the distribution of system states and to replace the model/system error covariance matrix with the sample covariance matrix from the ensemble. The goal is to perform an EKF-like analysis for each member in the ensemble, and the EnKF also consists of two steps of analytical prediction as shown in the following.
where is the index of a different member in the ensemble, is the same as previously defined , [30], and are the analysis state and forecast/model state of the i-th member in the ensemble, and is the state transition operator (i.e., model). The ensemble mean is used to approximately replace , and is used to approximately replace . On the other hand, the prediction steps become
where is the Kalman gain and is the observation operator. To prevent the system from diverging quickly, a perturbation to is often used. Since the observation y and appear simultaneously in the formula, they can be called the perturbation of . This EnKF of the “” disturbance is also called stochastic EnKF. is called the observational perturbation and follows a Gaussian distribution with zero mean and covariance .
The EnKF overcomes some of the problems that exist in the previous generation of the Kalman filter (i.e., KF and EKF). Its actual computations do not require an explicit forecast error covariance matrix () and an analysis error covariance matrix (), but only and to complete the prediction, reducing the computational burden when compared with the KF and EKF.
In addition, the introduction of an ensemble can improve computation speed because the EnKF’s ensemble members are independent to each other during prediction and analysis except for error statistics, which means that the small-scale calculation of multiple sets can be carried out at the same time. This is the key factor to improve the computation speed. Parallel computing is the most effective method to solve large-scale scientific computations. However, the parallelization of a numerical model is largely restricted by the data exchange among processes. The larger the amount of data that needs to be exchanged among processes, the lower the parallel efficiency. This implies that the iterative algorithm in the KF and EKF is greatly affected by data exchange, and their speeds will slower than the EnKF.
The problem of the near-linearity requirement in the EKF can also be effectively addressed using the ensemble way. The EnKF hides the prediction of error statistics in the prediction of a group of model variables with disturbance. Tangent linear approximations do not exist in the development of error statistics and model variables, along with that of nonlinear model [29].
The EnKF is widely used in the data assimilation applications of atmosphere, ocean, and land due to its advantages, such as fast computational speed and excellent outcome. It has become an important branch of the sequential data assimilation algorithm. For example, Houtekamer et al. explored the possibility of the EnKF assimilation of unconventional data using a T21 global atmospheric quasi-geostrophic spectral model with simulated observational data and concluded that it is a relatively perfect model [31]. In terms of ocean data assimilation, Evensen used a two-layer quasi-geostrophic ocean model to simulate ocean currents by assimilating satellite altimeter data with the EnKF [29]. In addition, the following are two examples of EnKF applications in the field of climate science.
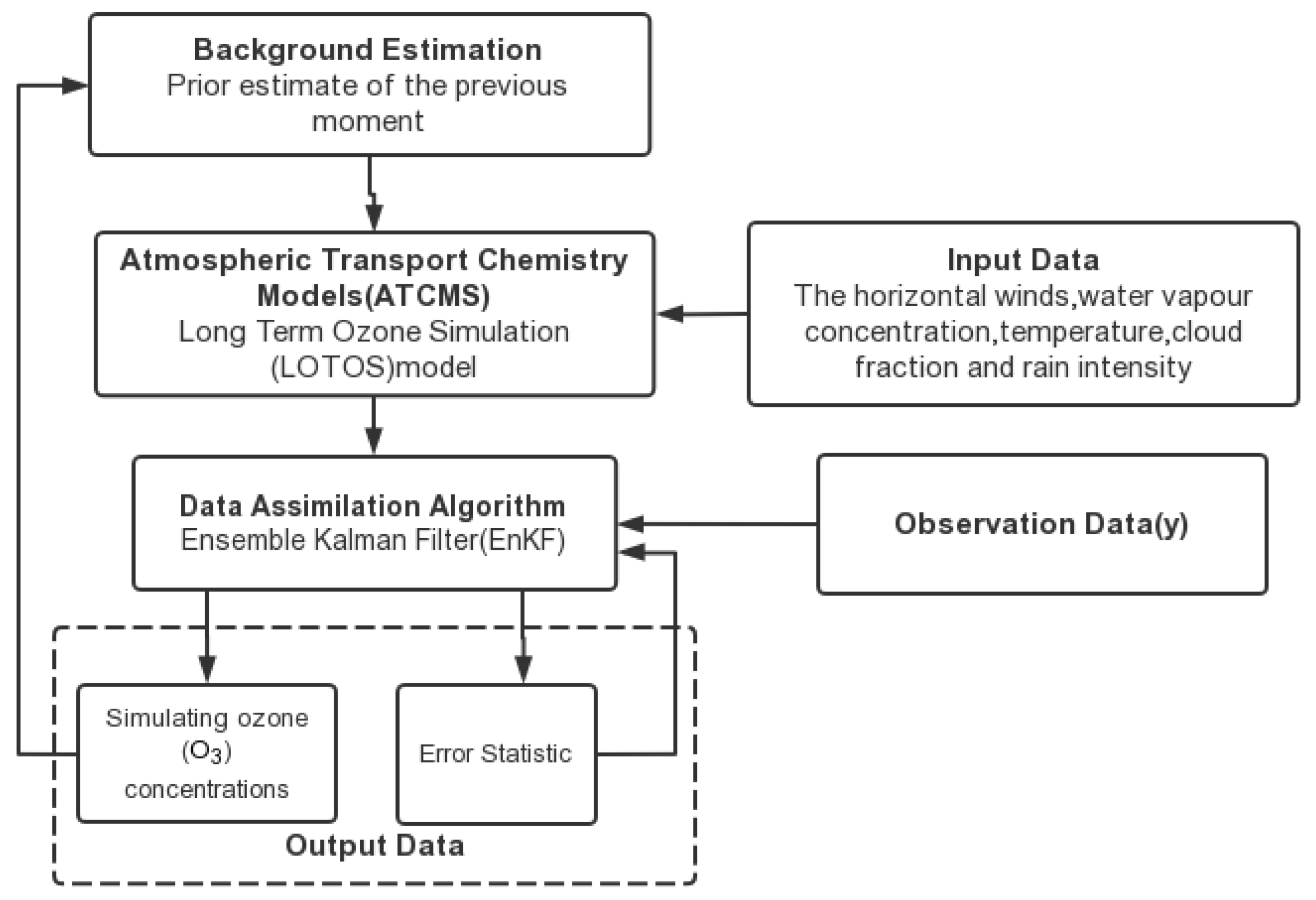
The first example is to simulate ozone (O3) concentrations using the EnKF [18]. Based on the Long-Term Ozone Simulation model (LOTOS), it is possible to improve the Atmospheric Transport Chemistry Models’ (ATCM) simulations of tropospheric ozone using the EnKF via the following flow chart in Figure 2.
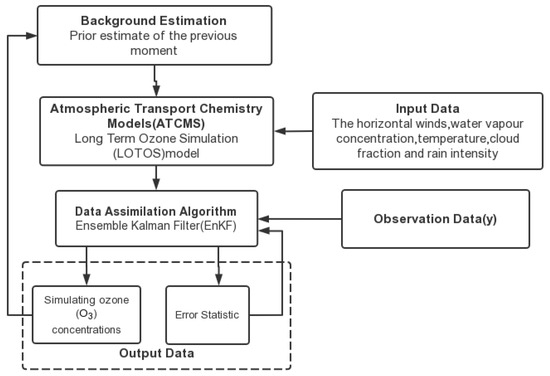
Figure 2.
The framework of simulating ozone (O3) concentrations [18].
Based on the comparison of assimilation results with observations, the use of the EnKF in combination with ATCMs can effectively optimize the predictions regarding ozone concentrations with the LOTOS. In several different country regions with different errors, it can still manage to optimize the predictions close to the observations.
The second example is to study soil moisture using the EnKF [4]. Based on the simple biosphere model (SiB2), soil moisture was estimated in the surface, root zone, and deep layers of the soil using the EnKF. Compared with the simple SiB2 simulation, the data assimilation with the EnKF has significantly improved the estimation accuracy of soil moisture in the surface, root zone, and deep layer. In particular, when there is precipitation or the difference between simulations and observations is large, the assimilation effect is more significant.
However, the EnKF is not perfect. For example, the uncertainty operation of perturbing observations in the EnKF has both advantages and disadvantages. One of the most practical problems in the EnKF is the feasibility problem, meaning that the matrix used in the calculations might not be full rank.
In the previous KF-type algorithms, it is always assumed that the error covariance matrix is a positive definite invertible matrix, which makes the calculation of the matrix inverse in the Kalman gain feasible. In the EnKF, due to the perturbation of the observations y, is no longer guaranteed to remain a positive definite invertible matrix, and matrix is meaningless to inverse if it is not a full rank matrix. inverse can be approximated with the eigenvalue decomposition if the difference in dimensionality between the ensemble members and the observations is not too great. However, when the difference is great, it will be impossible to find a reasonable gain matrix. In addition to this, the inclusion of perturbations and the selection of the ensemble are likely to lead to filter divergence.
2.4. Unscented Kalman Filter
To solve the problem under strong nonlinear conditions, in 1995, Julier and Uhlmann [32] proposed the Unscented Kalman filter (UKF) algorithm, which was further improved by Wan and Merwe [33] later.
The UKT is an improvement on the original Kalman filter based on unscented transform (UT), which investigates the problem of determining the posterior distribution of a nonlinearly transformed Gaussian random variable by capturing a defined number of sampling points. Once the corresponding statistical properties have been obtained by UT, the Unscented Kalman filter is obtained by combining it with the standard Kalman filter framework [34].
The unscented transformation refers to the deterministic sampling of the probability distribution of random variables according to a certain rule, and the distribution of weights (mean weight and variance weight) to the sampling points. The sampling points are commonly referred to as sigma points. Each sigma point can be transformed using a known nonlinear function to obtain a new sigma point, weighting and summing the new nonlinearly transformed sigma points, calculating the weighted mean and weighted variance, respectively, and using the weighted mean and weighted variance to approximate the nonlinearly transformed probability distribution of the random variable.
Compared with the KF and EKF, the UKF intersperses the steps of sigma sampling between the two steps of analysis and prediction. First, sigma sampling is performed on the posterior probability distribution at the previous time. The selected sigma points are defined as follows:
where is the system mean satisfied by the optimal estimate of the system state at the moment , is the system variance, is the weight of each sigma point when calculating the mean, and is the weight of each sigma point when calculating the variance, where parameter is satisfied by: , parameters and are scaling parameters that determine how far away from the mean the sigma points are distributed. Parameter is used to describe the distribution of the state variables.
The non-linear prediction was then performed to obtain the weighted mean and covariance matrix , with the main equation:
where is the sigma point after the nonlinear transformation, followed by sigma sampling of the prior estimate at the current moment:
It should be noted that, for efficiency, it is possible to directly use the sigma points of the moment after the state transformation to obtain as the sigma points of the moment a priori estimate , but this will reduce the accuracy to a certain extent.
Finally, the analysis steps are as follows:
where and describe the probability distribution of y, which are the mean and variance of respectively, and is the covariance matrix of analysis value and observation value.
Compared with the EKF, the UKF avoids the calculation of the Jacobian matrix and Hessian matrix, reducing the complex calculation with high dimensions. Moreover, the UKF does not ignore the high-order terms of the Taylor expansion of the nonlinear equation, like the EKF, but retains the equation using unscented transformation, which makes the prediction accuracy of the UKF higher than that of the EKF. In addition, the UKF does not need to be linearized, which reduces the requirements of the system state equation and observation equation. Especially when the system equation is highly nonlinear, the performance of the UKF is significantly better than that of the EKF.
In addition, in order to improve the accuracy of results, the parameters in the UKF can be continuously adjusted by fitting known prediction results and true states in advance to achieve optimal estimations. This is impossible for other Kalman filters.
The UKF, as a main method to solve nonlinear data assimilation problems, has been widely used in many fields, such as flight target tracking [35], visual tracking [36], real-time camera tracking, highway navigation systems, and vehicle and public transport systems. It has been further introduced into the field of machine learning, including nonlinear system identification, neural network training, and dual estimation [37].
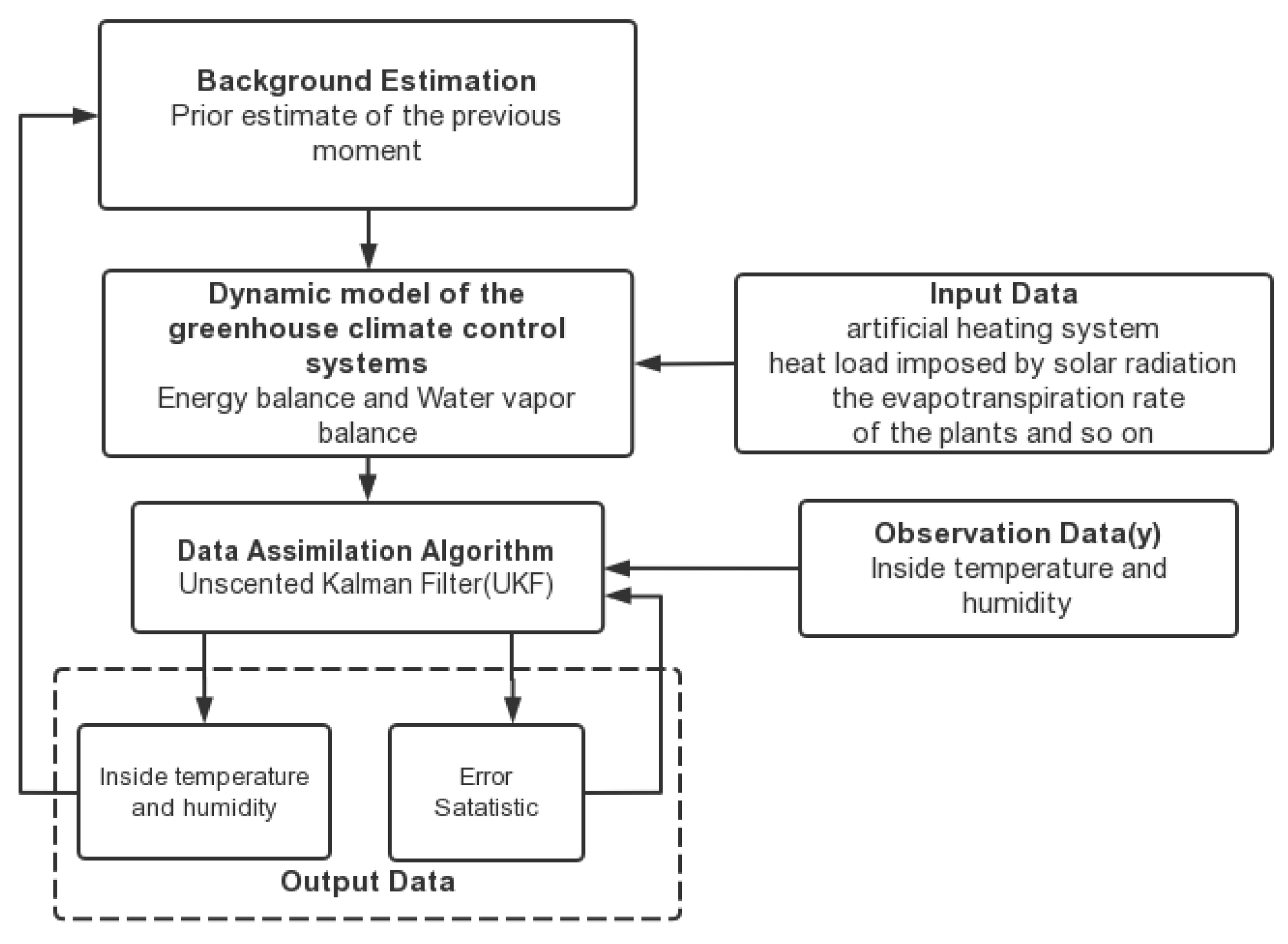
As an example, in Figure 2, the UKF has been applied into a greenhouse climate control system [38].
As a complex control system, a greenhouse climate control system creates difficulties in regulating the greenhouse environment because of highly coupled nonlinear dynamics and strong disturbances from surrounding environments, such as global radiation, wind speed and direction, and external air temperature and humidity. In addition, the climate control inside a greenhouse largely depends on the accuracy of sensors outside the greenhouse. The unconventional noise and incomplete measurement caused by weather or other accidents can also affect the quality of climate control.
The dynamic change in a greenhouse is determined by the difference of energy and mass content in between its internal and external air. A greenhouse’s climate state can be expressed by two variables: the internal air temperature and the absolute humidity. A simplified greenhouse climate model for control purposes describes the dynamic of the state variable with the energy balance and water vapor balance equations [39]. The former is affected by energy supply and energy loss, and the latter is mainly affected by the transpiration rate of plants.
The ability of the UKF to accurately estimate non-linearities makes it attractive for the implementation of greenhouse climate control systems, where the UKF is used to estimate the states of a greenhouse climate control system with missing measurements and to filter out noise. Please refer to Figure 3 for the process.
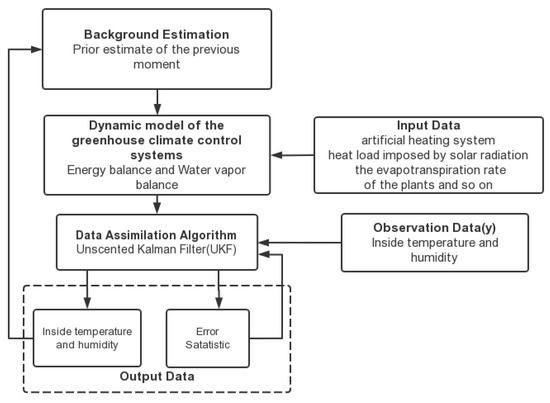
Figure 3.
The framework for the greenhouse climate control system with UKF [38].
Through simulation experiments, results show that the UKF algorithm without considering missing measurements has a higher order of accuracy than that with measurement losses.
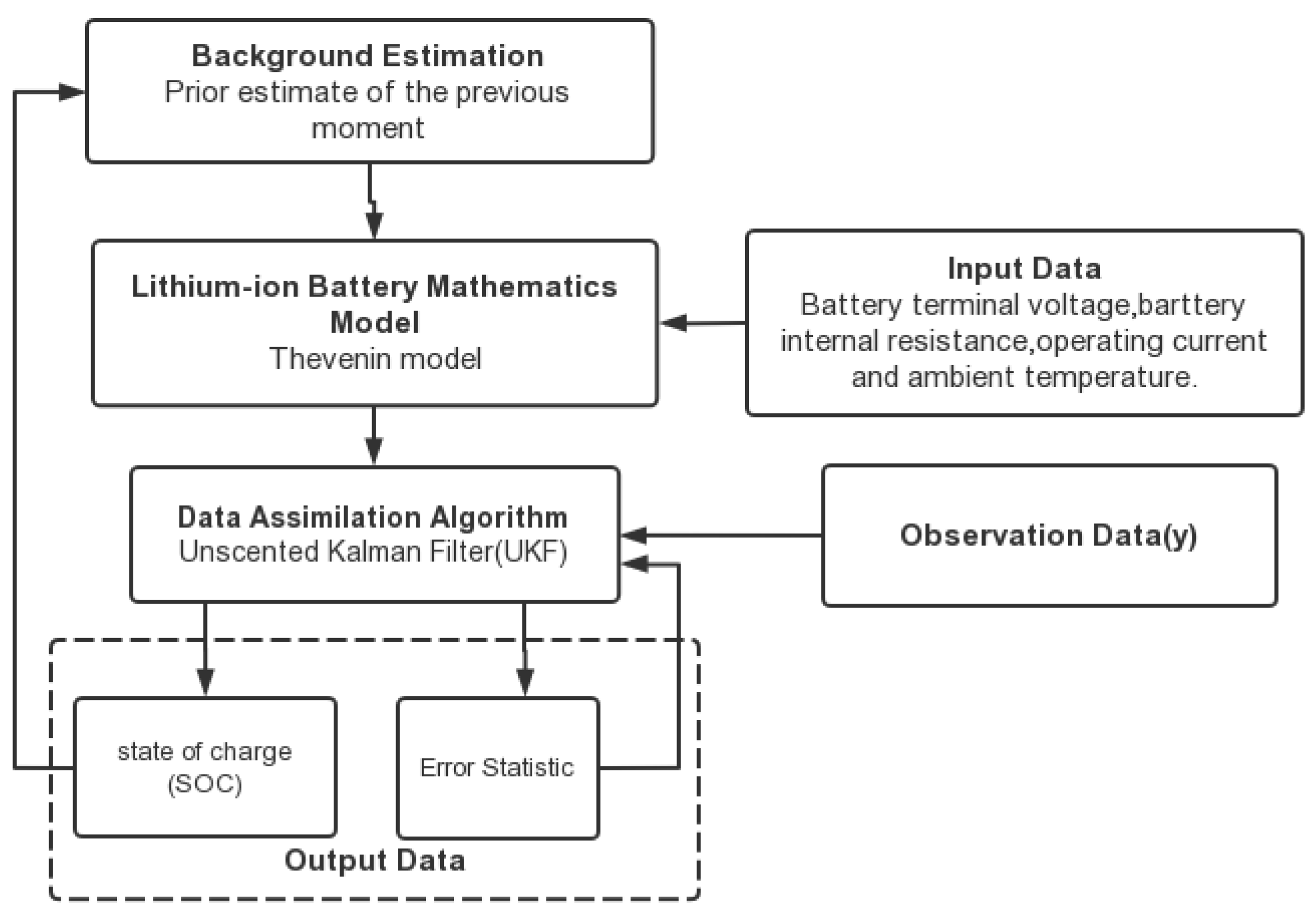
Another example of estimating the state of charge (SOC) of a lithium-ion battery can illustrate the unique advantages of the UKF [40]. The capacity of the lithium-ion battery and internal parameters obviously vary with temperature, so accurately estimating the state of the cell charge at various temperatures is the key technology of the battery management system in electric vehicles. Based on the Thevenin model, using the Unscented Kalman filter (UKF), the SOC of the Li-ion battery at various temperatures and discharge currents was estimated. Its specific estimation steps are shown in Figure 4.
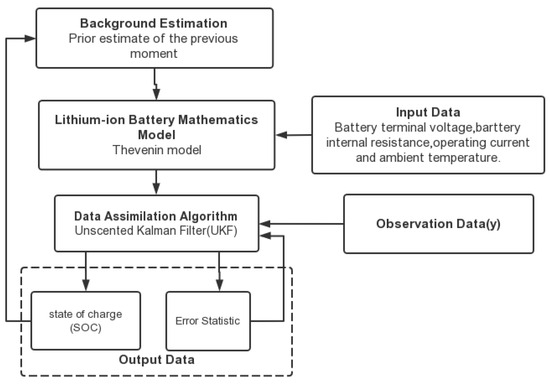
Figure 4.
The framework for the SOC estimation of Li-ion battery with UKF [40].
Results show that the UKF algorithm adapts to the estimation of the battery’s SOC under different discharge currents. It has a strong correction effect on the initial error, and the convergence speed slows down as the temperature decreases in the estimation process. However, the estimation of the steady-state accuracy is almost unaffected by the temperature, and the steady-state accuracy is very high. Therefore, the UKF algorithm is suitable for estimating the SOC of lithium-ion battery packs under different temperatures and discharge currents.
3. Other Kalman Filters
3.1. Adaptive Kalman Filter
In the KF, there is a premise that the model error and observation error are assumed to be fixed values given in advance, which is inappropriate when some filters are in a changing environment. The Adaptive Kalman filter (AKF) [41] can effectively solve this problem. The main change in the AKF relative to the KF is that the AKF updates the original fixed mean and covariance matrices, and observational errors are updated. The AKF’s analysis and prediction steps are consistent with the KF, and the update steps for [41] are
is usually taken as or , where b (0 < b < 1) is the forgetting factor; as time moves forward, 1 − gradually converges to 1 or b in two different modes, so is often between 0.95 and 0.99. More information about the parameter can be found in reference [42]. If then the AKF is transformed into the KF, and the AKF will tend to be a standard KF.
The AKF uses the observational data to constantly determine whether the system dynamics have been changed by the filter itself. It estimates and corrects model parameters and noise’s statistical characteristics so as to improve the filter design and reduce the actual error of the filter. This filter method combines system identification and filter estimation together.
It is clear that the AKF’s idea is applicable to not only the KF but also other Kalman filter algorithms. The addition of an adaptive filter greatly improves the problem that the default scene in the Kalman filter algorithms is static.
3.2. Derivative Algorithms of EnKF
In order to solve the problems in the EnKF, many more practical computational methods have emerged to optimize the existing EnKF.
The Ensemble Square Root filter (EnSRF) [43] uses the traditional Kalman gain for updating the ensemble mean but uses a ‘‘reduced’’ Kalman gain to update deviations from the ensemble mean. There is no additional computational cost incurred by EnSRF relative to the EnKF when observations have independent errors and are processed one at a time. It is demonstrated that the elimination of the sampling error associated with perturbed observations makes the EnSRF more accurate than the EnKF for a same ensemble size.
In Section 2.3, in order to ensure the feasibility of the EnKF and to solve the problem of filter dispersion, observations are perturbed. The filter dispersion can also be avoided by other schemes. For example, changing the Kalman gain in the EnKF into [43]
Since the computation with respect to involves the square root of the observation error covariance matrix , this EnKF is referred to as the ensemble square root Kalman algorithm.
The Ensemble Transform Kalman filter (ETKF) [44] differs from other ensemble Kalman filters in that it uses ensemble transformation and a normalization to rapidly obtain the prediction error covariance matrix associated with a particular deployment of observational resources. This rapidity enables it to quickly assess the ability of a large number of future feasible sequences of observational networks to reduce forecast error variance.
The Ensemble Adjustment Kalman filter (EAKF) [45] can perform viable data assimilation and prediction in models where the model state dimension is large compared with the ensemble size. It has an ability to assimilate observations with complex nonlinear relations to state variables and has extremely favorable computational scaling for large-scale models.
To facilitate the introduction of the ETKF and EATF, another idea for understanding the EnKF is introduced as the following.
Since it is difficult to compute in high-dimensional cases, can be updated by computing the transformation matrix and applying it to an ensemble of perturbation matrices in the square root form [46]. As a further explanation, let
where is a matrix in which each column is a set-analysis mean, and the set can be obtained by adding different perturbations to a fixed , respectively. Then, can be written as
From the equation in the KF algorithm, it can lead to
where is called the ensemble perturbation matrix in the observation space. F is defined as
and it is called the new interest rate covariance.
To determine the perturbation , needs to be computed, such that
where T is called the transformation matrix. Then, , resulting in . Different EnKFs can use different methods to solve the transformation matrix. For example, the eigenvalue decomposition of yields , which is called the Ensemble Transformed Kalman filter (ETKF) and can be calculated as . For more related detailed information, please refer to reference [46], which provides a large number of derivative algorithms of the EnKF organized through the above ideas.
All these filters solve the problem of the EnKF divergence to some extent. In addition, they can also be combined with the variational method. For example, Whitaker et al. tried to combine the EnKF and 3DVAR [43], and the results showed that with the increase in the sample number, the greater covariance weight of the EnKF would achieve better results. Hansen et al. proposed an assimilation method combining the EnKF and 4DVAR [47], and the results showed that their method is better than the single EnKF or 4DVAR method. Pleases refer to Appendix A for a brief description of 3DVAR and 4DVAR.
3.3. Derivative Algorithms of UKF
After introducing unscented transform into the KF, the UKF has become the mainstream algorithm replacing the EKF to solve nonlinear problems, and other methods can often combine with it to solve practical problems. For example, the UKF is combined with a particle filter [48] to improve the efficiency of the particle filter algorithm. There is also a Square Root Kalman filter (SR-UKF) [49] corresponding to the ensemble Kalman, where square root forms have the added benefit of numerical stability and guaranteed positive semi-definiteness of covariances.
4. Conclusions
Aiming at sequential assimilation algorithms in data assimilation, this paper introduces the basic principles and derivation formulas of the Kalman filter (KF), Extended Kalman filter (EKF), Ensemble Kalman filter (EnKF), and Unscented Kalman filter (UKF). This paper is primarily based on the following two aspects of interpretation: ① The system process model and observation model are established, mainly by establishing the system’s state equations and observation equations, as well as determining the statistical characteristics of the model error and the observation error using statistical measurements for the estimation of the noise-related parameters and establishing the system process of the mathematical model; ② the filter computational model and the mathematical model are established as the basis for the determination of the time update equations of the filter and the state update equation; the main coefficients in the filter coefficients are determined, including state transition matrices and the related factor matrix. Furthermore, it not only analyses and summaries their respective advantages and disadvantages, but also discusses their applications in the field of data assimilation.
The development of the Kalman filter algorithm has been moving towards a wider range of applications, higher accuracy, and faster speed over the decades. It has matured into application models in a number of fields, such as climate science, target tracking, and artificial intelligence. It has become an integral and important part of data assimilation.
Although the KF has been introduced for so many years, it has many limitations, such as being only applicable to linear conditions and slow speed. The EKF enables the application of the Kalman filter to nonlinear conditions through the linearization of the Taylor expansion, while the EnKF and UKF also combine the Kalman filter with the Monte Carlo algorithm and unscented transform, respectively, resulting in a more applicable and faster Kalman filter. For a detailed summary of those algorithms, please refer to Appendix C.
In addition to these four types of the Kalman filter, many derivative algorithms of the Kalman filter have been developed. There is still great potential for the Kalman filter and its derivatives to be developed. Various filter methods that more or less existed at present have weaknesses, such as the complex structure of algorithms and the lack of real-time reliability. It is hoped that with the rapid development of numerical computing technology, more scholars will devote themselves to the research on the Kalman filter algorithms in order to improve the accuracy and computational efficiency of the algorithms when solving practical problems.
Author Contributions
Conceptualization, Z.S.; validation, Z.S.; writing—original draft preparation, B.W.; writing—review and editing, B.W., Z.S., X.J., J.Z. and R.L.; supervision, Z.S.; funding acquisition, Z.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Nanjing Normal University (Grant No. 184080H202B371).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Acknowledgments
The authors would like to thank the anonymous reviewers for their valuable comments to this article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The Variational Data Assimilation Algorithms
The variational algorithm constructs a cost function to describe the difference between the analysis state and the truth of the state quantity and uses the variational idea to transform the data assimilation problem into an extreme value solving problem by minimizing the “distance” between the prediction of the state and the observation under the condition of satisfying some dynamic constraints [50] so that the estimated state with the smallest “distance” is the optimal state. The variational approach together with the use of remote sensing data is generally considered to be the key factor for the continuous improvement of the quality of numerical weather prediction in the 1990s, and variational assimilation algorithms have, therefore, become one of the mainstream assimilation methods in the late 20th century. Common variational algorithms include three-dimensional variational (3DVAR) and four-dimensional variational algorithms (4DVAR).
The 3DVAR algorithm adjusts the trajectory of model predictions using all observations within the assimilation window, constructs a cost function to represent the error between the analysis state and the true state, and solves for the optimal solution with a very small cost function. The cost function is difficult to compute directly, and usually requires the help of a gradient function and an adjoint model [50]. The 3DVAR algorithm includes physical processes in the cost function and uses the model forecast as the background field of the state, so the 3DVAR assimilation results are physically consistent and dynamically coherent. During the assimilation process, 3DVAR does not need to filter observations and can use all valid observations. At the same time, 3DVAR can also assimilate observations that are not directly or linearly related to the state quantities because 3DVAR can use complex observational operators. However, in practice, due to the limitations of nonlinear changes of states and high dimensionality of state quantities, it is difficult to carry out direct computation, and it requires the use of concomitant modes and tangent linear equations. In addition, it is difficult to write concomitant modes for complicated model operators and observation operators, and the computational cost is also high. For more details on 3DVAR, please check reference [50].
The 4DVAR algorithm considers the change in state over time on the basis of 3DVAR, and the optimal estimation of the state at time t is the result of the comprehensive consideration of the change in state over time. It also requires the use of gradient function and concomitant patterns, and it is more computationally intensive, because it takes into account the change in time. It compensates to some extent for the shortcomings of 3DVAR in terms of the time variation of state quantities and the initialization; please refer to references [17,51] for a further understanding of 4DVAR.
Appendix B. The Derivation of Kalman Gain
In the process of describing a physical model, a simple but nontrivial estimation of the analysis state is derived as
where is the matrix with dimension , is the matrix with dimension and and are the analysis state and forecast state of the model, respectively. Then, according to assumptions, is a linear combination of and . Combined with observation equation , where is the model error and assumed to be unbiased, and the covariance matrix of is ; then, analysis error can be written as
According to the previous assumptions, and are unbiased, . In order to reach an optimal estimation and reduce the analysis error as much as possible, it is required that
making .
Therefore, the linear unbiased estimation of becomes
where is a linear mapping from to . Let vector be the innovation, which is the information brought by the observations compared with the forecast state.
With the linear estimation of Equation (21), the estimation problem is now transformed into finding a “satisfactory gain” .
Assuming that the optimal gain matrix is known, the analysis error covariance matrix is further investigated. From Equation (21) and , it will lead to
Then, can be calculated as
where is the forecast error covariance matrix. Knowing that and are linear independent, and and are linear, the following can be obtained from .
In order to reduce an analysis error, the trace of the analysis error covariance matrix needs to be further discussed. When the optimal gain is considered, the change of with respect to is
The symmetry of , and are used in the above derivations. In the optimal state (i.e., when ), there should be , thus
At this step, the optimal estimation of gain under the linear assumption can be obtained. From Equation (A3), the result of the estimation analysis on X and can be achieved, which is called BLUE (best linear unbiased estimator) analysis.
Appendix C

Table A1.
Application of the four types of Kalman filters in data assimilation.
Table A1.
Application of the four types of Kalman filters in data assimilation.
| Kalman Filter | Applicable Model | Application |
|---|---|---|
| Kalman filter (KF) | Linear | Navigation, Guidance and Control [11] (It is no longer often used as the preferred method for data assimilation due to its limitations.) |
| Extended Kalman filter (EKF) | Locally linear with strong continuity | Natural Geographical Sciences: Weather Forecast [1] Soil moisture prediction [4] Artificial Intelligence and Computer Science: Target Tracking [35] Navigation System Machine Learning [37] Agricultural Science: Crop yield estimation [6] Transportation Science: Freeway Navigation Public Transportation System [52] (Note: These three types of nonlinear filters have high repetition rate in applications. According to a specific problem, a more appropriate filter is selected for the experiment. Here only proves a summary) |
| Ensemble Kalman filter (EnKF) | Nonlinear | |
| Unscented Kalman filter (UKF) | Nonlinear |

Table A2.
Basic formulas, algorithms, and characteristics of four types of Kalman filter.
Table A2.
Basic formulas, algorithms, and characteristics of four types of Kalman filter.
| Kalman Filter | Applicable Model | Application |
|---|---|---|
| Kalman filter (KF) | The system model is adjusted by the observations to reach an optimal state at the current time. Then, the model is reinitialized by using the state estimation at the current time and continues time integrations. Compared with other algorithms, KF can adjust the model according to the observations, and it can have a general understanding of predictions through its updated covariance matrix. However, it is only applicable to linear conditions, and its computational effort is difficult to estimate. | |
| Extended Kalman filter (EKF) | This type of Kalman filter linearizes nonlinear equations by taking the first-order terms through Taylor expansion. It has good prediction results for data assimilation problems with locally linear and strong continuity. Neglecting the second-order and higher-order expansion terms leads to a decrease in the prediction accuracy of the system. It is computationally intensive. | |
| Ensemble Kalman filter (EnKF) | The combination of an ensemble prediction and the Kalman filter can be used to calculate the forecast error covariance by Monte Carlo methods. It can be used in the case of strong nonlinearity of a system, reducing the amount of calculation, making it easy for parallel calculation, and improving the calculation speed. The addition of disturbance will accelerate the filter divergence and affect the feasibility of filter calculation, which will lead to the case that the matrix is full-rank. It is also difficult to obtain its inverse matrix. | |
| Unscented Kalman filter (UKF) | The combination of unscented transformation and the Kalman filter avoids linearization by taking sigma points and calculating the weighted mean and variance. Its calculation is easy to implement and with high accuracy, which is better than EKF. |
References
- Galanis, G.; Louka, P.; Katsafados, P.; Pytharoulis, I.; Kallos, G. Applications of Kalman filters based on non-linear functions to numerical weather predictions. Ann. Geophys. 2006, 24, 2451–2460. [Google Scholar] [CrossRef]
- Larsen, J.; Hoyer, J.L.; She, J. Validation of a hybrid optimal interpolation and Kalman filter scheme for sea surface temperature assimilation. J. Mar. Syst. 2007, 65, 122–133. [Google Scholar] [CrossRef]
- Fukumori, I.; Malanotte-Rizzoli, P. An approximate Kaiman filter for ocean data assimilation: An example with an idealized Gulf Stream model. J. Geophys. Res. Ocean. 1995, 100, 6777–6793. [Google Scholar] [CrossRef]
- Huang, C.; Li, X. Experiments of Soil Moisture Data Assimilation System Based on Ensemble Kalman Filter. Plateau Meteorol. 2006, 25, 665–671. [Google Scholar]
- Sun, L.; Seidou, O.; Nistor, I.; Liu, K. Review of the Kalman-type hydrological data assimilation. Hydrol. Sci. J. 2016, 61, 2348–2366. [Google Scholar] [CrossRef]
- Shi, L.S.; Hu, S.; Zha, Y.Y. Estimation of sugarcane yield by assimilating UAV and ground measurements via ensemble Kalman filter. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8816–8819. [Google Scholar]
- Wei, H.; Huang, Y.; Hu, F.; Zhao, B.; Guo, Z.; Zhang, R. Motion Estimation Using Region-Level Segmentation and Extended Kalman Filter for Autonomous Driving. Remote Sens. 2021, 13, 1828. [Google Scholar] [CrossRef]
- Mahfouz, S.; Mourad-Chehade, F.; Honeine, P.; Farah, J.; Snoussi, H. Target Tracking Using Machine Learning and Kalman Filter in Wireless Sensor Networks. IEEE Sens. J. 2014, 14, 3715–3725. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Kalman, R.; Bucy, R. New results in linear prediction filtering theory. Trans. AMSE J. Basic Eng. 1961, 83, 95–108. [Google Scholar] [CrossRef]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter. Proc. SIGGRAPH Course 2006, 8, 1–16. [Google Scholar]
- Oh, S.M.; Johnson, E. Development of UAV Navigation System Based on Unscented Kalman Filter. In Proceedings of the AIAA Guidance, Navigation, & Control Conference & Exhibit, Keystone, CO, USA, 21–24 August 2006. [Google Scholar]
- Lee, H.J.; Jung, S. Gyro Sensor Drift Compensation by Kalman Filter to Control a Mobile Inverted Pendulum Robot System. In Proceedings of the 2009 IEEE International Conference on Industrial Technology, Churchill, Australia, 10–13 February 2009; IEEE: Piscataway, NJ, USA, 2009; Volume 1–3, pp. 108–113. [Google Scholar]
- Weng, S.; Kuo, C.; Tu, S. Video object tracking using adaptive Kalman filter. J. Vis. Commun. Image Represent. 2006, 17, 1190–1208. [Google Scholar] [CrossRef]
- Yu, D.; Wei, W.; Zhang, Y.H. Dynamic target tracking with Kalman filter as predictor. Opto-Electron. Eng. 2009, 36, 52–56. [Google Scholar]
- Matthies, L.; Kanade, T.; Szeliski, R. Kalman filter-based algorithms for estimating depth from image sequences. Int. J. Comput. Vis. 1989, 3, 209–238. [Google Scholar] [CrossRef]
- Cacuci, D.; Navon, I.; Ionescu-Bujor, M. Computational Methods for Data Evaluation and Assimilation; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar] [CrossRef]
- Van Loon, M.; Builtjes, P.; Segers, A.J. Data assimilation of ozone in the atmospheric transport chemistry model LOTOS. Environ. Model. Softw. 2000, 15, 603–609. [Google Scholar] [CrossRef]
- Evensen, G. The Ensemble Kalman Filter: Theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Bengtsson, L.; Ghil, M.; Källén, E. Dynamic Meteorology: Data Assimilation Methods; Springer: New York, NY, USA, 1981; Volume 36, ISBN 978-0-387-90632-4. [Google Scholar]
- Asch, M.; Bocquet, M.; Nodet, M. Data Assimilation: Methods, Algorithms, and Applications; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2016; ISBN 978-1-611974-53-9. [Google Scholar]
- Lorenc, A.C. Analysis methods for numerical weather prediction. Q. J. R. Meteorol. Soc. 1986, 112, 1177–1194. [Google Scholar] [CrossRef]
- Senne, K. Stochastic processes and filtering theory. IEEE Trans. Autom. Control 2003, 17, 752–753. [Google Scholar] [CrossRef]
- Shi, P.; Luan, X.L.; Liu, F.; Karimi, H.R. Kalman Filtering on Greenhouse Climate Control. In Proceedings of the 31st Chinese Control Conference, Hefei, China, 25–27 July 2012; pp. 779–784. [Google Scholar]
- Heemink, A.; Bolding, K.; Verlaan, M. Storm surge forecasting using Kalman filtering. J. Meteorol. Soc. Jpn. Ser. II 2001, 75, 305–318. [Google Scholar] [CrossRef]
- Li, Q.; Ranyang, L.; Ji, K.; Dai, W. Kalman Filter and Its Application. In Proceedings of the 2015 8th International Conference on Intelligent Networks and Intelligent Systems (ICINIS), Tianjin, China, 1–3 November 2015. [Google Scholar]
- Van Hinsbergen, C.P.I.J.; Schreiter, T.; Zuurbier, F.S.; Van Lint, J.W.C.; van Zuylen, H.J. Localized Extended Kalman Filter for Scalable Real-Time Traffic State Estimation. IEEE Trans. Intell. Transp. Syst. 2012, 13, 385–394. [Google Scholar] [CrossRef]
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. Ocean 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Evensen, G.; Van Leeuwen, P.J. Assimilation of Geosat Altimeter Data for the Agulhas Current using the Ensemble Kalman Filter with a Quasi-Geostrophic Model. Mon. Weather Rev. 1995, 124, 85–96. [Google Scholar] [CrossRef]
- Houtekamer, P.L.; Mitchell, H.L. Ensemble Kalman filtering. Q. J. R. Meteorol. Soc. 2005, 131, 3269–3289. [Google Scholar] [CrossRef]
- Houtekamer, P.; Mitchell, H. Data Assimilation Using an Ensemble Kalman Filter Technique. Mon. Weather Rev. 1998, 126, 796–811. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K.; Durrant-Whyte, H.F. A new approach for filtering nonlinear systems. In Proceedings of the 1995 American Control Conference—ACC’95, Seattle, WA, USA, 21–23 June 1995; pp. 1628–1632. [Google Scholar]
- Wan, E.A.; van der Merwe, R. The Unscented Kalman Filter; Wiley: New York, NY, USA, 2001; pp. 221–280. ISBN 9780471221548. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. A New Extension of the Kalman Filter to Nonlinear Systems. In Proceedings of the SPIE—The International Society for Optical Engineering, Orlando, FL, USA, 28 July 1997; Volume 3068, pp. 182–193. [Google Scholar] [CrossRef]
- Yan, H.L.; Huang, G.H.; Wang, H.W.; Shu, R. Application of Unscented Kalman Filter for Flying Target Tracking. In Proceedings of the 2013 International Conference on Information Science and Cloud Computing (ISCC), Guangzhou, China, 7–8 December 2013; pp. 61–66. [Google Scholar]
- Ding, Q.C.; Zhao, X.G.; Han, J.D. Adaptive Unscented Kalman Filters Applied to Visual Tracking. In Proceedings of the 2012 IEEE International Conference on Information and Automation (ICIA), Shenyang, China, 6–8 June 2012; pp. 491–496. [Google Scholar]
- Wan, E.; Merwe, R.; Nelson, A. Dual Estimation and the Unscented Transformation. Adv. Neural Inf. Process. Syst. 2000, 12, 666–672. [Google Scholar]
- Luan, X.L.; Shi, Y.; Liu, F. Unscented Kalman Filtering for Greenhouse Climate Control Systems with Missing Measurement. Int. J. Innov. Comput. Inf. Control. 2012, 8, 2173–2180. [Google Scholar]
- Tchamitchian, M.; Tantau, H. Optimal Control of the Daily Greenhouse Climate: Physical Approach. IFAC Proc. Vol. 1996, 29, 973–977. [Google Scholar] [CrossRef]
- Yan-Xia, S.; Yuan, Z. State of charge estimation of lithium-ion battery based on unscented Kalman filter. Chin. J. Power Sources 2014, 4, 15–34. [Google Scholar]
- Akhlaghi, S.; Zhou, N.; Huang, Z.Y. Adaptive Adjustment of Noise Covariance in Kalman Filter for Dynamic State Estimation. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, W. An Optimal Adaptive Kalman Filter. J. Geod. 2006, 80, 177–183. [Google Scholar] [CrossRef]
- Whitaker, J.S.; Hamill, T.M. Ensemble data assimilation without perturbed observations. Mon. Weather Rev. 2006, 134, 1722. [Google Scholar] [CrossRef]
- Bishop, C.H.; Etherton, B.J.; Majumdar, S.J. Adaptive sampling with the ensemble transform Kalman filter. Part I: Theoretical aspects. Mon. Weather Rev. 2001, 129, 420–436. [Google Scholar] [CrossRef]
- Anderson, J.L. An ensemble adjustment Kalman filter for data assimilation. Mon. Weather Rev. 2001, 129, 2884–2903. [Google Scholar] [CrossRef]
- Vetra-Carvalho, S.; Van Leeuwen, P.J.; Nerger, L.; Barth, A.; Altaf, M.U.; Brasseur, P.; Kirchgessner, P.; Beckers, J.-M. State-of-the-art stochastic data assimilation methods for high-dimensional non-Gaussian problems. Tellus A Dyn. Meteorol. Oceanogr. 2018, 70, 1445364. [Google Scholar] [CrossRef]
- Hansen, J.A.; Smith, L.A. Probabilistic noise reduction. Tellus A Dyn. Meteorol. Oceanogr. 2001, 53, 585–598. [Google Scholar] [CrossRef][Green Version]
- Merwe, R.V.D.; Doucet, A.; Freitas, N.D.; Wan, E. The Unscented Particle Filter. Adv. Neural Inf. Process. Syst. 2001, 13, 1–7. [Google Scholar]
- Merwe, R.V.D.; Wan, E.A. The square-root unscented Kalman filter for state and parameter-estimation. In Proceedings of the 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing. Proceedings (Cat. No.01CH37221), Salt Lake City, UT, USA, 7–11 May 2001; pp. 3461–3464. [Google Scholar]
- Dimet, F.L.; Talagrand, O. Variational algorithms for analysis and assimilation of meteorological observations: Theoretical aspects. Tellus A Dyn. Meteorol. Oceanogr. 1986, 38A, 97–110. [Google Scholar] [CrossRef]
- Courtier, P.; Talagrand, O. Variational Assimilation of Meteorological Observations with the Adjoint Vorticity Equation. Ii: Numerical Results. Q. J. R. Meteorol. Soc. 1987, 113, 1329–1347. [Google Scholar] [CrossRef]
- Kumar, S.V. Traffic Flow Prediction using Kalman Filtering Technique. In TRANSBALTICA 2017: Transportation Science and Technology; Bureika, G., Yatskiv, I., Prentkovskis, O., Maruschak, P., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; Volume 187, pp. 582–587. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).