Estimation of the Concentration of XCO2 from Thermal Infrared Satellite Data Based on Ensemble Learning
Abstract
1. Introduction
2. Data Sources and Processing
2.1. Data Sources
2.1.1. TCCON Data
2.1.2. CrIS
2.1.3. ERA5
2.1.4. Other Parameters
2.2. Data Processing
3. Methodology
3.1. Ensemble Learning Methods
3.2. Model Evaluation Methodology
3.3. Technical Flowchart
4. Feature and Model Experiments
4.1. Correlation and Significance Analysis
4.2. Principal Component Analysis
4.3. Model Training Comparison
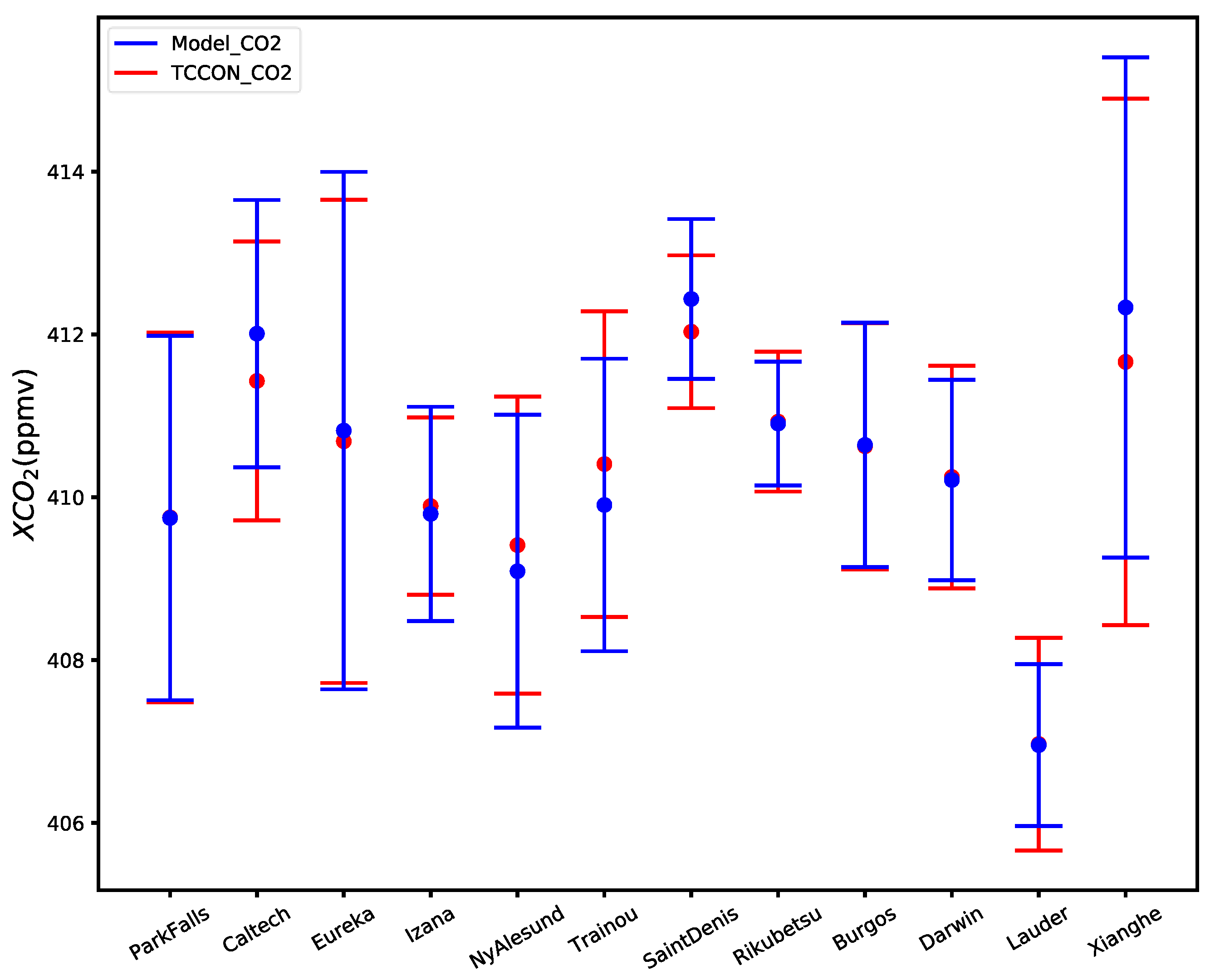
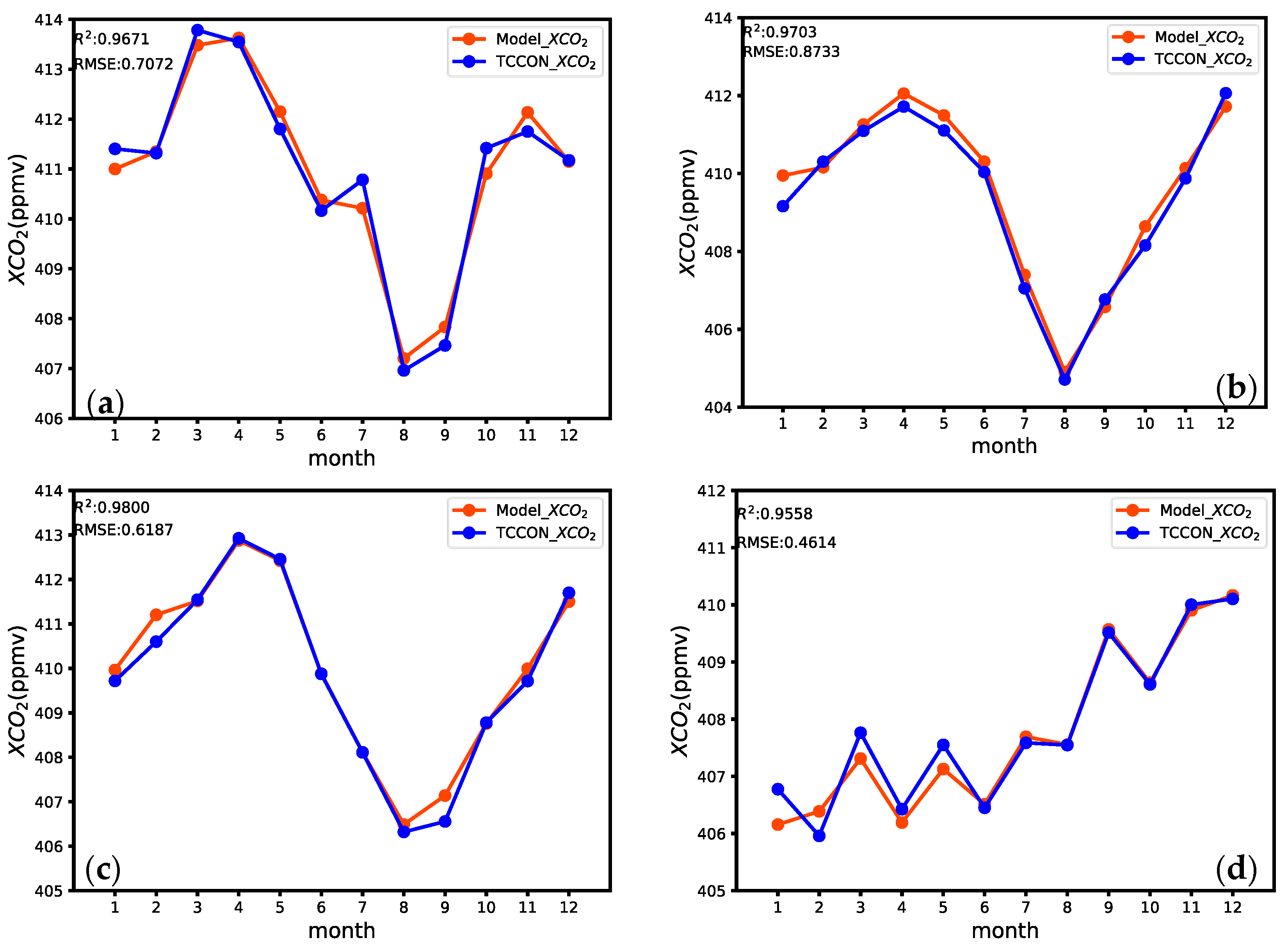
5. Validation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, L.Y.; Chen, L.F. Satellite remote sensing for global stocktaking: Methods, progress and perspectives. Natl. Remote Sens. Bull. 2022, 26, 243–267. [Google Scholar] [CrossRef]
- Yoro, K.O.; Daramola, M.O. CO2 emission sources, greenhouse gases, and the global warming effect. In Advances in Carbon Capture; Woodhead Publishing: Cambridge, UK, 2020; pp. 3–28. [Google Scholar]
- Rogelj, J.; Huppmann, D.; Krey, V.; Riahi, K.; Clarke, L.; Gidden, M.; Nicholls, Z.; Meinshausen, M. A new scenario logic for the Paris Agreement long-term temperature goal. Nature 2019, 573, 357–363. [Google Scholar] [CrossRef]
- Houweling, S.; Hartmann, W.; Aben, I.; Schrijver, H.; Skidmore, J.; Roelofs, G.J.; Breon, F.M. Evidence of systematic errors in SCIAMACHY-observed CO2; due to aerosols. Atmos. Chem. Phys. 2005, 5, 3003–3013. [Google Scholar] [CrossRef]
- Baker, D.F.; Bösch, H.; Doney, S.C.; O’Brien, D.; Schimel, D.S. Carbon source/sink information provided by column CO2 measurements from the Orbiting Carbon Observatory. Atmos. Chem. Phys. 2010, 10, 4145–4165. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Wang, K.; Chevallier, F.; Zhu, D.; Lian, J.; He, Y.; Tian, H.; Li, J.; Zhu, J.; et al. The size of the land carbon sink in China. Nature 2022, 603, E7–E9. [Google Scholar] [CrossRef] [PubMed]
- Rogalski, A. Recent progress in infrared detector technologies. Infrared Phys. Technol. 2011, 54, 136–154. [Google Scholar] [CrossRef]
- Suto, H.; Kataoka, F.; Kikuchi, N.; Knuteson, R.O.; Butz, A.; Haun, M.; Buijs, H.; Shiomi, K.; Imai, H.; Kuze, A. Thermal and near-infrared sensor for carbon observation Fourier transform spectrometer-2 (TANSO-FTS-2) on the Greenhouse gases Observing SATellite-2 (GOSAT-2) during its first year in orbit. Atmos. Meas. Tech. 2021, 14, 2013–2039. [Google Scholar] [CrossRef]
- Chen, L.F.; Zhang, Y. Overview of atmospheric CO2 remote sensing from space. Natl. Remote Sens. Bull. 2015, 19, 1–11. [Google Scholar]
- Ying, X. An Overview of Overfitting and its Solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Bai, L.; Tao, J.; Chen, L.; Zou, M.; Han, Z.; Wang, Z. Retrieval of Carbon Dioxide Using Cross-Track Infrared Sounder (CrIS) on S-NPP. Remote Sens. 2021, 13, 1163. [Google Scholar] [CrossRef]
- Li, J.B.; Zhang, Y.; Gai, R.L. CO2 satellite inversion method based on machine learning for short wave infrared channel. China Environ. Sci. 2023, 43, 1499–1509. [Google Scholar]
- Zhao, Z.; Xie, F.; Ren, T.; Zhao, C. Atmospheric CO2 retrieval from satellite spectral measurements by a two-step machine learning approach. J. Quant. Spectrosc. Radiat. Transf. 2022, 108006. [Google Scholar] [CrossRef]
- David, L.; Bréon, F.-M.; Chevallier, F. XCO2 estimates from the OCO-2 measurements using a neural network approach. Atmos. Meas. Tech. 2020, 14, 117–132. [Google Scholar] [CrossRef]
- Dong, X.; Yu, Z.; Cao, W.; Shi, Y.; Ma, Q. A survey on ensemble learning. Front. Comput. Sci. 2019, 14, 241–258. [Google Scholar] [CrossRef]
- He, Q.; Ye, T.; Chen, X.; Dong, H.; Wang, W.; Liang, Y.; Li, Y. Full-coverage mapping high-resolution atmospheric CO2 concentrations in China from 2015 to 2020: Spatiotemporal variations and coupled trends with particulate pollution. J. Clean. Prod. 2023, 428, 139290. [Google Scholar] [CrossRef]
- Messerschmidt, J.; Geibel, M.C.; Blumenstock, T.; Chen, H.; Deutscher, N.M.; Engel, A.; Feist, D.G.; Gerbig, C.; Gisi, M.; Hase, F.; et al. Calibration of TCCON column-averaged CO2: The first aircraft campaign over European TCCON sites. Atmos. Chem. Phys. 2011, 11, 10765–10777. [Google Scholar] [CrossRef]
- Wunch, D.; Toon, G.C.; Blavier, J.F.L.; Washenfelder, R.A.; Notholt, J.; Connor, B.J.; Griffith, D.W.T.; Sherlock, V.; Wennberg, P.O. The total carbon column observing network. Philos. Trans. R. Soc. A 2011, 369, 2087–2112. [Google Scholar] [CrossRef]
- Dupuy, E.; Morino, I.; Deutscher, N.M.; Yoshida, Y.; Uchino, O.; Connor, B.J.; De Mazière, M.; Griffith, D.W.T.; Hase, F.; Heikkinen, P.; et al. Comparison of XH2O Retrieved from GOSAT Short-Wavelength Infrared Spectra with Observations from the TCCON Network. Remote Sens. 2016, 8, 414. [Google Scholar] [CrossRef]
- Total Carbon Column Observing Network (TCCON) Team. 2020 TCCON Data Release; CaltechDATA: Pasadena, CA, USA, 2022. [Google Scholar] [CrossRef]
- Fu, D.; Bowman, K.W.; Worden, H.M.; Natraj, V.; Worden, J.R.; Yu, S.; Veefkind, P.; Aben, I.; Landgraf, J.; Strow, L.; et al. High-resolution tropospheric carbon monoxide profiles retrieved from CrIS and TROPOMI. Atmos. Meas. Tech. 2016, 9, 2567–2579. [Google Scholar] [CrossRef]
- Gambacorta, A.; Barnet, C.D. Methodology and Information Content of the NOAA NESDIS Operational Channel Selection for the Cross-Track Infrared Sounder (CrIS). IEEE Trans. Geosci. Remote Sens. 2013, 51, 3207–3216. [Google Scholar] [CrossRef]
- Smith, N.; Barnet, C.D. Uncertainty characterization and propagation in the community long-term infrared microwave combined atmospheric product system (CLIMCAPS). Remote Sens. 2019, 11, 1227. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Y.; Cai, K.; Zhu, S.; Zhang, X.; Chen, L. Evaluating the performance of ozone products derived from CrIS/NOAA20, AIRS/aqua and ERA5 reanalysis in the polar regions in 2020 using ground-based observations. Remote Sens. 2021, 13, 4375. [Google Scholar] [CrossRef]
- He, Z.; Lei, L.; Zeng, Z.C.; Sheng, M.; Welp, L.R. Evidence of carbon uptake associated with vegetation greening trends in eastern China. Remote Sens. 2020, 12, 718. [Google Scholar] [CrossRef]
- MOD13GA. Available online: https://ladsweb.modaps.eosdis.nasa.gov/missions-and-measurements/products/MOD13GA (accessed on 5 March 2022).
- Yang, J.; Yao, Y.; Wei, Y.; Zhang, Y.; Jia, K.; Zhang, X.; Shang, K.; Bei, X.; Guo, X. A Robust Method for Generating High-Spatiotemporal-Resolution Surface Reflectance by Fusing MODIS and Landsat Data. Remote Sens. 2020, 12, 2312. [Google Scholar] [CrossRef]
- Zhao, L.; Chen, S.; Xue, Y.; Cui, T. Study of Atmospheric Carbon Dioxide Retrieval Method Based on Normalized Sensitivity. Remote Sens. 2022, 14, 1106. [Google Scholar] [CrossRef]
- MOD13Q1. Available online: https://ladsweb.modaps.eosdis.nasa.gov/missions-and-measurements/products/MOD13Q1 (accessed on 20 March 2022).
- National Geophysical Data Center. Global Land One-km Base Elevation Project (GLOBE Topography); National Geophysical Data Center: Boulder, Colorado, 1999. [Google Scholar]
- Kumar, Y.; Kaur, K.; Singh, G. Machine learning aspects and its applications towards different research areas. In Proceedings of the 2020 International Conference on Computation, Automation and Knowledge Management (ICCAKM), Dubai, United Arab Emirates, 9–10 January 2020; pp. 150–156. [Google Scholar]
- Zhang, M.; Liu, G. Mapping contiguous XCO2 by machine learning and analyzing the spatio-temporal variation in China from 2003 to 2019. Sci. Total Environ. 2023, 858, 159588. [Google Scholar] [CrossRef] [PubMed]
- Song, S.P.; Fan, M. Estimating ground-level ozone concentration in China using ensemble learning methods. Natl. Remote Sens. Bull. 2023, 27, 1792–1806. [Google Scholar]
- Kunapuli, G. Ensemble Methods for Machine Learning; Simon and Schuster: New York City, NY, USA, 2023. [Google Scholar]
- Tang, W.Y.; Zhou, Z.H. Bagging-based selective clusterer ensemble. J. Softw. 2005, 16, 496–502. [Google Scholar] [CrossRef][Green Version]
- Yu, L.; Wu, D.J. Assemble Learning: A Survey of Boosting Algorithms. Pattern Recognit. Artif. Intell. 2004, 17, 52–59. [Google Scholar]
- Polikar, R. Ensemble learning. In Ensemble Machine Learning: Methods and Applications; Springer: New York, NY, USA, 2012; pp. 1–34. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Xu, S.; Ni, C.; Hu, X. Predicting Terrestrial Heat Flow in North China Using Multiple Geological and Geophysical Datasets Based on Machine Learning Method. Energies 2023, 16, 1620. [Google Scholar] [CrossRef]
- He, S.; Yuan, Y.; Wang, Z.; Luo, L.; Zhang, Z.; Dong, H.; Zhang, C. Machine Learning Model-Based Estimation of XCO2 with High Spatiotemporal Resolution in China. Atmosphere 2023, 14, 436. [Google Scholar] [CrossRef]
- Nagelkerke, N.J.D. A note on a general definition of the coefficient of determination. Biometrika 1991, 78, 691–692. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Hodson, T.O. Root-mean-square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Armstrong, R.A. Should Pearson’s correlation coefficient be avoided. Ophthalmic Physiol. Opt. 2019, 39, 316–327. [Google Scholar] [CrossRef]
- Goïta, K.; Magagi, R.; Beauregard, V.; Wang, H. Retrieval of Surface Soil Moisture over Wheat Fields during Growing Season Using C-Band Polarimetric SAR Data. Remote Sens. 2023, 15, 4925. [Google Scholar] [CrossRef]
- Frappart, F.; Ramillien, G.; Seoane, L. Monitoring Water Mass Redistributions on Land and Polar Ice Sheets Using the GRACE Gravimetry from Space Mission. In Land Surface Remote Sensing in Continental Hydrology; Elsevier: Amsterdam, The Netherlands, 2016; pp. 255–279. [Google Scholar]
- Song, W.; Han, X.; Qi, J. Prediction of Gas Emission in the Working Face Based on LASSO-WOA-XGBoost. Atmosphere 2023, 14, 1628. [Google Scholar] [CrossRef]
- Stephen, B.; Hastie, T.; Tibshirani, R. Cross-validation: What does it estimate and how well does it do it. J. Am. Stat. Assoc. 2023, 1–12. [Google Scholar] [CrossRef]
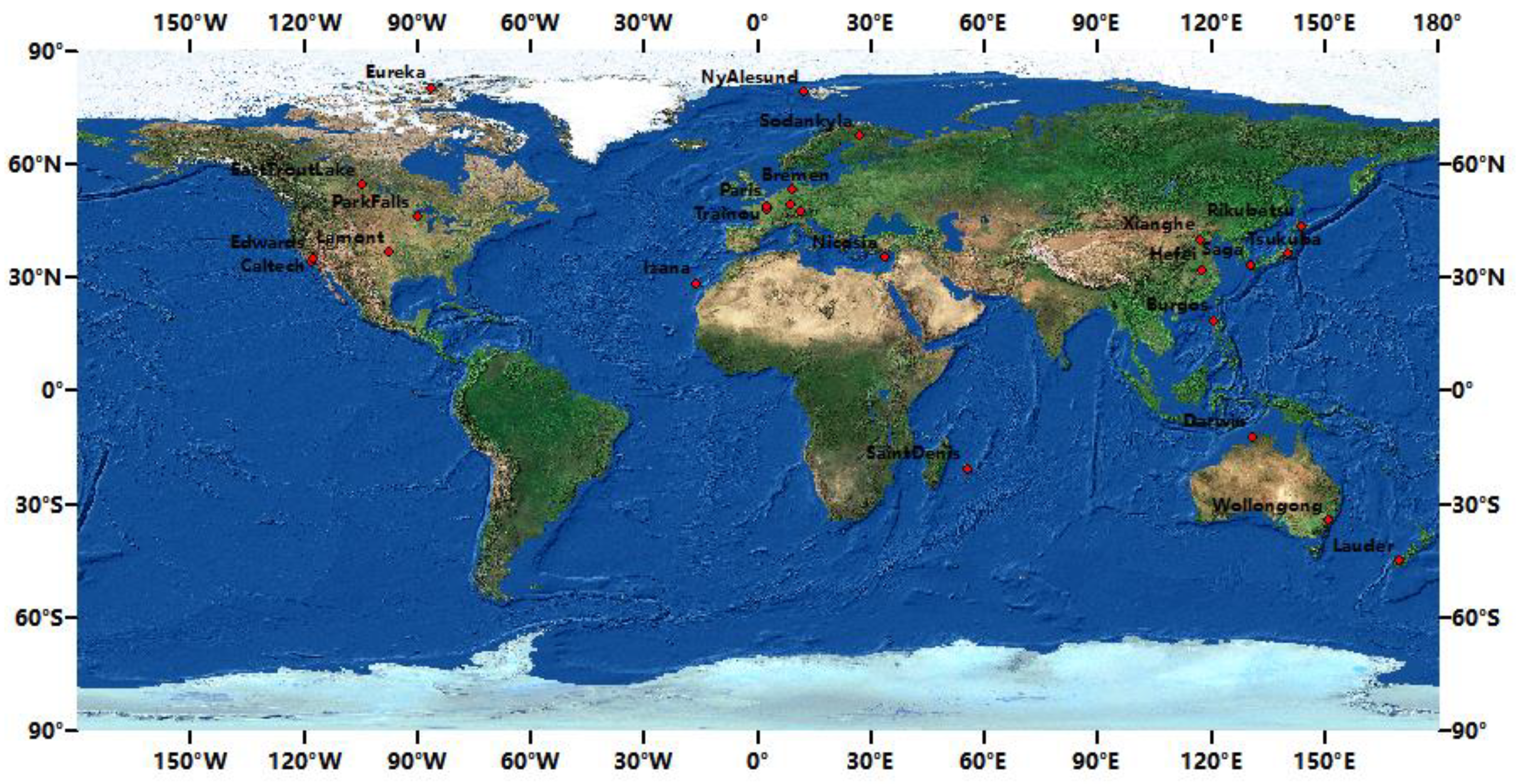






| Name | Lon | Lat | Number | Name | Lon | Lat | Number |
|---|---|---|---|---|---|---|---|
| Xianghe | 116.96 | 39.8 | 16,075 | Rikubetsu | 143.77 | 43.46 | 3976 |
| Hefei | 117.17 | 31.91 | 3002 | SaintDenis | 26.63 | 67.37 | 9825 |
| Zugspitze | 10.98 | 47.42 | 3567 | Paris | 2.36 | 48.85 | 21,442 |
| Wollongong | 150.88 | −34.41 | 19,508 | ParkFalls | −90.27 | 45.94 | 21,986 |
| Tsukuba | 140.12 | 36.05 | 13,990 | Trainou | 2.11 | 47.97 | 15,753 |
| NyAlesund | 11.92 | 78.92 | 4736 | Lamont | −97.49 | 36.6 | 28,766 |
| Lauder | 169.68 | −45.04 | 42,984 | Eureka | −86.42 | 80.05 | 7652 |
| Karlsruhe | 8.44 | 49.1 | 8229 | EastTrout | −104.99 | 54.36 | 39,992 |
| Saga | 130.29 | 33.24 | 15,147 | Edwards | −117.88 | 34.96 | 57,555 |
| Izana | −16.48 | 28.3 | 12,940 | Darwin | 130.89 | −12.43 | 12,838 |
| Garmisch | 47.48 | 11.06 | 8803 | Caltech | −118.13 | 34.14 | 36,000 |
| Bremen | 8.85 | 53.1 | 1451 | Burgos | 120.65 | 18.53 | 32,649 |
| Sodankyla | 26.63 | 67.37 | 13,050 | Nicosia | 33.38 | 35.14 | 10,476 |
| Variable Abbreviation | Full Name of the Variable | Unit | Temporal Resolution | Spatial Resolution | Data Sources |
|---|---|---|---|---|---|
| XCO2 | Column-averaged CO2 dry air mole fraction | ppmv | - | - | TCCON |
| lon | Longitude | 6 min | 50 km × 50 km | Cloud-cleared radiances V2 | |
| lat | Latitude | ||||
| month | Month | m | |||
| dd | Days | d | |||
| band | Radiance | mw/(m2 sr cm−1) | |||
| sza | Solar zenith angle | - | |||
| saa | Solar azimuth angle | degree | |||
| za | Zenith angle | - | |||
| aa | Azimuth angle | - | |||
| P1 * | 100 hpa | hPa | 1 h | 0.25° × 0.25° | ERA5 |
| T1 * | Temperature at 100 hpa | K | |||
| U1 * | U-component of wind at 100 hpa | m/s | |||
| V1 * | V-component of wind at 100 hpa | m/s | |||
| W1 * | Vertical velocity at 100 hpa | pa/s | |||
| blh | Boundary layer height | m | |||
| cbh | Cloud bottom height | m | |||
| tp | Total precipitation | - | |||
| cl | Lake cover | - | |||
| tcc | Total cloud coverage | - | |||
| skt | Skin temperature | K | |||
| t2m | 2 m Temperature | K | |||
| tco3 | Total column ozone | kg/m−2 | |||
| NDVI | Normalized difference vegetation index | - | 16 d | 250 m × 250 m | MOD13Q1 |
| SR | Surface reflectance | % | 1 d | 500 m × 500 m | MOD09GA |
| DEM | Digital elevation model | m | - | - | GLOBE Topography |
| Model | n_Estimators | Max_Depth | Min_Samples_Split | Min_Samples_Leaf |
|---|---|---|---|---|
| ERT | 400 | 30 | 5 | 1 |
| GBRT | 300 | 25 | 5 | 5 |
| XGBoost | 400 | 30 | 8 | 0.2 |
| Model | R2 | RMSE (ppmv) | MAE (ppmv) |
|---|---|---|---|
| ERT (PCA) | 0.9231 | 0.7552 | 0.5568 |
| ERT (CSA) | 0.9029 | 0.8026 | 0.5704 |
| GBRT (PCA) | 0.9067 | 0.7907 | 0.5812 |
| GBRT (CSA) | 0.8938 | 0.8458 | 0.6163 |
| XGBoost (PCA) | 0.8995 | 0.8382 | 0.6371 |
| XGBoost (CSA) | 0.8701 | 0.9368 | 0.6777 |
| Model | R2 | RMSE (ppmv) | MAE (ppmv) |
|---|---|---|---|
| ERT | 0.9006 | 0.7994 | 0.5804 |
| GBRT | 0.8720 | 0.9068 | 0.6705 |
| XGBoost | 0.8768 | 0.8897 | 0.6624 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, X.; Zhang, Y.; Fan, M.; Zhang, X.; Song, S.; Li, Z. Estimation of the Concentration of XCO2 from Thermal Infrared Satellite Data Based on Ensemble Learning. Atmosphere 2024, 15, 118. https://doi.org/10.3390/atmos15010118
Gong X, Zhang Y, Fan M, Zhang X, Song S, Li Z. Estimation of the Concentration of XCO2 from Thermal Infrared Satellite Data Based on Ensemble Learning. Atmosphere. 2024; 15(1):118. https://doi.org/10.3390/atmos15010118
Chicago/Turabian StyleGong, Xiaoyong, Ying Zhang, Meng Fan, Xinxin Zhang, Shipeng Song, and Zhongbin Li. 2024. "Estimation of the Concentration of XCO2 from Thermal Infrared Satellite Data Based on Ensemble Learning" Atmosphere 15, no. 1: 118. https://doi.org/10.3390/atmos15010118
APA StyleGong, X., Zhang, Y., Fan, M., Zhang, X., Song, S., & Li, Z. (2024). Estimation of the Concentration of XCO2 from Thermal Infrared Satellite Data Based on Ensemble Learning. Atmosphere, 15(1), 118. https://doi.org/10.3390/atmos15010118








