Spatial Distribution Characteristics and Analysis of PM2.5 in South Korea: A Geographically Weighted Regression Analysis
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Dataset Materials
2.2.1. Air Pollution Data
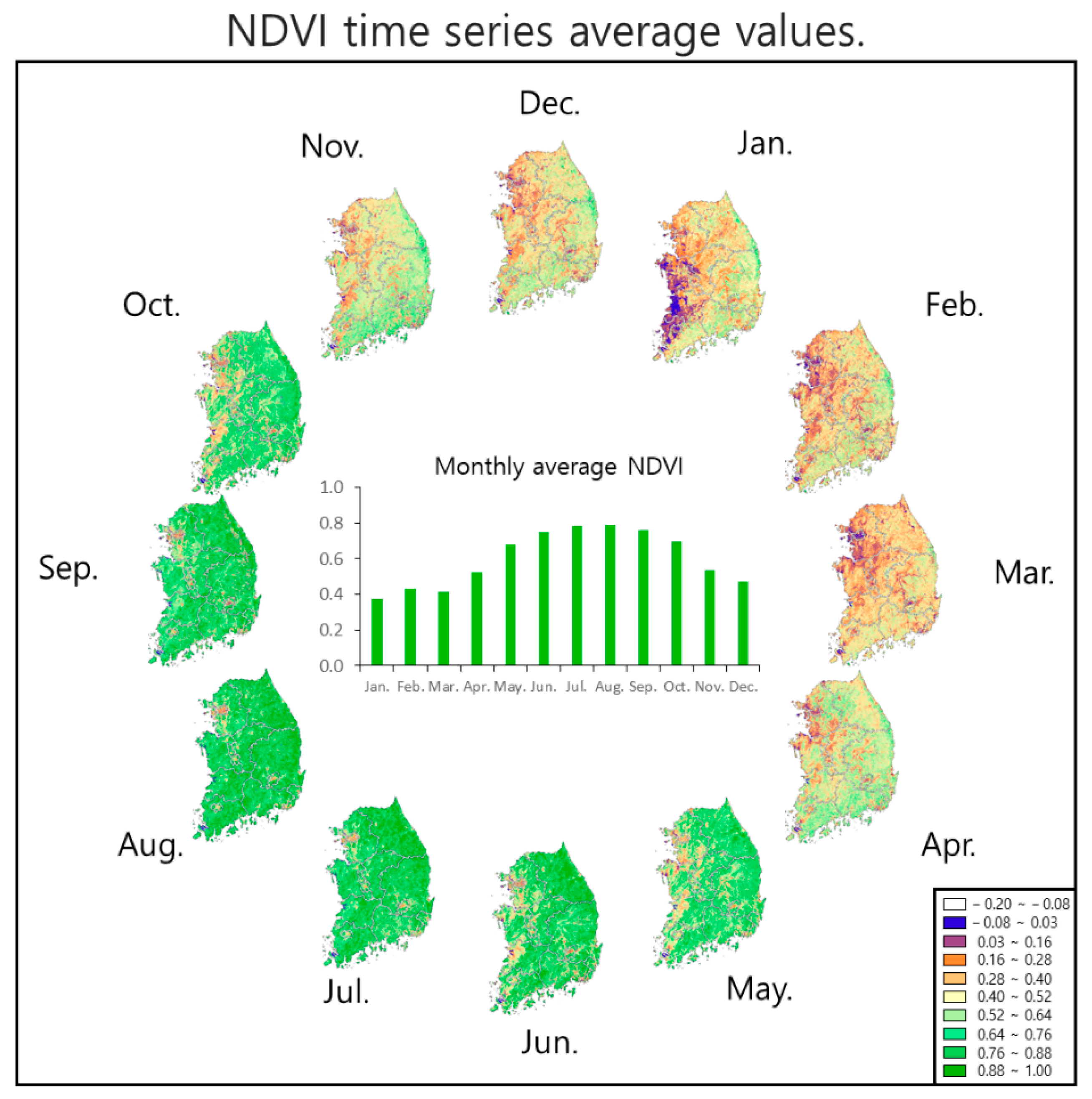
2.2.2. NDVI
2.2.3. Meteorological Data
2.3. Methods
2.3.1. Empirical Bayesian Kriging
2.3.2. Pearson’s Correlation Coefficient Method
2.3.3. Variance Inflation Factor
2.3.4. Global Moran’s Index
2.3.5. GWR Model
3. Results and Discussion
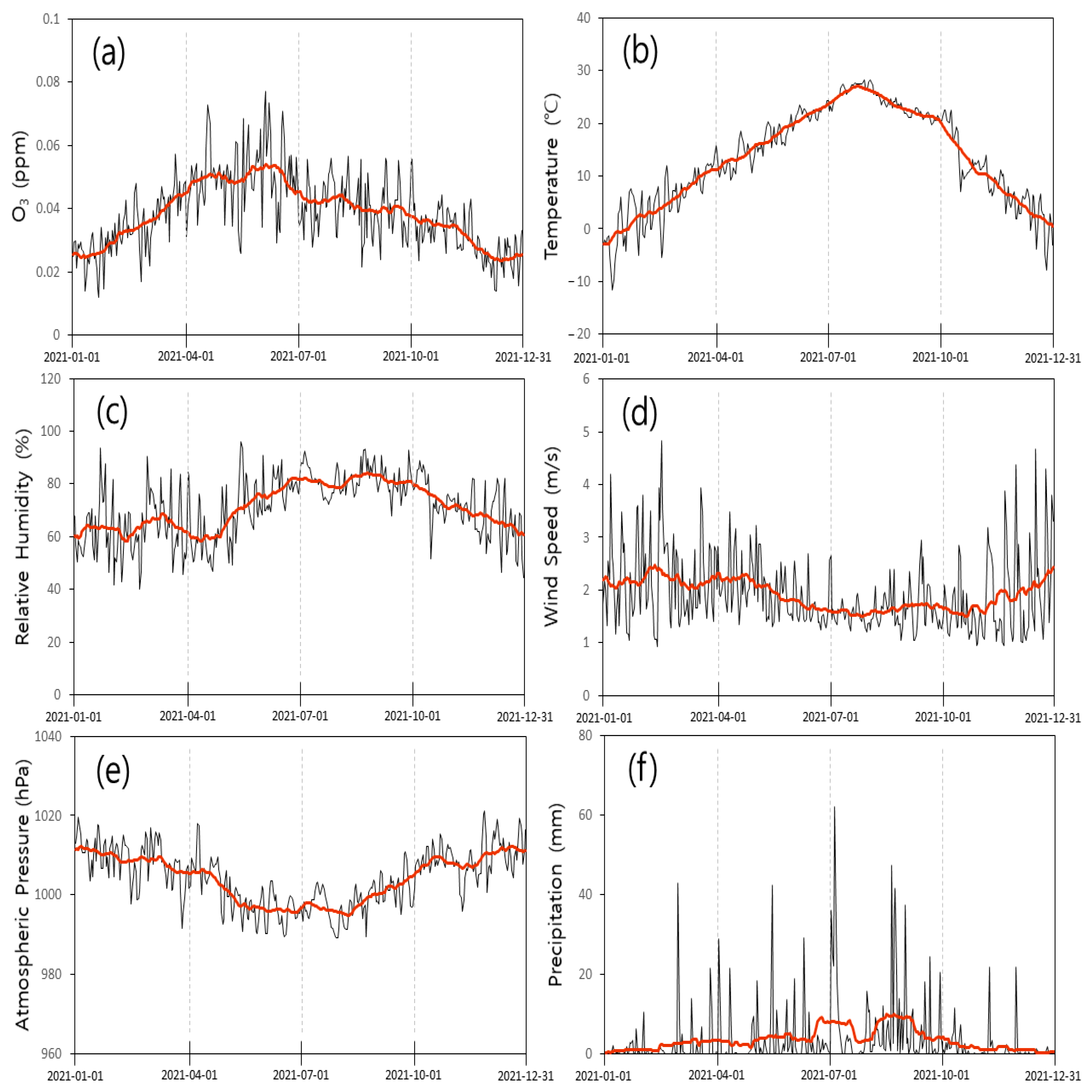
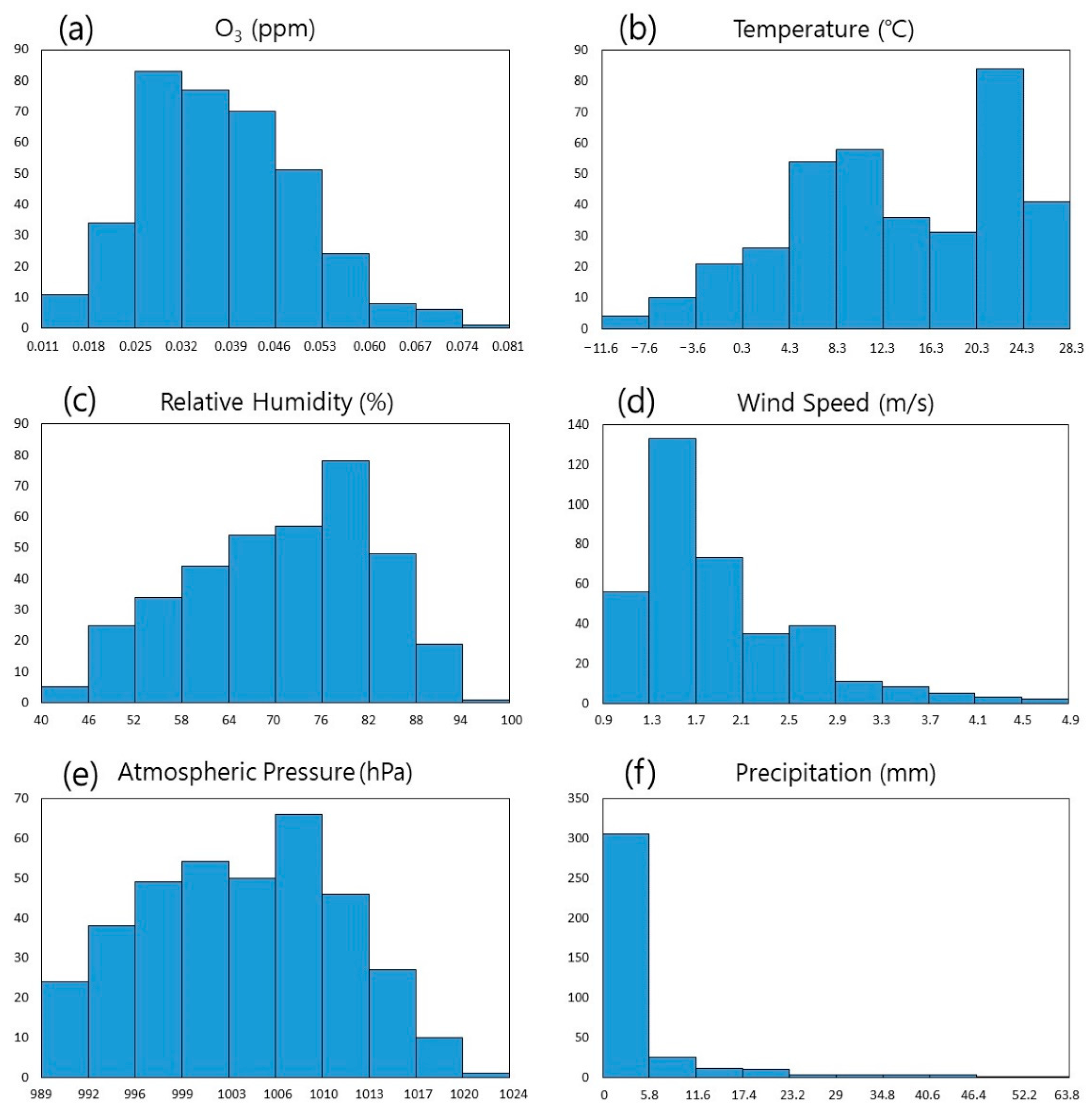
3.1. Analysis of Independent Variable Data
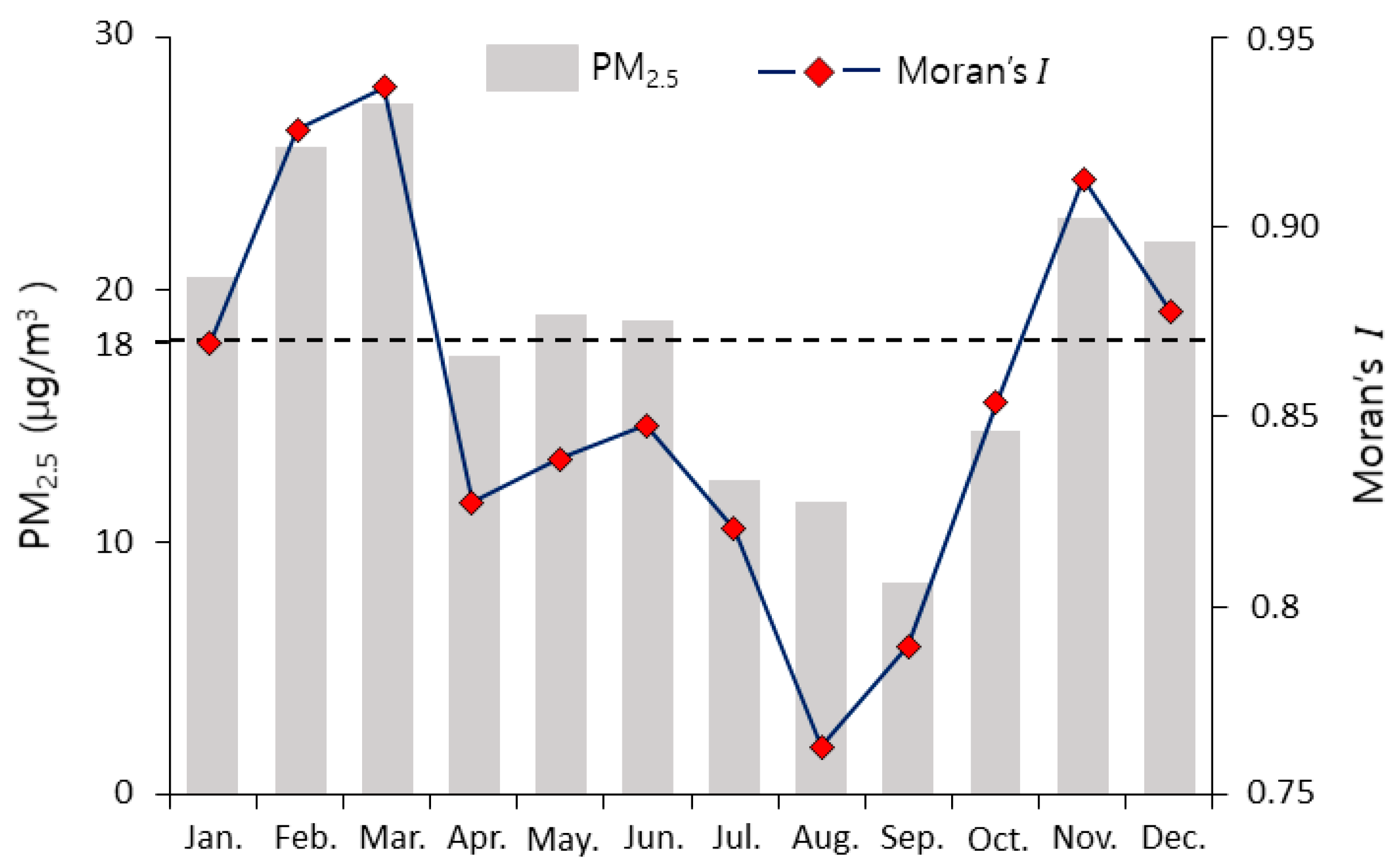
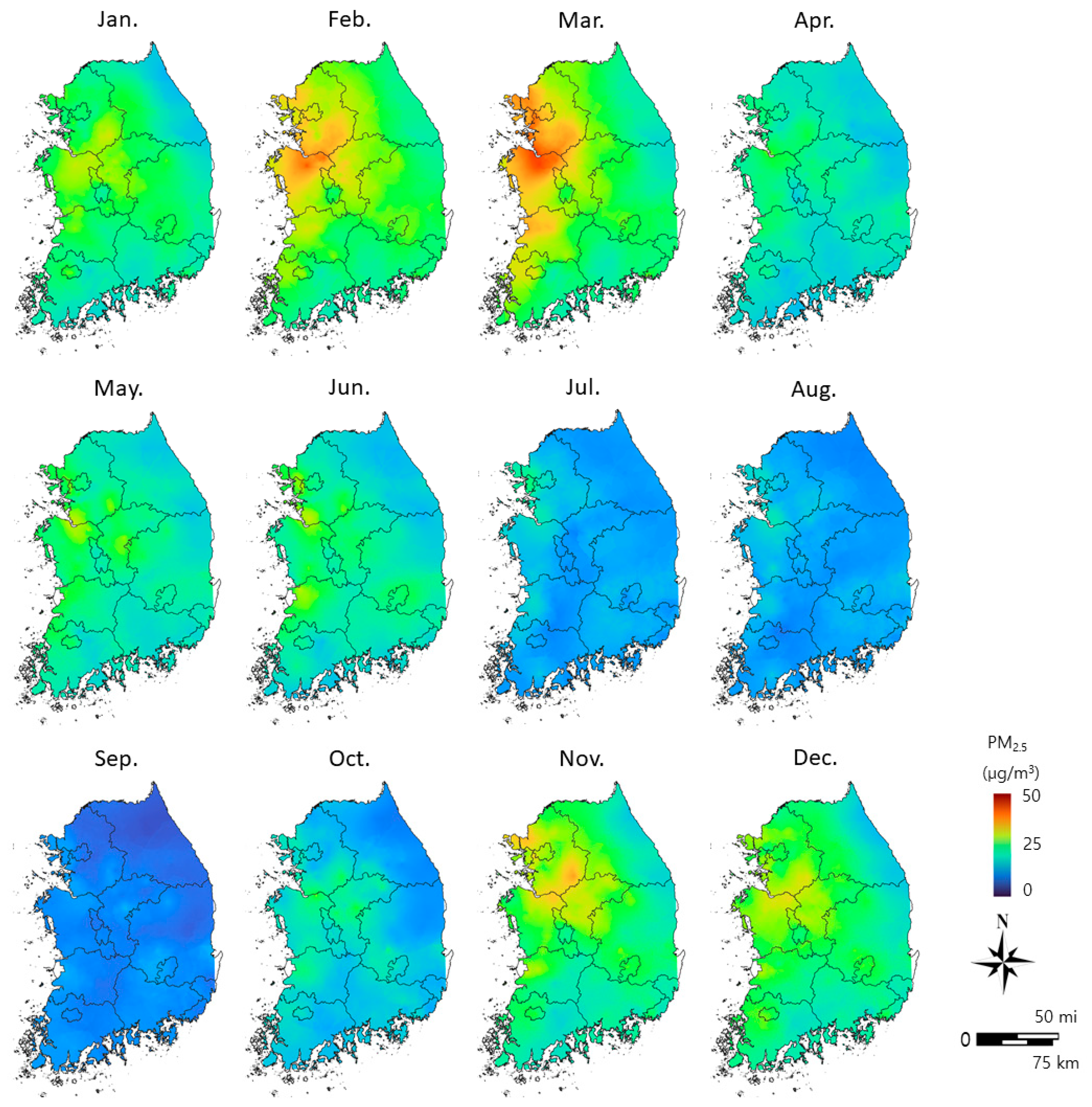
3.2. Spatiotemporal Distribution Characteristics of PM2.5
3.3. Pearson’s Correlation Analysis
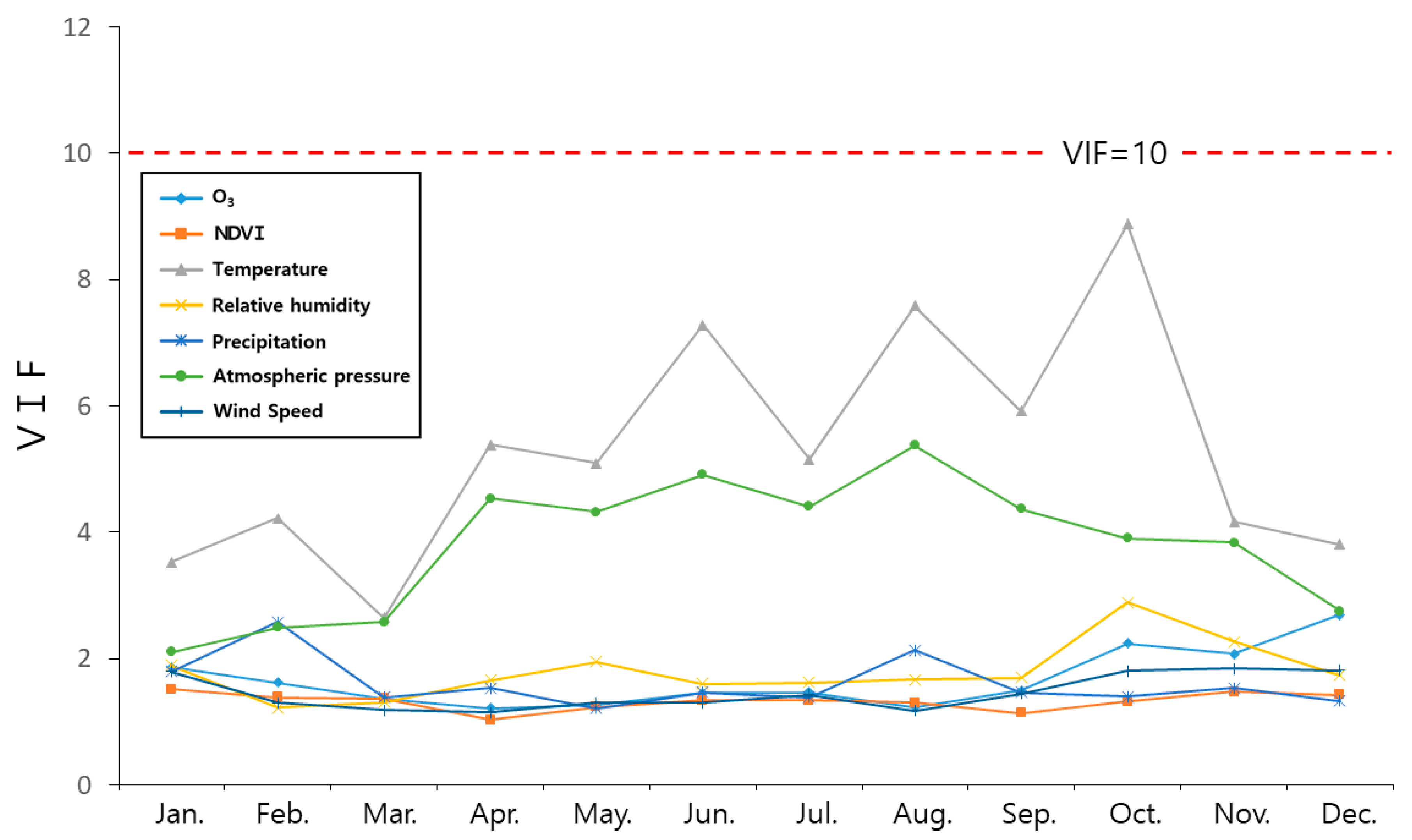
3.4. Multicollinearity Analysis
3.5. GWR Model Analysis
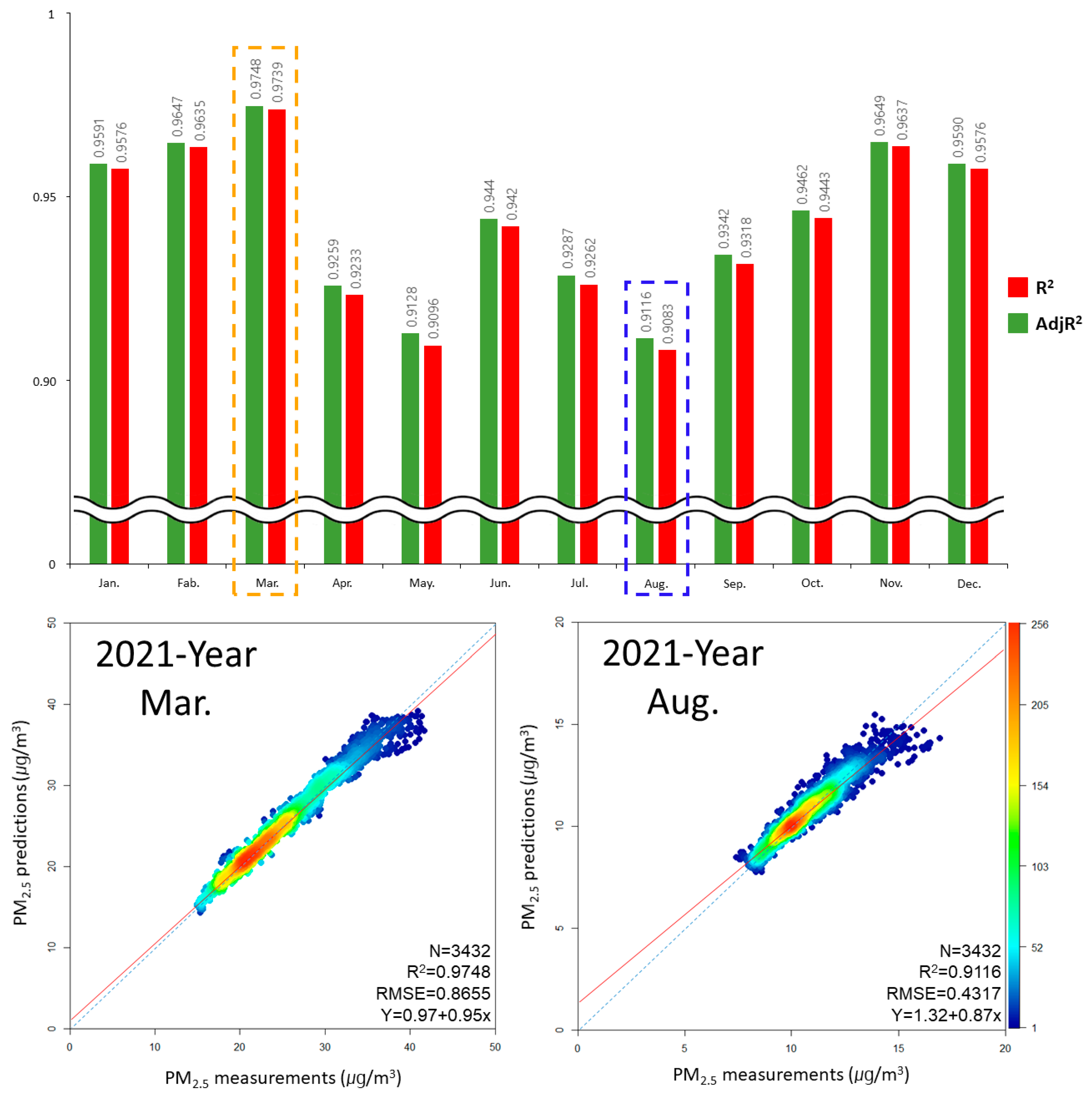
3.5.1. Analysis of the Coefficient of Determination
3.5.2. Spatiotemporal Heterogeneity Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brunekreef, B.; Holgate, S.T. Air pollution and health. Lancet 2002, 360, 1233–1242. [Google Scholar] [CrossRef] [PubMed]
- Xing, Y.F.; Xu, Y.H.; Shi, M.H.; Lian, Y.X. The impact of PM2.5 on the human respiratory system. J. Thorac. Dis. 2016, 8, E69. [Google Scholar] [PubMed]
- IARC. Air Pollution and Cancer (Scientific Publication No. 161); WHO Press: Geneva, Switzerland, 2013. [Google Scholar]
- Calvo, A.I.; Alves, C.; Castro, A.; Pont, V.; Vicente, A.M.; Fraile, R. Research on aerosol sources and chemical composition: Past, current and emerging issues. Atmos. Res. 2013, 120–121, 1–28. [Google Scholar] [CrossRef]
- Pacyna, E.G.; Pacyna, J.M.; Fudala, J.; Strzelecka-Jastrzab, E.; Hlawiczka, S.; Panasiuk, D.; Nitter, S.; Pregger, T.; Pfeiffer, H.; Friedrich, R. Current and future emissions of selected heavy metals to the atmosphere from anthropogenic sources in Europe. Atmos. Environ. 2007, 41, 8557–8566. [Google Scholar] [CrossRef]
- Liousse, C.; Penner, J.E.C.; Chuang, J.; Walton, J.; Eddleman, H.; Cachier, H. A global three-dimensional model study of carbonaceous aerosols. J. Geophys. Res. Atmos. 1996, 101, 19411–19432. [Google Scholar] [CrossRef]
- Vu, T.V.; Delgado-Saborit, J.M.; Harrison, R.M. Particle number size distributions from seven major sources and implications for source apportionment studies. Atmos. Environ. 2015, 122, 114–132. [Google Scholar] [CrossRef]
- Tucker, W.G. An overview of PM2.5 sources and control strategies. Fuel Process Technol. 2000, 65, 379–392. [Google Scholar] [CrossRef]
- Tomasi, C.; Lupi, A. Primary and secondary sources of atmospheric aerosol. In Atmospheric Aerosols: Life Cycles and Effects on Air Quality and Climate; Wiley: Hoboken, NJ, USA, 2017; pp. 1–86. [Google Scholar]
- Gehrig, R.; Buchmann, B. Characterising seasonal variations and spatial distribution of ambient PM10 and PM2.5 concentrations based on long-term Swiss monitoring data. Atmos. Environ. 2003, 37, 2571–2580. [Google Scholar] [CrossRef]
- Mei, C.L.; He, S.Y.; Fang, K.T. A note on the mixed geographically weighted regression model. J. Reg. Sci. 2004, 44, 143–157. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically weighted regression: A method for exploring spatial nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, B.; Zhang, Y.; Hu, H. Correlation between surface PM2.5 and O3 in eastern China during 2015–2019: Spatiotemporal variations and meteorological impacts. Atmos. Environ. 2023, 294, 119520. [Google Scholar] [CrossRef]
- Deng, X.; Gao, F.; Liao, S.; Li, S. Unraveling the association between the built environment and air pollution from a geospatial perspective. J. Clean. Prod. 2023, 386, 135768. [Google Scholar] [CrossRef]
- National Institute of Meteorological Sciences. 100 Years of Climate Change on the Korean Peninsula; National Institute of Meteorological Sciences: Jeju, Republic of Korea, 2018. [Google Scholar]
- Cressie, N. The origins of kriging. Math. Geol. 1990, 22, 239–252. [Google Scholar] [CrossRef]
- Gribov, A.; Krivoruchko, K. Empirical Bayesian kriging implementation and usage. Sci. Total Environ. 2020, 722, 137290. [Google Scholar] [CrossRef] [PubMed]
- Craney, T.A.; Surles, J.G. Model-dependent variance inflation factor cutoff values. Qual. Eng. 2002, 14, 391–403. [Google Scholar] [CrossRef]
- Moran, P.A. Notes on continuous stochastic phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef] [PubMed]
- National Istitute of Environmental Research. Annual Report of Air Quality in Korea 2020; National Istitute of Environmental Research: Inchen, Republic of Korea, 2020. [Google Scholar]
- Cha, Y.; Song, C.K.; Jeon, K.H.; Yi, S.M. Factors affecting recent PM2.5 concentrations in China and South Korea from 2016 to 2020. Sci. Total Environ. 2023, 881, 163524. [Google Scholar] [CrossRef]
- Kumar, N.; Park, R.J.; Jeong, J.I.; Woo, J.H.; Kim, Y.; Johnson, J.; Yarwood, G.; Kang, S.; Chun, S.; Knipping, E. Contributions of international sources to PM2.5 in South Korea. Atmos. Environ. 2021, 261, 118542. [Google Scholar] [CrossRef]
- Wei, P.; Xie, S.; Huang, L.; Liu, L.; Cui, L.; Tang, Y.; Zhang, Y.; Meng, C.; Zhang, L. Spatial interpolation of regional PM2.5 concentrations in China during COVID-19 incorporating multivariate data. Atmos. Pollut. Res. 2023, 14, 101688. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, L.; Liao, H.; Dang, R. Correlations between PM2.5 and ozone over China and associated underlying reasons. Atmosphere 2019, 10, 352. [Google Scholar] [CrossRef]
- Sun, J.; Wu, F.; Hu, B.; Tang, G.; Zhang, J.; Wang, Y. VOC characteristics, emissions and contributions to SOA formation during hazy episodes. Atmos. Environ. 2016, 141, 560–570. [Google Scholar] [CrossRef]
- Zhang, J.; Wei, Y.; Fang, Z. Ozone pollution: A major health hazard worldwide. Front. Immunol. 2019, 10, 2518. [Google Scholar] [CrossRef] [PubMed]
- Dickerson, R.R.; Kondragunta, S.; Stenchikov, G.; Civerolo, K.L.; Doddridge, B.G.; Holben, B.N. The impact of aerosols on solar ultraviolet radiation and photochemical smog. Science 1997, 278, 827–830. [Google Scholar] [CrossRef] [PubMed]
- Allabakash, S.; Lim, S.; Chong, K.S.; Yamada, T.J. Particulate matter concentrations over South Korea: Impact of meteorology and other pollutants. Remote Sens. 2022, 14, 4849. [Google Scholar] [CrossRef]
- Churkina, G.; Grote, R.; Butler, T.M.; Lawrence, M. Natural selection? Picking the right trees for urban greening. Environ. Sci. Policy 2015, 47, 12–17. [Google Scholar] [CrossRef]
- Calfapietra, C.; Fares, S.; Manes, F.; Morani, A.; Sgrigna, G.; Loreto, F. Role of biogenic volatile organic compounds (BVOC) emitted by urban trees on ozone concentration in cities: A review. Environ. Pollut. 2013, 183, 71–80. [Google Scholar] [CrossRef] [PubMed]
- Fitzky, A.C.; Sandén, H.; Karl, T.; Fares, S.; Calfapietra, C.; Grote, R.; Saunier, A.; Rewald, B. The interplay between ozone and urban vegetation—BVOC emissions, ozone deposition, and tree ecophysiology. Front. For. Glob. Chang. 2019, 2, 50. [Google Scholar] [CrossRef]
- Lu, S.; Yang, X.; Li, S.; Chen, B.; Jiang, Y.; Wang, D.; Xu, L. Effects of plant leaf surface and different pollution levels on PM2.5 adsorption capacity. Urban For. Urban Green. 2018, 34, 64–70. [Google Scholar] [CrossRef]
- Zenk, M.H. Heavy metal detoxification in higher plants—A review. Gene 1996, 179, 21–30. [Google Scholar] [CrossRef]
- Chang, S.Y.; Fang, G.C.; Chou, C.C.K.; Chen, W.N. Chemical compositions and radiative properties of dust and anthropogenic air masses study in Taipei Basin, Taiwan, during spring of 2004. Atmos. Environ. 2006, 40, 7796–7809. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, U.-J.; Kim, M.-J.; Kim, E.-J.; Lee, D.-W.; Lee, S.-D. Spatial Distribution Characteristics and Analysis of PM2.5 in South Korea: A Geographically Weighted Regression Analysis. Atmosphere 2024, 15, 69. https://doi.org/10.3390/atmos15010069
Lee U-J, Kim M-J, Kim E-J, Lee D-W, Lee S-D. Spatial Distribution Characteristics and Analysis of PM2.5 in South Korea: A Geographically Weighted Regression Analysis. Atmosphere. 2024; 15(1):69. https://doi.org/10.3390/atmos15010069
Chicago/Turabian StyleLee, Ui-Jae, Myeong-Ju Kim, Eun-Ji Kim, Do-Won Lee, and Sang-Deok Lee. 2024. "Spatial Distribution Characteristics and Analysis of PM2.5 in South Korea: A Geographically Weighted Regression Analysis" Atmosphere 15, no. 1: 69. https://doi.org/10.3390/atmos15010069
APA StyleLee, U.-J., Kim, M.-J., Kim, E.-J., Lee, D.-W., & Lee, S.-D. (2024). Spatial Distribution Characteristics and Analysis of PM2.5 in South Korea: A Geographically Weighted Regression Analysis. Atmosphere, 15(1), 69. https://doi.org/10.3390/atmos15010069




