Synthetic Wind Estimation for Small Fixed-Wing Drones
Abstract
:1. Introduction
1.1. Pitot Tube: Differential Pressure Sensor
1.2. Analytical Redundancy
Flight Control System
1.3. Wind Estimation in the Environmental Engineering
1.4. Flushed Air Data Systems
1.5. Summary of Existing Works on Wind Estimation
- 1.
- Tethered balloons and anemometers.
- 2.
- Multi-copter-based wind estimation with/without airspeed sensors.
- 3.
- Fixed-wing drones using single-hole/multi-hole pitot tubes and/or distributed sensing modalities for wind estimation.
- 4.
- Fixed-wing/Multi-copters using wind-tunnel calibrated aerodynamic models for wind estimation.
1.6. Problem Statement and Contributions
1.7. Distinction from Closely Related Work
1.8. Motivation and Inspiration
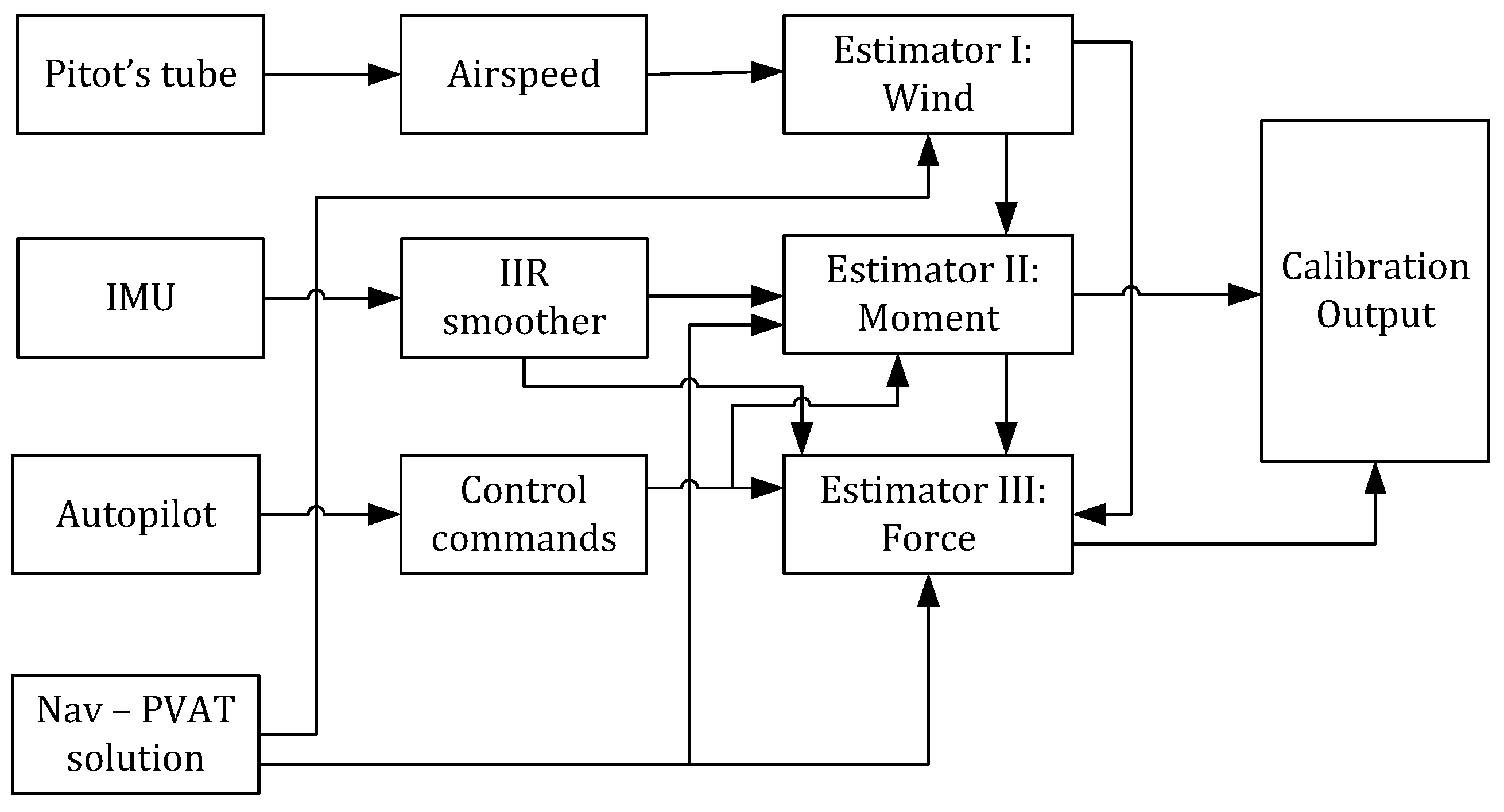
2. Materials and Methods
2.1. VDM-Based Navigation System
2.1.1. Notation
- 1.
- i for the inertial frame;
- 2.
- e for the Earth Centered Earth Fixed (ECEF) frame;
- 3.
- l for the navigation frame (local level parameterized by north, east, and down directions);
- 4.
- b for the body (drone) frame.
- 1.
- Let be the drone’s position in ellipsoidal coordinates (latitude, longitude, and height);
- 2.
- Let be the velocity of the drone in the navigation frame;
- 3.
- Let be the attitude of the drone represented using quaternions (from the body frame to navigation frame);
- 4.
- Let be the angular velocity of the drone with respect to the inertial frame, expressed in drone’s reference frame.
- 1.
- Let be the wind velocity in navigation frame;
- 2.
- . Let define the airspeed, be the angle of attack, and be the angle of side slip; note that ;
- 3.
- Let be the air density and be the dynamic pressure;
- 4.
- n denotes propeller speed;
- 5.
- Let denote ailerons, elevator, and rudder deflections, respectively, for a conventional fixed-wing drone;
- 6.
- For a delta wing drone, denote the deflections of left and right control surfaces (also known as elevons);
- 7.
- , denote wing span, wing surface, mean aerodynamic chord, propeller diameter, inertia tensor, and mass of the drone, respectively;
- 8.
- denotes Jacobian from Cartesian (NED) to ellipsoidal coordinates.
2.1.2. State-Space Representation
2.1.3. VDM for Conventional Fixed-Wing Drone
2.2. VDM for Delta-Wing Drone
2.3. Identifying Aerodynamic Model Parameters
2.4. Kinematics-Based Wind Estimation
2.5. Hardware: Conventional Fixed-Wing Drone
2.6. Hardware: Delta-Wing Drone
3. Results
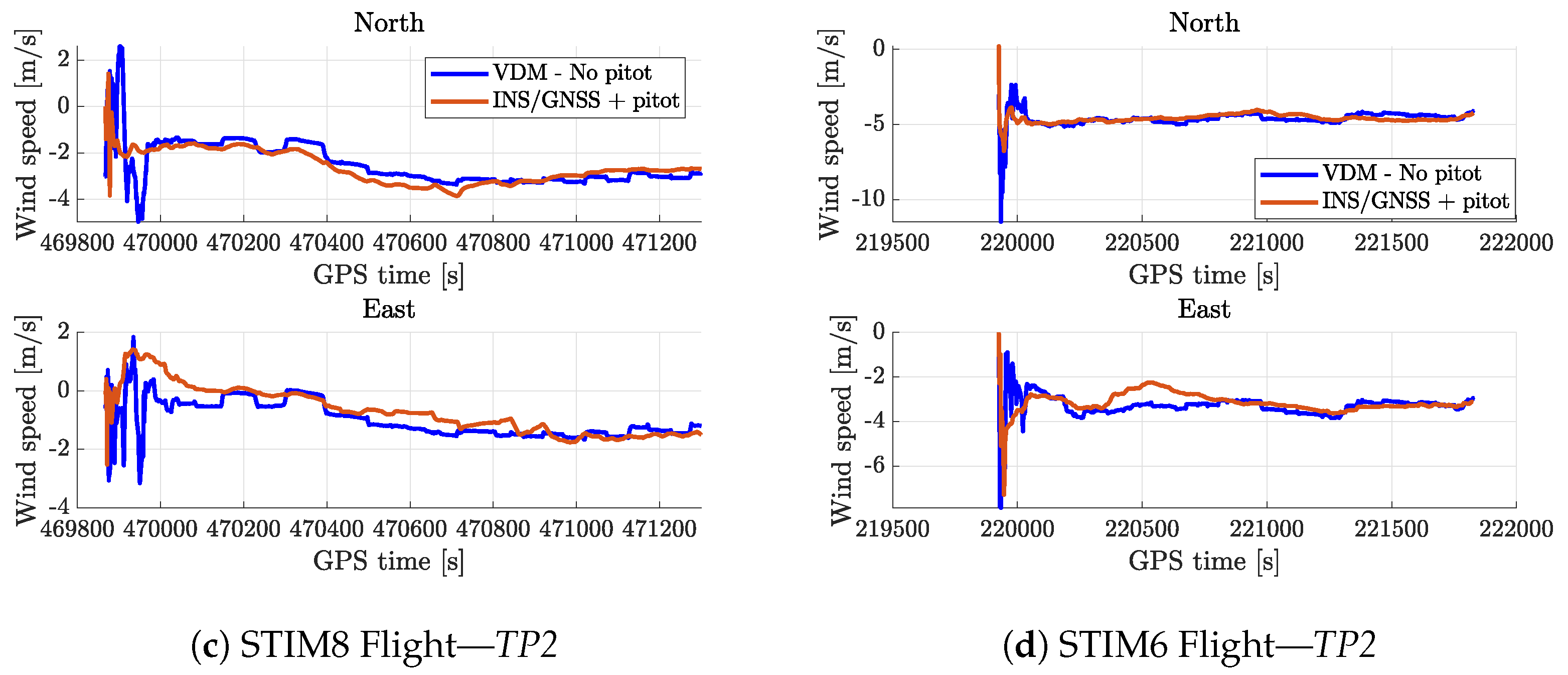
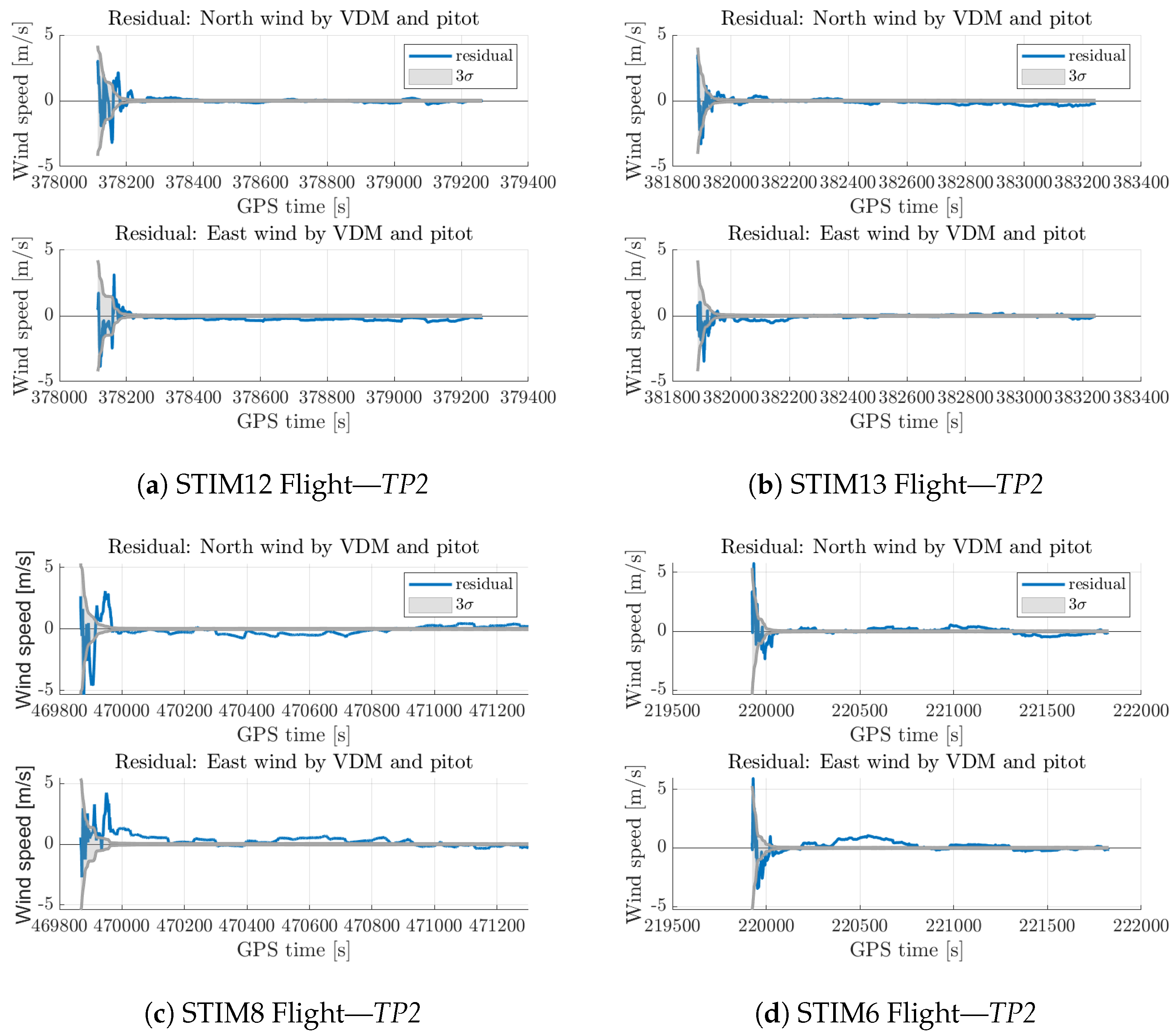
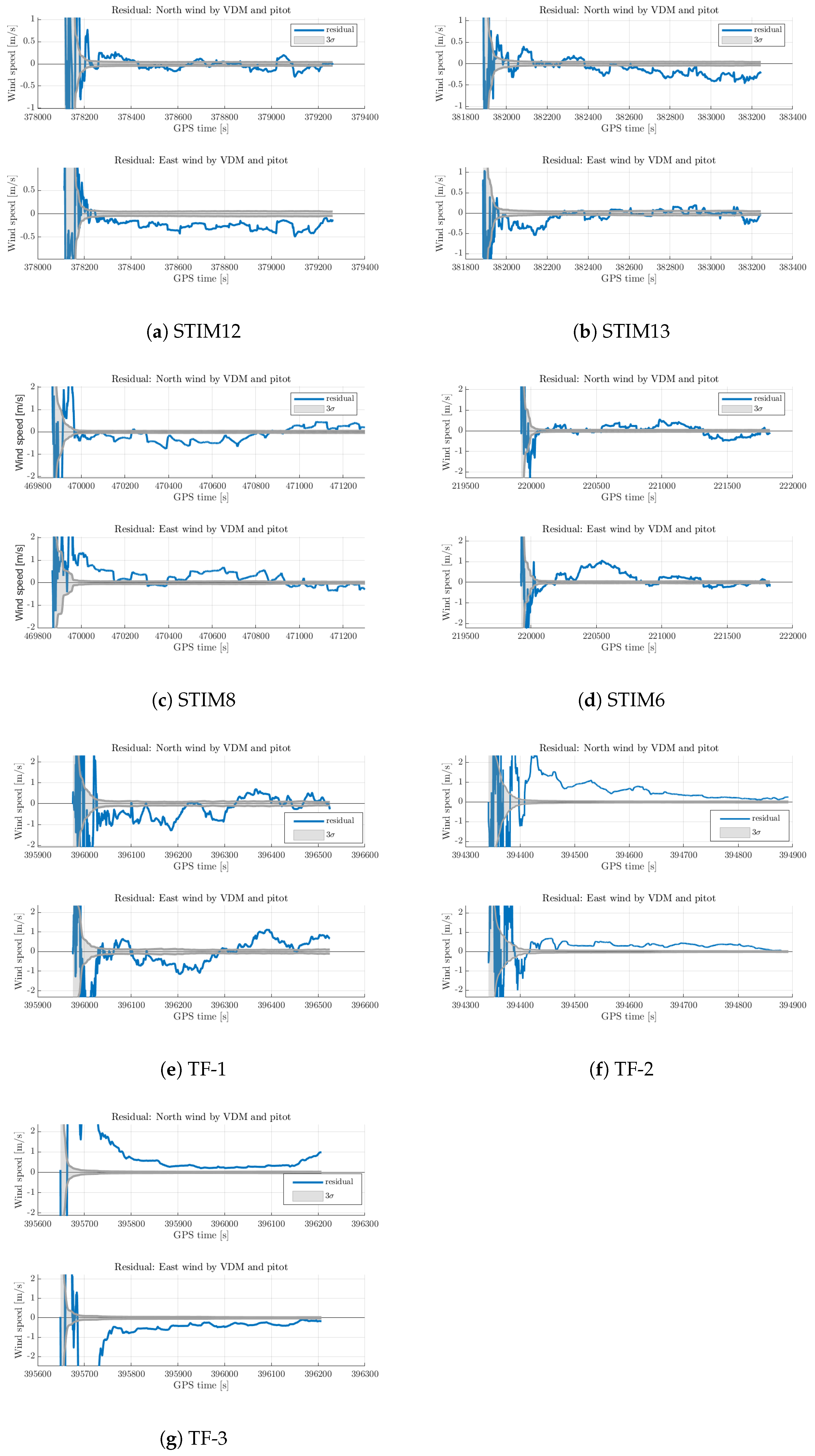
3.1. Conventional Fixed-Wing Drone
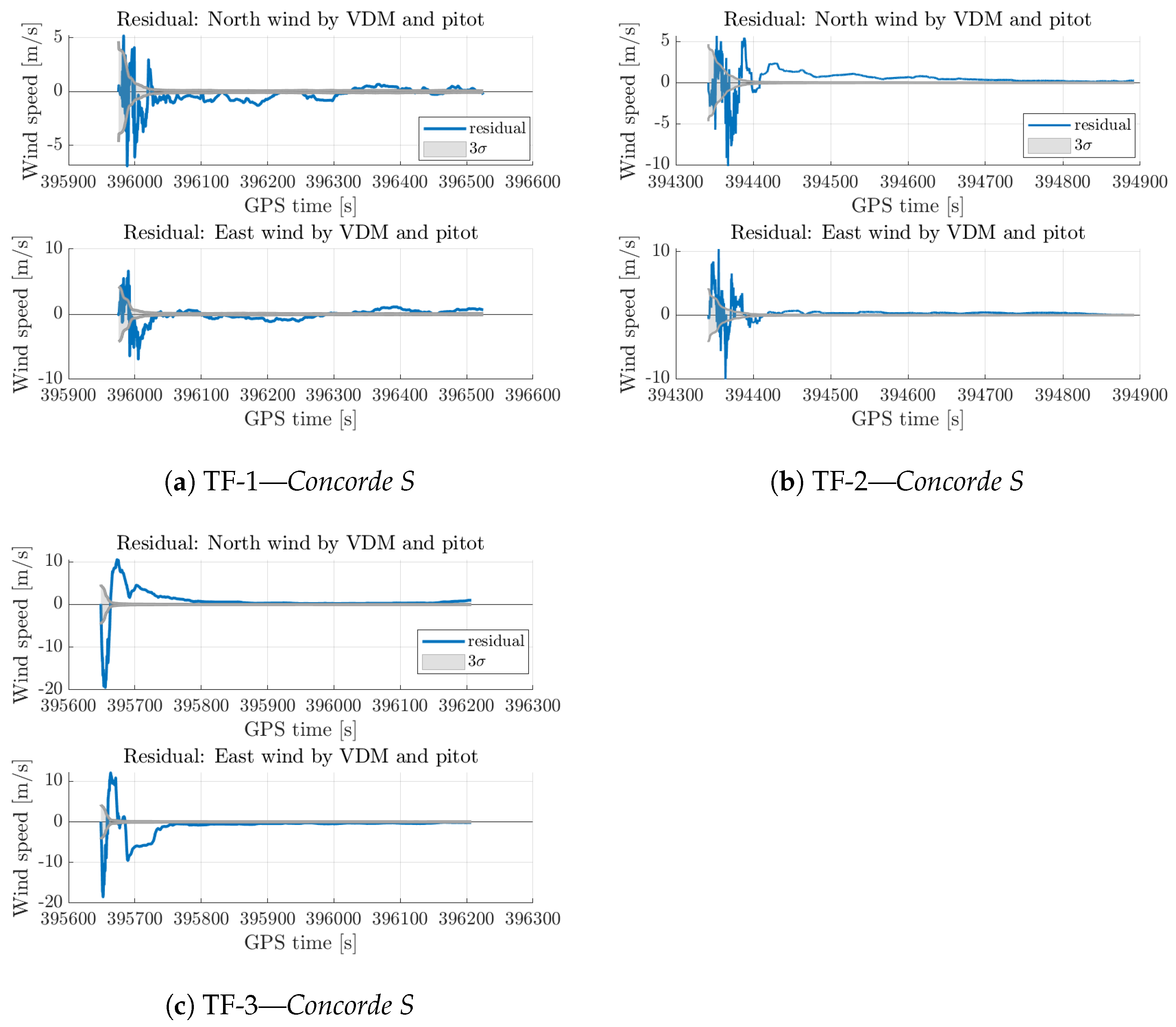
3.2. Delta-Wing Drone
4. Additional Discussion
4.1. Integrating VDM of Different Drones in the Navigation Filter for Wind Estimation
- 1.
- Aerodynamic models are encapsulated by the terms in Equations (2) and (4). These models vary depending on the type of the drone. For a conventional fixed-wing drone, the aerodynamic forces and moments are modeled by Equations (8)–(14) and then subsequently integrated into the state-dynamics/observation models (the equations can be found in [55]) via Equations (15) and (16). On the other hand, for a delta-wing drone, the model is governed by Equations (20)–(27) and then integrated into the state dynamics/observations via Equations (15) and (30). Following similar lines, the aerodynamics of a new drone should be modeled so as to obtain a mathematical expression for . Deducing a new functional model structure is beyond the scope of this paper and more details on this can be found in [68]. It should be noted that we have relied on the models already existing in literature [5,72] for VDM-based wind estimation.
- 2.
- Aerodynamic model parameters, represented as , are included in the state vector as described by Equation (7). The dimensionality of depends on the structure of the model. For a conventional fixed-wing drone, comprises 21 parameters segregated by force and moment identifier as shown in Equations (18) and (19). These are altogether combined in Equation (17). Meanwhile, for a delta-wing drone, 15 parameters constitute ; these are segregated by force and moment identifier in Equations (28) and (29) and later combined in Equation (17). For a new drone platform, depending on the nature of its model, the force and moment parameters should be included in the state vector in a way similar to the two drones in our work.
- 3.
- A priori estimates of aerodynamic model parameters are assumed to be known for this work. We rely on [4] for their values for the conventional fixed-wing and [5] for the delta-wing drone. However, for a new drone, methodologies described in [4,5,61] could be used to obtain their a priori values. Note that knowledge of insufficient quality can result in erroneous wind estimates as further highlighted in Appendix A.
- 4.
4.2. Benefits of Fixed-Wing Drones
4.3. Observability
4.3.1. Observability of GNSS/IMU/Pitot Based Wind Estimators
4.3.2. Observability of Synthetic Wind Estimator
4.4. Insights on VDM-Based Navigation Filter: A Focus on Wind-Estimation
4.5. Wind Model
4.6. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VDM | Vehicle Dynamic Model |
| GNSS | Global Navigation Satellite System |
| IMU | Inertial Measurement Unit |
| ADS | Air Data System |
| AHRS | Attitude and Heading Reference System |
| SWAP | Size, Weight and Power |
| LOS | Line of Sight |
| BVLOS | Beyond Visual Line of Sight |
| EKF | Extended Kalman Filter |
| INS | Inertial Navigation System |
| FADS | Flush Air Data System |
| AOA | Angle of attack |
| SSA | Sideslip angle |
| RLS | Recursive Least Squares |
| ECEF | Earth-Centered Earth Fixed |
| NED | North, East Down |
| WMF | Wind, Moment Force |
| CAD | Computer-Aided Design |
| PPS | Pulse Per Second |
| RPM | Rotation Per Minute |
| RMSE | Root Mean Square Error |
| GPS | Global Positioning System |
Appendix A. Adversarial Testing
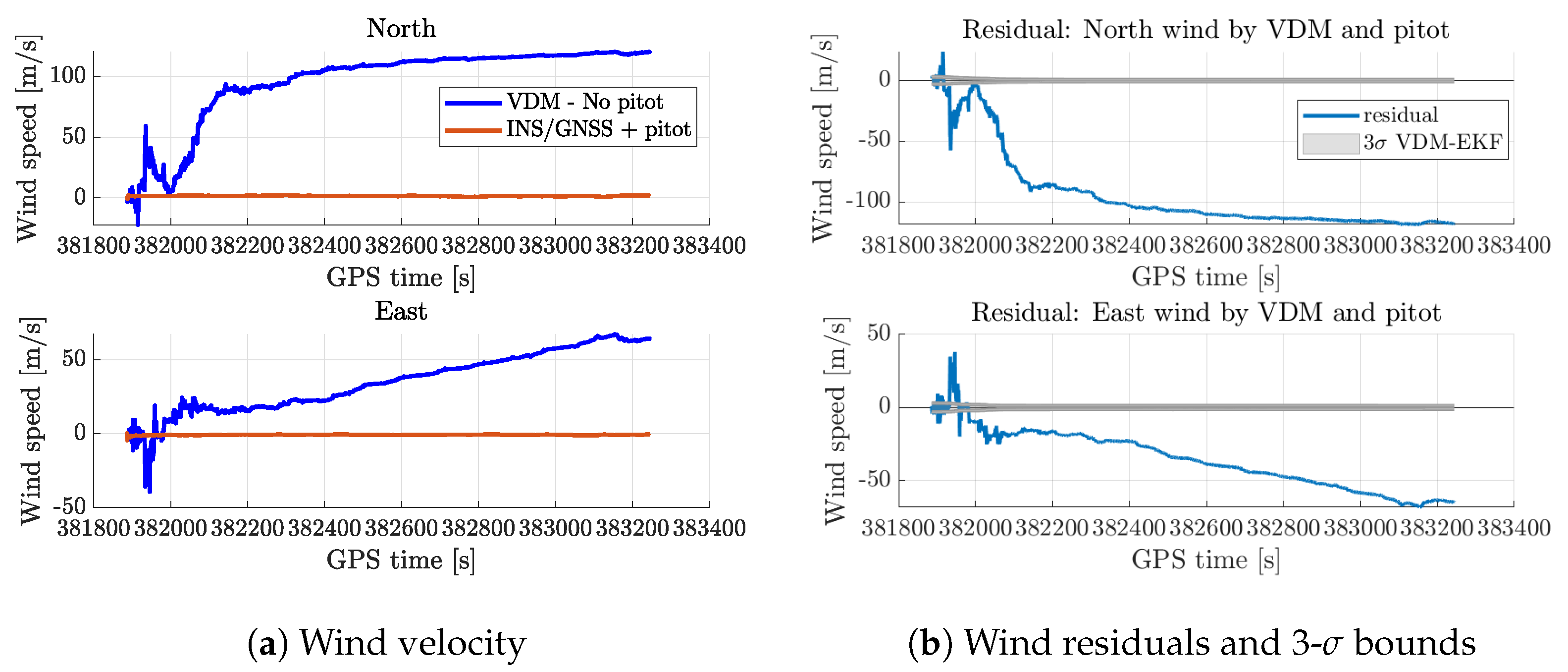
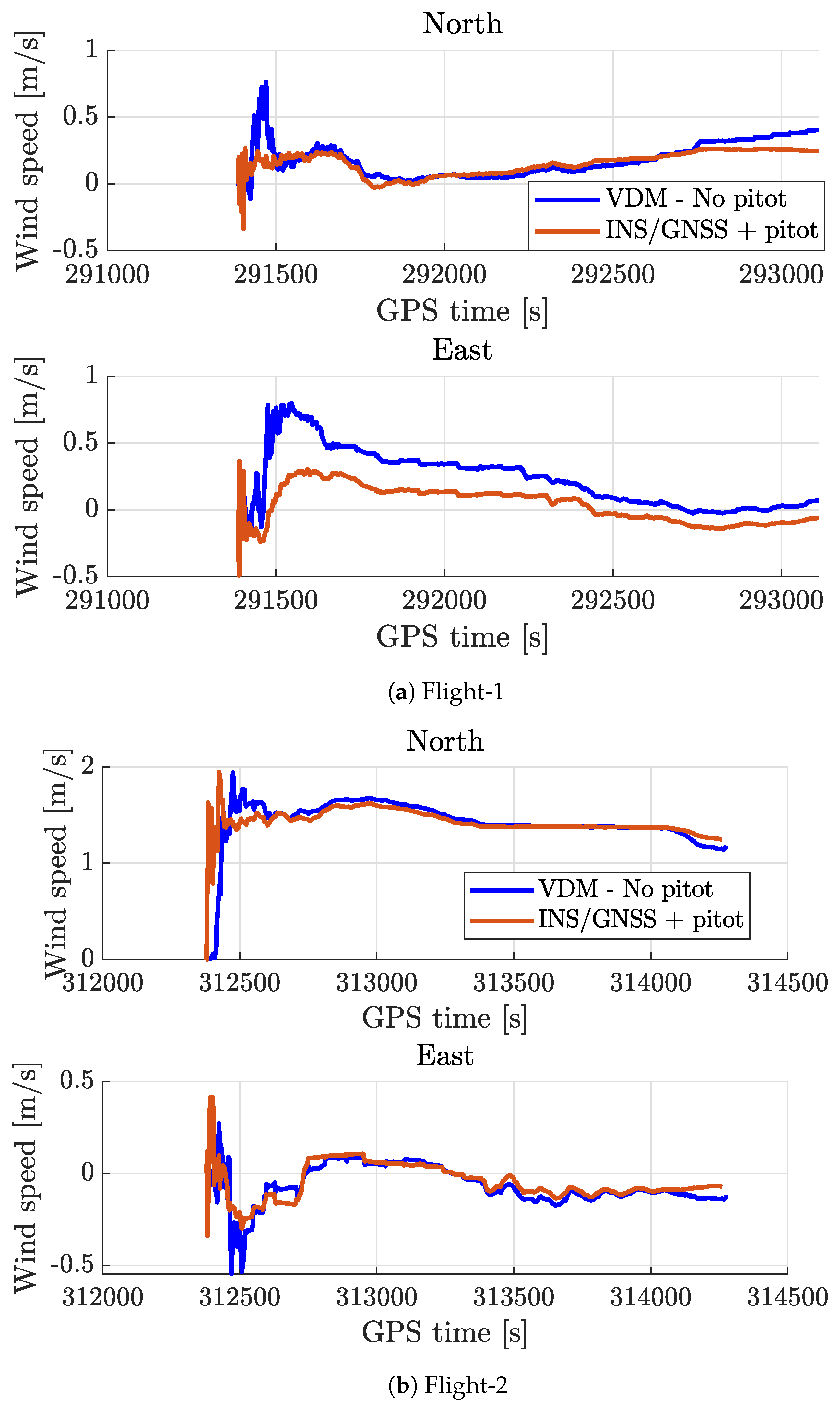
Appendix B. eBeeX Wind Estimation

References
- O’Shea, O.R.; Hamann, M.; Smith, W.; Taylor, H. Predictable pollution: An assessment of weather balloons and associated impacts on the marine environment—An example for the Great Barrier Reef, Australia. Mar. Pollut. Bull. 2014, 79, 61–68. [Google Scholar] [CrossRef]
- Meier, K.; Hann, R.; Skaloud, J.; Garreau, A. Wind Estimation with Multirotor UAVs. Atmosphere 2022, 13, 551. [Google Scholar] [CrossRef]
- Johansen, T.A.; Cristofaro, A.; Sørensen, K.; Hansen, J.M.; Fossen, T.I. On estimation of wind velocity, angle-of-attack and sideslip angle of small UAVs using standard sensors. In Proceedings of the 2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 9–12 June 2015; pp. 510–519. [Google Scholar] [CrossRef]
- Sharma, A.; Laupré, G.F.; Skaloud, J. Identifying Aerodynamics of Small Fixed-Wing Drones Using Inertial Measurements for Model-Based Navigation. NAVIGATION J. Inst. Navig. 2023, 70, navi.611. [Google Scholar] [CrossRef]
- Longobardi, P.; Sharma, A.; Skaloud, J. Identifying Aerodynamics of Delta-Wing Drones for Model-Based Navigation: A Comparative Study. IEEE Access 2024, 12, 91649–91663. [Google Scholar] [CrossRef]
- Borup, K.T.; Fossen, T.I.; Johansen, T.A. A nonlinear model-based wind velocity observer for unmanned aerial vehicles. IFAC-PapersOnLine 2016, 49, 276–283. [Google Scholar] [CrossRef]
- Wenz, A.; Johansen, T.A. Estimation of wind velocities and aerodynamic coefficients for UAVs using standard autopilot sensors and a moving horizon estimator. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 1267–1276. [Google Scholar] [CrossRef]
- Wenz, A.; Johansen, T.A. Real-Time Moving Horizon Estimation of Air Data Parameters and Wind Velocities for fixed-wing UAVs. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020; pp. 998–1006. [Google Scholar] [CrossRef]
- Wenz, A.; Johansen, T.A. Moving horizon estimation of air data parameters for UAVs. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 2101–2121. [Google Scholar] [CrossRef]
- Flight Safety Foundation. 2022. Available online: http://aviation-safety.net/database (accessed on 14 July 2022).
- 14 AC Part 135 Air Carrier and Operator Certification. 2022. Available online: https://www.faa.gov/licenses_certificates/airline_certification/135_certification (accessed on 14 July 2022).
- Kurtz, J.; Wittig, S.; O’Byrne, S. Applicability of a counterpropagating laser airspeed sensor to aircraft flight regimes. J. Aircr. 2016, 53, 439–450. [Google Scholar] [CrossRef]
- Wheeler, T.J.; Seiler, P.; Packard, A.K.; Balas, G.J. Performance analysis of fault detection systems based on analytically redundant linear time-invariant dynamics. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 214–219. [Google Scholar] [CrossRef]
- Zeis, J., Jr.; Lambert, H.; Calcio, R.; Gleason, D. Angle of attack estimation using an inertial reference platform. In Proceedings of the 15th Atmospheric Flight Mechanics Conference, Minneapolis, MN, USA, 15–17 August 1988. [Google Scholar] [CrossRef]
- Myschik, S.; Holzapfel, F.; Sachs, G. Low-cost sensor based integrated airdata and navigation system for general aviation aircraft. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; p. 7423. [Google Scholar] [CrossRef]
- Murch, A. A flight control system architecture for the NASA AirSTAR flight test infrastructure. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; p. 6990. [Google Scholar] [CrossRef]
- Colgren, R. The Feasibility of using an INS for control system feedbacks. In Proceedings of the AIAA and SAE, 1998 World Aviation Conference, Anaheim, CA, USA, 28–30 September 1998; p. 5517. [Google Scholar] [CrossRef]
- Colgren, R.; Frye, M.; Olson, W. A proposed system architecture for estimation of angle-of-attack and sideslip angle. In Proceedings of the Guidance, Navigation, and Control Conference and Exhibit, Portland, OR, USA, 9–11 August 1999; p. 4078. [Google Scholar] [CrossRef]
- Colgren, R.; Martin, K. Flight Test validation of sideslip estimation using inertial accelerations. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Dever, CO, USA, 14–17 August 2000; p. 4448. [Google Scholar] [CrossRef]
- Colgren, R.D. Method and System for Estimation and Correction of Angle-of-Attack and Sideslip Angle from Acceleration Measurements. US Patent 6,273,370, 14 August 2001. [Google Scholar]
- Wise, K.A. Computational Air Data System for Angle-of-Attack and Angle-of-Sideslip. US Patent 6,928,341, 9 August 2005. [Google Scholar]
- Wise, K. Flight testing of the X-45A J-UCAS computational alpha-beta system. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006. [Google Scholar] [CrossRef]
- Giebel, G.; Schmidt Paulsen, U.; Bange, J.; la Cour-Harbo, A.; Reuder, J.; Mayer, S.; van der Kroonenberg, A.; Mølgaard, J. Autonomous Aerial Sensors for Wind Power Meteorology—A Pre-Project; Danmarks Tekniske Universitet: Copenhagen, Denmark, 2012. [Google Scholar]
- Emeis, S.; Schafer, K.; Munkel, C. Surface-based remote sensing of the mixing-layer height-a review. Meteorol. Z. 2008, 17, 621–630. [Google Scholar] [CrossRef]
- Lenschow, D. The Measurement of Air Velocity and Temperature Using the NCAR Buffalo Aircraft Measuring System; National Center for Atmospheric Research Boulder: Boulder, CO, USA, 1972. [Google Scholar]
- Cho, J.Y.; Newell, R.E.; Anderson, B.E.; Barrick, J.D.; Thornhill, K.L. Characterizations of tropospheric turbulence and stability layers from aircraft observations. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Aberson, S.D.; Franklin, J.L. Impact on hurricane track and intensity forecasts of GPS dropwindsonde observations from the first-season flights of the NOAA Gulfstream-IV jet aircraft. Bull. Am. Meteorol. Soc. 1999, 80, 421–428. [Google Scholar] [CrossRef]
- Elston, J.; Argrow, B.; Stachura, M.; Weibel, D.; Lawrence, D.; Pope, D. Overview of small fixed-wing unmanned aircraft for meteorological sampling. J. Atmos. Ocean. Technol. 2015, 32, 97–115. [Google Scholar] [CrossRef]
- Spiess, T.; Bange, J.; Buschmann, M.; Vorsmann, P. First application of the meteorological Mini-UAV’M2AV’. Meteorol. Z. 2007, 16, 159–170. [Google Scholar] [CrossRef]
- Mansour, M.; Kocer, G.; Lenherr, C.; Chokani, N.; Abhari, R.S. Seven-sensor fast-response probe for full-scale wind turbine flowfield measurements. J. Eng. Gas Turbines Power 2011, 133, 081601. [Google Scholar] [CrossRef]
- Reineman, B.D.; Lenain, L.; Statom, N.M.; Melville, W.K. Development and testing of instrumentation for UAV-based flux measurements within terrestrial and marine atmospheric boundary layers. J. Atmos. Ocean. Technol. 2013, 30, 1295–1319. [Google Scholar] [CrossRef]
- Van den Kroonenberg, A.; Martin, T.; Buschmann, M.; Bange, J.; Vörsmann, P. Measuring the wind vector using the autonomous mini aerial vehicle M 2 AV. J. Atmos. Ocean. Technol. 2008, 25, 1969–1982. [Google Scholar] [CrossRef]
- Wildmann, N.; Ravi, S.; Bange, J. Towards higher accuracy and better frequency response with standard multi-hole probes in turbulence measurement with remotely piloted aircraft (RPA). Atmos. Meas. Tech. 2014, 7, 1027–1041. [Google Scholar] [CrossRef]
- Kocer, G.; Mansour, M.; Chokani, N.; Abhari, R.S.; Müller, M. Full-scale wind turbine near-wake measurements using an instrumented uninhabited aerial vehicle. J. Sol. Energy Eng. 2011, 133, 041011. [Google Scholar] [CrossRef]
- Reuder, J.; Jonassen, M.O. First results of turbulence measurements in a wind park with the Small Unmanned Meteorological Observer SUMO. Energy Procedia 2012, 24, 176–185. [Google Scholar] [CrossRef]
- Wildmann, N.; Hofsäß, M.; Weimer, F.; Joos, A.; Bange, J. MASC—A small Remotely Piloted Aircraft (RPA) for wind energy research. Adv. Sci. Res. 2014, 11, 55–61. [Google Scholar] [CrossRef]
- Dias, N.; Gonçalves, J.; Freire, L.; Hasegawa, T.; Malheiros, A. Obtaining potential virtual temperature profiles, entrainment fluxes, and spectra from mini unmanned aerial vehicle data. Bound.-Layer Meteorol. 2012, 145, 93–111. [Google Scholar] [CrossRef]
- Crowe, W.; Davis, K.; la Cour-Harbo, A.; Vihma, T.; Lesenkov, S.; Eppi, R.; Weatherhead, E.; Liu, P.; Raustein, M.; Abrahamsson, M.; et al. Enabling Science Use of Unmanned Aircraft Systems for Arctic Environmental Monitoring; Arctic Monitoring and Asessment Programme (AMAP): Oslo, Norway, 2012. [Google Scholar]
- Houston, A.L.; Argrow, B.; Elston, J.; Lahowetz, J.; Frew, E.W.; Kennedy, P.C. The collaborative Colorado–Nebraska unmanned aircraft system experiment. Bull. Am. Meteorol. Soc. 2012, 93, 39–54. [Google Scholar] [CrossRef]
- Balsley, B.B.; Lawrence, D.A.; Woodman, R.F.; Fritts, D.C. Fine-scale characteristics of temperature, wind, and turbulence in the lower atmosphere (0–1,300 m) over the south Peruvian coast. Bound.-Layer Meteorol. 2013, 147, 165–178. [Google Scholar] [CrossRef]
- Quindlen, J.; Langelaan, J. Flush air data sensing for soaring-capable UAVs. In Proceedings of the 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar] [CrossRef]
- Samy, I.; Postlethwaite, I.; Gu, D.W.; Green, J. Neural-network-based flush air data sensing system demonstrated on a mini air vehicle. J. Aircr. 2010, 47, 18–31. [Google Scholar] [CrossRef]
- Whitmore, S.; Cobleigh, B.; Haering, E., Jr. Design and calibration of the X-33 flush airdata sensing (FADS) system. In Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12–15 January 1998; p. 201. [Google Scholar] [CrossRef]
- Pruett, C.D.; Wolf, H.; Heck, M.L.; Siemers, P.M., III. Innovative air data system for the space shuttle orbiter. J. Spacecr. Rocket. 1983, 20, 61–69. [Google Scholar] [CrossRef]
- Shen, H.; Xu, Y.; Remeikas, C. Pitch control of a micro air vehicle with micropressure sensors. J. Aircr. 2013, 50, 239–248. [Google Scholar] [CrossRef]
- Shyy, W.; Bernal, L.; Yeo, D.; Atkins, E. Aerodynamic sensing for a fixed wing uas operating at high angles of attack. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Minneapolis, MN, USA, 13–16 August 2012. [Google Scholar] [CrossRef]
- Marino, M.; Ravi, S.; Watkins, S. Optimum location of pressure measurments around a wing as a dynamic control input in smooth and turbulent conditions. In Proceedings of the 28th International Congress of the Aeronautical Sciences; ICAS: Bonn, Germany, 2012; Volume 2, pp. 955–962. [Google Scholar]
- Mohamed, A.; Watkins, S.; Fisher, A.; Marino, M.; Massey, K.; Clothier, R. Bioinspired wing-surface pressure sensing for attitude control of micro air vehicles. J. Aircr. 2015, 52, 827–838. [Google Scholar] [CrossRef]
- Laurence, R.J., III; Argrow, B.M.; Frew, E.W. Wind tunnel results for a distributed flush airdata system. J. Atmos. Ocean. Technol. 2017, 34, 1519–1528. [Google Scholar] [CrossRef]
- Thompson, K.; Xu, Y.; Dickinson, B.T. Aerodynamic moment model calibration from distributed pressure arrays. J. Aircr. 2017, 54, 716–723. [Google Scholar] [CrossRef]
- Fei, H.; Zhu, R.; Zhou, Z.; Wang, J. Aircraft flight parameter detection based on a neural network using multiple hot-film flow speed sensors. Smart Mater. Struct. 2007, 16, 1239. [Google Scholar] [CrossRef]
- Que, R.; Zhu, R. Aircraft aerodynamic parameter detection using micro hot-film flow sensor array and BP neural network identification. Sensors 2012, 12, 10920–10929. [Google Scholar] [CrossRef]
- Keshavan, J.; Humbert, J.S. MAV stability augmentation using weighted outputs from distributed hair sensor arrays. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 4445–4450. [Google Scholar] [CrossRef]
- Lee, L.; Dickinson, B.; Baur, J.; Reich, G. Embedded Sensors for Autonomous Air Systems, LRIR 09rw10cor. 2012. Available online: https://api.semanticscholar.org/CorpusID:136535505 (accessed on 25 October 2024).
- Khaghani, M.; Skaloud, J. Assessment of VDM-based autonomous navigation of a UAV under operational conditions. Robot. Auton. Syst. 2018, 106, 152–164. [Google Scholar] [CrossRef]
- Lie, F.A.P.; Gebre-Egziabher, D. Synthetic air data system. J. Aircr. 2013, 50, 1234–1249. [Google Scholar] [CrossRef]
- Owens, B.; Cox, D.; Morelli, E. Development of a low-cost sub-scale aircraft for flight research: The FASER project. In Proceedings of the 25th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, San Francisco, CA, USA, 5–8 June 2006. [Google Scholar] [CrossRef]
- Mwenegoha, H.A.; Moore, T.; Pinchin, J.; Jabbal, M. Error characteristics of a model-based integration approach for fixed-wing unmanned aerial vehicles. J. Navig. 2021, 74, 1353–1366. [Google Scholar] [CrossRef]
- Mwenegoha, H.A.; Moore, T.; Pinchin, J.; Jabbal, M. Enhanced fixed wing UAV navigation in extended GNSS outages using a vehicle dynamics model and raw GNSS observables. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019; pp. 2552–2565. [Google Scholar] [CrossRef]
- Mwenegoha, H.A.; Moore, T.; Pinchin, J.; Jabbal, M. Model-based autonomous navigation with moment of inertia estimation for unmanned aerial vehicles. Sensors 2019, 19, 2467. [Google Scholar] [CrossRef]
- Mwenegoha, H.A.; Moore, T.; Pinchin, J.; Jabbal, M. A model-based tightly coupled architecture for low-cost unmanned aerial vehicles for real-time applications. IEEE Access 2020. [Google Scholar] [CrossRef]
- Laupré, G.; Longobardi, P.; Skaloud, J.; Charlaix, J.C. Model Based Navigation of Delta-Wing UAV-In-Flight Calibration and Autonomous Performance. Eur. J. Navig. 2021, 21, 22–30. [Google Scholar]
- Laupré, G.; Skaloud, J. On the self-calibration of aerodynamic coefficients in vehicle dynamic model-based navigation. Drones 2020, 4, 32. [Google Scholar] [CrossRef]
- Laupré, G.; Khaghani, M.; Skaloud, J. Sensitivity to time delays in VDM-based navigation. Drones 2019, 3, 11. [Google Scholar] [CrossRef]
- Laupré, G.; Pirlet, L.; Skaloud, J. Reliable strategies for implementing model-based navigation on fixed-wing drones. J. Navig. 2023, 76, 413–431. [Google Scholar] [CrossRef]
- Longobardi, P.; Skaloud, J. On the scalability of experimentally determined aerodynamic model for model-based navigation on a delta-wing UAV. In Proceedings of the 2023 IEEE 10th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Milan, Italy, 19–21 June 2023; pp. 19–24. [Google Scholar] [CrossRef]
- Longobardi, P.; Bonneau, G.; Skaloud, J. Wind Tunnel Characterization of a Delta-Wing UAV for—Model-Based Navigation. In Proceedings of the 2023 Aerospace Europe Conference 10th EUCASS and 9th CEAS Conference, CEAS, Lausanne, Switzerland, 9–13 July 2023. [Google Scholar] [CrossRef]
- Longobardi, P.; Skaloud, J. Aerodynamic Modeling of a Delta-Wing UAV for ModelBased Navigation. CEAS Aeronaut. J. 2024, 15, 283–301. [Google Scholar] [CrossRef]
- Laupré, G.F.; Sharma, A.; Skaloud, J. VDMNav: Software Architecture for Aerodynamically Constrained Navigation on Small Fixed-Wing Drones. IEEE Robot. Autom. Lett. 2024, 9, 2869–2876. [Google Scholar] [CrossRef]
- Sharma, A.; Gilgien, S.; Skaloud, J. Model-Based Fusion of GNSS and Multiple-IMUs. In Proceedings of the 2024 11th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Lublin, Poland, 3–5 June 2024; pp. 266–271. [Google Scholar] [CrossRef]
- Khaghani, M.; Skaloud, J. Autonomous Vehicle Dynamic Model-Based Navigation for Small UAVs. NAVIGATION J. Inst. Navig. 2016, 63, 345–358. [Google Scholar] [CrossRef]
- Ducard, G.J. Nonlinear Aircraft Model; Chapter Fault-tolerant Flight Control and Guidance Systems: Practical Methods for Small Unmanned Aerial Vehicles; Springer: London, UK, 2009; pp. 27–41. [Google Scholar] [CrossRef]
- Laupré, G.; Skaloud, J. Calibration of Fixed-Wing UAV Aerodynamic Coefficients with Photogrammetry for VDM-based Navigation. In Proceedings of the 2021 International Technical Meeting of The Institute of Navigation, Online, 25–28 January 2021; pp. 775–786. [Google Scholar] [CrossRef]
- Albrektsen, S.M.; Johansen, T.A. User-configurable timing and navigation for UAVs. Sensors 2018, 18, 2468. [Google Scholar] [CrossRef]
- Anderson, B.D.; Moore, J.B. Optimal Filtering; Dover Publications, Inc.: New York, NY, USA, 2005. [Google Scholar]
- Sastry, S. Nonlinear Systems Analysis, Stability, and Control; Springer: New York, NY, USA, 1999. [Google Scholar]
- Sun, K.; Regan, C.D.; Egziabher, D.G. GNSS/INS based estimation of air data and wind vector using flight maneuvers. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 838–849. [Google Scholar] [CrossRef]
- Sun, K.; Regan, C.D.; Gebre-Egziabher, D. Observability and performance analysis of a model-free synthetic air data estimator. J. Aircr. 2019, 56, 1471–1486. [Google Scholar] [CrossRef]
- Burkhard, J.; Sharma, A.; Skaloud, J. Linear Estimation of Deterministic Accelerometer Errors. NAVIGATION J. Inst. Navig. 2024, 71, navi.656. [Google Scholar] [CrossRef]
- Paul, K.J.; Cucci, D.A.; Skaloud, J. Model-based constraints for trajectory determination of quad-copters: Design, calibration & merits for direct orientation. ISPRS Open J. Photogramm. Remote Sens. 2023, 7, 100030. [Google Scholar] [CrossRef]





| Parameters | Value | Unit |
|---|---|---|
| Accelerometer | ||
| Temperature calibration | Yes | – |
| Bias repeatability (1 year) | 1.5 | mg |
| In run bias stability | 0.003 | mg |
| Velocity random walk | 0.014 | m/s/ |
| Gyroscope | ||
| Temperature calibration | Yes | – |
| Bias repeatability | 250 | deg/h |
| In run bias stability | 0.3 | deg/h |
| Angular random walk | 0.15 | deg/ |
| IMU | Accelerometer | Gyroscope | ||
|---|---|---|---|---|
| Bias | Noise Density | Bias | Noise Density | |
| [mg] | [mg/] | [deg/h] | [deg/s/] | |
| ICM-20689 | ±18,000 | |||
| BMI-055 | ||||
| Drone | Flight | Prevailing Wind [m/s] | RMSE [m/s] |
|---|---|---|---|
| TP2 | STIM12 | ∼1 | 0.30 |
| STIM13 | ∼1.5–2 | 0.28 | |
| STIM8 | ∼2–3 | 0.52 | |
| STIM6 | ∼4–6 | 0.50 | |
| ConcordeS | TF-1 | ∼3–4 | 0.78 |
| TF-2 | ∼4–6 | 0.74 | |
| TF-3 | ∼3–5 | 0.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, A.; Laupré, G.F.; Longobardi, P.; Skaloud, J. Synthetic Wind Estimation for Small Fixed-Wing Drones. Atmosphere 2024, 15, 1339. https://doi.org/10.3390/atmos15111339
Sharma A, Laupré GF, Longobardi P, Skaloud J. Synthetic Wind Estimation for Small Fixed-Wing Drones. Atmosphere. 2024; 15(11):1339. https://doi.org/10.3390/atmos15111339
Chicago/Turabian StyleSharma, Aman, Gabriel François Laupré, Pasquale Longobardi, and Jan Skaloud. 2024. "Synthetic Wind Estimation for Small Fixed-Wing Drones" Atmosphere 15, no. 11: 1339. https://doi.org/10.3390/atmos15111339
APA StyleSharma, A., Laupré, G. F., Longobardi, P., & Skaloud, J. (2024). Synthetic Wind Estimation for Small Fixed-Wing Drones. Atmosphere, 15(11), 1339. https://doi.org/10.3390/atmos15111339







