The Return Period Wind Speed Prediction of Beijing Urban Area Based on Short-Term Measured Wind Speed
Abstract
1. Introduction
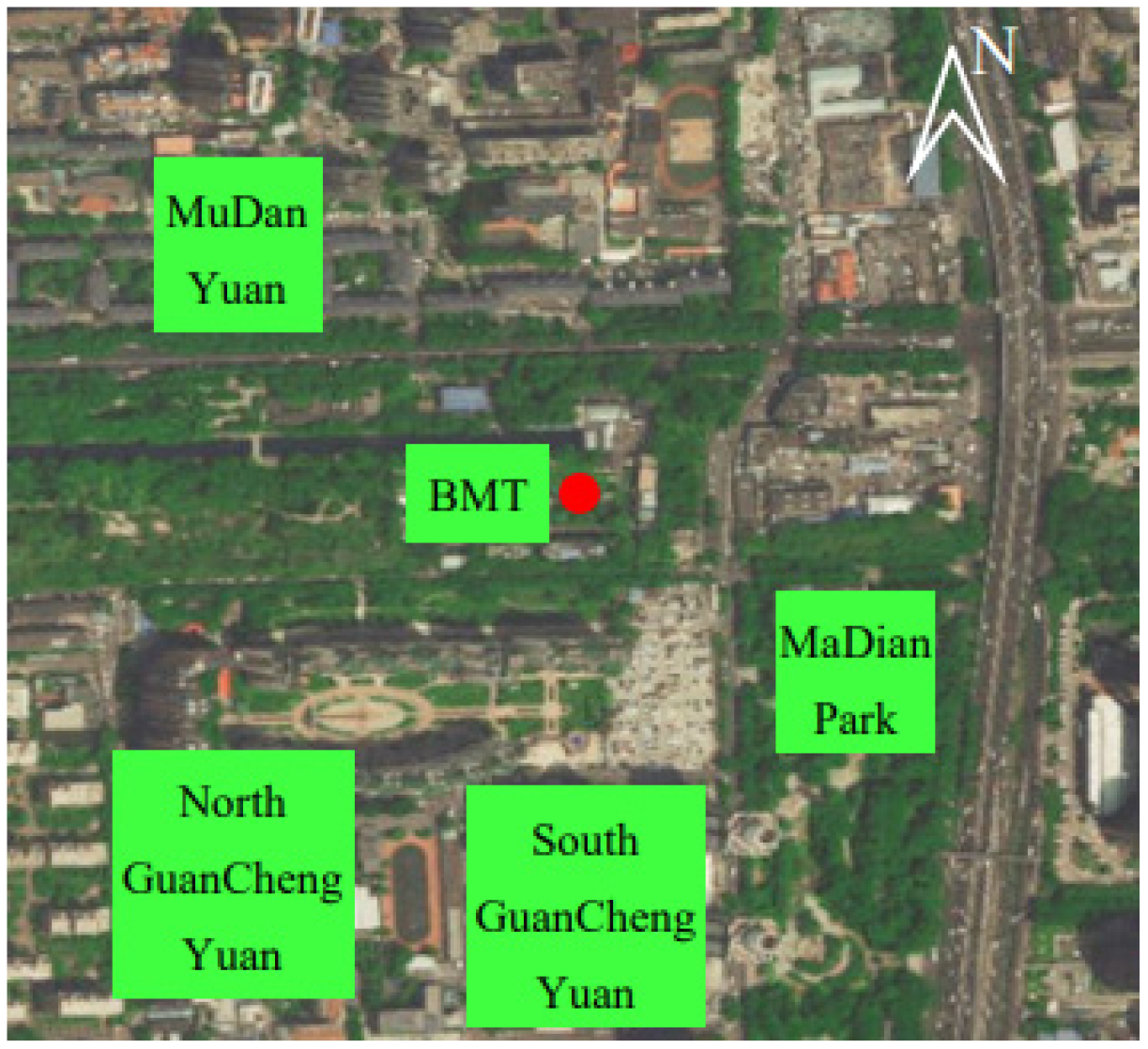
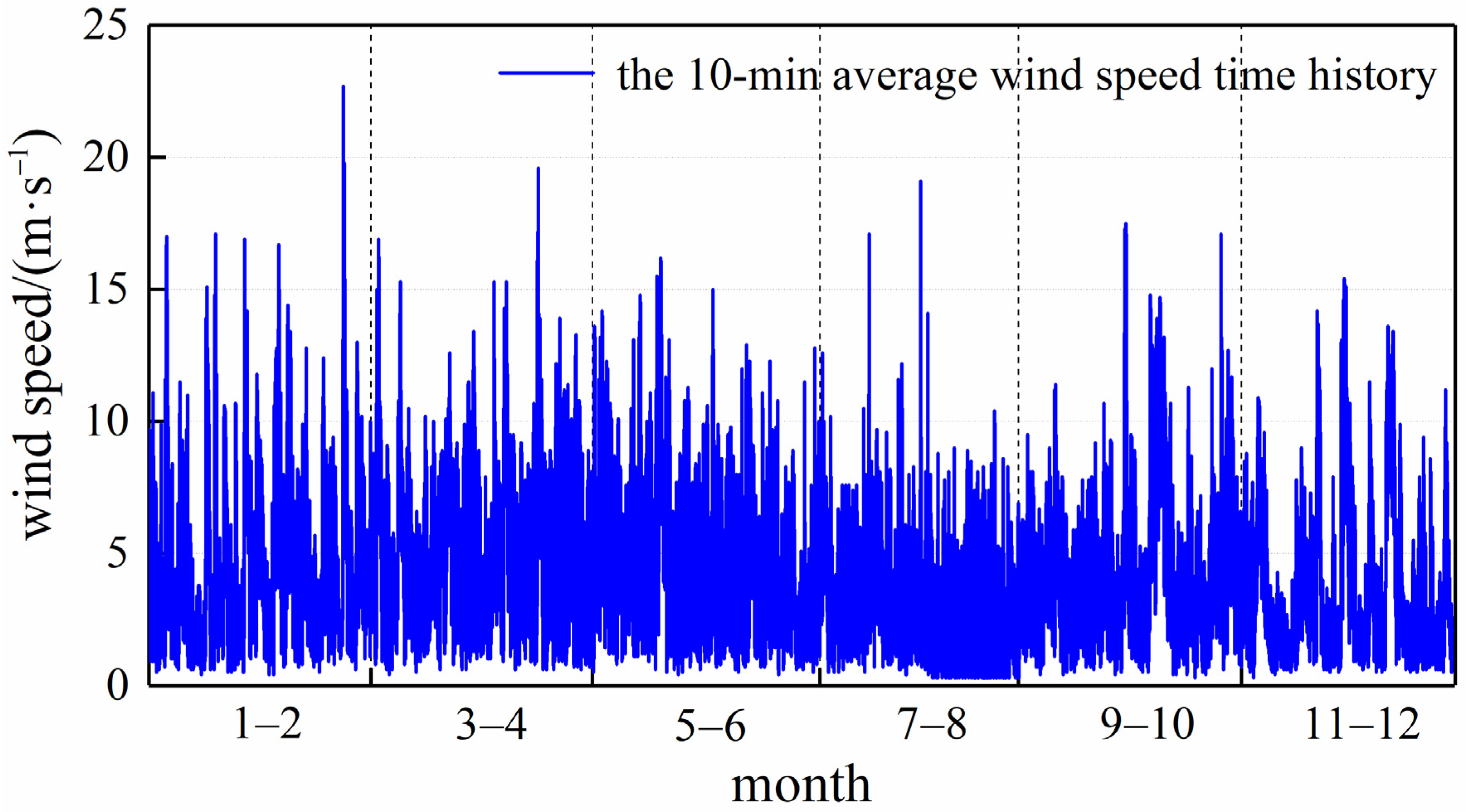
2. Measured Wind Speed Data Statistics
3. Monte–Carlo Simulation for Generating PISPS
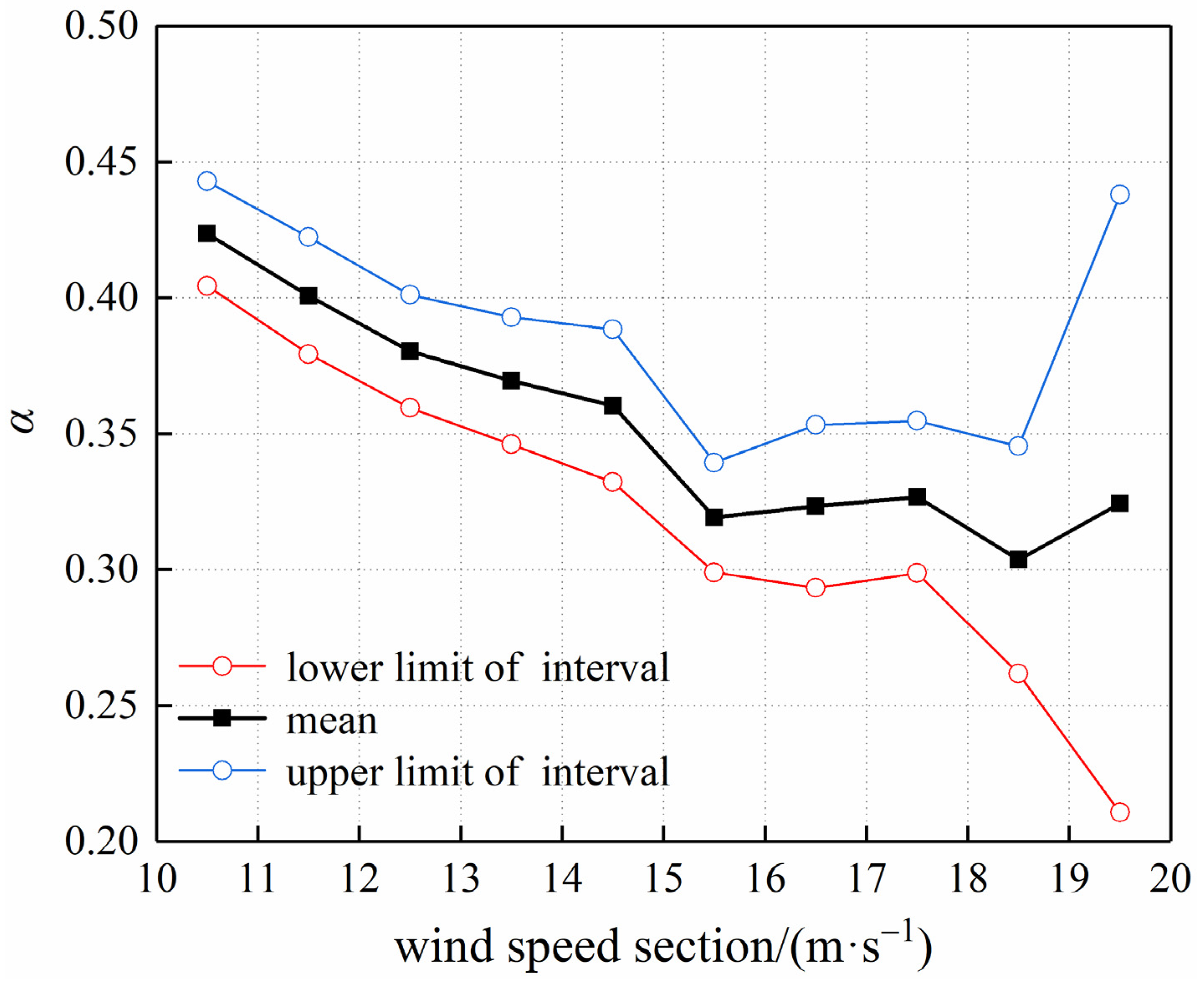
3.1. Fitting the Distribution of Measured ISPS
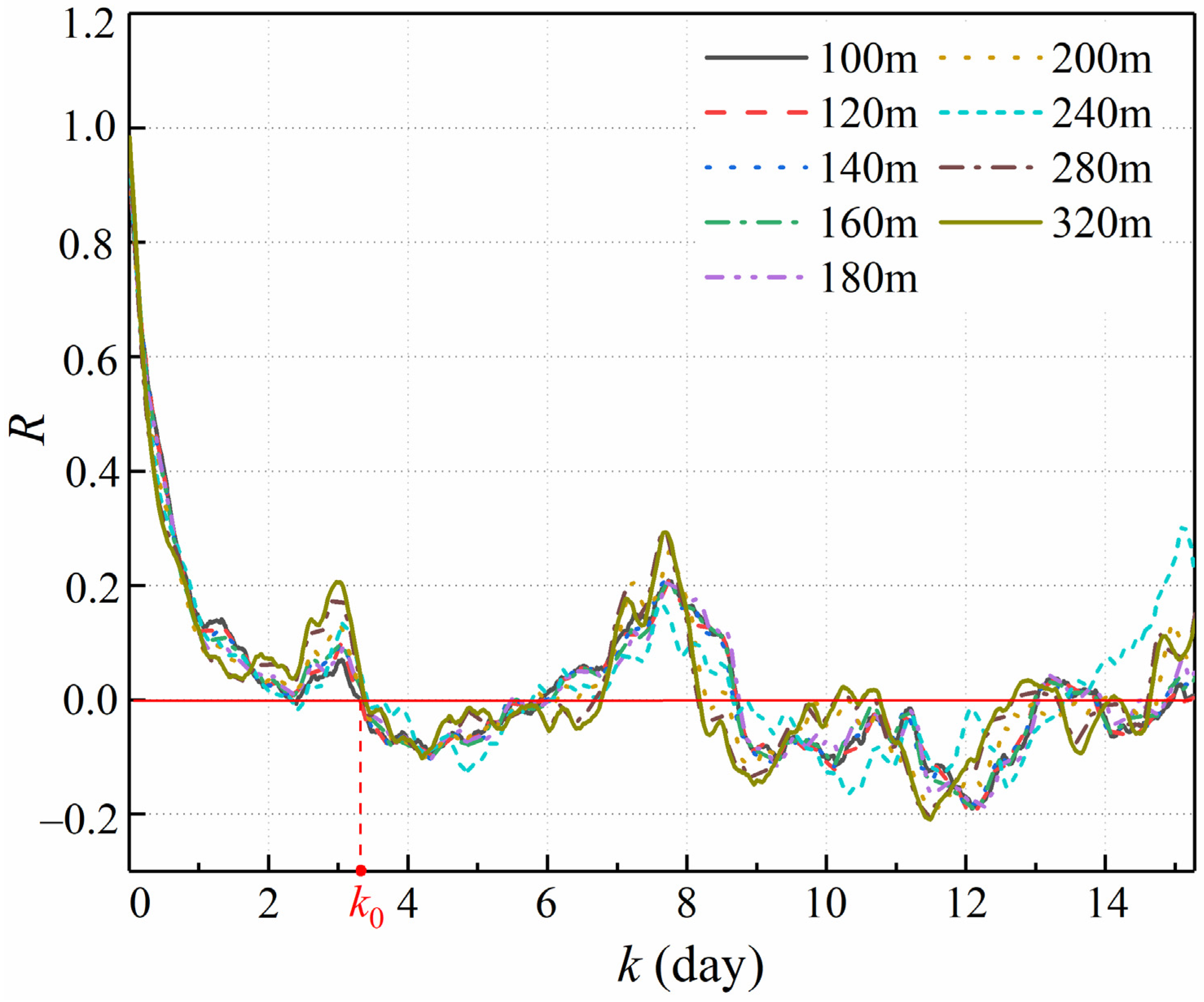
3.2. Generation of the PISPS
4. RPWS Prediction for the Whole Wind Direction
4.1. RPWS Prediction Based on PISPS
- (1)
- EVT I distribution model
- (2)
- EVT III distribution model
4.2. RPWS Prediction Based on the Measured OISPS
4.3. RPWS Prediction Results for the Whole Wind Direction
5. RPWS Prediction Considering Wind Direction
5.1. Analysis of Wind Speed–Direction Distribution
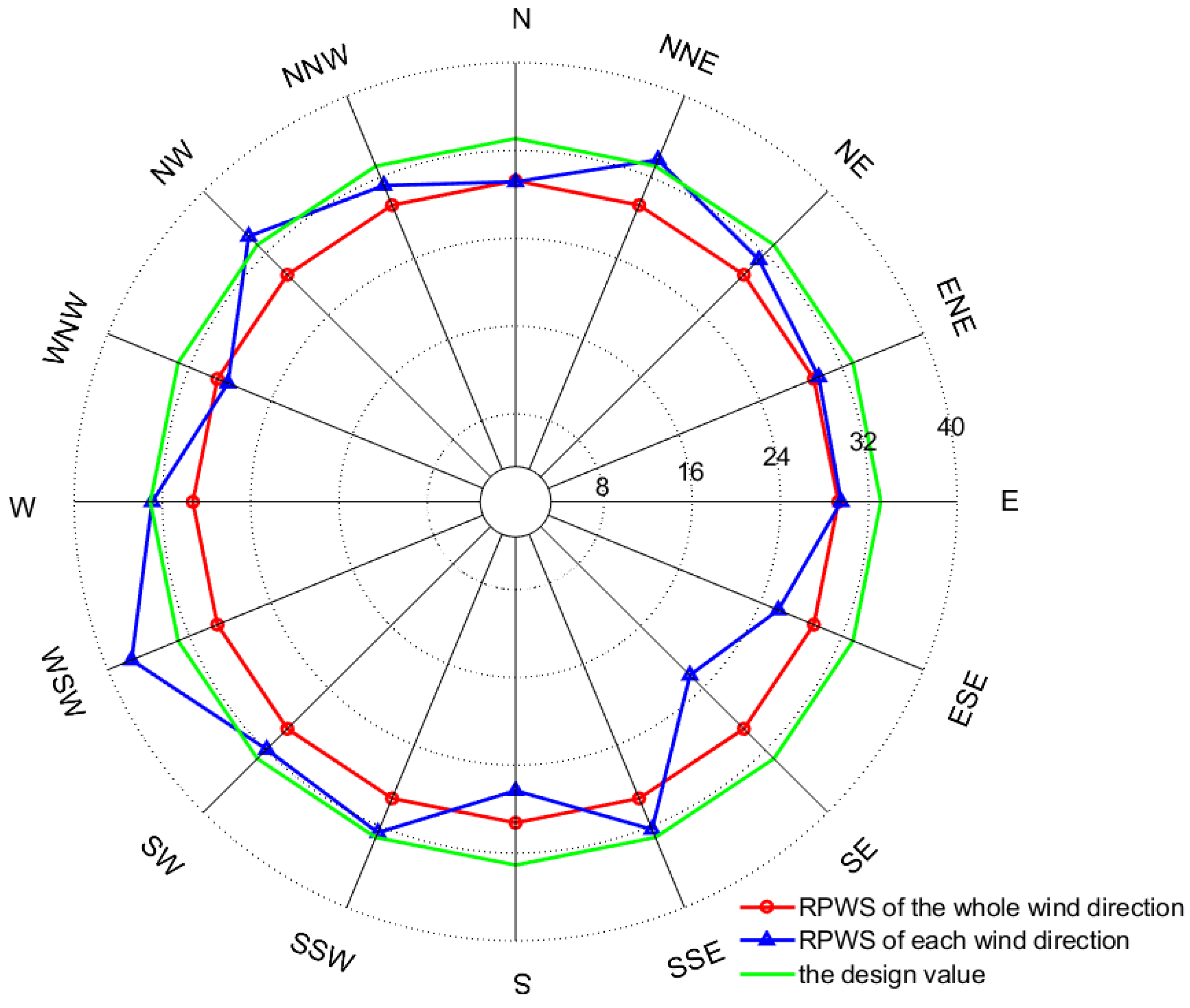
5.2. RPWS Prediction for Each Wind Direction Using the Cook Method
5.3. Analysis of RPWS Prediction Results
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Load Code for the Design of Building Structures: GB 50009—2012; China Architecture & Building Press: Beijing, China, 2012.
- Wang, B.; Dong, Y.; Dong, L. Calculation of basic wind pressure based on short-term wind speed data. J. Jilin Univ. (Eng. Technol. Ed.) 2020, 50, 1739–1746. [Google Scholar]
- Cook, N.J. Towards better estimation of extreme winds. J. Wind. Eng. Ind. Aerodyn. 1982, 9, 295–323. [Google Scholar] [CrossRef]
- Luo, Y.; Zhu, L.S. A new model of peaks over threshold for multivariate extremes. China Ocean. Eng. 2014, 28, 761–776. [Google Scholar] [CrossRef]
- Duthinh, D.; Pintar, A.L.; Simiu, E. Estimating peaks of stationary random processes: A peaks-over-threshold approach. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2017, 3, 04017028. [Google Scholar]
- Harris, R.I. Improvements to the Method of Independent Storms. J. Wind. Eng. Ind. Aerodyn. 1999, 80, 1–30. [Google Scholar] [CrossRef]
- Luo, Y.; Huang, G.-Q.; Chen, B.-Z.; Liu, W.-Z.; Li, M.-S.; Liao, H.-L. Design wind speed estimation for puli bridge based on short-term measured data. Eng. Mech. 2018, 35, 74–82. [Google Scholar]
- Di, W.; Yue, W.; Qingshan, Y.; Long, C. Improved method of independent storms for extreme value estimation of non-Gaussian wind pressure. J. Build. Struct. 2014, 35, 151–156. [Google Scholar]
- Shi, D. Practical Statistical Methods for Extremes; Tianjin Science and Technology Press: Tianjin, China, 2006. [Google Scholar]
- Wang, J.; Qin, S.; Jin, S.; Wu, J. Estimation methods review and analysis of offshore extreme wind speeds and wind energy resources. Renew. Sustain. Energy Rev. 2015, 42, 26–42. [Google Scholar] [CrossRef]
- An, Y.; Pandey, M.D. A comparison of methods of extreme wind speed estimation. J. Wind. Eng. Ind. Aerodyn. 2005, 93, 535–545. [Google Scholar] [CrossRef]
- D’Amico, G.; Petroni, F.; Prattico, F. Wind speed prediction for wind farm applications by extreme value theory and copulas. J. Wind. Eng. Ind. Aerodyn. 2015, 145, 229–236. [Google Scholar]
- Duan, Z.; Ou, J.; Zhou, D. The optimal probabilistic distribution for extreme wind speed. China Civ. Eng. J. 2002, 35, 11–16. [Google Scholar]
- Zhao, L.; Ge, Y.; Xiang, H. Optimization strategy of extreme wind speed fitting. J. Tongji Univ. (Nat. Sci.) 2003, 31, 383–388. [Google Scholar]
- Lu, A.; Zhao, L.; Guo, Z.; Ge, Y. A comparative study of extreme value distribution and parameter estimation based on the Monte Carlo method. J. Harbin Inst. Technol. 2013, 45, 88–95. [Google Scholar]
- Morgan, E.C.; Lackner, M.; Vogel, R.M.; Baise, L.G. Probability distributions for offshore wind speeds. Energy Convers. Manag. 2011, 52, 15–26. [Google Scholar] [CrossRef]
- Patlakas, P.; Galanis, G.; Barranger, N.; Kallos, G. Extreme wind events in a complex maritime environment: Ways of quantification. J. Wind. Eng. Ind. Aerodyn. 2016, 149, 89–101. [Google Scholar]
- Chen, Z.; Guan, Q. Simulating of asymptotic distributions of extreme wind speed in Chongqing using short-term wind speed records. J. Chongqing Univ. 2006, 29, 88–92. [Google Scholar]
- Gugliani, G.K.; Sarkar, A.; Bhadani, S.; Mandal, S. A novel approach for accurate assessment of design wind speed for variable wind climate. KSCE J. Civ. Eng. 2019, 23, 608–623. [Google Scholar]
- Li, B.; Li, C.; Yang, Q.; Tian, Y.; Zhang, X. Full-scale wind speed spectra of 5 Year time series in urban boundary layer observed on a 325 m meteorological tower. J. Wind. Eng. Ind. Aerodyn. 2021, 218, 104791. [Google Scholar] [CrossRef]
- Simiu, E.; Heckert, N.A. Extreme wind distribution tails: A peaks over threshold approach. J. Struct. Eng. 1996, 122, 539–547. [Google Scholar] [CrossRef]
- ESDU (Engineering Science Data Unit). World-Wide Extreme Wind Speeds: Part 1: Origins and Methods of Analysis; HIS (Information Handling Service): London, UK, 2012. [Google Scholar]
- Cook, N.J. Designers Guide to Wind Loading of Building Structures. Part 1: Background, Damage Survey, Wind Data and Structural Classification; Building Research Establishment Report; Butterworths: London, UK, 1986; pp. 99–116. [Google Scholar]
- Cook, N.J. Note on directional and seasonal assessment of extreme winds for design. J. Wind. Eng. Ind. Aerodyn. 1983, 12, 365–372. [Google Scholar]
- Cook, N.J.; Miller, C.A. Further note on directional assessment of extreme winds for design. J. Wind. Eng. Ind. Aerodyn. 1999, 79, 201–208. [Google Scholar] [CrossRef]
- Quan, Y.; Liu, L.; Gu, M. Improvement of Cook method considering directional extreme wind speed. J. Tongji Univ. (Nat. Sci.) 2015, 43, 189–192. [Google Scholar]


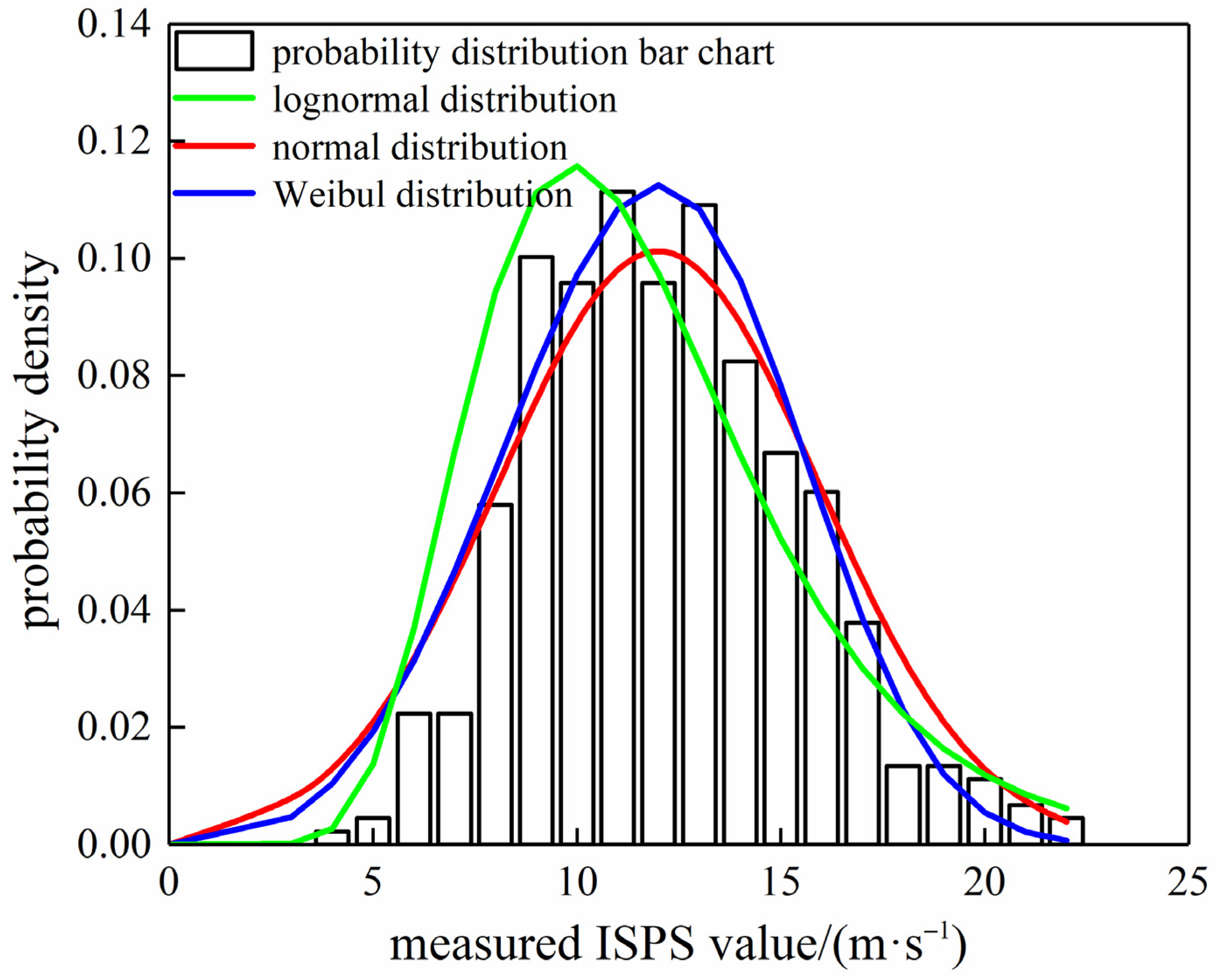

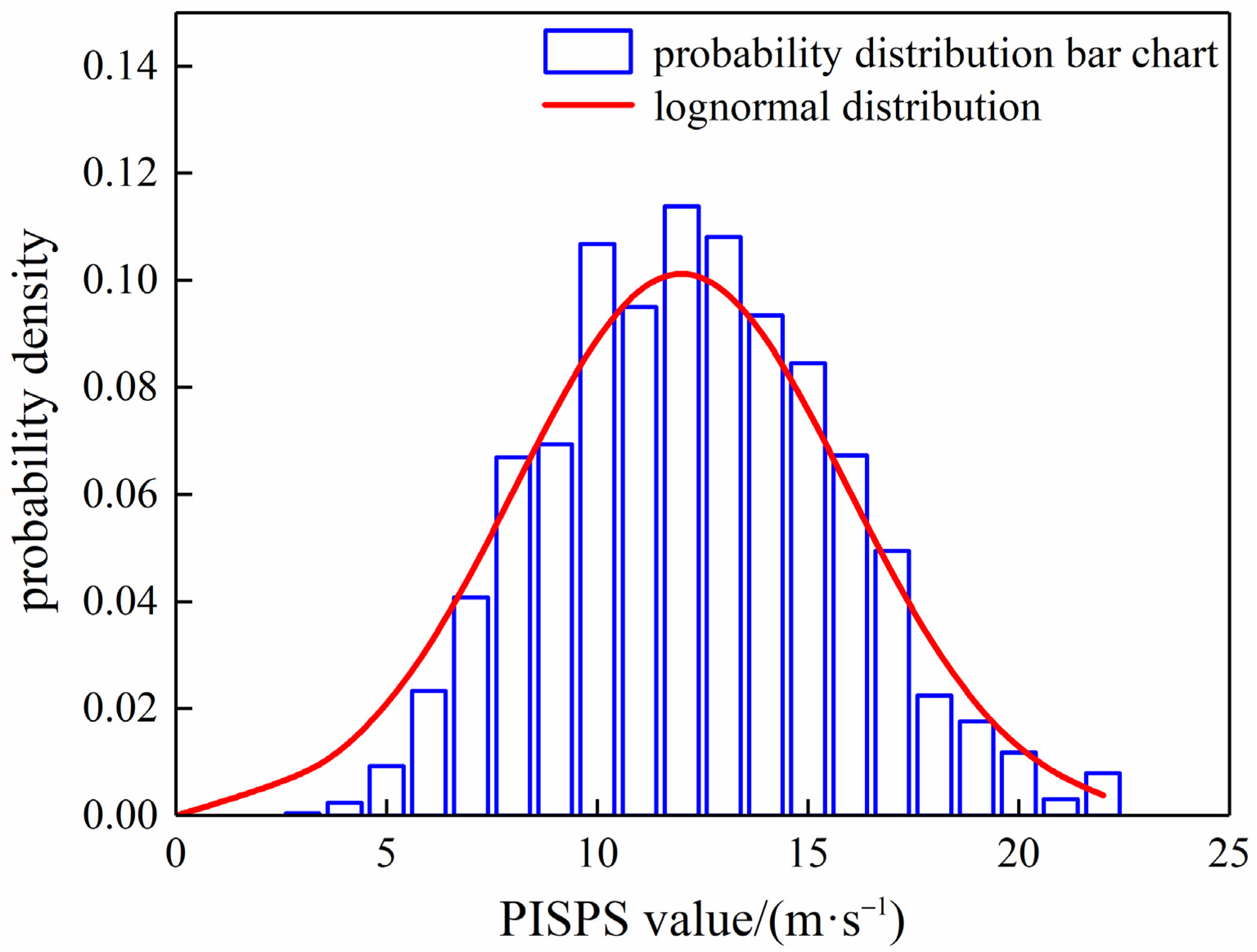
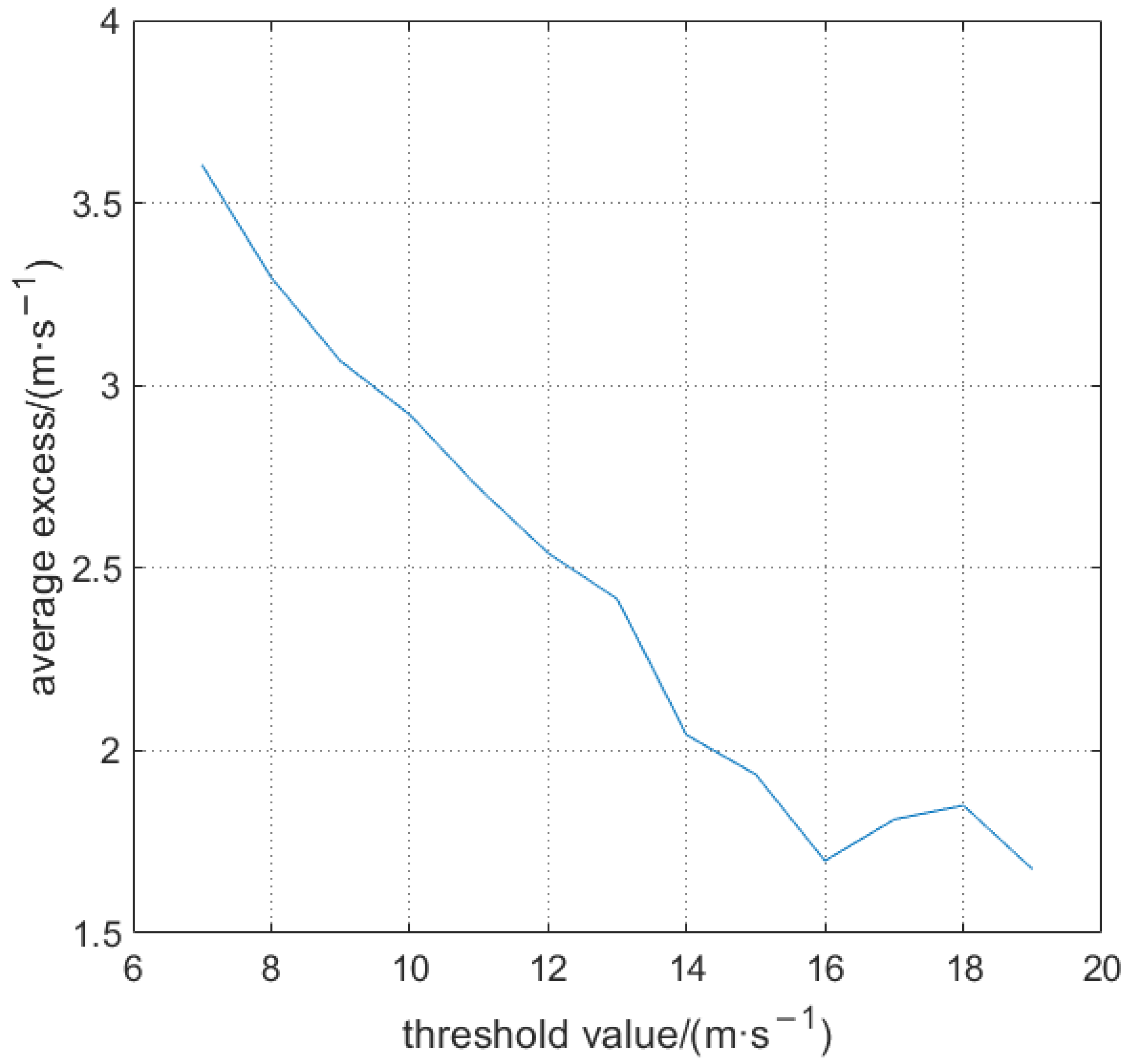

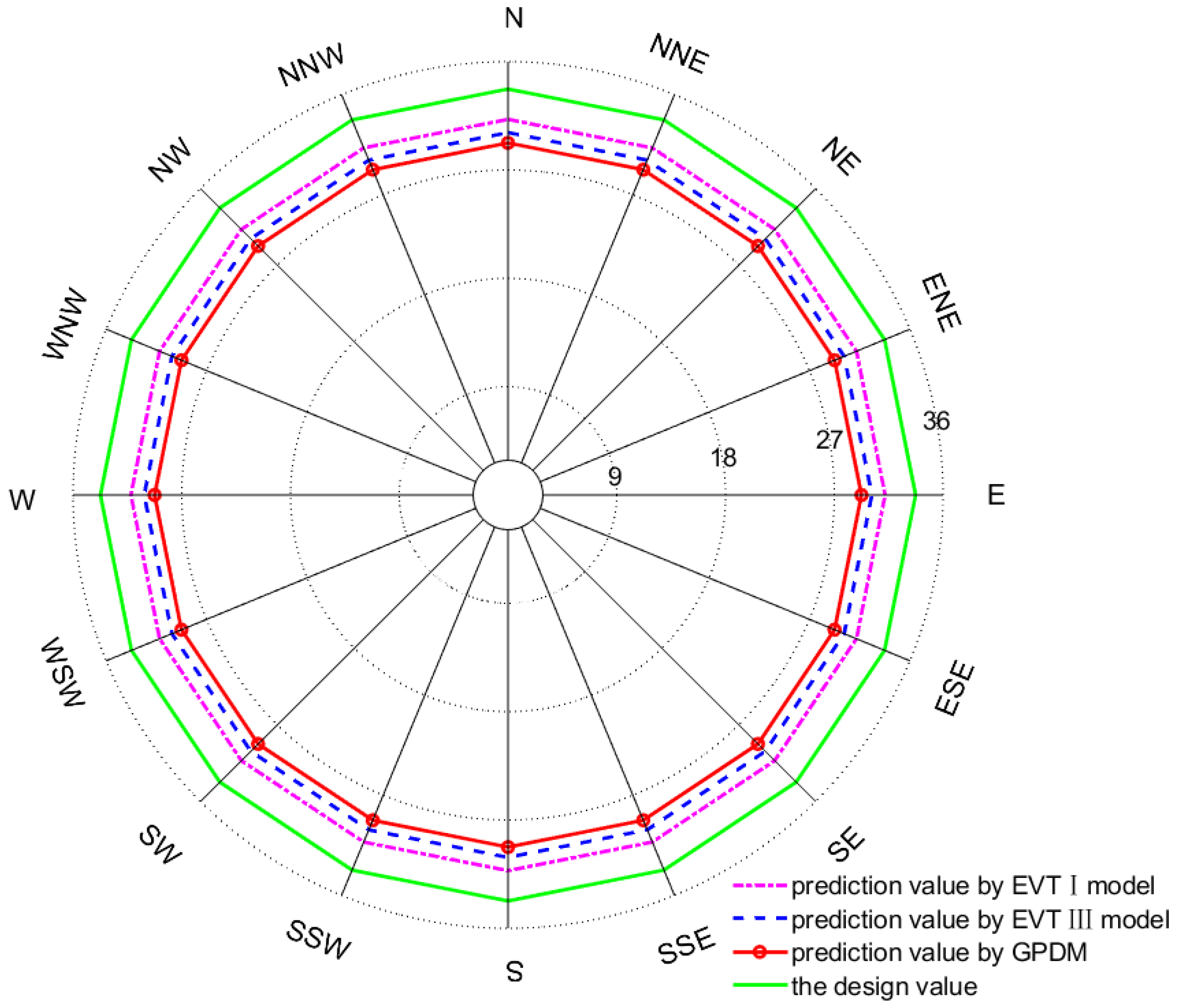
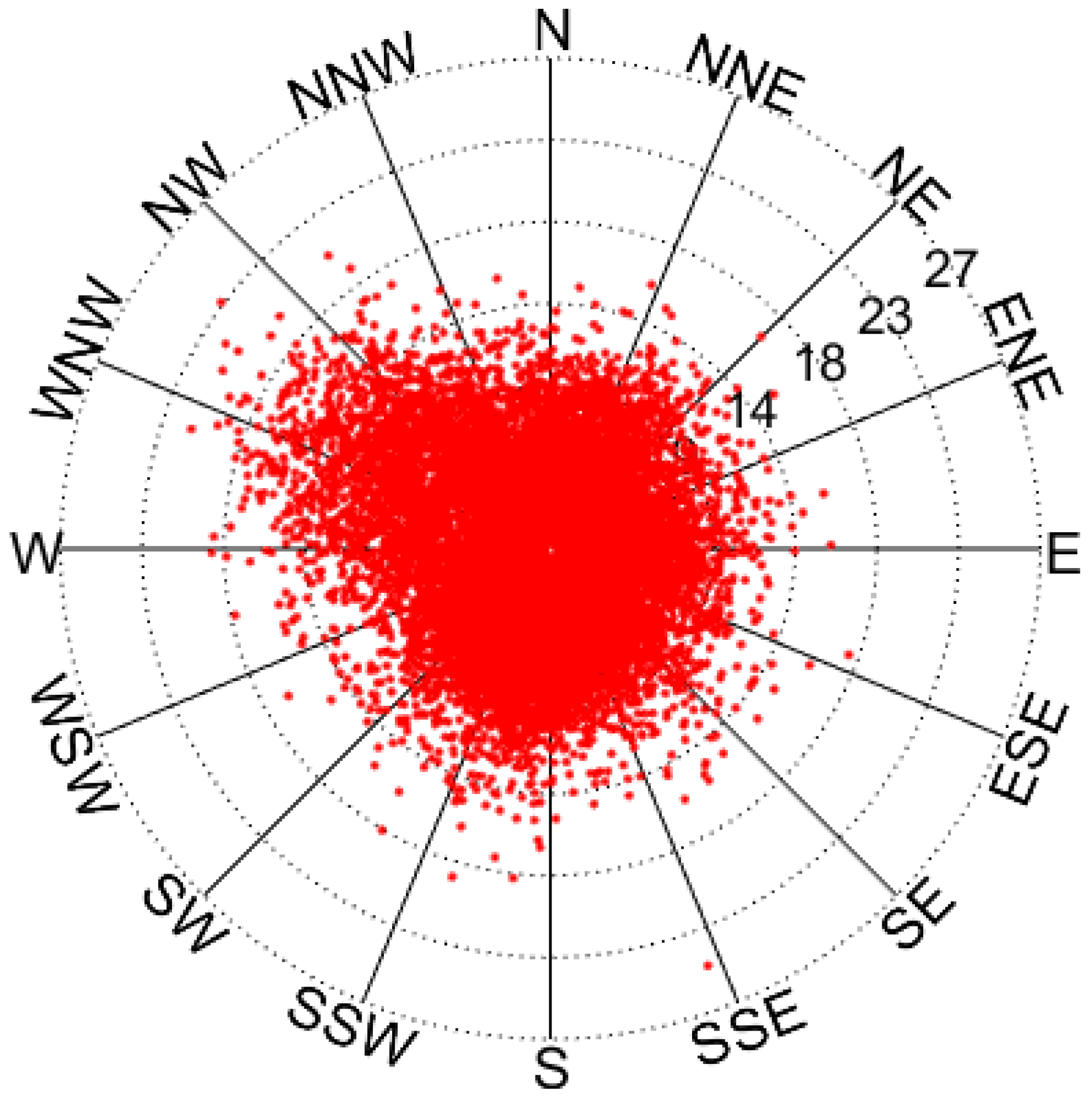
| Model | Position Parameters | Scale Parameters | Shape Parameters | Ks | R2 |
|---|---|---|---|---|---|
| lognormal | 2.4 | 0.33 | 0.89 | 0.80 | |
| normal | 12 | 3.9 | 0.79 | 0.85 | |
| Weibull | 13 | 3.83 | 0.96 | 0.79 |
| Model | Position Parameters | Scale Parameters | Shape Parameters |
|---|---|---|---|
| EVT I | 22.04 | 2.35 | |
| EVT III | 38.94 | 16.76 | 6.09 |
| Wind Direction | /(m·s−1) | (%) | (%) |
|---|---|---|---|
| N | 29.15 | 0.34 | 0.3 |
| NNE | 33.72 | 15.28 | 13.5 |
| NE | 31.19 | 6.62 | 5.85 |
| ENE | 29.73 | 1.63 | 1.44 |
| E | 29.50 | 0.86 | 0.76 |
| ESE | 25.77 | 11.9 | 10.52 |
| SE | 22.34 | 23.63 | 20.88 |
| SSE | 32.31 | 10.45 | 9.23 |
| S | 26.32 | 10.02 | 8.86 |
| SSW | 32.62 | 11.54 | 10.2 |
| SW | 31.90 | 9.07 | 8.01 |
| WSW | 37.66 | 28.76 | 25.42 |
| W | 32.94 | 12.61 | 11.14 |
| WNW | 28.22 | 3.53 | 3.12 |
| NW | 34.20 | 16.94 | 14.97 |
| NNW | 31.19 | 6.63 | 5.86 |
| Mean | 30.55 | 10.6 | 9.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Tian, Y. The Return Period Wind Speed Prediction of Beijing Urban Area Based on Short-Term Measured Wind Speed. Atmosphere 2024, 15, 159. https://doi.org/10.3390/atmos15020159
Chen W, Tian Y. The Return Period Wind Speed Prediction of Beijing Urban Area Based on Short-Term Measured Wind Speed. Atmosphere. 2024; 15(2):159. https://doi.org/10.3390/atmos15020159
Chicago/Turabian StyleChen, Weihu, and Yuji Tian. 2024. "The Return Period Wind Speed Prediction of Beijing Urban Area Based on Short-Term Measured Wind Speed" Atmosphere 15, no. 2: 159. https://doi.org/10.3390/atmos15020159
APA StyleChen, W., & Tian, Y. (2024). The Return Period Wind Speed Prediction of Beijing Urban Area Based on Short-Term Measured Wind Speed. Atmosphere, 15(2), 159. https://doi.org/10.3390/atmos15020159





