Abstract
Due to the complexity and uncertainty of meteorological systems, traditional precipitation forecasting methods have certain limitations. Therefore, based on the common characteristics of meteorological data, a precipitation forecasting model named MultiPred is proposed, with the goal of continuously predicting precipitation for 4 h in a specific region. This model combines the multimodal fusion method with recursive spatiotemporal prediction models. The training and testing process of the model roughly involves using spatial feature extraction networks and temporal feature extraction networks to generate preliminary predictions for multimodal data. Subsequently, a modal fusion layer is employed to further extract and fuse the spatial features of the preliminary predictions from the previous step, outputting the predicted precipitation values for the target area. Experimental tests and training were conducted using ERA5 multi-meteorological modal data and GPM satellite precipitation data from 2017 to 2020, covering longitudes from 110° to 122° and latitudes from 20° to 32°. The training set used data from the first three years, while the validation set and test set each comprised 50% of the data from the fourth year. The initial learning rate for the experiment was set to 1 × 10−4, and training was performed for 1000 epochs. Additionally, the training process utilized a loss function composed of Mean Absolute Error (MAE), Mean Squared Error (MSE), and Structural Similarity Index (SSIM). The model was evaluated using the Critical Success Index (CSI), Probability of Detection (POD), and the Heidke Skill Score (HSS). Experimental results demonstrate that MultiPred excels in precipitation forecasting, particularly for light precipitation events with amounts greater than or equal to 0.1 mm and less than 2 mm. It achieves optimal performance in both light and heavy precipitation forecasting tasks.
1. Introduction
Precipitation is one of the most common weather events in our daily lives [1]. From traditional rain gauges to modern meteorological radars and satellites, the automation and precision of sensors for measuring precipitation have significantly improved. These advancements provide a data foundation for Numerical Weather Prediction (NWP) [2]. NWP involves the long-term simulation of the Earth’s atmosphere, a typical nonlinear system, through the establishment of mathematical and physical models. It exhibits good interpretability. However, NWP models are grounded in the mathematical modeling principles of atmospheric physics and dynamics, rendering them more suitable for long-term meteorological forecasting tasks. They encounter challenges in predicting rapid changes in local weather conditions, particularly in the short-term forecasting of precipitation within specific local areas [3].
The radar extrapolation method [4] is a precipitation forecasting technique based on radar reflectivity data. This method predicts the development trend and intensity of precipitation by analyzing the characteristics of radar echoes. One advantage of this approach is its real-time capability, allowing for precipitation forecasts within a relatively short time range. However, due to the fact that motion can be highly dynamic and nonlinear, and its intensity can vary over time, radar extrapolation still has the problem of low accuracy in practical applications [5]. Due to limitations such as insufficient data update frequency and insensitivity to dynamic changes, the radar echo extrapolation method faces challenges in meeting the demands of short-term precipitation forecasting.
With the rise of deep learning science, there have been new development directions in the field of precipitation forecasting, and many scholars have conducted research in this area [6,7,8,9,10]. Deep learning models for short-term precipitation forecasting tasks can be categorized into four main types: Convolutional Neural Networks (CNNs), Recurrent Neural Networks (RNNs), Generative Networks, and Graph Neural Networks (GNNs). CNN structures, notably UNet [11] and its variants, have been extensively developed and applied in the study of hurricanes and extreme precipitation events. However, CNN models exhibit limitations in handling time series data, particularly for rapidly changing weather events.
Generative Adversarial Networks (GANs) find application in synthesizing meteorological scenarios, especially precipitation scenes. By learning distributions from existing observational data, GANs can generate synthetic data, aiding in augmenting training samples to enhance model performance. Meng et al. [12] introduced TCR-GAN for predicting extreme precipitation events caused by cyclones. Graph Neural Networks (GNNs) excel in capturing spatiotemporal relationships between nodes in graph structures, which is crucial for handling complex spatiotemporal correlations in meteorological data.
Recently, with the popularity of Transformer [13], Zhang et al. [14] employed a deep learning framework based on Automated Machine Learning (AutoML) techniques and Transformers. Experimental validation on datasets of two different resolutions confirmed the algorithm’s effectiveness. In addition, Transformer variants such as FourCastNet [15], Rainformer [16], and Earthformer [17] are also applied in the field of short-term precipitation forecasting.
Compared to other models, RNN models are more suitable for short-term precipitation forecasting due to their outstanding performance in handling time-series data. These models, by incorporating recurrent structures, effectively capture dependencies in the temporal dimension, showcasing notable performance when dealing with rapidly changing weather events.
However, typical RNN models such as ConvLSTM [18] treat the short-term precipitation forecasting problem as a spatiotemporal prediction issue based on radar echo sequences and have only been tested on radar echo datasets. Due to the instability of meteorological systems, radar data can be subject to noise interference, making it challenging to accurately reflect the true distribution of precipitation and leading to significant prediction errors.
In addition to radar echo data, there are other data sources in the meteorological field, such as satellite observation data, which can reflect real precipitation conditions. Furthermore, unlike other spatiotemporal prediction problems, meteorological data often interact with each other, exhibiting multimodality. Most current precipitation forecasting models do not fully exploit this characteristic. Therefore, our research focuses on the question of how to effectively leverage multimodal data to enhance the accuracy of precipitation forecasting.
Moreover, we hypothesize that the limitations of spatiotemporal prediction models such as ConvLSTM in short-term precipitation forecasting stem from an excessive reliance on radar echo sequences, neglecting the multimodality and spatial feature complexity of meteorological data. Based on this assumption, we propose a novel short-term precipitation forecasting model that combines a multimodal fusion structure with spatiotemporal prediction models, termed the multimodal fusion and prediction model (MultiPred).
Our goal is to integrate multimodal data and thoroughly explore the implicit causal relationships between precipitation data and other meteorological elements, aiming to enhance the accuracy of short-term local precipitation forecasts. The model leverages historical multimodal data from the target area to forecast subsequent precipitation events. Specifically, MultiPred comprises three components for precipitation prediction. Firstly, a spatial feature extraction network (SFEN) is employed to fuse spatial features from historical multimodal data. Secondly, a time feature extraction network consisting of convolutional long short-term memory (ConvLSTM) is utilized for the initial prediction of historical multimodal data. Thirdly, a modal fusion layer (MFL) is incorporated to fuse spatial features from the initial prediction, amalgamating the spatial features obtained from multiple meteorological modal data in the first stage. This enables the model to focus on predicting and outputting precipitation in the target region. The model was tested using ERA5 and GPM data, and the experimental results demonstrate that, compared to other models, MultiPred exhibits higher accuracy. The main contributions of this paper are as follows:
- In this study, a precipitation forecasting model named MultiPred is introduced, incorporating a multimodal fusion structure to integrate historical multimodal data from various sources, including satellite observations. This approach maximizes the diversity of meteorological data and enhances the model’s ability to reflect real precipitation.
- A novel spatial feature attention layer is proposed for constructing the spatial feature extraction network (SFEN), enabling a more specialized and efficient implementation of spatial feature fusion for historical multimodal data.
- Experimental validation on ERA5 and GPM datasets demonstrates that the MultiPred model exhibits higher accuracy compared to other models. This provides a novel and more effective direction and methodology for the future field of meteorological forecasting.
2. Related Work
2.1. Spatiotemporal Prediction Model
Traditional RNN models, such as LSTM and GRU, are commonly used in natural language processing [19]. RNN models flexibly handle sequence data through their autoregressive structure and effectively learn in the temporal dimension. However, traditional RNN models have some limitations in handling spatial features. When dealing with meteorological data with significant spatiotemporal variations, traditional RNN models often struggle to capture complex spatial correlations and multimodal characteristics.
To overcome these limitations, Shi et al. [18] replaced the matrix multiplication in the LSTM network with convolutional connections, forming the ConvLSTM model. This improvement enables the model to better capture the spatial features in meteorological data, resulting in superior performance in tasks such as short-term precipitation forecasting.
In order to enhance precipitation forecasting, Shi et al. [20] introduced TrajGRU in 2017. This method utilizes optical flow and a GRU model to extract trajectory information from historical precipitation observations, enhancing the accuracy of predicting future precipitation based on trajectory information. Wang et al. [21] introduced spatiotemporal memory units (M) into ConvLSTM and connected them through a zigzag structure, proposing the PredRNN model, which demonstrates outstanding performance in precipitation forecasting tasks. In 2018, Wang et al. extended PredRNN to PredRNN++ [22], which uses gradient highways (GHU) to alleviate the vanishing gradient problem. Subsequently, they further improved unit structures and the overall framework, introducing models such as MIM [23], E3D-LSTM [24], and PredRNN-V2 [25], achieving significant success in precipitation forecasting and other spatiotemporal prediction problems.
2.2. Multimodal Fusion
Multimodal fusion technology is another hot topic in current meteorological forecasting research. This technology integrates data from various observation methods, such as satellite remote sensing, ground observations, reanalysis data, and radar data, to enhance the model’s comprehensive understanding of meteorological phenomena. In this field, researchers actively explore and propose various innovative approaches to address the complexity and diversity in meteorological forecasting.
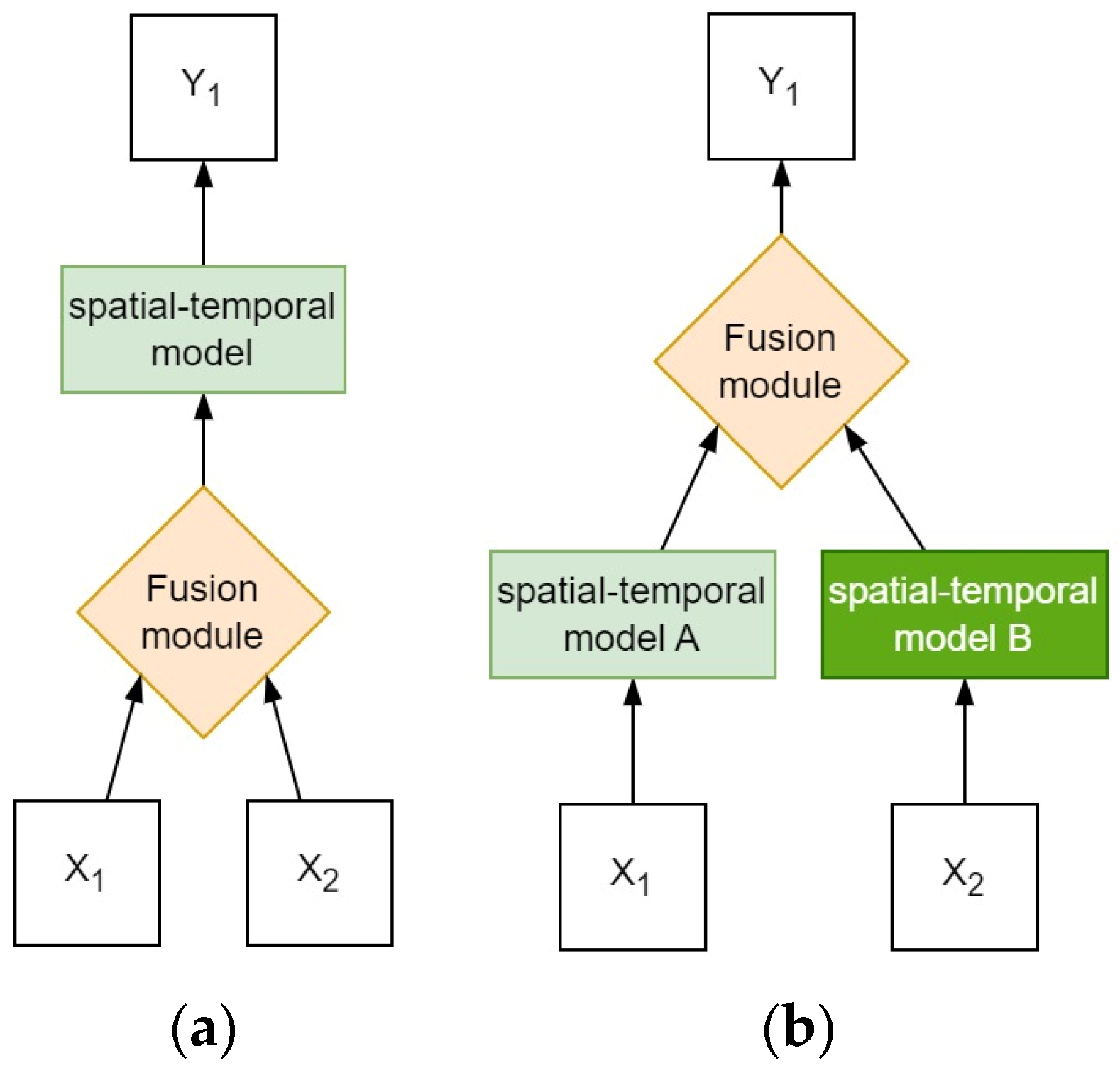
Multimodal fusion can be classified into early fusion and late fusion based on the fusion stage [26], as shown in Figure 1.
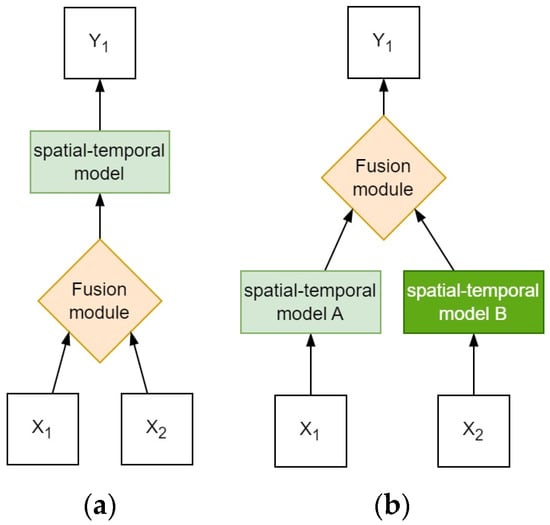
Figure 1.
The structure of different multimodal models. X1 and X2 represent inputs from different data sources, while Y represents outputs. (a) Early fusion strategy. (b) Late fusion strategy.
In early fusion models, Zhang et al. [14] developed an early fusion structure based on a deep learning framework using automatic machine learning techniques and Transformers. This structure, based on CNN, aims to extract spatial context from multimodal meteorological data. Through this algorithm, the research team successfully validated the empirical verification of two different resolution datasets, confirming the effectiveness of the algorithm in improving meteorological forecasting accuracy. Jin et al. [27] proposed an early fusion structure named Spatiotemporal-Aware Convolutional Neural Network (STACNN) for short-term precipitation forecasting tasks. This structure effectively integrates multimodal information, including temperature, humidity, and wind, establishing more efficient and comprehensive correlations between different modal data.
In late fusion models, Ma et al. [28] proposed a late fusion recurrent neural network, which not only provides accurate short-term precipitation forecasts but also predicts other meteorological elements. It demonstrates high flexibility and compatibility with various recurrent neural network models. They conducted experiments on two multimodal datasets, and MM-RNN outperformed conventional RNN networks that use a single radar modality. In 2019, Geng et al. [29] introduced LightNet, which utilizes ConvLSTM to extract spatiotemporal features from both lightning observation data and WRF model data. The features from these two types of data are then fused using a convolutional neural network to form a more comprehensive feature representation. Later, in 2023, they proposed LightNet+ [30], an extension of LightNet, introducing a bidirectional propagator and a non-local fusion unit. Specifically, LightNet+ employs an encoder based on ConvLSTM to encode lightning observation data, obtaining a compact feature representation. It then utilizes a bidirectional propagator to extract temporal trend information from the WRF model data in both forward and backward directions in the time dimension. Finally, a non-local fusion unit seamlessly integrates the features of the two types of data, providing more accurate and comprehensive information for the final lightning prediction results.
Compared to late fusion, early fusion has lower model complexity. In late fusion, different data sources need to be handled separately, while early fusion allows for feature extraction and data integration at an earlier stage, making the model more concise and efficient. Therefore, in the MultiPred model, early fusion is chosen to achieve precipitation forecasting.
3. Data
Data Set
The datasets used in the MultiPred model include global precipitation measurement data (GPM) related to precipitation and the ERA5 reanalysis dataset. The following paragraph will introduce these two types of data.
GPM refers to global precipitation measurement data obtained through the Integrated Multi-satellite Retrievals for GPM (IMERG) technology developed by the National Aeronautics and Space Administration (NASA) [31]. GPM data are grid data with a spatial resolution of 0.1° × 0.1° and a temporal resolution of 30 min. IMERG combines data from all passive microwave instruments in the GPM to provide rainfall estimates. In this study, GPM data can be approximated as actual precipitation values.
ERA5 data represents a new generation of global climate and atmospheric reanalysis data developed by the European Centre for Medium-Range Weather Forecasts [32]. ERA5 data includes various meteorological variables, such as temperature, humidity, wind speed, and other commonly used data, with a spatial resolution of 0.25° × 0.25° and a temporal resolution of 1 h. The data used in this study include eight meteorological variables at 700 hPa, 800 hPa, and 850 hPa levels, comprising temperature, U-component wind, V-component wind, vertical wind, and specific humidity. The reanalysis data from ERA5 are illustrated in Figure 2.

Figure 2.
Examples of ERA5 dataset, In the figure, color depth is used to represent the numerical strength of the corresponding meteorological mode. The darker the color, the higher the intensity, and vice versa. For example, in temperature images, the darker the color, the higher the temperature.
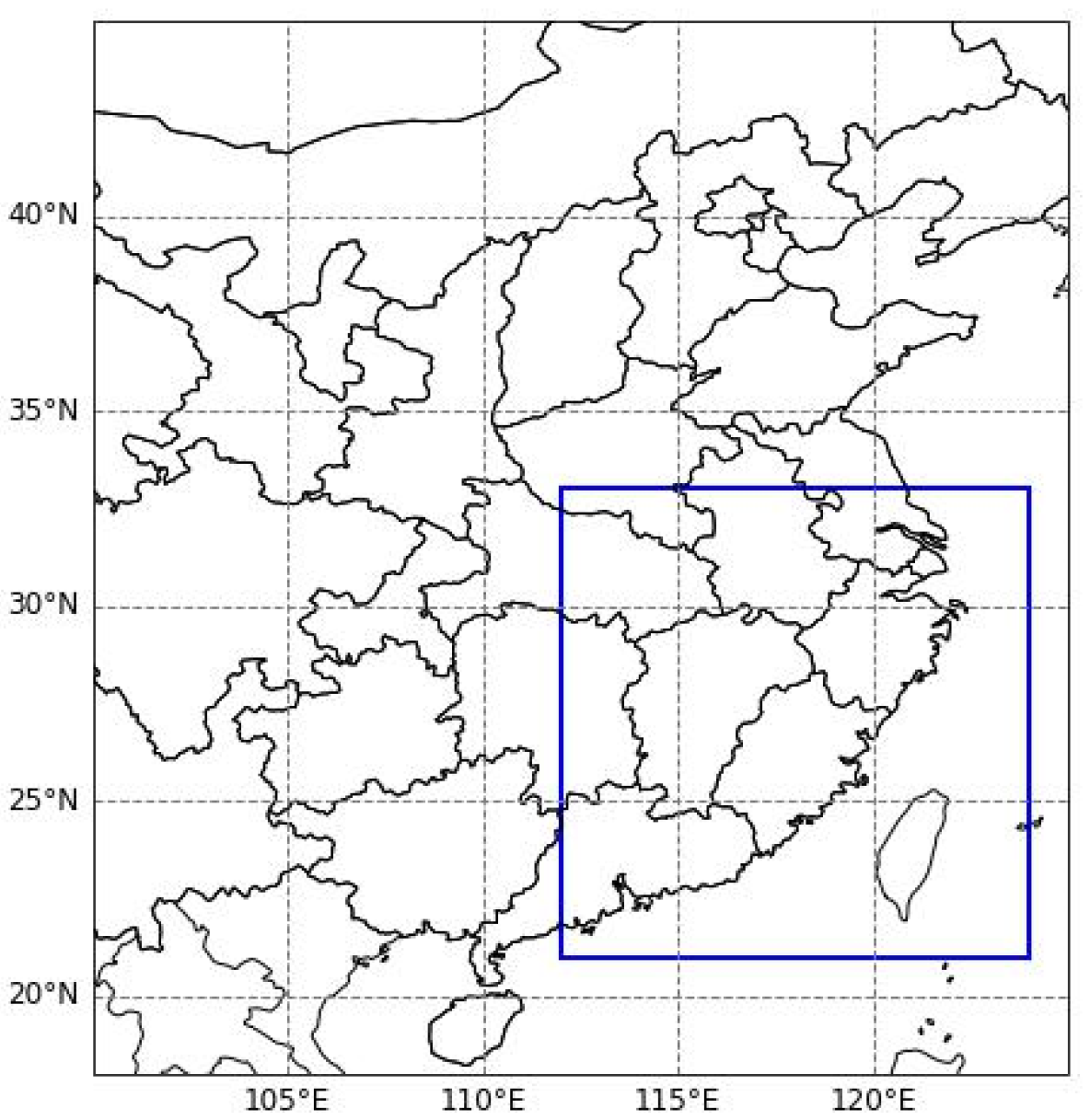
Our experiment aims to perform precipitation forecasting for a target region with dimensions of 120 × 120, covering the longitude from 110° to 122° and the latitude from 20° to 32°. Figure 3 displays the study area.
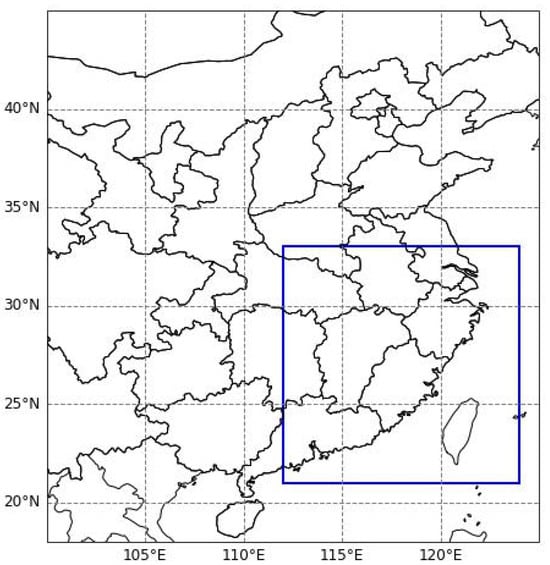
Figure 3.
The blue box indicates the input region for GPM grid data and ERA5 multimodal meteorological data.
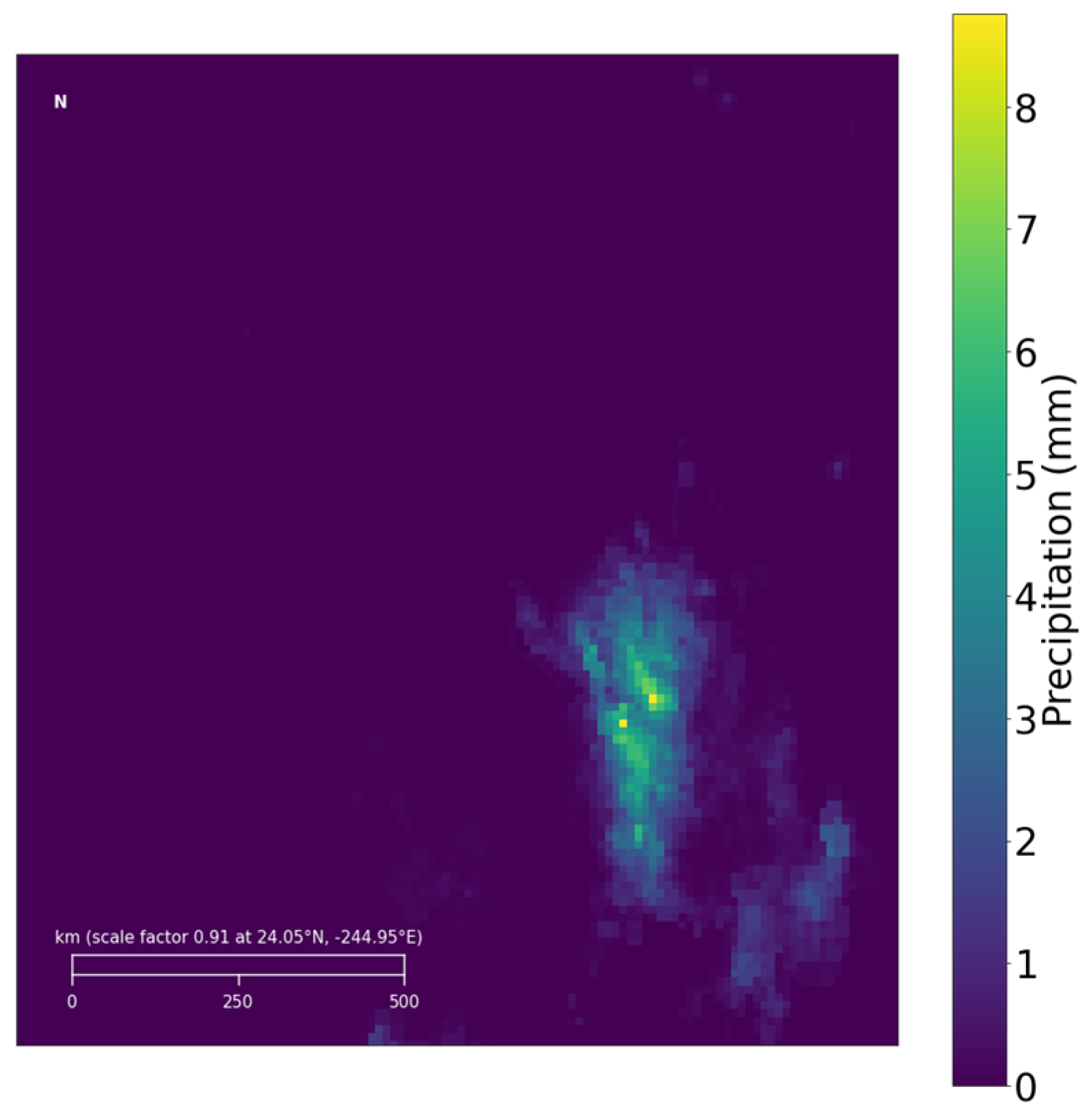
The precipitation data for the target region from GPM is illustrated in Figure 4. Additionally, to simulate the climatic environment of this area, ERA5 multimodal meteorological data have been chosen, covering the same range as the GPM grid data for the target region, with the ERA5 data represented in a 48 × 48 grid.
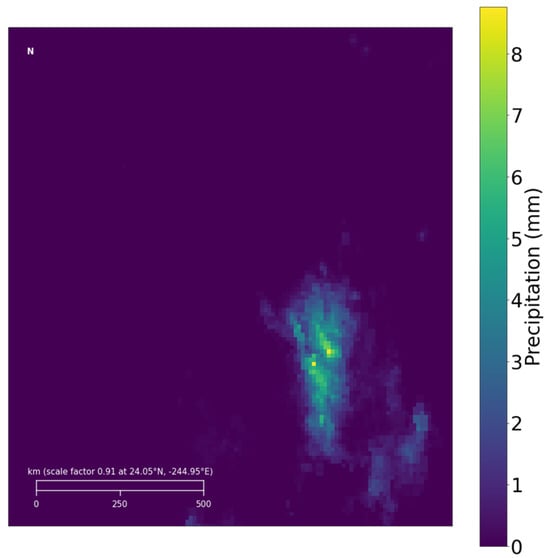
Figure 4.
Examples of GPM precipitation data in the target area.
4. Model
4.1. Spatiotemporal Sequence Prediction
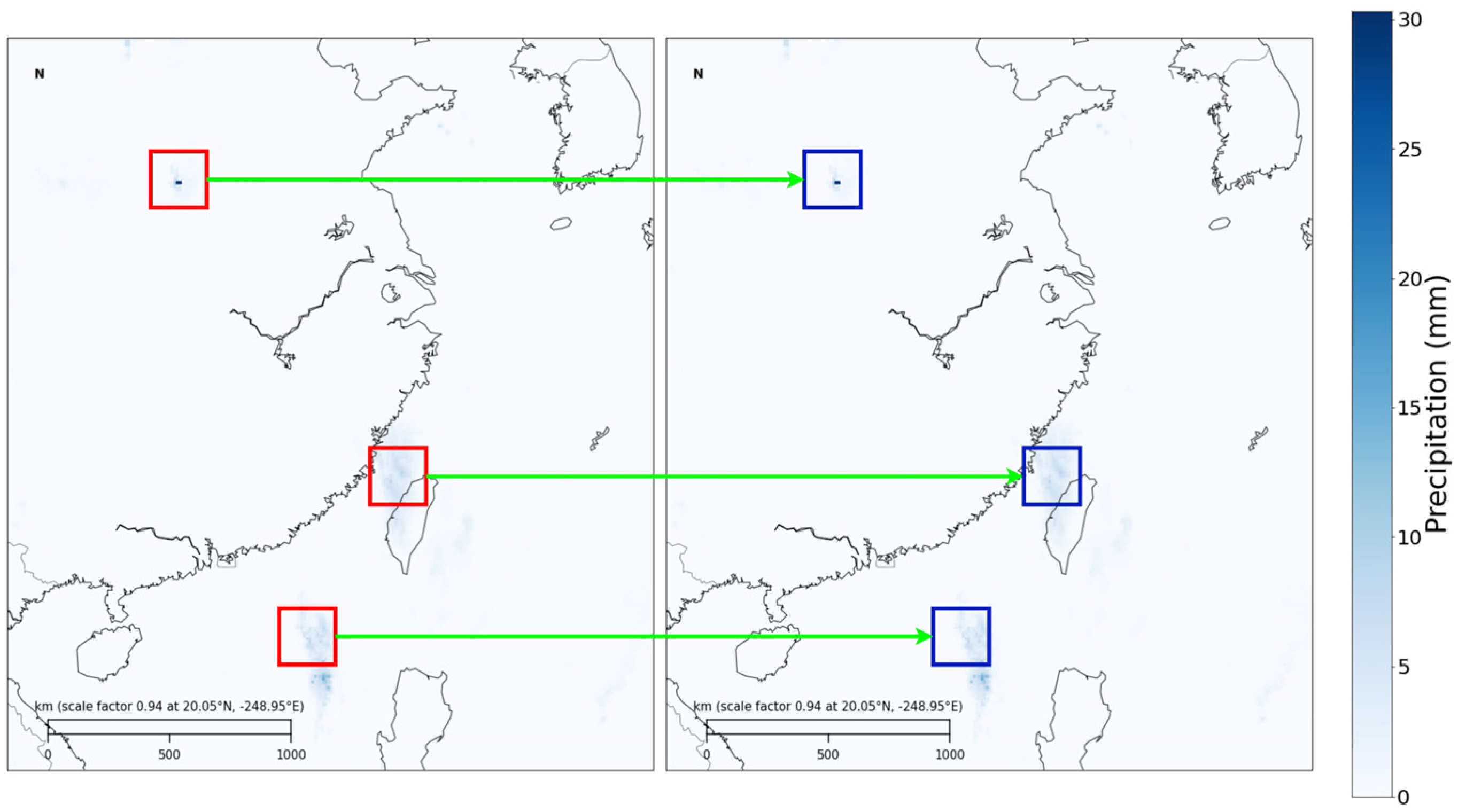
Given the spatial resolution, temporal intervals, and uneven distribution in meteorological observation data and meteorological reanalysis data, certain meteorological data, for instance, precipitation in coastal areas, may simultaneously be more prominent than in inland regions. In the same region, spring precipitation is typically less than summer precipitation, as illustrated in Figure 5.
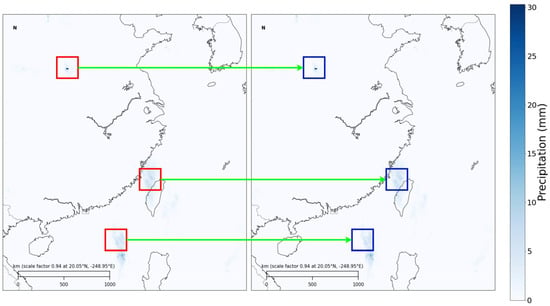
Figure 5.
Changes in precipitation in the eastern region of China on 1 May 2017 and 14 August 2017. From the figure, it can be observed that coastal precipitation is more frequent and intense. Additionally, the red and blue boxed areas in the figure indicate significant changes in the same region over time.
Therefore, meteorological observations can be formalized as meteorological data sequences with specific spatiotemporal resolutions [32]. For a local region at time , the -th type of meteorological observation data can be represented by the tensor , where and represent the grid length and width, based on latitude and longitude resolution, respectively. The entire meteorological observation sequence can be represented by concatenating all meteorological modality data, i.e., , where represents the number of modalities. By modeling meteorological data, meteorological forecasting tasks can be formalized as a spatiotemporal prediction task from sequence to sequence [33]. The goal is to infer the future meteorological states based on the historical observation sequence .
4.2. ConvLSTM
The ConvLSTM layer comprises two states: the cell state () and the hidden state (H), as well as three gates—the input gate, the forget gate, and the output gate. Along the time dimension, the forget gate () is activated first to determine which parts of the cell state () should be “forgotten”. Subsequently, new information accumulates in the cell state through the input gate (). Finally, the output gate () controls which information will propagate to the next time step. Formally, given an input Ft, the key equations of the ConvLSTM are as follows:
where ∗ denotes the convolution operator, ⊙ represents element-wise multiplication; and b are parameters for each gate; σ is the sigmoid function. As the third component of the model, ConvLSTM serves as a temporal feature extraction network, predicting multimodal meteorological data across multiple time steps. This can further enhance the accuracy and robustness of precipitation forecasting.
4.3. Basic Network Structure
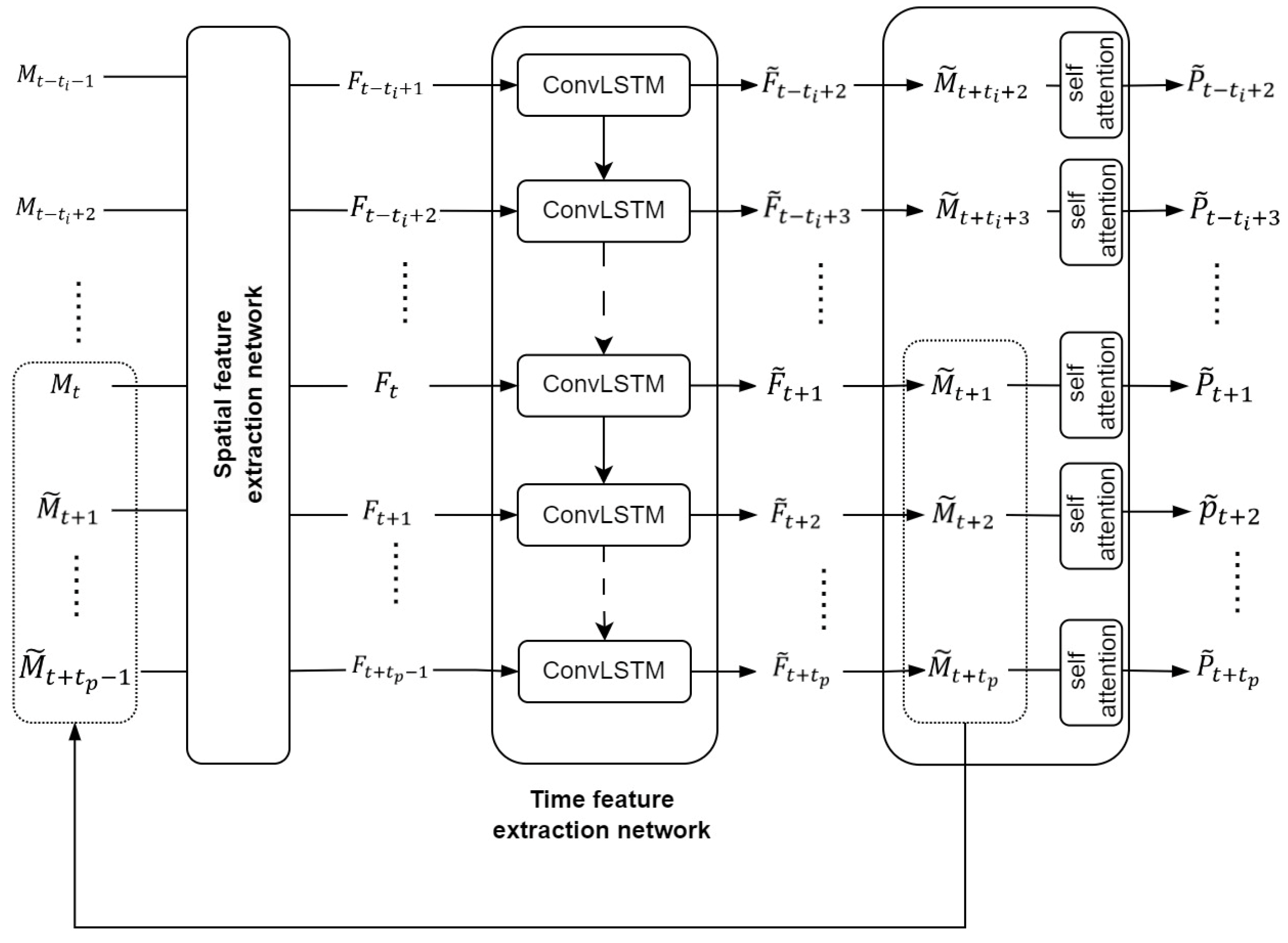
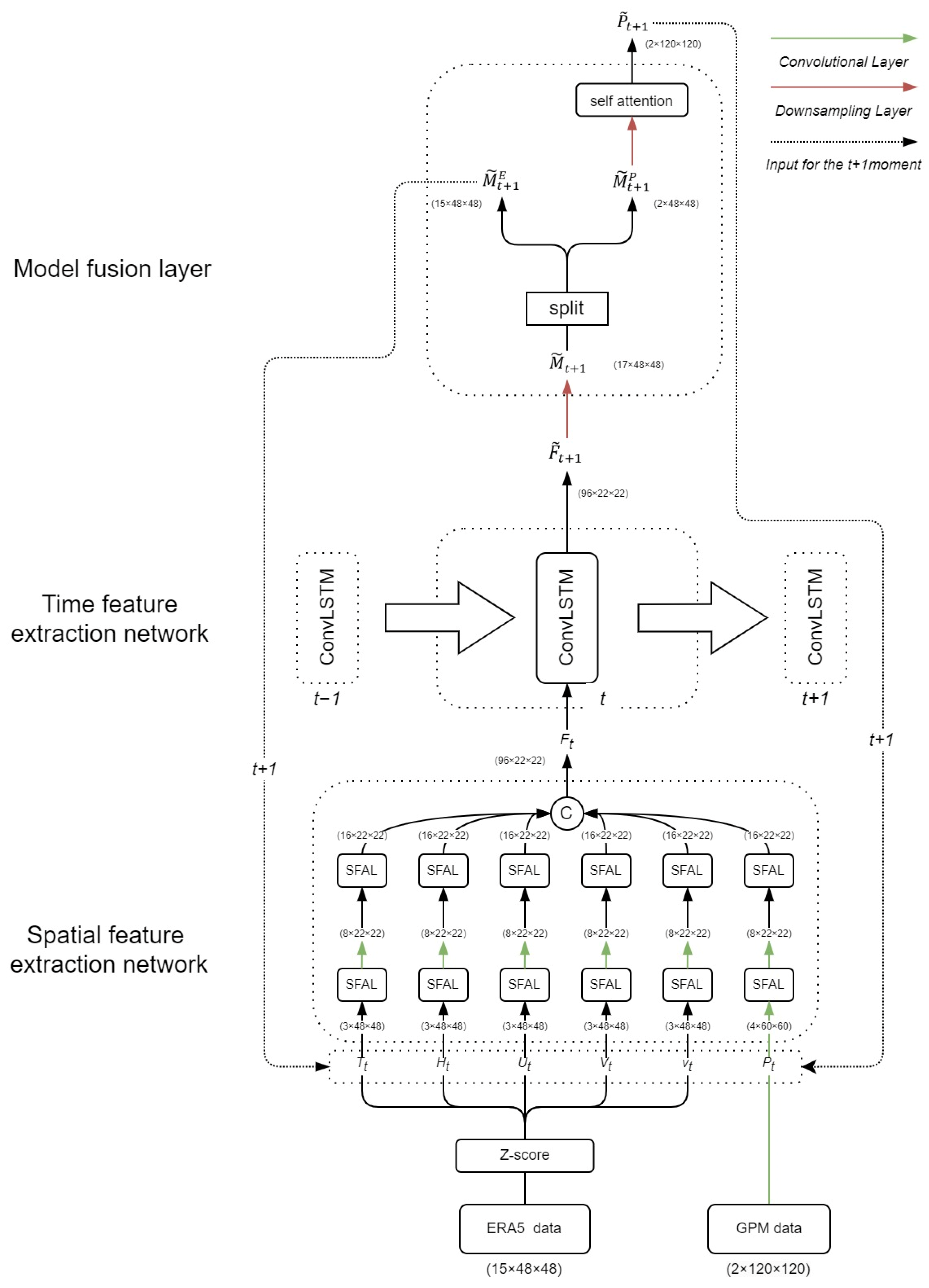
The precipitation forecasting problem in the field of meteorology is commonly regarded as a spatiotemporal prediction challenge in the realm of deep learning. In response to this, the MultiPred model has been devised, consisting primarily of three parts. The model structure is depicted in Figure 6.
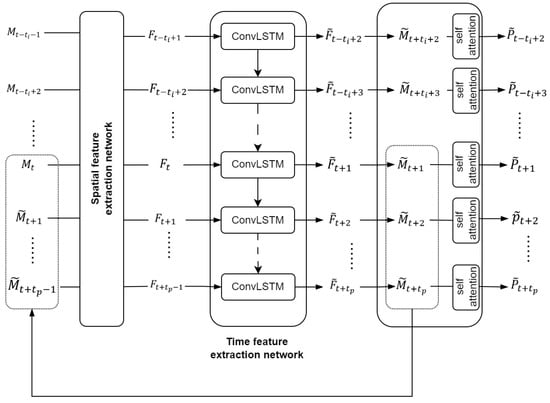
Figure 6.
Model structure diagram.
The first part is the spatial feature extraction network, which inputs multiple meteorological modal data sequences, including precipitation, , and outputs the encoded multimodal feature sequence, . The second part is the ConvLSTM network, which inputs the multimodal feature string and outputs the multimodal feature prediction sequence . The third part is the modal fusion layer, which integrates the spatial features of that have been upsampled by , and then, via the MFL, outputs the predicted precipitation value for the target area. The first part is the spatial feature extraction network, which can be formulated as follows:
In this context, represents a multimodal meteorological sequence with t_i observations at time t, where consists of denoting the U-component wind, V-component wind, humidity, temperature, vertical velocity, and precipitation at time , respectively. and represent the number of channels, the length of the tensor, and the width of the tensor, respectively.
In the first part of the model, the spatial feature extraction network extracts and integrates the spatial features of the reanalysis data sequence , and outputs a spatially encoded multimodal feature sequence .
The second part is the time feature extraction network, which, based on the output of the first part, , further extracts the temporal features of multimodal data and outputs the predicted multimodal data values for the target region, with a length of . This stage can be formalized as follows:
The third part is the spatial regression layer. Based on the output of the second part, F, of the model, this layer first obtains by upsampling , further fusing multimodal data, and outputting the predicted precipitation value for the target area. This stage can be formalized as follows:
4.4. Spatial Feature Extraction Network
4.4.1. Spatial Feature Attention Layer
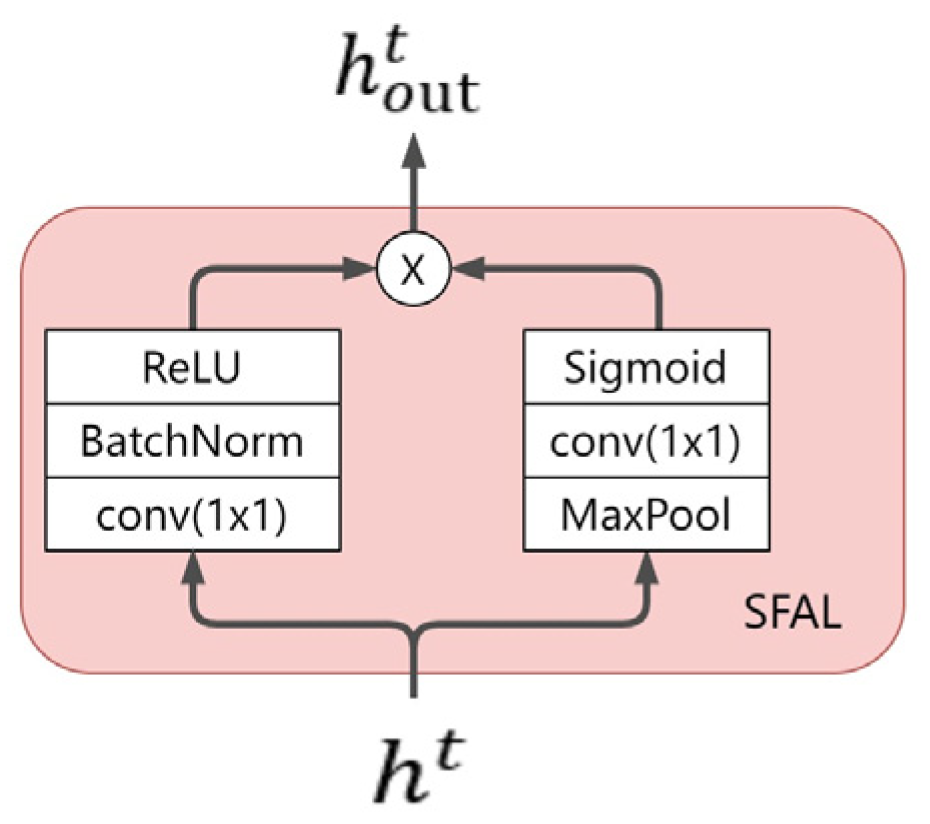
The spatial feature extraction network comprises a spatial feature attention layer (SFAL). Extreme values in meteorological data represent anomalies in the meteorological system, often associated with extreme weather events, such as heavy rain, typhoons, and so on. These extreme weather events can significantly impact precipitation, and the occurrence of extreme values can lead to changes in meteorological patterns, thereby influencing the distribution and intensity of precipitation. Therefore, these extreme values should be emphasized, and SFAL has been designed inspired by spatial attention mechanisms. The process of SFAL is as follows:
Assuming where represents the multimodal meteorological sequence, is input into both the left and right branches. In the left branch, a 1 × 1 convolutional layer is employed to halve the dimensions of and W, double the number of channels C, followed by Batch Normalization (BatchNorm) and ReLU activation operations. The left branch ultimately outputs the feature map . In the right branch, max-pooling is applied to halve the dimensions of and , followed by a 1 × 1 convolutional layer to double the number of channels C, and finally, the sigmoid activation function yields the feature map . Finally, and undergo element-wise multiplication, achieving different degrees of enhancement and suppression for the spatial positions of . The SFAL ultimately outputs the feature map . SFAL can be formalized as follows:
The structure of SFAL is illustrated in Figure 7.
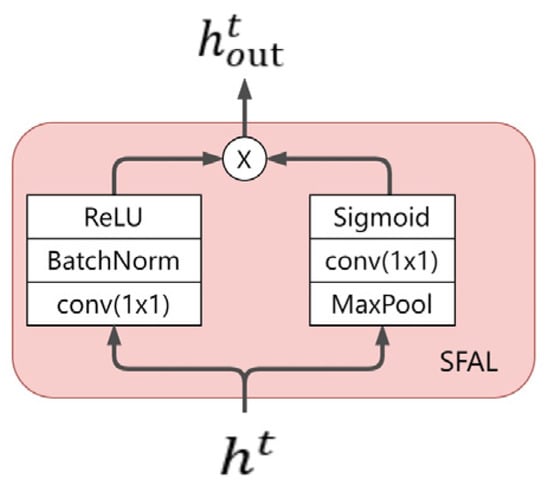
Figure 7.
SFAL structure.
SFAL utilizes a spatial attention mechanism to learn spatial attention weight maps, achieving different degrees of enhancement and suppression for the spatial positions of the original feature map. This allows the final feature map to focus more on spatial positions containing extreme values. Compared to directly using convolutional layers to extract spatial features, the SFAL module adds a pooling layer, resulting in fewer computations. Simultaneously, it complements the original features, obtaining a feature map with richer semantics.
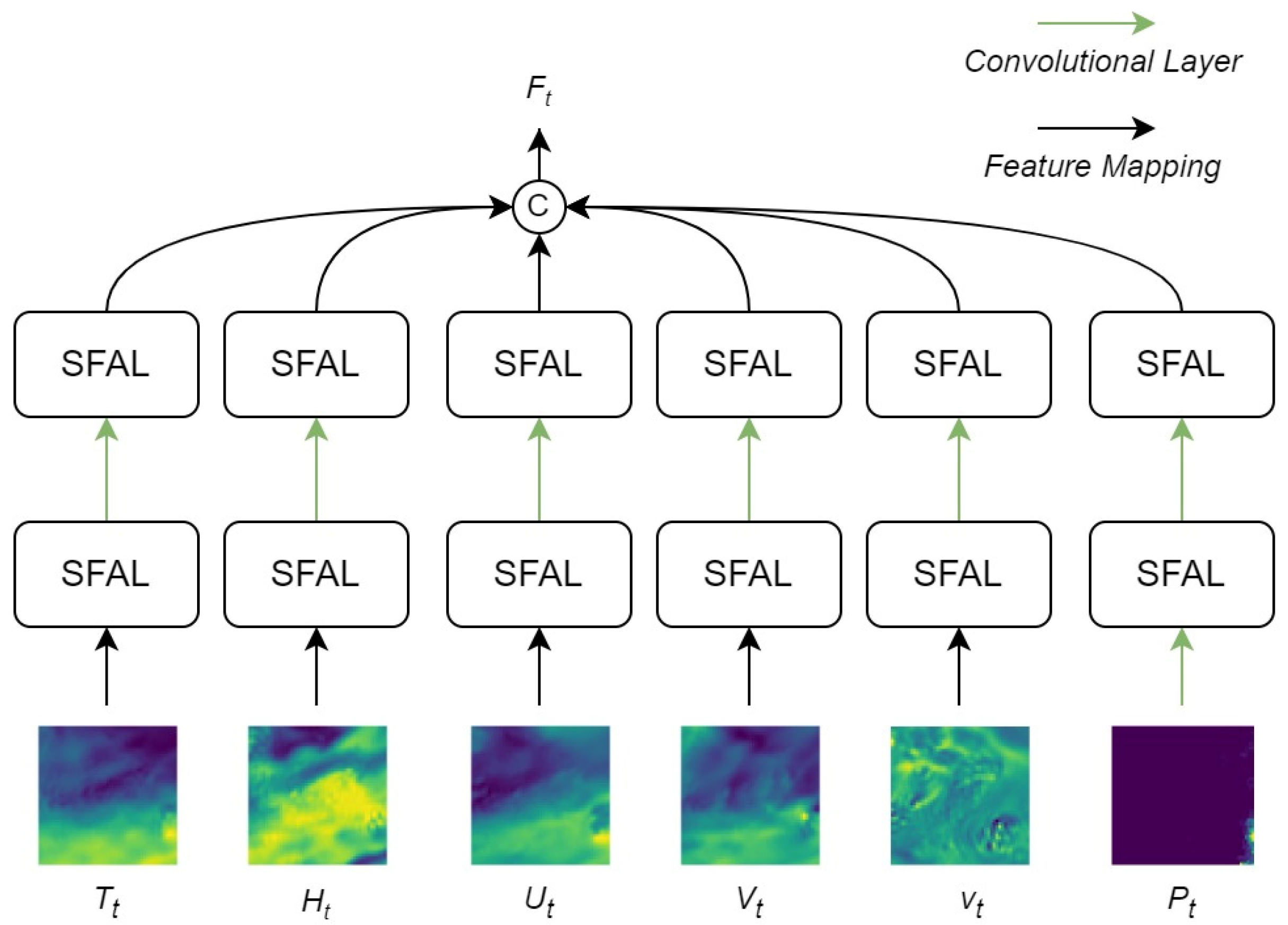
4.4.2. Spatial Feature Extraction Network
The role of the spatial feature extraction network is to preliminarily integrate the spatial information of different meteorological data and establish spatial relationships between various meteorological data. This module primarily employs multiple layers of SFAL to process input data. SFAL convolves and max-pools the three-dimensional tensor of the form across all channels, producing a new tensor in the form . During this process, SFAL performs element-wise multiplication and addition on feature maps from different channels, capturing spatial relationships between various meteorological data. By stacking multiple layers of SFAL, the module gradually extracts and integrates spatial information of different meteorological data, establishing spatial relationships between them.
The structure of the multimodal spatial encoding module is illustrated in Figure 8.
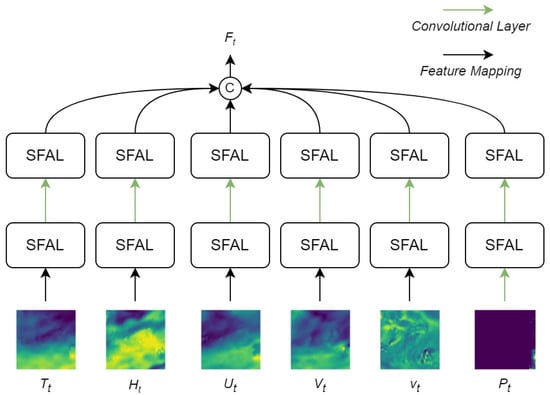
Figure 8.
Schematic diagram of SFEN. SFEN is based on convolutional layers and SFAL, consisting of six multimodal branches: precipitation, temperature, U-direction wind speed, V-direction wind speed, Vertical velocity, and specific humidity. “SFAL” refers to a spatial feature attention layer designed based on spatial attention mechanism. In the figure, color depth is used to represent the numerical strength of the corresponding meteorological mode.
4.5. Spatial Feature Extraction Network
The primary function of the ConvLSTM network is to provide a self-regressive recurrent prediction structure. The multimodal spatial encoding module inputs the encoded data at time into the ConvLSTM network. The ConvLSTM network generates multimodal data prediction results containing the predicted precipitation, which is then used to generate subsequent multimodal data prediction results , forming a self-regressive recurrent prediction.
In the second part, the continuous integration and reconstruction of the spatiotemporal features of multimodal meteorological data enhance the overall prediction accuracy of multimodal data and significantly improve the precision of precipitation prediction.
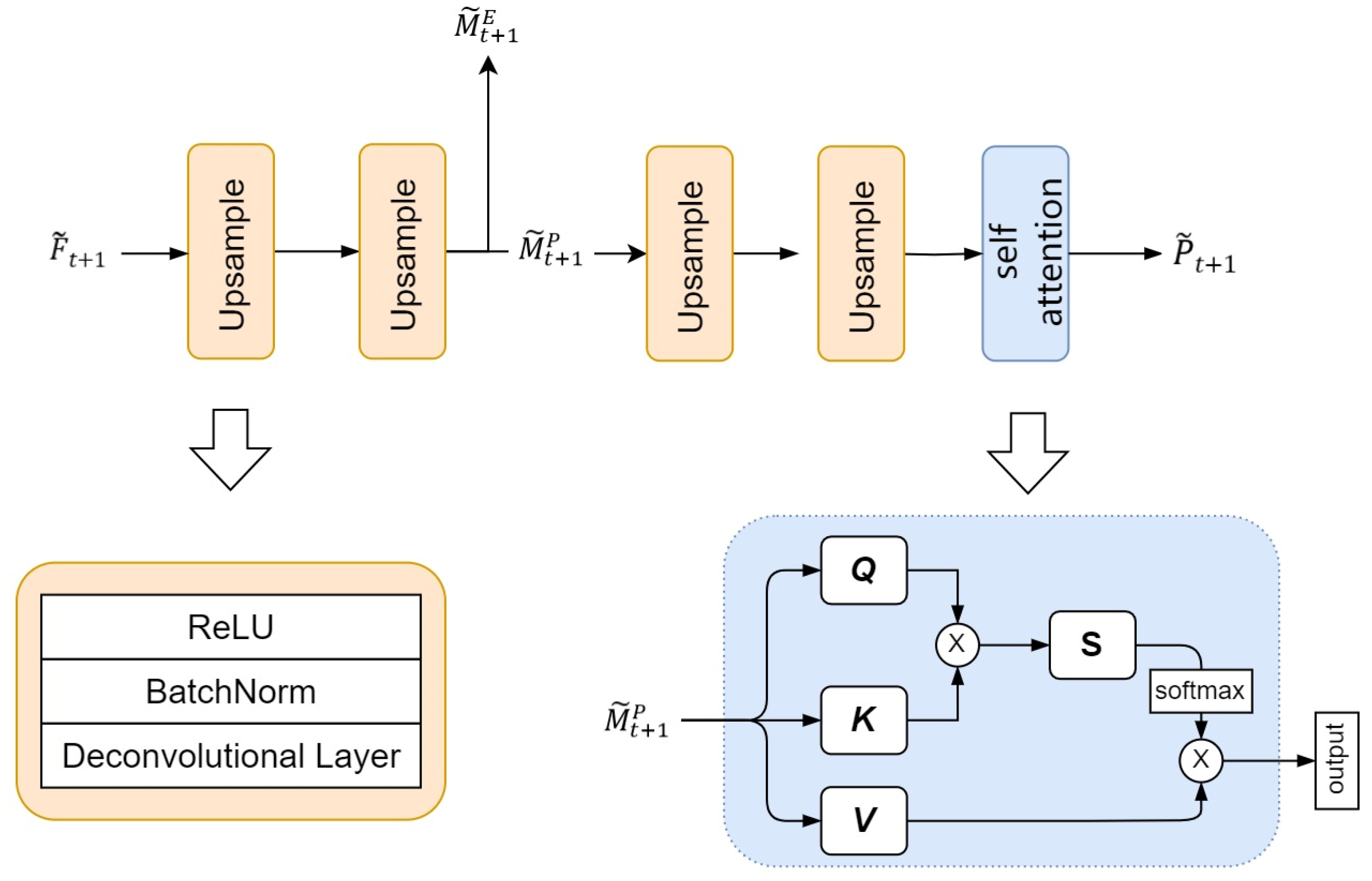
4.6. Modal Fusion Layer
The third component of this model is the modality fusion layer, primarily implemented through upsampling and a self-attention mechanism. In this section, the initial feature map generated by the temporal feature extraction network undergoes transformation to obtain a higher-resolution feature map. The upsampling part of the modality fusion layer includes a series of stacked deconvolution layers and ReLU activation functions. The deconvolution layer plays a crucial role in this module, enlarging the spatial resolution of the input tensor through the inverse operation of convolution. Through a sequence of deconvolution layers and activation functions, the modality fusion layer first reconstructs the predicted result into a representation with a higher spatial resolution ratio. Subsequently, is split into and by channel. Finally, by refining and adjusting through a self-attention mechanism, the precipitation forecast for time step t + 1 is ultimately obtained.
The schematic diagram of the modal fusion layer is shown in Figure 9.
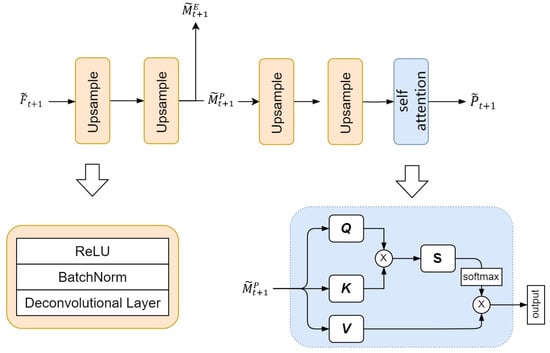
Figure 9.
Schematic diagram of the modal fusion layer, where the orange section represents the upsampling operation, and the blue section denotes the self-attention layer.
5. Experiment
5.1. Data Preprocessing
The input data for the model includes GPM precipitation data and ERA5 multimodal data for the target region. Due to the 30 min resolution of GPM data, data for each preceding half-hour is added to the input data to capture more spatiotemporal features of precipitation. The experiment utilizes ERA5 and GPM data from 2017 to 2020, with the first three years as the training set, and the fourth year divided into a validation set and a test set. The training set contains a total of 52,560 precipitation data points, and the ERA5 data consist of 26,280 points. Both the validation and test sets have 8760 precipitation data points and 4380 ERA5 data points each. Each batch inputted into the model consists of 8 h of data, where the first 4 h serve as the model input, and the GPM precipitation data for the following 4 h act as the model prediction label.
Given the different time resolutions (30 min for GPM and 1 h for ERA5), two GPM precipitation data sets within one hour are channel-merged to form the (2 × 120 × 120) input precipitation data.
Standard score transformation is applied to the ERA5 multimodal meteorological data to convert different modal data into standard normal distribution, facilitating statistical analysis and modeling. This transformation aids in better understanding and analyzing patterns and trends within ERA5 multimodal data.
The standard score transformation formula is given by , where is the initial value of ERA5 meteorological data, is the standardized value after standard score transformation, is the mean of the overall data, and is the standard deviation of each modality.
5.2. Loss Function
Zhao et al. [34]. believe that combining different loss functions can also achieve better image quality. Therefore, during the training phase, we combine MAE, MSE, and SSIM loss as the network’s loss functions. The loss function is shown in Formula (6).
where represents the ground truth, and represents the predicted value.
The Structural Similarity Index (SSIM) [35] loss is a metric used to measure the structural similarity between two images, commonly employed for image quality assessment. In the calculation process, the two images are divided into small blocks for computation. SSIM loss takes into account information regarding brightness, contrast, and structure, evaluating the similarity between two images by comparing these features.
The range of SSIM loss is between , where a value closer to 1 indicates a higher similarity between two images, while a value closer to 0 suggests a greater dissimilarity. When the SSIM loss is 1, it signifies that the two images are identical.
In the formula, the SSIM loss can be expressed as:
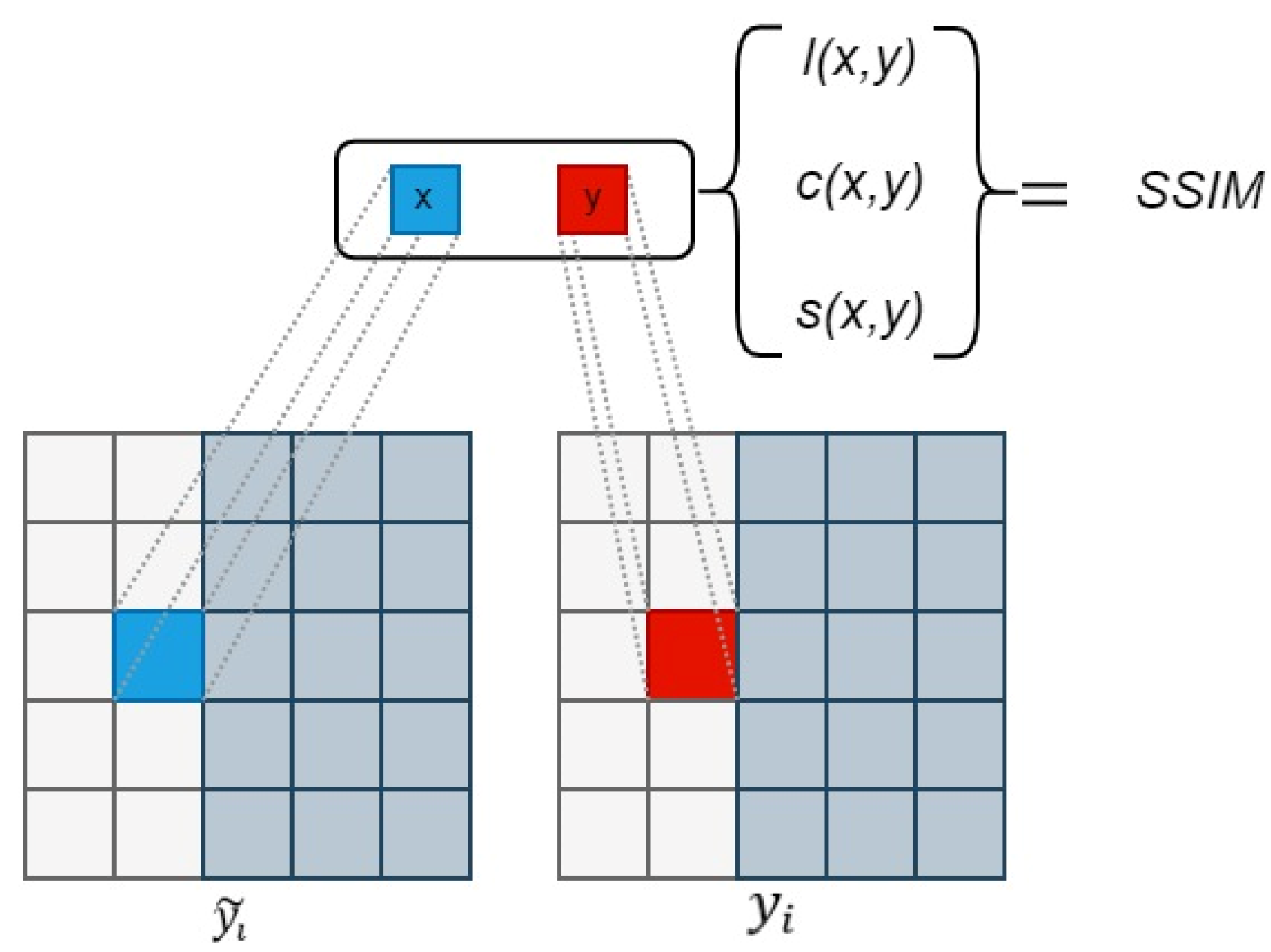
where and respectively, represent patches from and the corresponding patches from . and respectively, represent the average of and . and , respectively, represent the variance of and . represents the covariance between and . ,, and represent the luminance similarity, contrast similarity, and structure score between the two patches, respectively. , and represent weights. The schematic diagram of the computation process is shown in Figure 10.
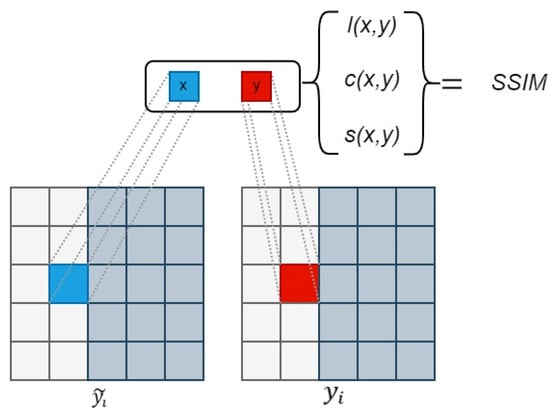
Figure 10.
SSIM Computation Process.
Due to the fact that an SSIM value closer to 1 indicates greater similarity between two images, an SSIM loss closer to 0 implies that the model prediction is more similar to the actual target. Therefore, subtracting the SSIM value from 1 provides a loss value consistent with the degree of similarity, facilitating the optimization process. The formula for SSIM loss is as follows:
MSE and MAE are common loss functions in spatiotemporal prediction models. The calculation formulas for MSE and MAE are shown in Equation (9).
where is the true value and is the predicted result.
5.3. Hyperparameter Settings
Before the actual training process, a series of experiments were conducted to carefully select the most suitable hyperparameter configurations, with the key parameters being batch size and learning rate. We examined three different batch sizes (4, 8) and three different learning rates (5 × 10−4, 3 × 10−4, 1 × 10−4) separately, conducting training for 300 epochs to investigate the model performance under different prediction time steps, as illustrated in Table 1.

Table 1.
Training results for different combinations of learning rates and batch sizes.
Observing the results table, it is evident that under the relatively low learning rate of 1 × 10−4, the model with a batch size of 4 consistently exhibited the minimum loss (LOSS) across various scenarios, with particularly outstanding performance when the learning rate was set to 1 × 10−4. Consequently, for the formal training phase, we have opted for the configuration of a batch size of 4 and a learning rate of 1 × 10−4 in anticipation of achieving superior model performance.
In this experiment, we utilized the Adam optimizer [36] for training. All network parameters were initialized using a normal distribution, and the training process concluded after 1000 iterations. The proposed neural network was implemented using PyTorch1.8.1 [37] and trained end-to-end. To prevent overfitting, an early stopping strategy was implemented in the experiment, meaning that if the loss value did not decrease within 5 epochs, the training process would stop. Our experimental platform featured 32 GB of memory and was equipped with a Nvidia RTX 2080 GPU, running Ubuntu 16.04.
5.4. Training Process
The overall training process of the model is illustrated in Figure 11. At time , the model’s input data is divided into GPM precipitation data and ERA5 reanalysis data. ERA5 reanalysis data include meteorological information for five modalities: U-wind, V-wind, humidity, temperature, and vertical wind speed, with a temporal resolution of 1 h and spatial dimensions of (3 × 48 × 48). The GPM precipitation data has a temporal resolution of 30 min. To align with the temporal resolution of ERA5 data, two GPM precipitation data with dimensions (120 × 120) within one hour are channel-merged to obtain precipitation data with dimensions (2 × 120 × 120). At the beginning of the model training, ERA5 data and GPM precipitation data are input into the spatial feature extraction network. It is worth noting that, to align the spatial dimensions of the two types of data, the precipitation data is downsampled to (4 × 48 × 48) through a convolution operation before entering the spatial feature extraction network.
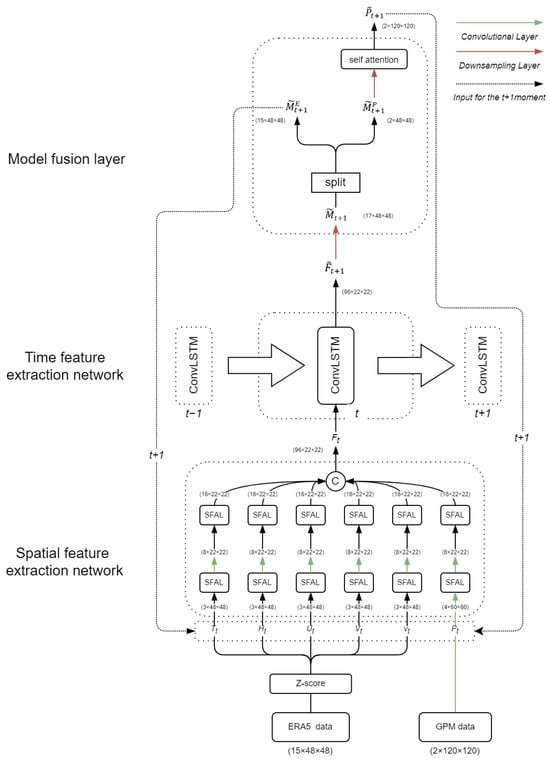
Figure 11.
Model flowchart at time step t.
In the spatial feature extraction network, the SFAL-enhanced model with six branches focuses on extreme values in the input feature map and performs channel expansion. After two layers of SFAL, the model extracts key features related to extreme weather events from the two types of data. Between the first and second layers of the SFAL branch handling precipitation, a convolution layer is used to further downsample the precipitation feature map.
In the final stage of the spatial feature extraction network, the output feature maps of each of the six branches are channel-merged to obtain a feature map with dimensions (192 × 22 × 22). Then, this feature map is input into the temporal feature extraction network, where a single layer of PredRNN extracts the spatiotemporal features of the input data, generating multimodal data predictions for time step . Through the temporal feature extraction network, the model enhances its ability to predict multimodal data in future time steps, further improving the accuracy of precipitation forecasting.
Next, is input into the modality fusion layer, and through deconvolution operations, is upsampled to the size of (17 × 48 × 48). Subsequently, is split into (15 × 48 × 48) and . is further upsampled and refined through self-attention to obtain precipitation prediction for time step . Additionally, and will form the input data for the model at the next time step to achieve autoregressive prediction.
5.5. Evaluation Metrics
A series of six model comparison experiments were meticulously designed to elucidate the efficacy of the MultiPred model in precipitation forecasting. To finely evaluate the experimental results, three widely recognized metrics, namely the Critical Success Index (CSI), Probability of Detection (POD), and the Heidke Skill Score (HSS), were employed. The calculation formulas for CSI, POD, and HSS are shown in Equation (10).
where TP stands for true positives, indicating the number of times the model correctly predicted precipitation events; FP stands for false positives, representing the number of times the model incorrectly predicted precipitation events, i.e., when there was no actual precipitation, but the model predicted precipitation; FN stands for false negatives, indicating the number of times the model incorrectly failed to predict precipitation events, i.e., when there was actual precipitation, but the model predicted no precipitation; TN stands for true negatives, representing the number of times the model correctly predicted the absence of precipitation events.
Both CSI and POD stand as pivotal indicators employed for the meticulous assessment of the precipitation forecasting model’s accuracy. The inclusion of the Heidke Skill Score (HSS) in the evaluation process provides a more comprehensive measure of the model’s accuracy. HSS takes into account both correct and incorrect predictions and is calculated as the difference between the proportion of true positives correctly predicted and the proportion of false positives incorrectly predicted.
As shown in Table 2, three different levels have been established: mild, when the precipitation d is less than 2 mm and greater than 0.1 mm; moderate, when the precipitation d is less than 6 mm and greater than 2 mm; and heavy, when the precipitation d is greater than 6 mm.

Table 2.
Correspondence between threshold and precipitation level.
5.6. Experimental Results and Analysis
The first group used the complete MultiPred model, with input data consisting of multiple meteorological modalities covering a large area for the preceding 4 h (including time encoding), and the output data representing continuous precipitation in the target area for the subsequent 4 h. The second group used the MultiPred model without the ERA5 meteorological data. The input data included continuous GPM precipitation and time encoding data for the past 4 h, with the same output as the first group. The third to sixth groups used the ConvLSTM, PredRNN, TrajGRU, and MIM models, respectively, with inputs and outputs similar to the first group. The comparative results on the ERA5 and GPM datasets are shown in Table 3, Table 4, Table 5 and Table 6.

Table 3.
Evaluation results for precipitation forecast in the previous hour.

Table 4.
Evaluation results for precipitation forecast in the first 2 h.

Table 5.
Evaluation results for precipitation forecast in the first 3 h.

Table 6.
Evaluation results for precipitation forecast in the first 4 h.
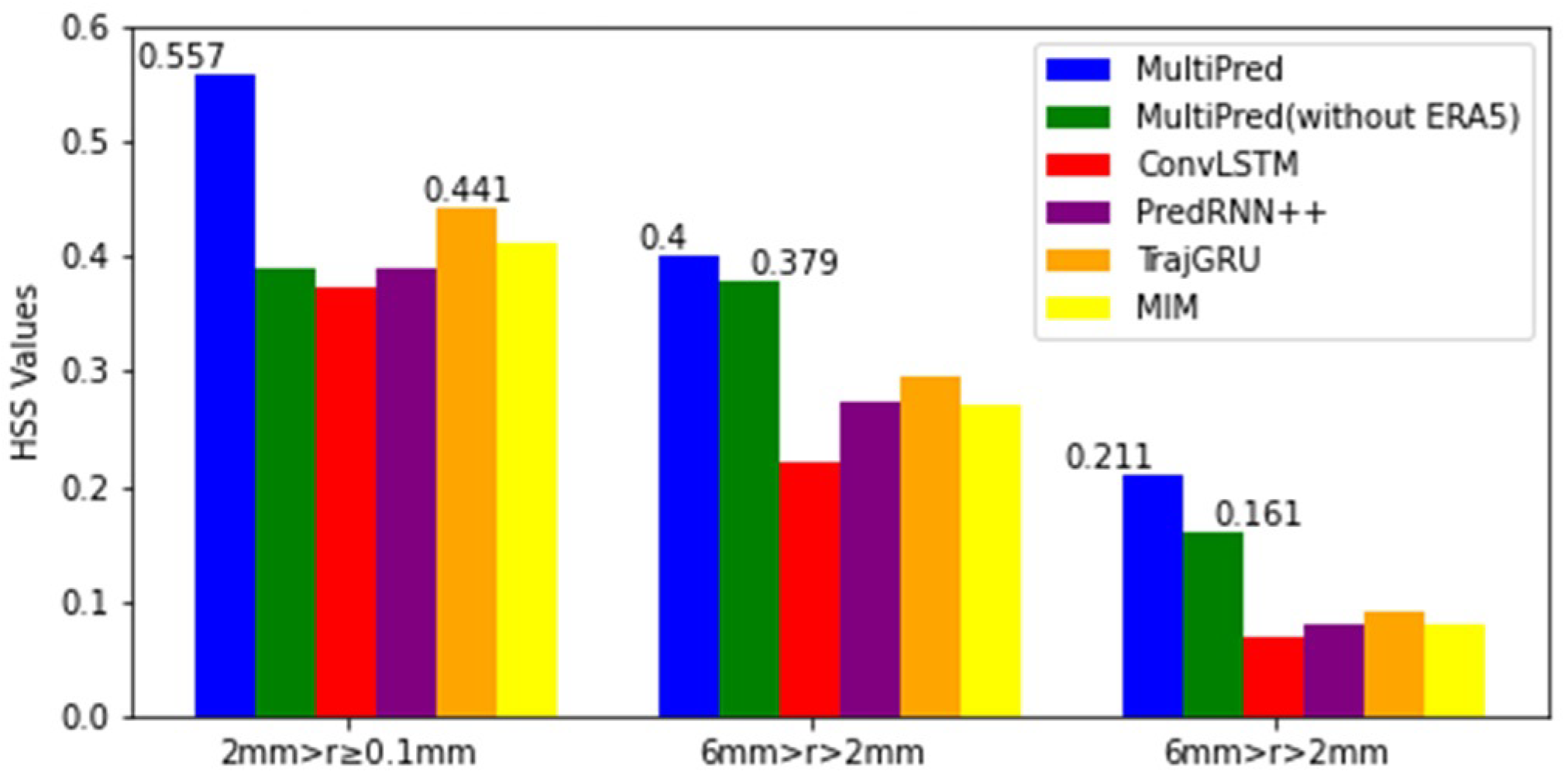
To more effectively analyze the precipitation forecasting capabilities of these six models, the CSI, POD, and HSS indices for each forecasting moment were selected and categorized into three precipitation levels for display. The comparative results on the GPM precipitation dataset and ERA5 reanalysis dataset are shown in Table 3, Table 4, Table 5 and Table 6. It can be observed (from Table 3, Table 4, Table 5 and Table 6) that over time, all indicators for the six models are gradually decreasing. In the prediction tasks for light precipitation with Light and heavy precipitation with over the entire four hours, the complete MultiPred model consistently exhibits the highest indicator values.
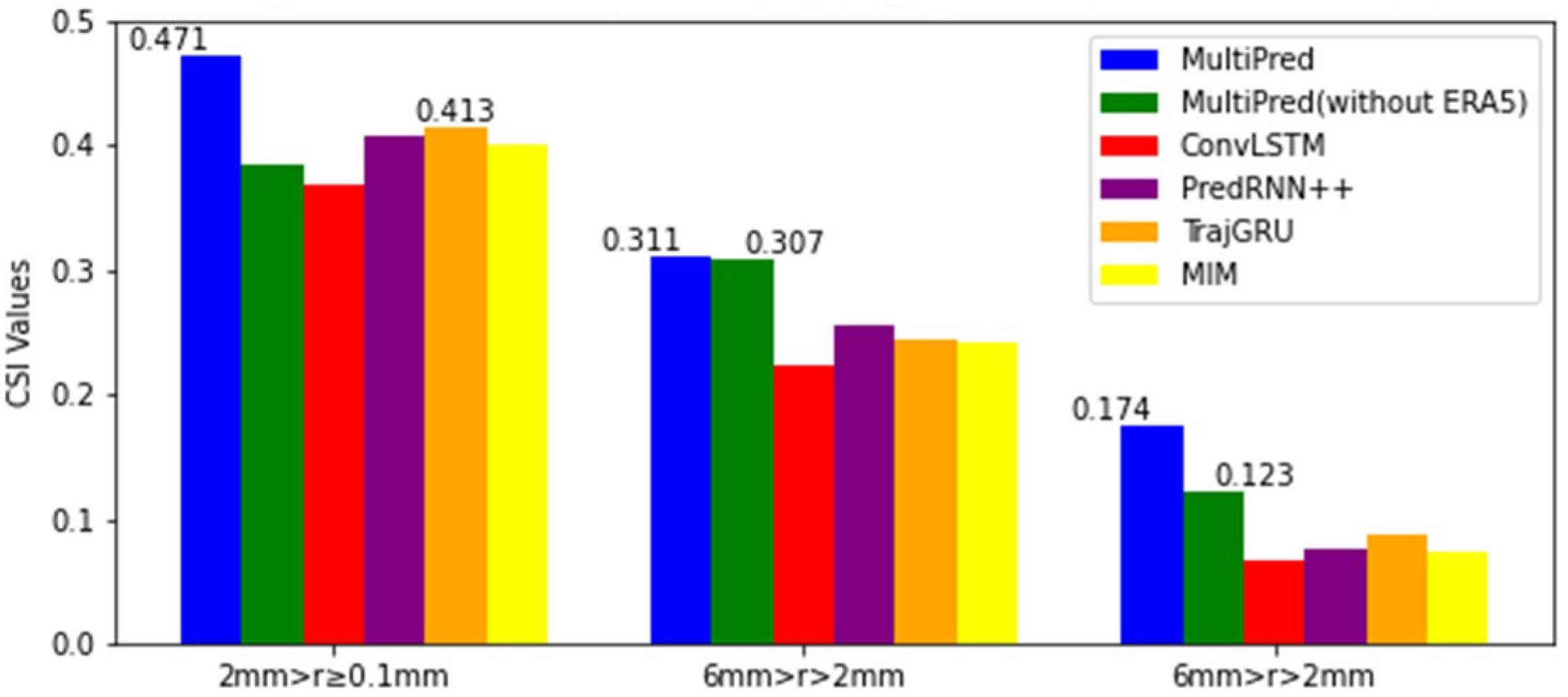
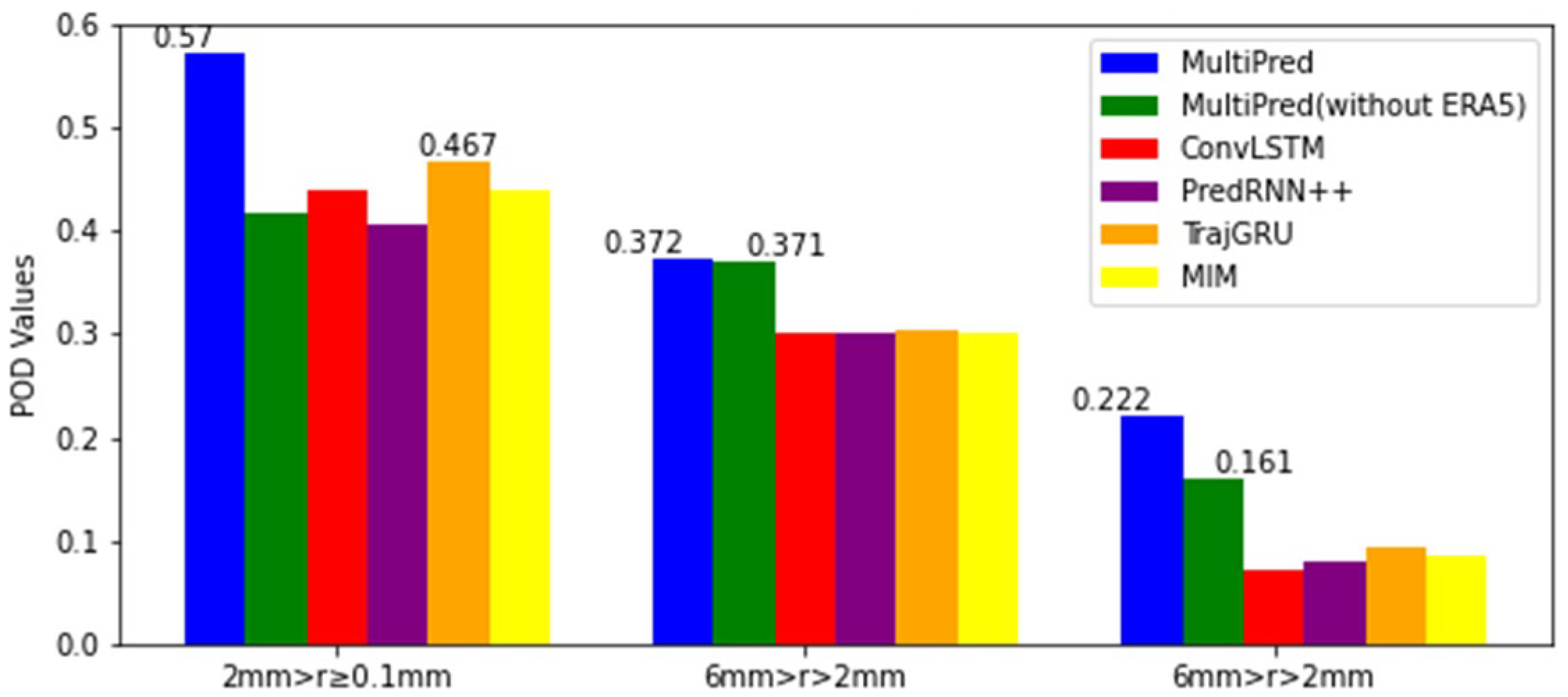
However, in the prediction task for moderate precipitation, the MultiPred model without ERA5 achieved the highest scores in the first and second hours. Additionally, the CSI, POD, and HSS index means for these models at the four forecasting moments were selected and categorized into three precipitation levels for display. From Figure 12, Figure 13 and Figure 14, it can be seen that the proposed MultiPred model obtained the highest score in the prediction task for light precipitation, with mean CSI, POD, and HSS values reaching 0.471, 0.570, and 0.557, respectively. Among all compared methods, E3D-LSTM is the best-performing precipitation forecasting model. Compared to E3D-LSTM, the MultiPred model improved the CSI, POD, and HSS indices by 14.03%, 22.05%, and 26.31%, respectively.
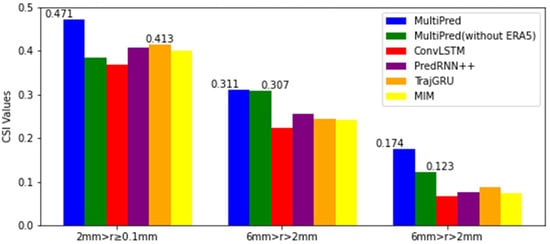
Figure 12.
Three sets of CSI indicators for an average of four hours and six models.
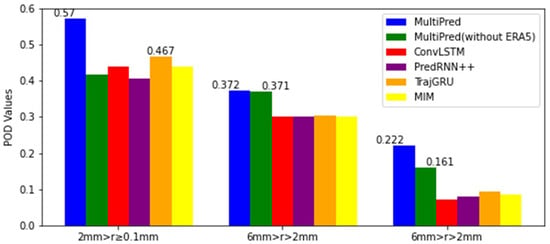
Figure 13.
Three sets of POD indicators compared for an average of four hours and across six models.
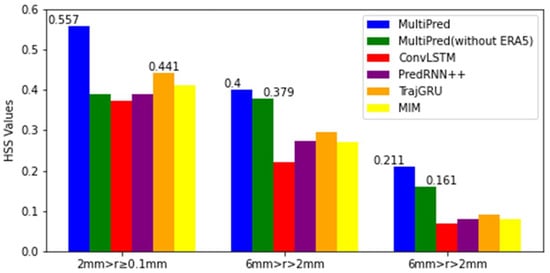
Figure 14.
Three sets of HSS indicators compared for an average of four hours and across six models.
For the prediction task of heavy precipitation, all indicators of the six models decreased compared to the light precipitation prediction task. Among them, the proposed MultiPred model also obtained the highest score. Compared to the MultiPred model without ERA5 data, the MultiPred model improved the CSI, POD, and HSS indices by 41.46%, 37.89%, and 31.06%, respectively.
This indicates that using only historical precipitation data to predict subsequent precipitation in light and heavy precipitation prediction tasks has clear limitations, as it does not consider the overall climate environment of the region. However, in the prediction task for moderate precipitation, the information from historical precipitation data is crucial for short-term forecasting. Nevertheless, in subsequent hours of forecasting, the complete MultiPred model achieved higher scores, indicating that information about the overall climate environment is necessary for long-term forecasting.
5.7. Visual Analysis
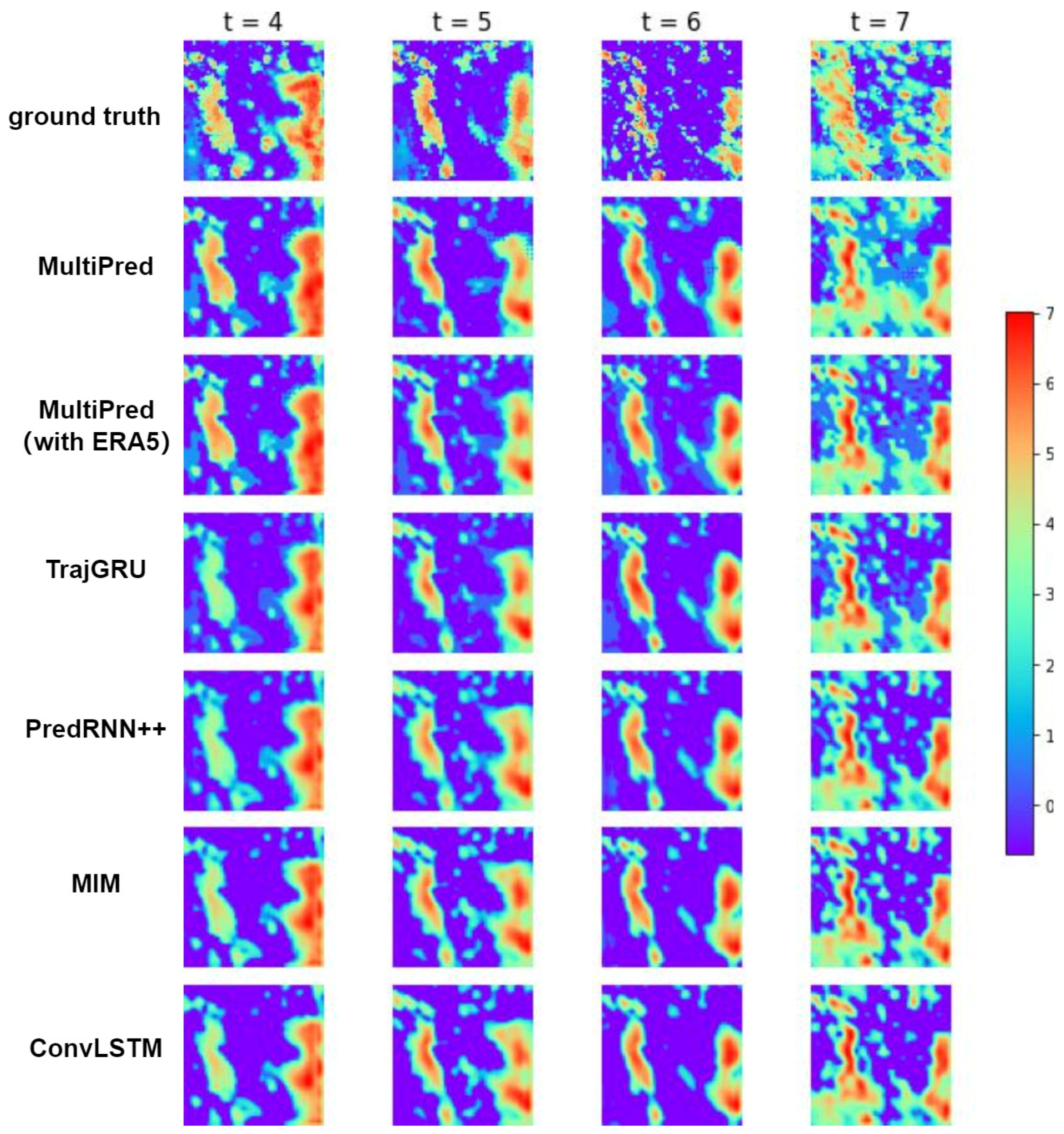
Figure 15 presents visual comparisons of precipitation forecast images for the target area at the first, second, third, and fourth hours, using different networks. The visualized models include the complete MultiPred model, MultiPred (without ERA5), TrajGRU, PredRNN++, MIM and ConvLSTM. The blue area represents regions where the model predicts no precipitation, while the precipitation values in the middle are mapped to green or yellow, and larger precipitation values are mapped to orange or red.
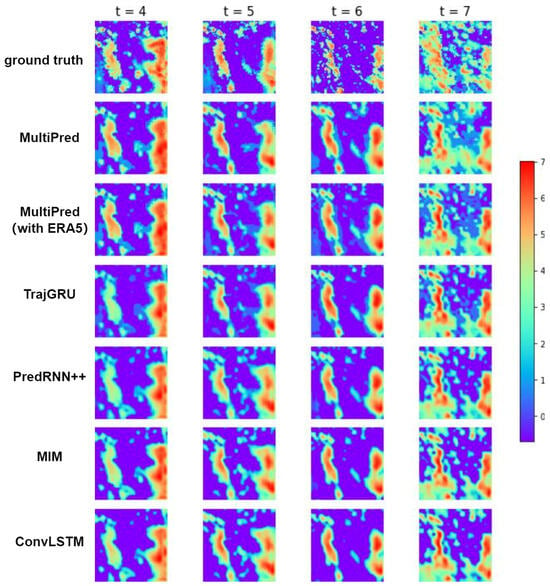
Figure 15.
Prediction results of precipitation for four consecutive hours using six models.
The first row in the figure shows the ground truth precipitation values at the four moments. It can be observed that, similar to MultiPred (without ERA5), in the method of predicting subsequent precipitation in the target area using only historical precipitation data, other methods compared to the complete MultiPred model exhibit issues with unclear boundaries and less accurate distribution of predicted precipitation in the regions with heavy precipitation. The complete MultiPred model performs well in predicting light and moderate precipitation areas, showing clearer boundaries, and the predicted results are closer to the true values. The network’s performance in predicting light and moderate precipitation areas depends on its ability to extract more abundant boundary features. In this regard, the complete MultiPred model, utilizing a multimodal fusion structure, demonstrates excellent forecasting capabilities for light and moderate precipitation amounts. This suggests that the multimodal fusion approach can effectively enhance the stability and accuracy of the prediction model.
Compared to the fifth row (PredRNN++), it is evident that the complete MultiPred model exhibits a slight improvement in predictive capabilities. This indicates that adding the multimodal spatial encoding module and the spatial regression module can better capture correlations between various meteorological data and perform feature fusion, thereby improving the model’s predictive accuracy.
Compared to TrajGRU and MIM, the complete MultiPred model shows improved index values and predictive performance, suggesting that the model has certain advantages in multi-factor precipitation forecasting compared to traditional spatiotemporal prediction models.
6. Discussion
Currently, mainstream deep learning-driven short-term precipitation forecasting models commonly face the challenge of not effectively integrating multimodal data.Therefore, we conducted an in-depth study on the organic integration of a multimodal fusion structure with spatiotemporal prediction models, leading to the proposal of a spatiotemporal prediction model based on early fusion, namely MultiPred. In MultiPred, we achieved outstanding performance in experiments by integrating precipitation data and reanalysis data, aligning with previous relevant research results by Sun et al. [38], who studied the enhancement of downscaling coarse-resolution precipitation forecasting results using satellite precipitation data and reanalysis data. Analyzing the experimental results, we observed that the MultiPred model exhibits poorer predictive performance in continuous 3 h and 4 h forecasts when not using ERA5 data. This suggests that in long-term precipitation forecasting, relying solely on historical precipitation information to predict future precipitation, without considering other meteorological modal information in the region, poses significant challenges.
Furthermore, through visual analysis, it is evident that compared to ConvLSTM, the MultiPred model produces clearer boundaries in its predictive results and captures light and moderate precipitation more sensitively. This aligns with the viewpoint in Ma et al.’s research [28] regarding the enhancement of model accuracy through multimodal fusion structures. Finally, short-term precipitation forecasting models commonly face the challenge of insufficient accuracy in precipitation datasets in practical applications, especially when predicting heavy precipitation using satellite precipitation data. This aligns with Kumar et al.’s findings [39] about the inadequacy of satellite data resolution. Despite the success of deep learning models in improving spatial feature extraction capabilities, there is still a need for datasets with higher spatial resolution. Therefore, in our next research step, we plan to utilize higher-resolution radar data to address this issue.
7. Conclusions
This study introduces a model named MultiPred for predicting precipitation in a target area. The model emphasizes a fusion structure of multimodal data and a combination of spatiotemporal prediction models. In the experiments, we utilized the ERA5 dataset and corresponding precipitation data from the eastern coastal region of China, conducting six sets of model control experiments to forecast continuous precipitation in the target area for the next 4 h. Through quantitative evaluation of multiple indicators and visualization of results, it can be concluded that the MultiPred model excels in both light and heavy precipitation forecasting tasks, demonstrating significantly superior performance compared to other methods. This validates the effectiveness of the multimodal fusion structure in precipitation forecasting, and empirical evidence confirms that the use of ERA5 data further enhances prediction accuracy.
To further enhance short-term precipitation forecasting performance, there is considerable room for improvement in the MultiPred model, primarily in two aspects: in terms of model structure, one can consider introducing more complex network structures or improving existing ones to enhance predictive performance; in terms of data, efforts can be made to add more input features or improve data quality to enhance model input information and prediction accuracy. For instance, introducing more meteorological observation data, geographical information data, or other relevant data could increase the model’s understanding and judgment capabilities in precipitation forecasting.
Author Contributions
Conceptualization, J.T., Z.F., X.J. and B.W.; methodology, B.W.; software, B.W.; validation, J.T. and B.W.; formal analysis, B.W.; investigation, B.W.; resources, B.W.; data curation, B.W.; writing—original draft preparation, B.W.; writing—review and editing, B.W.; visualization, B.W.; supervision, B.W.; project administration, B.W.; funding acquisition, J.T. and Z.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Project No. U2033218).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The GPM data presented in this study are openly available in [GPM_3IMERGHH] at 10.5067/GPM/IMERG/3B-HH/06, reference number [31]. The ERA5 data presented in this study are openly available in [ERA5 hourly data on pressure levels from 1940 to present] at 10.24381/cds.bd0915c6, reference number [32].
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, Y.; Wang, K. Global Precipitation System Scale Increased from 2001 to 2020. J. Hydrol. 2023, 616, 128768. [Google Scholar] [CrossRef]
- Palmer, T. A Vision for Numerical Weather Prediction in 2030. arXiv 2022, arXiv:2007.04830. [Google Scholar]
- Vogel, P.; Knippertz, P.; Fink, A.H.; Schlueter, A.; Gneiting, T. Skill of Global Raw and Postprocessed Ensemble Predictions of Rainfall over Northern Tropical Africa. Weather Forecast. 2018, 33, 369–388. [Google Scholar] [CrossRef]
- Shi, E.; Li, Q.; Gu, D.; Zhao, Z. A Method of Weather Radar Echo Extrapolation Based on Convolutional Neural Networks. In MultiMedia Modeling; Schoeffmann, K., Chalidabhongse, T.H., Ngo, C.W., Aramvith, S., O’Connor, N.E., Ho, Y.-S., Gabbouj, M., Elgammal, A., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2018; Volume 10704, pp. 16–28. ISBN 978-3-319-73602-0. [Google Scholar]
- Tian, L.; Li, X.; Ye, Y.; Xie, P.; Li, Y. A Generative Adversarial Gated Recurrent Unit Model for Precipitation Nowcasting. IEEE Geosci. Remote Sens. Lett. 2020, 17, 601–605. [Google Scholar] [CrossRef]
- Sønderby, C.K.; Espeholt, L.; Heek, J.; Dehghani, M.; Oliver, A.; Salimans, T.; Agrawal, S.; Hickey, J.; Kalchbrenner, N. MetNet: A Neural Weather Model for Precipitation Forecasting. arXiv 2020, arXiv:2003.12140. [Google Scholar]
- Gamboa-Villafruela, C.J.; Fernández-Alvarez, J.C.; Márquez-Mijares, M.; Pérez-Alarcón, A.; Batista-Leyva, A.J. Convolutional LSTM Architecture for Precipitation Nowcasting Using Satellite Data. In Proceedings of the 4th International Electronic Conference on Atmospheric Sciences, Online, 16–31 July 2021; MDPI: Basel, Switzerland; p. 33. [Google Scholar]
- Ehsani, M.R.; Zarei, A.; Gupta, H.V.; Barnard, K.; Lyons, E.; Behrangi, A. NowCasting-Nets: Representation Learning to Mitigate Latency Gap of Satellite Precipitation Products Using Convolutional and Recurrent Neural Networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4706021. [Google Scholar] [CrossRef]
- Grönquist, P.; Yao, C.; Ben-Nun, T.; Dryden, N.; Dueben, P.; Li, S.; Hoefler, T. Deep Learning for Post-Processing Ensemble Weather Forecasts. Phil. Trans. R. Soc. A 2021, 379, 20200092. [Google Scholar] [CrossRef]
- Scarchilli, G.; Gorgucci, V.; Chandrasekar, V.; Dobaie, A. Self-Consistency of Polarization Diversity Measurement of Rainfall. IEEE Trans. Geosci. Remote Sens. 1996, 34, 22–26. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2015; Volume 9351, pp. 234–241. ISBN 978-3-319-24573-7. [Google Scholar]
- Meng, F.; Song, T.; Xu, D. TCR-GAN: Predicting Tropical Cyclone Passive Microwave Rainfall Using Infrared Imagery via Generative Adversarial Networks 2022. arXiv 2022, arXiv:2201.07000. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30, pp. 1–11. [Google Scholar]
- Zhang, X.; Jin, Q.; Yu, T.; Xiang, S.; Kuang, Q.; Prinet, V.; Pan, C. Multi-Modal Spatio-Temporal Meteorological Forecasting with Deep Neural Network. ISPRS J. Photogramm. Remote Sens. 2022, 188, 380–393. [Google Scholar] [CrossRef]
- Pathak, J.; Subramanian, S.; Harrington, P.; Raja, S.; Chattopadhyay, A.; Mardani, M.; Kurth, T.; Hall, D.; Li, Z.; Azizzadenesheli, K.; et al. FourCastNet: A Global Data-Driven High-Resolution Weather Model Using Adaptive Fourier Neural Operators 2022. arXiv 2022, arXiv:2202.11214. [Google Scholar]
- Bai, C.; Sun, F.; Zhang, J.; Song, Y.; Chen, S. Rainformer: Features Extraction Balanced Network for Radar-Based Precipitation Nowcasting. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4023305. [Google Scholar] [CrossRef]
- Gao, Z.; Shi, X.; Wang, H.; Zhu, Y.; Wang, Y.; Li, M.; Yeung, D.-Y. Earthformer: Exploring Space-Time Transformers for Earth System Forecasting. Adv. Neural Inf. Process. Syst. 2022, 35, 25390–25403. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28, 802–810. [Google Scholar]
- Mikolov, T.; Karafiát, M.; Burget, L.; Černocký, J.; Khudanpur, S. Recurrent Neural Network Based Language Model. In Proceedings of the Interspeech 2010, Chiba, Japan, 26 September 2010; ISCA: Singapore, 2010; pp. 1045–1048. [Google Scholar]
- Shi, X.; Gao, Z.; Lausen, L.; Wang, H.; Yeung, D.-Y.; Wong, W.-C. Deep learning for precipitation nowcasting: A benchmark and a new model. Adv. Neural Inf. Process. Syst. 2017, 30, 5617–5627. [Google Scholar]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. Predrnn: Recurrent neural networks for predictive learning using spatiotemporal lstms. Adv. Neural Inf. Process. Syst. 2017, 30, 879–888. [Google Scholar]
- Wang, Y.; Gao, Z.; Long, M.; Wang, J.; Philip, S.Y. Predrnn++: Towards a resolution of the deep-in-time dilemma in spatiotemporalpredictive learning. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 5123–5132. [Google Scholar]
- Wang, Y.; Zhang, J.; Zhu, H.; Long, M.; Wang, J.; Yu, P.S. Memory in Memory: A Predictive Neural Network for Learning Higher-Order Non-Stationarity from Spatiotemporal Dynamics. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 9146–9154. [Google Scholar]
- Wang, Y.; Jiang, L.; Yang, M.-H.; Li, L.-J.; Long, M.; Fei-Fei, L. Eidetic 3D LSTM: A model for video prediction and beyond. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Wang, Y.; Wu, H.; Zhang, J.; Gao, Z.; Wang, J.; Yu, P.S.; Long, M. PredRNN: A Recurrent Neural Network for Spatiotemporal Predictive Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 2208–2225. [Google Scholar] [CrossRef] [PubMed]
- Gadzicki, K.; Khamsehashari, R.; Zetzsche, C. Early vs Late Fusion in Multimodal Convolutional Neural Networks. In Proceedings of the 2020 IEEE 23rd International Conference on Information Fusion (FUSION), Rustenburg, South Africa, 6–9 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Jin, Q.; Zhang, X.; Xiao, X.; Wang, Y.; Meng, G.; Xiang, S.; Pan, C. SpatioTemporal Inference Network for Precipitation Nowcasting with Multimodal Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 1299–1314. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, H.; Liu, J. MM-RNN: A Multimodal RNN for Precipitation Nowcasting. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Geng, Y.; Li, Q.; Lin, T.; Jiang, L.; Xu, L.; Zheng, D.; Yao, W.; Lyu, W.; Zhang, Y. LightNet: A Dual Spatiotemporal Encoder Network Model for Lightning Prediction. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 25 July 2019; ACM: New York, NY, USA, 2019; pp. 2439–2447. [Google Scholar]
- Zhou, X.; Geng, Y.; Yu, H.; Li, Q.; Xu, L.; Yao, W.; Zheng, D.; Zhang, Y. LightNet+: A Dual-Source Lightning Forecasting Network with Bi-Direction Spatiotemporal Transformation. Appl. Intell. 2022, 52, 11147–11159. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P.; Yoo, S.H. NASA global precipitation measurement (GPM) integrated multi-satellite retrievals for GPM (IMERG). Algorithm Theor. Basis Doc. (ATBD) 2015, 4, 30. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems 27 (NIPS 2014), Montreal, QC, Canada, 8–13 December 2014. [Google Scholar] [CrossRef]
- Zhao, H.; Gallo, O.; Frosio, I.; Kautz, J. Loss Functions for Image Restoration with Neural Networks. IEEE Trans. Comput. Imaging 2017, 3, 47–57. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization In Conference T Rack Proceedings, Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015; Bengio, Y., LeCun, Y., Eds.; ACM: New York, NY, USA, 2015. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; pp. 8026–8037. [Google Scholar]
- Sun, Y.; Tang, G. Downscaling satellite and reanalysis precipitation products using atten-tion-based deep convolutional neural nets. Front. Water 2020, 2, 536743. [Google Scholar] [CrossRef]
- Kumar, A.; Islam, T.; Sekimoto, Y.; Mattmann, C.; Wilson, B. Convcast: An Embedded Convolutional LSTM Based Architecture for Precipitation Nowcasting Using Satellite Data. PLoS ONE 2020, 15, e0230114. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).