Resonant Forcing by Solar Declination of Rossby Waves at the Tropopause and Implications in Extreme Events, Precipitation, and Heat Waves—Part 1: Theory
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Wavelet Analysis
2.3. Equations of Motion of Rossby Waves
2.4. Quasi-Stationary Rossby Waves Resonantly Forced
3. Results
3.1. Warm and Cold Airflows
3.1.1. The Northern Hemisphere
3.1.2. The Southern Hemisphere
3.2. First Case Study: Flood in Japan (July 2012)
3.3. Second Case Study: Heatwave in Europe (July–August 2015)
4. Discussion
5. Conclusions
- From a conceptual approach of polar and subtropical Rossby waves embedded in the jet streams, within a characteristic period range, the polar and subtropical MAs are warm or cold depending on their direction of propagation. They are generally in opposite phases. Similar stationary Rossby waves are also evidenced above the tropospheric polar vortex and, more sporadically, over the inter-tropical convergence zone (ITCZ) in the summer.
- The Rossby waves are resonantly forced by the variations in solar irradiance due to solar declination. This assertion arises from the wavelet spectrum of harmonics of the wind velocity at 250 mb. The adjustment variable to tune the natural period of the Rossby waves to the forcing period is the meandering of the MAs. Due to the formation of cold drops according to harmonic modes, Rossby waves play an essential role in the genesis of EPEs. The duration of the blocking is a half-period of the harmonic involved.
- Rossby waves are also evidenced above the descending air column, at the center of the tropospheric polar vortex, as well as above the ascending air column of the ITCZ.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Palmer, T.N. Climate extremes and the role of dynamics. Proc. Natl. Acad. Sci. USA 2013, 110, 5281–5282. [Google Scholar] [CrossRef] [PubMed]
- Hoskins, B.J.; Woollings, T. Persistent extratropical regimes and climate extremes. Curr. Clim. Change Rep. 2015, 1, 115–124. [Google Scholar] [CrossRef]
- Wirth, V.; Riemer, M.; Chang, E.K.M.; Martius, O. Rossby wave packets on the midlatitude waveguide—A review. Mon. Weather Rev. 2018, 146, 1965–2001. [Google Scholar] [CrossRef]
- Holton, J.R. An Introduction to Dynamic Meteorology, 3rd ed.; Academic Press: San Diego, CA, USA, 1992; 511p. [Google Scholar]
- Kornhuber, K.; Coumou, D.; Vogel, E.; Lesk, C.; Donges, J.F.; Lehmann, J.; Horton, R.M. Amplified Rossby waves enhance risk of concurrent heatwaves in major breadbasket regions. Nat. Clim. Change 2019, 10, 48–53. [Google Scholar] [CrossRef]
- Hoskins, B.J.; McIntyre, M.E.; Robertson, A.W. On the use and significance of isentropic potential vorticity maps. Q. J. R. Meteorol. Soc. 1985, 111, 877–946. [Google Scholar] [CrossRef]
- Schubert, S.; Wang, H.; Suárez, M.J. Warm season subseasonal variability and climate extremes in the Northern hemisphere: The role of stationary Rossby waves. J. Clim. 2011, 24, 4773–4792. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T. Climate extremes and climate change: The Russian heat wave and other climate extremes of 2010. J. Geophys. Res. 2012, 117, D17103. [Google Scholar] [CrossRef]
- Teng, H.; Branstator, G.; Wang, H.; Meehl, G.A.; Washington, W.M. Probability of US heat waves affected by a subseasonal planetary wave pattern. Nat. Geosci. 2013, 6, 1056–1061. [Google Scholar] [CrossRef]
- Chen, G.; Lu, J.; Burrows, D.A.; Leung, L.R. Local finite-amplitude wave activity as an objective diagnostic of midlatitude extreme weather. Geophys. Res. Lett. 2015, 42, 10952–10960. [Google Scholar] [CrossRef]
- Wolf, G.; Brayshaw, D.J.; Klingaman, N.P.; Czaja, A. Quasi-stationary waves and their impact on European weather and extreme events. Q. J. R. Meteorol. Soc. 2018, 144, 2431–2448. [Google Scholar] [CrossRef]
- Röthlisberger, M.; Frossard, L.; Bosart, L.F.; Keyser, D.; Martius, O. Recurrent synoptic scale Rossby wave patterns and their effect on the persistence of cold and hot spells. J. Clim. 2019, 32, 3207–3226. [Google Scholar] [CrossRef]
- Petoukhov, V.; Rahmstorf, S.; Petri, S.; Schellnhuber, H.J. Quasi-resonant amplification of planetary waves and recent Northern Hemisphere weather extremes. Proc. Natl. Acad. Sci. USA 2013, 110, 5336–5341. [Google Scholar] [CrossRef] [PubMed]
- Blackburn, M.; Methven, J.; Roberts, N. Large-scale context for the UK floods in summer 2007. Weather 2008, 63, 280–288. [Google Scholar] [CrossRef]
- Screen, J.A.; Simmonds, I. Amplified mid-latitude planetary waves favour particular regional weather extremes. Nat. Clim. Change 2014, 4, 704–709. [Google Scholar] [CrossRef]
- McKinnon, K.A.; Rhines, A.; Tingley, M.P.; Huybers, P. Long-lead predictions of eastern United States hot days from Pacific sea surface temperatures. Nat. Geosci. 2016, 9, 389–394. [Google Scholar] [CrossRef]
- Röthlisberger, M.; Pfahl, S.; Martius, O. Regional-scale jet waviness modulates the occurrence of midlatitude weather extremes. Geophys. Res. Lett. 2016, 43, 2016GL070944. [Google Scholar] [CrossRef]
- Rodrigues, R.R.; Woollings, T. Impact of atmospheric blocking on South America in austral summer. J. Clim. 2017, 30, 1821–1837. [Google Scholar] [CrossRef]
- Davis, C.A. A potential-vorticity diagnosis of the importance of initial structure and condensational heating in observed extratropical cyclogenesis. Mon. Weather Rev. 1992, 120, 2409–2428. [Google Scholar] [CrossRef]
- Romero, R. Sensitivity of a heavy-rain-producing western Mediterranean cyclone to embedded potential-vorticity anomalies. Q. J. R. Meteorol. Soc. 2001, 127, 2559–2597. [Google Scholar] [CrossRef]
- Ahmadi-Givi, F.; Graig, G.C.; Plant, R.S. The dynamics of a midlatitude cyclone with very strong latent-heat release. Q. J. R. Meteorol. Soc. 2004, 130, 295–323. [Google Scholar] [CrossRef]
- Romero, R. A method for quantifying the impacts and interactions of potential-vorticity anomalies in extratropical cyclones. Q. J. R. Meteorol. Soc. 2008, 134, 385–402. [Google Scholar] [CrossRef]
- Kim, K.-Y.; Na, H.; Jhun, J.-G. Oceanic response to midlatitude Rossby waves aloft and its feedback in the lower atmosphere in winter Northern Hemisphere. J. Geophys. Res. 2012, 117, D07110. [Google Scholar] [CrossRef]
- Davis, C.A.; Emanuel, K.A. Potential vorticity diagnostics of cyclogenesis. Mon. Weather Rev. 1991, 119, 1929–1953. [Google Scholar] [CrossRef]
- Horton, R.M.; Mankin, J.S.; Lesk, C.; Coffel, E.; Raymond, C. A review of recent Advances in research on extreme heat events. Curr. Clim. Change Rep. 2016, 2, 242–259. [Google Scholar] [CrossRef]
- Kornhuber, K.; Petoukhov, V.; Petri, S.; Rahmstorf, S.; Coumou, D. Evidence for wave resonance as a key mechanism for generating high-amplitude quasi-stationary waves in boreal summer. Clim. Dyn. 2017, 49, 1961–1979. [Google Scholar] [CrossRef]
- Petoukhov, V.; Petri, S.; Rahmstorf, S.; Coumou, D.; Kornhuber, K.; Schellnhuber, H.J. Role of quasiresonant planetary wave dynamics in recent boreal spring-to-autumn extreme events. Proc. Natl. Acad. Sci. USA 2016, 113, 6862–6867. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Zhu, X.; Sheng, Z.; He, M. Resonant waves play an important role in the increasing heat waves in Northern Hemisphere mid-latitudes under global warming. Geophys. Res. Lett. 2023, 50, e2023GL104839. [Google Scholar] [CrossRef]
- Frankignoul, C.; Müller, P. Quasi-geostrophic response of an infiniteβ-plane ocean to stochastic forcing by the atmosphere. J. Phys. Oceanogr. 1979, 9, 104–127. [Google Scholar] [CrossRef][Green Version]
- Willebrand, J.; Philander, S.G.H.; Pacanowski, R.C. The oceanic response to large-scale atmospheric disturbances. J. Phys. Oceanogr. 1980, 10, 411–429. [Google Scholar] [CrossRef][Green Version]
- Müller, P.; Frankignoul, C. Direct atmospheric forcing of geostrophic eddies. J. Phys. Oceanogr. 1981, 11, 287–308. [Google Scholar] [CrossRef][Green Version]
- Stott, P.A.; Stone, D.A.; Allen, M.R. Human contribution to the European heatwave of 2003. Nature 2004, 432, 610–614. [Google Scholar] [CrossRef]
- Otto, F.E.L.; Massey, N.; van Oldenborgh, G.J.; Jones, R.G.; Allen, M.R. Reconciling two approaches to attribution of the 2010 Russian heat wave. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Dong, B.; Sutton, R.T.; Shaffrey, L.C.; Wilcox, L.J. The 2015 European heat wave. Bull. Am. Meteorol. Soc. 2016, 97, S57–S62. [Google Scholar] [CrossRef]
- Kornhuber, K.; Osprey, S.M.; Coumou, D.; Petri, S.; Petoukhov, V.; Rahmstorf, S.; Gray, L.J. Extreme weather events in early summer 2018 connected by a recurrent hemispheric wave-7 pattern. Environ. Res. Lett. 2019, 14, 054002. [Google Scholar] [CrossRef]
- Mitchell, D.M.; Kornhuber, K.; Huntingford, C.; Uhe, P. The day the 2003 European heatwave record was broken. Lancet Planet. Health 2019, 3, e290–e292. [Google Scholar] [CrossRef] [PubMed]
- Rosner, B.; Benedict, I.; van Heerwaarden, C.; Weerts, A.; Hazeleger, W.; Bissoli, P.; Trachte, K. The long heat wave and drought in Europe in 2018 [in “State of the Climate in 2018”]. Bull. Am. Meteorol. Soc. 2019, 100, S222–S223. [Google Scholar]
- Vautard, R.; Yiou, P.; Otto FE, L.; Stott, P.A.; Christidis, N.; van Oldenborgh, G.J.; Schaller, N. Attribution of human-induced dynamical and thermodynamical contributions in extreme weather events. Environ. Res. Lett. 2016, 11, 114009. [Google Scholar] [CrossRef]
- Amengual, A.; Homar, V.; Romero, R.; Brooks, H.; Ramis, C.; Gordaliza, M.; Alonso, S. Projections of heat waves with high impact on human health in Europe. Glob. Planet. Change 2014, 119, 71–84. [Google Scholar] [CrossRef]
- Field, C.B.; Barros, V.; Stocker, T.F.; Qin, D.; Dokken, D.J.; Ebi, K.L.; Mastrandrea, M.D.; Mach, K.J.; Plattner, G.-K.; Allen, S.K.; et al. (Eds.) Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation; Cambridge University Press: Cambridge, UK, 2012; 582p. [Google Scholar]
- King, A.D.; Harrington, L.J. The inequality of climate change from 1.5 to 2 °C of global warming. Geophys. Res. Lett. 2018, 45, 5030–5033. [Google Scholar] [CrossRef]
- Perkins-Kirkpatrick, S.E.; Lewis, S.C. Increasing trends in regional heatwaves. Nat. Commun. 2020, 11, 3357. [Google Scholar] [CrossRef]
- Rogers, C.D.W.; Kornhuber, K.; Perkins-Kirkpatrick, S.E.; Loikith, P.C.; Singh, D. Six-fold increase in historical Northern Hemisphere concurrent large heatwaves driven by warming and changing atmospheric circulations. J. Clim. 2021, 35, 1063–1078. [Google Scholar] [CrossRef]
- Chan, P.W.; Catto, J.L.; Collins, M. Heatwave–blocking relation change likely dominates over decrease in blocking frequency under global warming. Npj Clim. Atmos. Sci. 2022, 5, 68. [Google Scholar] [CrossRef]
- Ogi, M.; Yamazaki, K.; Tachibana, Y. The summer northern annular mode and abnormal summer weather in 2003. Geophys. Res. Lett. 2005, 32, L04706. [Google Scholar] [CrossRef]
- Tachibana, Y.; Nakamura, T.; Komiya, H.; Takahashi, M. Abrupt evolution of the summer Northern Hemisphere annular mode and its association with blocking. J. Geophys. Res. 2010, 115, D12125. [Google Scholar] [CrossRef]
- Xu, P.; Wang, L.; Vallis, G.K.; Geen, R.; Screen, J.A.; Wu, P.; Ding, S.; Huang, P.; Chen, W. Amplified waveguide teleconnections along the polar front jet favor summer temperature extremes over Northern Eurasia. Geophys. Res. Lett. 2021, 48, e2021GL093735. [Google Scholar] [CrossRef]
- Xu, P.; Wang, L.; Huang, P.; Chen, W. Disentangling dynamical and thermodynamical contributions to the record-breaking heatwave over Central Europe in June 2019. Atmos. Res. 2021, 252, 105446. [Google Scholar] [CrossRef]
- White, R.H.; Kornhuber, K.; Martius, O.; Wirth, V. From Atmospheric Waves to Heatwaves a Waveguide Perspective for Understanding and Predicting Concurrent, Persistent, and Extreme Extratropical Weather. Am. Meteorol. Soc. 2022, 103, E923–E935. [Google Scholar] [CrossRef]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.-K.; Hnilo, J.J.; Fiorino, M.; Potter, G.L. NCEP-DOE AMIP-II Reanalysis (R-2). Bull. Am. Meteorol. Soc. 2002, 83, 1631–1643. [Google Scholar] [CrossRef]
- Pinault, J.-L. Long Wave Resonance in Tropical Oceans and Implications on Climate: The Atlantic Ocean. Pure Appl. Geophys. 2013, 170, 1913–1930. [Google Scholar] [CrossRef]
- Available online: https://www.weatherandradar.co.uk/weather-news/weather-explained-video-what-is-a-cold-drop--7zpm19glZwvxDiTfYroIlJ (accessed on 13 May 2024).
- Nie, J.; Sobel, A.H.; Shaevitz, D.A.; Wang, S. Dynamic amplification of extreme precipitation sensitivity. Proc. Natl. Acad. Sci. USA 2018, 115, 9467–9472. [Google Scholar] [CrossRef]
- Pinault, J.-L. Resonance of baroclinic waves in the tropical oceans: The Indian Ocean and the far western Pacific. Dyn. Atmos. Ocean. 2020, 89, 101119. [Google Scholar] [CrossRef]
- Pinault, J.-L. A Review of the Role of the Oceanic Rossby Waves in Climate Variability. J. Mar. Sci. Eng. 2022, 10, 493. [Google Scholar] [CrossRef]
- Gill, A.E. Atmosphere-Ocean Dynamics; International Geophysics Series; Academic Press: Cambridge, MA, USA, 1982; 662p. [Google Scholar]
- Pinault, J.-L. Resonantly Forced Baroclinic Waves in the Oceans: Harmonic Modes. J. Mar. Sci. Eng. 2018, 6, 78. [Google Scholar] [CrossRef]
- Choi, M.Y.; Thouless, D.J. Topological interpretation of subharmonic mode locking in coupled oscillators with inertia. Phys. Rev. B 2001, 64, 014305. [Google Scholar] [CrossRef]
- Duan, W.; Bin, H.; Kaoru, T.; Pingping, L.; Daniel, N.; Yosuke, Y.; Wenrui, H. Anomalous atmospheric events leading to Kyushu’s flash floods, July 11–14, 2012. Nat. Hazards 2014, 73, 1255–1267. [Google Scholar] [CrossRef]
- Muthers, S.; Gudrun Laschewski, G.; Matzarakis, A. The Summers 2003 and 2015 in South-West Germany: Heatwaves and Heat-Related Mortality in the Context of Climate Change. Atmosphere 2017, 8, 224. [Google Scholar] [CrossRef]
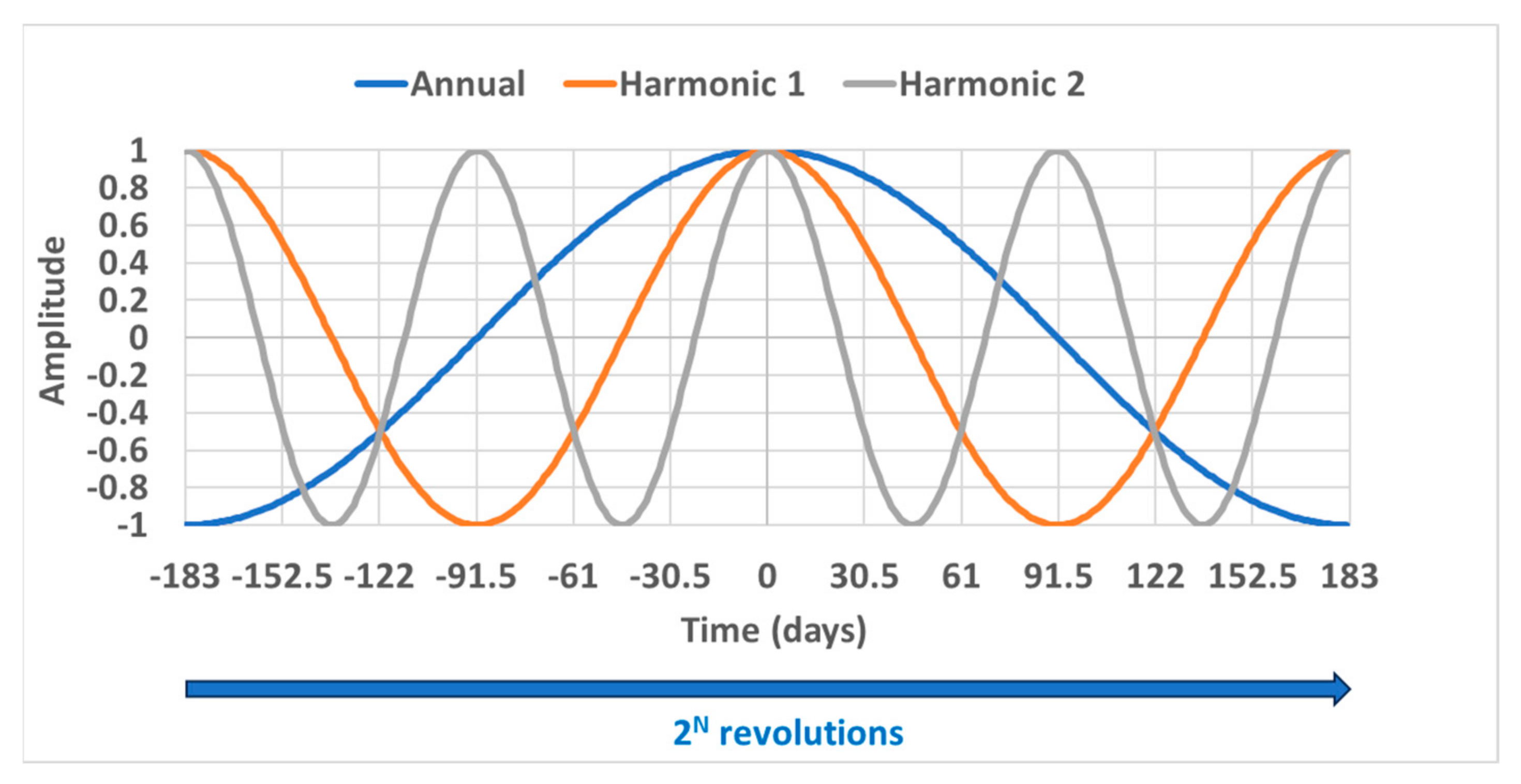
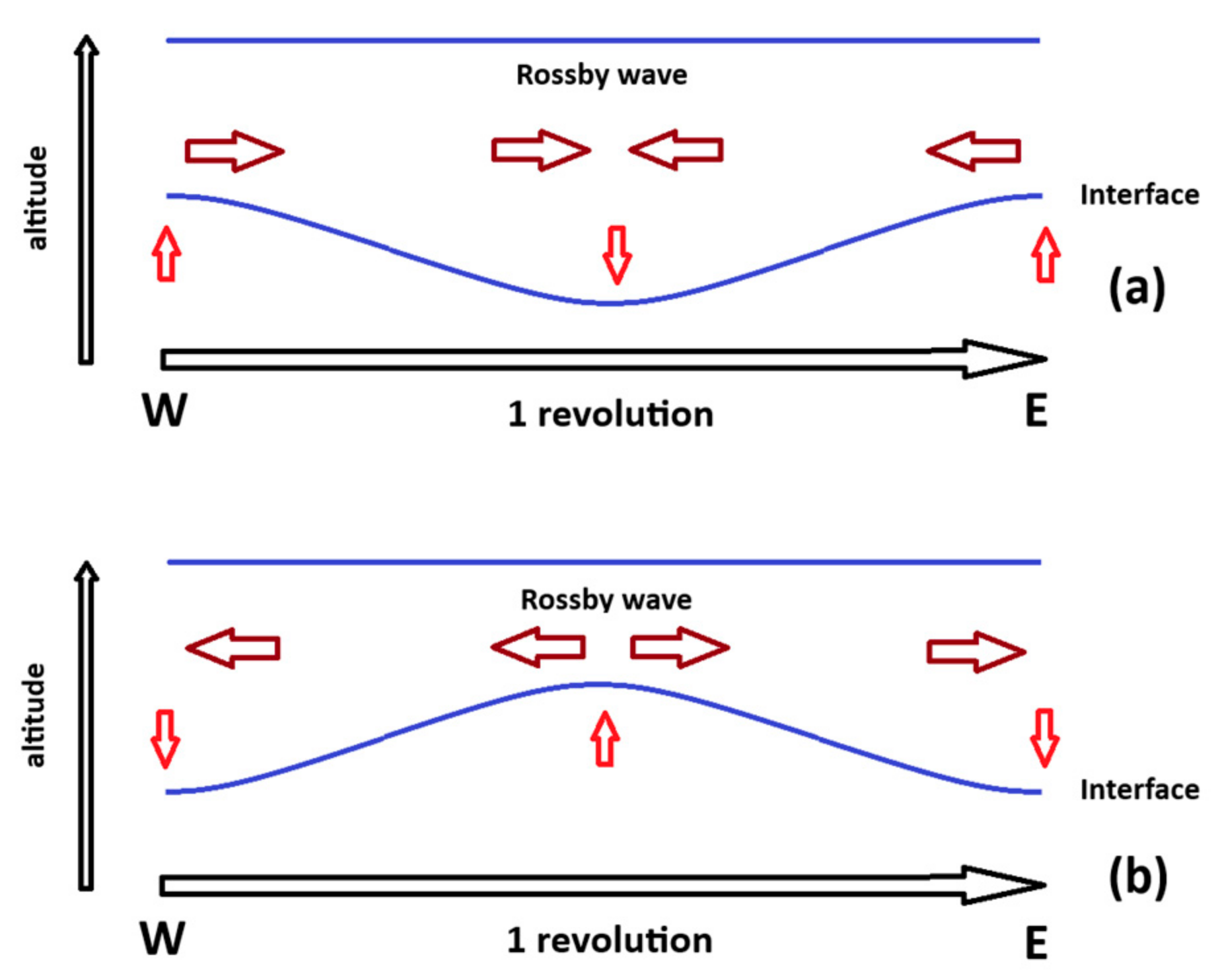
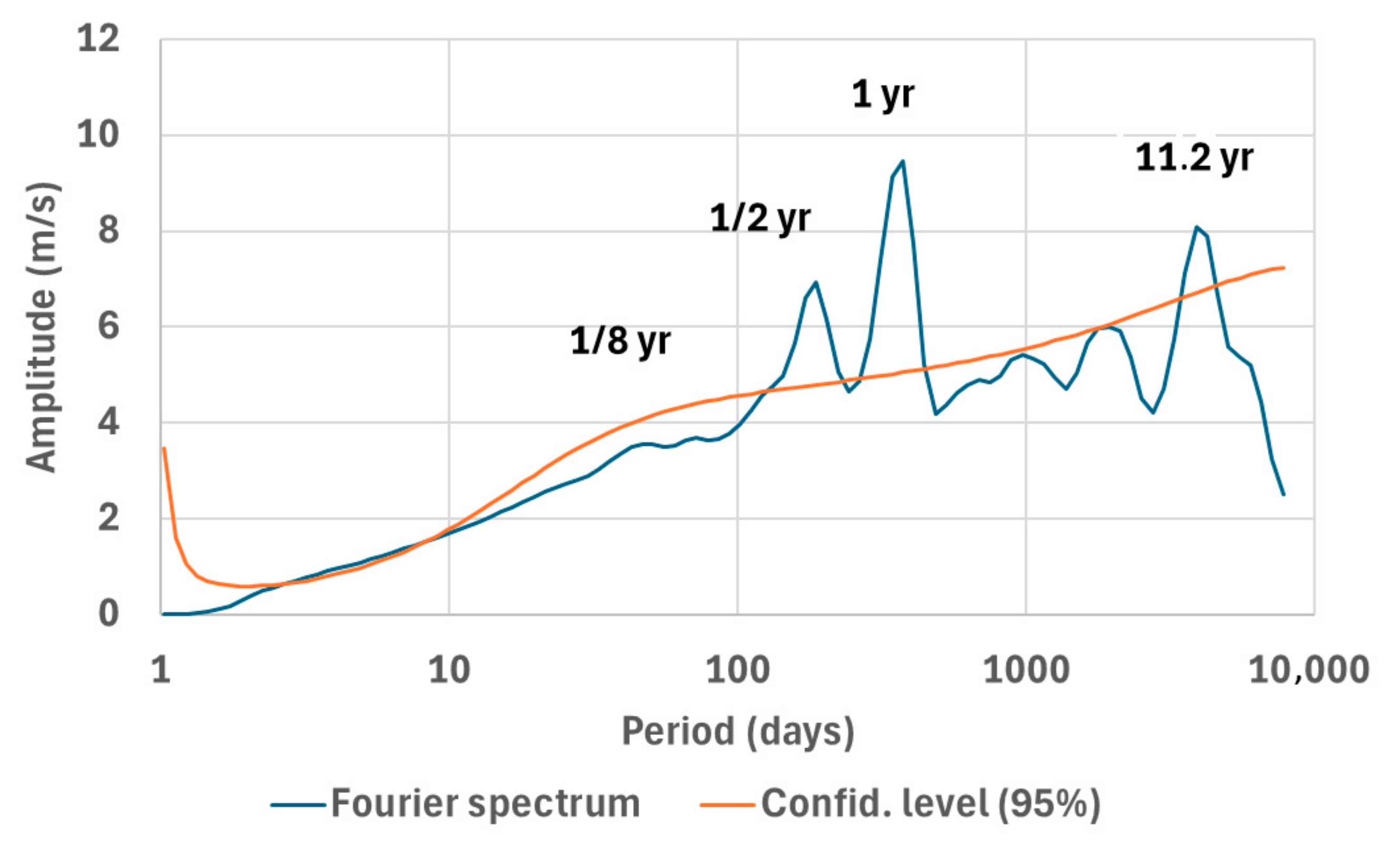

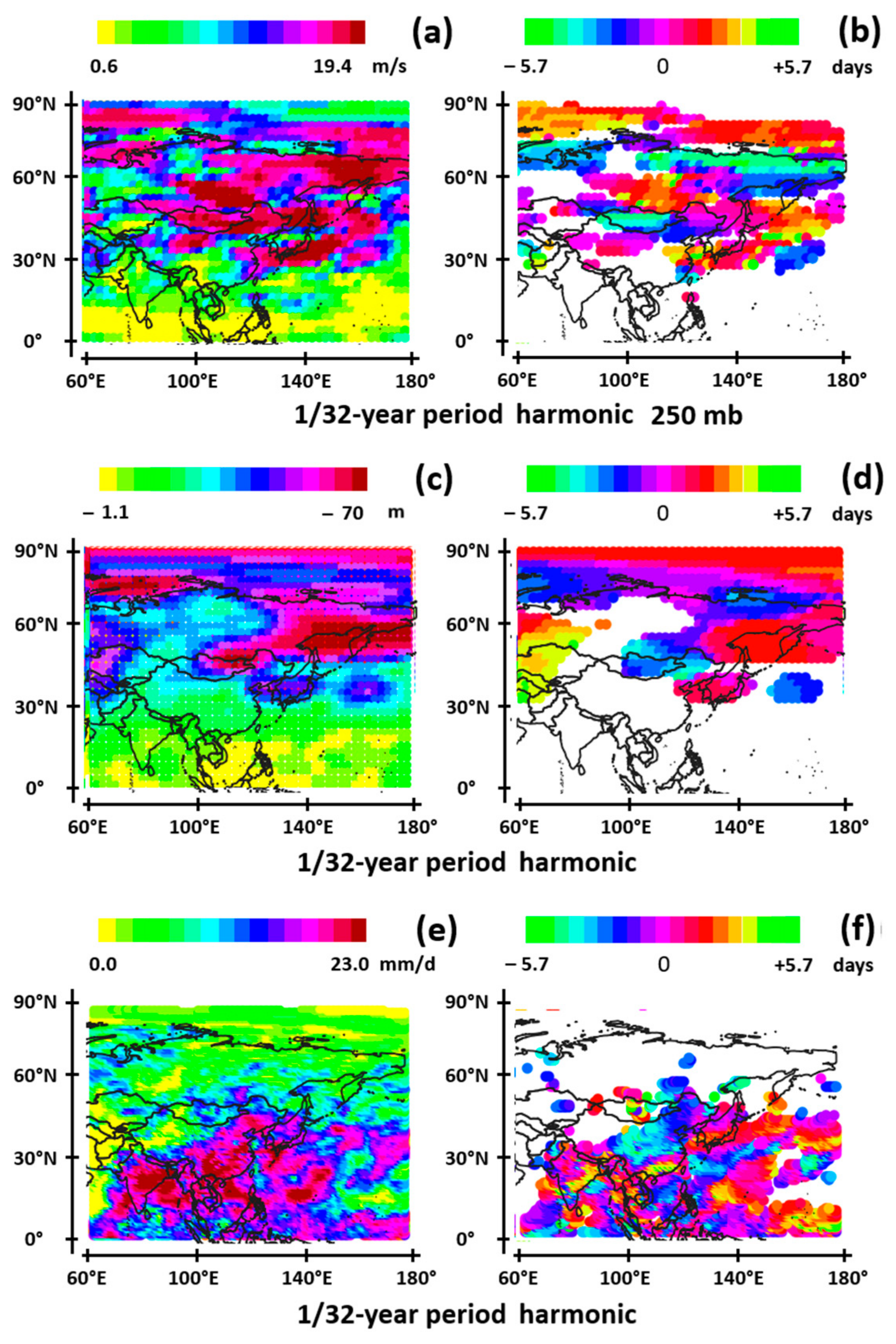
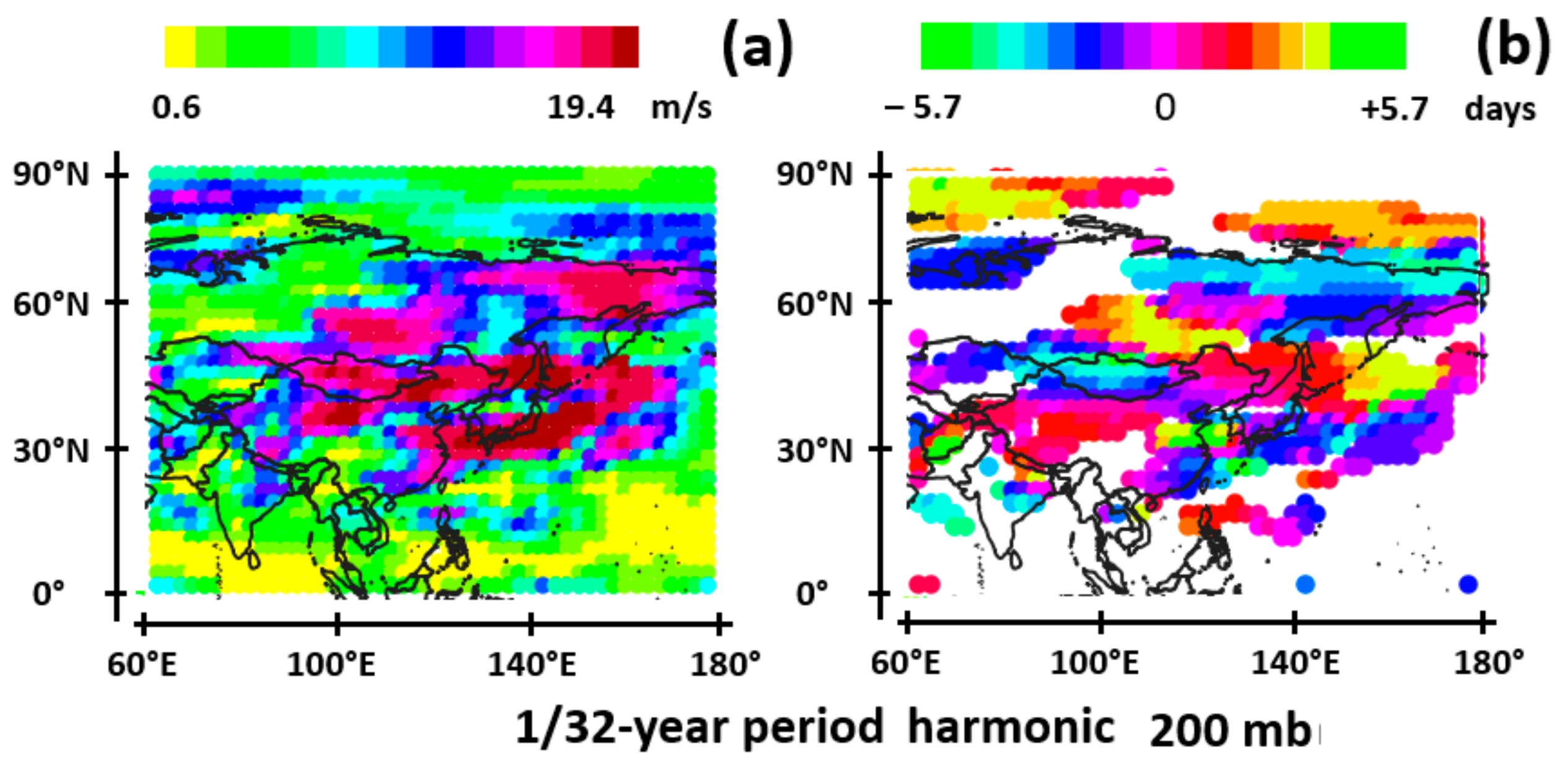


| Mean Period | Period Range |
|---|---|
| 1/8 year (45.7 days) | 34.2 to 68 days |
| 1/16 year (22.8 days) | 17.1 to 34.2 days |
| 1/32 year (11.4 days) | 8.56 to 17.1 days |
| 1/64 year (5.7 days) | 4.28 to 8.56 days |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinault, J.-L. Resonant Forcing by Solar Declination of Rossby Waves at the Tropopause and Implications in Extreme Events, Precipitation, and Heat Waves—Part 1: Theory. Atmosphere 2024, 15, 608. https://doi.org/10.3390/atmos15050608
Pinault J-L. Resonant Forcing by Solar Declination of Rossby Waves at the Tropopause and Implications in Extreme Events, Precipitation, and Heat Waves—Part 1: Theory. Atmosphere. 2024; 15(5):608. https://doi.org/10.3390/atmos15050608
Chicago/Turabian StylePinault, Jean-Louis. 2024. "Resonant Forcing by Solar Declination of Rossby Waves at the Tropopause and Implications in Extreme Events, Precipitation, and Heat Waves—Part 1: Theory" Atmosphere 15, no. 5: 608. https://doi.org/10.3390/atmos15050608
APA StylePinault, J.-L. (2024). Resonant Forcing by Solar Declination of Rossby Waves at the Tropopause and Implications in Extreme Events, Precipitation, and Heat Waves—Part 1: Theory. Atmosphere, 15(5), 608. https://doi.org/10.3390/atmos15050608








