Why the Real Atmosphere Has More Energy than Climate Models: Implications for Ground-Based Telescopes

Abstract

The calculation of Gibbs free energy via the statistical multifractal analysis of airborne observations indicates that the atmosphere is not at local thermodynamic equilibrium. Both climate models and meteorological analyses assume that it is. Satellite retrievals use spectroscopic data taken at equilibrium in laboratories, leading to apparent consistency that is to some degree faulty. Line shapes of radiatively active species, the rotational energy of molecular nitrogen and oxygen, and the translational energy of all molecules are involved, resulting in less energy in models than exists in the real atmosphere. The resulting formulation of turbulence is from the smallest scales up and has implications for astronomical observation by adaptive optics. Kolmogorov (isotropy) is not evident. The effect of temperature on the overhead water vapour column at ground-based telescopes is also open to the effects of climate change. The degree to which the dynamic operational temperature differs from that obtained by the use of local thermodynamic equilibrium assumptions needs to be established by observational measurements. Some of the considerations will apply to the atmospheres of exoplanets with regard to photochemistry and signatures of life.

1. Introduction

Atmospheric chemistry in Earth’s atmosphere is driven by the absorption of solar photons by some of the constituent molecules, most notably molecular oxygen. This process, called photodissociation, results in the production of photofragments—oxygen atoms, in the case of molecular oxygen. Depending upon the photon energy and the quantum levels of the parent molecules and their photofragments, the photofragments will have excitation energies above their ground state, which may be translational and electronic in all cases, plus rotational and vibrational in the case of molecules [1]. Although the assumption that excited photofragments are instantaneously thermalized is widely employed in numerical models of the atmosphere, the issue has been raised in, for example, Faraday Discussions meetings [2,3]. Initially, the fate of photofragments was raised in the context of modelled OH production in the troposphere [4,5] and of the shortfall of ozone production in the stratosphere [6]. However, evidence has emerged that photofragments have agency in affecting the determination of the intermittency of temperature via the initiation of turbulence on molecular scales followed by upscale propagation [7,8]. These later results were obtained using the methods of statistical multifractality [9]. Atmospheric turbulence is involved in the operation of ground-based astronomical telescopes via adaptive optics [10]. The fluctuations in density caused by turbulence result in fluctuations in optical refractive index, blurring the images of stars and galaxies in ground-based telescopes. It is not known with certainty how turbulence and the intermittency of temperature will vary with climate change, but there is evidence that it will at jet stream altitudes [11].

Statistical multifractality is summarized in

Table 1. The equivalence between statistical thermodynamic and scaling variables.

Variable	Statistical Thermodynamics	Scaling Equivalent
Temperature	T	1/qkBoltzmann
Partition function	f	e−K(q)
Energy	E	γ
Entropy	−S(E)	c(γ)
Gibbs free energy	−G	K(q)/q

.

More details about how these variables are obtained can be found in [1]. Briefly, q is the qth-order structure function of the observed variable. The scaling exponent K(q) is derived from the slope of a log–log plot [1]. Equation (1) expresses the relation of the Hurst exponent H to the Gibbs free energy equivalent.

$$H=H\left(q\right)+K\left(q\right)/q$$

(1)

The examination of energy E in terms of a scale ratio produces an expression for the fractal co-dimension c(γ). C₁ is the co-dimension of the mean, characterizing the intensity of the intermittency. The Lévy exponent α characterizes the generator of the intermittency (see [1]). We will examine the intermittency of temperature and its correlation with the ozone photodissociation rate and with temperature itself in the lower stratosphere.

A second factor affecting ground-based astronomical telescopes is the water vapour content of the overlying atmosphere, a variable that is known to increase as the surface temperature of the oceans increases. This will particularly affect telescopes operating at infrared, millimetre-wave and microwave wavelengths, where water vapour has rich rotational and vibrational spectra. There is pronounced hemispheric asymmetry in the water vapour content of the upper troposphere and lower stratosphere, with the Southern Hemisphere showing the drying effects of the Antarctic ice dome [12,13,14]. The effects on radiative transfer and the resulting temperature influence have been modelled. There is clear evidence that meteorological analyses fail to reproduce the diurnal temperature variation in the upper stratosphere and also show a cold bias [15], which will be discussed briefly in Section 4.

Significant effort has been made to detect atmospheric signs of life on exoplanets, even of intelligent and technological presence. Getting the spectroscopic interference from Earth’s spectra correct is an important consideration in this context, as are the characteristics of our terrestrial atmosphere in relation to the chemistry of life and its evolution from a prebiotic state

2. Materials and Methods

The observational data used in this paper were taken during a variety of airborne missions. They are cited in references [1,7,8,16,17], and the figures will be referred to as the figure number in the appropriate reference. There is one exception: the concept upon which this paper is based appears here as Figure 1. It is Figure 3 in [1]; an earlier version appeared as Figure 19 in [17].

The airborne observations analysed here were taken between 1987 and 2006 from the NASA ER-2, DC-8 and WB57F aircraft, using meteorological measurements [18], the ozone [19], an ozone photodissociation radiometer [20], total water measurements [21], and the NOAA Gulfstream 4-SP using GPS dropsondes [22]. The space and time coverage can be found in [23,24] and in the following Special Issues: J. Geophys. Res. D 1989, 94(D9, D14); Geophys. Res. Lett. 1990, 17(4); J. Geophys. Res. D 1992, 97(D8); J. Geophys. Res. D 1997, 102(D3); J. Geophys. Res. D 1999, 104, 481–495; and J. Geophys. Res. D 2002, 107, 8259.

3. Results

Results will be called up by reference; within the references, figures will be indicated by the number they have in the particular reference. The exception is Figure 1 above, included to illustrate the phenomenon we are discussing.

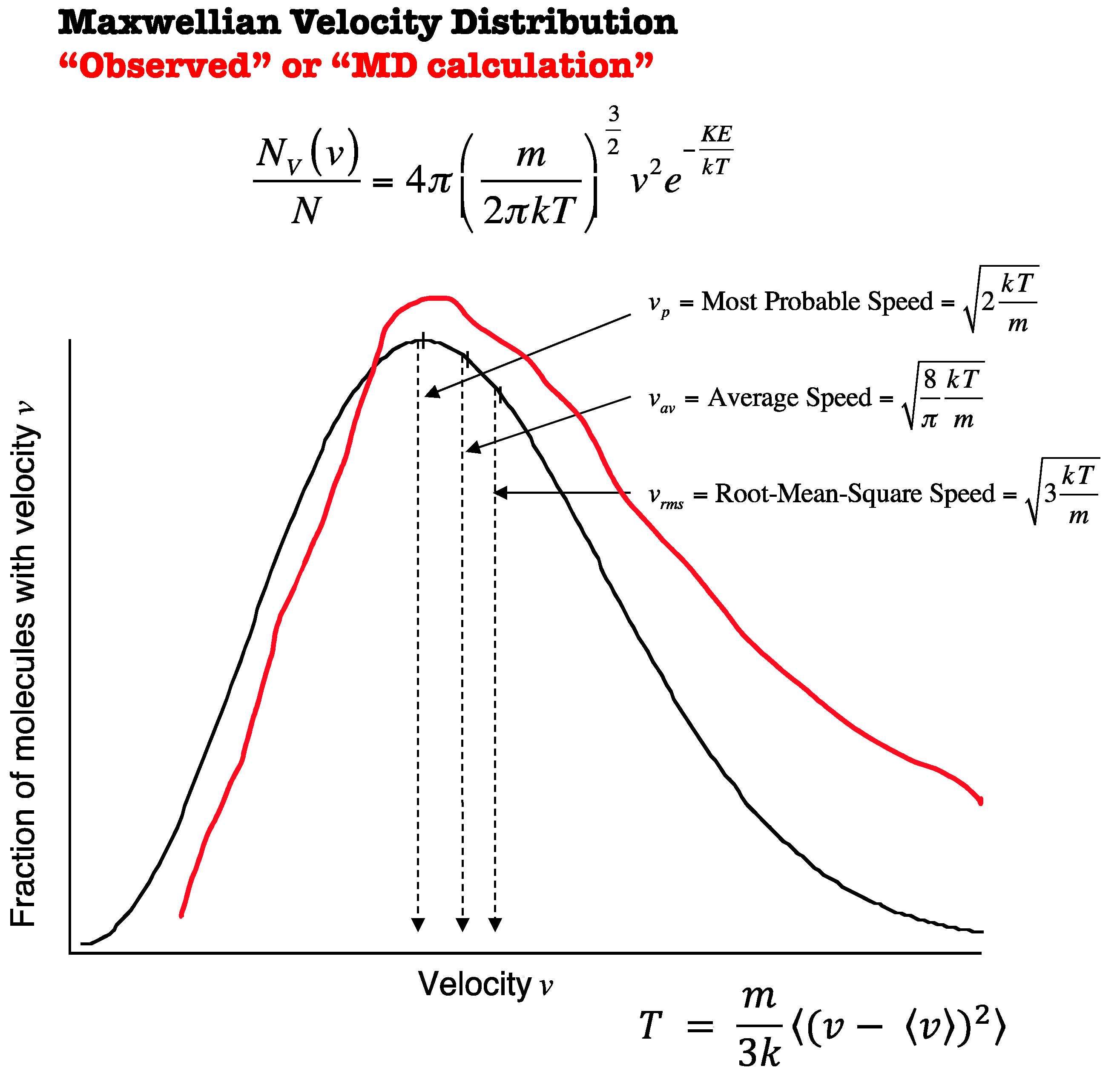
3.1. Turbulent Effects

The observation of non-classical turbulent exponents in airborne observations was reported as soon as statistical multifractal analysis was applied. The conclusion was that the atmosphere exhibited 23/9 multifractal dimensionality [8]. Application to the dropsonde observations resulted in the conclusion that isotropic, Kolmogorov exponents were never observed, with the exponent expressing the scaling of the vertical shear of the horizontal wind increasing as height increased from the ocean surface to 13 km altitude [22], and so resolving the question posed in [9] as regards the adaptive optics procedure for ground-based astronomical interferometers for astronomy. Figure 12 in [22] displays the result. Note that the aircraft observations extend from pole to pole [17]. The molecular origins of turbulence imply translational and rotational energy distributions in the major constituents N₂ and O₂ that are not Maxwell–Boltzmann populations [7]. Temperature in real air is thus not defined by the black curves in Figure 1, but is characterized by a curve resembling the hypothesized red one. The exponent characterizing temperature intermittency is less at night than during daylight hours but does not go to zero in the absence of solar radiation.

3.2. Radiative Effects

Radiative effects upon astronomical observations can arise in two further ways: the effect of molecular-driven turbulence upon spectroscopic line shapes [16,17] and the characterization of the atmospheric spectrum, particularly that of water vapour and its hydrogen-bonded dimer [25]. The population of the dimer and higher oligomers will depend nonlinearly upon temperature. Water vapour has a rich rovibrational spectrum from the near infrared to the microwave; it is an astronomical observable of interest too.

Airborne observations showed that a downward-looking high-resolution interferometer showed a temperature structure below the ER-2 over Antarctica that was more pronounced than that calculated by meteorological assimilation. Sensitivity to skin temperature and cloud cover was evident, factors that will respond to climatic heating.

3.3. Water Vapour Effects

Water vapour shows asymmetries between the Northern and Southern Hemispheres [12,13,14]. The drying effects of the Antarctic ice dome extend to the Southern Hemisphere mid-latitudes in the troposphere, as well as the stratosphere [13,14]. This implies that lower stratospheric and upper tropospheric air in the mid-latitudes of the Southern Hemisphere is not exclusively dried in the tropics at the “cold trap” but is significantly affected by the presence of Antarctica. The siting of ground-based telescopes in the montane upper troposphere of the Atacama Desert reflects this fact. It is a factor likely to be sensitive to sea surface temperatures via the Clapeyron–Clausius equation, as well as to the effect of melting sea ice and glaciers. Warmer sea surface temperatures globally are likely to increase the water vapour content in the air column above ground-based telescopes. In turn, this will make it more difficult to detect and analyse water vapour spectra from exoplanets.

4. Discussion

The argument that real air contains more energy than that simulated by numerical models that assume local thermodynamic equilibrium rests on results obtained by the statistical multifractal analysis of airborne and dropsonde observations. The manner in which that extra real energy manifests itself will affect the operation of adaptive optics in ground-based telescopes directly via the representation of atmospheric turbulence [10]; isotropy (Kolmogorov) was never observed [17,22]. This is shown in Figure 1 and Figure 12 of these references, respectively. While the intermittency of temperature is less at night, when ground-based telescopes operate, it is not zero. At any one time, half the atmosphere is subject to solar radiation and the resulting anisotropic turbulence propagates. There is evidence that clear air turbulence has increased under climate heating [11]. Note that measurements taken from dropsondes are free of the turbulent wake of the balloon, unlike the data taken on ascent by routine operational radiosondes.

A second way in which anisotropic turbulence will affect ground-based interferometric telescopes is in the calculation of spectral line shapes, especially of water vapour and its oligomers [8,25]. There is a need to check the rotational and translational population distributions of the major constituents, N₂ and O₂. Although these are homonuclear diatomic molecules possessing no electric dipole moment, there are collision-induced spectra in nitrogen accessible by coherent anti-Stokes Raman spectroscopy (CARS) [26,27]. Oxygen possesses a magnetic dipole moment in its ³Σ_g^- ground state via the coupling of electron spins to the rotation of the internuclear axis [26], which is evident as a spectrum in the 50–60 Ghz frequency range. Oxygen also has a CARS spectrum [26]. Nonlocal thermodynamic equilibrium conditions and their effect on molecular spectra will be of relevance for observations of exoplanetary atmospheres as an end in themselves and as a complicating factor arising from Earth’s atmosphere. The translational energy distribution of N₂ and O₂ in air may be measured using current molecular beam techniques, although it is likely to be a demanding observation.

The observation that led to the conclusion that local thermodynamic equilibrium does not exist in the Earth’s lower stratosphere was the correlation between the intermittency of temperature with both the ozone photodissociation rate and with temperature itself, as illustrated in Figures 2 and 3 of reference [7] and Figure 16 of [26]. It should be extended downwards to the troposphere and upwards throughout the stratosphere.

The abundance of water molecules in the air column above ground-based telescopes is open to perturbation, in the form of a probable increase, under climate heating. Both the temperature and the pressure distribution will in principle be involved. Rises in sea surface temperature will be the basic driver. Observations of water in exoplanetary atmospheres will be affected.

Satellite retrievals are based on spectra taken under equilibrium conditions in laboratories. This has the potential to fold thermodynamic equilibrium into analyses of the atmosphere, possibly a source of error that would cause unrealistic agreement between the analyses and forecast integrations by the models. The effects of turbulence and non-Maxwellian velocity distributions upon the line shapes of carbon dioxide and water vapour, particularly in the important unsaturated wings of the IR spectral lines, are critical in global heating. The two molecules in real air will trap more upwelling IR radiation than those in a model atmosphere employing local thermodynamic equilibrium.

Carbon dioxide increases affect ozone abundance, as well as that of water vapour in theory, and arguably did so in fact from 1926 to the early 1970s. Ozone is a significant ’blanket’ infrared absorber, as well as a ‘parasol molecule’ in the Earth’s atmosphere, and could therefore be such in exoplanets. Overall, the chemistry of Earth’s atmosphere constitutes a complex, scale-free network that is affected by a multitude of radiative, chemical and fluid mechanical processes. It is not currently predictable with any certainty how most of these, except water, carbon dioxide and ozone, will evolve under global heating. This further implies that exoplanetary atmospheres are likely to be both complex and different to Earth in their atmospheric composition, as well as in signatures of ‘civilizations’. There are basic considerations derived from Earth’s atmospheric photochemistry that will apply to the different compositions in exoplanets [28,29].

Aerosols, their air–water interface and the physics that produces them are thus important, particularly in the search for life on exoplanets. Examples on Earth can be found in [30,31]. Lightning is one such example, having been observed on Jupiter [32]. Its similarity to Earth’s lightning makes Earth observations relevant [32,33,34,35]. These processes are dependent on deep convection, which in turn will be increased by the heating of the Earth’s surface. The Martian atmosphere has photochemistry [36,37] and displays statistical multifractal behaviour [38]. The Martian atmosphere’s surface pressure is about 7 mbar, like the upper stratosphere on Earth, where there is a significant shortfall in temperature calculations by models [15,17]. Another example is the aerosol composition introduced by meteorite impacts in Earth’s upper atmosphere [30,39]. Will aerosols and meteorites be observable on exoplanets from ground-based telescopes? Technetium or plutonium, for example, would be a signature of a technological civilization. That would also be true of combinations of ordinary elements into unusual molecules; or alloys of transition metals, lanthanides, and actinides [39]. The chemical composition of atmospheric aerosols is accessible by spectroscopic methods [40,41]. The detection of the entropy production necessitated by the organization of a civilization would add conviction—for example, the increase in so-called ‘greenhouse’ gases in our atmosphere and in the outgoing infrared radiation to space that is the entropy production for Earth’s organized biosphere [17].

The cold bias in many current atmospheric models may be attributable to other processes that are absent or imperfectly represented, such as gravity waves and subgrid-scale parametrizations. Indeed, the scatter in the simulations from such models may be caused by such inadequacies. The cause proposed here stems from extensive observations. Note that there are recent theoretical arguments as to why different definitions of temperature tend to converge [42]. These cannot account for the correlation of observed air temperature intermittency with ozone photodissociation rate and with temperature itself, as reported in [1,17].

5. Conclusions

The above discussion implies the need for a research program to make the measurements necessary to characterize the extent of the turbulent extra energy in Earth’s atmosphere arising from global heating and departures from local thermodynamic equilibrium, and how these factors are and will be manifested. See [1] for further details. Population distributions of the translational and rotational energies of N₂ and O₂ are required from the surface to the stratopause. Real air contains more energy than that simulated in current climate models. The same consideration will apply in the different compositions likely on exoplanets.