Assessment of Rainfall Frequencies from Global Precipitation Datasets
Abstract
:1. Introduction
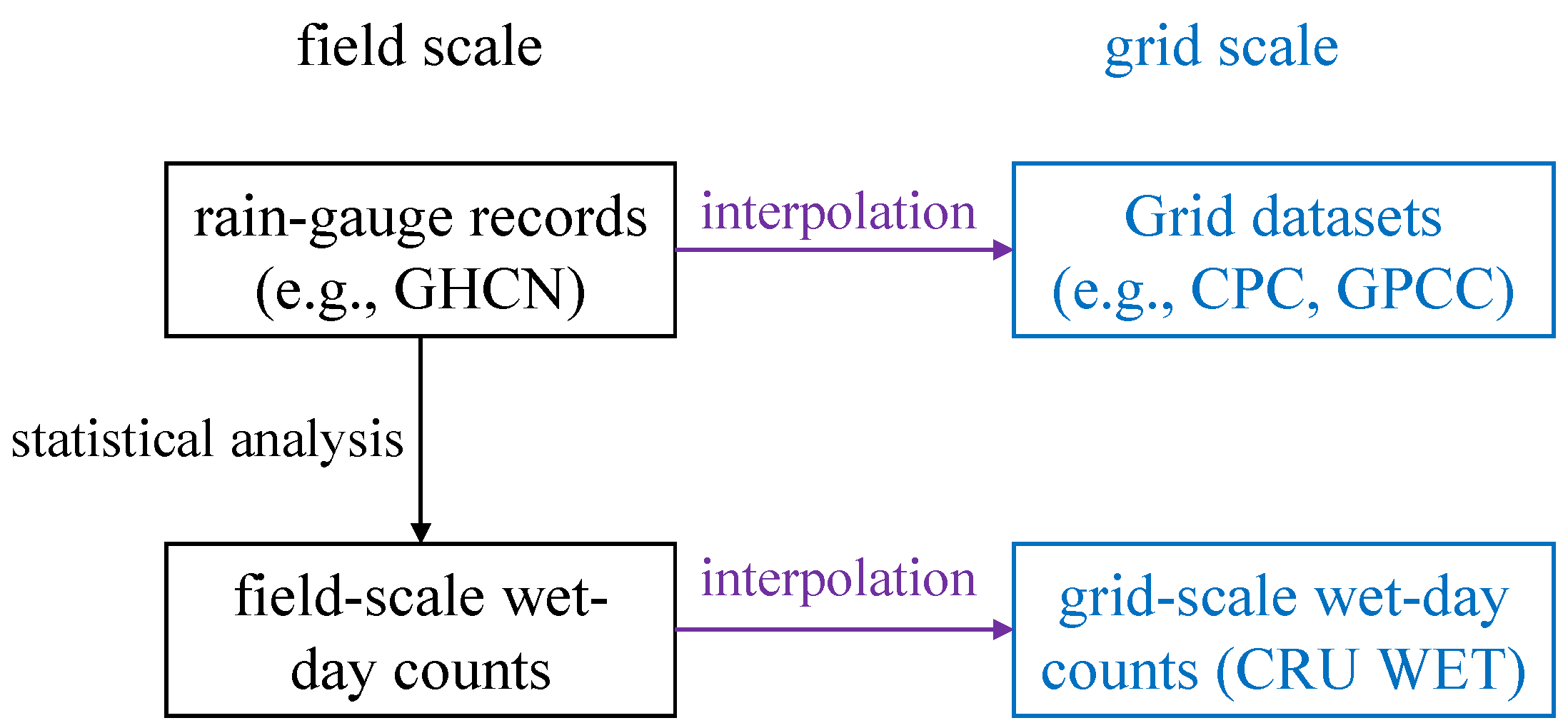
2. Data and Methods
3. Results and Discussions
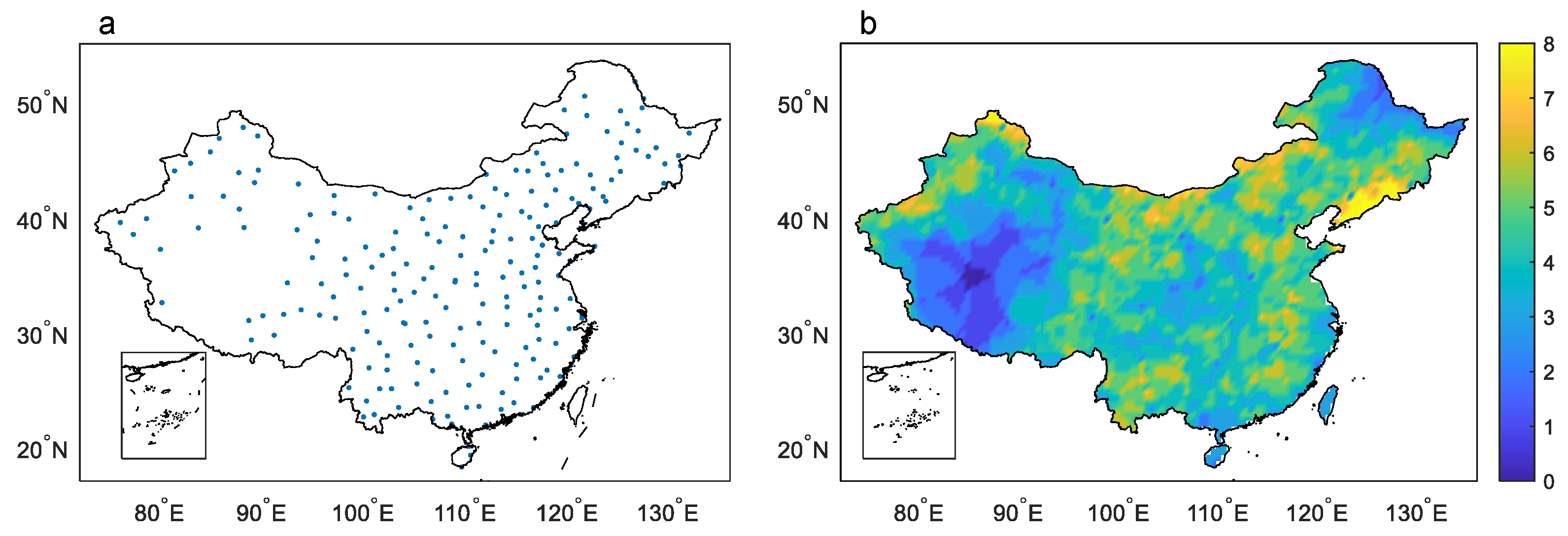
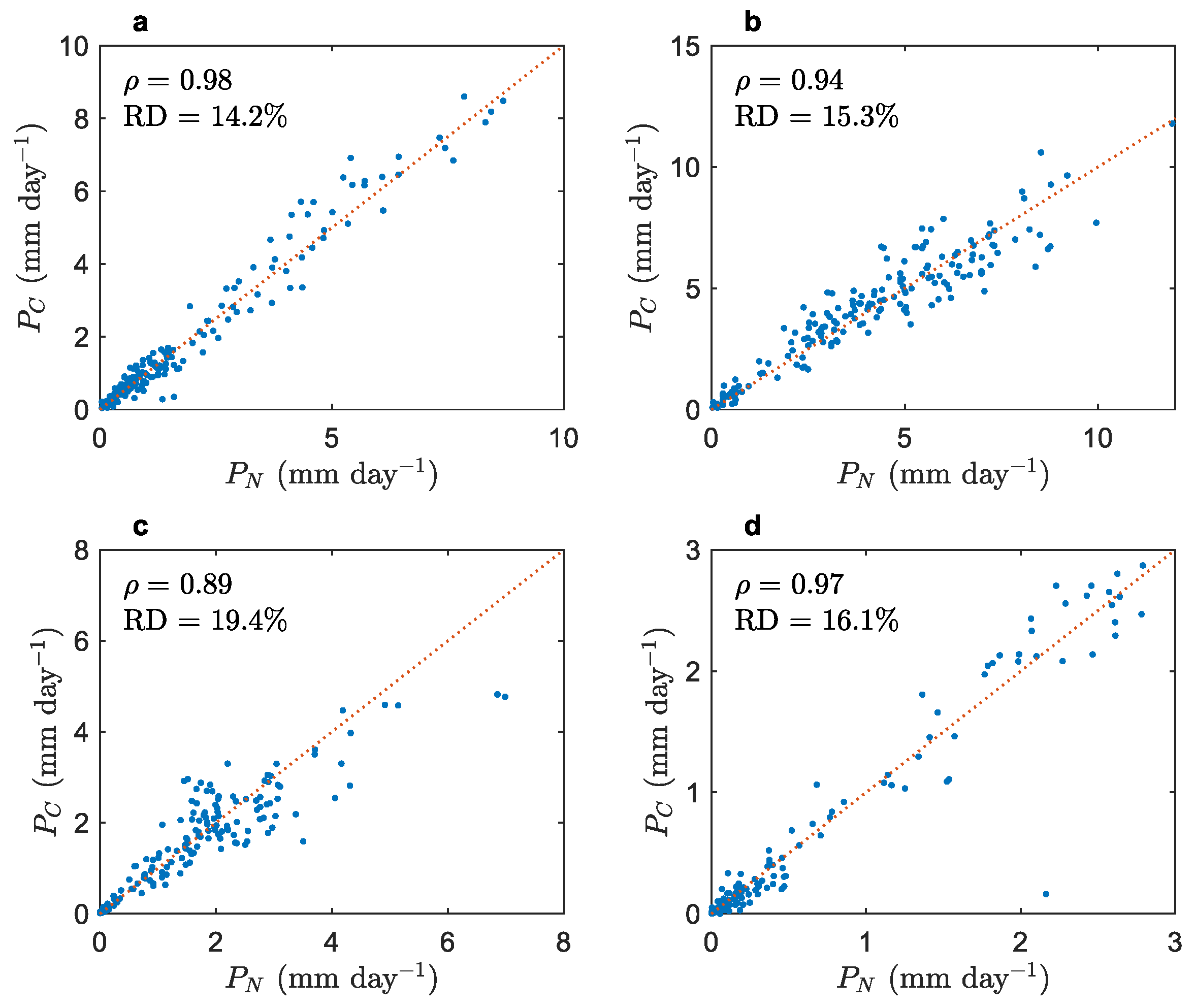
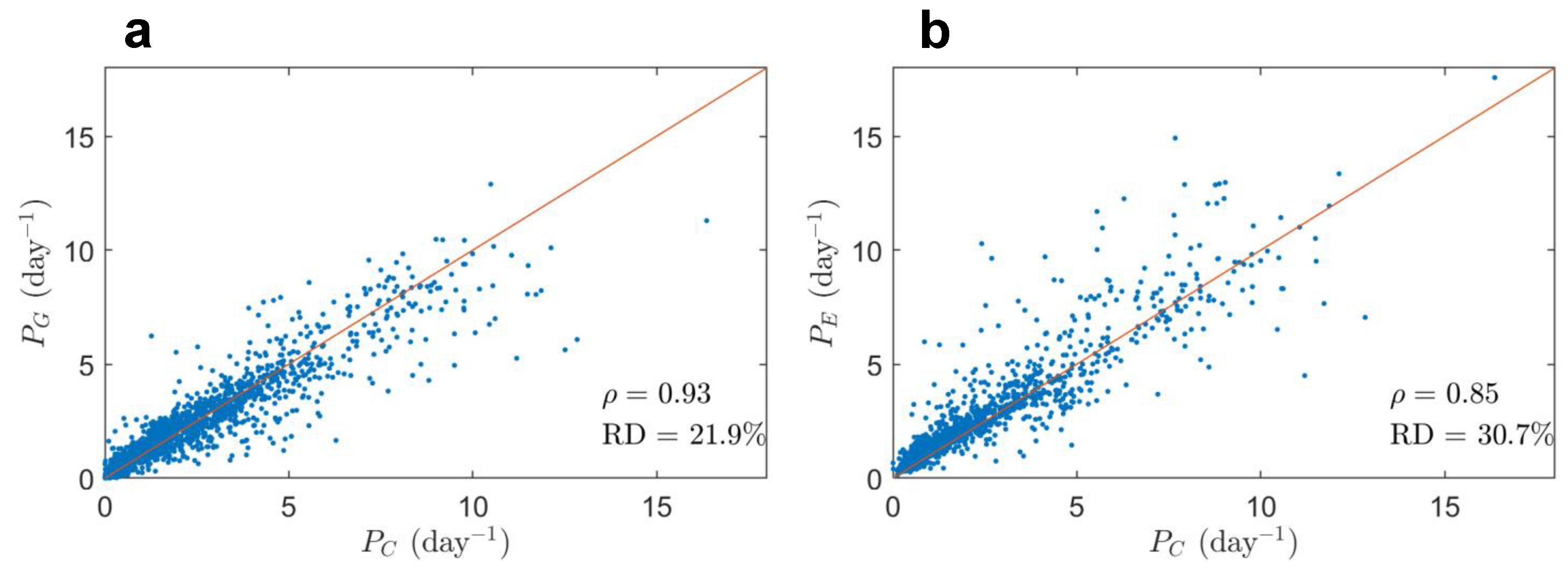
3.1. Field-Scale Rainfall Frequency
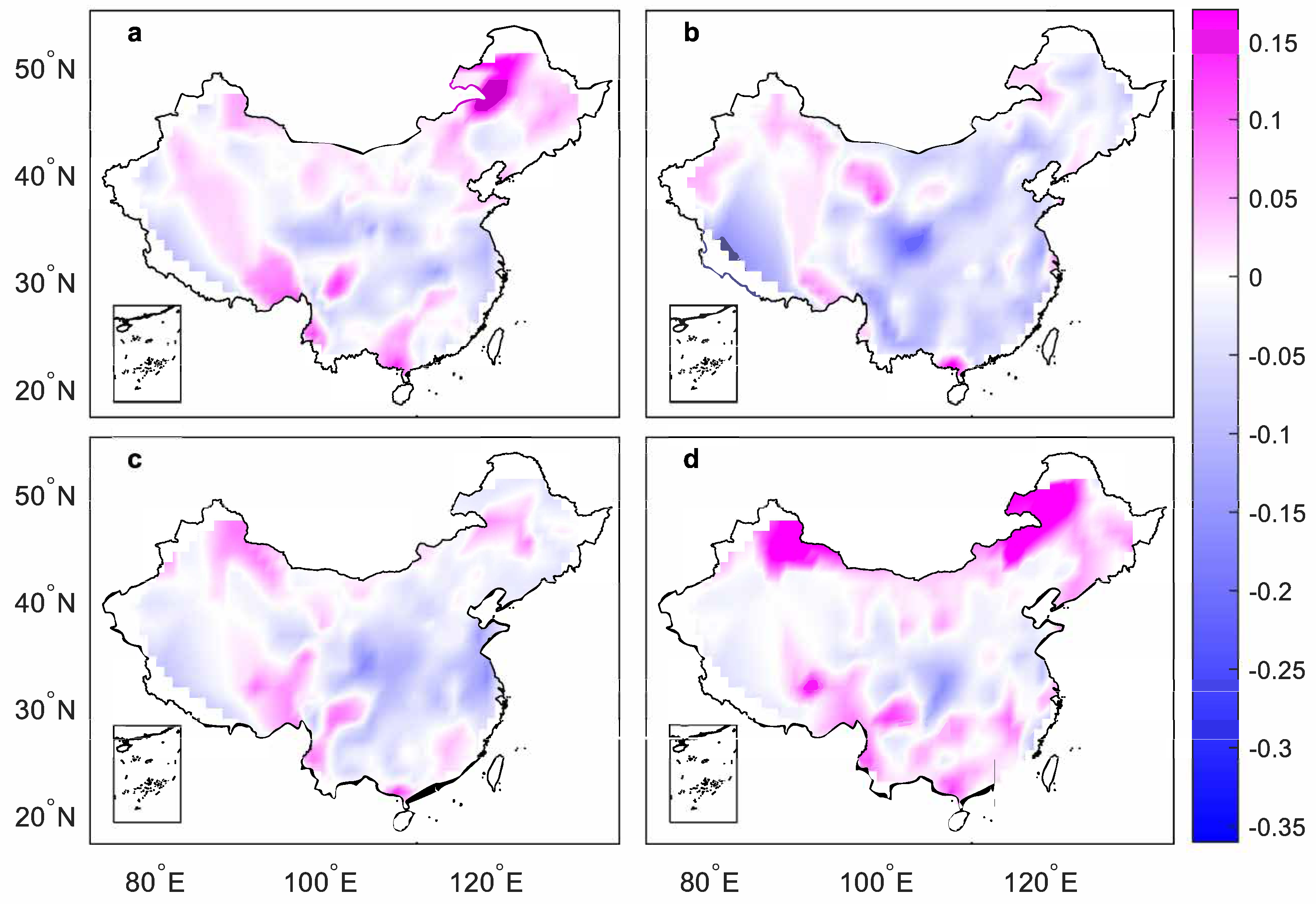
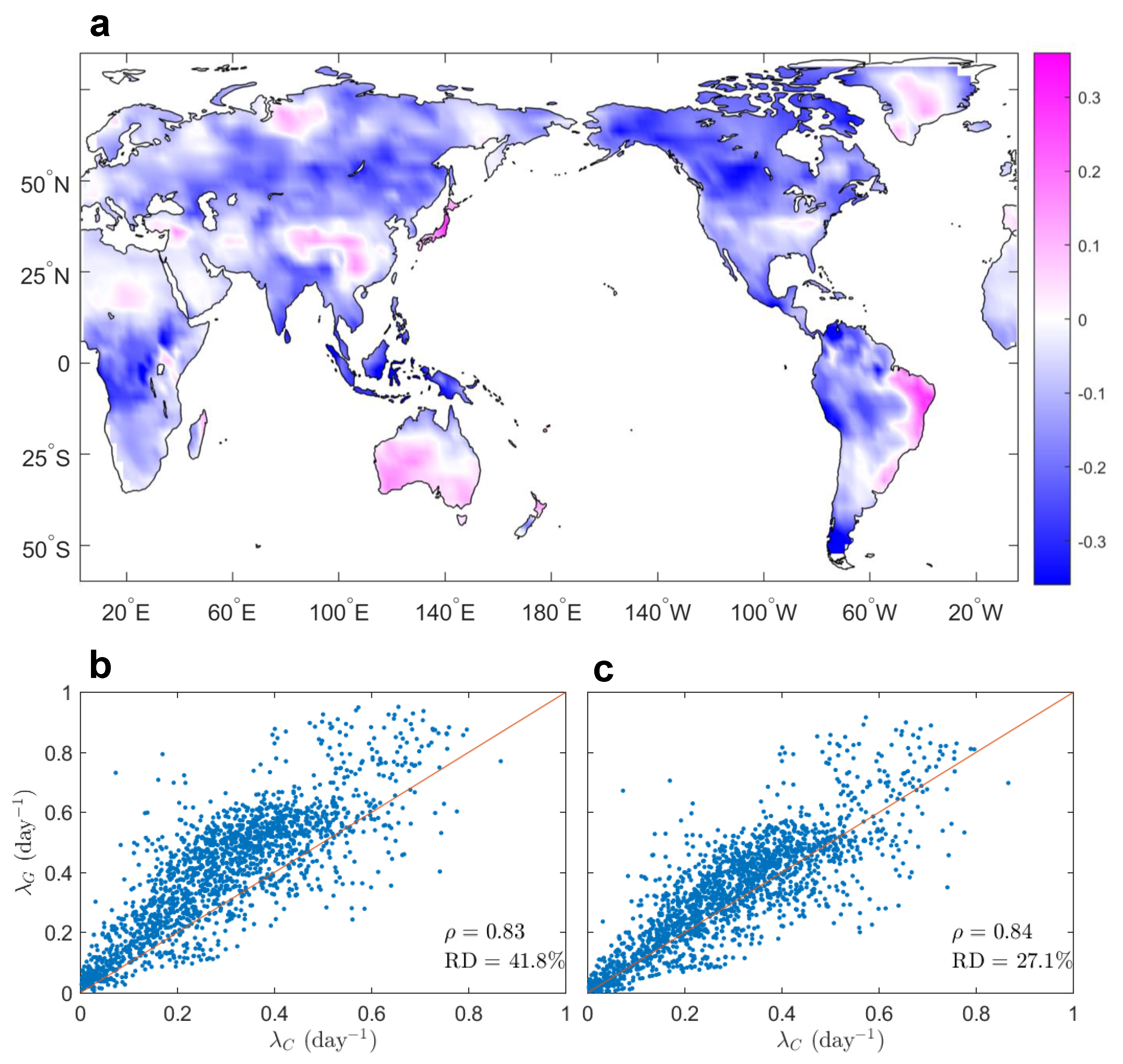
3.2. Grid-Scale Rainfall Frequency
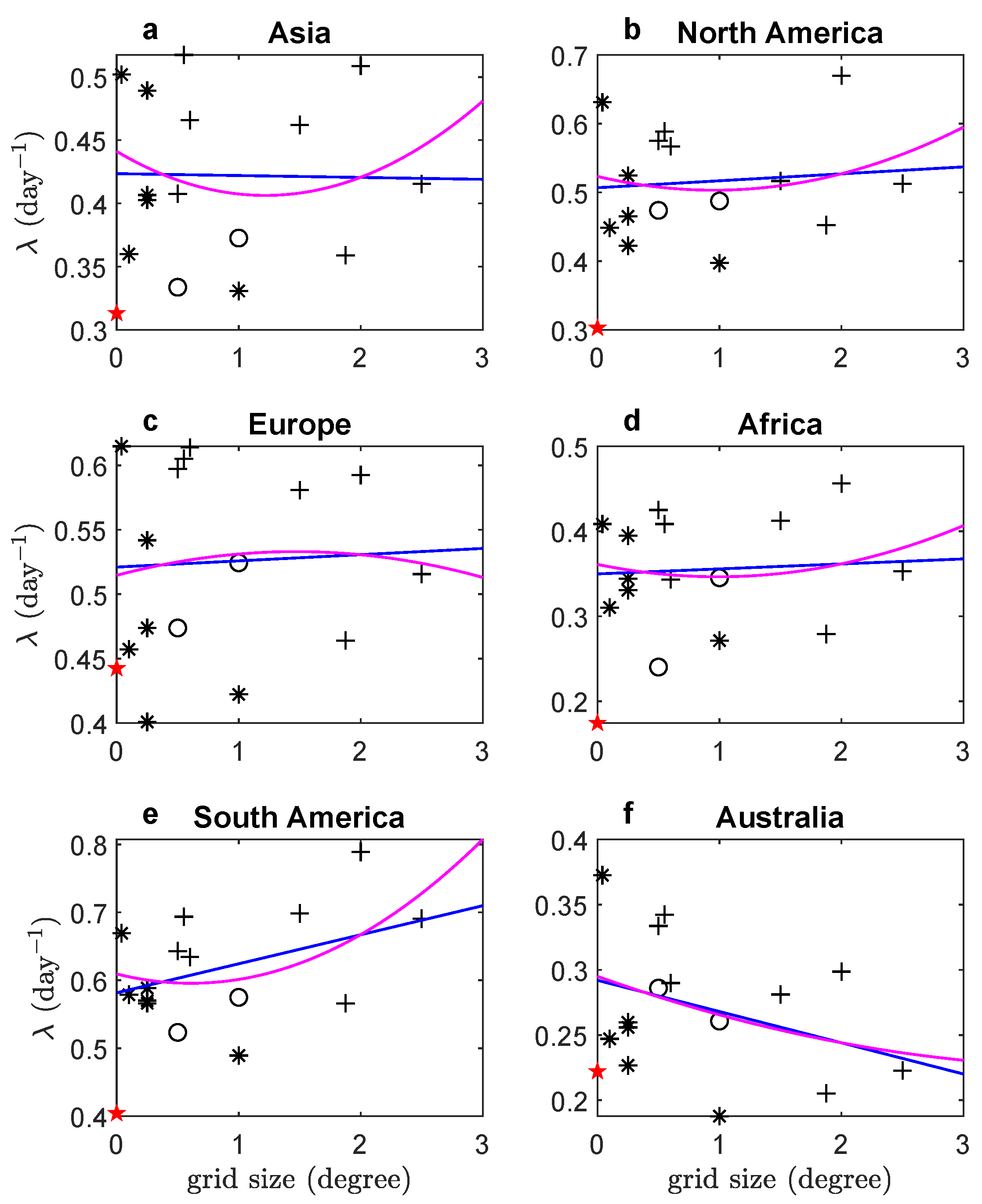
3.3. Independence of Rainfall Frequencies on Grid Resolutions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GPCP 1dd | Global Precipitation Climatology Project 1 degree of daily precipitation analysis |
| CPC | Climate Prediction Center |
| 20CR | Twentieth-century reanalysis system |
| CFSR | Climate Forest System Reanalysis system |
| NECP1 | National Centers for Environmental Prediction version 1 |
| NCEP2 | National Centers for Environmental Prediction version 2 |
| JRA55 | Japanese 55-year Reanalysis |
| ERA Interim | European Centre for Medium-Range Weather Forecasts Reanalysis interim |
| MERRA | Modern-Era Retrospective Analysis for Research and Application system |
| GPCC-daily | Global Precipitation Climatology Centre daily precipitation analysis |
| CMORPH | Climate Prediction Center morphing technique |
| TRMM 3B42 | Tropical Rainfall Measuring Mission 3B42 daily precipitation analysis |
| PERSIANN CCS | Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks Cloud Classification System |
| PERSIANN CDR | Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks Climate Data Record |
| MSWEP | Multi-Source Weighted-Ensemble Precipitation |
References
- Eagleson, P.S. Climate, soil, and vegetation: 1. Introduction to water balance dynamics. Water Resour. Res. 1978, 14, 705–712. [Google Scholar] [CrossRef]
- Austin, A.T.; Yahdjian, L.; Stark, J.M.; Belnap, J.; Porporato, A.; Norton, U.; Ravetta, D.A.; Schaeffer, S.M. Water pulses and biogeochemical cycles in arid and semiarid ecosystems. Oecologia 2004, 141, 221–235. [Google Scholar] [CrossRef] [PubMed]
- Liang, M.; Feng, X.; Gornish, E.S. Rainfall pulses mediate long-term plant community compositional dynamics in a semi-arid rangeland. J. Appl. Ecol. 2021, 58, 708–717. [Google Scholar] [CrossRef]
- Breinl, K.; Lun, D.; Müller-Thomy, H.; Blöschl, G. Understanding the relationship between rainfall and flood probabilities through combined intensity-duration-frequency analysis. J. Hydrol. 2021, 602, 126759. [Google Scholar] [CrossRef]
- MC Fernandes, V.; Rudgers, J.A.; Collins, S.L.; Garcia-Pichel, F. Rainfall pulse regime drives biomass and community composition in biological soil crusts. Ecology 2022, 103, e3744. [Google Scholar] [CrossRef] [PubMed]
- Porporato, A.; Yin, J. Ecohydrology: Dynamics of Life and Water in the Critical Zone; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Feldman, A.F.; Feng, X.; Felton, A.J.; Konings, A.G.; Knapp, A.K.; Biederman, J.A.; Poulter, B. Plant responses to changing rainfall frequency and intensity. Nat. Rev. Earth Environ. 2024, 5, 276–294. [Google Scholar] [CrossRef]
- Fay, P.a.; Kaufman, D.M.; Nippert, J.B.; Carlisle, J.D.; Harper, C.W. Changes in grassland ecosystem function due to extreme rainfall events: Implications for responses to climate change. Glob. Chang. Biol. 2008, 14, 1600–1608. [Google Scholar] [CrossRef]
- Peng, S.; Piao, S.; Shen, Z.; Ciais, P.; Sun, Z.; Chen, S.; Bacour, C.; Peylin, P.; Chen, A. Precipitation amount, seasonality and frequency regulate carbon cycling of a semi-arid grassland ecosystem in Inner Mongolia, China: A modeling analysis. Agric. For. Meteorol. 2013, 178–179, 46–55. [Google Scholar] [CrossRef]
- Fay, P.A.; Blair, J.M.; Smith, M.D.; Nippert, J.B.; Carlisle, J.D.; Knapp, A.K. Relative effects of precipitation variability and warming on tallgrass prairie ecosystem function. Biogeosciences 2011, 8, 3053–3068. [Google Scholar] [CrossRef]
- Robinson, T.M.P.; La Pierre, K.J.; Vadeboncoeur, M.A.; Byrne, K.M.; Thomey, M.L.; Colby, S.E. Seasonal, not annual precipitation drives community productivity across ecosystems. Oikos 2012, 122, 727–738. [Google Scholar] [CrossRef]
- Arnbjerg-Nielsen, K.; Willems, P.; Olsson, J.; Beecham, S.; Pathirana, A.; Bülow Gregersen, I.; Madsen, H.; Nguyen, V.T.V. Impacts of climate change on rainfall extremes and urban drainage systems: A review. Water Sci. Technol. 2013, 68, 16–28. [Google Scholar] [CrossRef]
- Schwinning, S.; Sala, O.E. Hierarchy of responses to resource pulses in arid and semi-arid ecosystems. Oecologia 2004, 141, 211–220. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T.; Shepherd, T.G. Attribution of climate extreme events. Nat. Clim. Chang. 2015, 5, 725–730. [Google Scholar] [CrossRef]
- Siteur, K.; Eppinga, M.B.; Karssenberg, D.; Baudena, M.; Bierkens, M.F.; Rietkerk, M. How will increases in rainfall intensity affect semiarid ecosystems? Water Resour. Res. 2014, 50, 5980–6001. [Google Scholar] [CrossRef]
- Wang, J.; Liu, D.; Ciais, P.; Peñuelas, J. Decreasing rainfall frequency contributes to earlier leaf onset in northern ecosystems. Nat. Clim. Chang. 2022, 12, 386–392. [Google Scholar] [CrossRef]
- Xie, P.; Arkin, P.A. Analyses of Global Monthly Precipitation Using Gauge Observations, Satellite Estimates, and Numerical Model Predictions. J. Clim. 1996, 9, 840–858. [Google Scholar] [CrossRef]
- Kidd, C. Satellite rainfall climatology: A review. Int. J. Climatol. 2001, 21, 1041–1066. [Google Scholar] [CrossRef]
- Bosilovich, M.G.; Chen, J.; Robertson, F.R.; Adler, R.F. Evaluation of Global Precipitation in Reanalyses. J. Appl. Meteorol. Climatol. 2008, 47, 2279–2299. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M.; Rudolf, B. GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 2013, 115, 15–40. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Turk, F.; Petersen, W.; Hou, A.Y.; García-Ortega, E.; Machado, L.A.; Angelis, C.F.; Salio, P.; Kidd, C.; Huffman, G.J.; et al. Global precipitation measurement: Methods, datasets and applications. Atmos. Res. 2012, 104–105, 70–97. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; van Dijk, A.I.J.M.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Hydrol. Earth Syst. Sci. 2017, 21, 6201–6217. [Google Scholar] [CrossRef]
- Paredes Trejo, F.J.; Álvarez Barbosa, H.; Peñaloza-Murillo, M.A.; Moreno, M.A.; Farias, A. Intercomparison of improved satellite rainfall estimation with CHIRPS gridded product and rain gauge data over Venezuela. Atmósfera 2016, 29, 323–342. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; Momin, I.M.; Rajagopal, E.N.; Basu, S.; Collins, M.; Turner, A.G.; Achuta Rao, K.; Ashok, K. Seasonal intercomparison of observational rainfall datasets over India during the southwest monsoon season: Comparison of monsoon rainfall. Int. J. Climatol. 2014, 35, 2326–2338. [Google Scholar] [CrossRef]
- Tanarhte, M.; Hadjinicolaou, P.; Lelieveld, J. Intercomparison of temperature and precipitation data sets based on observations in the Mediterranean and the Middle East. J. Geophys. Res. Atmos. 2012, 117, D12102. [Google Scholar] [CrossRef]
- Tapiador, F.; Navarro, A.; Levizzani, V.; García-Ortega, E.; Huffman, G.; Kidd, C.; Kucera, P.; Kummerow, C.; Masunaga, H.; Petersen, W.; et al. Global precipitation measurements for validating climate models. Atmos. Res. 2017, 197, 1–20. [Google Scholar] [CrossRef]
- Serreze, M.C.; Hurst, C.M. Representation of Mean Arctic Precipitation from NCEP–NCAR and ERA Reanalyses. J. Clim. 2000, 13, 182–201. [Google Scholar] [CrossRef]
- Zolina, O.; Kapala, A.; Simmer, C.; Gulev, S.K. Analysis of extreme precipitation over Europe from different reanalyses: A comparative assessment. Glob. Planet. Chang. 2004, 44, 129–161. [Google Scholar] [CrossRef]
- Romilly, T.G.; Gebremichael, M. Evaluation of satellite rainfall estimates over Ethiopian river basins. Hydrol. Earth Syst. Sci. 2011, 15, 1505–1514. [Google Scholar] [CrossRef]
- McCollum, J.R.; Krajewski, W.F.; Ferraro, R.R.; Ba, M.B. Evaluation of Biases of Satellite Rainfall Estimation Algorithms over the Continental United States. J. Appl. Meteorol. 2002, 41, 1065–1080. [Google Scholar] [CrossRef]
- Chen, M.; Shi, W.; Xie, P.; Silva, V.B.S.; Kousky, V.E.; Wayne Higgins, R.; Janowiak, J.E. Assessing objective techniques for gauge-based analyses of global daily precipitation. J. Geophys. Res. Atmos. 2008, 113, D04110. [Google Scholar] [CrossRef]
- Wagner, P.D.; Fiener, P.; Wilken, F.; Kumar, S.; Schneider, K. Comparison and evaluation of spatial interpolation schemes for daily rainfall in data scarce regions. J. Hydrol. 2012, 464, 388–400. [Google Scholar] [CrossRef]
- Kidd, C.; Becker, A.; Huffman, G.J.; Muller, C.L.; Joe, P.; Skofronick-Jackson, G.; Kirschbaum, D.B. So, how much of the Earth’s surface is covered by rain gauges? Bull. Am. Meteorol. Soc. 2017, 98, 69–78. [Google Scholar] [CrossRef] [PubMed]
- Krajewski, W.; Smith, J.A. Radar hydrology: Rainfall estimation. Adv. Water Resour. 2002, 25, 1387–1394. [Google Scholar] [CrossRef]
- Moreau, E.; Testud, J.; Le Bouar, E. Rainfall spatial variability observed by X-band weather radar and its implication for the accuracy of rainfall estimates. Adv. Water Resour. 2009, 32, 1011–1019. [Google Scholar] [CrossRef]
- Schamm, K.; Ziese, M.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Schneider, U.; Schröder, M.; Stender, P. Global gridded precipitation over land: A description of the new GPCC First Guess Daily product. Earth Syst. Sci. Data 2014, 6, 49–60. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef]
- Jaffrés, J.B. GHCN-Daily: A treasure trove of climate data awaiting discovery. Comput. Geosci. 2019, 122, 35–44. [Google Scholar] [CrossRef]
- Dinku, T.; Alessandrini, S.; Evangelisti, M.; Rojas, O. A description and evaluation of FAO satellite rainfall estimation algorithm. Atmos. Res. 2015, 163, 48–60. [Google Scholar] [CrossRef]
- Harris, I.; Jones, P.; Osborn, T.; Lister, D. Updated high-resolution grids of monthly climatic observations—The CRU TS3.10 Dataset. Int. J. Climatol. 2013, 34, 623–642. [Google Scholar] [CrossRef]
- Lin, J.; Bryan, B.A.; Zhou, X.; Lin, P.; Do, H.X.; Gao, L.; Gu, X.; Liu, Z.; Wan, L.; Tong, S.; et al. Making China’s water data accessible, usable and shareable. Nat. Water 2023, 1, 328–335. [Google Scholar] [CrossRef]
- Adler, R.; Sapiano, M.; Huffman, G.; Wang, J.J.; Gu, G.; Bolvin, D.; Chiu, L.; Schneider, U.; Becker, A.; Nelkin, E.; et al. The Global Precipitation Climatology Project (GPCP) Monthly Analysis (New Version 2.3) and a Review of 2017 Global Precipitation. Atmosphere 2018, 9, 138. [Google Scholar] [CrossRef] [PubMed]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Gehne, M.; Hamill, T.M.; Kiladis, G.N.; Trenberth, K.E. Comparison of Global Precipitation Estimates across a Range of Temporal and Spatial Scales. J. Clim. 2016, 29, 7773–7795. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Menne, M.J.; Durre, I.; Vose, R.S.; Gleason, B.E.; Houston, T.G. An Overview of the Global Historical Climatology Network-Daily Database. J. Atmos. Ocean. Technol. 2012, 29, 897–910. [Google Scholar] [CrossRef]
- Ha, K.J.; Heo, K.Y.; Lee, S.S.; Yun, K.S.; Jhun, J.G. Variability in the East Asian monsoon: A review. Meteorol. Appl. 2012, 19, 200–215. [Google Scholar] [CrossRef]
- Porporato, A.; Daly, E.; Rodriguez-Iturbe, I. Soil Water Balance and Ecosystem Response to Climate Change. Am. Nat. 2004, 164, 625–632. [Google Scholar] [CrossRef]
- Daly, E.; Calabrese, S.; Yin, J.; Porporato, A. Linking parametric and water-balance models of the Budyko and Turc spaces. Adv. Water Resour. 2019, 134, 103435. [Google Scholar] [CrossRef]
- Yin, J.; Porporato, A. Global Distribution of Climatic Aridity. Geophys. Res. Lett. 2023, 50, e2023GL105228. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, X.; Zhang, Z.; Lin, Z.; Yin, J. Assessment of Rainfall Frequencies from Global Precipitation Datasets. Atmosphere 2025, 16, 66. https://doi.org/10.3390/atmos16010066
Yin X, Zhang Z, Lin Z, Yin J. Assessment of Rainfall Frequencies from Global Precipitation Datasets. Atmosphere. 2025; 16(1):66. https://doi.org/10.3390/atmos16010066
Chicago/Turabian StyleYin, Xueyi, Ziyang Zhang, Zhi Lin, and Jun Yin. 2025. "Assessment of Rainfall Frequencies from Global Precipitation Datasets" Atmosphere 16, no. 1: 66. https://doi.org/10.3390/atmos16010066
APA StyleYin, X., Zhang, Z., Lin, Z., & Yin, J. (2025). Assessment of Rainfall Frequencies from Global Precipitation Datasets. Atmosphere, 16(1), 66. https://doi.org/10.3390/atmos16010066




