Spatio-Temporal Analysis of Drought with SPEI in the State of Mexico and Mexico City
Abstract
1. Introduction
2. Materials and Methods
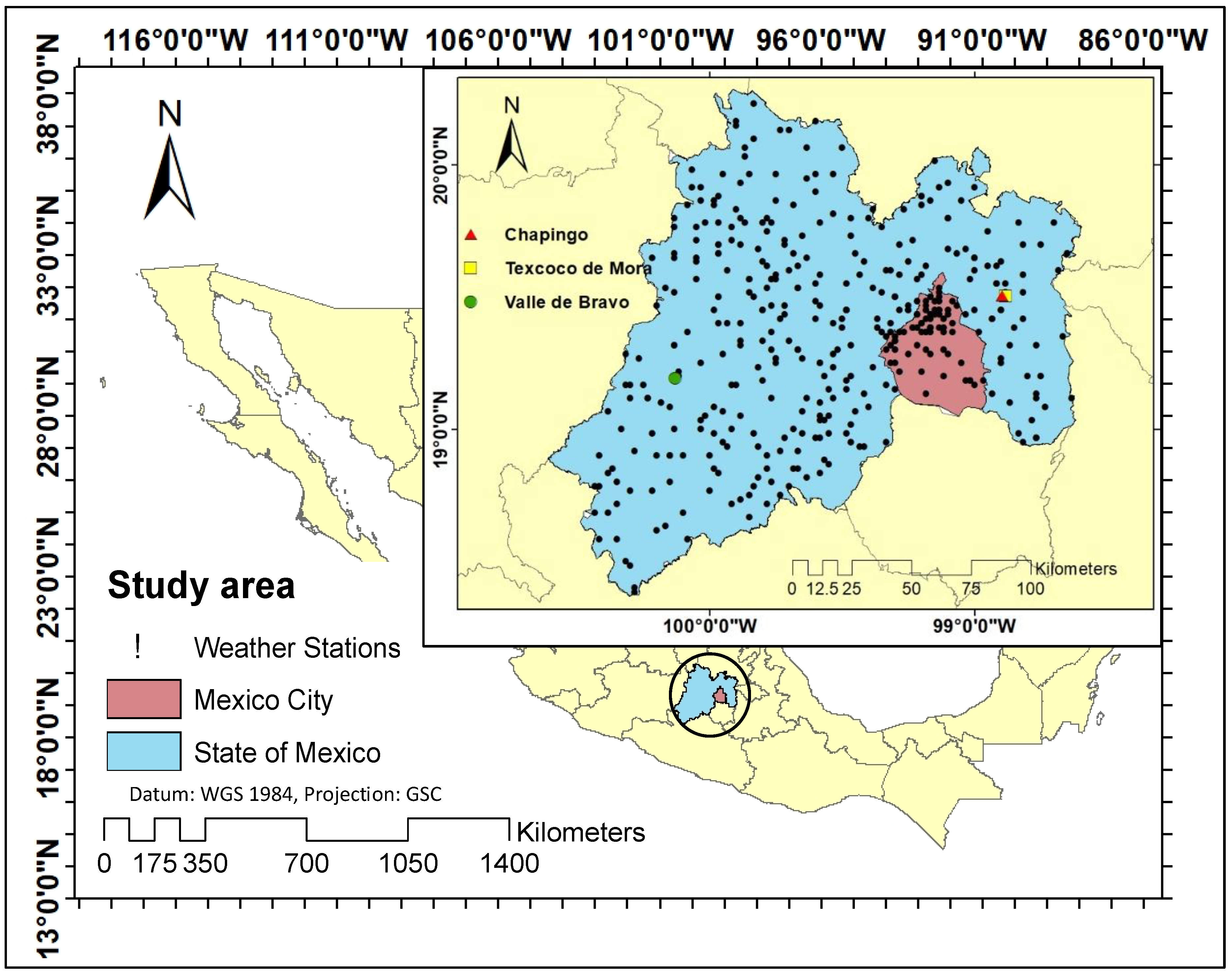
2.1. Description of the Study Area
2.2. Climatological Databases
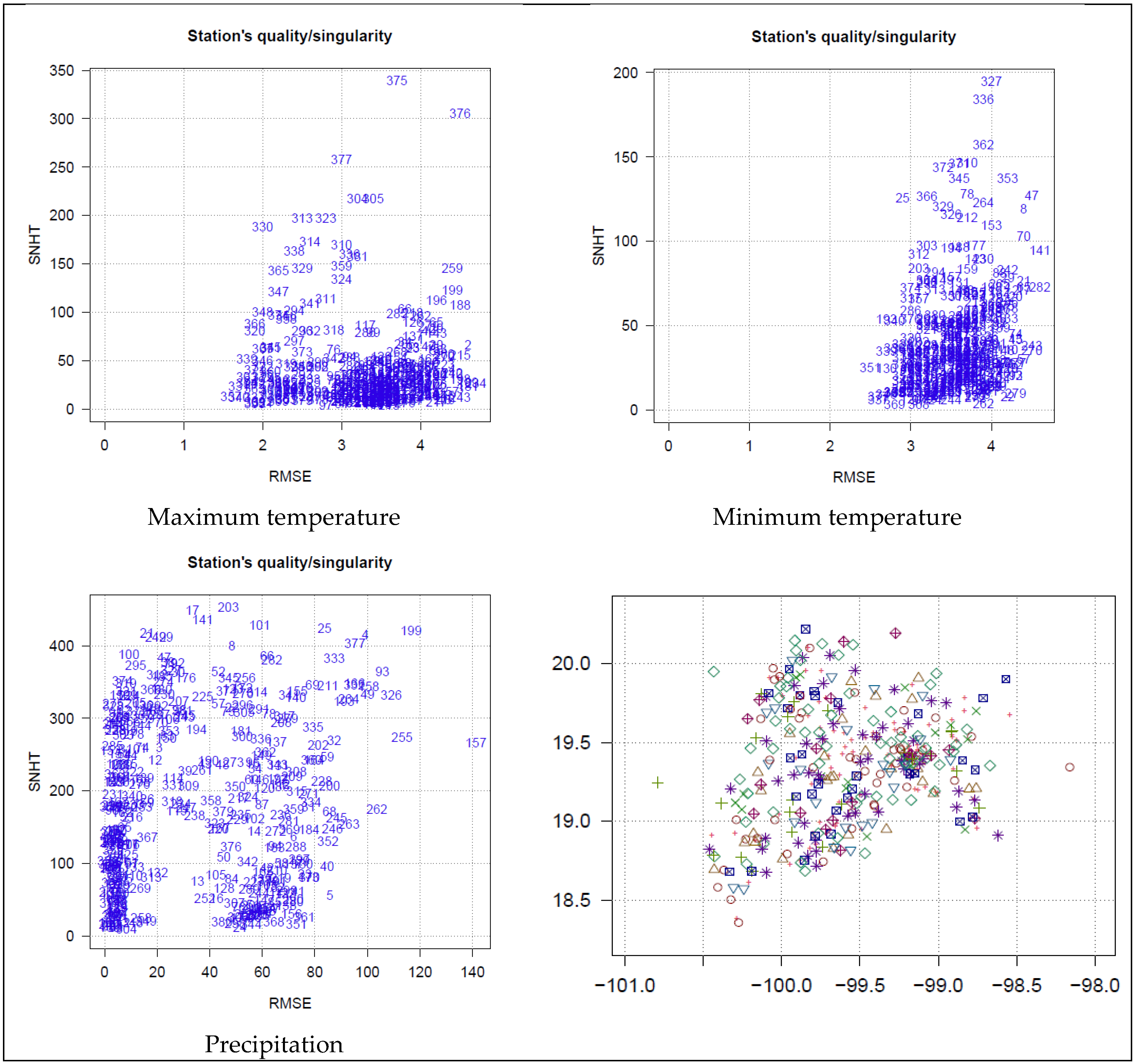
2.3. Climatol: Software for the Validation and Analysis of Climate Data
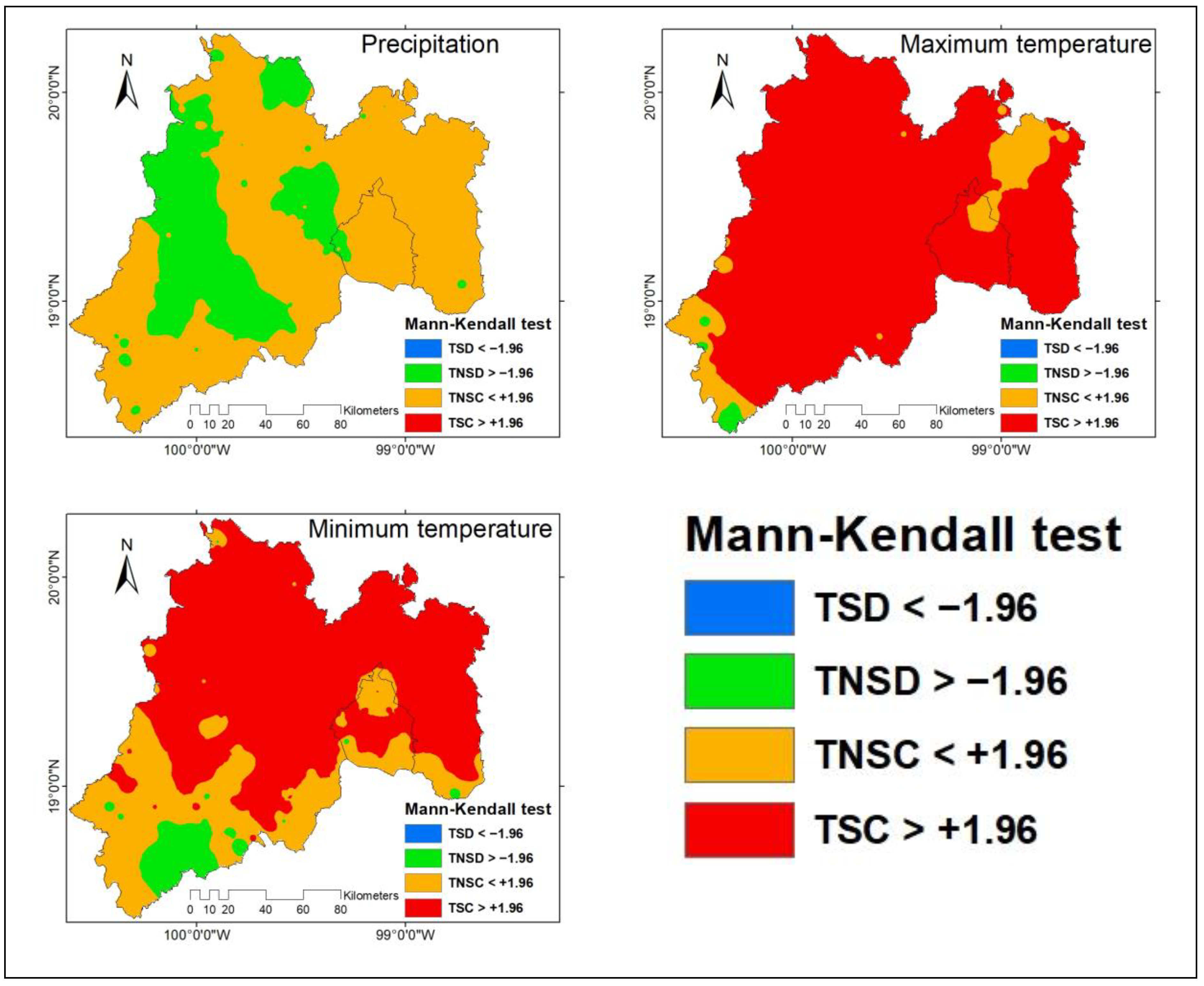
2.4. Mann–Kendall Statistical Test
2.5. Climate Engine
2.6. CHIRPS Satellite Data
2.7. DAYMET Satellite Data
2.8. Potential Evapotranspiration Equations (PETs)
2.9. Drought Indices
2.9.1. The Palmer Drought Severity Index (PDSI)
2.9.2. Standardized Precipitation Index (SPI)
2.9.3. Standardized Precipitation Evapotranspiration Index (SPEI)
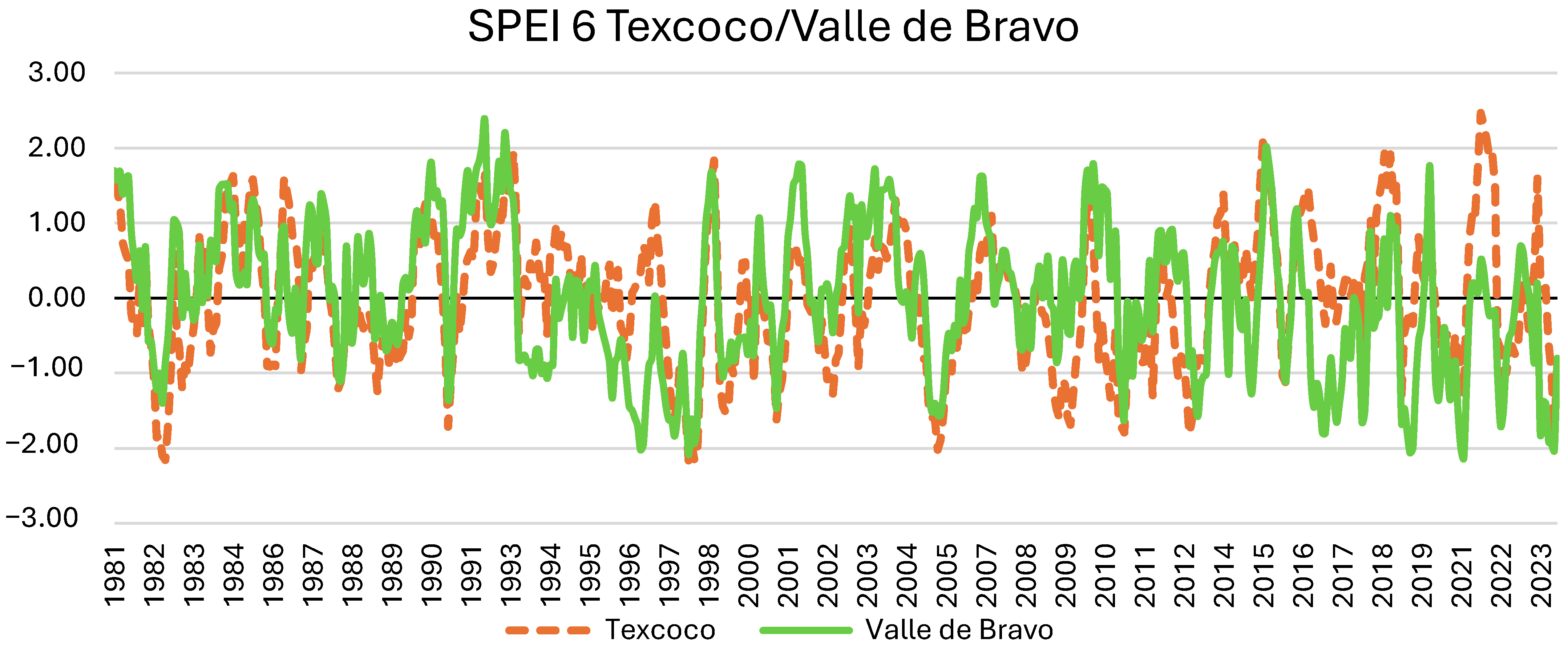
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Smakhtin, V.U.; Schipper, E.L.F. Droughts: The impact of semantics and perceptions. Water Policy 2008, 10, 131. [Google Scholar] [CrossRef]
- Stahl, K.; Kohn, I.; Blauhut, V.; Urquijo, J.; de Stefano, L.; Acácio, V.; Dias, S.; Stagge, J.H.; Tallaksen, L.M.; Kampragou, E.; et al. Impacts of European drought events: Insights from an international database of text-based reports. Nat. Hazards Earth Syst. Sci. 2016, 16, 801–819. [Google Scholar] [CrossRef]
- Dai, A. Drought under global warming: A review. WIREs Clim Chang. 2011, 2, 45–65. [Google Scholar] [CrossRef]
- Zhang, Q.; Yao, Y.B.; Li, Y.H.; Huang, J.P.; Ma, Z.G.; Wang, Z.L.; Wang, S.P.; Wang, Y.; Zhang, Y. Progress and prospect on the study of causes and variation regularity of droughts in China. Acta Meteorol. Sin. 2020, 78, 500–521. [Google Scholar] [CrossRef]
- Meyer, S.J.; Hubbard, K.G.; Wilhite, D.A. A crop-specific drought index for corn: I. Model development and validation. Agron. J. 1993, 85, 388–395. [Google Scholar] [CrossRef]
- Calviño, P.A.; Andrade, F.H.; Sadras, V.O. Maize yield as affected by water availability, soil depth, and crop management. Agron. J. 2003, 95, 275–281. [Google Scholar] [CrossRef]
- Hunt, E.D.; Svoboda, M.; Wardlow, B.; Hubbard, K.; Hayes, M.; Arkebauer, T. Monitoring the effects of rapid onset of drought on non-irrigated maize with agronomic data and climate-based drought indices. Agric. For. Meteorol. 2014, 191, 1–11. [Google Scholar] [CrossRef]
- Real-Rangel, R.A.; Pedrozo-Acuña, A.; Breña-Naranjo, J.A.; Alcocer-Yamanaka, V.H. Monitorización de sequías en México a través del índice estandarizado multivariado de sequía. In Proceedings of the XXIV Congreso Nacional de Hidráulica, Acapulco, Guerrero, México, 22–25 March 2017. [Google Scholar]
- Wilhite, D.A. Drought as a natural hazard: Concepts and definitions. In Drought: A Global Assessment; Wilhite, D., Ed.; Routledge: London, UK, 2000; Volume 1, pp. 3–18. [Google Scholar]
- Burton, I.; Kates, R.W.; White, G.F. The Environment as Hazard; Oxford University Press: New York, NY, USA, 1978; 240p. [Google Scholar]
- Sun, Y.; Chen, X.; Yu, Y.; Qian, J.; Wang, M.; Huang, S.; Xing, X.; Song, S.; Sun, X. Spatiotemporal Characteristics of Drought in Central Asia from 1981 to 2020. Atmosphere 2022, 13, 1496. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; American Meteorological Society: Boston, MA, USA, 1993; pp. 179–183. [Google Scholar]
- Guttman, N.B. Comparing the Palmer drought index and the Standardized Precipitation Index. J. Am. Water Resour. Assoc. 1998, 34, 113–121. [Google Scholar] [CrossRef]
- WMO. Drought Monitoring and Early Warning: Concepts, Progress and Future Challenges; WMO: Geneva, Switzerland, 2006. [Google Scholar]
- Hayes, M.; Svoboda, M.; Wall, N.; Widhalm, M. The Lincoln declaration on drought indices: Universal meteorological drought index recommended. Bull. Am. Meteorol. Soc. 2011, 92, 485–488. [Google Scholar] [CrossRef]
- Hao, Z.; AghaKouchak, A.; Phillips, T.J. Changes in concurrent monthly precipitation and temperature extremes. Environ. Res. Lett. 2013, 8, 034014. [Google Scholar] [CrossRef]
- Ren, L.; Zhou, T.; Zhang, W. Attribution of the record-breaking heat event over Northeast Asia in summer 2018: The role of circulation. Environ. Res. Lett. 2020, 15, 054018. [Google Scholar] [CrossRef]
- Wang, L.Y.; Yuan, X. Two types of flash drought and their connections with seasonal drought. Adv. Atmos. Sci. 2018, 35, 1478–1490. [Google Scholar] [CrossRef]
- Yuan, X.; Wang, Y.M.; Zhang, M.; Wang, L.Y. A few thoughts on the study of flash drought (in Chinese). Trans. Atmos. Sci. 2020, 43, 1086–1095. [Google Scholar]
- Monitor de Sequía en México. Servicio Meteorológico Nacional. 2024. Available online: https://smn.conagua.gob.mx/es/climatologia/monitor-de-sequia/monitor-de-sequia-en-mexico (accessed on 30 October 2024).
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multi-scalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index—SPEI. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Castillo-Castillo, M.; Ibáñez-Castillo, L.; Valdés, J.B.; Arteaga-Ramirez, R. Análisis de sequías meteorológicas en la cuenca del río Fuerte, México. Tecnol. Y Cienc. Del Agua 2017, 8, 35–52. [Google Scholar] [CrossRef]
- Hernández-Vásquez, C.C.; Ibáñez-Castillo, L.A.; Gómez-Díaz, J.D.; Arteaga-Ramírez, R. Analysis of meteorological droughts in the Sonora River basin Mexico. Atmósfera 2022, 35, 467–482. [Google Scholar] [CrossRef]
- Dinku, T.; Funk, C.; Peterson, P.; Maidment, R.; Tadesse, T.; Gadain, H.; Ceccato, P. Validation of the CHIRPS satellite rainfall estimates over eastern Africa. Q. J. R. Meteorol. Soc. 2018, 144 (Suppl. 1), 292–312. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards group infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
- CONAGUA (Comisión Nacional del Agua). Programa de medidas preventivas y de mitigación de la sequía. In Consejo de Cuenca ríos Fuerte y Sinaloa; Comisión Nacional del Agua, Secretaría de Medio Ambiente y Recursos Naturales: Ciudad de México, Mexico, 2014; p. 262. [Google Scholar]
- INEGI Monografías. 2024. Available online: https://cuentame.inegi.org.mx/monografias/ (accessed on 4 November 2024).
- INEGI (Instituto Nacional de Estadística, Geografía e Informática). 2020 Censo de Población y Vivienda. México. 2023. Available online: https://www.inegi.org.mx/datosabiertos/ (accessed on 10 September 2023).
- Guijarro, J.A. Climatol: A software tool for the validation and analysis of climate data. Environ. Model. Softw. 2018, 105, 1–10. [Google Scholar]
- Kuya, E.K.; Gjelten, H.M.; Tveito, O.E. Homogenization of Norwegian monthly precipitation series for the period 1961–2018. Adv. Sci. Res. 2022, 19, 73–80. [Google Scholar] [CrossRef]
- Tudorache, G. Analysing the homogeneity of air temperature, relative air humidity, precipitation and wind data series using ‘Climatol’ and meteorological metadata. Aerul Şi Apa Compon. Ale Mediului. 2017, 2017, 50–57. [Google Scholar] [CrossRef]
- HydroGeoLogic, Inc. -OU-1 Informe Anual de Monitoreo de Aguas Subterráneas de 2004; HydroGeoLogic, Inc.: Antiguo Fort Ord, CA, USA, 2005. [Google Scholar]
- Kendall, M.G. Rank Correlation Methods; Charles Griffin: London, UK, 1975; p. 120. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Yu, J.-Y.; Kao, H.-Y. Decadal changes of El Niño persistence barrier in SST and ocean heat content indices: 1958–2001. Geophys. Res. Lett. 2007, 112, D13106. [Google Scholar] [CrossRef]
- Silva, D.G. Evolução Paleoambiental dos Depósitos de Tanques em Fazenda Nova, Município de Brejo da Madre de Deus—Pernambuco. Master’s Thesis, UFPE, Recife, Brazil, 2007. [Google Scholar]
- Climate Engine. Desert Research Institute and University of California, Merced. version 2.1. 2024. Available online: http://climateengine.org (accessed on 7 April 2024).
- Funk, C.; Michaelsen, J.; Marshall, M. Mapping recent decadal climate variations in precipitation and temperature across Eastern Africa and the Sahel. In Remote Sensing of Drought—Innovative Monitoring Approaches; Wardlow, B., Anderson, M., Verdin, J., Eds.; Taylor and Francis: London, UK, 2012; pp. 331–357. [Google Scholar]
- Funk, C.; Verdin, J.; Michaelsen, J.; Peterson, P.; Pedreros, D.; Husak, G. A global satellite assisted precipitation climatology. Earth Syst. Sci. Data Discuss. 2015, 7, 1–13. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Rowland, J.; Romero, B.; Husak, G.; Michaelsen, J.; Verdin, A. A quasi-global precipitation time series for drought monitoring. U.S. Geol. Surv. Data Ser. 2014, 832, 4. [Google Scholar] [CrossRef]
- Maidment, R.; Grimes, D.; Black, E.; Tarnavsky, E.; Young, M.; Greatrex, H.; Allan, R.P.; Stein, T.; Nkonde, E.; Senkunda, S.; et al. A new, long-term daily satellite-based rainfall dataset for operational monitoring in Africa. Sci. Data 2017, 4, 170063. [Google Scholar] [CrossRef]
- Thornton, M.M.; Shrestha, R.; Wei, Y.; Thornton, P.E.; Kao, S.-C.; Wilson, B.E. Daymet: Daily Surface Weather Data on a 1-km Grid for North America, Version 4 R1; ORNL DAAC: Oak Ridge, TN, USA, 2022. [Google Scholar] [CrossRef]
- McMahon, T.A.; Peel, M.C.; Lowe, L.; Srikanthan, R.; McVicar, T.R. Estimating actual, potential, reference crop and pan evaporation using standard meteorological data: A pragmatic synthesis. Hydrol. Earth Syst. Sci. 2013, 17, 1331–1363. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference Crop Evapotranspiration from Ambient Air Temperature; American Society of Agricultural Engineers: St. Joseph, MI, USA, 1985; pp. 96–99. [Google Scholar]
- Allen, R.; Pereira, L.; Raes, D.; Smith, M. Crop evapotranspiration. In FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 10. [Google Scholar]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather. Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Jensen, M.E. Consumptive Use of Water and Irrigation Water Requirements; American Society of Civil Engineers: New York, NY, USA, 1973. [Google Scholar]
- Amatya, D.; Skaggs, R.; Gregory, J. Comparison of methods for estimating REF-ET. J. Irrig. Drain. Div. ASCE 1995, 121, 427–435. [Google Scholar] [CrossRef]
- WFD; Hadley Centre for Climate Prediction and Research/Met Office/Ministry of Defence/United Kingdom. WATer and global CHange (WATCH) Forcing Data (WFD)—20th Century. In Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory; NCAR: Boulder, CO, USA, 2018. [Google Scholar] [CrossRef]
- NIDIS, National Integrated Drought Information System, US Government. Drought Basics. 2025. Available online: https://www.drought.gov/what-is-drought/drought-basics (accessed on 3 February 2025).
- Wells, N.; Goddard, S.; Hayes, M.J. A self-calibrating Palmer Drought Severity Index. J. Clim. 2004, 17, 2335–2351. [Google Scholar] [CrossRef]
- Moazzam, M.F.U.; Rahman, G.; Munawar, S.; Farid, N.; Lee, B.G. Spatiotemporal Rainfall Variability and Drought Assessment during Past Five Decades in South Korea Using SPI and SPEI. Atmosphere 2022, 13, 292. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; National Center for Atmospheric Research Staff. (Eds.) The Climate Data Guide: Standardized Precipitation Evapotranspiration Index (SPEI). 2024. Available online: https://climatedataguide.ucar.edu/climate-data/standardized-precipitation-evapotranspiration-index-spei (accessed on 19 April 2023).
- Keyantash, J.; Dracup, J. The quantification of drought: An evaluation of drought indices. Bull. Am. Meteorol. Soc. 2002, 83, 1167–1180. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente, S.; Calculation of the Standardized Precipitation-Evapotranspiration Index. Package SPEI.R for R or RStudio Program. 2014. Available online: https://cran.r-project.org/web/packages/SPEI/index.html (accessed on 14 May 2023).
- RStudio, Inc. RStudio® Version 2023.03.1; RStudio, Inc.: Boston, MA, USA, 2023. [Google Scholar]
- Sung, J.H.; Park, J.; Jeon, J.-J.; Seo, S.B. Assessment of inter-model variability in meteorological drought characteristics using CMIP5 GCMs over South Korea. KSCE J. Civ. Eng. 2020, 24, 2824–2834. [Google Scholar] [CrossRef]
- Jang, D. Assessment of meteorological drought indices in Korea using RCP 8.5 scenario. Water 2018, 10, 283. [Google Scholar] [CrossRef]
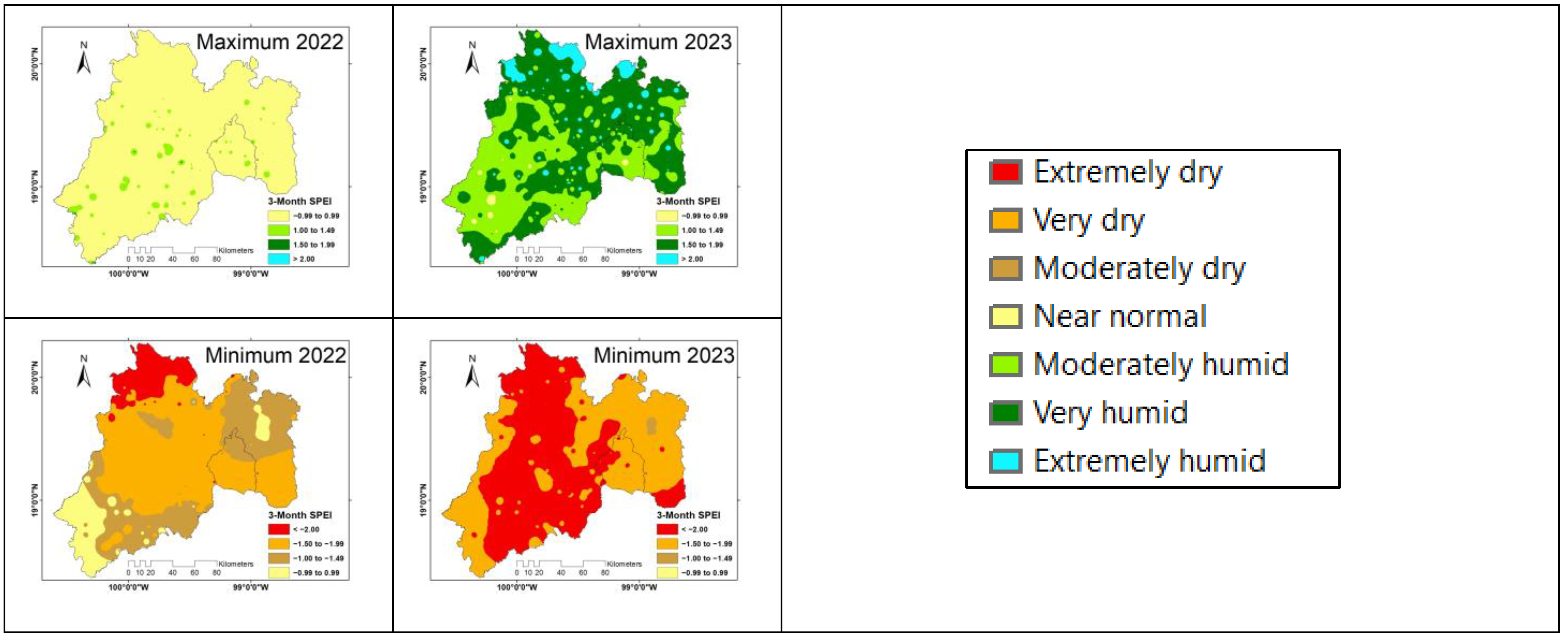
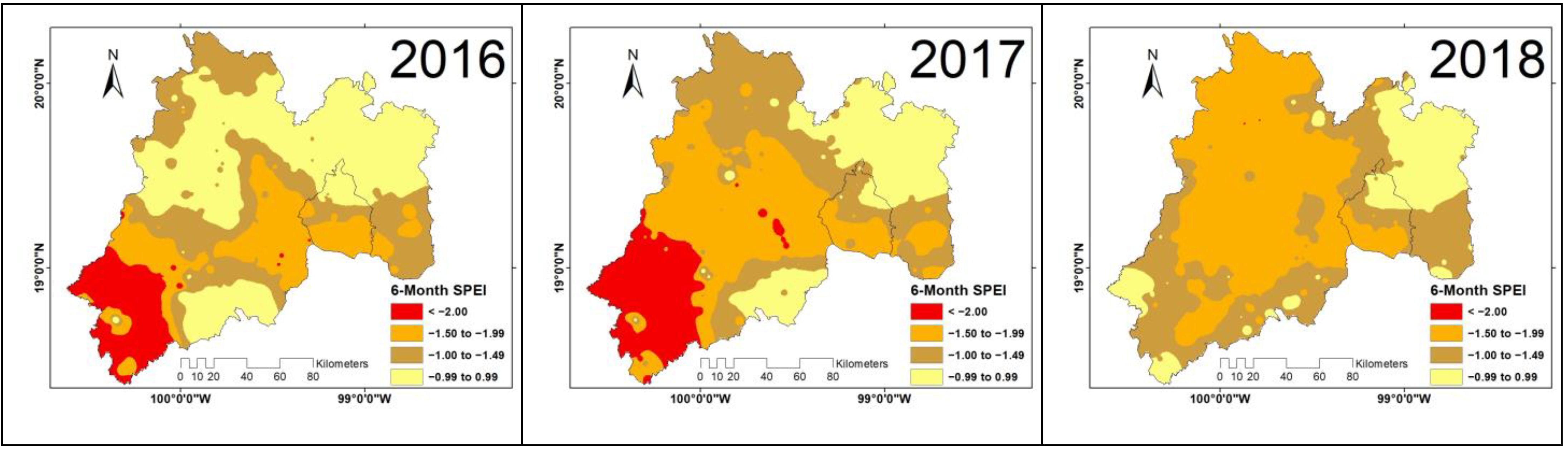
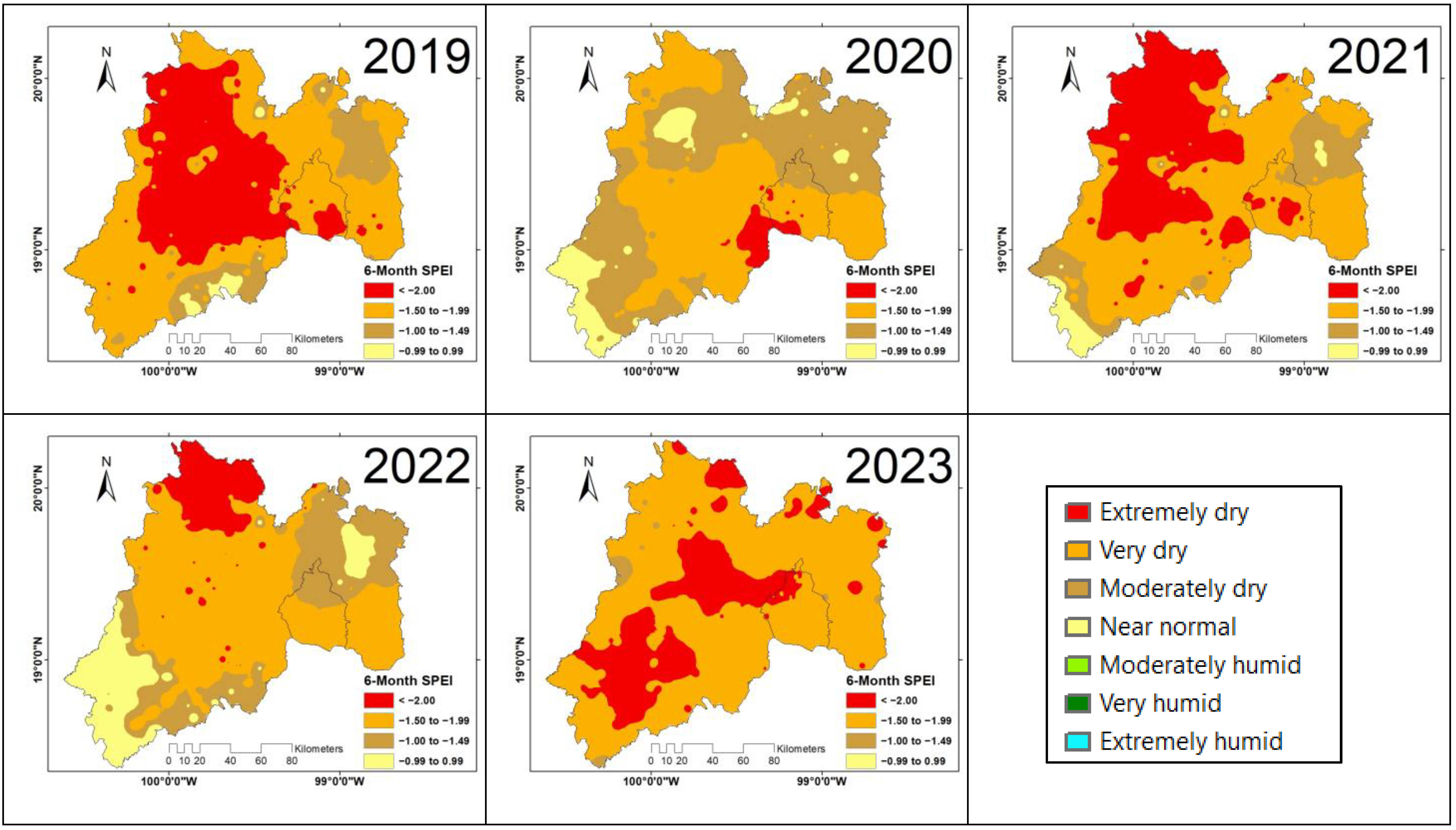
| Index Value | Category |
|---|---|
| >2.00 | Extremely humid |
| 1.50 to 1.99 | Very humid |
| 1.00 to 1.49 | Moderately humid |
| −0.99 to 0.99 | Near normal |
| −1.00 to −1.49 | Moderately dry |
| −1.50 to −1.99 | Very dry |
| <−2.00 | Extremely dry |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carrillo-Carrillo, M.; Ibáñez-Castillo, L.; Arteaga-Ramírez, R.; Arévalo-Galarza, G. Spatio-Temporal Analysis of Drought with SPEI in the State of Mexico and Mexico City. Atmosphere 2025, 16, 202. https://doi.org/10.3390/atmos16020202
Carrillo-Carrillo M, Ibáñez-Castillo L, Arteaga-Ramírez R, Arévalo-Galarza G. Spatio-Temporal Analysis of Drought with SPEI in the State of Mexico and Mexico City. Atmosphere. 2025; 16(2):202. https://doi.org/10.3390/atmos16020202
Chicago/Turabian StyleCarrillo-Carrillo, Mauricio, Laura Ibáñez-Castillo, Ramón Arteaga-Ramírez, and Gustavo Arévalo-Galarza. 2025. "Spatio-Temporal Analysis of Drought with SPEI in the State of Mexico and Mexico City" Atmosphere 16, no. 2: 202. https://doi.org/10.3390/atmos16020202
APA StyleCarrillo-Carrillo, M., Ibáñez-Castillo, L., Arteaga-Ramírez, R., & Arévalo-Galarza, G. (2025). Spatio-Temporal Analysis of Drought with SPEI in the State of Mexico and Mexico City. Atmosphere, 16(2), 202. https://doi.org/10.3390/atmos16020202







