Analyzing the Precise Point Positioning Performance of Different Dual-Frequency Ionospheric-Free Combinations with BDS-3 and Galileo
Abstract
:1. Introduction
2. Materials and Methods
2.1. Ionosphere-Free PPP Observation Model
2.2. Selected BDS-3 and Galileo DFIF Combinations
3. Experimental Setup
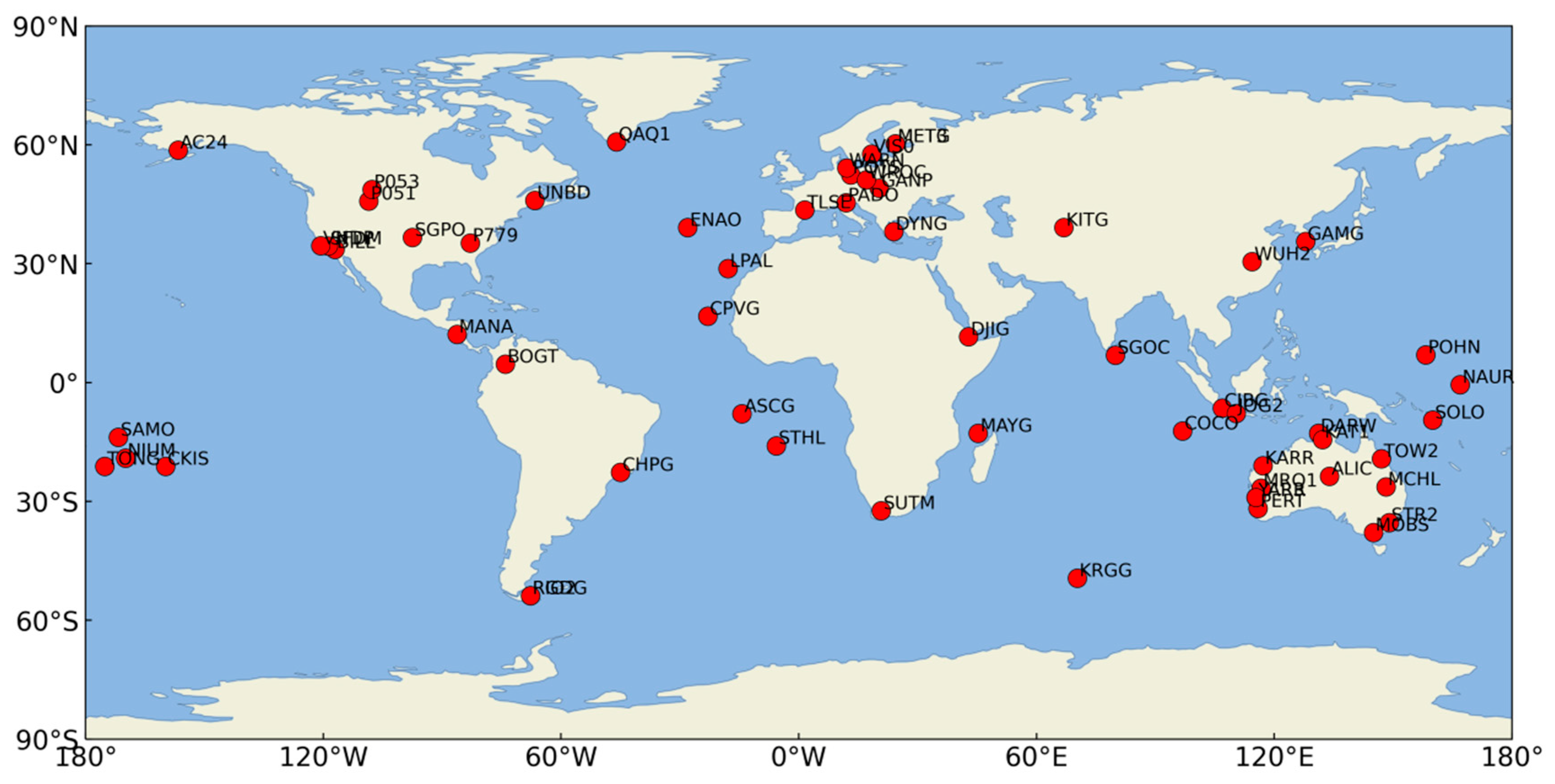
3.1. Observation Dataset
3.2. Processing Strategy
4. Results
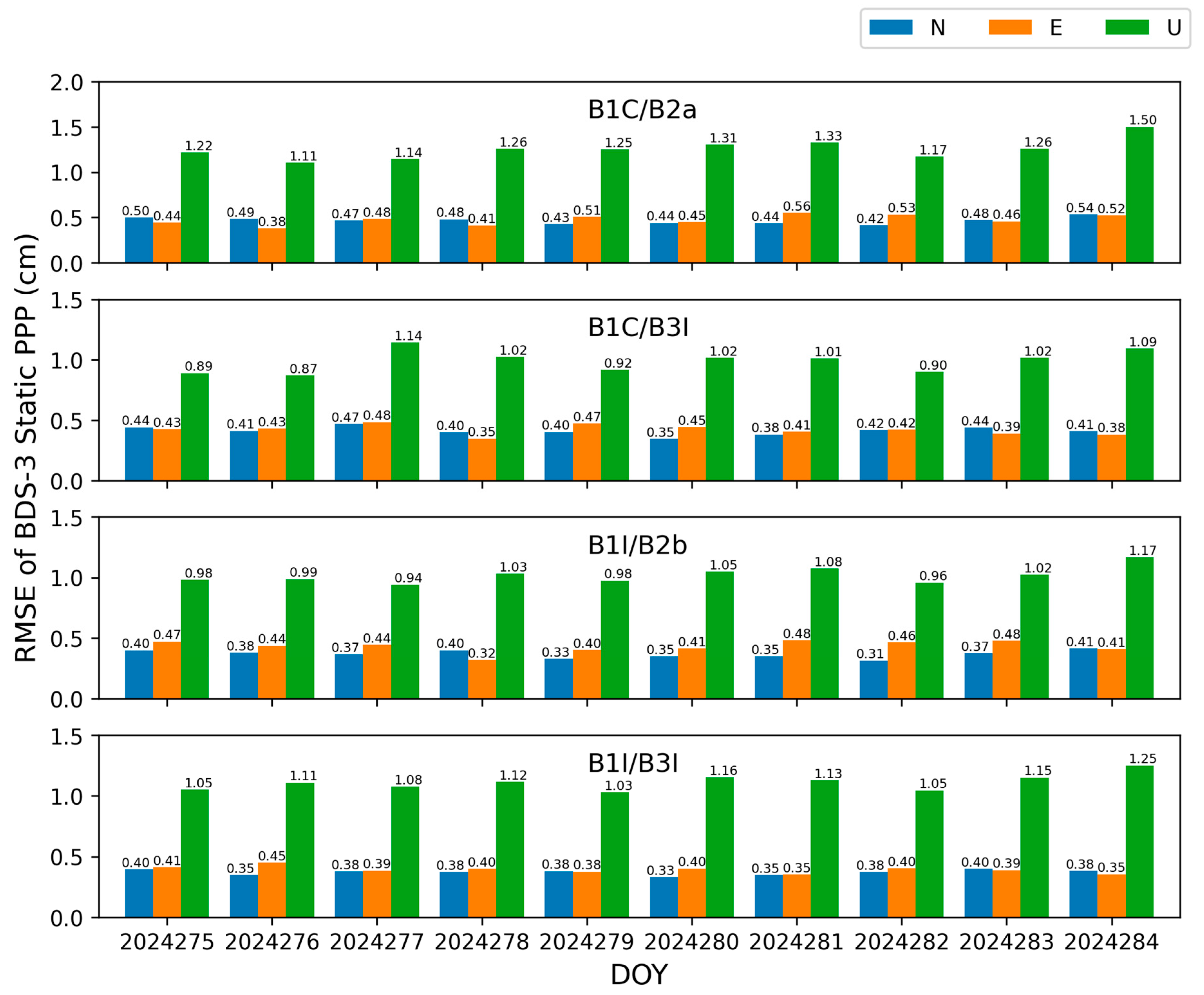
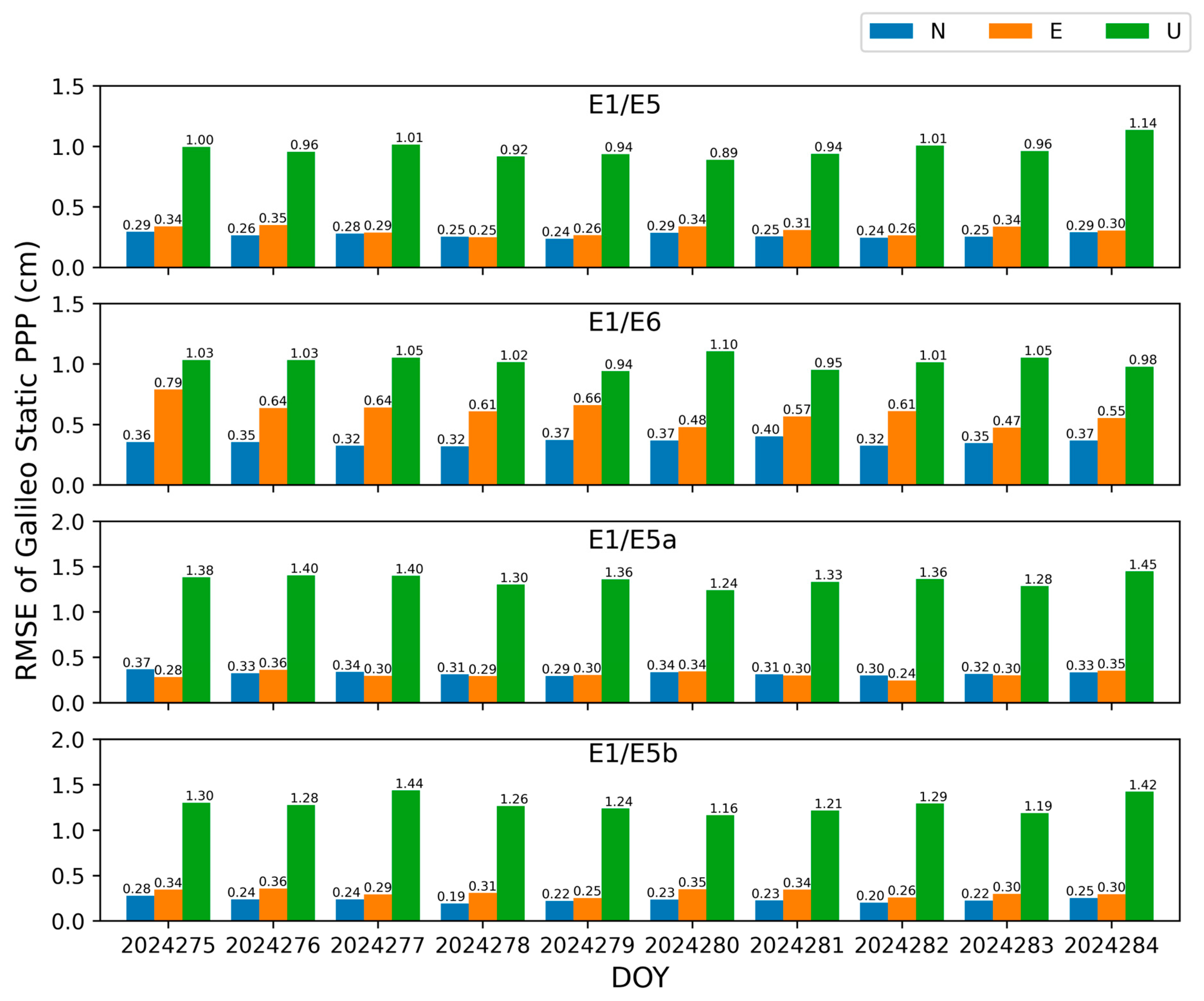
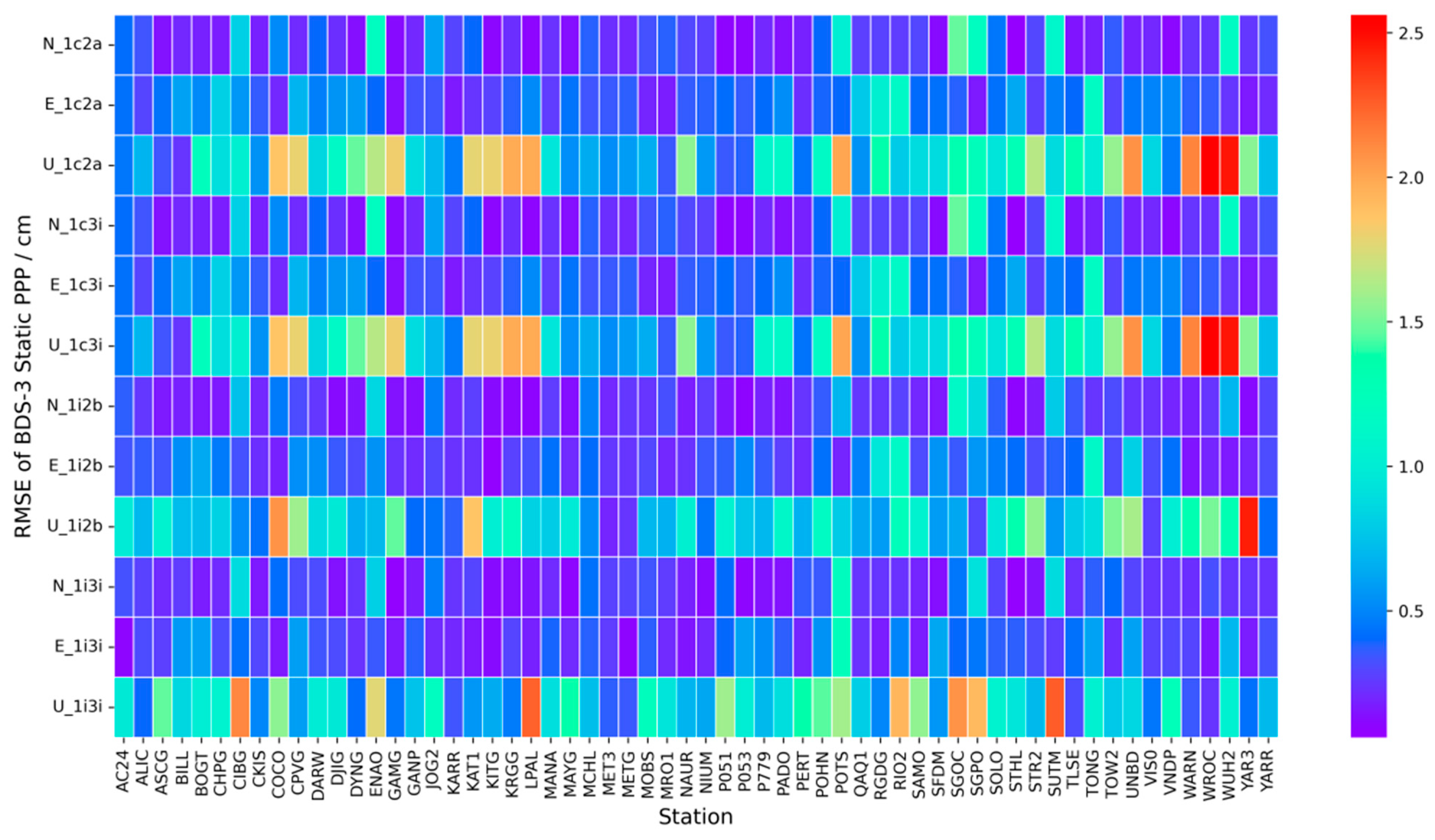
4.1. Static Results
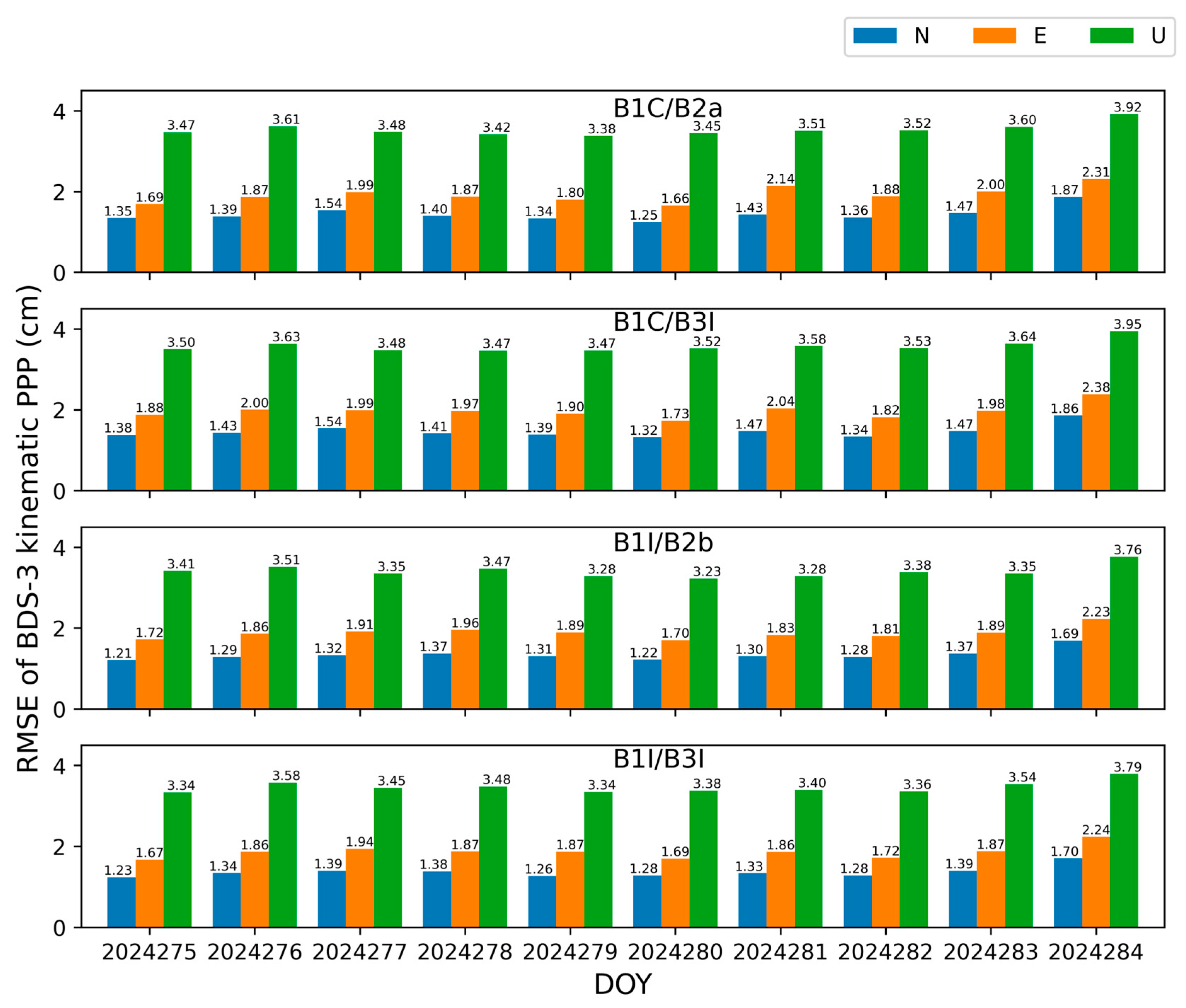
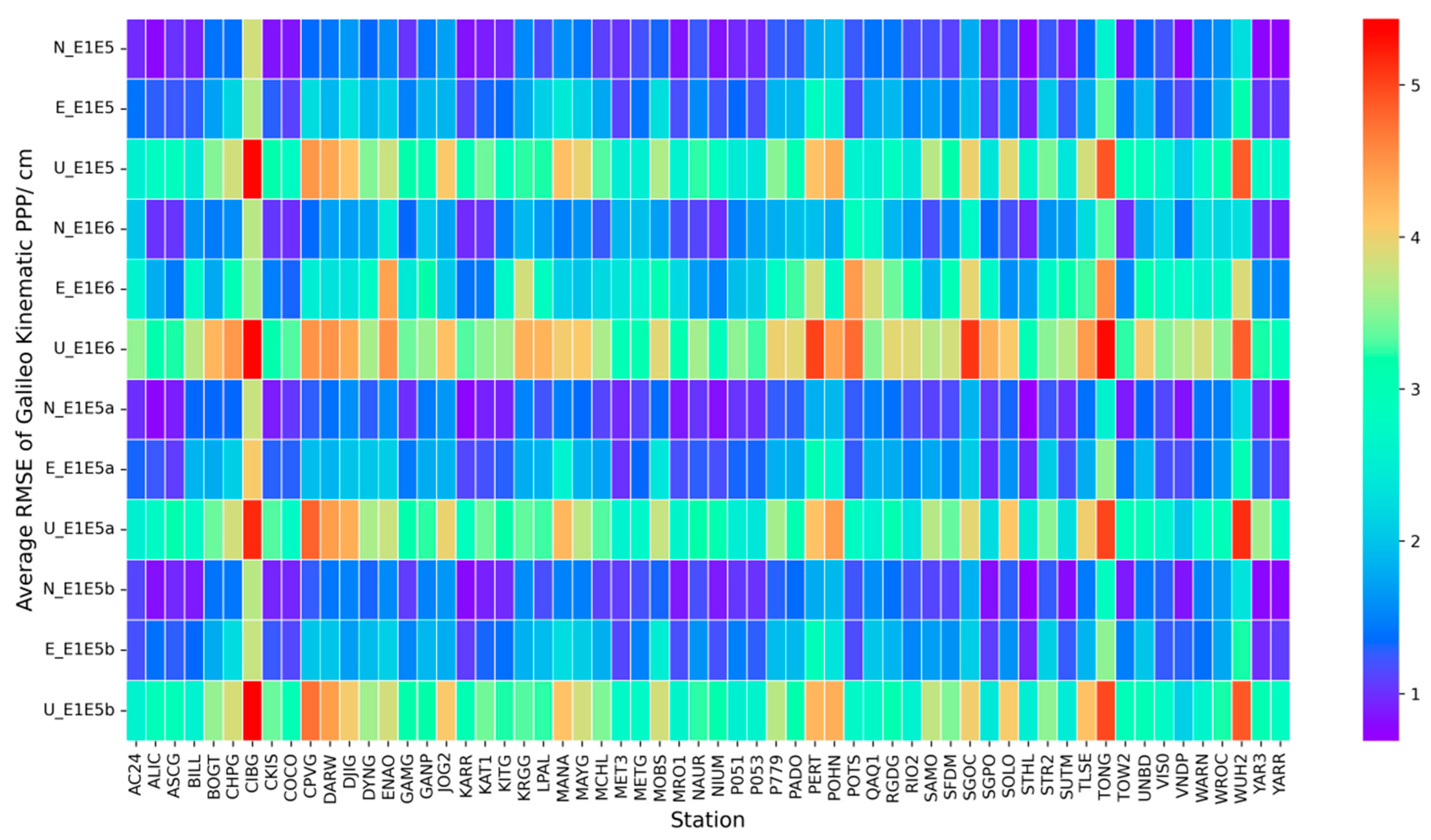
4.2. Kinematic Results
5. Discussion
6. Conclusions
- (1)
- The PPP DFIF combinations of BDS-3 are competitive with those of Galileo. Both BDS-3 and Galileo can achieve independent PPP globally in static and kinematic modes.
- (2)
- Among the four combinations of BDS-3-only, B1C/B3I showed the best performance in PPP accuracy, with an RMSE of the NEU components of 0.41 cm, 0.42 cm, and 0.99 cm, respectively. B1C/B2a performed the worst, with an RMSE of the NEU components of 0.47 cm, 0.48 cm, and 1.26 cm, respectively, in static mode. Among the four combinations of Galileo-only, E1/E5 showed the best performance in PPP accuracy, with the RMSE of the NEU components being 0.27 cm, 0.31 cm, and 0.98 cm, respectively; E1/E5a performed the worst, with the RMSE of the NEU components being 0.32 cm, 0.31 cm, and 1.35 cm, respectively, in static mode.
- (3)
- Similarly to the analysis of static mode, among the four BDS-3-only combinations, B1I/B2b showed the best performance in PPP accuracy, with the RMSE of the NEU components being 1.34 cm, 1.88 cm, and 3.40 cm, respectively. B1C/B2a performed the worst, with the RMSE of the NEU components being 1.44 cm, 1.92 cm, and 3.53 cm, respectively, in kinematic mode. Among the four Galileo-only combinations, E1/E5 showed the best performance in PPP accuracy, with the RMSE of the NEU components being 1.28 cm, 1.71 cm, and 3.25 cm, respectively. E1/E6 performed the worst, with the RMSE of the NEU components being 1.70 cm, 2.60 cm, and 3.85 cm, respectively, in kinematic mode.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Receiver | JAVAD TRE_3S/TRE_3 | JAVAD TRE_3 DELTA | |
|---|---|---|---|
| Autonomous | <2 m | <2 m | |
| Static, Fast Static accuracy | H | 0.3 cm + 0.1 ppm | 0.3 cm + 0.1 ppm |
| V | 0.35 cm + 0.4 ppm | 0.35 cm + 0.4 ppm | |
| Kinematic accuracy | H | 1 cm + 1 ppm | 1 cm + 1 ppm |
| V | 1.5 cm + 1 ppm | 1.5 cm + 1.5 ppm | |
| RTK (OTF) accuracy | H: | 1 cm + 1 ppm | 1 cm + 1 ppm |
| V | 1.5 cm + 1. ppm | 1.5 cm + 1.5 ppm | |
| Receiver | TRIMBLE ALLOY | |
|---|---|---|
| Differential positioning | H | 0.25 m + 1 ppm RMS |
| V | 0.50 m + 1 ppm RMS | |
| SBAS differential positioning | H | 0.50 m RMS |
| V | 0.85 m RMS | |
| High-precision static | H | 3 mm + 0.1 ppm RMS |
| V | 3.5 mm + 0.4 ppm RMS | |
| Static and fast static | H | 3 mm + 0.5 ppm RMS |
| V | 5 mm + 0.5 ppm RMS | |
| Single baseline (<30 km) RTK | H | 8 mm + 1 ppm RMS |
| V | 15 mm + 1 ppm RMS | |
| Network RTK | H | 8 mm + 0.5 ppm RMS |
| V | 8 mm + 0.5 ppm RMS | |
| Initialization time | Typically <10 s | |
| Initialization reliability | Typically >99.9% | |
| Receiver | LEICA GR30/LEICA GR50 | |||
|---|---|---|---|---|
| Code Differential | H: 0.25m + 1 ppm, V: 0.5m +1 ppm | |||
| Site Monitor | RTK Positioning modes | Reference station (smoothed) | Monitoring (instantaneous) | Network RTK (instantaneous] |
| Single baseline (<30 km) | H: 6 mm + 1 ppm, V: 10 mm +1 ppm | H: 8 mm + 1 ppm, V: 15 mm +1 ppm | H: 8 mm + 1 ppm, V: 15 mm +1 ppm | |
| VRS, FKP, iMAX, MAC (RTCM SC 104) | H: 6 mm + 0.5 ppm, V: 10 mm +0.5 ppm | H: 8 mm + 0.5 ppm, V: 15 mm +0.5 ppm | H: 8 mm + 0.5 ppm, V: 15 mm +0.5 ppm | |
| Time for initialization (typical) | 10 s | 10 s | 4 s | |
| Speed and Displacement Measurement (VADASE) | Velocity | H: 0.003 m/s, V: 0.005 m/s. | ||
| displacement engine (typical) | H: 1 cm/s, V: 2 cm/s | |||
| Receiver | SEPT POLARX5 | SEPT POLARX5TR | SEPT POLARX5S | SEPT ASTERX4 |
|---|---|---|---|---|
| Application scenario | Multi-frequency GNSS Reference Receiver | Multi-frequency GNSS Time and Frequency Transfer Receiver | Ionospheric Monitoring GNSS Receiver | Multi-frequency dual-antenna receiver |
| Measurement precision | Carrier phase: All signals 1–1.3 mm | Code < 0.5 ns Phase < 5 ps | Phi60 noise floor: 0.03 rad | - |
| Position accuracy | Static high precision H: 3 mm + 0.1 ppm V: 3.5 mm + 0.4 ppm | - | - | RTK H: 0.6 cm + 0.5 ppm V: 1 cm + 1 ppm |
| Time accuracy | 1 PPS out 5: ns | 1 PPS out: 5 ns | - | xPPS out: 10 ns |
| Time to first fix | Cold start < 45 s Warm start < 20 s | - | - | Cold start < 45 s Warm start < 20 s |
| Tracking performance | Tracking 20 db Hz, Acquisition 33 db Hz | |||
| Receiver | Stonex SC2200 | ||
|---|---|---|---|
| Position accuracy | Static | H: 3 mm + 0.1 ppm | V: 3.5 mm + 1 ppm |
| RTK | H: 15 mm + 1 ppm | V: 15 mm + 1 ppm | |
| Initialization time: | <10s | ||
| Initialization reliability | >99.9% | ||
References
- Rebeiz, G.M. RF MEMS: Theory, Design, and Technology; Wiley: New York, NY, USA, 2003. [Google Scholar]
- Titterton, D.H.; Weston, J.L. Strapdown Inertial Navigation Technology; Aerospace & Electronic Systems Magazine IEEE; The Institution of Engineering and Technology: Stevenage, UK, 2004. [Google Scholar] [CrossRef]
- Suvorkin, V.; Garcia-Fernandez, M.; González-Casado, G.; Li, M.; Rovira-Garcia, A. Assessment of Noise of MEMS IMU Sensors of Different Grades for GNSS/IMU Navigation. Sensors 2024, 24, 1953. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Ouyang, C.; Huang, Y.; Peng, W. Assessment of BDS-3 Global Positioning Service: Ephemeris, SPP, PPP, RTK, and New Signal. GPS Solut. 2020, 24, 81. [Google Scholar] [CrossRef]
- Rovira-Garcia, A.; Juan, J.M.; Sanz, J.; Gonzalez-Casado, G. A Worldwide Ionospheric Model for Fast Precise Point Positioning. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4596–4604. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J.G.; Odijk, D. Combined BDS, Galileo, QZSS and GPS Single-Frequency RTK. GPS Solut. 2015, 19, 151–163. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Odolinski, R.; Odijk, D. Instantaneous BeiDou+GPS RTK Positioning with High Cut-off Elevation Angles. J. Geod. 2014, 88, 335–350. [Google Scholar] [CrossRef]
- He, X.; Zhang, X.; Tang, L.; Liu, W. Instantaneous Real-Time Kinematic Decimeter-Level Positioning with BeiDou Triple-Frequency Signals over Medium Baselines. Sensors 2015, 16, 1. [Google Scholar] [CrossRef] [PubMed]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Malys, S.; Jensen, P.A. Geodetic Point Positioning with GPS Carrier Beat Phase Data from the CASA UNO Experiment. Geophys. Res. Lett. 1990, 17, 651–654. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS Carrier-Phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Aginiparthi, A.S.; Vankadara, R.K.; Mokkapati, R.K.; Panda, S.K. Evaluating the Single-Frequency Static Precise Point Positioning Accuracies from Multi-Constellation GNSS Observations at an Indian Low-Latitude Station. J. Appl. Geod. 2024, 18, 699–707. [Google Scholar] [CrossRef]
- Cai, C.; Gao, Y. Modeling and Assessment of Combined GPS/GLONASS Precise Point Positioning. GPS Solut. 2013, 17, 223–236. [Google Scholar] [CrossRef]
- Yue, C.; Dang, Y.; Xue, S.; Wang, H.; Gu, S.; Xu, C. A New Optimal Subset Selection Method of Partial Ambiguity Resolution for Precise Point Positioning. Remote Sens. 2022, 14, 4819. [Google Scholar] [CrossRef]
- Pan, Y.; Geng, J.; Liu, K.; Chen, X.; Fang, R. Evaluation of Rapid Phase Clock/Bias Products for PPP Ambiguity Resolution and Its Application to the M7.1 2019 Ridgecrest, California Earthquake. Adv. Space Res. 2020, 65, 2586–2594. [Google Scholar] [CrossRef]
- Kim, H.; Hyun, C.-U.; Park, H.-D.; Cha, J. Image Mapping Accuracy Evaluation Using UAV with Standalone, Differential (RTK), and PPP GNSS Positioning Techniques in an Abandoned Mine Site. Sensors 2023, 23, 5858. [Google Scholar] [CrossRef] [PubMed]
- Goudarzi, M.A.; Banville, S. Application of PPP with Ambiguity Resolution in Earth Surface Deformation Studies: A Case Study in Eastern Canada. Surv. Rev. 2018, 50, 531–544. [Google Scholar] [CrossRef]
- Meng, X.; Wang, J.; Han, H. Optimal GPS/Accelerometer Integration Algorithm for Monitoring the Vertical Structural Dynamics. J. Appl. Geod. 2014, 8, 265–272. [Google Scholar] [CrossRef]
- Guo, J.; Li, X.; Li, Z.; Hu, L.; Yang, G.; Zhao, C.; Fairbairn, D.; Watson, D.; Ge, M. Multi-GNSS Precise Point Positioning for Precision Agriculture. Precis. Agric. 2018, 19, 895–911. [Google Scholar] [CrossRef]
- Zhang, X.; Li, P.; Zuo, X. Kinematic Precise Orbit Determination Based on Ambiguity-Fixed PPP. Geomat. Inf. Sci. Wuhan Univ. 2013, 38, 1009–1013. [Google Scholar]
- Grayson, B.; Penna, N.T.; Mills, J.P.; Grant, D.S. GPS Precise Point Positioning for UAV Photogrammetry. Photogramm. Record. 2018, 33, 427–447. [Google Scholar] [CrossRef]
- Zhang, B.; Ou, J.; Yuan, Y.; Li, Z. Extraction of Line-of-Sight Ionospheric Observables from GPS Data Using Precise Point Positioning. Sci. China Earth Sci. 2012, 55, 1919–1928. [Google Scholar] [CrossRef]
- Zhang, F.; Tang, L.; Li, J.; Du, X. A Simple Approach to Determine Single-Receiver Differential Code Bias Using Precise Point Positioning. Sensors 2023, 23, 8230. [Google Scholar] [CrossRef] [PubMed]
- Geng, J.; Bock, Y. Triple-Frequency GPS Precise Point Positioning with Rapid Ambiguity Resolution. J. Geod. 2013, 87, 449–460. [Google Scholar] [CrossRef]
- Lou, Y.; Zheng, F.; Gu, S.; Wang, C.; Guo, H.; Feng, Y. Multi-GNSS Precise Point Positioning with Raw Single-Frequency and Dual-Frequency Measurement Models. GPS Solut. 2016, 20, 849–862. [Google Scholar] [CrossRef]
- Afifi, A.; El-Rabbany, A. Performance Analysis of Several GPS/Galileo Precise Point Positioning Models. Sensors 2015, 15, 14701–14726. [Google Scholar] [CrossRef]
- Li, P.; Jiang, X.; Zhang, X.; Ge, M.; Schuh, H. GPS + Galileo + BeiDou Precise Point Positioning with Triple-Frequency Ambiguity Resolution. GPS Solut. 2020, 24, 78. [Google Scholar] [CrossRef]
- Chen, C.; Xiao, G.; Chang, G.; Xu, T.; Yang, L. Assessment of GPS/Galileo/BDS Precise Point Positioning with Ambiguity Resolution Using Products from Different Analysis Centers. Remote Sens. 2021, 13, 3266. [Google Scholar] [CrossRef]
- Hou, Z.; Zhou, F. Assessing the Performance of Precise Point Positioning (PPP) with the Fully Serviceable Multi-GNSS Constellations: GPS, BDS-3, and Galileo. Remote Sens. 2023, 15, 807. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Dai, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Accuracy and Reliability of Multi-GNSS Real-Time Precise Positioning: GPS, GLONASS, BeiDou, and Galileo. J. Geod. 2015, 89, 607–635. [Google Scholar] [CrossRef]
- Liu, T.; Yuan, Y.; Zhang, B.; Wang, N.; Tan, B.; Chen, Y. Multi-GNSS Precise Point Positioning (MGPPP) Using Raw Observations. J. Geod. 2017, 91, 253–268. [Google Scholar] [CrossRef]
- Zhou, F.; Cao, X.; Ge, Y.; Li, W. Assessment of the Positioning Performance and Tropospheric Delay Retrieval with Precise Point Positioning Using Products from Different Analysis Centers. GPS Solut. 2020, 24, 12. [Google Scholar] [CrossRef]
- Li, M.; Qu, L.; Zhao, Q.; Guo, J.; Su, X.; Li, X. Precise Point Positioning with the BeiDou Navigation Satellite System. Sensors 2014, 14, 927–943. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.; Zhang, X.; Wang, J.; Ren, X. Modeling and Assessment of Triple-Frequency BDS Precise Point Positioning. J. Geod. 2016, 90, 1223–1235. [Google Scholar] [CrossRef]
- Xia, F.; Ye, S.; Xia, P.; Zhao, L.; Jiang, N.; Chen, D.; Hu, G. Assessing the Latest Performance of Galileo-Only PPP and the Contribution of Galileo to Multi-GNSS PPP. Adv. Space Res. 2019, 63, 2784–2795. [Google Scholar] [CrossRef]
- Liu, S.; Zhu, S.; Zhang, J. Investigating Performance of BDS-2+3 Dual-Frequency Absolute Positioning With Broadcast Ephemerides, RTS and Final MGEX Products. IEEE Access 2023, 11, 22034–22050. [Google Scholar] [CrossRef]
- China Satellite Navigation Office. Available online: http://www.beidou.gov.cn/ (accessed on 1 November 2024).
- China Satellite Navigation Office. BeiDou Navigation Satellite System Signal in Space Interface Control Document Open Service Signal B1I (Version 3.0). Available online: http://www.beidou.gov.cn/xt/gfxz/201902/P020190227593621142475.pdf (accessed on 1 November 2024).
- China Satellite Navigation Office. BeiDou Navigation Satellite System Signal in Space Interface Control Document Open Service Signal B1C (Version 1.0). Available online: http://www.beidou.gov.cn/xt/gfxz/201712/P020171226741342013031.pdf (accessed on 1 November 2024).
- China Satellite Navigation Office. BeiDou Navigation Satellite System Signal in Space Interface Control Document Open Service Signal B2a (Version 1.0). Available online: http://www.beidou.gov.cn/xt/gfxz/201712/P020171226742357364174.pdf (accessed on 1 November 2024).
- China Satellite Navigation Office. BeiDou Navigation Satellite System Signal in Space Interface Control Document Open Service Signal B2b (Version 1.0). Available online: http://www.beidou.gov.cn/xt/gfxz/202008/P020230516558683155109.pdf (accessed on 1 November 2024).
- China Satellite Navigation Office. BeiDou Navigation Satellite System Signal in Space Interface Control Document Open Service Signal B3I (Version 3.0). Available online: http://www.beidou.gov.cn/xt/gfxz/201802/P020180209623601401189.pdf (accessed on 1 November 2024).
- European GNSS Service Centre (GSC). Available online: https://www.gsc-europa.eu/system-service-status/constellation-information (accessed on 1 November 2024).
- The European GNSS (Galileo) Open Service Signal-In-Space Interface Control Document (Issue 2.0). Available online: https://galileognss.eu/wp-content/uploads/2021/01/Galileo_OS_SIS_ICD_v2.0.pdf (accessed on 1 November 2024).
- Zhou, F.; Dong, D.; Li, W.; Jiang, X.; Wickert, J.; Schuh, H. GAMP: An Open-Source Software of Multi-GNSS Precise Point Positioning Using Undifferenced and Uncombined Observations. GPS Solut. 2018, 22, 33. [Google Scholar] [CrossRef]
- Collins, P.; Bisnath, S.; Lahaye, F.; Héroux, P. Undifferenced GPS Ambiguity Resolution Using the Decoupled Clock Model and Ambiguity Datum Fixing. Navigation 2010, 57, 123–135. [Google Scholar] [CrossRef]
- Héroux, P.; Kouba, J. GPS Precise Point Positioning Using IGS Orbit Products. Phys. Chem. Earth Part A Solid Earth Geod. 2001, 26, 573–578. [Google Scholar] [CrossRef]
- Vankadara, R.; Dashora, N.; Panda, S.K.; Dabbakuti, J.R.K.K. A Comparative Analysis of the Effect of Orbital Geometry and Signal Frequency on the Ionospheric Scintillations over a Low Latitude Indian Station: First Results from the 25th Solar Cycle. Remote Sens. 2024, 16, 1698. [Google Scholar] [CrossRef]
- Ogutcu, S.; Alcay, S.; Ozdemir, B.N.; Li, P.; Zhang, Y.; Konukseven, C.; Atiz, O.F. Assessing the Performance of BDS-3 for Multi-GNSS Static and Kinematic PPP-AR. Adv. Space Res. 2023, 71, 1543–1557. [Google Scholar] [CrossRef]
- De Oliveira, P.S.; Morel, L.; Fund, F.; Legros, R.; Monico, J.F.G.; Durand, S.; Durand, F. Modeling Tropospheric Wet Delays with Dense and Sparse Network Configurations for PPP-RTK. GPS Solut. 2017, 21, 237–250. [Google Scholar] [CrossRef]
- Zhou, F.; Dong, D.; Ge, M.; Li, P.; Wickert, J.; Schuh, H. Simultaneous Estimation of GLONASS Pseudorange Inter-Frequency Biases in Precise Point Positioning Using Undifferenced and Uncombined Observations. GPS Solut. 2018, 22, 19. [Google Scholar] [CrossRef]
- Misra, P.; Enge, P. Global Positioning System-Signals, Measurements, and Performance; Ganga-Jamuna Press: Kathmandu, Nepal, 2001. [Google Scholar]
- Zhang, Y.; Kubo, N.; Chen, J.; Wang, J.; Wang, H. Initial Positioning Assessment of BDS New Satellites and New Signals. Remote Sens. 2019, 11, 1320. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, J.; Gong, X.; Chen, Q. The Update of BDS-2 TGD and Its Impact on Positioning. Adv. Space Res. 2020, 65, 2645–2661. [Google Scholar] [CrossRef]
- Böhm, J.; Möller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an Improved Empirical Model for Slant Delays in the Troposphere (GPT2w). GPS Solut. 2015, 19, 433–441. [Google Scholar] [CrossRef]
- Yue, C.; Dang, Y.; Gu, S.; Wang, H.; Zhang, J. Optimization of Undifferenced and Uncombined PPP Stochastic Model Based on Covariance Component Estimation. GPS Solut. 2022, 26, 119. [Google Scholar] [CrossRef]
- Malik, J.S. Analysis of Position Coordinate Accuracy of Triple GNSS System by Post-Processing Dual Frequency Observations Using Open Source GAMP: A Case Study. Acta Geodyn. Geomater. 2020, 17, 485–499. [Google Scholar] [CrossRef]
- Zhou, F.; Xu, T. Modeling and assessment of GPS/BDS/Galileo triple-frequency precise point positioning. Acta Geod. Cartogr. Sin. 2021, 50, 61–70. [Google Scholar] [CrossRef]
- Cheng, S.; Cheng, J.; Zang, N.; Zhang, Z.; Zhao, G.; Chen, S. Stochastic Characteristics Analysis on GNSS Observations and Real-Time ROTI-Based Stochastic Model Compensation Method in the Ionospheric Scintillation Environment. GPS Solut. 2024, 28, 130. [Google Scholar] [CrossRef]
- Hoque, M.M.; Jakowski, N. Higher Order Ionospheric Effects in Precise GNSS Positioning. J. Geod. 2007, 81, 259–268. [Google Scholar] [CrossRef]
- Cai, C.; Liu, G.; Yi, Z.; Cui, X.; Kuang, C. Effect Analysis of Higher-Order Ionospheric Corrections on Quad-Constellation GNSS PPP. Meas. Sci. Technol. 2019, 30, 024001. [Google Scholar] [CrossRef]
- Luo, X.; Li, H.; Gong, X.; Xie, Z.; Li, Y. BDS-3 B1I Signal Tracking Error Characteristic and Its Advantage in PPP Under Ionospheric Scintillation at Low Latitudes. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–10. [Google Scholar] [CrossRef]
- Luo, X.; Liu, Z.; Lou, Y.; Gu, S.; Chen, B. A Study of Multi-GNSS Ionospheric Scintillation and Cycle-Slip over Hong Kong Region for Moderate Solar Flux Conditions. Adv. Space Res. 2017, 60, 1039–1053. [Google Scholar] [CrossRef]
- Zhou, Y.; Kuang, C.; Cai, C. Analysis of Higher-Order Ionospheric Effects on GNSS Precise Point Positioning in the China Area. Surv. Rev. 2019, 51, 442–449. [Google Scholar] [CrossRef]



| GNSS | IFC | Noise Amplification Factors | ||
|---|---|---|---|---|
| BDS-3 | B1C/B2a | 2.26 | 1.26 | 2.59 |
| B1C/B3I | 2.84 | 1.84 | 3.39 | |
| B1I/B2b | 2.49 | 1.49 | 2.90 | |
| B1I/B3I | 2.94 | 1.94 | 3.53 | |
| Galileo | E1/E5 | 2.34 | 1.34 | 2.69 |
| E1/E6 | 2.93 | 1.93 | 3.51 | |
| E1/E5a | 2.26 | 1.26 | 2.59 | |
| E1/E5b | 2.42 | 1.42 | 2.81 |
| Receiver Brand | Site Name | Receiver | Number |
|---|---|---|---|
| JAVAD | SGPO00USA | JAVAD TRE_3S | 1 |
| ENAO00PRT,POTS00DEU,SGOC00LKA,SUTM00ZAF,WUH200CHN | JAVAD TRE_3 | 5 | |
| BOGT00COL,MET300FIN,STHL00GBR,WARN00DEU | JAVAD TRE_3 DELTA | 4 | |
| LEICA | WROC00POL | LEICA GR30 | 1 |
| LPAL00ESP | LEICA GR50 | 1 | |
| SEPT | AC2400USA,ALIC00AUS,BILL00USA,CKIS00COK,COCO00AUS,DARW00AUS,DJIG00DJI,DYNG00GRC,JOG200IDN,KARR00AUS,KAT100AUS,KITG00UZB, MANA00NIC,METG00FIN,MOBS00AUS,NAUR00NRU,NIUM00NIU,P05100USA,P05300USA,P77900USA,POHN00FSM,QAQ100GRL,SAMO00WSM,SFDM00USA,SOLO00SLB,TONG00TON,TOW200AUS,VIS000SWE,VNDP00USA,YAR300AUS,YARR00AUS | SEPTPOLARX5 | 31 |
| GAMG00KOR | SEPT POLARX5TR | 1 | |
| UNBD00CAN | SEPT POLARX5S | 1 | |
| RIO200ARG | SEPT ASTERX4 | 1 | |
| STONEX | PADO00ITA | STONEX SC2200 | 1 |
| TRIMBLE | ASCG00SHN, CHPG00BRA,CIBG00IDN,CPVG00CPV,GANP00SVK,KRGG00ATF, MAYG00MYT,MCHL00AUS,MRO100AUS,PERT00AUS,RGDG00ARG,STR200AUS,TLSE00FRA | TRIMBLE ALLOY | 13 |
| Item | Strategies |
|---|---|
| PPP modes | BDS-3 Standalone, Galileo Standalone |
| Frequencies | BDS-3: B1C/B2a, B1C/B3I, B1I/B2b, and B1I/B3I; Galileo: E1/E5, E1/E6, E1/E5a, and E1/E5b, |
| Parameter adjustment | Kalman filter |
| Troposphere | Zenith: GPT2w. Mapping function: VMF1. The residual part estimated as a random walk parameter. |
| Ionosphere | Ionosphere-free combination |
| Satellite phase center offset | Corrected using the European Space Agency (ESA) model |
| Receiver phase center offset | Corrected by IGS antenna model |
| Satellite orbit and clock | Precise product of GFZ’s GBM |
| Daily DCB | CAS’s DCB product |
| Station displacement | Corrected according to IERS 2010 conventions |
| Phase windup effect | Corrected |
| Elevation mask | 10° |
| Station coordinates | Estimated white noise for kinematic mode; constant parameters for static mode. |
| Receiver clock | Estimated as white noise |
| Cycle slip detection | GF+MW |
| Phase ambiguities | Float for BDS-3 and Galileo |
| GNSS | DFIF | RMSE | ||||
|---|---|---|---|---|---|---|
| N | E | U | H | 3D | ||
| BDS-3 | B1C/B2a | 0.47 | 0.48 | 1.26 | 0.67 | 1.43 |
| B1C/B3I | 0.41 | 0.42 | 0.99 | 0.59 | 1.15 | |
| B1I/B2b | 0.37 | 0.43 | 1.02 | 0.57 | 1.17 | |
| B1I/B3I | 0.37 | 0.39 | 1.11 | 0.54 | 1.24 | |
| Galileo | E1/E5 | 0.27 | 0.31 | 0.98 | 0.41 | 1.06 |
| E1/E6 | 0.35 | 0.61 | 1.01 | 0.70 | 1.24 | |
| E1/E5a | 0.32 | 0.31 | 1.35 | 0.45 | 1.42 | |
| E1/E5b | 0.23 | 0.31 | 1.28 | 0.39 | 1.34 | |
| GNSS | DFIF | RMSE | ||||
|---|---|---|---|---|---|---|
| N | E | U | H | 3D | ||
| BDS-3 | B1C/B2a | 1.55 | 2.13 | 3.65 | 2.64 | 4.50 |
| B1C/B3I | 1.57 | 2.17 | 3.69 | 2.68 | 4.56 | |
| B1I/B2b | 1.45 | 2.13 | 3.53 | 2.58 | 4.37 | |
| B1I/B3I | 1.48 | 2.08 | 3.58 | 2.55 | 4.40 | |
| Galileo | E1/E5 | 1.42 | 1.89 | 3.38 | 2.36 | 4.13 |
| E1/E6 | 1.85 | 2.85 | 3.96 | 3.40 | 5.22 | |
| E1/E5a | 1.41 | 1.90 | 3.46 | 2.37 | 4.19 | |
| E1/E5b | 1.44 | 1.92 | 3.48 | 2.40 | 4.23 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Shu, Z.; Yao, J. Analyzing the Precise Point Positioning Performance of Different Dual-Frequency Ionospheric-Free Combinations with BDS-3 and Galileo. Atmosphere 2025, 16, 316. https://doi.org/10.3390/atmos16030316
Sun X, Shu Z, Yao J. Analyzing the Precise Point Positioning Performance of Different Dual-Frequency Ionospheric-Free Combinations with BDS-3 and Galileo. Atmosphere. 2025; 16(3):316. https://doi.org/10.3390/atmos16030316
Chicago/Turabian StyleSun, Xingli, Zhan Shu, and Jinjie Yao. 2025. "Analyzing the Precise Point Positioning Performance of Different Dual-Frequency Ionospheric-Free Combinations with BDS-3 and Galileo" Atmosphere 16, no. 3: 316. https://doi.org/10.3390/atmos16030316
APA StyleSun, X., Shu, Z., & Yao, J. (2025). Analyzing the Precise Point Positioning Performance of Different Dual-Frequency Ionospheric-Free Combinations with BDS-3 and Galileo. Atmosphere, 16(3), 316. https://doi.org/10.3390/atmos16030316





