Some Recent Key Aspects of the DC Global Electric Circuit
Abstract
1. Introduction to the DC Global Electric Circuit
2. Electrical Balance Sheet of the DC GEC
3. Positive Charge near the Earth’s Surface
4. Influence of Space Weather on the DC GEC
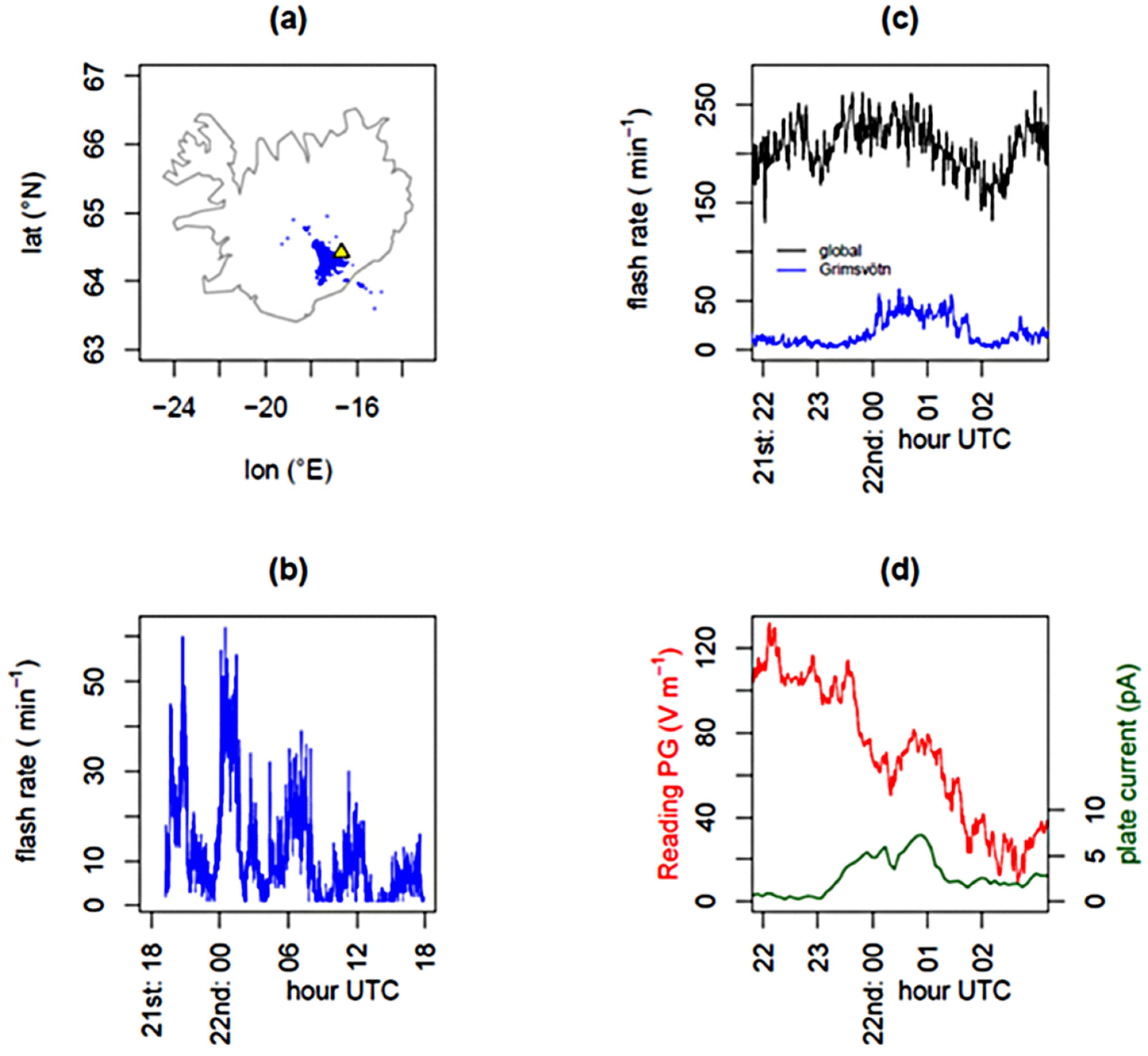
5. The GEC and Ionospheric Currents Generated by Thunderstorms
6. The Time Constant of the GEC
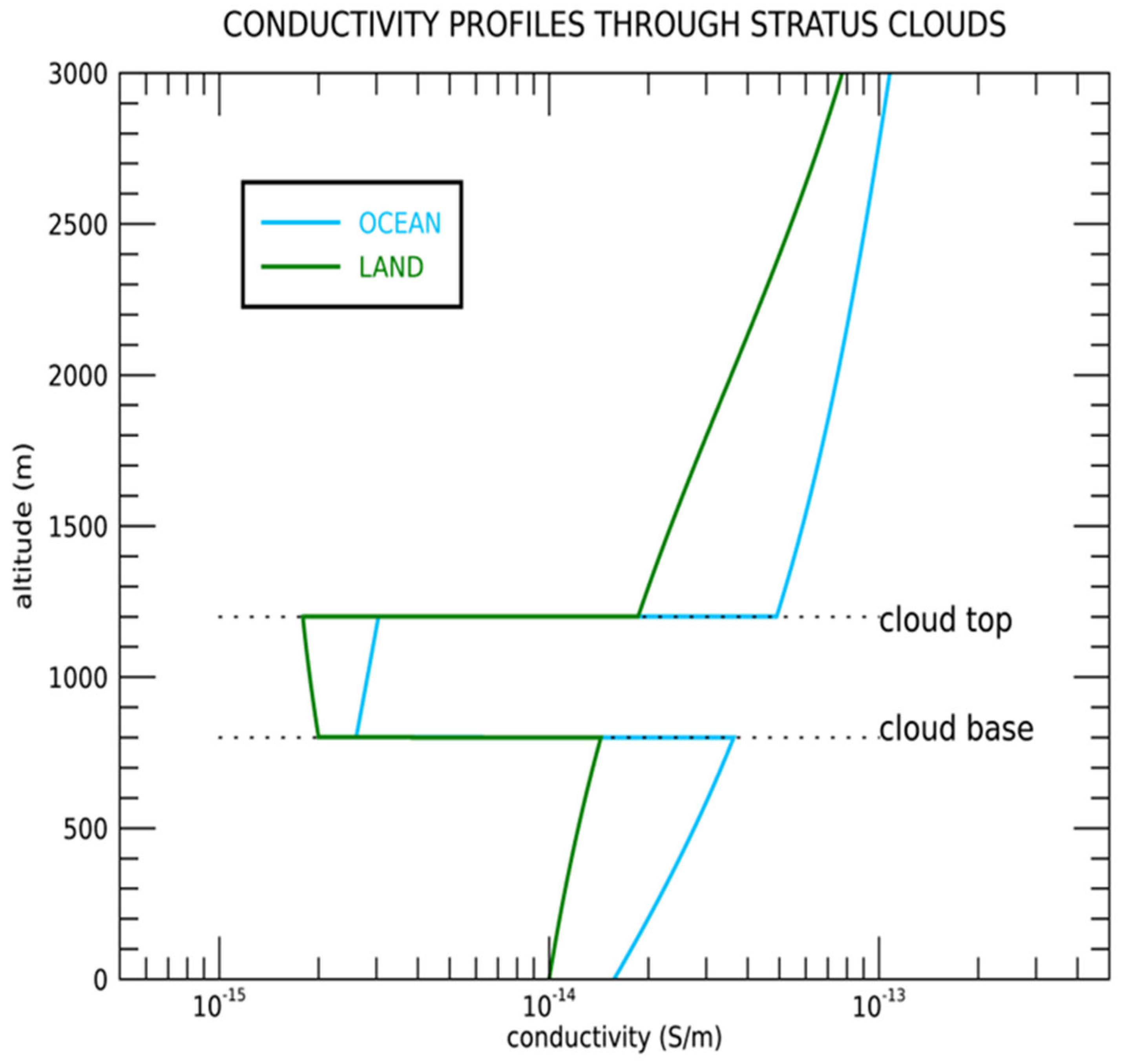
- A value of 1.6 × 10−14 S/m at mean sea level over the unpolluted ocean;
- A value of 1.0 × 10−14 S/m above the land surface, where the air is polluted so that the ions are larger, heavier, and hence less mobile than in pure air;
- The air conductivity inside the stratus cloud is less than that in the surrounding air at the same level by a factor ~10 for the same reason, the ions being scavenged by small water droplets; observations and a theoretical discussion which support these profiles have been presented by Harrison et al. [47].
7. Recent Observations of GEC Parameters
- Solar flares or coronal mass ejections;
- Forbush decreases;
- Solar proton events;
- Auroral activity; and
- Gigantic jets.
8. Can Pre-Seismic or Seismic Phenomena Affect the GEC?
- Understanding the physical background of the earthquake precursors’ generation, some of which involve the GEC;
- Developing technologies for their reliable identification, and determining the main earthquake parameters, namely their time, place, and magnitude;
- Organising their real-time monitoring and developing short-term forecasts.
- An earthquake of magnitude 7 on the Richter scale could generate a noisy ULF signal (up to ~1 nT or ~1 µV/m) that could be detectable above other ULF noise in the global electric circuit at a distance of only up to 100 or perhaps 300 km from the epicentre of the earthquake (his Section 2.2);
- There is no direct experimental evidence for the mobile positive hole (p-hole) theory of current carriers responsible for the rock conductivity in stressed rocks presented by Freund et al. [88]; because of contradictions with the values of three different realistic parameters, this theory presents unrealistic estimates of the magnitude of the earthquake precursor signals which are present in the GEC (his Section 2.3);
- The increased conductivity of air at up to ~1 km above the surface following the enhanced emission of radon from the Earth associated with seismic activity (Harrison et al. [79], Pulinets et al. [89]) decreases the total resistance of the column of air up to the ionosphere by ~20%; this would locally increase the current up to the ionosphere, which would increase the fair-weather current in the GEC (his Section 5.1);
- Any aerosol ions present will reduce the conductivity, which, in the presence of light winds (up to ~2 m/s) under fair-weather conditions, could cause large changes in the PG, up to 400 V/m, and for ~2 h, as has been observed before earthquakes (Smirnov [90]) (his Section 5.2);
- The possible coupling between infrared radiation anomalies and earthquakes (Pulinets and Ouzounov [91]) is “implausible” because quantitative estimates of the signals present in the GEC arising from these models are unrealistic and do not agree with observations (his Section 5.3);
- There is no theoretical explanation for how the claimed changes (e.g., Galvan et al. [92], Sunardi et al. [93], Li et al. [76]) to the total electron content of a column of ionospheric ionisation (in TEC units, 1016 m−2) before an earthquake could occur, although they might be caused by upward-propagating acoustic gravity waves in the atmosphere which could change the ionosphere and also the GEC (his Section 6);
- The increased current up to the ionosphere discussed in (3 above would increase the E-region density at night by ~0.004% and by day by an even smaller amount; such a small increase would not be detectable experimentally, so this aspect of the mechanism is “hardly plausible” (his Section 6.3);
- Because the timescale of discharging in natural ionisation levels by attachment is of the order of minutes at most, an enhanced emission of charged aerosols (rather than radon) from the ground before an earthquake (Sorokin and Novikov [94]) produces “only very weak ionospheric currents”, making models for this mechanism “seem questionable” (his Section 6.4).
9. The DC and AC GECs and Human Health
10. Conclusions
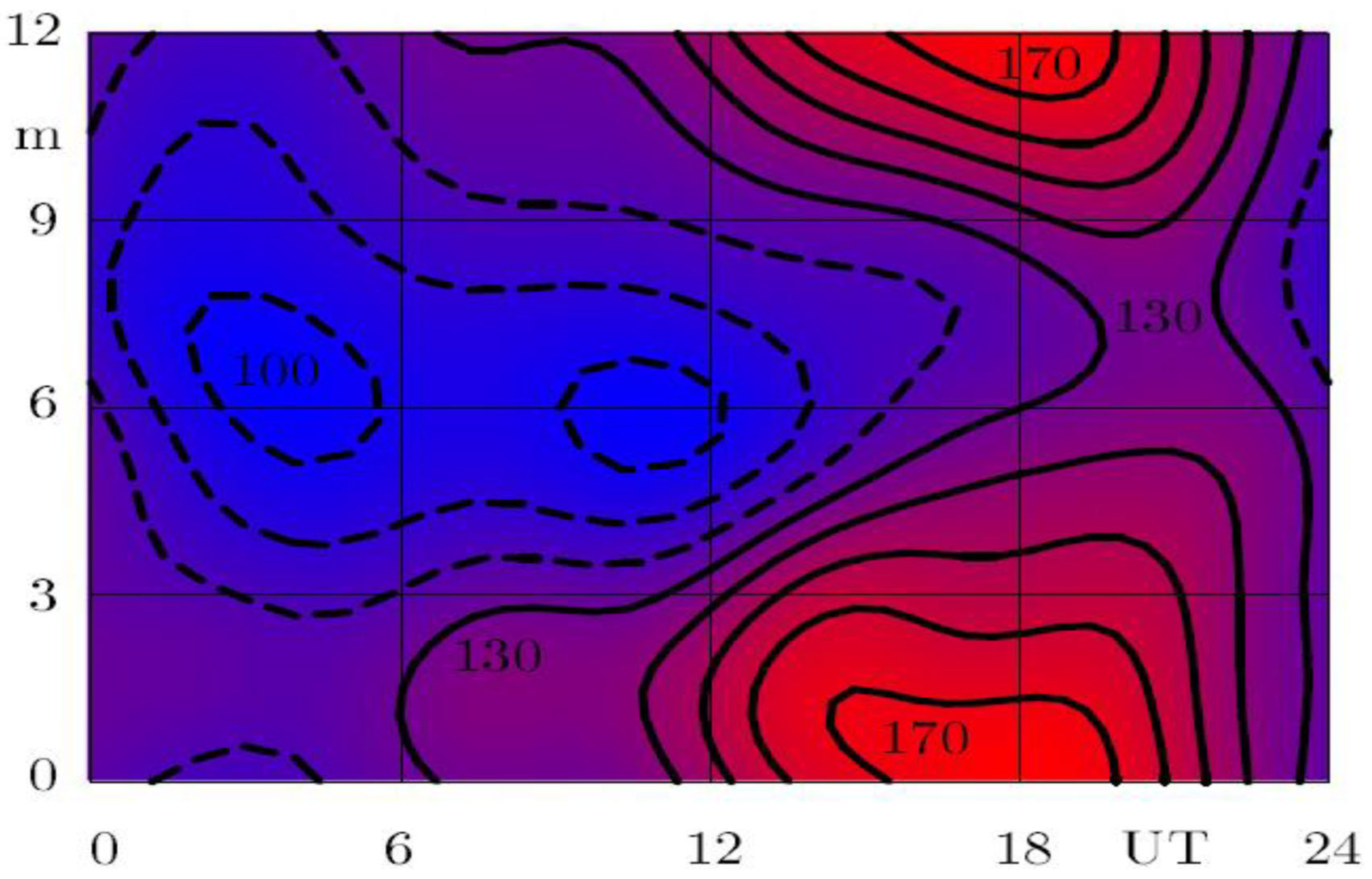
- The current I in the DC GEC of ~1 kA is generated by thunderstorms and electrified shower clouds; this maintains the ionospheric potential V at ~250 kV with respect to the Earth’s surface. The current flowing down through the fair-weather and semi-fair-weather atmosphere has a density J ~2 pA/m2, and the resistance of the atmosphere, R, is ~250 Ω. The electric field E (or potential gradient, with the opposite sign) above the surface of the Earth varies from ~100 V/m at 04 UT during July to ~170 V/m at 18 UT in January; the UT variation on a particular day is called the Carnegie curve (Section 1 and Section 2).
- The positive charge density in the atmosphere near the Earth’s surface associated with the operation of the DC GEC and the consequent charge Q of −6 × 105 C on the Earth (Wilson [3]) is only 0.3 pC/m3; this is smaller than typical values of the measured charge density that range from ~−20 to + 20 pC/m3. It is therefore impossible to gain information about the GEC, other than for its existence, from such observations (Section 3).
- A comprehensive theoretical model of the DC GEC has been published by Denisenko et al. [38]); using it, thunderstorm-generated electric fields can be estimated in the ionosphere. These cause low-latitude electrojets to flow in the ionosphere, which produce geomagnetic perturbations ~0.1 nT; they are too small to be detectable in the presence of those generate by ionospheric-wind-driven dynamo currents (Section 4).
- With the capacitance C of the GEC being ~1.5 F, its CR time constant, τ, is modelled to be ~8 min. With a more complex model involving status clouds over 30% of the Earth, this value of τ is confirmed. More recent modelling studies by Rycroft et al. [28] have put τ at 10 min. The time constant derived experimentally from observations of the sudden excitation of the GEC by volcanic lightning is found to lie between 7 and 12 min (Section 5).
- It is unlikely that seismic activity, or earthquake precursors, can produce large enough electric fields in the ionosphere to cause detectable effects there, either by enhanced radon emission or by enhanced thermal emission from the earthquake region (Section 6).
- There is some evidence that, via a melatonin mechanism, Schumann resonance signals and alpha waves in the human brain may somehow be linked (Section 7).
Funding
Acknowledgments
Conflicts of Interest
References
- Wilson, C.T.R. On the measurement of earth-air current and on the origin of atmospheric electricity. Proc. Camb. Phil. Soc. 1906, 13, 363–382. [Google Scholar]
- Wilson, C.T.R. On the Measurement of the Atmospheric Electric Potential Gradient and the Earth-air Current. Proc. R. Soc. Lond. A 1908, 80, 537–547. [Google Scholar] [CrossRef]
- Wilson, C.T.R. Investigations on lightning discharges and on the electric field of thunderstorms, Philos. Trans. R. Soc. Lond. A 1921, 221, 73–115. [Google Scholar] [CrossRef]
- Wilson, C.T.R. Some thundercloud problems. J. Franklin Inst. 1929, 208, 1–12. [Google Scholar] [CrossRef]
- Rycroft, M.J.; Israelsson, S.; Price, C. The global atmospheric electric circuit, solar activity and climate change. J. Atmos. Sol-Terr. Phys. 2000, 62, 1563–1576. [Google Scholar] [CrossRef]
- Williams, E.R. The global electrical circuit: A review. Atmos. Res. 2009, 91, 140–152. [Google Scholar] [CrossRef]
- Williams, E.R. Electricity in the Atmosphere: Global Electrical Circuit. Ref. Collect. Earth Syst. Environ. Sci. 2024, 13. [Google Scholar] [CrossRef]
- Harrison, R.G. The cloud chamber and CTR Wilson’s legacy to atmospheric science. Weather 2011, 66, 276–279. [Google Scholar] [CrossRef]
- Harrison, R.G. Fair Weather Atmospheric Electricity. J. Phys. Conf. Ser. 2011, 301, 012001. [Google Scholar] [CrossRef]
- Rycroft, M.J.; Odzimek, A.; Harrison, R.G. Determining the time constant of the global atmospheric electric circuit through modelling and observations. J. Atmos. Sol.-Terr. Phys. 2024, 260, 106267. [Google Scholar] [CrossRef]
- Wormell, T.W. Vertical electric currents below thunderstorms and showers. Proc. R. Soc. Lond. A. 1930, 127, 567–590. [Google Scholar] [CrossRef]
- Wormell, T.W. Atmospheric electricity; some recent trends and problems. Q. J. R. Met. Soc. 1953, 79, 3–38. [Google Scholar] [CrossRef]
- Wormell, T.W. Obituary. Q. J. R. Met. Soc. 1985, 111, 675. [Google Scholar] [CrossRef]
- Aplin, K.L.; Harrison, R.G.; Füllekrug, M.; Lanchester, B.; Becker, F. A scientific career launched at the start of the space age: Michael Rycroft at 80. Hist. Geo Space Sci. 2020, 11, 105–121. [Google Scholar] [CrossRef]
- Schumann, W.O. Über die strahlungslosen Eigenschwingungen einer leitenden Kugel, die von einer Luftschicht und einer Ionosphärenhülle umgeben ist. Z. Für Naturforschung. 1952, 7A, 149–154. [Google Scholar] [CrossRef]
- Balser, M.; Wagner, C.A. Observations of Earth–Ionosphere Cavity Resonances. Nature 1960, 188, 638–641. [Google Scholar]
- Rycroft, M.J. Resonances of the Earth-Ionosphere Cavity Observed at Cambridge, England. Radio Sci. J. Res. NBS 1965, 69D, 1071–1081. [Google Scholar]
- Barr, R.; Llanwyn Jones, D.; Rodger, C.J. ELF and VLF Radio Waves. J. Atmos. Sol.-Terr. Phys. 2000, 62, 1689–1718. [Google Scholar]
- Nickolaenko, A.P.; Hayakawa, M. Resonances in the Earth-Ionosphere Cavity; Springer: Berlin/Heidelberg, Germany, 2002; 380p, ISBN 9781402007545. [Google Scholar]
- Nickolaenko, A.; Hayakawa, M. Schumann Resonance for Tyros: Essentials of Global Electromagnetic Resonance in the Earth–Ionosphere Cavity; Springer: Berlin/Heidelberg, Germany, 2014; 348p. [Google Scholar] [CrossRef]
- Liu, J.; Huang, J.; Li, Z.; Zhao, Z.; Zeren, Z.; Shen, X.; Wang, Q. Recent Advances and Challenges in Schumann Resonance Observations and Research. Remote Sens. 2023, 15, 3557. [Google Scholar] [CrossRef]
- Siingh, D.; Singh, R.P.; Jeni Victor, N.; Kamra, A.K. The DC and AC global electric circuits and climate. Earth-Sci. Rev. 2023, 244, 104542. [Google Scholar] [CrossRef]
- Mülheisen, R. The global circuit and its parameters. In Electrical Processes in Atmospheres; Dolezalek, H., Reiter, R., Eds.; Steinkopf Verlag: Heidelberg, Germany, 1977; pp. 467–476. [Google Scholar]
- Harrison, R.G. The global atmospheric electrical circuit and climate. Surv. Geophys. 2004, 25, 441–484. [Google Scholar] [CrossRef]
- Harrison, R.G. The Carnegie curve. Surv. Geophys. 2013, 34, 209–232. [Google Scholar] [CrossRef]
- Harrison, R.G. Behind the curve: A comparison of historical sources for the Carnegie curve of the global atmospheric electric circuit. Hist. Geo Space Sci. 2020, 11, 207–213. [Google Scholar] [CrossRef]
- Harrison, R.G.; Nicoll, K.A. Fair weather criteria for atmospheric electricity measurements. J. Atmos. Sol.-Terr. Phys. 2018, 179, 239–250. [Google Scholar] [CrossRef]
- Rycroft, M.J.; Nickolaenko, A.P.; Harrison, R.G.; Odzimek, A. The global circuit capacitor and two new ways of deriving the time constant of the global atmospheric electric circuit. J. Atmos. Sol.-Terr. Phys. 2025; submitted. [Google Scholar]
- Aplin, K.L. Instrumentation for Atmospheric Ion Measurements. Ph.D. Thesis, University of Reading, Reading, UK, 2000; 274p. [Google Scholar]
- Aplin, K.L.; Harrison, R.G.; Rycroft, M.J. Investigating Earth’s atmospheric electricity: A role model for planetary studies. Space Sci. Rev. 2008, 137, 11–27. [Google Scholar] [CrossRef]
- Anisimov, S.V.; Galichenko, S.V.; Aphinogenov, K.V.; Klimanova, E.V.; Kozmina, A.S. Small air ion statistics near the earth’s surface. Atmos. Res. 2022, 267, 105193. [Google Scholar]
- Nicoll, K.A.; Harrison, R.G. Experimental determination of layer cloud edge charging from cosmic ray ionisation. Geophys. Res. Lett. 2010, 37, L13802. [Google Scholar] [CrossRef]
- Nicoll, K.A.; Harrison, R.G. Charge measurements in stratiform cloud from a balloon based sensor. J. Phys. Conf. Ser. 2011, 301, 012003. [Google Scholar] [CrossRef]
- Nicoll, K.A.; Harrison, R.G. Stratiform cloud electrification: Comparison of theory with multiple in-cloud measurements. Q. J. R. Met. Soc. 2016, 142, 2679–2691. [Google Scholar] [CrossRef]
- Anisimov, S.V.; Galichenko, S.V.; Aphinogenov, K.V.; Klimanova, E.V.; Prokhorchuk, A.A.; Kozmina, A.S.; Guriev, A.V. Mid-latitude atmospheric boundary layer electricity: A study by using a tethered balloon platform. Atmos. Res. 2021, 250, 105355. [Google Scholar] [CrossRef]
- Hirsikko, A.; Nieminen, T.; Gagn’e, S.; Lehtipalo, K.; Manninen, H.E.; Ehn, M.; Hõrrak, U.; Kerminen, V.-M.; Laakso, L.; McMurry, P.H.; et al. Atmospheric ions and nucleation: A review of observations. Atmos. Phys. Chem. 2011, 11, 767–798. [Google Scholar] [CrossRef]
- Tinsley, B.A. The influence of the solar wind electric and magnetic fields on the latitude and temporal variations of the current density, Jz, of the global electric circuit, with relevance to weather and climate. J. Atmos. Sol.-Terr. Phys. 2024, 265, 106355. [Google Scholar] [CrossRef]
- Denisenko, V.V.; Rycroft, M.J.; Harrison, R.G. Mathematical Simulation of the Ionospheric Electric Field as a Part of the Global Electric Circuit. Surv. Geophys. 2019, 40, 1–35, Erratum in Surv. Geophys. 2019, 40, 37. [Google Scholar] [CrossRef]
- Harrison, R.G. Measuring electrical properties of the lower troposphere using enhanced meteorological radiosondes. Geosci. Instrum. Method Data Syst. 2022, 11, 37–57. [Google Scholar] [CrossRef]
- Khegai, V.V.; Korsunova, L.P.; Legen’ka, A.D. Estimation of a Tropospheric Electric Field Associated with the African Zone of Thunderstorm Activity that Penetrates the Ionosphere. Geomagn. Aeron. 2021, 61, 559–564. [Google Scholar] [CrossRef]
- Liu, X.; Li, L.; Zhang, Y.; Xue, H. Ionospheric currents and nightside ionospheric magnetic fields calculated by TIE-GCM (in Chinese). Chin. J. Space Sci. 2018, 38, 29–36. [Google Scholar] [CrossRef]
- Denisenko, V.V.; Rycroft, M.J. The ionospheric equatorial electrojets generated by low latitude thunderstorms. J. Atmos. Sol.-Terr. Phys. 2021, 221, 105704. [Google Scholar] [CrossRef]
- Denisenko, V.V.; Rycroft, M.J. WWLLN data used to model the ionospheric electric field generated by thunderstorms. Ann. Geophys. 2022, 65, PA536. [Google Scholar] [CrossRef]
- Denisenko, V.V.; Rycroft, M.J. Seasonal dependence of the equatorial electrojets generated by thunderstorms. Adv. Space Res. 2023, 73, 3464–3471. [Google Scholar] [CrossRef]
- Holzworth, R.H.; Bering, E.A., III; Kokorowski, M.F.; Lay, E.H.; Reddell, B.; Kadokura, A.; Yamagishi, H.; Sato, N.; Ejiri, M.; Hirosawa, H.; et al. Balloon observations of temporal variation in the global circuit compared to global lightning activity. Adv. Space Res. 2005, 36, 2223–2228. [Google Scholar] [CrossRef]
- Haldoupis, C.; Rycroft, M.; Williams, E.; Price, C. Is the “Earth-ionosphere capacitor” a valid component in the atmospheric global electric circuit? J. Atmos. Sol.-Terr. Phys. 2017, 164, 127–131. [Google Scholar] [CrossRef]
- Harrison, R.G.; Nicoll, K.A.; Mareev, E.; Slyunyaev, N.; Rycroft, M.J. Extensive layer clouds in the global electric circuit: Their effects on vertical charge distribution and storage. Proc. R. Soc. A 2020, 476, 20190758. [Google Scholar] [CrossRef] [PubMed]
- Bór, J.; Bozóki, T.; Sátori, G.; Williams, E.; Behnke, S.A.; Rycroft, M.J.; Buzás, A.; Silva, H.G.; Kubicki, M.; Said, R.; et al. Responses of the AC/DC Global Electric Circuit to Volcanic Electrical Activity in the Hunga Tonga-Hunga Ha’apai Eruption on 15 January 2022. J. Geophys. Res. Atmos. 2023, 128, e2022JD038238. [Google Scholar] [CrossRef]
- Rycroft, M.J.; Harrison, R.G. Electromagnetic atmosphere-plasma coupling: The global electric circuit. Space Sci. Rev. 2012, 168, 363–384. [Google Scholar] [CrossRef]
- Tacza, J.; Raulin, J.-P.; Macotela, E.; Norabuena, E.; Fernandez, G.; Correia, E.; Rycroft, M.J.; Harrison, R.G. A new South American network to study the atmospheric electric field and its variations related to geophysical phenomena. J. Atmos. Sol.-Terr. Phys. 2014, 120, 70–79. [Google Scholar] [CrossRef]
- Tacza, J.; Li, G.; Raulin, J.-P. Effects of Forbush Decreases on the global electric circuit. Space Weather 2024, 22, e2023SW003852. [Google Scholar] [CrossRef]
- Michnowski, S.; Odzimek, A.; Kleimenova, N.G.; Kozyreva, O.V.; Kubicki, M.; Klos, Z.; Israelsson, S.; Nikiforova, N.N. Review of Relationships Between Solar Wind and Ground-Level Atmospheric Electricity: Case Studies from Hornsund, Spitsbergen, and Swider, Poland. Surv. Geophys. 2021, 42, 757–801. [Google Scholar] [CrossRef]
- Lavigne, T.; Liu, C.; Hill, J.; Bruning, E. Observations from the one year electric field Study-North Slope of Alaska (OYES-NSA) field campaign, and their implications for observing the distribution of global electrified cloud activity. J. Atmos. Sol.-Terr. Phys. 2021, 214, 105528. [Google Scholar] [CrossRef]
- Lavigne, T.; Liu, C. Relationships among diurnal variations of polar night cloud, precipitation, surface temperatures, and the fair-weather return current of the global electric circuit (GEC). J. Atmos. Sol.-Terr. Phys. 2023, 244, 106026. [Google Scholar] [CrossRef]
- Nicoll, K.A.; Harrison, R.G.; Barta, V.; Bor, J.; Brugge, R.; Chillingarian, A.; Chum, J.; Georgoulias, A.K.; Guha, A.; Kourtidis, K.; et al. A global atmospheric electricity monitoring network for climate and geophysical research. J. Atmos. Sol.-Terr. Phys. 2019, 184, 18–29. [Google Scholar] [CrossRef]
- Yair, Y.; Yaniv, R. The Effects of Fog on the Atmospheric Electrical Field Close to the Surface. Atmosphere 2023, 14, 549. [Google Scholar] [CrossRef]
- Povschenko, O.; Bazhenov, V. Analysis of Modern Atmospheric Electrostatic Field Measuring Instruments and Methods. Technol. Audit. Prod. Reserves 2023, 4, 16–24. [Google Scholar] [CrossRef]
- Harrison, R.G.; Marlton, G.J. Fair weather electric field meter for atmospheric science platforms. J. Electrostat. 2020, 107, 103489. [Google Scholar] [CrossRef]
- Büsken, M.; for the Pierre Auger Collaboration. A new network of electric field mills at the Pierre Auger Observatory. J. Phys. Conf. Ser. 2022, 2398, 012004. [Google Scholar] [CrossRef]
- Lyu, F.; Zhang, Y.; Lu, G.; Zhu, B.; Zhang, H.; Xu, W.; Xiong, S.; Lyu, W. Recent observations and research progresses of terrestrial gamma-ray flashes during thunderstorms. Sci. China Earth Sci. 2023, 66, 435–455. [Google Scholar] [CrossRef]
- Lucas, G.M.; Thayer, J.P.; Deierling, W. Statistical analysis of spatial and temporal variations in atmospheric electric fields from a regional array of field mills. J. Geophys. Res. Atmos. 2017, 122, 1158–1174. [Google Scholar] [CrossRef]
- Riabova, S.A.; Spivak, A.A. Variations of Electrical Characteristics of the Surface Atmosphere during Magnetic Storms. Dokl. Earth Sci. 2021, 497, 246–251. [Google Scholar] [CrossRef]
- Anisimov, S.V.; Shikhova, N.M.; Kleimenova, N.G. Response of a Magnetospheric Storm in the Atmospheric Electric Field of the Midlatitudes. Geomagn. Aeron. 2021, 61, 180–190. [Google Scholar] [CrossRef]
- Li, L.; Chen, T.; Shen, C.; Ti, S.; Wang, S.; Cai, C.; Li, W.; Luo, J. Near-surface atmospheric electric field changes through magnetic clouds via coronal mass ejections. Geosci. Lett. 2023, 10, 45. [Google Scholar] [CrossRef]
- Li, W.; Sun, Z.; Chen, T.; Yan, Z.; Luo, J.; Xu, Q.; Ma, Z. Different Effects of a Super Storm on Atmospheric Electric Fields at Different Latitudes. Atmosphere 2024, 15, 1314. [Google Scholar] [CrossRef]
- Pilipenko, V.; Smirnov, S.E.; Frank-Kamenetsky, A.V.; Martinez-Bedenko, V.A. An electrical storm during a magnetic storm on April 5, 2010. Izv. Atmos. Ocean. Phys. 2024, 60, 1555-628X. Available online: https://link.springer.com/journal/volumesAndIssues/11485 (accessed on 10 March 2025).
- Yaniv, R.; Yair, Y.; Price, C.; Reuveni, Y. No Response of Surface-Level Atmospheric Electrical Parameters in Israel to Severe Space Weather Events. Atmosphere 2023, 14, 1649. [Google Scholar] [CrossRef]
- Tacza, J.; Odzimek, A.; Tueros Cuadros, E.; Raulin, J.-P.; Kubicki, M.; Fernandez, G.; Marun, A. Investigating effects of solar proton events and Forbush decreases on ground-level potential gradient recorded at middle and low latitudes and different altitudes. Space Weather 2022, 20, e2021SW002944. [Google Scholar] [CrossRef]
- Tacza, J.; Raulin, J.-P.; Mendonca, R.R.S.; Makhmutov, V.S.; Marun, A.; Fernandez, G. Solar effects on the atmospheric electric field during 2010–2015 at low latitudes. J. Geophys. Res. Atmos. 2018, 123, 11970–11979. [Google Scholar] [CrossRef]
- Kleimenova, N.; Kozyrova, O.; Michnowski, S.; Kubicki, M. Influence of geomagnetic disturbances on atmospheric electric field (Ez) variations at high and middle latitudes. J. Atmos. Sol.-Terr. Phys. 2013, 99, 117–122. [Google Scholar] [CrossRef]
- Nickolaenko, A.P.; Hayakawa, M.; Koloskov, O. Schumann resonance as a remote sensor of lower ionosphere and global thunderstorms as based on the long-term observations at Antarctic and Arctic stations. J. Atmos. Sol.-Terr. Phys. 2025, 269, 106465. [Google Scholar] [CrossRef]
- Parrot, M.; Tramutoli, V.; Liu, T.J.Y.; Pulinets, S.; Ouzounov, D.; Genzano, N.; Lisi, M.; Hattori, K.; Namgaladze, A. Atmospheric and ionospheric coupling phenomena associated with large earthquakes. Eur. Phys. J. Spec. Top. 2021, 230, 197–225. [Google Scholar] [CrossRef]
- Chen, H.; Han, P.; Hattori, K. Recent Advances and Challenges in the Seismo-Electromagnetic Study: A Brief Review. Remote Sens. 2022, 14, 5893. [Google Scholar] [CrossRef]
- Peddi Naidu, P.; Madhavi Latha, T.; Madhusudhana Rao, D.N.; Indira Devi, M. Anomalous behavior of the ionosphere before strong earthquakes. Indian J. Phys. 2017, 91, 1467–1476. [Google Scholar] [CrossRef]
- Boudjada, M.Y.; Biagi, P.F.; Eichelberger, H.U.; Nico, G.; Schwingenschuh, K.; Galopeau, P.H.M.; Solovieva, M.; Contadakis, M.; Denisenko, V.; Lammer, H.; et al. Unusual Sunrise and SunsetTerminator Variations in the Behavior of Sub-Ionospheric VLF Phase and Amplitude Signals Prior to the Mw7.8 Turkey Syria Earthquake of 6 February 2023. Remote Sens. 2024, 16, 4448. [Google Scholar] [CrossRef]
- Li, Z.; Tao, Z.; Zhang, J.; Cao, Y. Analysis of Seismo-ionospheric Anomaly Disturbance Associated with the Mw7.6 Mexico Earthquake on 19 September 2022. Res. Sq. 2025; submitted. [Google Scholar] [CrossRef]
- Sorokin, V.M.; Chmyrev, V.M.; Hayakawa, M. A Review on Electrodynamic Influence of Atmospheric Processes to the Ionosphere. Open J. Earthq. Res. 2020, 9, 113–141. [Google Scholar] [CrossRef]
- Denisenko, V.V.; Bakhmetieva, N.V. Disturbance of the Electric Field in the D-Region of the Ionosphere with an Increase in Radon Emanation. Geomagn. Aeron. 2024, 64, 673–681. [Google Scholar] [CrossRef]
- Harrison, R.G.; Aplin, K.L.; Rycroft, M.J. Atmospheric electricity coupling between earthquake regions and the ionosphere. J. Atmos. Sol.-Terr. Phys. 2010, 72, 376–381. [Google Scholar] [CrossRef]
- Harrison, R.G.; Aplin, K.L.; Rycroft, M.J. Brief Communication: Earthquake–cloud coupling through the global atmospheric electric circuit. Nat. Hazards Earth Syst. Sci. 2014, 14, 773–777. [Google Scholar] [CrossRef]
- Píša, D.; Parrot, M.; Santolík, O. Ionospheric density variations recorded before the 2010 Mw 8.8 earthquake in Chile. J. Geophys. Res. 2011, 116, A08309. [Google Scholar] [CrossRef]
- Píša, D.; Nemec, F.; Santolík, O.; Parrot, M.; Rycroft, M. Additional attenuation of natural VLF electromagnetic waves observed by the DEMETER spacecraft resulting from preseismic activity. J. Geophys. Res. Space Phys. 2013, 118, 5286–5295. [Google Scholar] [CrossRef]
- Pulinets, S.A. Physical bases of the short-term forecast of earthquakes. Astron. Astrophys. Trans. (AApTr) 2023, 34, 65–84. [Google Scholar] [CrossRef]
- Pulinets, S.; Herrera, V.M.V. Earthquake Precursors: The Physics, Identification, and Application. Geosciences 2024, 14, 209. [Google Scholar] [CrossRef]
- Surkov, V.V. An Overview of Theoretical Studies of Non-Seismic Phenomena Accompanying Earthquakes. Surv. Geophys. 2025, 46, 7–70. [Google Scholar] [CrossRef]
- Ouzounov, D.; Pulinets, S.; Hattori, K.; Taylor, P. (Eds.) Pre-Earthquake Processes; a Multidisciplinary Approach to Earthquake Prediction Studies; AGU/Wiley: Washington, DC, USA, 2018; 365p. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D.; Karelin, A.; Boyarchuk, K. Earthquake Precursors in the Atmosphere and Ionosphere: New Concepts; Springer: Dordrecht, The Netherlands, 2023; 314p. [Google Scholar] [CrossRef]
- Freund, F.; Ouillon, G.; Scoville, J.; Sornette, D. Earthquake precursors in the light of peroxy defects theory: Critical review of systematic observations. Eur. Phys. J. Spec. Top. 2021, 230, 7–46. [Google Scholar] [CrossRef]
- Pulinets, S.; Mironova, I.; Miklyaev, P.; Petrova, T.; Shitov, A.; Karagodin, A. Radon Variability as a Result of Interaction with the Environment. Atmosphere 2024, 15, 167. [Google Scholar] [CrossRef]
- Smirnov, S. Negative anomalies of the Earth’s electric field as earthquake precursors. Geosciences 2020, 10, 10. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D. Lithosphere-Atmosphere-Ionosphere Coupling (LAIC) model—A unified concept for earthquake precursors validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar]
- Galvan, D.A.; Komjathy, A.; Hickey, M.P.; Stephens, P.; Snively, J.; Song, Y.T.; Butala, M.D.; Mannucci, A.J. Ionospheric signatures of Tohoku-Oki tsunami of March 11, 2011: Model comparisons near the epicenter. Radio Sci. 2012, 47, RS4003. [Google Scholar] [CrossRef]
- Sunardi, B.; Muslim, B.; Sakya, A.E.; Rohadi, S.; Sulastri, S.; Murjaya, J. Ionospheric earthquake effects detection based on Total Electron Content (TEC) GPS correlation. IOP Conf. Ser. Earth Environ. Sci. 2018, 132, 012014. [Google Scholar] [CrossRef]
- Sorokin, V.M.; Novikov, V.A. A model of TEC perturbations possibly related to seismic activity. Ann. Geoph. 2023, 66, 642. [Google Scholar] [CrossRef]
- SCENIHR. Health Effects of Electromagnetic Fields; European Commission: Brussels, Belgium, 2015; 288p, ISBN 978-92-79-30134-6. [Google Scholar]
- WHO. Environmental Health Criteria 238, Extremely Low Frequency Fields; WHO: Geneva, Switzerland, 2007; 510p, ISBN 978-92-4-157238-5. [Google Scholar]
- Palmer, S.J.; Rycroft, M.J.; Cermack, M. Solar and geomagnetic activity, extremely low frequency magnetic and electric fields and human health at the Earth’s surface. Surv. Geophys. 2006, 27, 537–595. [Google Scholar] [CrossRef]
- Cherry, N. Schumann Resonances, a plausible biophysical mechanism for the human health effects of solar/geomagnetic activity. Nat. Hazards 2002, 26, 279–331. [Google Scholar] [CrossRef]
- Jammoul, M.; Lawand, N. Melatonin: A Potential Shield against Electromagnetic Waves. Curr. Neuropharmacol. 2022, 20, 648–660. [Google Scholar] [CrossRef]
- Price, C.; Williams, E.; Elhalel, G.; Sentman, D. Natural ELF fields in the atmosphere and in living organisms. Int. J. Biometeorol. 2021, 65, 85–92. [Google Scholar] [CrossRef]
- Brazier, M.A. The analysis of brain waves. Sci. Am. 1962, 206, 152–153. [Google Scholar] [PubMed]
- Hima, C.S.; Asheeta, A.; Nair, C.C.; Nair, S.M.J. A review on brainwave therapy. World J. Pharm. Sci. 2020, 8, 59–66. [Google Scholar]
- Martel, J.; Chang, S.-H.; Chevalier, G.; Ojcius, D.M.; Young, J.D. Influence of electromagnetic fields on the circadian rhythm: Implications for human health and disease. Biomed. J. 2023, 46, 48–59. [Google Scholar] [CrossRef] [PubMed]
- Martel, J.; Rouleau, N.; Murugan, N.J.; Chin, W.-C.; Ojcius, D.M.; Young, J.D. Effects of light, electromagnetic fields and water on biological rhythms. Biomed. J. 2024, 100824. [Google Scholar] [CrossRef]
- Nevoit, G.; Landauskas, M.; McCarty, R.; Bumblyte, I.A.; Potyazhenko, M.; Taletaviciene, G.; Jarusevicius, G.; Vainoras, A. Schumann Resonances and the Human Body: Questions About Interactions, Problems and Prospects. Appl. Sci. 2025, 15, 449. [Google Scholar] [CrossRef]
- Mavromichalaki, H.; Papailiou, M.-C.; Gerontidou, M.; Dimitrova, S.; Kudela, K. Human Physiological Parameters Related to Solar and Geomagnetic Disturbances: Data from Different Geographic Regions. Atmosphere 2021, 12, 1613. [Google Scholar] [CrossRef]
- Cui, H.; Ding, H.; Hu, L.; Zhao, Y.; Shu, Y.; Voon, V. A novel dual-site OFCdlPFC accelerated repetitive transcranial stimulation for depression: A pilot randomized controlled study. Psychol. Med. 2024, 54, 3849–3862. [Google Scholar] [CrossRef]
- Mironova, I.; Füllekrug, M.; Kourtidis, K.; Mareev, E. Editorial: Atmospheric Electricity. Front. Earth Sci. 2022, 10, 853584. [Google Scholar] [CrossRef]
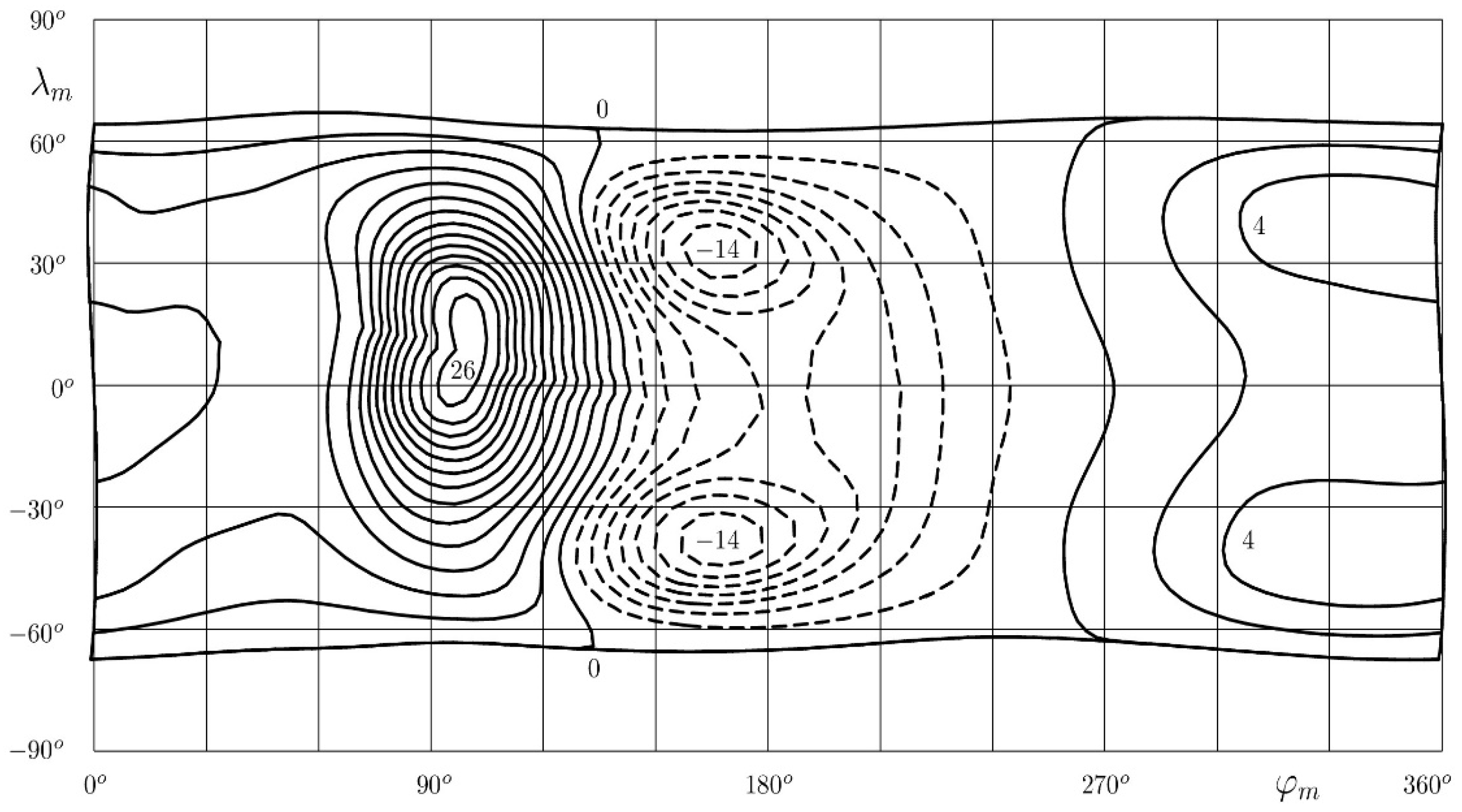
| Point discharge currents | −100 C |
| Lightning discharges | −20 C |
| Fair-weather conduction current | +60 C |
| Precipitation, i.e., rain or snow | +20 C |
| Net gain of negative charge on Earth’s surface | 40 C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rycroft, M.J. Some Recent Key Aspects of the DC Global Electric Circuit. Atmosphere 2025, 16, 348. https://doi.org/10.3390/atmos16030348
Rycroft MJ. Some Recent Key Aspects of the DC Global Electric Circuit. Atmosphere. 2025; 16(3):348. https://doi.org/10.3390/atmos16030348
Chicago/Turabian StyleRycroft, Michael J. 2025. "Some Recent Key Aspects of the DC Global Electric Circuit" Atmosphere 16, no. 3: 348. https://doi.org/10.3390/atmos16030348
APA StyleRycroft, M. J. (2025). Some Recent Key Aspects of the DC Global Electric Circuit. Atmosphere, 16(3), 348. https://doi.org/10.3390/atmos16030348







