Backward Integration of Nonlinear Shallow Water Model: Part 2: Vortex Merger
Abstract
1. Introduction
2. Basic Equations and Numerical Model
3. Numerical Results
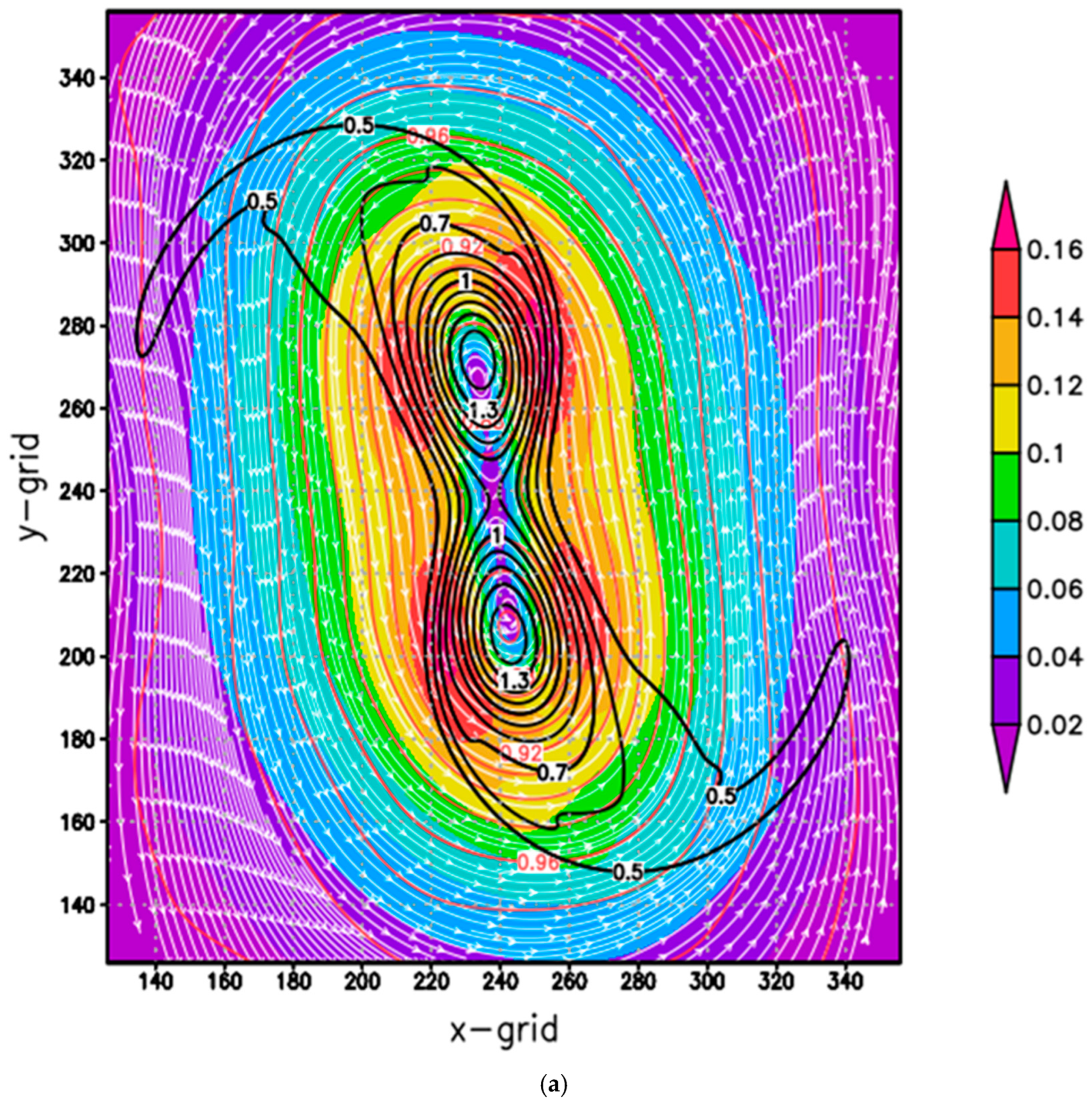
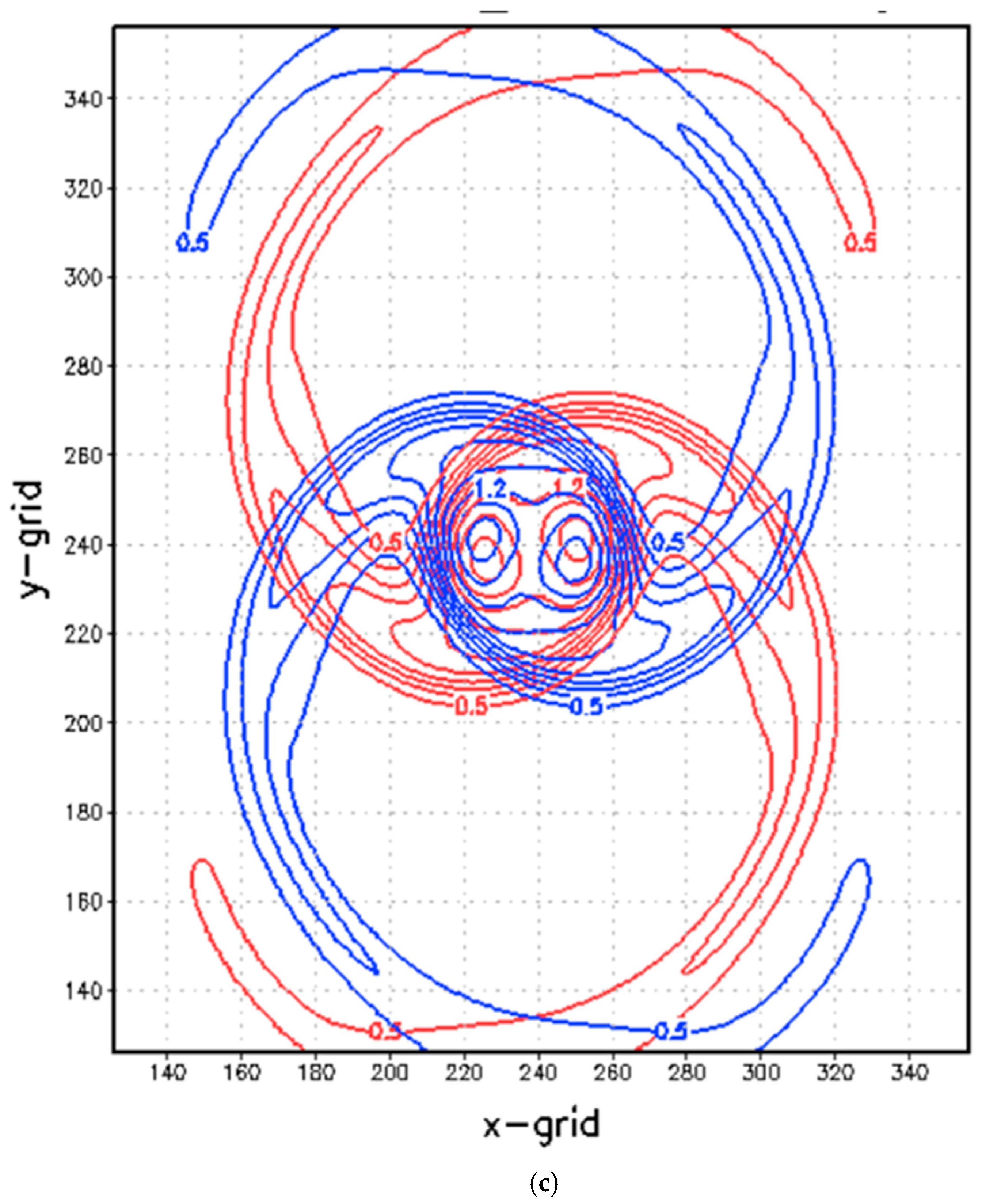
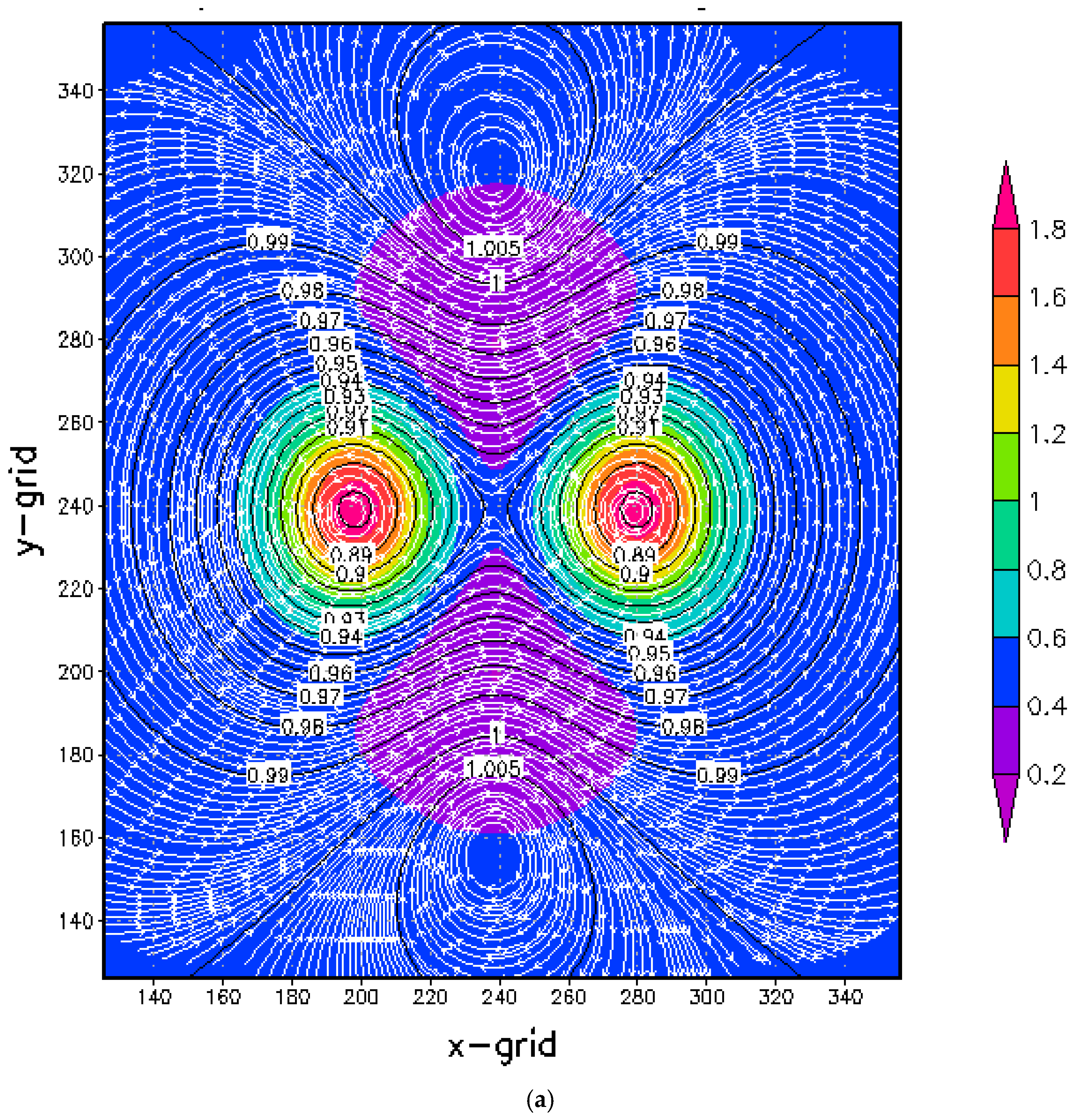
3.1. Case A: Initial Condition and Numerical Simulations
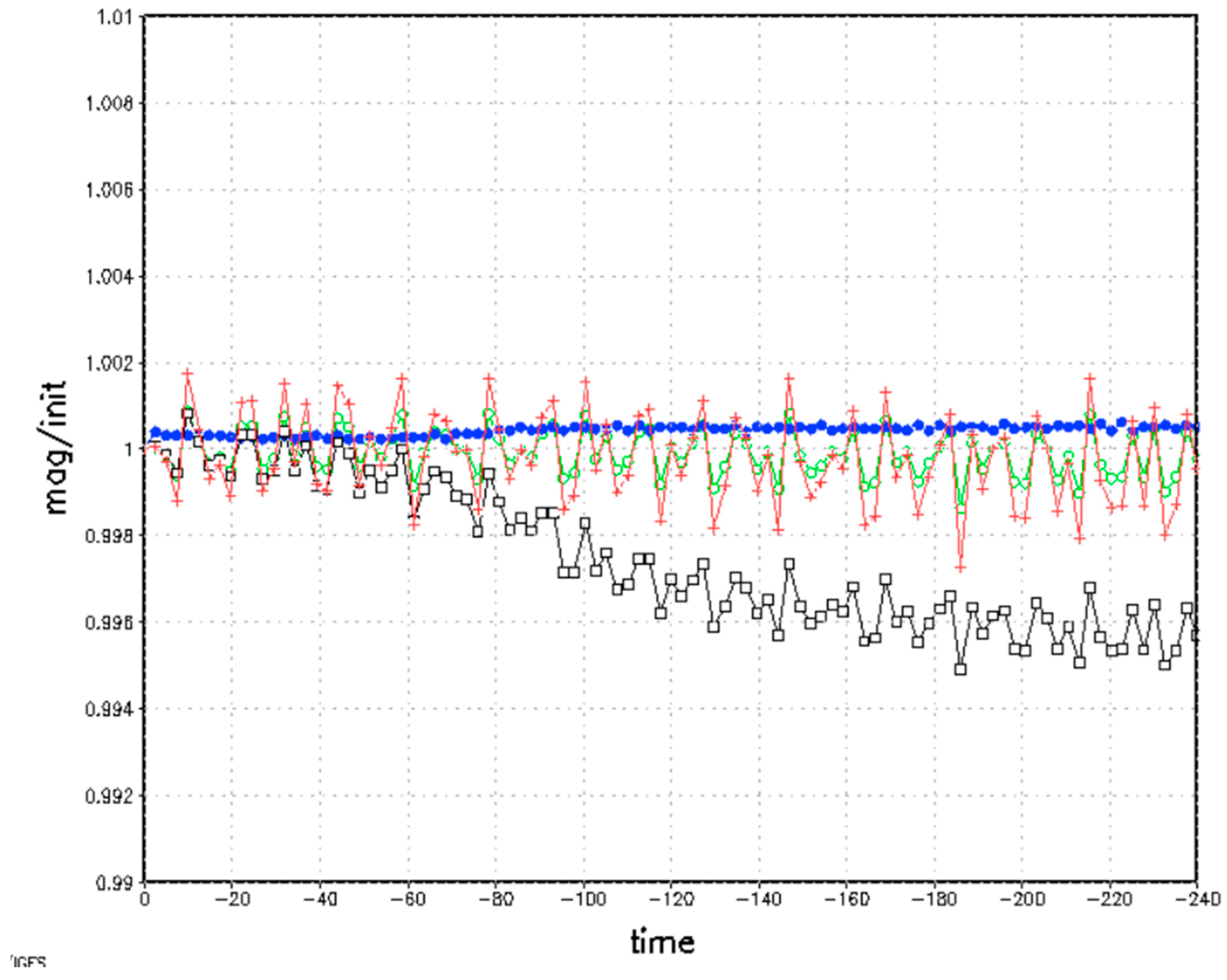
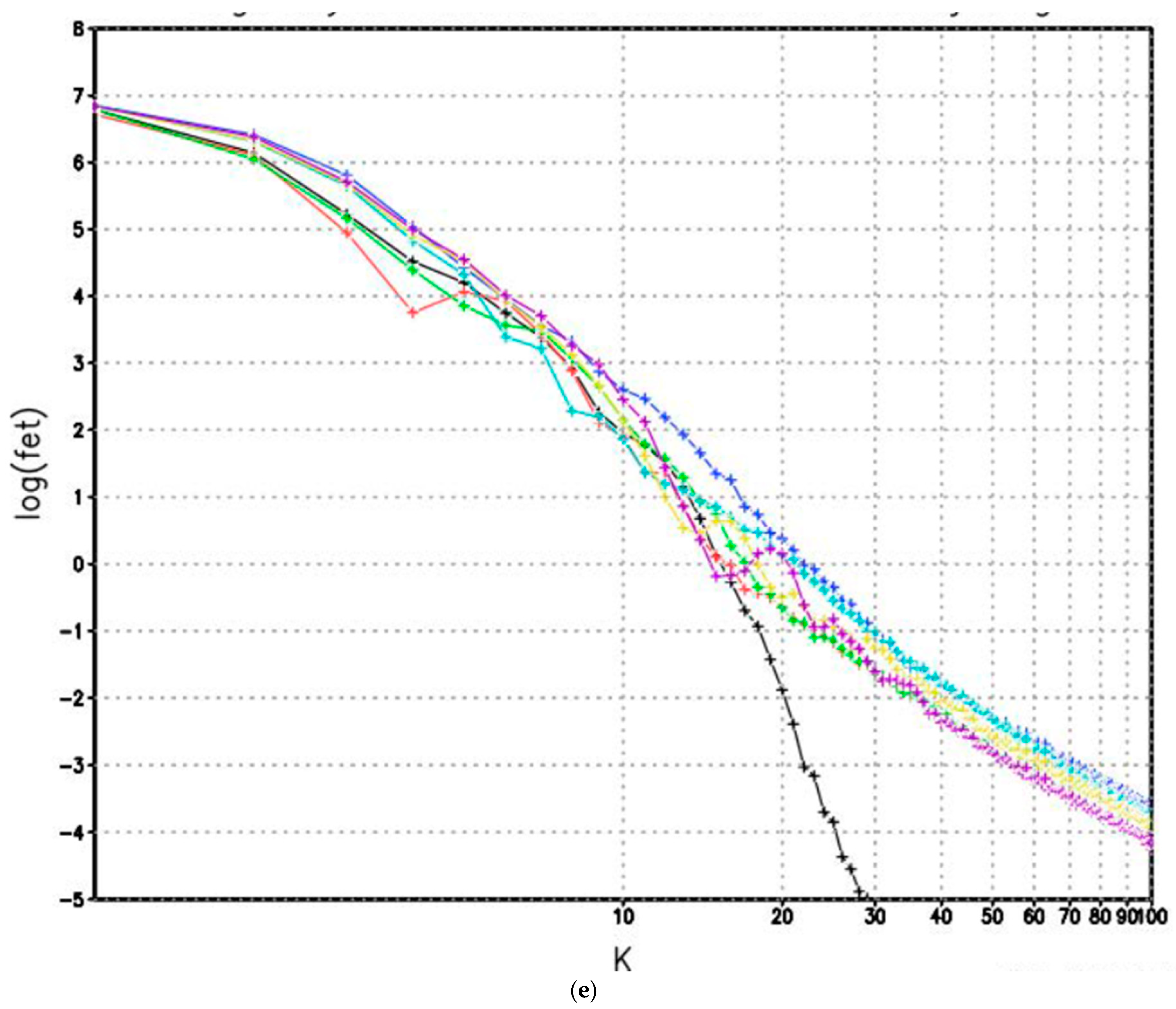
3.2. Energy and Enstrophy
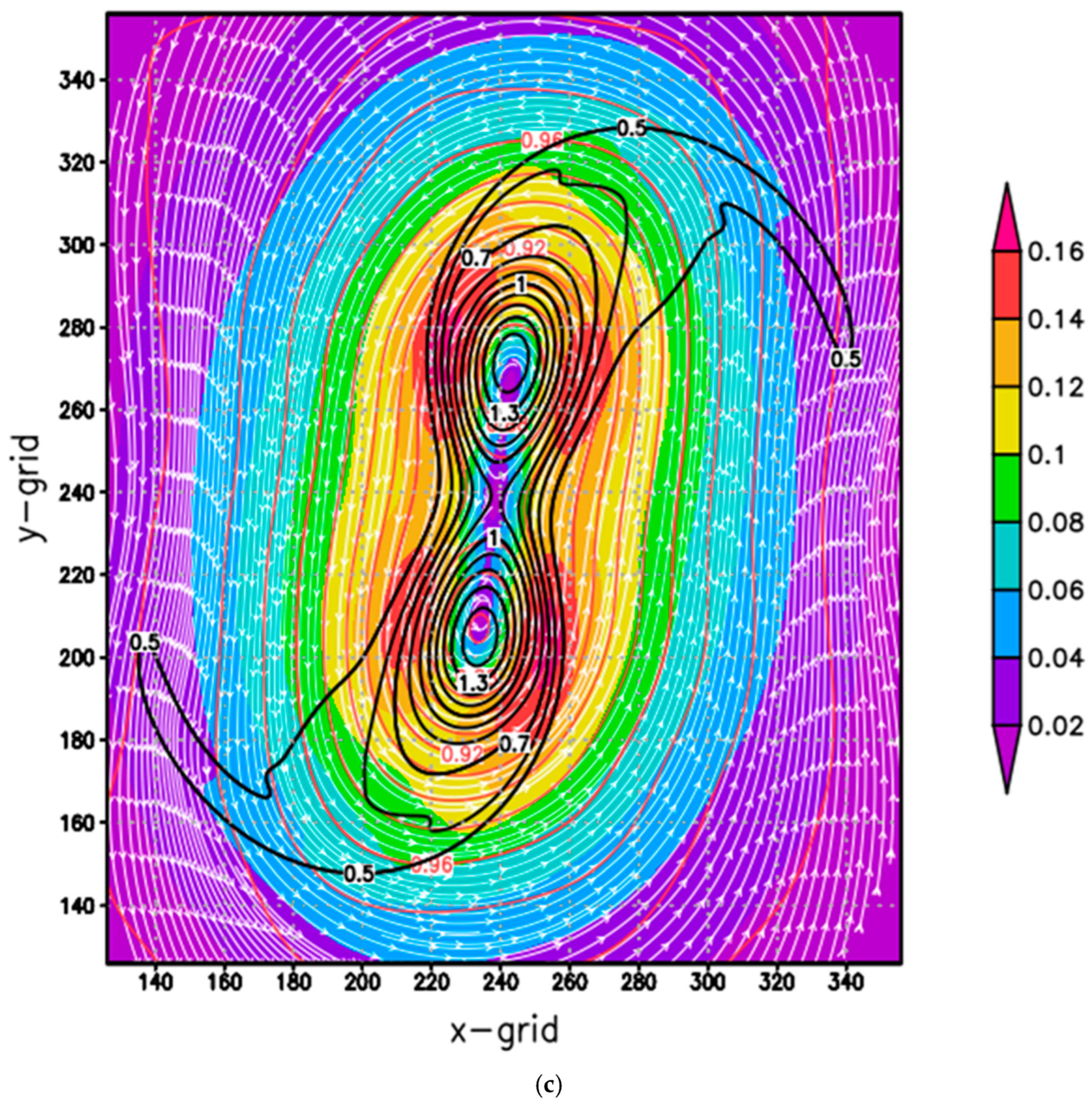
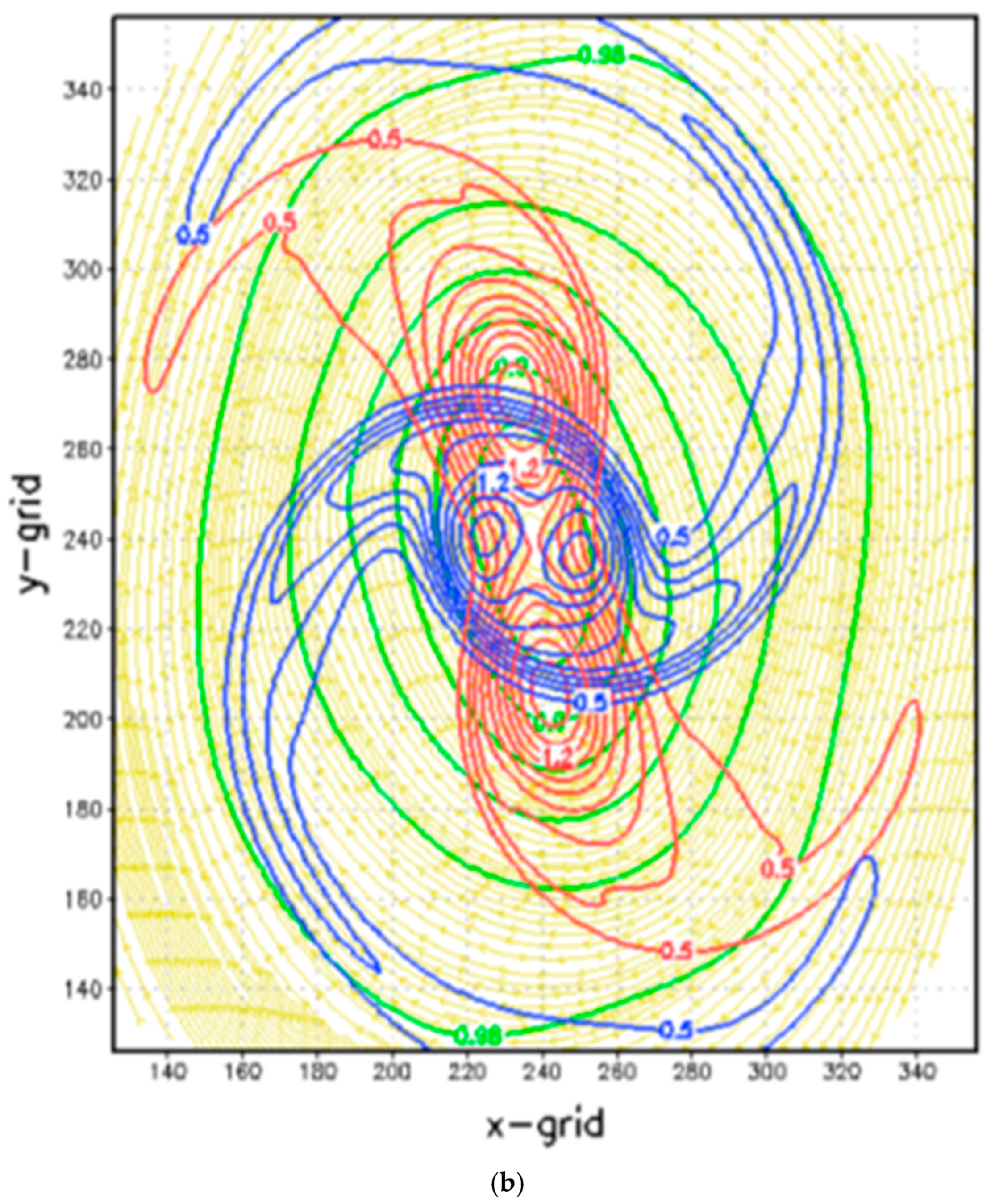
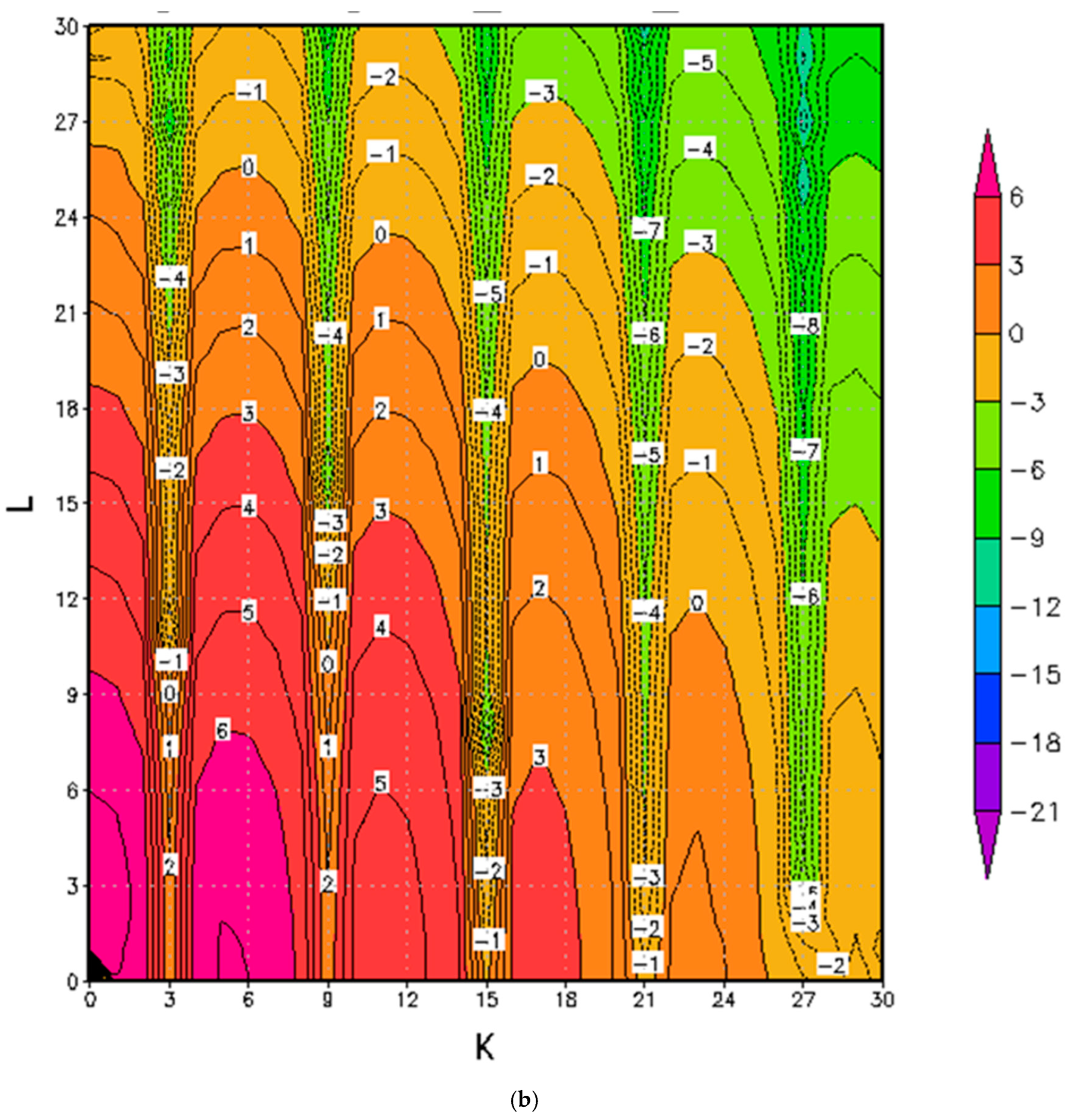
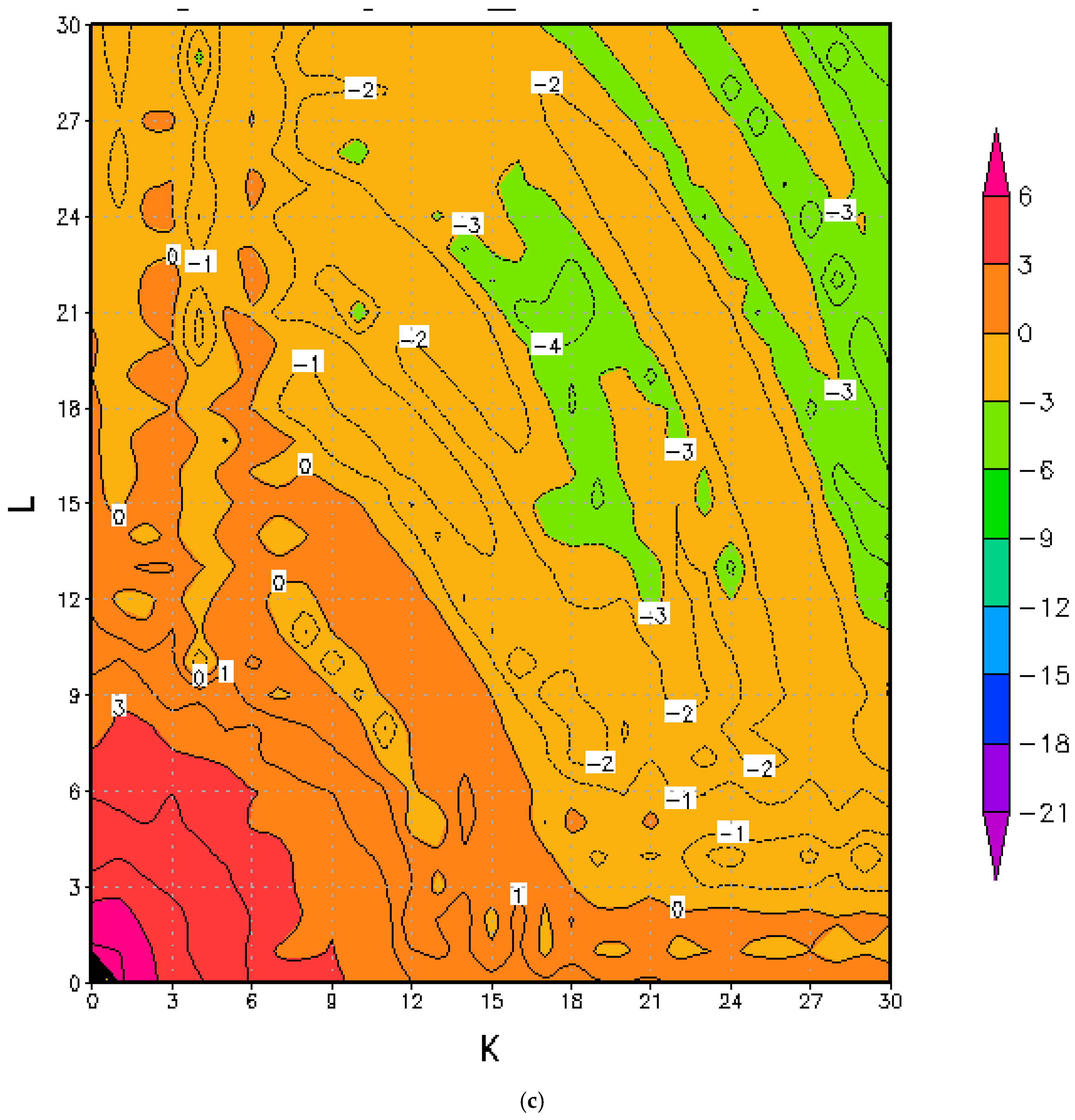
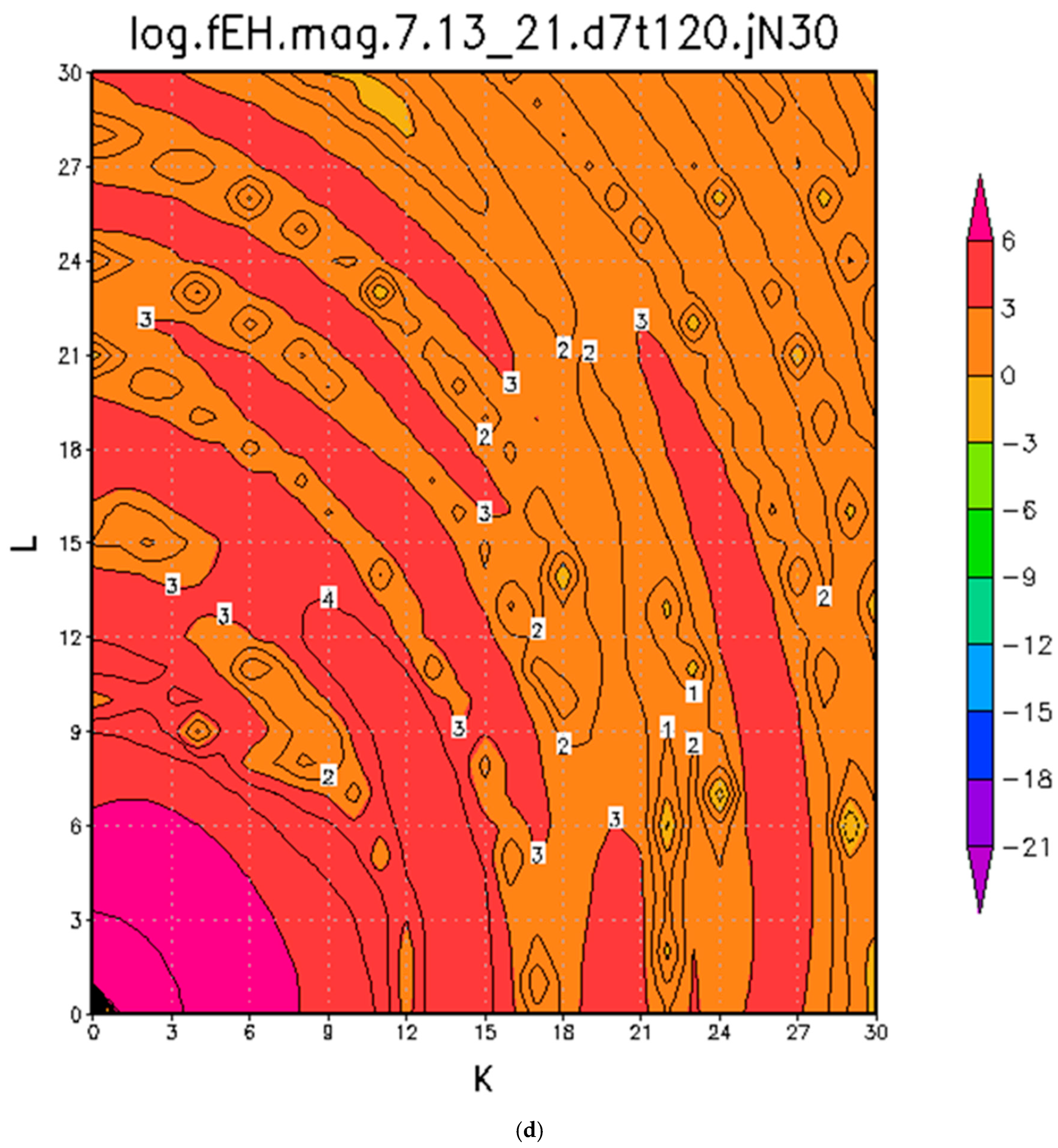
4. Retrieval from Backward Integration
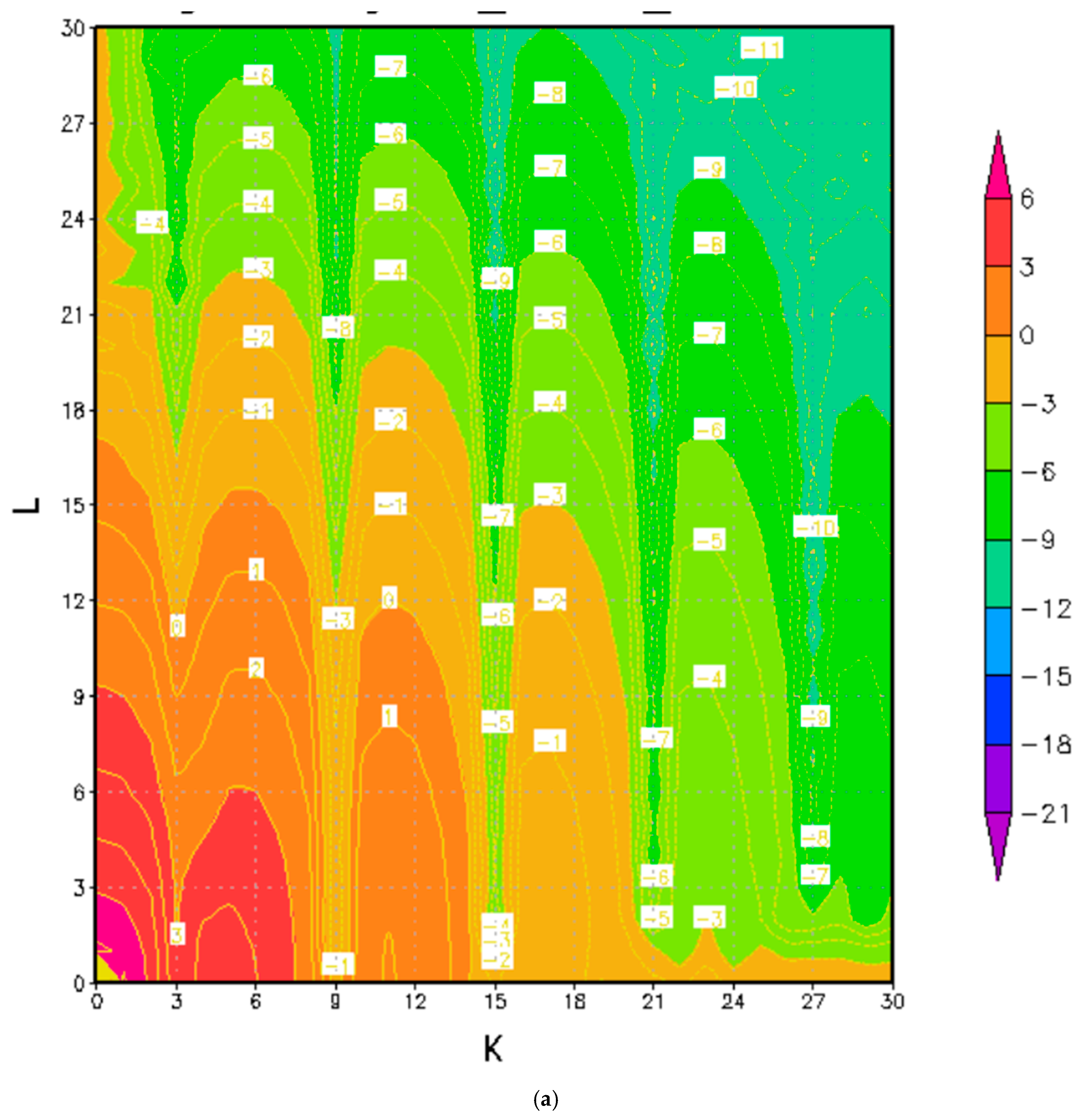
4.1. Backward Integration to Retrieve Initial Condition for Case A
4.2. Integrations for Case B
5. Discussion
6. Summary
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boussinesq, J. Essai sur la Theorie des Eaux Courantes. Memoires Presentes par Divers Savants a L’academie des Sciences de L’institut National de France, 13th ed.; Imprimerie Nationale: Paris, France, 1877; pp. 1–680. [Google Scholar]
- Wikipedia Korteweg-de Vries Equation. Available online: https://en.wikipedia.org/wiki/Korteweg%E2%80%93De_Vries_equation (accessed on 20 March 2025).
- Korteweg, D.J.; de Vries, G. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. London Edinburgh Dublin Philos. Mag. J. Sci. 1895, 39, 422–443. [Google Scholar]
- Konno, K.; Wadati, M. Simple derivation of Backlund Transformation from Riccati form of inverse method. Prog. Theor. Phys. 1975, 53, 1652–1656. [Google Scholar]
- Griffiths, G.W. Ba¨cklund Transformation. Phys. Rev. Lett. 2012, 31, 1386. Available online: https://www.researchgate.net/profile/Graham-Griffiths2/publication/269408982_Backlund_Transformation/links/58b942ac45851591c5d811d3/Baecklund-Transformation.pdf (accessed on 1 January 2024).
- Gadioux, R. Using Ba¨cklund Transformations to Find Soliton Solutions. 2022. Available online: https://www.universityofgalway.ie/media/collegeofscience/schools/schoolofmathematics/files/Romain-Gadioux---Using-B%C3%A4cklund-Transformations-to-Find-Soliton-Solutions.pdf (accessed on 12 December 2024).
- Gao, X.-Y. Symbolic Computation on a (2 + 1)-Dimensional generalized nonlinear evolution system in fluid dynamics, Plasma Physics, Nonlinear Optics and Quantum Mechanics. Qual. Theory Dyn. Syst. 2024, 23, 202. [Google Scholar] [CrossRef]
- Gao, X.Y. Hetero-Bäcklund transformation, bilinear forms and multi-solitons for a (2+1)-dimensional generalized modified dispersive water-wave system for the shallow water. Chin. J. Phys. 2024, 92, 1233–1239. [Google Scholar] [CrossRef]
- Hu, X.-R.; Chen, Y. Bäcklund transformations and explicit solutions of (2+1)-dimensional barotropic and Quasi-Geostrophic Potential Vorticity equation. Commun. Theor. Phys. 2010, 53, 803–808. [Google Scholar]
- Kuo, H.L.; Platzman, G.W. An Investigation of the Nonlinear Solution of the Rayleigh Convection Problem by Means of Characteristic Functions; Department of Meteorology, University of Chicago: Chicago, IL, USA, 1960; p. 76. [Google Scholar]
- Segur, H. Lecture 5: Waves in Shallow Water, Part I: The Theory. 2009. Available online: https://gfd.whoi.edu/wp-content/uploads/sites/18/2018/03/lecture5-harvey_136544.pdf (accessed on 20 January 2025).
- Boyd, J.P. Equatorial solitary waves. Part-1: Rossby solitons. J. Phys. Ocean. 1980, 10, 1699–1717. [Google Scholar]
- Boyd, J.P. Equatorial solitary waves. Part 3: Westward-traveling motions. J. Phys. Ocean. 1985, 15, 46–54. [Google Scholar]
- Liao, S. An optimal homotopy-analysis approach for strongly nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simulat. 2009, 15, 2003–2016. [Google Scholar] [CrossRef]
- Fourier, J.B.J. Theorie Analytique de la Chaleur; Didot: Paris, France, 1822; pp. 499–508. [Google Scholar]
- Keller, J.J. Inverse Euler equation. Z. Angew. Math. Phys. 1966, 49, 363–383. [Google Scholar]
- Kalnay, E.; Park, S.K.; Pu, Z.-X.; Gao, J. Application of the Quasi-Inverse Method to Data Assimilation. Mon. Wea. Rev. 2000, 128, 864–875. [Google Scholar] [CrossRef]
- Van Leeuwen, T.; Brune, C. 10 Lectures on Inverse Problems and Imaging. 2025. Available online: https://tristanvanleeuwen.github.io/IP_and_Im_Lectures/intro.html (accessed on 10 January 2025).
- Sun, W.Y.; Sun, O.M. Backward Integration of Diffusion Equation. Aerosol Air Qual. Res. 2017, 17, 278–289. [Google Scholar] [CrossRef]
- Sun, W.Y. Backward Integration of Nonlinear Shallow Water Model: Part I: Solitary Rossby Waves. Atmosphere 2024, 15, 1161. [Google Scholar] [CrossRef]
- Sun, W.Y. Instability in leapfrog and forward–backward schemes: Part II: Numerical simulations of dam break. Comput. Fluids 2011, 45, 70–76. [Google Scholar] [CrossRef][Green Version]
- Melander, M.V.; Zabusky, N.J.; McWilliams, J.C. Symmetric vortex merger in two dimensions: Causes and conditions. J. Fluid. Mech. 1988, 195, 303–340. [Google Scholar] [CrossRef]
- Waugh, D.W. The efficiency of symmetric vortex merger. Phys. Fluid Dyn. 1992, 4, 1745–1758. [Google Scholar] [CrossRef]
- Oh, T.J. The Development and Testing of Characteristic-based Semi-Lagrangian Two-Dimensional Shallow Water Equations Model. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2020. Available online: https://docs.lib.purdue.edu/dissertations/AAI3278686/ (accessed on 20 March 2025).
- Huang, S.; Xiang, J.; Du, H.; Cao, X. Inverse problems in atmospheric science and their application. J. Phys. Conf. Ser. 2005, 12, 45–57. [Google Scholar] [CrossRef]
- Meunier, P.; Le Dizès, S.; Leweke, T. Physics of vortex merging. Comptes Rendus Phys. 2005, 6, 431–450. [Google Scholar] [CrossRef]
- Sun, W.Y.; Oh, T.J. Vortex merger in shallow water model. Asia-Pacific J. Atmos. Sciences 2022, 58, 533–547. [Google Scholar] [CrossRef]
- Duponcheel, M.; Orlandi, P.; Winckelmans, G. Time-reversibility of the Euler equations as a benchmark for energy conserving schemes. J. Comput. Phys. 2008, 19, 8736–8752. [Google Scholar] [CrossRef]
- Eckhardt, B.; Hascoet, E. Breaking time reversal symmetry by viscous dephasing. Phys. Rev. E 2005, 72, 037301. [Google Scholar]
- Fang, L.; Bos, W.J.T.; Liang, S.; Bertoglio, J.-P.; Shao, L. Time reversibility of Navier-Stokes turbulence and its implication for subgrid scale models. J. Turbul. 2012, 13, 639777. [Google Scholar]
- Sun, W.Y. The Vortex Moving toward Taiwan and the influence of the Central Mountain Range. Geosci. Lett. 2016, 3, 21. [Google Scholar] [CrossRef][Green Version]
- Sun, W.Y. Challenges and Progress in Computational Geophysical Fluid Dynamics in Recent Decades. Atmosphere 2023, 14, 1324. [Google Scholar] [CrossRef]
- Miller, A. MODULE Fast Fourier. 2005. Available online: https://jblevins.org/mirror/amiller/fft.f90 (accessed on 4 October 2024).
- Vallis, G.K. Fundamentals and Large Scale Circulation. In Atmospheric and Oceanic Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2005; p. 774. [Google Scholar]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Acad. Sci. USSR 1941, 30, 299–303. [Google Scholar]
- Obukhov, A.M. Energy distribution in the spectrum of turbulent flow. Izv. Akad. Nauk. SSR Ser. Geogr. Geofiz. 1941, 5, 453–466. [Google Scholar]
- Batchelor, G.K. The theory of homogeneous turbulence. In Cambridge Monographs on Mechanics and Applied Mathematics; Cambridge University Press: Cambridge, UK, 1953; p. 197. [Google Scholar]
- Fjørtoft, R. On the changes in the spectral distribution of kinetic energy for two dimensional nondivergent flow. Tellus 1953, 5, 225–230. [Google Scholar]
- Batchelor, G.K. Computation of the energy spectrum in homogeneous two dimensional turbulence. Phys. Fluids Suppl. 1969, 12, 233–239. [Google Scholar]
- Kraichnan, R. Inertial ranges in two-dimensional turbulence. Phys. Fluids 1967, 10, 1417–1423. [Google Scholar]
- Kraichnan, R.; Montgomery, D. Two-dimensional turbulence. Rep. Prog. Phys. 1980, 43, 547–619. [Google Scholar]
- Nastrom, G.; Gage, K.; Jasperson, W. Kinetic energy spectrum of large-and mesoscale atmospheric processes. Nature 1984, 310, 36–38. [Google Scholar] [CrossRef]
- Kraichnan, R. Inertial-range transfer in two- and three-dimensional turbulence. J. Fluid Mech. 1971, 47, 525–535. [Google Scholar] [CrossRef]
- Deusebio, E.; Boffetta, G.; Lindborg, E.; Musacchio, S. Dimensional transition in rotating turbulence. Phys. Rev. E 2014, 90, 023005. [Google Scholar] [CrossRef]
- Taylor, G.I. Experiments with rotating fluids. Proc. Roy. Soc. Lond. A 1921, 100, 114–121. [Google Scholar]
- Xiao, Z.; Wang, X.; Chen, S.; Eyink, G. Physical mechanism of the inverse energy cascade of two-dimensional turbulence: A numerical investigation. J. Fluid Mech. 2009, 619, 1–44. [Google Scholar]
- Boffetta, G.; Ecke, R.E. Two-Dimensional Turbulence Annu. Rev. Fluid Mech. 2012, 44, 427–451. [Google Scholar]
- Morize, C.; Moisy, F. Energy decay of rotating turbulence with confinement effects. Phys. Fluids 2006, 18, 065107. [Google Scholar]
- Zhou, Y. A phenomenological treatment of rotating turbulence. Phys. Fluids 1995, 7, 2092. [Google Scholar]
- Pouquet, A.; Sen, A.; Rosenberg, D.; Mininni, P.D.; Baerenzung, J. Inverse cascades in turbulence and the case of rotating flows. Phys. Scr. 2013, T155, 014032. [Google Scholar] [CrossRef]
- Sun, W.Y.; Yeh, K.S.; Sun, R.Y. A simple Semi-Lagrangian Scheme for advection equation. Q. J. R. Meteorol. Soc. 1996, 122, 1211–1226. [Google Scholar]
- Sun, W.Y. An efficient forward semi-Lagrangian model. Terr. Atmos. Ocean. Sci. 2024, 35, 2. [Google Scholar] [CrossRef]
- Sun, W.Y. Numerical experiments for advection equation. J. Comput. Phys. 1993, 108, 264–271. [Google Scholar] [CrossRef]
- Poincaré, H. Sur les Fonctions Fuchsiennes. Comptes Rendus Hebd. L’académie Sci. Paris 1882, 94, 1166–1167. [Google Scholar]
- Poincaré, H. Solutions Periodiques, Non-Existence des Integrales Uniformes, Solutions Asymptotiques; Gauthier-Villars: Paris, France, 1892; Volume 1. (In French) [Google Scholar]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.-Y. Backward Integration of Nonlinear Shallow Water Model: Part 2: Vortex Merger. Atmosphere 2025, 16, 365. https://doi.org/10.3390/atmos16040365
Sun W-Y. Backward Integration of Nonlinear Shallow Water Model: Part 2: Vortex Merger. Atmosphere. 2025; 16(4):365. https://doi.org/10.3390/atmos16040365
Chicago/Turabian StyleSun, Wen-Yih. 2025. "Backward Integration of Nonlinear Shallow Water Model: Part 2: Vortex Merger" Atmosphere 16, no. 4: 365. https://doi.org/10.3390/atmos16040365
APA StyleSun, W.-Y. (2025). Backward Integration of Nonlinear Shallow Water Model: Part 2: Vortex Merger. Atmosphere, 16(4), 365. https://doi.org/10.3390/atmos16040365





