The Positive Effects of Linked Control Policy for Vessels Passing Through Locks on Air Quality—A Case Study of Yichang, China
Abstract
:1. Introduction
2. Materials and Methods
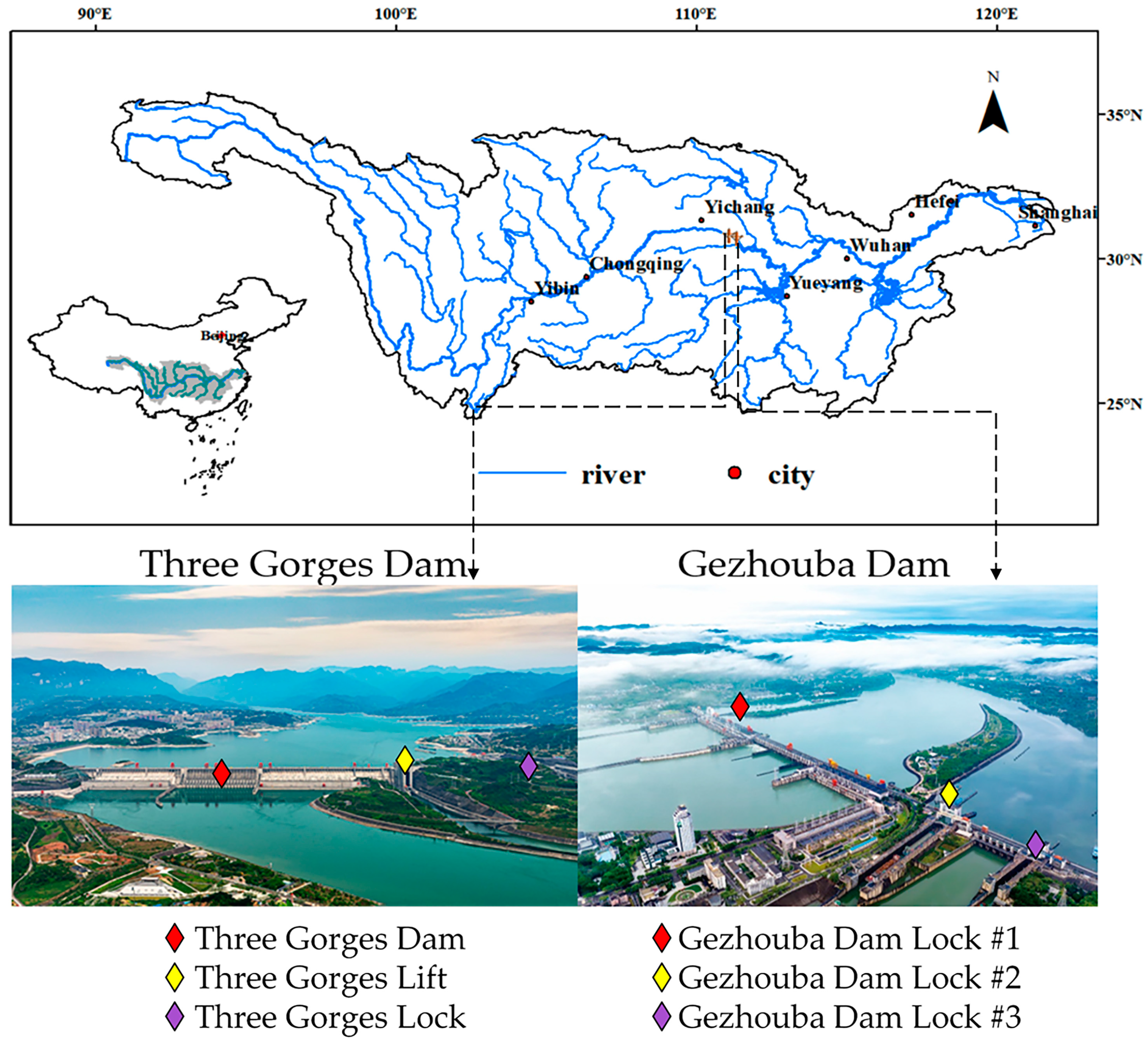
2.1. Location
2.2. Policy
2.3. Data
2.4. Model
3. Results
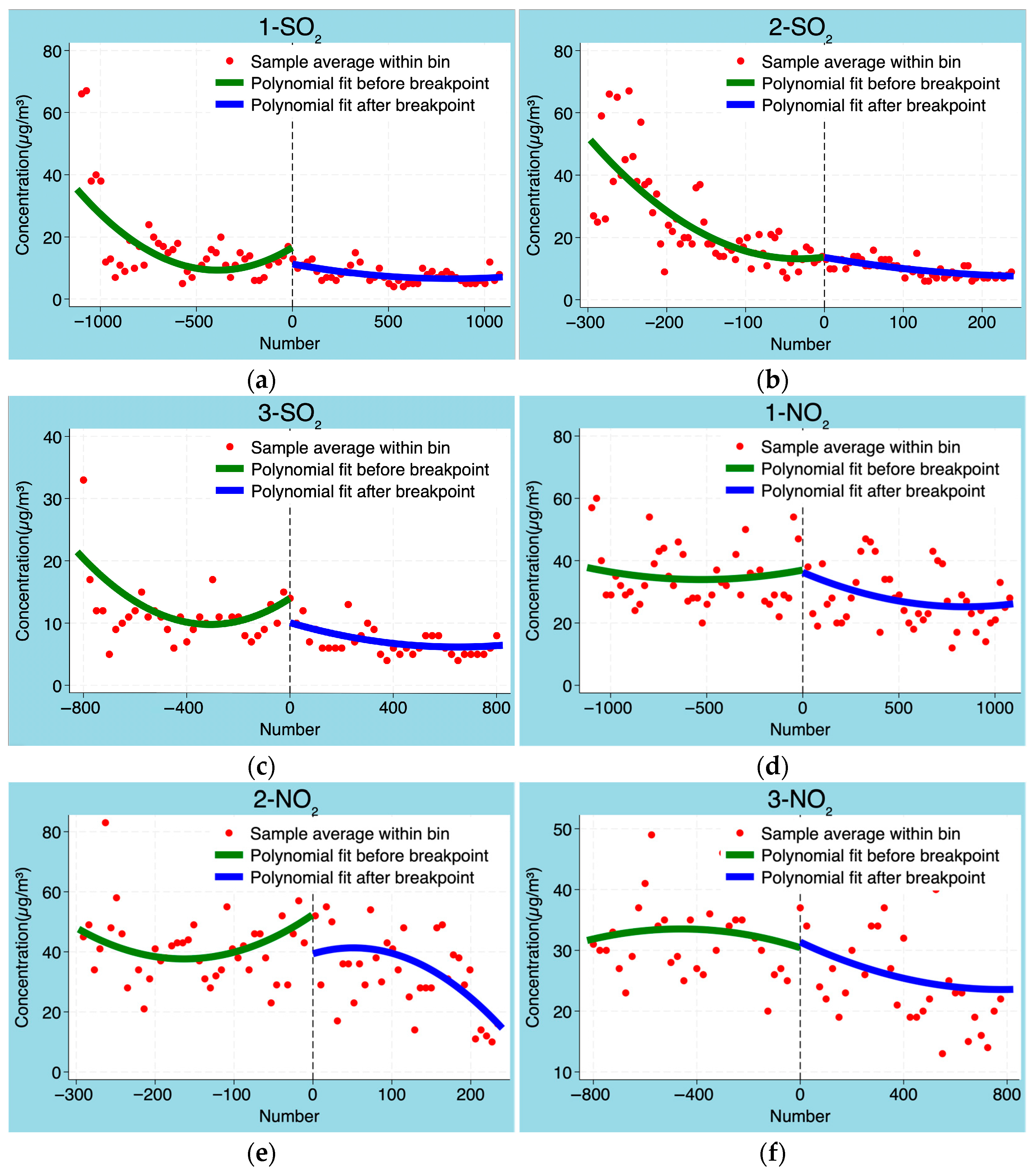
3.1. The Influence of Policy Implementation on SO2 and NO2
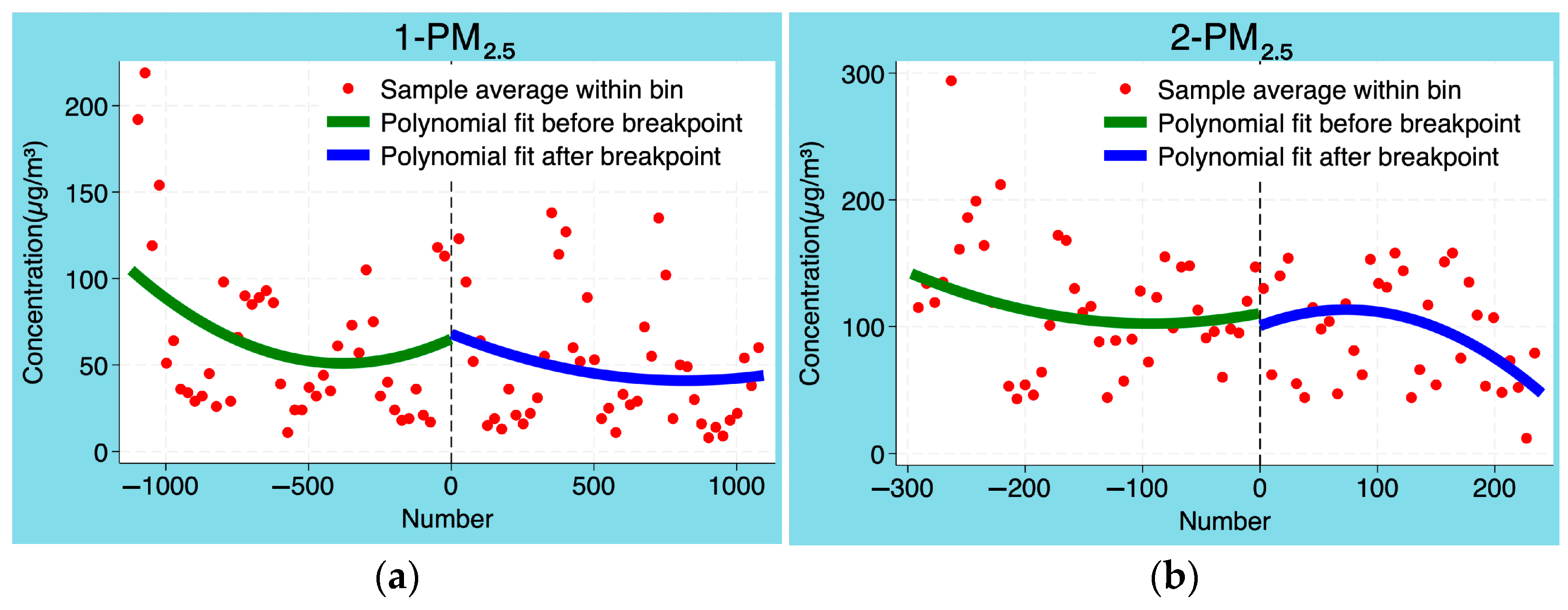
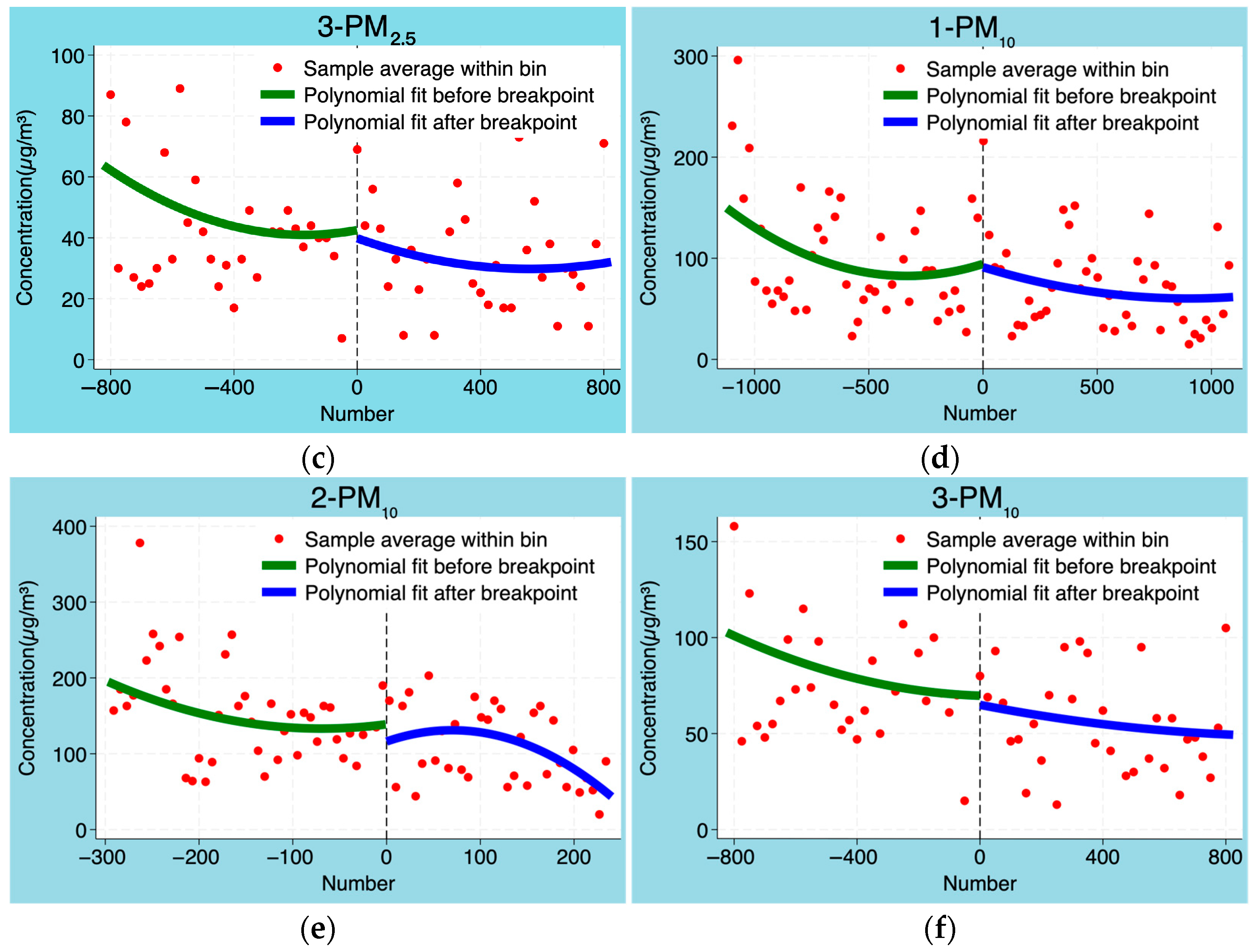
3.2. The Influence of Policy Implementation on PM2.5 and PM10
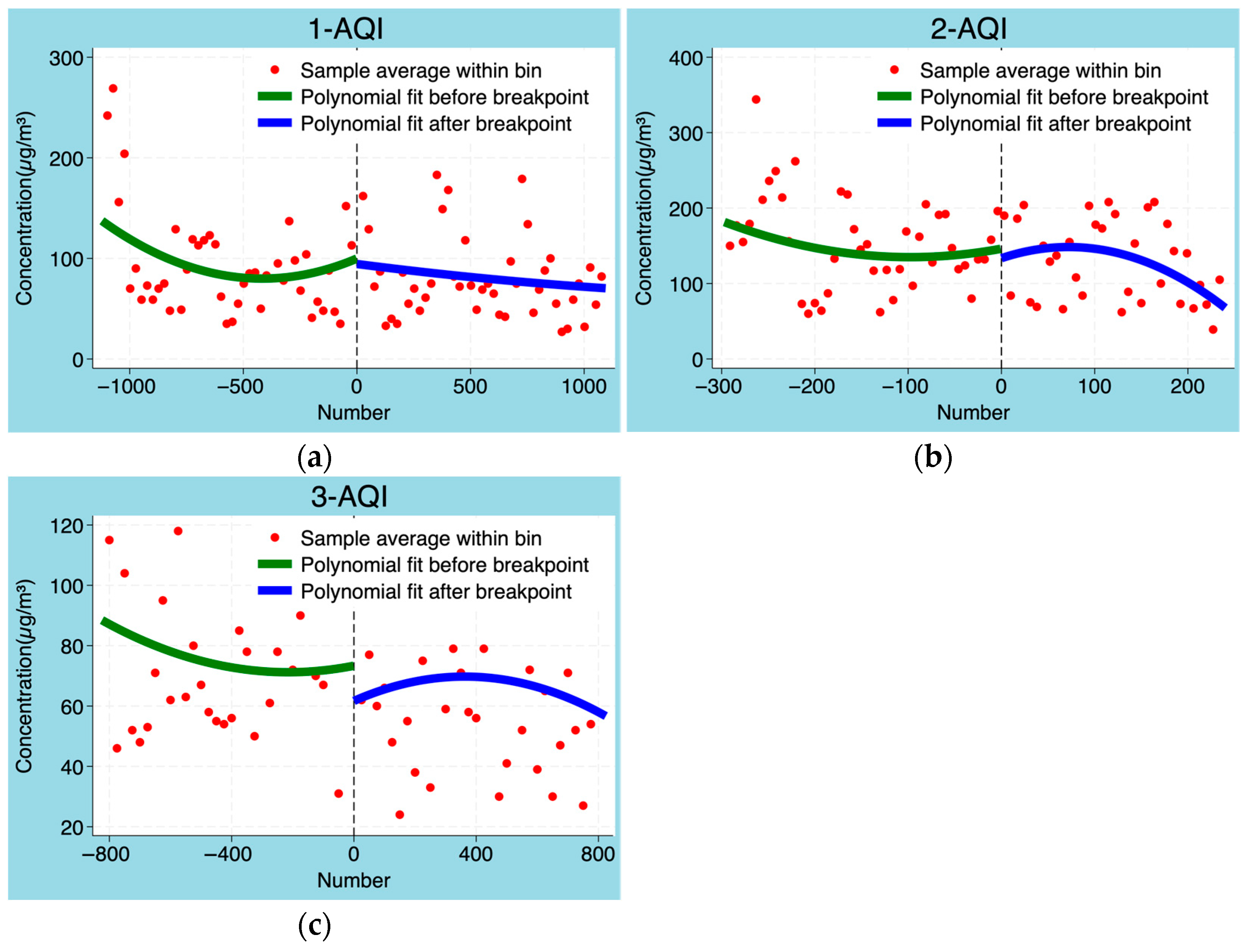
3.3. The Influence of Policy Implementation on AQI
4. Robustness Tests
4.1. Polynomial Order Test
4.2. Local Linear Regression Test Based on Rectangular Kernel Function
4.3. Local Linear Regression Test Based on Triangular Kernel Function
4.4. Continuity Test for Covariates
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Yang, X.; Brown, R.; Yang, L.; Morawska, L.; Ristovski, Z.; Fu, Q.; Huang, C. Shipping emissions and their impacts on air quality in China. Sci. Total Environ. 2017, 581, 186–198. [Google Scholar] [PubMed]
- Liu, Y.S.; Ge, Y.S.; Tan, J.W.; Fu, M.L.; Shah, A.N.; Li, L.Q.; Ji, Z.; Ding, Y. Emission characteristics of offshore fishing ships in the Yellow Bo Sea, China. J. Environ. Sci. 2018, 65, 83–91. [Google Scholar]
- Mueller, N.; Westerby, M.; Nieuwenhuijsen, M. Health Impact Assessments of Shipping and Port-Sourced Air Pollution on a Global Scale: A Scoping Literature Review. Environ. Res. 2023, 216, 114460. [Google Scholar] [PubMed]
- Matthias, V.; Bewersdorff, I.; Aulinger, A.; Quante, M. The contribution of ship emissions to air pollution in the North Sea regions. Environ. Pollut. 2010, 158, 2241–2250. [Google Scholar]
- Zhang, X.; Aikawa, M. The Variation of PM2.5 from Ship Emission under Low-Sulfur Regulation: A Case Study in the Coastal Suburbs of Kitakyushu, Japan. Sci. Total Environ. 2023, 858, 159968. [Google Scholar]
- Sofiev, M.; Winebrake, J.J.; Johansson, L.; Carr, E.W.; Prank, M.; Soares, J.; Vira, J.; Kouznetsov, R.; Jalkanen, J.-P.; Corbett, J.J. Cleaner Fuels for Ships Provide Public Health Benefits with Climate Tradeoffs. Nat. Commun. 2018, 9, 406. [Google Scholar]
- Yuan, T.; Song, H.; Wood, R.; Wang, C.; Oreopoulos, L.; Platnick, S.E.; Von Hippel, S.; Meyer, K.; Light, S.; Wilcox, E. Global Reduction in Ship-Tracks from Sulfur Regulations for Shipping Fuel. Sci. Adv. 2022, 8, eabn7988. [Google Scholar]
- Liu, H.; Fu, M.; Jin, X.; Shang, Y.; Shindell, D.; Faluvegi, G.; Shindell, C.; He, K. Health and Climate Impacts of Ocean-Going Vessels in East Asia. Nat. Clim. Chang. 2016, 6, 1037–1041. [Google Scholar]
- Zhou, F.; Hou, L.; Zhong, R.; Chen, W.; Ni, X.; Pan, S.; Zhao, M.; An, B. Monitoring the Compliance of Sailing Ships with Fuel Sulfur Content Regulations Using Unmanned Aerial Vehicle (UAV) Measurements of Ship Emissions in Open Water. Atmos. Meas. Tech. 2020, 13, 4899–4909. [Google Scholar]
- Fu, M.; Ding, Y.; Ge, Y.; Yu, L.; Yin, H.; Ye, W.; Liang, B. Real-World Emissions of Inland Ships on the Grand Canal, China. Atmos. Environ. 2013, 81, 222–229. [Google Scholar] [CrossRef]
- Kurtenbach, R.; Vaupel, K.; Kleffmann, J.; Klenk, U.; Schmidt, E.; Wiesen, P. Emissions of NO, NO2, and PM from Inland Shipping. Atmos. Chem. Phys. 2016, 16, 14285–14295. [Google Scholar]
- Zhou, F.; Wang, Y.; Hou, L.; An, B. Air Pollutant Emission Factors of Inland River Ships under Compliance. J. Mar. Sci. Eng. 2024, 12, 1732. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, Y.; Sun, P.; Wang, X. An Analysis on Convergence of Data-Driven Approach to Ship Lock Scheduling. Math. Comput. Simul. 2013, 88, 31–38. [Google Scholar]
- Zhao, X.; Lin, Q.; Yu, H. A Co-Scheduling Problem of Ship Lift and Ship Lock at the Three Gorges Dam. IEEE Access 2020, 8, 132893–132910. [Google Scholar]
- Wu, Z.; Ji, B.; Yu, S.S. Modeling and Solution Algorithm for Green Lock Scheduling Problem on Inland Waterways. Mathematics 2024, 12, 1192. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, Y.; Guo, W.; Tian, H.; Tang, K. Ship Scheduling Problem Based on Channel-Lock Coordination in Flood Season. Expert Syst. Appl. 2024, 254, 124393. [Google Scholar]
- Zhang, H.; Ke, J. An Intelligent Scheduling System and Hybrid Optimization Algorithm for Ship Locks of the Three Gorges Hub on the Yangtze River. Mech. Syst. Signal Process. 2024, 208, 110974. [Google Scholar]
- Zhang, Y.; Zheng, Q.-Q.; He, L.-J.; Tian, H.-W. Ship Traffic Optimization Method for Solving the Approach Channel and Lock Co-Scheduling Problem of the Three Gorges Dam on the Yangzi River. Ocean Eng. 2023, 276, 114196. [Google Scholar] [CrossRef]
- Ji, B.; Yuan, X.; Yuan, Y.; Lei, X.; Fernando, T.; Iu, H.H.C. Exact and Heuristic Methods for Optimizing Lock-Quay System in Inland Waterway. Eur. J. Oper. Res. 2019, 277, 740–755. [Google Scholar]
- Xin, Q.; Wang, Y.; Zhang, M.; Wang, R.; Wang, Y. Quantitative Analysis of Influencing Factors on Changzhou Ship Lock Capacity. Appl. Sci. 2024, 14, 4958. [Google Scholar] [CrossRef]
- Li, X.; Mou, J.; Chen, L.; Huang, Y.; Chen, P. Ship–Infrastructure Cooperation: Survey on Infrastructure Scheduling for Waterborne Transportation Systems. J. Mar. Sci. Eng. 2022, 11, 31. [Google Scholar] [CrossRef]
- Schwarzkopf, D.A.; Petrik, R.; Matthias, V.; Quante, M.; Yu, G.; Zhang, Y. Comparison of the Impact of Ship Emissions in Northern Europe and Eastern China. Atmosphere 2022, 13, 894. [Google Scholar] [CrossRef]
- Golak, J.A.P.; Defryn, C.; Grigoriev, A. Optimizing Fuel Consumption on Inland Waterway Networks: Local Search Heuristic for Lock Scheduling. Omega 2022, 109, 0305–0483. [Google Scholar]
- Smith, L.D.; Ii, D.C.S.; Campbell, J.F. Simulation of Alternative Approaches to Relieving Congestion at Locks in a River Transportion System. Oper. Res. 2010, 50, 105–106. [Google Scholar]
- Segovia, P.; Negenborn, R.R.; Reppa, V. Vessel Passage Scheduling through Cascaded Bridges Using Mixed-integer Programming. IFAC Pap. 2022, 55, 248–253. [Google Scholar]
- Pang, Q.H.; Wu, X.Y. Optimization Scheduling Model of Double Line Shiplock Based on Nonlinear Goal Programming. J. Appl. Res. Technol. 2014, 12, 192–200. [Google Scholar]
- National Economic and Social Development Statistical Bulletin of Yichang City. 2023. Available online: http://www.yichang.gov.cn/zfxxgk/show.html?aid=1&id=233339 (accessed on 8 March 2024).
- Three Gorges Navigation Authority. The Throughput of the Three Gorges Hub Will Be Nearly 160 Million Tons in 2024. 2025. Available online: https://sxth.mot.gov.cn/xw_1/thyw_5769/202501/t20250102_427449.html (accessed on 6 January 2025).
- Ma, Y.; Chen, D.; Fu, X.; Shang, F.; Guo, X.; Lang, J.; Zhou, Y. Impact of Sea Breeze on the Transport of Ship Emissions: A Comprehensive Study in the Bohai Rim Region, China. Atmosphere 2022, 13, 1094. [Google Scholar] [CrossRef]
- Zhou, F.; Fan, Y.; Zou, J.; An, B. Ship Emission Monitoring Sensor Web for Research and Application. Ocean Eng. 2022, 249, 110980. [Google Scholar]
- Three Gorges Navigation Authority. The Traffic Organization of Yangtze River Trunk Line Crossing Dam by Coordinated Control of Ships. 2017. Available online: https://sxth.mot.gov.cn/fw/thfw/thgg_5774/202103/P020210327592677984068.pdf (accessed on 6 January 2025).
- GB 3095—2012; Ministry of Ecology and Environment Ambient Air Quality Standards. 2012. Available online: https://www.mee.gov.cn/ywgz/fgbz/bz/bzwb/dqhjbh/dqhjzlbz/201203/W020120410330232398521.pdf (accessed on 8 February 2025).
- Zhang, Q.; Zheng, Z.; Wan, Z.; Zheng, S. Does Emission Control Area Policy Reduce Sulfur Dioxides Concentration in Shanghai? Transp. Res. Part Transp. Environ. 2020, 81, 102289. [Google Scholar]
- Zhang, Q.; Liu, H.; Wan, Z. Evaluation on the effectiveness of ship emission control area policy: Heterogeneity detection with the regression discontinuity method. Environ. Impact Assess. Rev. 2022, 94, 106747. [Google Scholar]
- Song, S.K.; Shon, Z.H.; Moon, S.H.; Lee, T.H.; Kim, H.S.; Kang, S.H.; Park, G.H.; Yoo, E.C. Impact of international Maritime Organization 2020 sulfur content regulations on port air quality at international hub port. J. Clean. Prod. 2022, 347, 131298. [Google Scholar]
- Xiao, G.; Xu, L. Challenges and Opportunities of Maritime Transport in the Post-Epidemic Era. J. Mar. Sci. Eng. 2024, 12, 1685. [Google Scholar] [CrossRef]
- Xiao, G.; Wang, Y.; Wu, R.; Li, J.; Cai, Z. Sustainable Maritime Transport: A Review of Intelligent Shipping Technology and Green Port Construction Applications. J. Mar. Sci. Eng. 2024, 12, 1728. [Google Scholar] [CrossRef]
| Groups | Variable | Obs. | Mean. | Std. Dev. | Min. | Max. |
|---|---|---|---|---|---|---|
| 1 | SO2 | 2187 | 12 | 9 | 3 | 92 |
| NO2 | 32 | 11 | 8 | 83 | ||
| PM2.5 | 56 | 43 | 3 | 318 | ||
| PM10 | 84 | 52 | 8 | 407 | ||
| AQI | 87 | 48 | 21 | 368 | ||
| IDE | 44 | 19 | 21 | 82 | ||
| ISE | 72 | 59 | 16 | 199 | ||
| IWE | 26 | 12 | 16 | 50 | ||
| 2 | SO2 | 538 | 18 | 14 | 5 | 92 |
| NO2 | 38 | 13 | 8 | 83 | ||
| PM2.5 | 105 | 50 | 10 | 318 | ||
| PM10 | 131 | 63 | 16 | 407 | ||
| AQI | 138 | 60 | 26 | 368 | ||
| IDE | 46 | 19 | 21 | 82 | ||
| ISE | 72 | 59 | 16 | 199 | ||
| IWE | 27 | 13 | 16 | 50 | ||
| 3 | SO2 | 1649 | 10 | 5 | 3 | 56 |
| NO2 | 29 | 9 | 12 | 64 | ||
| PM2.5 | 40 | 25 | 3 | 206 | ||
| PM10 | 68 | 35 | 8 | 286 | ||
| AQI | 71 | 28 | 21 | 256 | ||
| IDE | 43 | 19 | 21 | 82 | ||
| ISE | 72 | 59 | 25 | 199 | ||
| IWE | 26 | 12 | 16 | 50 |
| 1-SO2 | 2-SO2 | 3-SO2 | ||||
|---|---|---|---|---|---|---|
| (a) | (b) | (a) | (b) | (a) | (b) | |
| r | −9.60 *** (1.50) | −8.06 *** (1.46) | −6.78 ** (2.68) | −4.81 ** (2.14) | −4.51 *** (0.82) | −2.89 *** (0.82) |
| Cons. | 24.40 *** (1.34) | 24.39 *** (1.96) | 20.17 *** (2.01) | 23.85 *** (2.94) | 16.68 *** (0.53) | 19.02 *** (1.04) |
| IDE | −0.06 (0.05) | 0.01 (0.10) | −0.18 *** (0.03) | |||
| ISE | 0.07 ** (0.03) | 0.01 (0.05) | 0.12 *** (0.01) | |||
| IWE | −0.14 * (0.07) | −0.37 *** (0.12) | −0.20 *** (0.04) | |||
| Obs. | 2187 | 2187 | 538 | 538 | 1649 | 1649 |
| R2 | 0.718 | 0.732 | 0.774 | 0.780 | 0.663 | 0.671 |
| AIC | 13,023.29 | 12,915.82 | 3541.99 | 3529.52 | 8457.41 | 8420.76 |
| BIC | 13,068.81 | 12,978.41 | 3584.87 | 3580.98 | 8500.68 | 8480.25 |
| Order | 9 | 9 | 9 | 9 | 7 | 7 |
| 1-NO2 | 2-NO2 | 3-NO2 | ||||
|---|---|---|---|---|---|---|
| (a) | (b) | (a) | (b) | (a) | (b) | |
| r | −20.31 *** (3.38) | −18.52 *** (3.32) | −21.38 *** (6.22) | −21.94 *** (6.47) | −9.75 *** (3.10) | −9.37 *** (3.47) |
| Cons. | 74.19 *** (2.10) | 56.59 *** (3.92) | 76.55 *** (3.29) | 73.05 *** (6.10) | 54.24 *** (2.34) | 43.01 *** (3.74) |
| IDE | 0.84 *** (0.15) | 0.06 (0.21) | 0.61 *** (0.13) | |||
| ISE | −0.06 ** (0.02) | 0.048 (0.04) | −0.17 *** (0.05) | |||
| IWE | −0.75 *** (0.14) | −0.10 (0.22) | −0.16 (0.13) | |||
| Obs. | 2187 | 2187 | 538 | 538 | 1649 | 1649 |
| R2 | 0.420 | 0.445 | 0.439 | 0.441 | 0.379 | 0.388 |
| AIC | 15,395.96 | 15,300.48 | 3974.99 | 3975.72 | 11,080.51 | 11,057.79 |
| BIC | 15,441.48 | 15,363.07 | 4017.87 | 4031.46 | 11,123.78 | 11,117.27 |
| Order | 9 | 9 | 8 | 8 | 9 | 9 |
| 1-PM2.5 | 2-PM2.5 | 3-PM2.5 | ||||
|---|---|---|---|---|---|---|
| (a) | (b) | (a) | (b) | (a) | (b) | |
| r | −17.71 (14.26) | −15.10 (14.52) | −37.59 (28.15) | −24.11 (25.58) | −13.28 * (7.44) | −23.16 *** (8.59) |
| Cons. | 174.0 *** (9.42) | 213.9 *** (15.70) | 155.4 *** (14.29) | 189.9 *** (27.37) | 90.34 *** (5.69) | 106.5 *** (10.13) |
| IDE | −1.61 *** (0.58) | −1.08 (1.13) | −0.21 (0.37) | |||
| ISE | 0.30 ** (0.15) | 0.16 (0.25) | −0.24 (0.17) | |||
| IWE | 0.35 (0.62) | −0.22 (1.14) | 0.61 (0.42) | |||
| Obs. | 2187 | 2187 | 538 | 538 | 1649 | 1649 |
| R2 | 0.381 | 0.397 | 0.263 | 0.267 | 0.287 | 0.294 |
| AIC | 21,641.10 | 21,587.13 | 5581.02 | 5580.75 | 14,686.53 | 14,671.92 |
| BIC | 21,686.63 | 21,649.72 | 5623.89 | 5636.50 | 14,729.80 | 14,731.40 |
| Order | 9 | 9 | 9 | 9 | 9 | 9 |
| 1-PM10 | 2-PM10 | 3-PM10 | ||||
|---|---|---|---|---|---|---|
| (a) | (b) | (a) | (b) | (a) | (b) | |
| r | −49.13 *** (15.09) | −46.81 *** (15.15) | −39.03 (26.82) | −21.40 (24.28) | −55.31 *** (11.44) | −57.63 *** (11.95) |
| Cons. | 211.5 *** (9.63) | 246.5 *** (16.11) | 192.8 *** (14.41) | 233.6 *** (31.30) | 127.9 *** (7.32) | 159.2 *** (14.54) |
| IDE | −0.99 * (0.58) | −1.55 (1.29) | −0.33 (0.52) | |||
| ISE | 0.31 * (0.17) | 0.28 (0.28) | −0.09 (0.24) | |||
| IWE | −0.92 (0.66) | −0.01 (1.33) | −0.55 (0.56) | |||
| Obs. | 2187 | 2187 | 538 | 538 | 1649 | 1649 |
| R2 | 0.390 | 0.403 | 0.353 | 0.356 | 0.283 | 0.299 |
| AIC | 22,372.91 | 22,329.05 | 5760.36 | 5758.96 | 15,896.35 | 15,863.89 |
| BIC | 22,424.12 | 22,397.34 | 5807.52 | 5814.70 | 15,945.02 | 15,928.79 |
| Order | 9 | 1 | 9 | 9 | 8 | 9 |
| 1-AQI | 2-AQI | 3-AQI | ||||
|---|---|---|---|---|---|---|
| (a) | (b) | (a) | (b) | (a) | (b) | |
| r | −20.12 (16.36) | −17.92 (16.45) | −40.17 (34.07) | −25.14 (31.22) | −43.35 *** (9.60) | −44.62 *** (9.86) |
| Cons. | 208.7 *** (10.46) | 251.6 *** (17.49) | 198.6 *** (18.60) | 244.0 *** (34.75) | 110.3 *** (6.52) | 141.3 *** (12.11) |
| IDE | −1.61 ** (0.64) | −1.35 (1.42) | −0.71 * (0.43) | |||
| ISE | 0.35 ** (0.16) | 0.15 (0.29) | 0.21 (0.21) | |||
| IWE | −0.10 (0.70) | −0.22 (1.41) | −0.78 (0.49) | |||
| Obs. | 2187 | 2187 | 538 | 538 | 1649 | 1649 |
| R2 | 0.325 | 0.340 | 0.254 | 0.259 | 0.157 | 0.168 |
| AIC | 22,324.73 | 22,279.16 | 5787.93 | 5785.12 | 15,439.75 | 15,420.65 |
| BIC | 22,375.94 | 22,347.45 | 5835.10 | 5840.86 | 15,488.42 | 15,485.54 |
| Order | 9 | 9 | 9 | 9 | 8 | 8 |
| 1-SO2 | 2-SO2 | 3-SO2 | ||||
|---|---|---|---|---|---|---|
| (a) | (b) | (a) | (b) | (a) | (b) | |
| r | −8.93 *** (1.33) | −1.25 (1.07) | −2.35 (2.07) | −1.72 (2.01) | −2.31 ** (0.94) | −3.43 *** (1.05) |
| Cons. | 20.91 *** (2.09) | 26.54 *** (1.85) | 23.99 *** (2.81) | 23.95 *** (2.76) | 20.09 *** (0.98) | 20.28 *** (1.13) |
| IDE | 0.03 (0.07) | −0.35 *** (0.06) | −0.08 (0.09) | −0.09 (0.09) | −0.20 *** (0.03) | −0.20 *** (0.03) |
| ISE | 0.09 *** (0.03) | 0.15 *** (0.03) | 0.04 (0.04) | 0.04 (0.04) | 0.10 *** (0.01) | 0.13 *** (0.01) |
| IWE | −0.38 *** (0.05) | −0.13 (0.08) | −0.46 *** (0.10) | −0.44 *** (0.11) | −0.06 (0.04) | −0.16 *** (0.04) |
| Obs. | 2187 | 2187 | 538 | 538 | 1649 | 1649 |
| Order | 8 | 7 | 7 | 8 | 9 | 8 |
| 1-NO2 | 2-NO2 | 3-NO2 | ||||
|---|---|---|---|---|---|---|
| (a) | (b) | (a) | (b) | (a) | (b) | |
| r | −20.26 *** (3.28) | −9.03 *** (3.14) | −18.79 *** (6.14) | −23.42 *** (6.86) | −16.99 *** (3.53) | −10.69 *** (3.33) |
| Cons. | 52.74 *** (3.73) | 61.50 *** (3.54) | 74.65 *** (6.07) | 74.26 *** (6.06) | 44.54 *** (4.18) | 43.11 *** (4.05) |
| IDE | 0.98 *** (0.15) | 0.37 *** (0.12) | −0.05 (0.22) | 0.03 (0.21) | 0.61 *** (0.14) | 0.57 *** (0.14) |
| ISE | −0.04 (0.03) | 0.05 ** (0.02) | 0.07 (0.04) | 0.04 (0.04) | −0.02 (0.06) | −0.11 ** (0.05) |
| IWE | −1.03 *** (0.12) | −0.71 *** (0.11) | −0.11 (0.22) | −0.01 (0.20) | −0.77 *** (0.13) | −0.46 *** (0.14) |
| Obs. | 2187 | 2187 | 538 | 538 | 1649 | 1649 |
| Order | 8 | 6 | 9 | 7 | 8 | 7 |
| 1-PM2.5 | 2-PM2.5 | 3-PM2.5 | ||||
|---|---|---|---|---|---|---|
| (a) | (b) | (a) | (b) | (a) | (b) | |
| r | 22.69 * (12.67) | −22.64 * (13.27) | −8.54 (27.07) | −0.16 (25.45) | −28.70 *** (8.50) | −30.73 *** (9.04) |
| Cons. | 186.9 *** (15.17) | 219.7 *** (14.35) | 195.3 *** (26.34) | 191.4 *** (26.77) | 104.0 *** (10.94) | 106.2 *** (11.17) |
| IDE | −3.10 *** (0.52) | −0.73 (0.60) | −1.98 * (1.07) | −2.01 * (1.08) | −0.15 (0.40) | −0.19 (0.40) |
| ISE | 0.86 *** (0.13) | 0.46 *** (0.14) | 0.39 * (0.22) | 0.40 * (0.22) | −0.09 (0.18) | −0.05 (0.20) |
| IWE | −0.39 (0.54) | −1.51 *** (0.54) | −0.58 (1.06) | −0.66 (1.12) | −0.19 (0.45) | −0.23 (0.44) |
| Obs. | 2187 | 2187 | 538 | 538 | 1649 | 1649 |
| Order | 8 | 6 | 7 | 8 | 7 | 8 |
| 1-PM10 | 2-PM10 | 3-PM10 | ||||
|---|---|---|---|---|---|---|
| (a) | (b) | (a) | (b) | (a) | (b) | |
| r | −54.86 *** (14.64) | 1.52 (13.17) | 16.06 (23.26) | 6.98 (24.96) | −46.17 *** (11.38) | −31.81 *** (11.79) |
| Cons. | 222.0 *** (15.68) | 258.9 *** (14.92) | 231.0 *** (27.77) | 236.0 *** (31.56) | 149.6 *** (13.05) | 155.6 *** (13.94) |
| IDE | −0.17 (0.59) | −3.03 *** (0.53) | −2.68 ** (1.11) | −2.61 ** (1.24) | −0.37 (0.51) | −0.23 (0.49) |
| ISE | 0.47 *** (0.16) | 0.97 *** (0.15) | 0.53 ** (0.21) | 0.57 ** (0.26) | −0.27 (0.23) | −0.57 ** (0.22) |
| IWE | −2.65 *** (0.57) | −1.49 ** (0.58) | −0.31 (1.15) | −0.55 (1.30) | −0.02 (0.57) | 1.20 ** (0.55) |
| Obs. | 2187 | 2187 | 538 | 538 | 1649 | 1649 |
| Order | 8 | 6 | 6 | 8 | 9 | 7 |
| 1-AQI | 2-AQI | 3-AQI | ||||
|---|---|---|---|---|---|---|
| (a) | (b) | (a) | (b) | (a) | (b) | |
| r | −25.70 (15.67) | 20.31 (14.83) | −7.08 (32.60) | 1.15 (30.79) | −41.54 *** (9.72) | −38.21 *** (9.35) |
| Cons. | 220.4 *** (16.97) | 266.3 *** (17.11) | 249.2 *** (33.50) | 245.0 *** (33.99) | 145.0 *** (12.26) | 141.3 *** (12.11) |
| IDE | −0.61 (0.66) | −3.24 *** (0.59) | −2.33 * (1.33) | −2.35 * (1.35) | −0.86 ** (0.43) | −0.74 * (0.43) |
| ISE | 0.54 *** (0.16) | 0.83 *** (0.16) | 0.40 (0.25) | 0.41 (0.25) | 0.16 (0.20) | 0.12 (0.20) |
| IWE | −2.24 *** (0.61) | −0.15 (0.73) | −0.62 (1.31) | −0.71 (1.38) | −0.37 (0.45) | −0.50 (0.50) |
| Obs. | 2187 | 2187 | 538 | 538 | 1649 | 1649 |
| Order | 8 | 7 | 7 | 8 | 6 | 7 |
| 1-SO2 | 2-SO2 | 3-SO2 | 1-NO2 | 2-NO2 | 3-NO2 | |
| r-Treat | 2.45 | 1.75 | −2.22 | −10.18 | −12.98 | −16.13 |
| r-0.5Treat | 4.26 | 4.26 | −0.4 | 4.2 | −4.22 | 4 |
| r-2Treat | 0.02 | 0.76 | −4.25 | −17.12 | −19.38 | −17.75 |
| Obs. | 2187 | 538 | 1649 | 2187 | 538 | 1649 |
| Bandwidth | 6.95 | 7.07 | 6.01 | 8.69 | 10.18 | 7.70 |
| 0.5Bandwidth | 3.47 | 3.53 | 3.00 | 4.34 | 5.09 | 3.85 |
| 2Bandwidth | 13.90 | 14.14 | 12.03 | 17.39 | 20.37 | 15.40 |
| 1-PM2.5 | 2-PM2.5 | 3-PM2.5 | 1-PM10 | 2-PM10 | 3-PM10 | |
| r-Treat | 50.16 | 53.88 | −36.75 | 43.11 | 37.18 | −71.80 |
| r-0.5Treat | 59.61 | 35.10 | −23.25 | 9.06 | 32.56 | −39.04 |
| r-2Treat | 24.05 | 13.28 | −16.87 | 7.01 | 7.16 | −33.34 |
| Obs. | 2187 | 538 | 1649 | 2187 | 538 | 1649 |
| Bandwidth | 11.12 | 13.76 | 10.34 | 12.84 | 16.05 | 11.59 |
| 0.5Bandwidth | 5.56 | 6.88 | 5.17 | 6.42 | 8.02 | 5.79 |
| 2Bandwidth | 22.24 | 27.52 | 20.69 | 25.69 | 32.10 | 23.18 |
| 1-AQI | 2-AQI | 3-AQI | ||||
| r-Treat | 65.91 | 73.74 | −41.42 | |||
| r-0.5Treat | 74.72 | 45.79 | −26.98 | |||
| r-2Treat | 31.85 | 11.13 | −41.42 | |||
| Obs. | 2187 | 538 | 1649 | |||
| Bandwidth | 11.87 | 15.13 | 10.82 | |||
| 0.5Bandwidth | 5.93 | 7.56 | 5.41 | |||
| 2Bandwidth | 23.75 | 30.27 | 21.64 |
| 1-SO2 | 2-SO2 | 3-SO2 | 1-NO2 | 2-NO2 | 3-NO2 | |
| r-Treat | 2.60 | 2.55 | −1.91 | −9.83 | −11.89 | −15.23 |
| r-0.5Treat | 4.95 | 4.96 | −0.42 | −0.08 | −2.89 | −2.81 |
| r-2Treat | 1.10 | 1.07 | −4.11 | −16.09 | −16.24 | −17.50 |
| Obs. | 2187 | 538 | 1649 | 2187 | 538 | 1649 |
| Bandwidth | 8.84 | 9.00 | 7.66 | 11.07 | 12.96 | 9.80 |
| 0.5Bandwidth | 4.42 | 4.50 | 3.83 | 5.53 | 6.48 | 4.90 |
| 2Bandwidth | 17.69 | 18.01 | 15.32 | 22.14 | 25.93 | 19.61 |
| 1-PM2.5 | 2-PM2.5 | 3-PM2.5 | 1-PM10 | 2-PM10 | 3-PM10 | |
| r-Treat | 48.20 | 48.01 | −32.75 | 38.41 | 30.46 | −62.95 |
| r-0.5Treat | 44.31 | 40.02 | −19.29 | 20.08 | 27.46 | −34.62 |
| r-2Treat | 26.76 | 18.93 | −16.30 | 15.24 | 10.03 | −40.28 |
| Obs. | 2187 | 538 | 1649 | 2187 | 538 | 1649 |
| Bandwidth | 14.16 | 17.51 | 13.17 | 16.35 | 20.43 | 14.76 |
| 0.5Bandwidth | 7.08 | 8.75 | 6.58 | 8.17 | 10.21 | 7.38 |
| 2Bandwidth | 28.32 | 35.03 | 26.35 | 32.70 | 40.87 | 29.52 |
| 1-AQI | 2-AQI | 3-AQI | ||||
| r-Treat | 64.47 | 60.99 | −36.70 | |||
| r-0.5Treat | 52.78 | 52.42 | −19.87 | |||
| r-2Treat | 32.92 | 19.09 | −15.97 | |||
| Obs. | 2187 | 538 | 1649 | |||
| Bandwidth | 15.12 | 19.27 | 13.77 | |||
| 0.5Bandwidth | 7.56 | 9.63 | 6.88 | |||
| 2Bandwidth | 30.24 | 38.54 | 27.55 |
| 1 | 2 | 3 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| IDE | ISE | IWE | IDE | ISE | IWE | IDE | ISE | IWE | |
| r | −5.46 *** (0.72) | −26.57 *** (3.12) | −2.69 *** (0.36) | 3.86 *** (1.24) | −1.09 (4.42) | 2.07 * (1.06) | −3.95 *** (0.73) | −8.41 *** (2.67) | −4.09 *** (0.64) |
| Cons. | 42.43 *** (0.60) | 77.47 *** (2.85) | 15.95 *** (0.24) | 37.64 *** (0.97) | 61.91 *** (3.64) | 12.76 *** (0.96) | 41.45 *** (0.39) | 65.47 *** (1.21) | 15.88 *** (0.24) |
| Obs. | 2187 | 2187 | 2187 | 538 | 538 | 538 | 1649 | 1649 | 1649 |
| R2 | 0.937 | 0.908 | 0.919 | 0.940 | 0.895 | 0.933 | 0.946 | 0.953 | 0.919 |
| Order | 8 | 9 | 7 | 9 | 9 | 9 | 8 | 8 | 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, L.; Zhang, B. The Positive Effects of Linked Control Policy for Vessels Passing Through Locks on Air Quality—A Case Study of Yichang, China. Atmosphere 2025, 16, 368. https://doi.org/10.3390/atmos16040368
Hou L, Zhang B. The Positive Effects of Linked Control Policy for Vessels Passing Through Locks on Air Quality—A Case Study of Yichang, China. Atmosphere. 2025; 16(4):368. https://doi.org/10.3390/atmos16040368
Chicago/Turabian StyleHou, Liwei, and Bowen Zhang. 2025. "The Positive Effects of Linked Control Policy for Vessels Passing Through Locks on Air Quality—A Case Study of Yichang, China" Atmosphere 16, no. 4: 368. https://doi.org/10.3390/atmos16040368
APA StyleHou, L., & Zhang, B. (2025). The Positive Effects of Linked Control Policy for Vessels Passing Through Locks on Air Quality—A Case Study of Yichang, China. Atmosphere, 16(4), 368. https://doi.org/10.3390/atmos16040368





