Assessing the Transferability of the Regional Climate Model REMO to Different COordinated Regional Climate Downscaling EXperiment (CORDEX) Regions
Abstract
:1. Introduction
2. Model and Experiment Setup
| Model Version | Vertical Coordinate/Levels | Advection Scheme | Time Step | Convective Scheme | Radiation Scheme | Turbulence Vertical Diffusion | Cloud Microphysics Scheme | Land Surface Scheme |
|---|---|---|---|---|---|---|---|---|
| REMO 2009 hydrostatic | Hybrid/ 27-31 | Semi-lagrangian | 240 s | Tiedtke [11], Nordeng [12], Pfeifer [13] | Morcrette et al. [14], Giorgetta and Wild [15] | Louis [16] | Lohmann and Roeckner [17] | Hagemann [18], Rechid et al. [19] |

3. Evaluation Framework
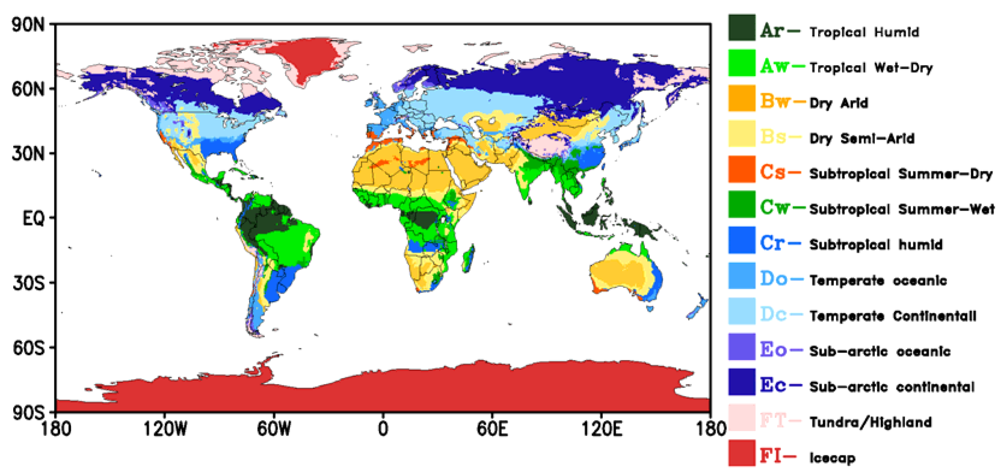

4. Evaluation of Model Results
4.1. Global Temperature and Precipitation Characteristics

| T | O | M | O | M | O | M | O | M | O | M | O | M | O | M | O | M | O | M | O | M | O | M | O | M |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DJF | Ar | Aw | Bs | Bw | Cr | Cs | Cw | Dc | Do | Ec | Eo | FT | ||||||||||||
| Eu | 1.2 | 0.9 | 2.3 | 2.4 | 1.1 | 1.1 | 3.1 | 3.0 | 2.0 | 2.2 | ||||||||||||||
| Med | 1.2 | 1.2 | 1.1 | 1.0 | 2.1 | 2.2 | 1.2 | 1.2 | ||||||||||||||||
| WA | 1.0 | 1.8 | 1.5 | 1.6 | 1.4 | 1.4 | 1.2 | 1.9 | 1.6 | 1.7 | 1.5 | 1.5 | 1.4 | 1.8 | ||||||||||
| Afr | 0.6 | 0.8 | 0.7 | 0.9 | 0.7 | 0.7 | 1.0 | 1.1 | 0.6 | 0.6 | ||||||||||||||
| NA | 1.5 | 1.3 | 2.4 | 2.0 | 2.7 | 3.1 | 2.8 | 3.1 | ||||||||||||||||
| SA | 0.4 | 0.8 | 0.3 | 0.8 | 0.6 | 0.6 | 0.7 | 0.9 | 0.8 | 1.0 | ||||||||||||||
| MAM | Ar | Aw | Bs | Bw | Cr | Cs | Cw | Dc | Do | Ec | Eo | FT | ||||||||||||
| Eu | 2.9 | 2.6 | 5.3 | 5.4 | 2.8 | 2.9 | 5.7 | 5.6 | 4.0 | 3.9 | ||||||||||||||
| Med | 3.7 | 4.2 | 3.0 | 2.8 | 5.0 | 5.0 | 2.9 | 2.8 | ||||||||||||||||
| WA | 1.3 | 1.2 | 4.5 | 4.7 | 4.4 | 4.5 | 2.5 | 2.4 | 4.6 | 4.2 | 4.4 | 4.2 | 3.8 | 4.5 | ||||||||||
| Afr | 0.5 | 0.6 | 0.7 | 0.7 | 0.6 | 0.6 | 2.3 | 2.5 | 0.5 | 0.6 | ||||||||||||||
| NA | 3.7 | 3.6 | 5.2 | 4.9 | 7.3 | 7.6 | 7.3 | 7.8 | ||||||||||||||||
| SA | 0.4 | 0.7 | 0.6 | 0.8 | 2.0 | 2.1 | 2.5 | 2.6 | 2.7 | 2.9 | ||||||||||||||
| JJA | Ar | Aw | Bs | Bw | Cr | Cs | Cw | Dc | Do | Ec | Eo | FT | ||||||||||||
| Eu | 1.5 | 1.7 | 1.3 | 1.3 | 1.5 | 1.5 | 1.8 | 2.0 | 1.6 | 1.7 | ||||||||||||||
| Med | 1.0 | 1.3 | 1.5 | 1.8 | 1.4 | 1.4 | 1.5 | 1.6 | ||||||||||||||||
| WA | 0.7 | 0.9 | 0.7 | 0.6 | 0.6 | 0.6 | 0.5 | 0.8 | 1.3 | 1.4 | 1.0 | 1.1 | 1.1 | 1.0 | ||||||||||
| Afr | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.7 | 0.5 | 0.3 | 0.6 | 0.9 | ||||||||||||||
| NA | 1.1 | 0.9 | 1.5 | 1.9 | 1.4 | 1.3 | 1.9 | 1.3 | ||||||||||||||||
| SA | 0.4 | 1.1 | 0.6 | 1.4 | 1.0 | 1.1 | 1.2 | 1.2 | 1.0 | 1.2 | ||||||||||||||
| SON | Ar | Aw | Bs | Bw | Cr | Cs | Cw | Dc | Do | Ec | Eo | FT | ||||||||||||
| Eu | 3.7 | 3.5 | 5.3 | 5.3 | 3.7 | 3.7 | 6.6 | 6.3 | 4.3 | 3.8 | ||||||||||||||
| Med | 4.6 | 5.4 | 3.8 | 3.9 | 5.1 | 5.0 | 3.8 | 3.7 | ||||||||||||||||
| WA | 1.1 | 1.5 | 4.6 | 4.8 | 4.6 | 4.9 | 2.6 | 3.3 | 5.3 | 5.0 | 4.8 | 4.9 | 5.4 | 6.3 | ||||||||||
| Afr | 0.6 | 0.5 | 0.6 | 0.5 | 0.6 | 0.6 | 2.7 | 3.4 | 1.0 | 1.5 | ||||||||||||||
| NA | 4.7 | 4.3 | 5.8 | 5.6 | 7.4 | 7.5 | 7.0 | 7.1 | ||||||||||||||||
| SA | 0.4 | 0.7 | 0.5 | 0.9 | 1.6 | 1.6 | 1.9 | 1.7 | 2.2 | 2.2 | ||||||||||||||
| P | O | M | O | M | O | M | O | M | O | M | O | M | O | M | O | M | O | M | O | M | O | M | O | M |
| DJF | Ar | Aw | Bs | Bw | Cr | Cs | Cw | Dc | Do | Ec | Eo | FT | ||||||||||||
| Eu | 34.5 | 36.6 | 9.7 | 14.8 | 21.4 | 23.8 | 8.1 | 10.1 | 23.0 | 27.1 | ||||||||||||||
| Med | 3.8 | 2.5 | 25.9 | 26.9 | 10.4 | 12.5 | 21.0 | 20.9 | ||||||||||||||||
| WA | 13.7 | 18.3 | 5.6 | 10.0 | 3.3 | 7.3 | 9.1 | 9.7 | 9.6 | 15.1 | 8.8 | 15.3 | 5.3 | 7.3 | ||||||||||
| Afr | 18.5 | 26.2 | 10.5 | 9.5 | 12.3 | 10.2 | 2.2 | 2.1 | 16.2 | 14.6 | ||||||||||||||
| NA | 7.9 | 16.2 | 10.9 | 13.6 | 6.0 | 6.8 | 5.8 | 8.0 | ||||||||||||||||
| SA | 41.4 | 33.6 | 24.7 | 35.5 | 22.2 | 26.8 | 29.4 | 35.9 | 9.7 | 15.0 | ||||||||||||||
| MAM | Ar | Aw | Bs | Bw | Cr | Cs | Cw | Dc | Do | Ec | Eo | FT | ||||||||||||
| Eu | 14.8 | 18.4 | 10.4 | 13.7 | 15.1 | 17.2 | 9.2 | 15.1 | 15.6 | 19.7 | ||||||||||||||
| Med | 3.9 | 2.6 | 14.2 | 15.6 | 11.4 | 12.6 | 15.4 | 17.4 | ||||||||||||||||
| WA | 53.1 | 82.2 | 5.7 | 7.0 | 4.5 | 5.1 | 48.6 | 82.2 | 12.7 | 15.9 | 12.8 | 17.2 | 11.8 | 10.5 | ||||||||||
| Afr | 22.9 | 27.7 | 13.9 | 11.6 | 8.6 | 9.1 | 1.7 | 2.7 | 38.7 | 27.5 | ||||||||||||||
| NA | 11.0 | 15.0 | 14.7 | 16.2 | 6.9 | 8.7 | 4.1 | 8.3 | ||||||||||||||||
| SA | 34.1 | 34.9 | 44.3 | 55.8 | 29.8 | 43.6 | 34.0 | 42.0 | 16.6 | 23.1 | ||||||||||||||
| JJA | Ar | Aw | Bs | Bw | Cr | Cs | Cw | Dc | Do | Ec | Eo | FT | ||||||||||||
| Eu | 8.2 | 9.9 | 13.2 | 14.0 | 14.7 | 12.2 | 13.4 | 15.6 | 17.4 | 18.1 | ||||||||||||||
| Med | 0.6 | 0.3 | 5.9 | 5.7 | 14.9 | 14.3 | 14.4 | 13.1 | ||||||||||||||||
| WA | 39.9 | 67.8 | 20.7 | 23.5 | 5.4 | 7.1 | 49.2 | 43.4 | 8.9 | 9.8 | 12.0 | 15.9 | 15.5 | 13.4 | ||||||||||
| Afr | 19.2 | 20.6 | 15.4 | 11.2 | 18.5 | 15.1 | 9.7 | 6.7 | 3.6 | 2.9 | ||||||||||||||
| NA | 13.4 | 12.6 | 12.9 | 13.0 | 9.4 | 8.7 | 8.8 | 10.5 | ||||||||||||||||
| SA | 38.4 | 40.5 | 8.9 | 9.5 | 5.3 | 5.0 | 21.0 | 19.6 | 18.9 | 27.9 | ||||||||||||||
| SON | Ar | Aw | Bs | Bw | Cr | Cs | Cw | Dc | Do | Ec | Eo | FT | ||||||||||||
| Eu | 29.7 | 31.3 | 13.2 | 17.1 | 20.1 | 18.9 | 11.0 | 18.4 | 18.8 | 24.6 | ||||||||||||||
| Med | 6.5 | 2.6 | 24.2 | 24.6 | 14.4 | 15.9 | 20.3 | 18.9 | ||||||||||||||||
| WA | 70.0 | 121.8 | 13.2 | 29.1 | 2.4 | 6.2 | 73.1 | 63.7 | 10.2 | 12.5 | 11.9 | 16.6 | 18.3 | 22.6 | ||||||||||
| Afr | 26.3 | 27.4 | 20.0 | 23.2 | 10.2 | 13.3 | 4.1 | 4.3 | 28.8 | 22.3 | ||||||||||||||
| NA | 19.4 | 21.8 | 10.0 | 13.6 | 11.5 | 12.8 | 8.1 | 11.4 | ||||||||||||||||
| SA | 27.5 | 32.1 | 30.6 | 34.1 | 20.4 | 29.7 | 29.5 | 37.2 | 10.3 | 16.3 | ||||||||||||||

4.2. Temperature Precipitation Relationship

4.3. PDF Skill Score

5. Conclusions
Acknowledgments
References
- WCRP CORDEX. Available online: http://wcrp.ipsl.jussieu.fr/SF_RCD_CORDEX.html (accessed on 20 October 2010).
- Jacob, D.; Barring, L.; Christensen, O.B.; Christensen, J.H.; de Castro, M.; Deque, M.; Giorgi, F.; Hagemann, S.; Lenderink, G.; Rockel, B.; et al. An inter-comparison of regional climate models for Europe: Model performance in present-day climate. Clim. Change 2007, 81, 31–52. [Google Scholar] [CrossRef]
- Simmons, A.; Uppala, S.; Dee, D.; Kobayashi, S. ERA-Interim: New ECMWF reanalysis products from 1989 onwards. ECMWF Newslett. 2006, 110, 25–35. [Google Scholar]
- Takle, E.S.; Roads, J.; Rockel, B.; Gutowski, W.J., Jr.; Arrit, R.W.; Meinke, I.; Jones, C.G.; Zadra, A. Transferability intercomparison: An opportunity for new insight on the global watercycle and energy budget. Bull. Am. Meteor. Soc. 2007, 88, 375–384. [Google Scholar] [CrossRef]
- Jacob, D.; Podzun, R. Sensitivity studies with the regional climate model REMO. Meteorol. Atmos. Phys. 1997, 63, 119–129. [Google Scholar] [CrossRef]
- Trewatha, G.T. An Introduction to Climate, 3rd ed; McGraw-Hill: New York, NY, USA, 1954. [Google Scholar]
- Perkins, S.E.; Pitman, A.J.; Holbrook, N.J.; McAneney, J. Evaluation of the AR4 climate model’s simulated daily maximum temperature, minimum temperature, and precipitation over Australia using probability density functions. J. Climate 2007, 20, 4356–4376. [Google Scholar] [CrossRef]
- Jacob, D. A note to the simulation of the annual and inter-annual variability of the water budget over the Baltic Sea drainage basin. Meteorol. Atmos. Phys. 2001, 77, 61–73. [Google Scholar] [CrossRef]
- Roeckner, E.; Arpe, K.; Bengtsson, L.; Christoph, M.; Claussen, M.; Dümenil, L.; Esch, M.; Giorgetta, M.; Schlese, U.; Schulzweida, U. The Atmospheric General Circulation Model Echam-4: Model Description and Simulation of the Present Day Climate; Report No. 218; Max-Planck-Institute for Meteorology: Hamburg, Germany, 1996. [Google Scholar]
- Majewski, D. The Europa-Modell of the Deutscher Wetterdienst. In Proceedings of the ECMWF Seminar on Numerical Methods in Atmospheric Models, Reading, UK, 9–13 September 1991; pp. 147–191.
- Tiedtke, M. A comprehensive mass flux scheme for cumulus parameterization in large scale models. Mon. Weather Rev. 1989, 117, 1779–1800. [Google Scholar] [CrossRef]
- Nordeng, T.E. Extended Versions of the Convective Parametrization Scheme at ECMWF and Their Impact on the Mean and Transient Activity of the Model in the Tropics; Technical Report No. 206; European Centre for Medium-Range Weather Forecasts: Reading, UK, 1994. [Google Scholar]
- Pfeifer, S. Modeling Cold Cloud Processes with the Regional Climate Model Remo; Reports on Earth System Science 23; Max-Planck-Institute for Meteorology: Hamburg, Germany, 2006. [Google Scholar]
- Morcrette, J.J.; Smith, L.; Fourquart, Y. Pressure and temperature dependance of the absorption in longwave radiation parameterizations. Beitr. Phys. Atmos. 1986, 59, 455–469. [Google Scholar]
- Giorgetta, M.; Wild, M. The Water Vapour Continuum and Its Representation in Echam4; Report No. 162; Max-Planck-Institute for Meteorology: Hamburg, Germany, 1995. [Google Scholar]
- Louis, J.F. A parametric model of vertical eddy fluxes in the atmosphere. Bound. Layer Meteorol. 1979, 17, 187–202. [Google Scholar] [CrossRef]
- Lohmann, U.; Roeckner, E. Design and performance of a new cloud microphysics scheme developed for the ECHAM4 general circulation model. Clim. Dyn. 1996, 12, 557–572. [Google Scholar] [CrossRef]
- Hagemann, S. An Improved Land Surface Parameter Dataset for Global and Regional Climate Models; Report No. 336; Max-Planck-Institute for Meteorology: Hamburg, Germany, 2002. [Google Scholar]
- Rechid, D.; Raddatz, T.J.; Jacob, D. Parameterization of snow-free land surface albedo as a function of vegetation phenology based on MODIS data and applied in climate modelling. Theor. Appl. Climatol. 2009, 95, 245–255. [Google Scholar] [CrossRef]
- Davies, H.C. A lateral boundary formulation for multi-level prediction models. Quart. J. R. Meteor. Soc. 1976, 102, 405–418. [Google Scholar]
- CRU Datasets-CRU TS Time-Series; British Atmospheric Data Centre: Didcot, UK, 2008. Available online: http://badc.nerc.ac.uk/view/badc.nerc.ac.uk__ATOM__dataent_1256223773328276 (accessed on 20 October 2010).
- Brohan, P.; Kennedy, J.J.; Harris, I.; Tett, S.F.B.; Jones, P.D. Uncertainty estimates in regional and global observed temperature changes: A new dataset from 1850. J. Geophys. Res. 2006, 111. [Google Scholar]
- Legates, D.R.; Willmott, C.J. Mean seasonal and spatial variability in gauge-corrected, global precipitation. Int. J. Climatol. 1990, 10, 111–127. [Google Scholar] [CrossRef]
- Lohmann, U.; Sausen, R.; Bengtsson, L.; Cubasch, U.; Perlwitz, J.; Roeckner, E. The Köppen climate classification as a diagnostic tool for general circulation models. Clim. Res. 1993, 3, 177–193. [Google Scholar] [CrossRef]
- de Castro, M.; Gallardo, C.; Jylha, K.; Tuomenvirta, H. The use of a climate-type classification for assessing climate change effects in Europe from an ensemble of nine regional climate models. Clim. Change 2007, 81, 329–341. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Sánchez, E.; Romera, R. Exploiting an ensemble of regional climate models to provide robust estimates of projected changes in monthly temperature and precipitation probability distribution functions. Tellus A 2009, 61, 57–71. [Google Scholar] [CrossRef]
- Kleidon, A.; Heimann, M. Assessing the role of deep rooted vegetation in the climate system with model simulations: Mechanism, comparison to observations and implications for Amazonian deforestation. Clim. Dyn. 2000, 16, 183–199. [Google Scholar] [CrossRef]
- Haensler, A.; Hagemann, S.; Jacob, D. Dynamical downscaling of ERA40 reanalysis data over southern Africa: Added value in the representation of seasonal rainfall characteristics. Int. J. Climatol. 2011, 31, 2338–2349. [Google Scholar] [CrossRef]
- Richter, I.; Mechoso, C.R. Orographic influences on subtropical stratocumulus. J. Atmos. Sci. 2006, 63, 2585–2601. [Google Scholar] [CrossRef]
- Yu, J.-Y.; Mechoso, C.R. Links between annual variations of peruvian stratocumulus clouds and of SST in the Eastern Equatorial Pacific. J. Clim. 1999, 12, 3305–3318. [Google Scholar]
- Yang, D.; Kane, D.; Zhang, Z.; Legates, D.; Goodison, B. Bias corrections of long-term (1973-2004) daily precipitation data over the northern regions. Geophys. Res. Lett. 2005, 32. [Google Scholar]
- Dai, A.; Qian, T.; Trenberth, K.E.; Milliman, J.D. Changes in continental freshwater discharge from 1948 to 2004. J. Clim. 2009, 22, 2773–2791. [Google Scholar] [CrossRef]
- Dai, A.; Trenberth, K.E. Estimates of freshwater discharge from continents: Latitudinal and seasonal variations. J. Hydrometeor. 2002, 3, 660–687. [Google Scholar] [CrossRef]
- Hagemann, S.; Duemenil, L. A parameterization of the lateral waterflow for the global scale. Clim. Dyn. 1998, 14, 17–31. [Google Scholar] [CrossRef]
- Jayaraman, K.S. Rival monsoon forecasts banned. Nature 2005, 436. [Google Scholar]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Jacob, D.; Elizalde, A.; Haensler, A.; Hagemann, S.; Kumar, P.; Podzun, R.; Rechid, D.; Remedio, A.R.; Saeed, F.; Sieck, K.; et al. Assessing the Transferability of the Regional Climate Model REMO to Different COordinated Regional Climate Downscaling EXperiment (CORDEX) Regions. Atmosphere 2012, 3, 181-199. https://doi.org/10.3390/atmos3010181
Jacob D, Elizalde A, Haensler A, Hagemann S, Kumar P, Podzun R, Rechid D, Remedio AR, Saeed F, Sieck K, et al. Assessing the Transferability of the Regional Climate Model REMO to Different COordinated Regional Climate Downscaling EXperiment (CORDEX) Regions. Atmosphere. 2012; 3(1):181-199. https://doi.org/10.3390/atmos3010181
Chicago/Turabian StyleJacob, Daniela, Alberto Elizalde, Andreas Haensler, Stefan Hagemann, Pankaj Kumar, Ralf Podzun, Diana Rechid, Armelle Reca Remedio, Fahad Saeed, Kevin Sieck, and et al. 2012. "Assessing the Transferability of the Regional Climate Model REMO to Different COordinated Regional Climate Downscaling EXperiment (CORDEX) Regions" Atmosphere 3, no. 1: 181-199. https://doi.org/10.3390/atmos3010181
APA StyleJacob, D., Elizalde, A., Haensler, A., Hagemann, S., Kumar, P., Podzun, R., Rechid, D., Remedio, A. R., Saeed, F., Sieck, K., Teichmann, C., & Wilhelm, C. (2012). Assessing the Transferability of the Regional Climate Model REMO to Different COordinated Regional Climate Downscaling EXperiment (CORDEX) Regions. Atmosphere, 3(1), 181-199. https://doi.org/10.3390/atmos3010181




