Joint Application of Concentration and ?18O to Investigate the Global Atmospheric CO Budget
Abstract
:1. Introduction

2. Observation of Atmospheric Carbon Monoxide and Its Isotopes

3. Forward Model Description
3.1. MOZART-4 and Its Tracer Version
3.2. Sources and Sinks of Atmospheric CO
| Sources | Northern Hemisphere | Southern Hemisphere |
|---|---|---|
| Fossil fuel | 340 | 25 |
| Biofuel | 276 | 38 |
| NMHC oxidation | 310 | 232 |
| Methane oxidation | 497 | 379 |
| Ocean | 8 | 12 |
| Biogenic | 104 | 57 |
| Biomass burning (year) | ||
| 1997 | 192 | 364 |
| 1998 | 397 | 193 |
| 1999 | 221 | 171 |
| 2000 | 199 | 137 |
| 2001 | 193 | 171 |
| 2002 | 222 | 196 |
| 2003 | 235 | 161 |
| 2004 | 192 | 212 |
3.3. Incorporation of Oxygen Isotopes
3.4. Simulated Atmospheric [CO] and δ18O: Model Evaluation

4. Methodology for Inverse Modeling Analysis
4.1. Bayesian Synthesis Inversion
4.2. Assigning Uncertainties in the Analyses
4.2.1. Uncertainties in Measurements: Se
| Quantity | Unit | Uncertainty (1σ) | e.m.a.u * | |
|---|---|---|---|---|
| Brenninkmeijer [41] | This Study | |||
| CO | ppbv | 1.70% | 1.31% | 2% |
| δ18O | ‰, VSMOW | 0.40‰ | 0.27‰ | 1‰ |
4.2.2. Uncertainties in a Priori Source Estimates: Sa


4.3. Inversion Schemes; Incorporation of Isotope Information to the Source Optimization
4.3.1. Decoupled Inversion
4.3.2. Coupled (Simultaneous) Inversion
4.3.3. Coupled (Sequential) Inversion
4.3.4. Optimization of Source Strengths and δ18O Signature in These Inversion Methods

5. Optimized Global CO Budget from Joint Inversion of [CO] and δ18O
5.1. Optimized Atmospheric CO Sources for 1997, 1998, and 2004
| Fossil fuel | Bio. burn. | CH4 ox. | NMHC ox. | Biofuel | Ocean | Biogenic | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f | e | f | e | f | e | f | e | f | e | f | e | f | e | ||
| NH | 1997 | 1.10 | 1.7 | 1.33 | 8.8 | 1.12 | 0.8 | 0.72 | 7.8 | 1.79 | 12.6 | 1.05 | 24.9 | 0.53 | 15.1 |
| 1998 | 0.98 | 2.3 | 0.89 | 4.0 | 1.11 | 0.8 | 1.48 | 9.1 | 1.64 | 12.5 | 1.06 | 24.9 | 0.79 | 20.0 | |
| 2004 | 0.87 | 1.6 | 0.94 | 18.4 | 1.10 | 0.8 | 1.07 | 9.4 | 1.31 | 10.9 | 1.00 | 24.9 | 0.47 | 16.9 | |
| SH | 1997 | 0.98 | 4.0 | 0.97 | 7.5 | 0.97 | 0.6 | 0.67 | 7.0 | 0.86 | 23.0 | 0.96 | 22.2 | 0.79 | 23.1 |
| 1998 | 1.00 | 4.0 | 0.75 | 6.9 | 0.98 | 0.7 | 0.85 | 7.8 | 1.01 | 23.8 | 0.98 | 22.4 | 0.99 | 23.0 | |
| 2004 | 0.99 | 4.0 | 0.93 | 4.7 | 0.98 | 0.7 | 0.52 | 6.5 | 0.96 | 23.1 | 0.98 | 22.5 | 0.84 | 23.0 | |
5.1.1. Optimized Fossil Fuel and Biofuel Source Strength
5.1.2. Optimized Biomass Burning Source Strength
5.1.3. Optimized Chemical Oxidation Source Strengths
5.1.4. Optimized Ocean and Biogenic Source Strengths
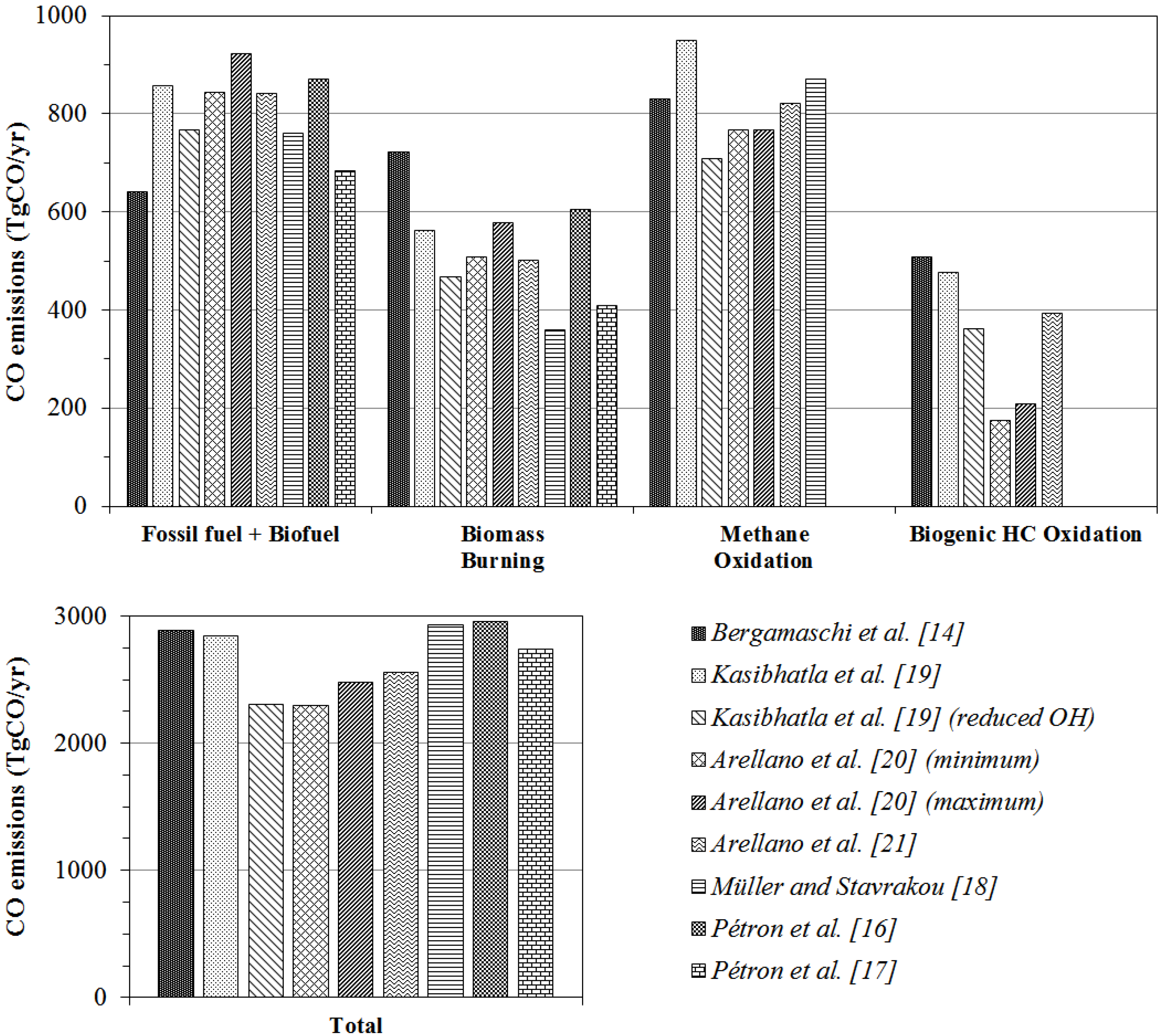
5.1.5. Comparison to the Previous CO Sources Strength Estimates Derived from Inversion Analyses
5.2. A Posteriori CO and δ18O
| This work | Bergamaschi et al. [14] | Petron et al. [16] | Petron et al. [17] | Muller and Stavrakou, [18] | Kasibhatla et al. [19] | Arellano et al. [20] | Arellano et al. [21] | Duncan et al. [67] | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a priori | a posteriori | |||||||||||
| Year of observational data | 1997 | 1998 | 2004 | 1993–1995 | 1990–1996 | Apr. 2000–Mar. 2001 | 1997 | 1993–1995 | 2000 | Apr. 2000–Apr. 2001 | 1988–1997 | |
| Fossil fuel (FF) | 365 | 397 | 359 | 321 | 309 | 365 | 464–487 | |||||
| Biofuel (BF) | 313 | 524 | 489 | 396 | 561 | 318 | 189 | |||||
| FF + BF | 678 | 922 | 849 | 716 | 642 | 870 | 683 | 760 | 768–857 | 844–923 | 841 | |
| Biomass burning | 516 * | 609 | 498 | 377 | 722 | 606 | 408 | 359 | 467–561 | 508–579 | 501 | 451–573 |
| Anthro. HC oxidation | 166 | |||||||||||
| Biogenic HC oxidation | 507 | 362–477 | 175–209 | 394 | 354–379 | |||||||
| Total NMHC oxidation | 543 | 377 | 656 | 454 | 774 | |||||||
| Methane oxidation | 875 | 923 | 923 | 919 | 830 | 870 | 709–949 | 767 | 820 | 778–861 | ||
| Ocean | 20 | 20 | 20 | 20 | 23 | 20 | 23 | |||||
| Biogenic | 160 | 100 | 138 | 97 | 167 | 142 | ||||||
| Total surface emission | 1375 | 1651 | 1505 | 1210 | 1364 | 1528–1694 | 1091 | 1261 | 1235–1418 | 1352–1502 | 1342 | |
| Total oxidation source | 1418 | 1300 | 1579 | 1373 | 1503 | 1461–1536 | 1650 | 1644 | ||||
| Total source | 2793 | 2951 | 3084 | 2583 | 2891 | 2960–3067 | 2741 | 2928 | 2306–2846 | 2294–2478 | 2556 | 2236–2489 |



5.3. Inversion Results by Different Inversion Schemes: CO-only, Sequential, and Simultaneous Inversion

5.4. The Influence of the Number of Observation Stations in the Inversion Results
| Fossil Fuel | Bio. Burn. | CH4 Ox. | NMHC Ox. | Biofuel | Oceanic | Biogenic | ||
|---|---|---|---|---|---|---|---|---|
| 1997NH | seq/sim | 0.99 | 0.98 | 0.99 | 0.98 | 1.04 | 0.99 | 1.00 |
| [CO]/sim | 1.01 | 0.99 | 0.96 | 1.14 | 0.92 | 0.98 | 1.17 | |
| 1998NH | seq/sim | 1.00 | 1.00 | 1.00 | 0.97 | 1.03 | 1.00 | 1.00 |
| [CO]/sim | 1.05 | 1.07 | 0.97 | 0.97 | 0.91 | 0.98 | 1.15 | |
| 2004NH | seq/sim | 1.00 | 1.00 | 1.00 | 0.94 | 1.00 | 0.99 | 1.18 |
| [CO]/sim | 1.05 | 1.06 | 0.96 | 0.96 | 0.94 | 1.00 | 1.38 | |
| 1997SH | seq/sim | 1.00 | 0.99 | 0.99 | 0.98 | 1.00 | 0.99 | 1.00 |
| [CO]/sim | 1.01 | 0.97 | 1.00 | 0.99 | 1.04 | 1.00 | 1.07 | |
| 1998SH | seq/sim | 1.00 | 1.01 | 1.00 | 0.97 | 0.99 | 0.99 | 0.99 |
| [CO]/sim | 1.00 | 1.04 | 1.00 | 0.98 | 0.98 | 1.00 | 0.98 | |
| 2004SH | seq/sim | 0.99 | 0.98 | 0.99 | 1.02 | 0.98 | 0.98 | 0.97 |
| [CO]/sim | 1.00 | 0.98 | 0.99 | 1.05 | 0.99 | 0.98 | 1.03 |

6. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Supplement
References
- Brenninkmeijer, C.A.M.; Röckmann, T.; Bräunlich, M.; Jöckel, P.; Bergamaschi, P. Review of progress in isotope studies of atmospheric carbon monoxide. Chemosphere Glob. Chang. Sci. 1999, 1, 33–52. [Google Scholar] [CrossRef]
- Ehhalt, D.; Prather, M.; Dentener, F.; Derwent, R.; Dlugokencky, E.; Holland, E.; Isaksen, I.; Katima, J.; Kirchhoff, V.; Matson, P.; et al. Climate chamge 2001: The scientific basis (atmospheric chemistry and greenhouse gases). In Intergovernmental Panel on Climate Change Third Assessment Report; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Crutzen, P.J.; Zimmermann, P.H. The changing photochemistry of the troposphere. Tellus Ser. A Dyn. Meteorol. Oceanogr. 1991, 43, 136–151. [Google Scholar] [CrossRef]
- Thompson, A.M. The oxidizing capacity of the earth’s atmosphere: Probable past and future changes. Science 1992, 256, 1157–1165. [Google Scholar] [CrossRef] [PubMed]
- Forster, P.; Ramaswamy, V.; Artaxo, P.; Berntsen, T.; Betts, R.; Fahey, D.; Haywood, J.; Lean, J.; Lowe, D.; Myhre, G.; et al. Changes in atmospheric constituents and in radiative forcing. In Climate Change 2007: The Physical Science Basis: Contribution of Working Group i to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K., Tignor, M., Miller, H., Eds.; Cambridge University Press: Cambridge, UK, 2007; pp. 129–234. [Google Scholar]
- Li, Q.; Jacob, D.J.; Bey, I.; Palmer, P.I.; Duncan, B.N.; Field, B.D.; Martin, R.V.; Fiore, A.M.; Yantosca, R.M.; Parrish, D.D.; et al. Transatlantic transport of pollution and its effects on surface ozone in Europe and North America. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Shim, C.; Li, Q.; Luo, M.; Kulawik, S.; Worden, H.; Worden, J.; Eldering, A.; Diskin, G.; Sachse, G.; Weinheimer, A.; et al. Satellite observations of mexico city pollution outflow from the Tropospheric Emissions Spectrometer (TES). Atmos. Environ. 2009, 43, 1540–1547. [Google Scholar] [CrossRef]
- Pfister, G.; Hess, P.G.; Emmons, L.K.; Lamarque, J.F.; Wiedinmyer, C.; Edwards, D.P.; Pétron, G.; Gille, J.C.; Sachse, G.W. Quantifying CO emissions from the 2004 alaskan wildfires using mopitt co data. Geophys. Res. Lett. 2005, 32, L11809. [Google Scholar] [CrossRef]
- Palmer, P.I.; Suntharalingam, P.; Jones, D.B.A.; Jacob, D.J.; Streets, D.G.; Fu, Q.; Vay, S.A.; Sachse, G.W. Using CO2: CO correlations to improve inverse analyses of carbon fluxes. J. Geophys. Res. 2006, 111, D12318. [Google Scholar] [CrossRef]
- Brenninkmeijer, C.A.M.; Rockmann, T. Principal factors determining the 18O/16O ratio of atmospheric CO as derived from observations in the southern hemispheric troposphere and lowermost stratosphere. J. Geophys. Res. Atmos. 1997, 102, 25477–25485. [Google Scholar] [CrossRef]
- Hauglustaine, D.A.; Brasseur, G.P.; Walters, S.; Rasch, P.J.; Muller, J.F.; Emmons, L.K.; Carroll, C.A. Mozart, a global chemical transport model for ozone and related chemical tracers 2. Model results and evaluation. J. Geophys. Res. Atmos. 1998, 103, 28291–28335. [Google Scholar] [CrossRef]
- Logan, J.A.; Prather, M.J.; Wofsy, S.C.; McElroy, M.B. Tropospheric chemistry: A global perspective. J. Geophys. Res. Oceans Atmos. 1981, 86, 7210–7254. [Google Scholar] [CrossRef]
- Weinstock, B.; Niki, H. Carbon monoxide balance in nature. Science 1972, 176, 290–292. [Google Scholar] [CrossRef] [PubMed]
- Bergamaschi, P.; Hein, R.; Heimann, M.; Crutzen, P.J. Inverse modeling of the global CO cycle 1. Inversion of CO mixing ratios. J. Geophys. Res. 2000, 105, 1909–1927. [Google Scholar] [CrossRef]
- Sanhueza, E.; Dong, Y.; Scharffe, D.; Lobert, J.M.; Crutzen, P.J. Carbon monoxide uptake by temperate forest soils: The effects of leaves and humus layers. Tellus Ser. B Chem. Phys. Meteorol. 1998, 50, 51–58. [Google Scholar] [CrossRef]
- Pétron, G.; Granier, C.; Khattatov, B.; Lamarque, J.-F.; Yudin, V.; Müller, J.-F.; Gille, J. Inverse modeling of carbon monoxide surface emissions using climate monitoring and diagnostics laboratory network observations. J. Geophys. Res. 2002, 107, 4761. [Google Scholar] [CrossRef]
- Pétron, G.; Granier, C.; Khattatov, B.; Yudin, V.; Lamarque, J.-F.; Emmons, L.; Gille, J.; Edwards, D.P. Monthly CO surface sources inventory based on the 2000–2001 mopitt satellite data. Geophys. Res. Lett. 2004, 31, L21107. [Google Scholar] [CrossRef]
- Müller, J.F.; Stavrakou, T. Inversion of CO and nox emissions using the adjoint of the images model. Atmos. Chem. Phys. 2005, 5, 1157–1186. [Google Scholar] [CrossRef]
- Kasibhatla, P.; Arellano, A.; Logan, J.A.; Palmer, P.I.; Novelli, P. Top-down estimate of a large source of atmospheric carbon monoxide associated with fuel combustion in asia. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Arellano, A.F., Jr.; Kasibhatla, P.S.; Giglio, L.; van der Werf, G.R.; Randerson, J.T. Top-down estimates of global CO sources using mopitt measurements. Geophys. Res. Lett. 2004, 31, L01104. [Google Scholar]
- Arellano, A.F., Jr.; Kasibhatla, P.S.; Giglio, L.; van der Werf, G.R.; Randerson, J.T.; Collatz, G.J. Time-dependent inversion estimates of global biomass-burning CO emissions using measurement of pollution in the troposphere (mopitt) measurements. J. Geophys. Res. 2006, 111, D09303. [Google Scholar]
- Hooghiemstra, P.B.; Krol, M.C.; Bergamaschi, P.; de Laat, A.T.J.; van der Werf, G.R.; Novelli, P.C.; Deeter, M.N.; Aben, I.; Röckmann, T. Comparing optimized CO emission estimates using mopitt or noaa surface network observations. J. Geophys. Res. Atmos. 2012, 117, D06309. [Google Scholar]
- Kopacz, M.; Jacob, D.J.; Fisher, J.A.; Logan, J.A.; Zhang, L.; Megretskaia, I.A.; Yantosca, R.M.; Singh, K.; Henze, D.K.; Burrows, J.P.; et al. Global estimates of CO sources with high resolution by adjoint inversion of multiple satellite datasets (mopitt, airs, sciamachy, tes). Atmos. Chem. Phys. 2010, 10, 855–876. [Google Scholar] [CrossRef]
- Bergamaschi, P.; Hein, R.; Brenninkmeijer, C.A.M.; Crutzen, P.J. Inverse modeling of the global CO cycle 2. Inversion of 13c/12c and 18o/16o isotope ratios. J. Geophys. Res. 2000, 105, 1929–1945. [Google Scholar] [CrossRef]
- Tans, P.P. A note on isotopic ratios and the global atmospheric methane budget. Glob. Biogeochem. Cycles 1997, 11, 77–81. [Google Scholar] [CrossRef]
- Rayner, P.J.; Law, R.M.; Allison, C.E.; Francey, R.J.; Trudinger, C.M.; Pickett-Heaps, C. Interannual variability of the global carbon cycle (1992–2005) inferred by inversion of atmospheric CO2 and δ13CO2 measurements. Glob. Biogeochem. Cycles 2008, 22, GB3008. [Google Scholar] [CrossRef]
- Rockmann, T.; Jockel, P.; Gros, V.; Braunlich, M.; Possnert, G.; Brenninkmeijer, C.A.M. Using 14C, 13C, 18O and 17O isotopic variations to provide insights into the high northern latitude surface CO inventory. Atmos. Chem. Phys. 2002, 2, 147–159. [Google Scholar] [CrossRef]
- Enting, I.G. Inverse Problems in Atmospheric Constituent Transport; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Tans, P.P.; Berry, J.A.; Keeling, R.F. Oceanic C-13/C-12 observations—A new window on ocean CO2 uptake. Glob. Biogeochem. Cycles 1993, 7, 353–368. [Google Scholar] [CrossRef]
- Mikaloff Fletcher, S.E.; Tans, P.P.; Bruhwiler, L.M.; Miller, J.B.; Heimann, M. CH4 sources estimated from atmospheric observations of CH4 and its 13C/12C isotopic ratios: 1. Inverse modeling of source processes. Glob. Biogeochem. Cycles 2004, 18, GB4004. [Google Scholar]
- Ciais, P.; Tans, P.P.; White, J. W. C.; Trolier, M.; Francey, R.J.; Berry, J. A.; Randall, D.R.; Sellers, P.J.; Collatz, J.G.; Schimel, D.S. Partitioning of ocean and land uptake of CO2 as inferred by delta13C measurements from the noaa climate monitoring and diagnostics laboratory global air sampling network. J. Geophys. Res. Atmos. 1995, 100, 5051–5070. [Google Scholar] [CrossRef]
- Houweling, S.; van der Werf, G.R.; Klein Goldewijk, K.; Röckmann, T.; Aben, I. Early anthropogenic CH4 emissions and the variation of CH4 and 13CH4 over the last millennium. Glob. Biogeochem. Cycles 2008, 22, GB1002. [Google Scholar] [CrossRef]
- Hein, R.; Crutzen, P.J.; Heimann, M. An inverse modeling approach to investigate the global atmospheric methane cycle. Glob. Biogeochem. Cycles 1997, 11, 43–76. [Google Scholar] [CrossRef]
- Emmons, L.K.; Walters, S.; Hess, P.G.; Lamarque, J.F.; Pfister, G.G.; Fillmore, D.; Granier, C.; Guenther, A.; Kinnison, D.; Laepple, T.; et al. Description and evaluation of the model for ozone and related chemical tracers, version 4 (mozart-4). Geosci. Model Dev. 2010, 3, 43–67. [Google Scholar] [CrossRef] [Green Version]
- Manning, M.R.; Brenninkmeijer, C.A.M.; Allan, W. Atmospheric carbon monoxide budget of the southern hemisphere: Implications of 13c/12c measurements. J. Geophys. Res. 1997, 102, 10673–10682. [Google Scholar] [CrossRef]
- Mak, J.E.; Kra, G.; Sandomenico, T.; Bergamaschi, P. The seasonally varying isotopic composition of the sources of carbon monoxide at barbados, west indies. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Novelli, P.C.; Masarie, K.A.; Lang, P.M.; Hall, B.D.; Myers, R.C.; Elkins, J.W. Reanalysis of tropospheric CO trends: Effects of the 1997–1998 wildfires. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Novelli, P.C.; Masarie, K.A.; Lang, P.M. Distributions and recent changes of carbon monoxide in the lower troposphere. J. Geophys. Res. 1998, 103, 19015–19033. [Google Scholar] [CrossRef]
- Pfister, G.G.; Emmons, L.K.; Hess, P.G.; Lamarque, J.F.; Orlando, J.J.; Walters, S.; Guenther, A.; Palmer, P.I.; Lawrence, P.J. Contribution of isoprene to chemical budgets: A model tracer study with the ncar ctm mozart-4. J. Geophys. Res. 2008, 113, D05308. [Google Scholar]
- Williams, J.; Fischer, H.; Wong, S.; Crutzen, P.J.; Scheele, M.P.; Lelieveld, J. Near equatorial CO and O3 profiles over the indian ocean during the winter monsoon: High O3 levels in the middle troposphere and interhemispheric exchange. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Mak, J.E.; Brenninkmeijer, C.A.M. Compressed air sample technology for the isotopic analysis of atmospheric carbon monoxide. J. Atmos. Ocean. Technol. 1994, 11, 425–431. [Google Scholar]
- Brenninkmeijer, C.A.M. Measurement of the abundance of 14CO in the atmosphere and the 13C/12C and 18O/16O ration of atmospheric co with applications in new zealand and antarctica. J. Geophys. Res. 1993, 98, 10595–10614. [Google Scholar] [CrossRef]
- Mak, J.; Kra, G. The isotopic composition of carbon monoxide at montauk point, long island. Chemosphere Glob. Chang. Sci. 1999, 1, 205–218. [Google Scholar] [CrossRef]
- Smiley, W.G. Note on a reagent for oxidation of carbon monoxide. Nucl. Sci. Abstr. 1965, 3, 391. [Google Scholar]
- Drori, R.; Dayan, U.; Edwards, D.P.; Emmons, L.K.; Erlick, C. Attributing and quantifying carbon monoxide sources affecting the eastern mediterranean: A combined satellite, modelling, and synoptic analysis study. Atmos. Chem. Phys. 2012, 12, 1067–1082. [Google Scholar] [CrossRef]
- Emmons, L.K.; Apel, E.C.; Lamarque, J.F.; Hess, P.G.; Avery, M.; Blake, D.; Brune, W.; Campos, T.; Crawford, J.; DeCarlo, P.F.; et al. Impact of mexico city emissions on regional air quality from mozart-4 simulations. Atmos. Chem. Phys. 2010, 10, 6195–6212. [Google Scholar] [CrossRef]
- Wespes, C.; Emmons, L.; Edwards, D.P.; Hannigan, J.; Hurtmans, D.; Saunois, M.; Coheur, P.F.; Clerbaux, C.; Coffey, M.T.; Batchelor, R.L.; et al. Analysis of ozone and nitric acid in spring and summer arctic pollution using aircraft, ground-based, satellite observations and mozart-4 model: Source attribution and partitioning. Atmos. Chem. Phys. 2012, 12, 237–259. [Google Scholar] [CrossRef] [Green Version]
- Pfister, G.G.; Hess, P.G.; Emmons, L.K.; Rasch, P.J.; Vitt, F.M. Impact of the summer 2004 alaska fires on top of the atmosphere clear-sky radiation fluxes. J. Geophys. Res. 2008, 113, D02204. [Google Scholar]
- Shindell, D.T.; Faluvegi, G.; Stevenson, D.S.; Krol, M.C.; Emmons, L.K.; Lamarque, J.F.; Pétron, G.; Dentener, F.J.; Ellingsen, K.; Schultz, M.G.; et al. Multimodel simulations of carbon monoxide: Comparison with observations and projected near-future changes. J. Geophys. Res. 2006, 111, D19306. [Google Scholar] [CrossRef]
- Stevenson, D.S.; Dentener, F.J.; Schultz, M.G.; Ellingsen, K.; van Noije, T.P.C.; Wild, O.; Zeng, G.; Amann, M.; Atherton, C.S.; Bell, N.; et al. Multimodel ensemble simulations of present-day and near-future tropospheric ozone. J. Geophys. Res. 2006, 111, D08301. [Google Scholar]
- Emmons, L.K.; Hess, P.G.; Lamarque, J.F.; Pfister, G.G. Tagged ozone mechanism for mozart-4, cam-chem and other chemical transport models. Geosci. Model Dev. 2012, 5, 1531–1542. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The ncep/ncar 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar]
- Kistler, R.; Collins, W.; Saha, S.; White, G.; Woollen, J.; Kalnay, E.; Chelliah, M.; Ebisuzaki, W.; Kanamitsu, M.; Kousky, V.; et al. The NCEP–NCAR 50–year reanalysis: Monthly means CD–ROM and documentation. Bull. Am. Meteorol. Soc. 2001, 82, 247–267. [Google Scholar]
- Van der Werf, G.R.; Randerson, J.T.; Giglio, L.; Collatz, G.J.; Kasibhatla, P.S.; Arellano, A.F. Interannual variability in global biomass burning emissions from 1997 to 2004. Atmos. Chem. Phys. 2006, 6, 3423–3441. [Google Scholar] [CrossRef]
- Tarr, M.A.; Miller, W.L.; Zepp, R.G. Direct carbon monoxide photoproduction from plant matter. J. Geophys. Res. Atmos. 1995, 100, 11403–11413. [Google Scholar] [CrossRef]
- Conrad, R.; Seiler, W.; Bunse, G.; Giehl, H. Carbon monoxide in seawater (Atlantic Ocean). J. Geophys. Res. 1982, 87, 8839–8852. [Google Scholar] [CrossRef]
- Stubbins, A.; Uher, G.; Kitidis, V.; Law, C.S.; Upstill-Goddard, R.C.; Woodward, E.M.S. The open-ocean source of atmospheric carbon monoxide. Deep Sea Res. Part II Top. Stud. Oceanogr. 2006, 53, 1685–1694. [Google Scholar] [CrossRef]
- Olivier, J.; Peters, J.; Granier, C.; Petron, G.; Müller, J.F.; Wallens, S. Present and future surface emissions of atmospheric compounds. POET report #2. 2003. EU project EVK2–1999–00011 Available online: http://tropo.aeronomie.be/pdf/POET_emissions_report.pdf (accessed on 17 April 2015).
- Horowitz, L.W.; Walters, S.; Mauzerall, D.L.; Emmons, L.K.; Rasch, P.J.; Granier, C.; Tie, X.; Lamarque, J.-F.; Schultz, M.G.; Tyndall, G.S.; et al. A global simulation of tropospheric ozone and related tracers: Description and evaluation of mozart, version 2. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Lawrence, M.G.; Jöckel, P.; von Kuhlmann, R. What does the global mean OH concentration tell us? Atmos. Chem. Phys. 2001, 1, 37–49. [Google Scholar] [CrossRef]
- Sanderson, M.G.; Collins, W.J.; Derwent, R.G.; Johnson, C.E. Simulation of global hydrogen levels using a lagrangian three-dimensional model. J. Atmos. Chem. 2003, 46, 15–28. [Google Scholar] [CrossRef]
- Stevens, C.M.; Wagner, A.F. The role of isotope fractionation effects in atmospheric chemistry. Z. Naturforschung 1989, 44, 376–384. [Google Scholar]
- Röckmann, T.; Brenninkmeijer, C.A.M.; Saueressig, G.; Bergamaschi, P.; Crowley, J.N.; Fischer, H.; Crutzen, P.J. Mass-independent oxygen isotope fractionation in atmospheric CO as a result of the reaction CO + OH. Science 1998, 281, 544–546. [Google Scholar] [CrossRef] [PubMed]
- Tsunogai, U.; Nakagawa, F.; Komatsu, D.D.; Gamo, T. Stable carbon and oxygen isotopic analysis of atmospheric carbon monoxide using continuous-flow isotope ratio ms by isotope ratio monitoring of CO. Anal. Chem. 2002, 74, 5695–5700. [Google Scholar] [CrossRef] [PubMed]
- Stevens, C.M.; Walling, D.; Venters, A.; Ross, L.E.; Engelkem, A.; Krout, L. Isotopic composition of atmospheric carbon-monoxide. Earth Planet. Sci. Lett. 1972, 16, 147–165. [Google Scholar] [CrossRef]
- Nakagawa, F.; Tsunogai, U.; Gamo, T.; Yoshida, N. Stable isotopic compositions and fractionations of carbon monoxide at coastal and open ocean stations in the Pacific. J. Geophys. Res. Oceans 2004, 109. [Google Scholar] [CrossRef]
- Guenther, A.; Geron, C.; Pierce, T.; Lamb, B.; Harley, P.; Fall, R. Natural emissions of non-methane volatile organic compounds; carbon monoxide, and oxides of nitrogen from North America. Atmos. Environ. 2000, 34, 2205–2230. [Google Scholar] [CrossRef]
- Duncan, B.N.; Logan, J.A.; Bey, I.; Megretskaia, I.A.; Yantosca, R.M.; Novelli, P.C.; Jones, N.B.; Rinsland, C.P. Global budget of co, 1988–997: Source estimates and validation with a global model. J. Geophys. Res. 2007, 112, D22301. [Google Scholar] [CrossRef]
- Palmer, P.I.; Jacob, D.J.; Jones, D.B.A.; Heald, C.L.; Yantosca, R.M.; Logan, J.A.; Sachse, G.W.; Streets, D.G. Inverting for emissions of carbon monoxide from asia using aircraft observations over the western pacific. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Bousquet, P.; Ciais, P.; Peylin, P.; Ramonet, M.; Monfray, P. Inverse modeling of annual atmospheric CO2 sources and sinks 1. Method and control inversion. J. Geophys. Res. 1999, 104, 26161–26178. [Google Scholar] [CrossRef]
- Bousquet, P.; Peylin, P.; Ciais, P.; Ramonet, M.; Monfray, P. Inverse modeling of annual atmospheric CO2 sources and sinks 2. Sensitivity study. J. Geophys. Res. 1999, 104, 26179–26193. [Google Scholar] [CrossRef]
- Chen, Y.-H.; Prinn, R.G. Estimation of atmospheric methane emissions between 1996 and 2001 using a three-dimensional global chemical transport model. J. Geophys. Res. 2006, 111, D10307. [Google Scholar] [CrossRef]
- Heimann, M.; Kaminski, T. Inverse modelling approaches to infer surface trace gas fluxes from observed atmospheric mixing ratios. In Developments in Atmospheric Science; Bouwman, A.F., Ed.; Elsevier: Amsterdam, Netherlands, 1999; Volume 24, pp. 277–295. [Google Scholar]
- Bian, H.; Chin, M.; Kawa, S.R.; Duncan, B.; Arellano, A.; Kasibhatla, P. Sensitivity of global co simulations to uncertainties in biomass burning sources. J. Geophys. Res. 2007, 112, D23308. [Google Scholar] [CrossRef]
- Heald, C.L.; Jacob, D.J.; Jones, D.B.A.; Palmer, P.I.; Logan, J.A.; Streets, D.G.; Sachse, G.W.; Gille, J.C.; Hoffman, R.N.; Nehrkorn, T. Comparative inverse analysis of satellite (mopitt) and aircraft (trace-p) observations to estimate asian sources of carbon monoxide. J. Geophys. Res. 2004, 109, D23306. [Google Scholar]
- Dentener, F.; Peters, W.; Krol, M.; van Weele, M.; Bergamaschi, P.; Lelieveld, J. Interannual variability and trend of ch4 lifetime as a measure for OH changes in the 1979–1993 time period. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Pilkington, M. Joint inversion of gravity and magnetic data for two-layer models. Geophysics 2006, 71, 35–42. [Google Scholar] [CrossRef]
- Miller, J.B.; Mack, K.A.; Dissly, R.; White, J.W.C.; Dlugokencky, E.J.; Tans, P.P. Development of analytical methods and measurements of 13C/12C in atmospheric ch4 from the NOAA climate monitoring and diagnostics laboratory global air sampling network. J. Geophys. Res. 2002, 107, 4178. [Google Scholar] [CrossRef]
- GLOBALVIEW-CH4. Cooperative atmospheric data integration project—Methane. CD-ROM, NOAA ESRL, Boulder, Colorado. Available online: ftp.Cmdl.Noaa.Gov, path: Ccg/ch4/globalview (accessed on 17 April 2015).
- Lines, L.R.; Schultz, A.K.; Treitel, S. Cooperative inversion of geophysical data. Geophysics 1988, 53, 8–20. [Google Scholar] [CrossRef]
- Tsunogai, U.; Hachisu, Y.; Komatsu, D.D.; Nakagawa, F.; Gamo, T.; Akiyama, K.-I. An updated estimation of the stable carbon and oxygen isotopic compositions of automobile CO emissions. Atmos. Environ. 2003, 37, 4901–4910. [Google Scholar] [CrossRef]
- Bergamaschi, P.; Brenninkmeijer, C.A.M.; Hahn, M.; Rockmann, T.; Scharffe, D.H.; Crutzen, P.J.; Elansky, N.F.; Belikov, I.B.; Trivett, N.B.A.; Worthy, D.E.J. Isotope analysis based source identification for atmospheric CH4 and CO sampled across russia using the trans-siberian railroad. J. Geophys. Res. Atmos. 1998, 103, 8227–8235. [Google Scholar] [CrossRef]
- Kato, S.; Akimoto, H.; Röckmann, T.; Bräunlich, M.; Brenninkmeijer, C.A.M. Stable isotopic compositions of carbon monoxide from biomass burning experiments. Atmos. Environ. 1999, 33, 4357–4362. [Google Scholar]
- Park, K.; Emmons, L.K.; Wang, Z.; Mak, J.E. Large interannual variations in nonmethane volatile organic compound emissions based on measurements of carbon monoxide. Geophys. Res. Lett. 2013, 40, 221–226. [Google Scholar] [CrossRef]
- Conny, J.M.; Verkouteren, R.M.; Currie, L.A. Carbon 13 composition of tropospheric CO in Brazil: A model scenario during the biomass burn season. J. Geophys. Res. Atmos. 1997, 102, 10,638–10,693. [Google Scholar] [CrossRef]
- Conny, J.M. The isotopic characterization of carbon monoxide in the troposphere. Atmos. Environ. 1999, 32, 2669–2683. [Google Scholar] [CrossRef]
- Quay, P.D.; King, S.L.; Stutsman, J.; Wilbur, D.O.; Steele, L.P.; Fung, I.; Gammon, R.H.; Brown, T.A.; Farwell, G.W.; Grootes, P.M.; Schmidt, F.H. Carbon isotopic composition of atmospheric CH4: Fossil and biomass burning source strengths. Glob. Biogeochem. Cycles 1991, 5, 25–47. [Google Scholar] [CrossRef]
- Röckman, T.; Brenninkmeijer, C.A.M.; Crutzen, P.J.; Platt, U. Short term variations in the 13C/12C ratio of CO as a measure of Cl activation during tropospheric ozone depletion events in the Arctic. J. Geophys. Res. Atmos. 1999, 104, 1691–1697. [Google Scholar] [CrossRef]
- Moss, R.; Manning, M.; Lowe, D.; Ferretti, D.; Knobben, R. Changes in atmospheric carbon monoxide in the Pacific region. In Workshop on the Science of Atmospheric Trace Gases; NIWA: Wellington, New Zealand, 1998; Clarkson, T., Ed.; pp. 74–77. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, K.; Emmons, L.K.; Wang, Z.; Mak, J.E. Joint Application of Concentration and ?18O to Investigate the Global Atmospheric CO Budget. Atmosphere 2015, 6, 547-578. https://doi.org/10.3390/atmos6050547
Park K, Emmons LK, Wang Z, Mak JE. Joint Application of Concentration and ?18O to Investigate the Global Atmospheric CO Budget. Atmosphere. 2015; 6(5):547-578. https://doi.org/10.3390/atmos6050547
Chicago/Turabian StylePark, Keyhong, Louisa K. Emmons, Zhihui Wang, and John E. Mak. 2015. "Joint Application of Concentration and ?18O to Investigate the Global Atmospheric CO Budget" Atmosphere 6, no. 5: 547-578. https://doi.org/10.3390/atmos6050547
APA StylePark, K., Emmons, L. K., Wang, Z., & Mak, J. E. (2015). Joint Application of Concentration and ?18O to Investigate the Global Atmospheric CO Budget. Atmosphere, 6(5), 547-578. https://doi.org/10.3390/atmos6050547





