UV Irradiance Enhancements by Scattering of Solar Radiation from Clouds
Abstract
:1. Introduction
2. Materials and Methods
2.1. Cloud Modification Factors


2.2. Diurnal Changes of UV Cloud Modification Factors
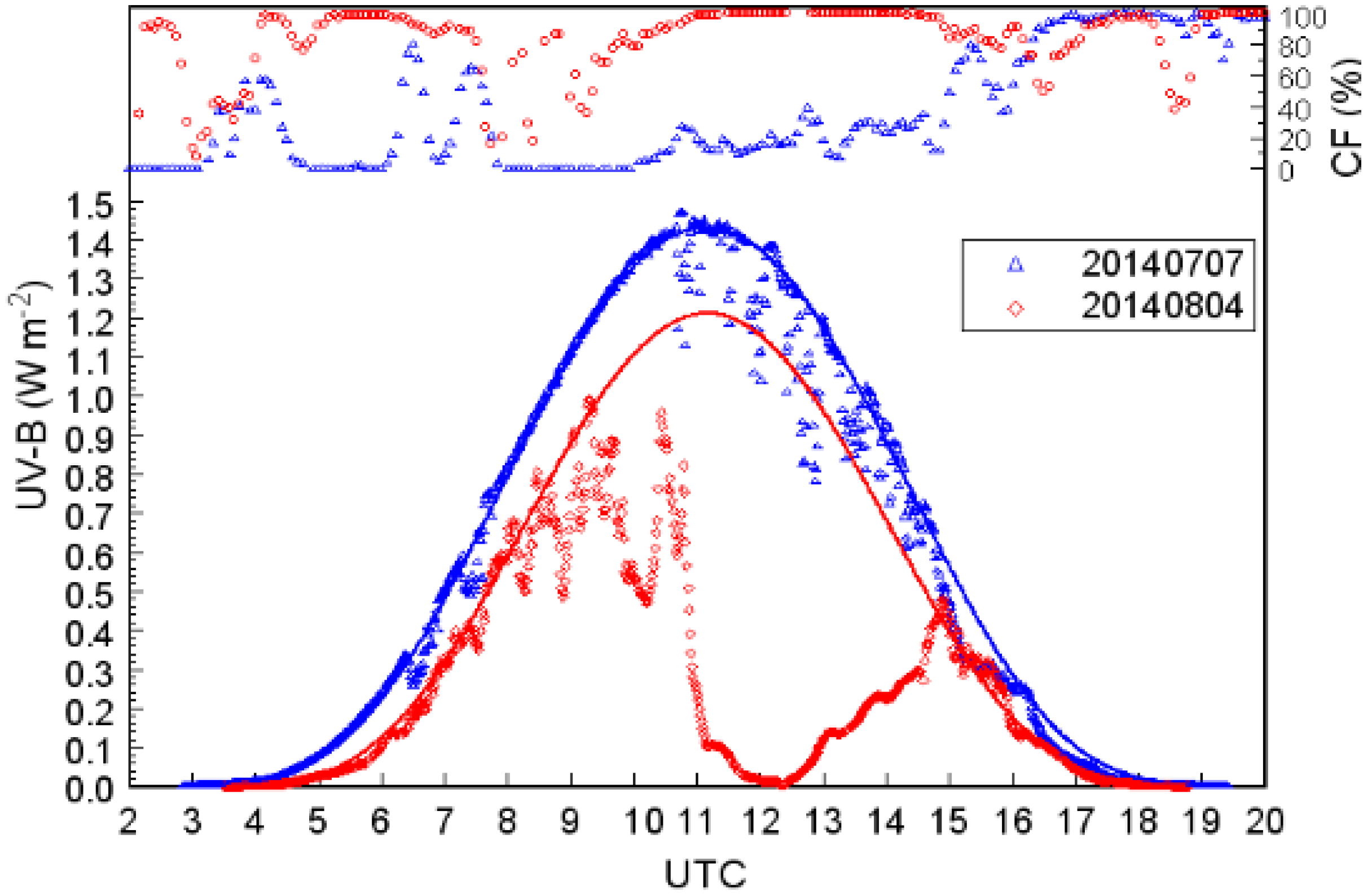
| 7 July 2014 | 4 August 2014 | |||
|---|---|---|---|---|
| MIN | MAX | MIN | MAX | |
| CMFUVB | 0.407 | 1.198 | 0.004 | 1.293 |
| CMFERY | 0.379 | 1.105 | 0.005 | 1.319 |
| CMFUVA | 0.350 | 1.153 | 0.010 | 1.337 |
| CMFUVB/UVA | 0.873 | 1.310 | 0.346 | 1.328 |
| CMFUVB/ERY | 0.970 | 1.143 | 0.768 | 1.157 |

3. Results
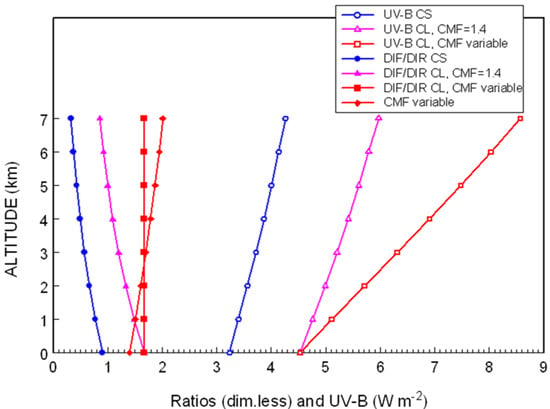
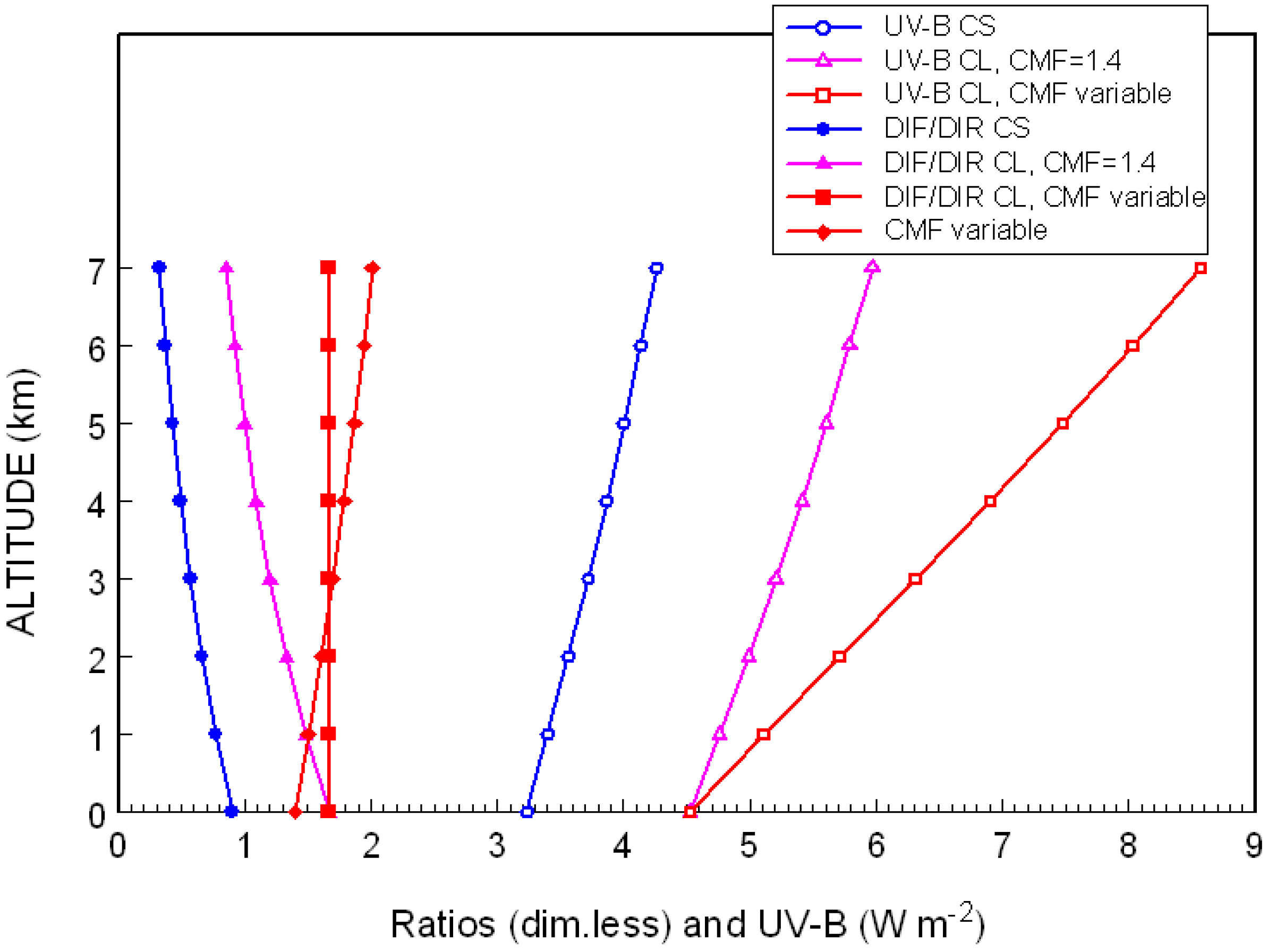
3.1. UV Irradiance Enhancement by Clouds in the Andes Region

| TST | SZA | UV-A | UV-ACS | CMFUVA | UV-B | CMFUVB/UVA | |
|---|---|---|---|---|---|---|---|
| 1 | 9.48 | 35.1 | 89.76 | 74.37 | 1.21 | 8.15 | 1.4 |
| 2 | 11.15 | 12.1 | 73.53 | 76.15 | 0.97 | 7.87 | 1.4 |
| 3 | 9.48 | 35.1 | 89.76 | 74.37 | 1.21 | 8.15 | 1.6 |
| 4 | 11.15 | 12.1 | 73.53 | 76.15 | 0.97 | 7.87 | 1.6 |
| 5 | 9.48 | 35.1 | 89.76 | 74.37 | 1.21 | 8.15 | 1.7 |
| 6 | 11.15 | 12.1 | 73.53 | 76.15 | 0.97 | 7.87 | 1.7 |
| 7 | 12.32 | 5.4 | 28.09 | 77.83 | 0.36 | 0.52 | 0.3 |
| CMFUVB | UVBCS | UVBCS/UVACS | CMFUVB/CMFERY | UVBCS/ERYCS | UVI | |
|---|---|---|---|---|---|---|
| 1 | 1.69 | 4.82 | 0.065 | 1.3 | 5.6 | 45 |
| 2 | 1.35 | 5.82 | 0.076 | 1.3 | 5.1 | 47 |
| 3 | 1.93 | 4.22 | 0.057 | 1.5 | 6.2 | 35 |
| 4 | 1.54 | 5.09 | 0.067 | 1.5 | 5.9 | 36 |
| 5 | 2.05 | 3.97 | 0.053 | 1.4 | 6.2 | 38 |
| 6 | 1.64 | 4.79 | 0.063 | 1.4 | 5.9 | 38 |
| 7 | 0.12 | 4.26 | 0.055 | 0.3 | 6.8 | 11 |
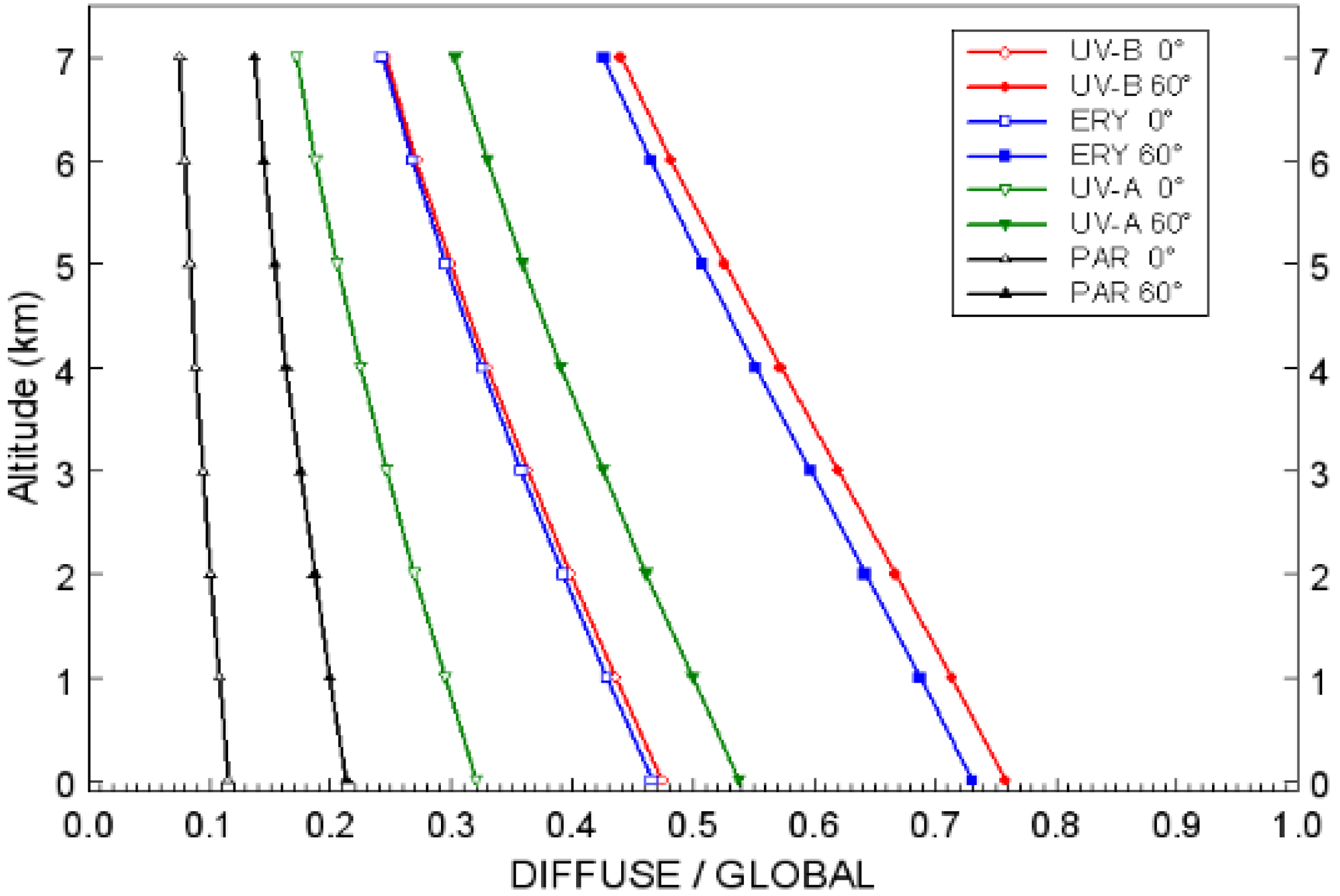

3.2. Conversion from UV-B Irradiance to Erythemal Irradiance or UV Index

4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations / Nomenclature
| AIRS | Atmospheric InfraRed Sounder |
| a.s.l | above sea level |
| Cb | Cumulonimbus |
| CF | cloud fraction, i.e., percentage of the upper hemisphere covered by clouds |
| CMF | cloud modification factor (dimensionless) |
| CL | index for cloudy sky |
| CS | index for cloudless sky |
| DIF, DIFFUSE | diffuse irradiance in the respective wavelength region (W·m−2) |
| DIR | direct irradiance in the respective wavelength region (W·m−2) |
| DU | Dobson unit |
| EPTOMS | Earth Probe Total Ozone Mapping Spectrometer |
| ERY | erythemal irradiance derived from spectral irradiance weighted by the erythemal action spectrum according to [8] |
| EXT | extraterrestrial irradiance in the respective wavelength region (W·m−2) |
| GLOBAL | global irradiance component in the respective wavelength region (W·m−2) |
| MEAS | index for measured irradiance |
| MOD | index for model calculation using the LibRadtran radiative transfer model |
| MODIS | Moderate Imaging Spectroradiometer |
| PAR | Photosynthetic Active Radiation defined as irradiance from 400 to 700 nm (W·m−2) |
| sc | index for irradiance including scattered radiation from clouds |
| SZA | solar zenith angle |
| TST | True Solar Time |
| TTL | tropical tropopause layer |
| UTC | Universal Time Coordinated |
| UV-A | irradiance from 315 to 400 nm (W·m−2) |
| UV-B | irradiance from 280 to 315 nm (W·m−2) |
| UVI | UV index (dimensionless) defined as the 40 fold of erythemal irradiance in W·m−2 |
References
- Gu, L.; Fuentes, J.D.; Garstang, M.; Tota da Silva, J.; Heitz, R.; Sigler, J.; Shugart, J.H. Cloud modulation of surface solar irradiance at a pasture site in southern Brazil. Agr. For. Meteorol. 2001, 106, 117–129. [Google Scholar] [CrossRef]
- Piacentini, R.D.; Cede, A.; Barcena, H. Extreme solar total and uv irradiances due to cloud effect measured near the summer solstice at the high-altitude desertic plateau puna of Atacama (Argentina). J. Atmos. Sol.-Terr. Phys. 2003, 65, 727–731. [Google Scholar] [CrossRef]
- Piacentini, R.D.; Salum, G.M.; Fraidenraich, N.; Tiba, C. Extreme total solar irradiance due to cloud enhancement at sea level of the Ne Atlantic Coast of Brazil. Renew. Energ. 2011, 36, 409–412. [Google Scholar] [CrossRef]
- Yordanov, G.H.; Midtgård, O.-M.; Saetre, T.O.; Nielsen, H.K.; Norum, L.E. Overirradiance (Cloud Enhancement) events at high latitudes. IEEE J. Photovoltaics 2013, 3, 271–277. [Google Scholar] [CrossRef]
- Mims, F.E., III; Frederick, J.E. Cumulus clouds and UV-B. Nature 1994, 371, 291. [Google Scholar] [CrossRef]
- Sabburg, J.M.; Long, C.N. Improved sky imaging for studies of enhanced uv irradiance. Atmos. Chem. Phys. Discuss. 2004, 4, 6213–6238. [Google Scholar] [CrossRef]
- Sabburg, J.; Calbó, J. Five Years of cloud enhanced surface uv radiation measurements at two sites (in the Northern and Southern Hemispheres). Atmos. Res. 2009, 93, 902. [Google Scholar] [CrossRef]
- McKinlay, A.F.; Diffey, B.L. A reference action spectrum for ultraviolet induced erythema in human skin. CIE-J. 1987, 6, 17–22. [Google Scholar]
- Webb, A.R.; Slaper, H.; Koepke, P.; Schmalwieser, A.W. Know your standard: clarifying the CIE erythema action spectrum. Photochem. Photobiol. 2011, 87, 483–486. [Google Scholar] [CrossRef] [PubMed]
- Schwander, H.; Koepke, P.; Kaifel, A.; Seckmeyer, G. Modification of spectral UV irradiance by clouds. J. Geophys. Res. 2002, 107, D16. [Google Scholar] [CrossRef]
- Lovengreen, C.; Fuenzalida, H.A.; Videla, L. On the spectral dependency of UV radiation enhancements due to clouds in Valdivia, Chile (39.8° S). J. Geophys. Res. 2005, 110, D14207. [Google Scholar] [CrossRef]
- Sabburg, J.M.; Parisi, A.V. Spectral dependency of cloud enhanced UV irradiance. Atmos. Res. 2006, 81, 206–214. [Google Scholar] [CrossRef]
- Lopez, M.L.; Palancar, G.G.; Toselli, B.M. Effect of different types of clouds on surface UV-b and total solar irradiance at southern mid-latitudes: cmf determinations at Cordoba, Argentina. Atmos. Environ. 2009, 43, 3130–3136. [Google Scholar] [CrossRef]
- Gelsor, N.; Pingcuo, N.; Wangmu, T.; Kjeldstad, B.; Chen, Y.C.; Frette, Ø.; Stamnes, J.J.; Bhattarai, B.K.; Dahlback, A. Solar UV irradiance measurements at four sites in Tibet. J. Ins. Eng. 2011, 8, 75–86. [Google Scholar]
- Cabrol, N.A.; Feister, U.; Häder, D.-P.; Piazena, H.; Grin, E.A.; Klein, A. Record solar UV irradiance in the tropical Andes. Front. Environ. Sci. 2014, 2, 1–6. [Google Scholar] [CrossRef]
- Balis, D.S.; Zerefos, C.S.; Kourtidis, K.; Bais, A.F.; Hofzumahaus, A.; Kraus, A.; Schmitt, R.; Blumthaler, M.; Gobbi, G.P. Measurements and modeling of photolysis rates during the Photochemical Activity and Ultraviolet Radiation (PAUR) II campaign. J. Geophys. Res. 2002, 107, 8138. [Google Scholar] [CrossRef]
- Zerefos, C.S.; Kourtidis, K.A.; Melas, D.; Balis, D.; Zanis, P.; Katsaros, L.; Mantis, H.T.; Repapis, C.; Isaksen, I.; Sundet, J.; et al. Photochemical activity and solar ultraviolet radiation (PAUR) modulation factors: An overview of the project. J. Geophys. Res. 2002, 107, 8134. [Google Scholar] [CrossRef]
- Mayer, B.; Kylling, A. Technical note: The LibRadtran software package for radiative transfer calculations-description and examples of use. Atmos. Chem. Phys. 2005, 5, 1855–1877. [Google Scholar] [CrossRef]
- den Outer, P.N.; Slaper, H.; Kaurola, J.; Lindfors, A.; Kazantzidis, A.; Bais, A.; Feister, U.; Junk, J.; Janouch, M.; Josefsson, W. Reconstructing of erythemal ultraviolet radiation levels in Europe for the past four decades. J. Geophys. Res. Atmos. 2010, 115, 1–17. [Google Scholar] [CrossRef]
- Staiger, H.; den Outer, P.; Bais, A.; Feister, U.; Johnsen, B.; Vuilleumier, L. Hourly resolved cloud modification factors in the ultraviolet. Atmos. Chem. Phys. 2008, 8, 2493–2508. [Google Scholar] [CrossRef]
- Feister, U.; Shields, J. Cloud and Radiance Measurements with the VIS/NIR Daylight Whole Sky Imager at Lindenberg (Germany). Meteorol. Zeitschr. 2005, 14, 627–639. [Google Scholar] [CrossRef]
- Feister, U.; Kaifel, A.; Grewe, R.-D.; Kaptur, J.; Reutter, O.; Wohlfart, M.; Gericke, K. Fast measurements of solar spectral irradiance-first performance results of two novel spectroradiometers. Opt. Eng. 2005, 44, 1–9. [Google Scholar]
- Mayer, B.; Kylling, A.; Madronich, S.; Seckmeyer, G. Enhanced absorption of UV radiation due to multiple scattering in clouds-experimental evidence and theoretical explanation. J. Geophys. Res. 1998, 103, 241–254. [Google Scholar] [CrossRef]
- Feister, U.; Laschewski, G.; Grewe, R.D. UV Index Forecasts and Measurements of Health-effective Radiation. J. Photochem. Photobiol. Bio. 2011, 102, 55–68. [Google Scholar] [CrossRef] [PubMed]
- Mishin, E. Ozone Layer Perturbation by a Single Blue Jet. Geophys. Res. Lett. 1997, 24, 1919–1922. [Google Scholar] [CrossRef]
- Pasko, V.P.; George, J.J. Three-dimensional modeling of blue jets and blue starters. J. Geophys. Res. 2002, 107, 1458. [Google Scholar] [CrossRef]
- Winkler, H.; Notholt, J. A Model study of the plasma chemistry of stratospheric blue jets. J. Atmos. Sol.-Terr. Phys. 2015, 122, 75–85. [Google Scholar] [CrossRef]
- Nirala, M. Multi-sensor data fusion and comparison of total column ozone. Int. J. Remote Sens. 2007, 29, 15, 4553–4573. [Google Scholar] [CrossRef]
- Hassim, M.E.E.; Lane, T.P. A Model study on the influence of overshooting convection on ttl water vapour. Atmos. Chem. Phys. 2010, 10, 9833–9849. [Google Scholar] [CrossRef]
- Wang, P.K.; Su, S.H.; Charvát, Z.; Šťástka, J.; Lin, H.M. Cross tropopause transport of water by mid-latitude deep convective storms: A review. Terr. Atmos. Ocean. Sci. 2011, 22, 447–462. [Google Scholar] [CrossRef]
- Aumann, H.H.; Gregorich, D.; DeSouza-Machado, S. AIRS observations of deep convective clouds. In Proceedings SPIE 6301of the Atmospheric and Environmental Remote Sensing Data Processing and Utilization II: Perspective on Calibration/Validation Initiatives and Strategies, San Diego, CA, USA, 13 August 2006.
- Weisz, E.; Li, J.; Menzel, J.W.; Heidinger, A.K.; Kahn, B.H.; Liu, C.-Y. Comparison of AIRS, MODIS, CloudSat and CALIPSO cloud top height retrievals. Geophys. Res. Lett. 2007, 34, L17811. [Google Scholar] [CrossRef]
- McKenzie, R.; Smale, D.; Kotkamp, M. Relationship between UVB and erythemally weighted radiation. Photochem. Photobiol. Sci. 2004, 3, 252–256. [Google Scholar] [CrossRef] [PubMed]
- Acker, J.G.; Leptoukh, G. Online Analysis enhances use of NASA earth science data. Eos Trans. AGU 2007, 88, 14–17. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feister, U.; Cabrol, N.; Häder, D. UV Irradiance Enhancements by Scattering of Solar Radiation from Clouds. Atmosphere 2015, 6, 1211-1228. https://doi.org/10.3390/atmos6081211
Feister U, Cabrol N, Häder D. UV Irradiance Enhancements by Scattering of Solar Radiation from Clouds. Atmosphere. 2015; 6(8):1211-1228. https://doi.org/10.3390/atmos6081211
Chicago/Turabian StyleFeister, Uwe, Nathalie Cabrol, and Donat Häder. 2015. "UV Irradiance Enhancements by Scattering of Solar Radiation from Clouds" Atmosphere 6, no. 8: 1211-1228. https://doi.org/10.3390/atmos6081211
APA StyleFeister, U., Cabrol, N., & Häder, D. (2015). UV Irradiance Enhancements by Scattering of Solar Radiation from Clouds. Atmosphere, 6(8), 1211-1228. https://doi.org/10.3390/atmos6081211