Interdecadal Variations in the Walker Circulation and Its Connection to Inhomogeneous Air Temperature Changes from 1961–2012
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. 3P-DGAC Method
2.3. Definition of the PWC Intensity
3. Capability of the Novel 3P-DGAC Method to Acquire Interdecadal Variations in the PWC
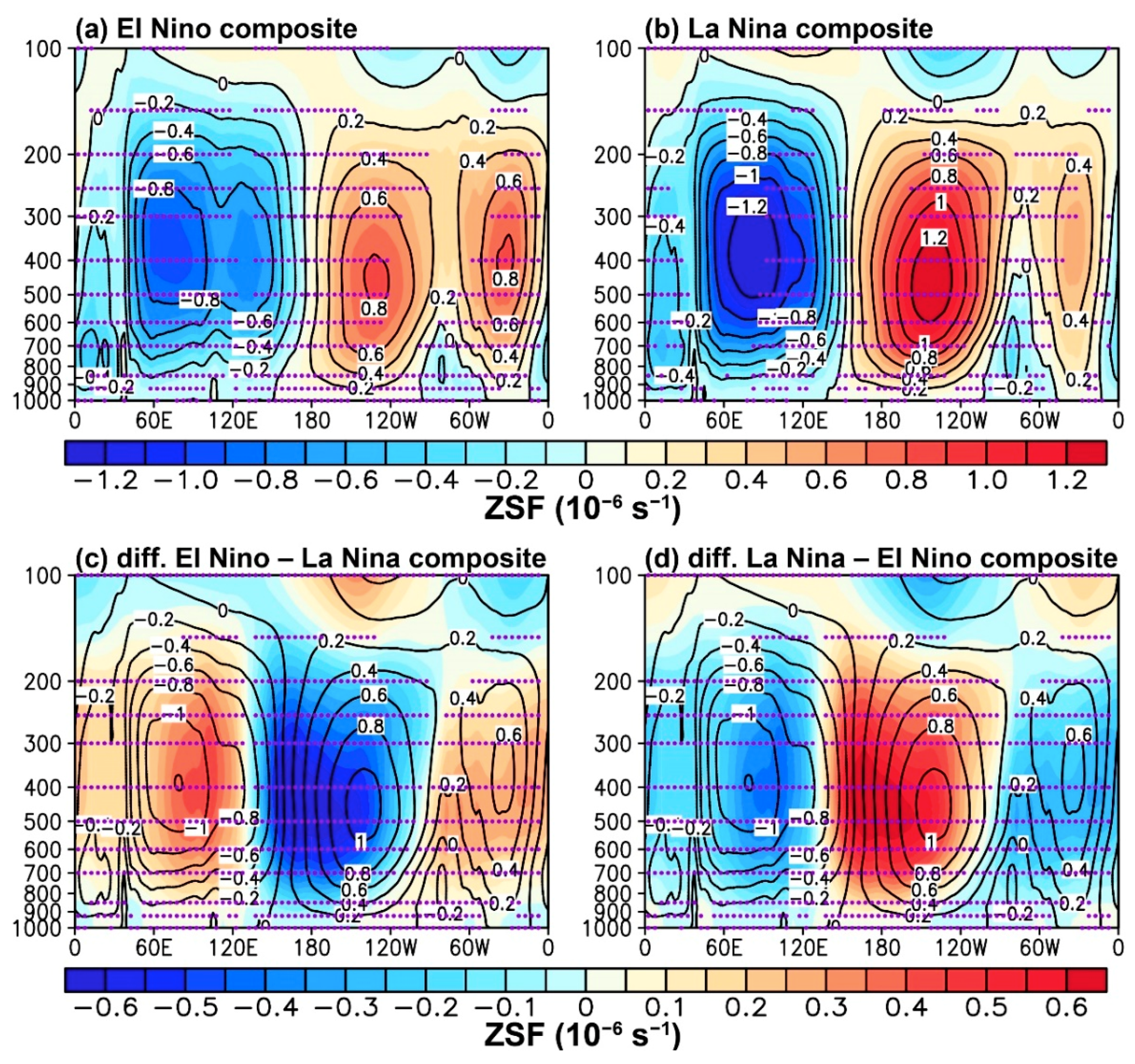
3.1. Response of the PWC to El Niño–Southern Oscillation (ENSO) Events
3.2. Interdecadal Variations of the PWC
3.3. Interdecadal Variations of the Precipitation, Zonal Winds at 1000 hPa, SST, and SLP in the Low Latitudes
4. Connections between the Interdecadal Variations in the PWC Intensity and the Air Temperature Gradient Changes
5. Novel Index for the PWC Intensity Based on Air Temperature
6. Summary
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Bjerknes, J. Atmospheric teleconnections from the equatorial Pacific. Mon. Weather Rev. 1969, 97, 163–172. [Google Scholar] [CrossRef]
- Philander, S.G.H. El Niño, La Niña, and the Southern Oscillation; Academic Press: San Diego, CA, USA, 1990. [Google Scholar]
- Power, S.; Casey, T.; Folland, C.; Colman, A.; Mehta, V. Inter-decadal modulation of the impact of ENSO on Australia. Clim. Dyn. 1999, 15, 319–324. [Google Scholar] [CrossRef]
- Kosaka, Y.; Xie, S.-P. Recent global-warming hiatus tied to equatorial Pacific surface cooling. Nature 2013, 501, 403–407. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- England, M.H.; Mcgregor, S.; Spence, P.; Meehl, G.A.; Timmermann, A.; Cai, W.; Gupta, A.S.; McPhaden, M.J.; Purich, A.; Santoso, A. Recent intensification of wind-driven circulation in the Pacific and the ongoing warming hiatus. Nat. Clim. Chang. 2014, 4, 222–227. [Google Scholar] [CrossRef] [Green Version]
- Ma, S.; Zhou, T. Changes of the tropical Pacific Walker circulation simulated by two versions of FGOALS model. Sci. China Earth Sci. 2014, 57, 2165–2180. [Google Scholar] [CrossRef]
- Ma, S.; Zhou, T. Robust strengthening and westward shift of the tropical Pacific Walker circulation during 1979–2012: A comparison of 7 sets of reanalysis data and 26 CMIP5 dodels. J. Clim. 2016, 29, 3097–3118. [Google Scholar] [CrossRef]
- Vecchi, G.A.; Soden, B.J.; Wittenberg, A.T.; Held, I.M.; Leetmaa, A.; Harrison, M.J. Weakening of tropical Pacific atmospheric circulation due to anthropogenic forcing. Nature 2006, 441, 73–76. [Google Scholar] [CrossRef] [PubMed]
- Vecchi, G.A.; Soden, B.J. Global warming and the weakening of the tropical circulation. J. Clim. 2007, 20, 4316–4340. [Google Scholar] [CrossRef]
- DiNezio, P.N.; Clement, A.C.; Vecchi, G.A.; Soden, B.J.; Kirtman, B.P.; Lee, S.K. Climate response of the equatorial Pacific to global warming. J. Clim. 2009, 22, 4873–4892. [Google Scholar] [CrossRef]
- Yu, B.; Zwiers, F.W. Changes in equatorial atmospheric zonal circulations in recent decades. Geophys. Res. Lett. 2010, 37, L05701. [Google Scholar] [CrossRef]
- Power, S.B.; Kociuba, G. What caused the observed twentieth-century weakening of the Walker circulation? J. Clim. 2011, 24, 6501–6514. [Google Scholar] [CrossRef]
- Tokinaga, H.; Xie, S.-P.; Deser, C.; Yu, K.; Okumura, Y.M. Slowdown of the Walker circulation driven by tropical Indo-Pacific warming. Nature 2012, 491, 439–443. [Google Scholar] [CrossRef] [PubMed]
- DiNezio, P.N.; Vecchi, G.A.; Clement, A.C. Detectability of changes in the Walker circulation in response to global warming. J. Clim. 2013, 26, 4038–4048. [Google Scholar] [CrossRef]
- Kociuba, G.; Power, S.B. Inability of CMIP5 models to simulate recent strengthening of the Walker circulation: Implications for projections. J. Clim. 2015, 28, 20–35. [Google Scholar] [CrossRef]
- Meng, Q.; Latif, M.; Park, W.; Keenlyside, N.S.; Semenov, V.A.; Martin, T. Twentieth century Walker circulation change: Data analysis and model experiments. Clim. Dyn. 2012, 38, 1757–1773. [Google Scholar] [CrossRef]
- L’Heureux, M.L.; Lee, S.; Lyon, B. Recent multidecadal strengthening of the Walker circulation across the tropical Pacific. Nat. Clim. Chang. 2013, 3, 571–576. [Google Scholar] [CrossRef]
- Sohn, B.J.; Yeh, S.W.; Schmetz, J.; Song, H.J. Observational evidences of Walker circulation change over the last 30 years contrasting with GCM results. Clim. Dyn. 2013, 40, 1721–1732. [Google Scholar] [CrossRef]
- McGregor, S.; Timmermann, A.; Stuecker, M.F.; England, M.H.; Merrifield, M.; Jin, F.-F.; Chikamoto, Y. Recent Walker circulation strengthening and Pacific cooling amplified by Atlantic warming. Nat. Clim. Chang. 2014, 4, 888–892. [Google Scholar] [CrossRef] [Green Version]
- Sandeep, S.; Stordal, F.; Sardeshmukh, P.D.; Compo, G.P. Pacific Walker circulation variability in coupled and uncoupled climate models. Clim. Dyn. 2014, 43, 103–117. [Google Scholar] [CrossRef]
- Dong, B.; Lu, R. Interdecadal enhancement of the Walker circulation over the tropical Pacific in the late 1990s. Adv. Atmos. Sci. 2013, 30, 247–262. [Google Scholar] [CrossRef]
- Allan, R.; Ansell, T. A New Globally complete monthly historical gridded mean sea level pressure dataset (HadSLP2): 1850–2004. J. Clim. 2006, 19, 5816–5842. [Google Scholar] [CrossRef]
- Deser, C.; Wallace, J.M. Large-scale atmospheric circulation features of warm and cold episodes in the tropical Pacific. J. Clim. 1990, 3, 1254–1281. [Google Scholar] [CrossRef]
- Garcia, S.R.; Kayano, M.T. Climatological aspects of Hadley, Walker and monsoon circulations in two phases of the Pacific decadal oscillation. Theor. Appl. Climatol. 2008, 91, 117–127. [Google Scholar] [CrossRef]
- Bayr, T.; Dommenget, D.; Martin, T.; Power, S.B. The eastward shift of the Walker circulation in response to global warming and its relationship to ENSO variability. Clim. Dyn. 2014, 43, 2747–2763. [Google Scholar] [CrossRef]
- Hu, S.; Cheng, J.; Xu, M.; Chou, J. Three-pattern decomposition of global atmospheric circulation: Part II—Dynamical equations of horizontal, meridional and zonal circulations. Clim. Dyn. 2018, 50, 2673–2686. [Google Scholar] [CrossRef]
- Bayr, T.; Dommenget, D. The tropospheric land-sea warming contrast as the driver of tropical sea level pressure changes. J. Clim. 2013, 26, 1387–1402. [Google Scholar] [CrossRef]
- Xu, M. Study on the Three Dimensional Decomposition of Large Scale Circulation and Its Dynamical Feature. Ph.D. Thesis, Lanzhou University, Lanzhou, China, May 2001. (In Chinese). [Google Scholar]
- Hu, S. The Three-Dimensional Expansion of Global Atmospheric Circumfluence and Characteristic Analyze of Atmospheric Vertical Motion. Ph.D. Thesis, Lanzhou University, Lanzhou, China, June 2006. (In Chinese). [Google Scholar]
- Liu, H.; Hu, S.; Xu, M.; Chou, J. Three-dimensional decomposition method of global atmospheric circulation. Sci. China Ser. D 2008, 51, 386–402. [Google Scholar] [CrossRef]
- Hu, S.; Cheng, J.; Chou, J. Novel three-pattern decomposition of global atmospheric circulation: Generalization of traditional two-dimensional decomposition. Clim. Dyn. 2017, 49, 3573–3586. [Google Scholar] [CrossRef]
- Hu, S.; Chou, J.; Cheng, J. Three-pattern decomposition of global atmospheric circulation: Part I—Decomposition model and theorems. Clim. Dyn. 2018, 50, 2355–2368. [Google Scholar] [CrossRef]
- Cheng, J.; Gao, C.; Hu, S.; Feng, G. High-stability algorithm for the three-pattern decomposition of global atmospheric circulation. Theor. Appl. Climatol. 2018, 133, 851–866. [Google Scholar] [CrossRef]
- Cheng, J.; Xu, Z.; Hu, P.; Hou, X.; Gao, C.; Hu, S.; Feng, G. Significant role of orography in shaping the northern Hadley circulation and its poleward expansion during boreal summer. Geophys. Res. Lett. 2018, 45, 6619–6627. [Google Scholar] [CrossRef]
- Ebita, A.; Kobayashi, S.; Ota, Y.; Moriya, M.; Kumabe, R.; Onogi, K.; Harada, Y.; Yasui, S.; Miyaoka, K.; Takahashi, K.; et al. The Japanese 55-year reanalysis “JRA-55”: An interim report. SOLA 2011, 7, 149–152. [Google Scholar] [CrossRef]
- Chen, M.; Xie, P.; Janowiak, J.E.; Arkin, P.A. Global land precipitation: A 50-y monthly analysis based on gauge observations. J. Hydrometeorol. 2002, 3, 249–266. [Google Scholar] [CrossRef]
- Huang, B.; Thorne, P.W.; Banzon, V.F.; Boyer, T.; Chepurin, G.; Lawrimore, J.H.; Menne, M.J.; Smith, T.M.; Vose, R.S.; Zhang, H.M. NOAA Extended Reconstructed Sea Surface Temperature (ERSST); Version 5; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2017. [Google Scholar] [CrossRef]
- Holton, J.R. Synoptic-scale motions I: Quasi-geostrophic analysis. In An Introduction to Dynamic Meteorology, 4th ed.; Cynar, F., Ed.; Elsevier Academic Press: Amsterdam, The Netherlands, 2004; pp. 139–176. [Google Scholar]
- Yu, B.; Zwiers, F.W.; Boer, G.J.; Ting, M.F. Structure and variances of equatorial zonal circulation in a multimodel ensemble. Clim. Dyn. 2012, 39, 2403–2419. [Google Scholar] [CrossRef]
- Schwendike, J.; Govekar, P.; Reeder, M.J.; Wardle, R.; Berry, G.J.; Jakob, C. Local partitioning of the overturning circulation in the tropics and the connection to the Hadley and Walker circulations. J. Geophys. Res. Atmos. 2014, 119, 1322–1339. [Google Scholar] [CrossRef] [Green Version]
- Graham, N.E. Decadal-scale climate variability in the tropical and North Pacific during the 1970s and 1980s: Observations and model results. Clim. Dyn. 1994, 10, 135–162. [Google Scholar] [CrossRef]
- Burgman, R.J.; Clement, A.C.; Mitas, C.M.; Chen, J.; Esslinger, K. Evidence for atmospheric variability over the Pacific on decadal timescales. Geophys. Res. Lett. 2008, 35, L01704. [Google Scholar] [CrossRef]
- Chen, J.; DelGenio, A.D.; Carlson, B.E.; Bosilovich, M.G. The spatiotemporal structure of twentieth-century climate variations in observations and reanalysis. Part II: Pacific pan-decadal variability. J. Clim. 2008, 21, 2634–2650. [Google Scholar] [CrossRef]
- Wang, H.; Mehta, V.M. Decadal variability of the Indo-Pacific warm pool and its association with atmospheric and oceanic variability in the NCEP-NCAR and SODA reanalyses. J. Clim. 2008, 21, 5545–5565. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, L.; Yu, L. Oceanic origin of a recent La Niña-like trend in the tropical Pacific. Adv. Atmos. Sci. 2011, 28, 1109–1117. [Google Scholar] [CrossRef]
- Schwendike, J.; Berry, G.J.; Reeder, M.J.; Jakob, C.; Govekar, P.; Wardle, R. Trends in the local Hadley and local Walker circulations. J. Geophys. Res. 2015, 120, 7599–7618. [Google Scholar] [CrossRef] [Green Version]










© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, X.; Cheng, J.; Hu, S.; Feng, G. Interdecadal Variations in the Walker Circulation and Its Connection to Inhomogeneous Air Temperature Changes from 1961–2012. Atmosphere 2018, 9, 469. https://doi.org/10.3390/atmos9120469
Hou X, Cheng J, Hu S, Feng G. Interdecadal Variations in the Walker Circulation and Its Connection to Inhomogeneous Air Temperature Changes from 1961–2012. Atmosphere. 2018; 9(12):469. https://doi.org/10.3390/atmos9120469
Chicago/Turabian StyleHou, Xiaoya, Jianbo Cheng, Shujuan Hu, and Guolin Feng. 2018. "Interdecadal Variations in the Walker Circulation and Its Connection to Inhomogeneous Air Temperature Changes from 1961–2012" Atmosphere 9, no. 12: 469. https://doi.org/10.3390/atmos9120469
APA StyleHou, X., Cheng, J., Hu, S., & Feng, G. (2018). Interdecadal Variations in the Walker Circulation and Its Connection to Inhomogeneous Air Temperature Changes from 1961–2012. Atmosphere, 9(12), 469. https://doi.org/10.3390/atmos9120469



