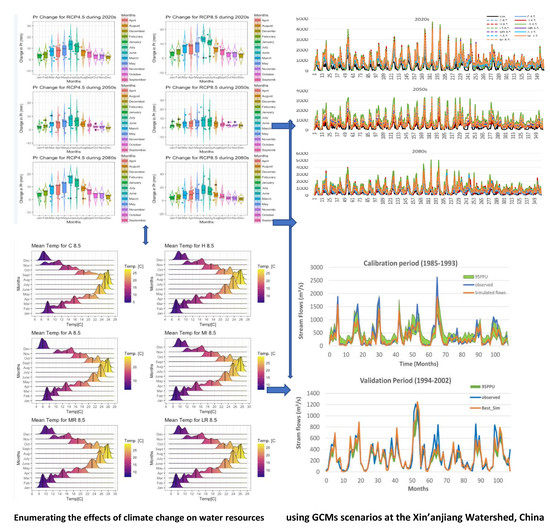
Enumerating the Effects of Climate Change on Water Resources Using GCM Scenarios at the Xin’anjiang Watershed, China
Abstract
:1. Introduction
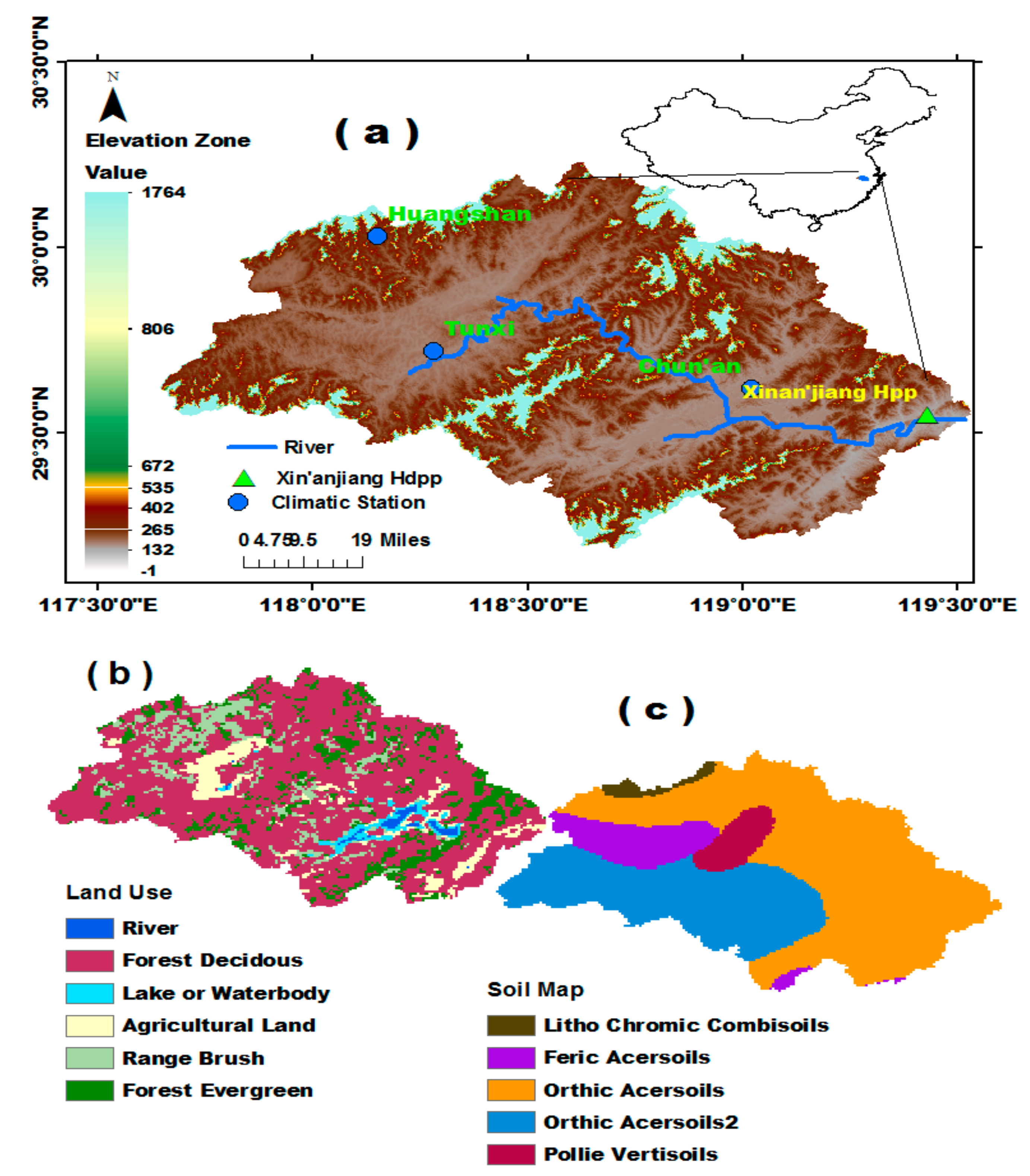
2. Location of the Study Area
3. Data Collection
4. Materials and Methods
4.1. Functionality of SWAT
4.2. SWAT Data Inputs
4.2.1. Spatial Datasets
4.2.2. Temporal Data
4.3. Model Efficiency
4.4. SWAT-CUP
4.5. Statistical Downscaling of Climatic Variables
4.6. Optimization of the Projected Flows for Hydropower
4.6.1. Proposed Mathematical Model for Xin’anjiang Hydropower
4.6.2. PSO
5. Results and Discussion
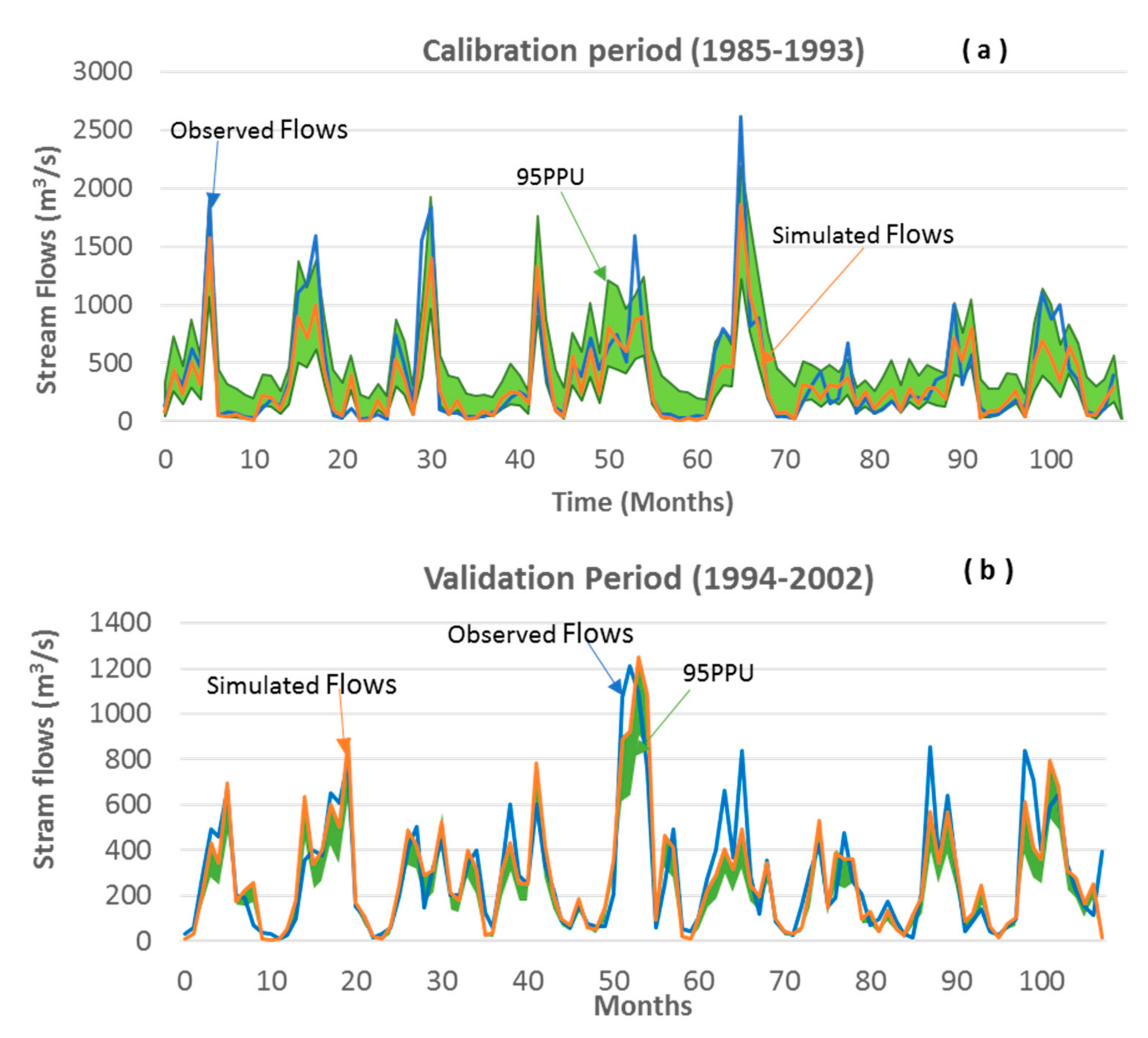
5.1. SWAT Evaluation
5.1.1. Sensitivity Analysis
5.1.2. Model Calibration and Validation
5.2. Climate Change Scenarios
5.2.1. Mean Monthly Maximum and Minimum Temperatures
5.2.2. Mean Temperature Distribution till 2100
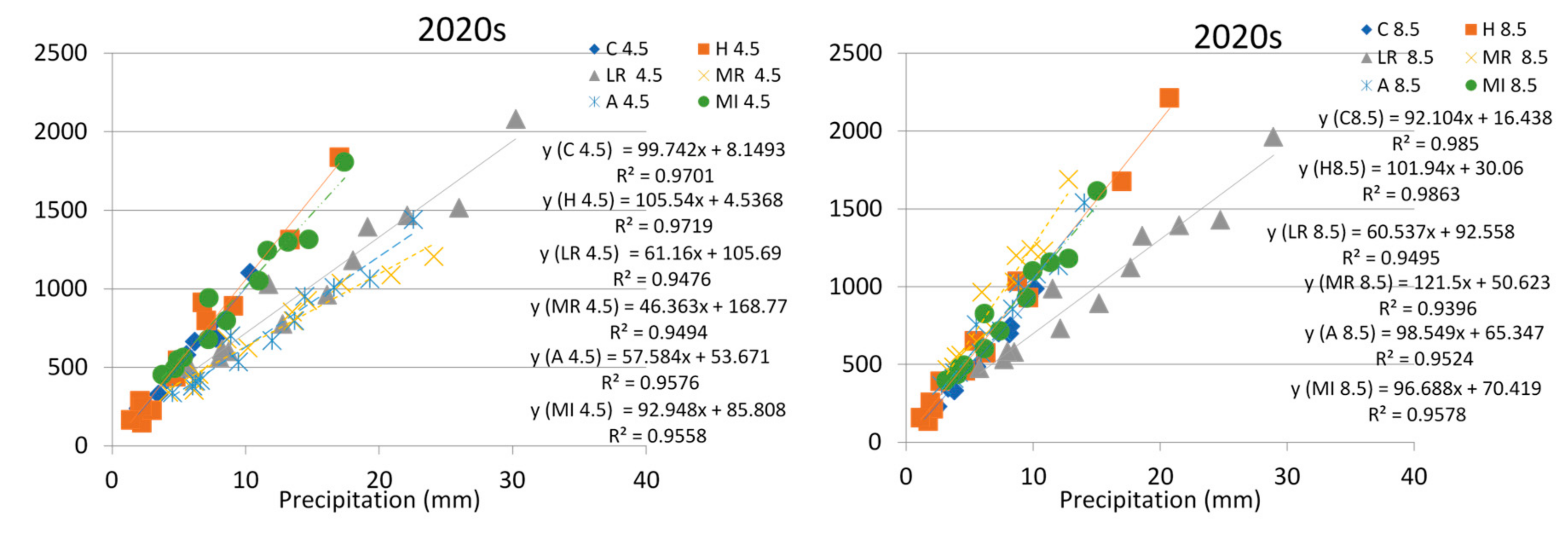
5.3. Change in Precipitation
5.4. Climate Change Impacts on Hydrological Behaviors
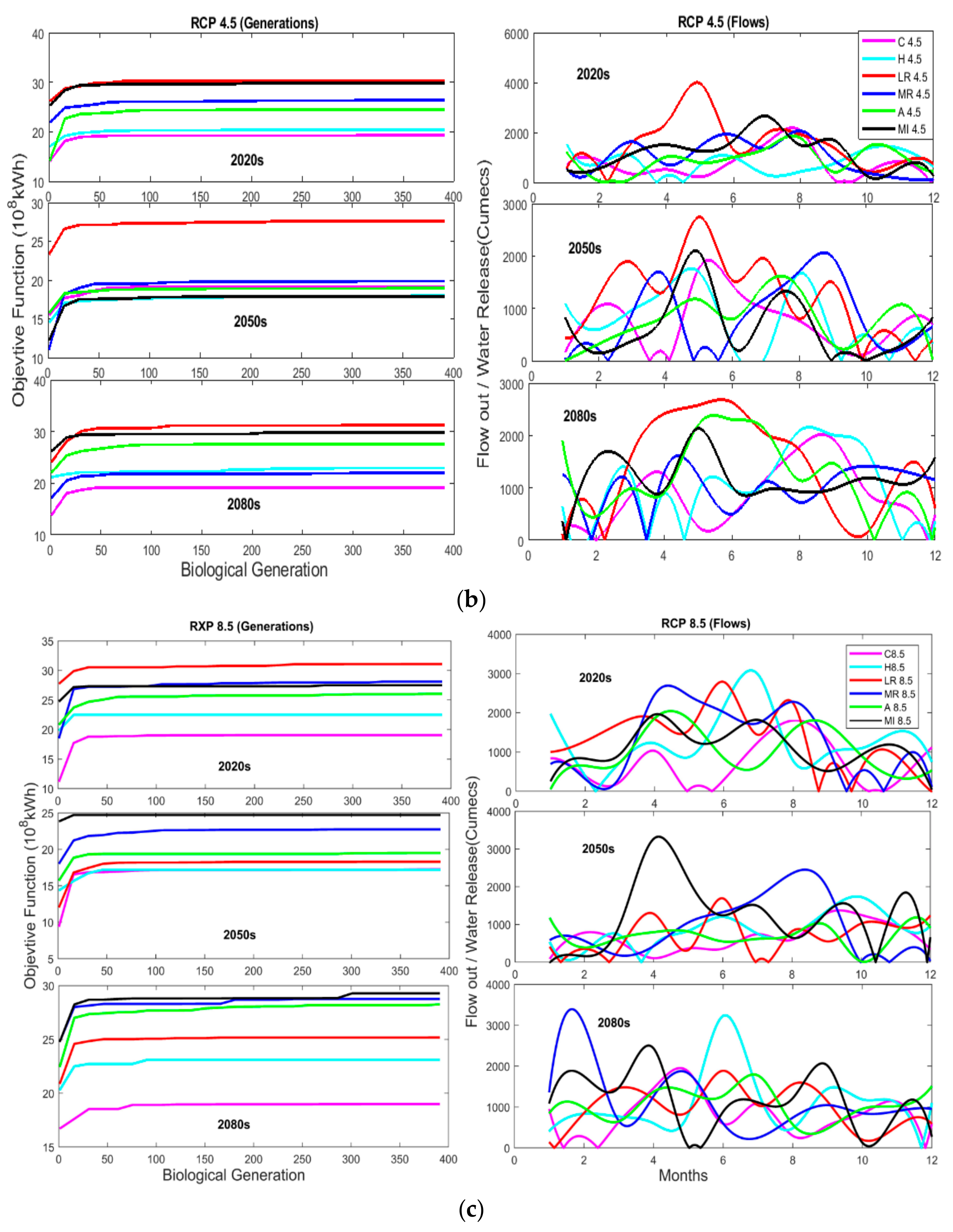
5.5. Projected Hydropower Generation and Optimization Using Future Stream Flows
6. Discussion on Uncertainties and Limitations of the Current Study
7. Conclusions and Recommendations
- (1)
- Calibration and validation of the SWAT indicated that evaluation indices e.g., NSE and R2, were satisfactory within monthly timescale. The calibrated SWAT accurately reproduced stream flows in the Xin’anjiang watershed.
- (2)
- The downscaled results of the GCMs and RCPs showed that maximum and minimum temperature will continually increase in the future with a maximum increase during April to July. However, future projections of precipitations for six GCMs grow more uncertain and complex, for monthly and seasonal series shows overall increase in precipitation (except HadGEM2-ES, which shows decrease in monthly and seasonal series during some months and seasons) with maximum increase during the months of June and July for monthly series and in summer season for seasonal series. Overall, monthly and seasonal precipitation will apparently increase during this century with a maximum increase for the 2020s followed by 2080s, but 2050s appear to less increase in future precipitation amount. The average increase in precipitation for seasonal and monthly series is more significant under RCP4.5 as compared to RCP8.5 scenarios.
- (3)
- Six GCMs generated large magnitude increase in stream flows during summer and autumn than in winter and spring seasons. The average of six GCMs and RCPs for monthly series stated that mostly GCMs and RCPs exhibit increase in streamflow with maximum increase during June and July. The mean of multi GCMs and RCPs showed that stream flow exhibits a strong correlation with precipitation and clearly indicated that any change in stream flows is typically affected by simultaneous variations in precipitations. The results of streamflows indicated that maximum increase in the stream flow is during the 2020s and 2080s as precipitation amount increases, while the lesser increase is expected in precipitation and stream flows during 2050s. Moreover, MPI-ESM-LR generated the large magnitude of stream flows in the 21st century than any other GCMs.
- (4)
- The ensemble optimization technique and mathematical model used for hydropower production for six GCMs under RCP scenarios can enhance the electricity amount than using the flows traditionally. The maximum amount of electricity generation is expected during the 2020s by optimal use of stream flows for GCMs. Results indicated that MPI-ESM-LR generated the maximum amount of electricity using 2020s flows under RCP8.5 and 4.5 followed by MIROC-ESM.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stocker, T. Change 2013: The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Wang, G.Q.; Zhang, J.Y.; Jin, J.L.; Pagano, T.C.; Calow, R.; Bao, Z.X.; Liu, C.S.; Liu, Y.L.; Yan, X.L. Assessing water resources in China using PRECIS projections and a VIC model. Hydrol. Earth Syst. Sci. 2012, 16, 231–240. [Google Scholar] [CrossRef] [Green Version]
- Solomon, S.; Intergovernmental Panel on Climate Change Working Group I. Climate Change 2007: The Physical Science Basis: Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Field, C.B.; Barros, V.R.; Intergovernmental Panel on Climate Change Working Group II. Climate Change 2014: Impacts, Adaptation, and Vulnerability: Working Group II Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Zhang, J.Y.; Wang, G. Impacts of Climate Change on Hydrology and Water Resources; Science Press: Beijing, China, 2007. (In Chinese) [Google Scholar]
- Piao, S.; Ciais, P.; Huang, Y.; Shen, Z.; Peng, S.; Li, J.; Zhou, L.; Liu, H.; Ma, Y.; Ding, Y.; et al. The impacts of climate change on water resources and agriculture in China. Nature 2010, 467, 43–51. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Ren, G.; Zhao, Z.; Xu, Y.; Luo, Y.; Li, Q.; Jin, Z. Detection, causes and projection of climate change over China: An overview of recent progress. Adv. Atmos. Sci. 2007, 24, 954–971. [Google Scholar] [CrossRef]
- ECSNCCA. Second National Climate Change Assessment Report [Internet]. Beijing, 2011. Available online: http://unfccc.int/resource/docs/natc/chnnc2e.pdf (accessed on 2 February 2018).
- Ding, Y.; Sun, Y.; Wang, Z.; Zhu, Y.; Song, Y. Inter-decadal variation of the summer precipitation in China and its association with decreasing Asian summer monsoon Part II: Possible causes. Int. J. Climatol. 2009, 29, 1926–1944. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Zhou, L. Observed trends in extreme precipitation events in China during 1961–2001 and the associated changes in large-scale circulation. Geophys. Res. Lett. 2005, 32, L09707. [Google Scholar] [CrossRef]
- Feng, L.; Zhou, T.; Wu, B.; Li, T.; Luo, J.-J. Projection of future precipitation change over China with a high-resolution global atmospheric model. Adv. Atmos. Sci. 2011, 28, 464–476. [Google Scholar] [CrossRef]
- Xie, Z.-H.; Zeng, Y.-J.; Xia, J.; Qin, P.-H.; Jia, B.-H.; Zou, J.; Liu, S. Coupled modeling of land hydrology–regional climate including human carbon emission and water exploitation. Adv. Clim. Chang. Res. 2017, 8, 68–79. [Google Scholar] [CrossRef]
- Ho, C.H.; Kim, J.H.; Lau, K.M.; Kim, K.M.; Gong, D.Y.; Lee, Y.B. Interdecadal Changes in Heavy Rainfall in China during the Northern Summer. Terr. Atmos. Ocean. Sci. 2005, 16, 1163–1176. [Google Scholar] [CrossRef]
- Lieting, C.; Renguang, W. Interannual and decadal variations of snow cover over Qinghai-Xizang Plateau and their relationships to summer monsoon rainfall in China. Adv. Atmos. Sci. 2000, 17, 18–30. [Google Scholar] [CrossRef]
- Zhou, T.; Gong, D.; Li, J.; Li, B. Detecting and understanding the multi-decadal variability of the East Asian Summer Monsoon Recent progress and state of affairs. Meteorol. Z. 2009, 18, 455–467. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, X.; Liu, Z.; Wang, D. Trend Analysis of Precipitation in the Jinsha River Basin in China. J. Hydrometeorol. 2013, 14, 290–303. [Google Scholar] [CrossRef]
- Zhen, L.; Yan, Z.-W. Homogenized Daily Mean/Maximum/Minimum Temperature Series for China from 1960–2008. Atmos. Ocean. Sci. Lett. 2009, 2, 237–243. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, Z.; Fu, G.; Chen, Y. Trends of major hydroclimatic variables in the Tarim River basin during the past 50 years. J. Arid Environ. 2010, 74, 256–267. [Google Scholar] [CrossRef]
- Xue, L.; Yang, F.; Yang, C.; Chen, X.; Zhang, L.; Chi, Y.; Yang, G. Identification of potential impacts of climate change and anthropogenic activities on streamflow alterations in the Tarim River Basin, China. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luo, K.; Tao, F.; Moiwo, J.P.; Xiao, D. Attribution of hydrological change in Heihe River Basin to climate and land use change in the past three decades. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Xu, C. Climate Change and Hydrologic Models: A Review of Existing Gaps and Recent Research Developments. Water Resour. Manag. 1999, 13, 369–382. [Google Scholar] [CrossRef]
- Kiely, G. Climate change in Ireland from precipitation and streamflow observations. Adv. Water Resour. 1999, 23, 141–151. [Google Scholar] [CrossRef]
- Shen, Y.; Oki, T.; Utsumi, N.; Kanae, S.; Hanasaki, N. Projection of future world water resources under SRES scenarios: Water withdrawal/Projection des ressources en eau mondiales futures selon les scénarios du RSSE: Prélèvement d’eau. Hydrol. Sci. J. 2008, 53, 11–33. [Google Scholar] [CrossRef]
- Arnell, N.W. Climate change and global water resources: SRES emissions and socio-economic scenarios. Glob. Environ. Chang. 2004, 14, 31–52. [Google Scholar] [CrossRef]
- Su, B.; Huang, J.; Gemmer, M.; Jian, D.; Tao, H.; Jiang, T.; Zhao, C. Statistical downscaling of CMIP5 multi-model ensemble for projected changes of climate in the Indus River Basin. Atmos. Res. 2016, 178–179, 138–149. [Google Scholar] [CrossRef]
- Leng, G.; Huang, M.; Tang, Q.; Leung, L.R. A modeling study of irrigation effects on global surface water and groundwater resources under a changing climate. J. Adv. Model. Earth Syst. 2015, 7, 1285–1304. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Y.; Xie, Z.; Zou, J. Hydrologic and Climatic Responses to Global Anthropogenic Groundwater Extraction. J. Clim. 2017, 30, 71–90. [Google Scholar] [CrossRef]
- Christensen, J.; Hesselbjerg, B.; Hewitson, A.; Busuioc, A.; Chen, X.; Gao, R.; Held, R.J. Regional Climate Projections. In Climate Change, 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2007; Chapter 11; pp. 847–940. [Google Scholar]
- Haerter, J.O.; Hagemann, S.; Moseley, C.; Piani, C. Climate model bias correction and the role of timescales. Hydrol. Earth Syst. Sci. 2011, 15, 1065–1079. [Google Scholar] [CrossRef] [Green Version]
- Hayhoe, K.; Wake, C.; Anderson, B.; Liang, X.-Z.; Maurer, E.; Zhu, J.; Bradbury, J.; DeGaetano, A.; Stoner, A.M.; Wuebbles, D. Regional climate change projections for the Northeast USA. Mitig. Adapt. Strateg. Glob. Chang. 2008, 13, 425–436. [Google Scholar] [CrossRef]
- Maurer, E.P.; Duffy, P.B. Uncertainty in projections of streamflow changes due to climate change in California. Geophys. Res. Lett. 2005, 32, L03704. [Google Scholar] [CrossRef]
- Wood, A.W.; Leung, L.R.; Sridhar, V.; Lettenmaier, D.P. Hydrologic Implications of Dynamical and Statistical Approaches to Downscaling Climate Model Outputs. Clim. Chang. 2004, 62, 189–216. [Google Scholar] [CrossRef]
- Maurer, E.P.; Ficklin, D.L.; Wang, W. Technical Note: The impact of spatial scale in bias correction of climate model output for hydrologic impact studies. Hydrol. Earth Syst. Sci. 2016, 20, 685–696. [Google Scholar] [CrossRef] [Green Version]
- Basheer, A.K.; Lu, H.; Omer, A.; Ali, A.B.; Abdelgader, A.M.S. Impacts of climate change under CMIP5 RCP scenarios on the streamflow in the Dinder River and ecosystem habitats in Dinder National Park, Sudan. Hydrol. Earth Syst. Sci. 2016, 20, 1331–1353. [Google Scholar] [CrossRef] [Green Version]
- Gudmundsson, L.; Bremnes, J.B.; Haugen, J.E.; Engen-Skaugen, T. Technical Note: Downscaling RCM precipitation to the station scale using statistical transformations—A comparison of methods. Hydrol. Earth Syst. Sci. 2012, 16, 3383–3390. [Google Scholar] [CrossRef]
- Lafon, T.; Dadson, S.; Buys, G.; Prudhomme, C. Bias correction of daily precipitation simulated by a regional climate model: A comparison of methods. Int. J. Climatol. 2013, 33, 1367–1381. [Google Scholar] [CrossRef] [Green Version]
- Maurer, E.P.; Das, T.; Cayan, D.R. Errors in climate model daily precipitation and temperature output: Time invariance and implications for bias correction. Hydrol. Earth Syst. Sci. 2013, 17, 2147–2159. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Is bias correction of regional climate model (RCM) simulations possible for non-stationary conditions? Hydrol. Earth Syst. Sci. 2013, 17, 5061–5077. [Google Scholar] [CrossRef] [Green Version]
- Behera, S.; Panda, R.K. Evaluation of management alternatives for an agricultural watershed in a sub-humid subtropical region using a physical process based model. Agric. Ecosyst. Environ. 2006, 113, 62–72. [Google Scholar] [CrossRef]
- Douglas-Mankin, K.R.; Srinivasan, R.; Arnold, J.G. Soil and Water Assessment Tool (SWAT) Model: Current Developments and Applications. Transactions of the ASABE. Am. Soc. Agric. Biol. Eng. 2010, 53, 1423–1431. [Google Scholar] [CrossRef]
- van Griensven, A.; Breuer, L.; Di Luzio, M.; Vandenberghe, V.; Goethals, P.; Meixner, T.; Arnold, J.; Srinivasan, R. Environmental and ecological hydroinformatics to support the implementation of the European Water Framework Directive for river basin management. J. Hydroinform. 2006, 8, 239. [Google Scholar] [CrossRef]
- Sun, H.; Cornish, P.S. Estimating shallow groundwater recharge in the headwaters of the Liverpool Plains using SWAT. Hydrol. Process. 2005, 19, 795–807. [Google Scholar] [CrossRef]
- Mapfumo, E.; Chanasyk, D.S.; Willms, W.D. Simulating daily soil water under foothills fescue grazing with the soil and water assessment tool model (Alberta, Canada). Hydrol. Process. 2004, 18, 2787–2800. [Google Scholar] [CrossRef]
- Ouyang, W.; Wang, X.; Fang, H.; Srinivasand, R. Temporal-spatial dynamics of vegetation variation on non-point source nutrient pollution. Ecol. Model. 2009, 220, 2702–2713. [Google Scholar] [CrossRef]
- Gosain, A.K.; Rao, S.; Srinivasan, R.; Reddy, N.G. Return-flow assessment for irrigation command in the Palleru river basin using SWAT model. Hydrol. Process. 2005, 19, 673–682. [Google Scholar] [CrossRef]
- Zaman, M.; Yuan, S.; Liu, J.; Ahmad, I.; Sultan, M.; Qamar, M.U.; Saifullah, M.; Adnan, M.; Anjum, M.N.; Nawaz, M.I.; et al. Investigating Hydrological Responses and Adaptive Operation of a Hydropower Station under a Climate Change Scenario. Pol. J. Environ. Stud. 2018, 27, 2337–2348. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.; Yuan, L. A drought early warning system on real-time multireservoir operations. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef] [Green Version]
- Mousavi, S.; Karamouz, M. Fuzzy-state stochastic dynamic programming for reservoir operation. J. Water Resour. 2004, 130. [Google Scholar] [CrossRef]
- Wurbs, R.A. Reservoir-System Simulation and Optimization Models. J. Water Resour. Plan. Manag. 1993, 119, 455–472. [Google Scholar] [CrossRef]
- Ganji, A.; Karamouz, M.; Khalili, D. Development of stochastic dynamic Nash game model for reservoir operation II. The value of players’ information availability and cooperative behaviors. Adv. Water Resour. 2007, 30, 157–168. [Google Scholar] [CrossRef]
- Labadie, J. Optimal operation of multireservoir systems: State-of-the-art review. J. Water Resour. Plan. Manag. 2004, 130, 93–111. [Google Scholar] [CrossRef]
- Kucukmehmetoglu, M. A game theoretic approach to assess the impacts of major investments on transboundary water resources: The case of the Euphrates and Tigris. Water Resour. Manag. 2009, 23, 3069. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the Proceedings of ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Lima, C.A.S., Jr.; Lapa, C.M.F.; do NA Pereira, C.M.; da Cunha, J.J.; Alvim, A.C.M. Comparison of computational performance of GA and PSO optimization techniques when designing similar systems–Typical PWR core case. Ann. Nucl. Energy 2011, 38, 1339–1346. [Google Scholar] [CrossRef]
- Rahi, O.; Chandel, A.; Sharma, M. Optimization of hydro power plant design by particle swarm optimization (PSO). Procedia Eng. 2012, 30, 418–425. [Google Scholar] [CrossRef]
- Zaman, M.; Yuan, S.; Liu, J.; Ahmad, I.; Ali Buttar, N.; Saifullah, M.; Nawaz, M.I. Optimization of Mangla Hydropower Station, Pakistan, using Optimization Techniques. MATEC Web Conf. 2017, 136, 02010. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, S.; Bai, X.; Shu, D.; Tian, Y. Runoff response to climate change and human activities in a typical karst watershed, SW China. PLoS ONE 2018, 13, e0193073. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.; Zhao, N.; Sun, H.; Ye, L.; Zhai, J. Changes and relationships of climatic and hydrological droughts in the Jialing River basin, China. PLoS ONE 2015, 10, e0141648. [Google Scholar] [CrossRef] [PubMed]
- Gu, H.; Yu, Z.; Wang, G.; Wang, J.; Ju, Q.; Yang, C. Impact of climate change on hydrological extremes in the Yangtze River Basin, China. Stoch. Environ. Res. Risk Assess. 2015, 29, 693–707. [Google Scholar] [CrossRef]
- Hu, X.; Lu, L.; Li, X.; Wang, J.; Guo, M. Land use/cover change in the middle reaches of the heihe river basin over 2000-2011 and its implications for sustainable water resource management. PLoS ONE 2015, 10, e0128960. [Google Scholar] [CrossRef] [PubMed]
- Yang, P.; Xia, J.; Zhang, Y.; Hong, S. Temporal and spatial variations of precipitation in Northwest China during 1960–2013. Atmos. Res. 2017, 183, 283–295. [Google Scholar] [CrossRef]
- Zhang, Y.; You, Q.; Chen, C.; Ge, J. Impacts of climate change on streamflows under RCP scenarios: A case study in Xin River Basin, China. Atmos. Res. 2016, 178–179, 521–534. [Google Scholar] [CrossRef]
- Zaman, M.; Fang, G.; Saifullah, M.; Javed, Q. Seasonal and Annual Precipitation Trend Prediction in Xin’Anjiang China. Fresenius Environ. Bull. 2016, 25, 89–102. [Google Scholar]
- Ouyang, F.; Zhu, Y.; Fu, G.; Lü, H.; Zhang, A.; Yu, Z.; Chen, L. Impacts of climate change under CMIP5 RCP scenarios on streamflow in the Huangnizhuang catchment. Stoch. Environ. Res. Risk Assess. 2015, 29, 1781–1795. [Google Scholar] [CrossRef]
- Zhu, Y.; Lin, Z.; Wang, J.; Zhao, Y.; He, F. Impacts of Climate Changes on Water Resources in Yellow River Basin, China. Procedia Eng. 2016, 154, 687–695. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Cibin, R.; Chaubey, I.; Engel, B. Simulated watershed scale impacts of corn stover removal for biofuel on hydrology and water quality. Hydrol. Process. 2012, 26, 1629–1641. [Google Scholar] [CrossRef]
- Te Chow, V.; Maidment, D.R.; Mays, L.W. Applied Hydrology; Tata McGraw-Hill Education: New Delhi, India, 2010. [Google Scholar]
- Sloan, P.G.; Moore, I.D. Modeling subsurface stormflow on steeply sloping forested watersheds. Water Resour. Res. 1984, 20, 1815–1822. [Google Scholar] [CrossRef] [Green Version]
- Arnold, J.G.; Allen, P.M. Automated methods for estimating baseflow and ground water recharge from streamflow records. J. Am. Water Resour. Assoc. 1999, 35, 411–424. [Google Scholar] [CrossRef]
- George, H.; Hargreaves, G.H.; Zohrab, A.; Samani, Z.A. Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Jimmy, R.; Williams, J.R. Flood Routing with Variable Travel Time or Variable Storage Coefficients. Trans. ASAE 1969, 12, 100–103. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Van Griensven, A.; Meixner, T.; Grunwald, S.; Bishop, T.; Diluzio, M.; Srinivasan, R. A global sensitivity analysis tool for the parameters of multi-variable catchment models. J. Hydrol. 2006, 324, 10–23. [Google Scholar] [CrossRef]
- Abbaspoura, K.C.; Yanga, J.; Maximova, I.; Sibera, R.; Bognerb, K.; Mieleitnera, J.; Zobrista, J.; Srinivasanc, R. Modelling hydrology and water quality in the pre-alpine/alpine Thur watershed using SWAT. J. Hydrol. 2007, 333, 413–430. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; KAbbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Daren Harmel, R.; van Griensven, A.; Liew, M.; et al. SWAT: Model Use, Calibration, and Validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Ma, L.; Ascough, J.C., II; Ahuja, L.R.; Shaffer, M.J.; Hanson, J.D.; Rojas, K.W. Root zone water quality model sensitivity analysis using monte carlo simulation. Trans. ASAE 2000, 43, 883–895. [Google Scholar] [CrossRef]
- Willems, P.; Olsson, J.; Arnbjerg-Nielsen, K.; Beecham, S.; Pathirana, A.; Gregersen, I.B.; Madsen, H. Impacts of Climate Change on Rainfall Extremes and Urban Drainage Systems; IWA Publishing: London, UK, 2012; Volume 11. [Google Scholar] [CrossRef]
- Library, W.O.; Tryhorn, L.; Degaetano, A. A comparison of techniques for downscaling extreme precipitation over the Northeastern United States. Int. J. Climatol. 2011, 31, 1975–1989. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Vonk, E. Dam Reoperation as an Adaptation Strategy for Shifting Patterns of Water Supply and Demand—A Case Study for the Xinánjiang—Fuchunjiang Reservoir Cascade, China. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2013. [Google Scholar]
- Knutti, R.; Sedláček, J. Robustness and uncertainties in the new CMIP5 climate model projections. Nat. Clim. Chang. Nat. Res. 2012, 3, 369–373. [Google Scholar] [CrossRef]
- Qian, W.; Lin, X.; Zhu, Y.; Xu, Y.; Fu, J. Climatic regime shift and decadal anomalous events in China. Clim. Chang. 2007, 84, 167–189. [Google Scholar] [CrossRef]
- Li, C.; He, J.; Zhu, J. A review of decadal/interdecadal climate variation studies in China. Adv. Atmos. Sci. 2004, 21, 425–436. [Google Scholar] [CrossRef]
- Qian, W.H.; Qin, A. Precipitation division and climate shift in China from 1960 to 2000. Theor. Appl. Climatol. 2008, 93, 1–17. [Google Scholar] [CrossRef]
- Fu, G.; Chen, S.; Liu, C.; Shepard, D. Hydro-climatic trends of the yellow river basin for the last 50 years. 2004, 65, 149–178. [Google Scholar] [CrossRef]
- Zaman, M.; Fang, G.; Mehmood, K.; Saifullah, M. Trend Change Study of Climate Variables in Xin’anjiang-Fuchunjiang Watershed, China. Adv. Meteorol. 2015, 2015, 507936. [Google Scholar] [CrossRef]
- Song, Y.; Achberger, C.; Linderholm, H.W. Rain-season trends in precipitation and their effect in different climate regions of China during 1961–2008. Environ. Res. Lett. 2011, 6. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, Y.; Booij, M.; Lin, S.; Zhang, Q. Detection of trends in precipitation extremes in Zhejiang, East China. Theor. Appl. 2012, 107, 201–210. [Google Scholar] [CrossRef]















| Model/RCP * | Institutes and Grid Resolution | RCP4.5 | RCP8.5 |
|---|---|---|---|
| CCSM4 | (National center for Atmospheric Research USA with 0.9424° × 1.25° grid resolution) | Designated as C 4.5 | Designated as C 8.5 |
| HadGEM2-ES | (Met office Hadley Centre UK with 1.875° × 1.25° grid resolution) | Designated as H 4.5 | Designated as H 8.5 |
| MPI-ESM-LR | (Max Plank Institute for Metrology, Hamburg, Germany with 1.8653° × 1.875° grid resolution) | Designated as LR 4.5 | Designated as LR 8.5 |
| MPI-ESM-MR | Max Plank Institute for Metrology, Hamburg, Germany with 1.865 × 1.875° grid resolution | Designated as MR 4.5 | Designated as MR 8.5 |
| ACCESS 1.0 | (Commonwealth Scientific and Industrial Research Organization (CSIRO) and Bureau of Metrology, Australia with 1.875° × 1.25° grid resolution) | Designated as A 4.5 | Designated as A 8.5 |
| MIROC-ESM | (University of Tokyo, NIES and JAMSTEC with 2.7906° × 2.8125° grid resolution) | Designated as MI 4.5 | Designated as MI 8.5 |
| Rank | Name | Description | LH-OAT Value |
|---|---|---|---|
| 1 | CN2 | Initial SCS runoff curve number | 3.13 |
| 2 | Alpha_BF | Baseflow recession constant | 2.44 |
| 3 | CH_N2 | Manning’s coefficient | 2.13 |
| 4 | ESCO | Soil evaporation compensation factor | 1.78 |
| 5 | SURLAG | Surface runoff lag time (days) | 0.41 |
| 6 | CH_K2 | Effective hydraulic conductivity (mm/h) | 0.39 |
| 7 | CANMX | Maximum canopy storage (mm) | 0.30 |
| 8 | SOL_AWC | Soil available water capacity (mm) | 0.26 |
| 9 | SOL_Z | Depth of soil layer | 0.22 |
| 10 | GW_DELAY | Groundwater delay time (days) | 0.19 |
| NSE | R2 | Relative Error (%) | |
|---|---|---|---|
| Calibration | 0.86 | 0.84 | −8.5 |
| Validation | 0.81 | 0.80 | 12.5 |
| Temperatures | Models | RCP4.5 | RCP8.5 | ||||
|---|---|---|---|---|---|---|---|
| 2020 | 2050 | 2080 | 2020 | 2050 | 2080 | ||
| TMax | CCSM4 | 1.1 | 2.1 | 3.3 | 1.1 | 2.2 | 3.6 |
| HadGEM2 | 1.3 | 2.3 | 3.3 | 1.8 | 3 | 4.4 | |
| MPI-ESM-LR | 1.1 | 1.94 | 2.4 | 0.6 | 2.8 | 3.8 | |
| MPI-ESM-MR | 0.8 | 1.5 | 1.9 | 1.0 | 2.1 | 3.8 | |
| ACCESS1.0 | 1.9 | 3.2 | 4.1 | 1.0 | 3.3 | 4.7 | |
| MIROC-ESM | 2.2 | 4.1 | 4.2 | 1.9 | 4.1 | 4.9 | |
| TMin | CCSM4 | 1.1 | 2.2 | 3 | 1.2 | 2.2 | 3.2 |
| HadGEM2 | 1.2 | 2.2 | 3.2 | 1.3 | 2.3 | 3.3 | |
| MPI-ESM-LR | 1.9 | 2.6 | 2.9 | 1.1 | 3.1 | 4.1 | |
| MPI-ESM-MR | 2.0 | 2.6 | 2.9 | 1.2 | 2.2 | 3.9 | |
| ACCESS1.0 | 2.2 | 3.2 | 4.0 | 0.9 | 3.0 | 4.6 | |
| MIROC-ESM | 2.1 | 3.5 | 4.1 | 1.4 | 3.3 | 4.8 | |
| Scenarios | % Change in Stream Flows | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C 4.5 | C8.5 | H4.5 | H8.5 | LR 4.5 | LR 8.5 | MR 4.5 | MR 8.5 | A 4.5 | A 8.5 | MI 4.5 | MI 8.5 | |
| 2020s | 72.6 | 67.1 | 112.9 | 131.6 | 170.0 | 180.6 | 142.9 | 130.0 | 127.0 | 135.8 | 119.9 | 128.6 |
| 2050s | 31.4 | 58.1 | 58.4 | 54.0 | 129.1 | 111.8 | 82.0 | 106.7 | 89.2 | 66.0 | 98.0 | 102.3 |
| 2080s | 63.0 | 75.5 | 95.81 | 117.0 | 158.9 | 155.8 | 100.4 | 129.3 | 118.7 | 103.0 | 114.1 | 117.2 |
| Scenarios | Energy Output (108 kW·h) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2020s | 2050s | 2080s | ||||||||
| Rainy Year | Average Year | Dry Year | Rainy Year | Average Year | Dry Year | Rainy Year | Average Year | Dry Year | ||
| RCP4.5 | C 4.5 | 19.23 | 15.04 | 11.137 | 18.7 | 15.1 | 10.14 | 14.23 | 11.71 | 8.36 |
| H 4.5 | 19.12 | 16.05 | 14.51 | 18.17 | 13.17 | 11.83 | 23.17 | 20.36 | 16.26 | |
| LR 4.5 | 30.03 | 23.38 | 21.83 | 27.84 | 22.53 | 18.79 | 28.81 | 24.59 | 22.23 | |
| MR 4.5 | 26.36 | 20.09 | 18.09 | 19.24 | 15.97 | 13.77 | 22.05 | 18.07 | 14.41 | |
| A 4.5 | 24.19 | 19.51 | 15.74 | 19.52 | 15.61 | 12.32 | 27.61 | 24.16 | 20.13 | |
| MI 4.5 | 30.0 | 23.68 | 20.02 | 17.48 | 14.05 | 11.17 | 29.46 | 22.83 | 19.92 | |
| RCP8.5 | C 8.5 | 18.26 | 14.62 | 12.49 | 17.55 | 13.56 | 12.34 | 18.89 | 15.23 | 12.59 |
| H 8.5 | 22.84 | 18.72 | 15.42 | 17.23 | 13.31 | 11.19 | 23.19 | 20.45 | 16.78 | |
| LR 8.5 | 31.41 | 25.86 | 21.54 | 19.07 | 15.25 | 11.38 | 24.39 | 20.61 | 16.94 | |
| MR 8.5 | 25.65 | 23.02 | 18.78 | 21.32 | 16.89 | 14.44 | 27.45 | 21.5 | 18.37 | |
| A 8.5 | 26.03 | 20.29 | 16.76 | 19.51 | 15.02 | 12.61 | 18.33 | 14.68 | 12.33 | |
| MI 8.5 | 27.15 | 20.8 | 17.34 | 25.12 | 22.23 | 19.77 | 29.28 | 23.75 | 20.8 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaman, M.; Naveed Anjum, M.; Usman, M.; Ahmad, I.; Saifullah, M.; Yuan, S.; Liu, S. Enumerating the Effects of Climate Change on Water Resources Using GCM Scenarios at the Xin’anjiang Watershed, China. Water 2018, 10, 1296. https://doi.org/10.3390/w10101296
Zaman M, Naveed Anjum M, Usman M, Ahmad I, Saifullah M, Yuan S, Liu S. Enumerating the Effects of Climate Change on Water Resources Using GCM Scenarios at the Xin’anjiang Watershed, China. Water. 2018; 10(10):1296. https://doi.org/10.3390/w10101296
Chicago/Turabian StyleZaman, Muhammad, Muhammad Naveed Anjum, Muhammad Usman, Ijaz Ahmad, Muhammad Saifullah, Shouqi Yuan, and Shiyin Liu. 2018. "Enumerating the Effects of Climate Change on Water Resources Using GCM Scenarios at the Xin’anjiang Watershed, China" Water 10, no. 10: 1296. https://doi.org/10.3390/w10101296
APA StyleZaman, M., Naveed Anjum, M., Usman, M., Ahmad, I., Saifullah, M., Yuan, S., & Liu, S. (2018). Enumerating the Effects of Climate Change on Water Resources Using GCM Scenarios at the Xin’anjiang Watershed, China. Water, 10(10), 1296. https://doi.org/10.3390/w10101296