Equivalent Small Hydro Power: A Simple Method to Evaluate Energy Production by Small Turbines in Collective Irrigation Systems
Abstract
:1. Introduction
2. Material and Methods
2.1. Outlines on the Original Method (OM)
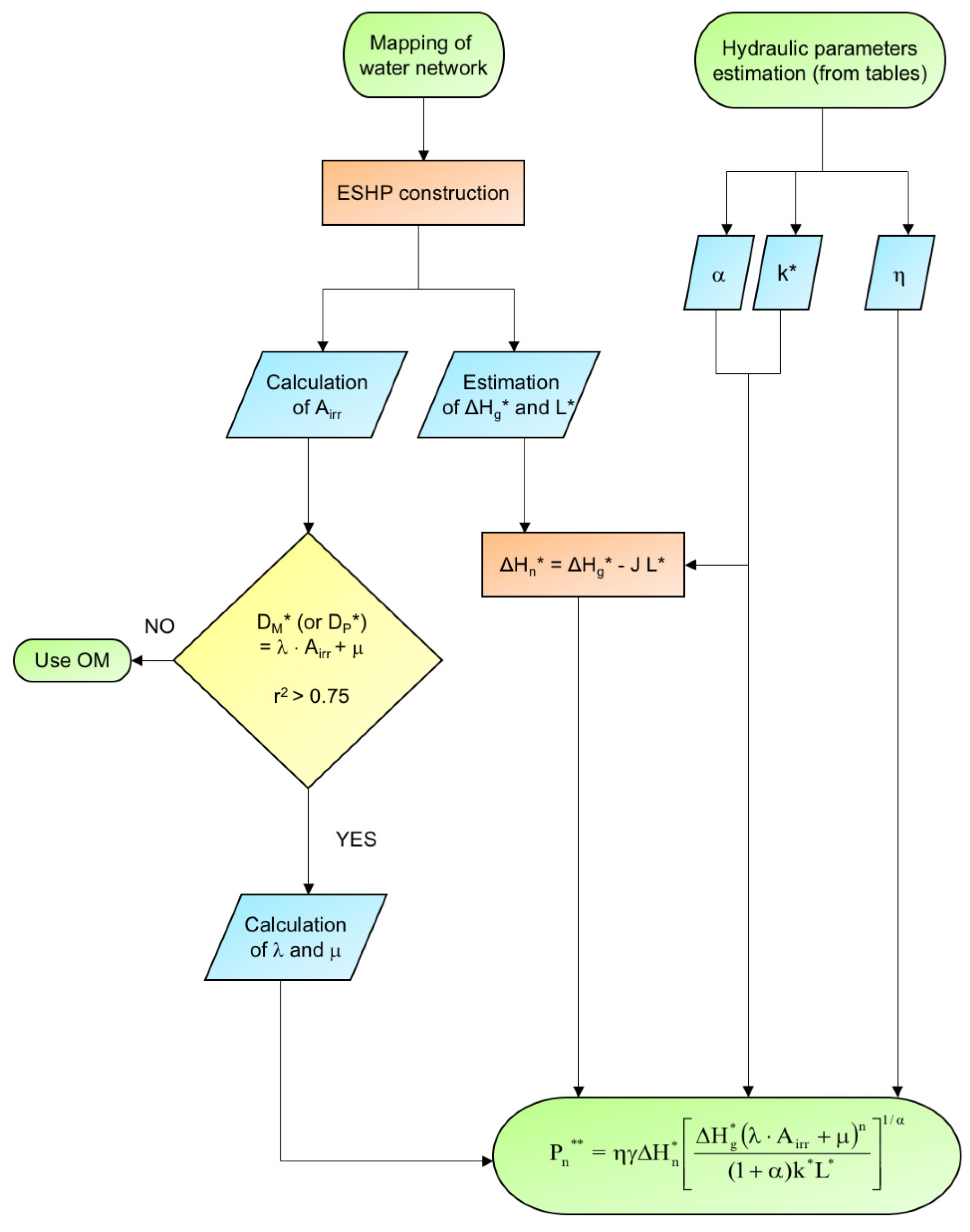
2.2. Description of the Simplified Method (SM)
- − A single pressured pipeline with constant diameter (D*) and roughness coefficient (k*);
- − A single turbine (SHP).
- a)
- k* (henceforth kP) equal to k of the material with prevalent length of the actual water network;
- b)
- k* (henceforth kM) equal to the arithmetic mean of the roughness coefficients (k) of all materials of the actual water network.
- − L*, equal to the total length of the main pipelines of the water network (that is, the feeders);
- − ΔHg* (gross hydraulic head), estimated as the difference between the altitudes of the water supply point (reservoir or river section) and the most depressed point of the irrigated areas.
2.3. SM Verification in Seven Case Studies of Calabria (Southern Italy)
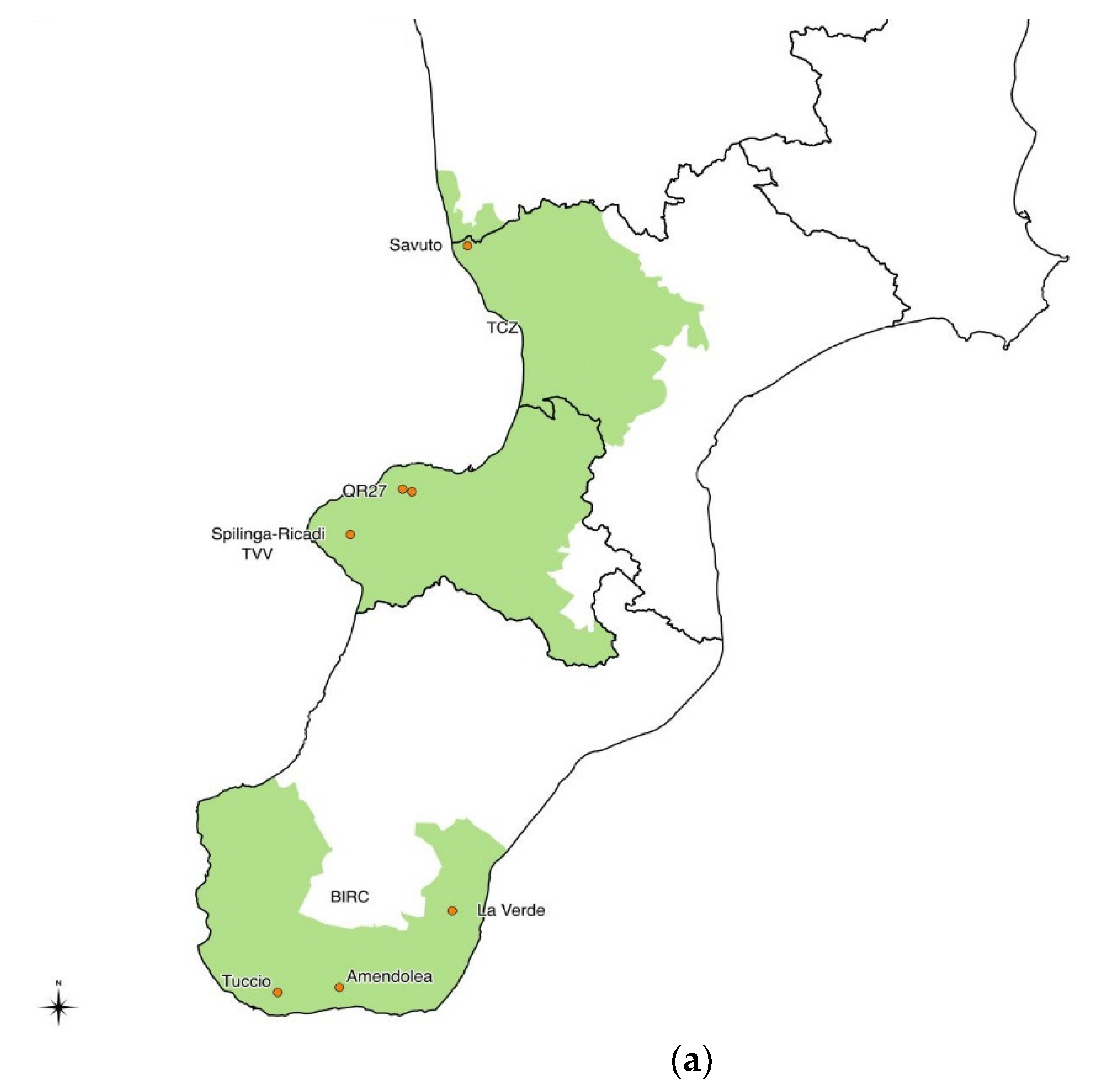
2.3.1. Study Area
2.3.2. Analysis of the Collective Irrigation Systems and SHP Plants
3. Results and Discussions
3.1. Analysis of the Seven Irrigation Systems and Calculation of the SHP Potential by the OM
3.2. Schematization and Calculation of the ESHP by the SM
3.3. Replacement of D of the SHP Plants with DP*/DM* in the ESHP Plants
3.4. Analysis of Differences in Hydraulic Parameters of the Water Networks Between OM and SM
3.5. Analysis of the Correlations between DP*/DM* and Airr in the ESHP Plants
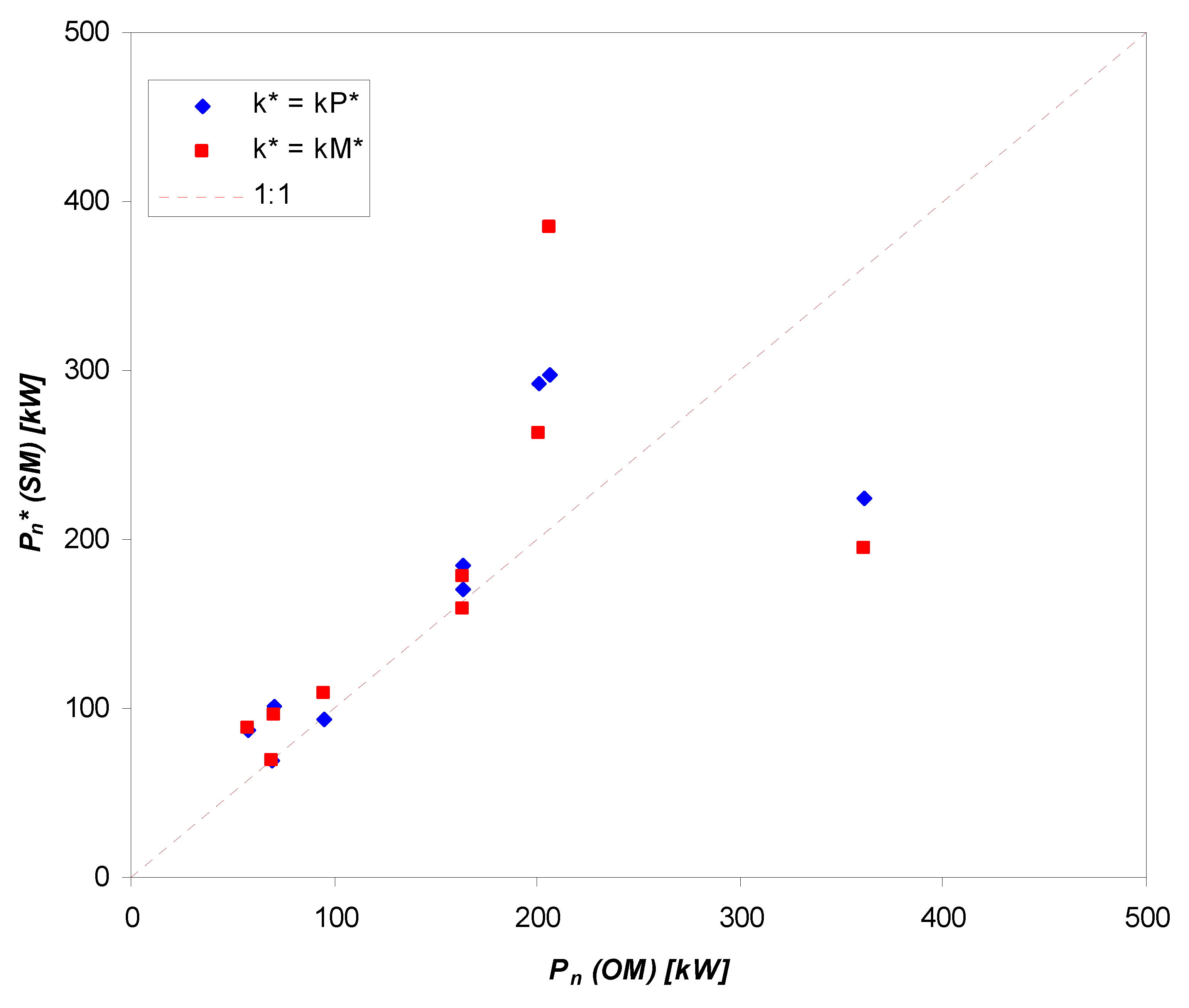
3.6. Analysis of the Reliability of Turbine Power Estimates by SM
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
List of Abbreviations
| D = Pipeline internal diameter (m) |
| D** = Pipeline internal diameter of the ESHP network (m) |
| DM* = Pipeline internal diameter of the ESHP network estimated for k* = kM (m) |
| DP* = Pipeline internal diameter of the ESHP network estimated for k* = kP (m) |
| g = Gravity acceleration (9.806 m s−2) |
| J = Hydraulic gradient (m km−1) |
| L = Pipeline length (km) |
| L* = Pipeline length of the ESHP network (km) |
| Pn = Net electrical power of the turbine (kW) |
| Pn* = Net electrical power of the turbines of the ESHP network (kW) |
| Pn** = Net electrical power of the turbines of the ESHP network (kW), estimated by the SM |
| Q = Water discharge (L s−1) |
| Q* = Optimal water discharge (maximizing the SHP power) (L s−1) |
| Q** = Optimal discharge of the ESHP network (L s−1) |
| Airr = Irrigated area (ha) |
| α, n, k, C = Coefficients of Hazen-Williams’ equation (dimensionless) |
| k* = k coefficient of Hazen-Williams’ equation of the ESHP network (dimensionless) |
| kP = k coefficient of Hazen-Williams’ equation of the ESHP network (adopting k of the prevalent material) (dimensionless) |
| kM = k coefficient of Hazen-Williams’ equation of the ESHP network (adopting k averaged among the different materials) (dimensionless) |
| SHP = Small Hydro Power |
| ESHP = Equivalent Small Hydro Power |
| WUA = Water User Association |
| γ = Water specific weight (9806 N m−3) |
| ΔHg = Gross hydraulic head (m) |
| ΔHn = Net hydraulic head (m) |
| ΔHg* = Gross hydraulic head of the ESHP network (m) |
| ΔHn* = Net hydraulic head of the ESHP network (m) |
| η = Turbine efficiency (dimensionless) |
References
- Yuksek, O.; Komurcu, M.I.; Yuksel, I.; Kaygusuz, K. The role of hydropower in meeting Turkey’s electric energy demand. Energy Policy 2006, 34, 3093–3103. [Google Scholar] [CrossRef]
- Yuksel, I. Hydropower in Turkey for a clean and sustainable energy future. Renew. Sustain. Energy Rev. 2008, 12, 1622–1640. [Google Scholar] [CrossRef]
- Okot, D.K. Review of small hydropower technology. Renew. Sustain. Energy Rev. 2013, 26, 515–520. [Google Scholar] [CrossRef]
- Nilsson, C.; Reidy, C.A.; Dynesius, M.; Revenga, C. Fragmentation and flow regulation of the world’s large river systems. Science 2005, 308, 405–408. [Google Scholar] [CrossRef] [PubMed]
- Jaramillo, F.; Destouni, G. Local flow regulation and irrigation raise global human water consumption and footprint. Science 2015, 350, 1248–1251. [Google Scholar] [CrossRef] [PubMed]
- Dragu, C.; Sels, T.; Belmans, R. Small hydro power—State of the art and applications. In Proceedings of the International Conference on Power Generation and Sustainable Development, Liège, Belgium, 8–9 October 2011; pp. 265–270. [Google Scholar]
- Paish, O. Small hydro power: Technology and current status. Renew. Sustain. Energy Rev. 2002, 6, 537–556. [Google Scholar] [CrossRef]
- Hosseini, S.M.H.; Forouzbakhsh, F.; Rahimpoor, M. Determination of the optimal installation capacity of small hydro-power plants through the use of technical, economic and reliability indices. Energy Policy 2005, 33, 1948–1956. [Google Scholar] [CrossRef]
- Cavazzini, G.; Santolin, A.; Pavesi, G.; Ardizzon, G. Accurate estimation model for small and micro hydropower plants costs in hybrid energy systems modelling. Energy 2016, 103, 746–757. [Google Scholar] [CrossRef]
- Zema, D.A.; Nicotra, A.; Tamburino, V.; Zimbone, S.M. Energy production by small hydro power plants in collective irrigation systems of Calabria (Southern Italy). Chem. Eng. Trans. 2017, 58, 523–528. [Google Scholar]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; López-Jiménez, P.A.; Ramos, H.M. PATs selection towards sustainability in irrigation networks: Simulated annealing as a water management tool. Renew. energy 2018, 116, 234–249. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Modeling irrigation networks for the quantification of potential energy recovering: A case study. Water 2016, 8. [Google Scholar] [CrossRef]
- Aggidis, G.A.; Luchinskaya, E.; Rothschild, R.; Howard, D.C. The costs of small-scale hydro power production: Impact on the development of existing potential. Renew. Energy 2010, 35, 2632–2638. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Energy recovery in existing water networks: Towards greater sustainability. Water 2017, 9. [Google Scholar] [CrossRef]
- Voros, N.G.; Kiranoudis, C.T.; Maroulis, Z.B. Short-cut design of small hydro-electric plants. Renew. Energy 2000, 19, 545–563. [Google Scholar] [CrossRef]
- Karlis, A.D.; Papadopoulos, D.P. A systematic assessment of the technical feasibility and economic viability of small hydroelectric system installations. Renew. Energy 2000, 20, 253–262. [Google Scholar] [CrossRef]
- Montanari, R. Criteria for the economic planning of a low power hydroelectric plant. Renew. Energy 2003, 28, 2129–2145. [Google Scholar] [CrossRef]
- Forouzbakhsh, F.; Hosseini, S.M.H.; Vakilian, M. An approach to the investment analysis of small and medium hydro-power plants. Energy Policy 2007, 35, 1013–1024. [Google Scholar] [CrossRef] [Green Version]
- Samora, I.; Manso, P.; Franca, M.J.; Schleiss, A.J.; Ramos, H.M. Opportunity and economic feasibility of inline microhydropower units in water supply networks. J. Water Resour. Plan. Manag. 2016, 142. [Google Scholar] [CrossRef]
- Lima, G.M.; Brentan, B.M.; Luvizotto, E., Jr. Optimal design of water supply networks using an energy recovery approach. Renew. Energy 2018, 117, 404–413. [Google Scholar] [CrossRef]
- Morillo, J.G.; McNabola, A.; Camacho, E.; Montesinos, P.; Díaz, J.A.R. Hydro-power energy recovery in pressurized irrigation networks: A case study of an Irrigation District in the South of Spain. Agric. Water Manag. 2018, 204, 17–27. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Optimization strategy for improving the energy efficiency of irrigation systems by micro hydropower: Practical application. Water 2017, 9. [Google Scholar] [CrossRef]
- Zema, D.A.; Nicotra, A.; Tamburino, V.; Zimbone, S.M. A simple method to evaluate the technical and economic feasibility of micro hydro power plants in existing irrigation systems. Renew. Energy 2016, 85, 498–506. [Google Scholar] [CrossRef]
- Zema, D.A.; Nicotra, A.; Tamburino, V.; Zimbone, S.M. Performance Assessment of collective irrigation in Water User Associations of Calabria (Southern Italy). Irrig. Drain. 2015, 64, 314–325. [Google Scholar] [CrossRef]
- Zema, D.A.; Nicotra, A.; Mateos, L.; Zimbone, S.M. Improvement of the irrigation performance in Water User Associations integrating data envelopment analysis and multi-regression models. Agric. Water Manag. 2018, 205, 38–49. [Google Scholar] [CrossRef]
- Zema, D.A.; Nicotra, A.; Zimbone, S.M. Diagnosis and improvement of the collective irrigation and drainage services in Water Users’ Associations of Calabria (Southern Italy). Irrig. Drain. 2018, in press. [Google Scholar] [CrossRef]
- Nicotra, A.; Zema, D.A.; Zimbone, S.M. Improvement of Current Performance in Collective Water Delivery Systems of Calabria (Southern Italy). Chem. Eng. Trans. 2017, 58, 733–738. [Google Scholar]



| Coefficient | Pipeline material | |||
|---|---|---|---|---|
| Concrete or Asbestos-Concrete | Steel | Cast Iron | Plastic (HDPE, PVC) | |
| C | 100 | 120 | 130 | 150 |
| kP 1 | 0.00211 | 0.00151 | 0.0013 | 0.00099 |
| kM 2 | 0.00148 | 0.00148 | 0.00148 | 0.00148 |
| Irrigation System | Pipeline Characteristics | Airr (ha) | Number of Turbines | ΔHg (m) | L (m) | Q* (L/s) | Pn (kW) | Total Pn (kW) | |
|---|---|---|---|---|---|---|---|---|---|
| Material | D (mm) | ||||||||
| Spilinga-Ricadi | Steel | 80, 125, 150, 200, 600 | 463 | 7 | 57–145 | 844–2892 | 31–64 | 10–47 | 171 |
| Plastic (PVC) | 200, 250, 315 | ||||||||
| Murria | Steel | 250, 300, 400, 450 | 282 | 4 | 21–102 | 2337–2786 | 165–280 | 29–122 | 206 |
| Plastic (HDPE) | 200, 280, 315 | ||||||||
| Plastic (PVC) | 250 | ||||||||
| QR27 | Steel | 250, 300, 400 | 393 | 4 | 18–118 | 1555–2227 | 334 | 33–82 | 200 |
| Concrete | 600 | ||||||||
| Plastic (PVC) | 250 | ||||||||
| La Verde | Steel | 350 | 463 | 7 | 47–57 | 622–1515 | 756 | 180–181 | 365 |
| Concrete | 400 | ||||||||
| Asbestos-concrete | 200, 225, 350, 400 | ||||||||
| Cast iron | 600 | ||||||||
| Plastic (HDPE) | 110, 140 | ||||||||
| Plastic (PVC) | 200, 250, 315 | ||||||||
| Amendolea | Steel | 100, 250, 300 | 642 | 4 | 24–66 | 1549– 3276 | 51–619 | 7–95 | 164 |
| Asbestos-concrete | 175, 300, 350, 400 | ||||||||
| Cast iron | 600 | ||||||||
| Plastic (HDPE) | 110, 140, 160, 280, 315 | ||||||||
| Tuccio | Concrete | 400 | 725 | 4 | 13–196 | 927–4054 | 161–235 | 25–64 | 207 |
| Savuto | Steel | 600 | 975 | 3 | 18–35 | 674–4308 | 291–427 | 28–70 | 168 |
| Concrete | 600 | ||||||||
| ESHP | Hydraulic Parameters | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ΔHg* (m) | L* (m) | JL* (m) | ΔHn* (m) | kP (-) | DP* (mm) | kM (-) | DM* (mm) | Q** (L/s) | ||
| Spilinga | I | 240 | 9763 | 84.2 | 156 | 0.001 | 211 | 0.0015 | 229 | 54 |
| II | 222 | 5859 | 77.8 | 144 | 0.001 | 199 | 0.0015 | 215 | 58 | |
| III | 312 | 7961 | 109.4 | 203 | 0.001 | 162 | 0.0015 | 176 | 34 | |
| Murria | 224 | 12,042 | 78.5 | 145 | 0.002 | 377 | 0.0015 | 376 | 170 | |
| QR27 | 246 | 7417 | 86.3 | 160 | 0.001 | 294 | 0.0015 | 319 | 150 | |
| La Verde | 176 | 22,000 | 61.7 | 114 | 0.001 | 559 | 0.0015 | 606 | 379 | |
| Amendolea | 155 | 23,695 | 54.3 | 101 | 0.001 | 453 | 0.0015 | 491 | 195 | |
| Tuccio | 215 | 12,752 | 75.4 | 140 | 0.002 | 419 | 0.0015 | 390 | 177 | |
| Savuto | 85 | 15,635 | 29.8 | 55 | 0.002 | 649 | 0.0015 | 646 | 364 | |
| ESHP | ΔHn vs. ΔHn* | L vs. L* | |||||
|---|---|---|---|---|---|---|---|
| OM (m) | SM (m) | Difference (%) | OM (m) | SM (m) | Difference (%) | ||
| Spilinga | I | 140 | 156 | −0.2 | 4942 | 9763 | −48.2 |
| II | 158 | 144 | 0.6 | 4687 | 5859 | −11.7 | |
| III | 174 | 203 | 16.7 | 2655 | 7961 | −53.1 | |
| Murria | 205 | 145 | 0.6 | 10,449 | 12,042 | −15.9 | |
| QR27 | 156 | 160 | −0.0 | 7770 | 7417 | 3.5 | |
| La Verde | 73 | 114 | −0.4 | 2137 | 22,000 | −198.6 | |
| Amendolea | 105 | 101 | 0.0 | 9461 | 23,695 | −142.3 | |
| Tuccio | 130 | 140 | −0.1 | 9028 | 12,752 | −37.2 | |
| Savuto | 54 | 55 | 0.0 | 9776 | 15,635 | −58.6 | |
| SHP/ESHP Plant | Pn (by OM) (kW) | k = kP* 1 | k = kM* 2 | |||||
|---|---|---|---|---|---|---|---|---|
| D** (mm) | Pn** (by SM) (kW) | Difference Pn**, Pn (%) | D** (mm) | Pn** (by SM) (kW) | Difference Pn**, Pn (%) | |||
| Spilinga | I | 70.0 | 243 | 100.8 | 43.9 | 259 | 96.5 | 37.8 |
| II | 69.5 | 199 | 69.6 | 0.1 | 216 | 69.8 | 0.4 | |
| III | 58.1 | 189 | 87.0 | 49.8 | 206 | 88.4 | 52.2 | |
| Murria | 95.0 | 279 | 93.3 | −1.8 | 295 | 108.6 | 14.4 | |
| QR27 | 200.4 | 339 | 291.7 | 45.5 | 353 | 263.1 | 31.3 | |
| La Verde | 361.6 | 467 | 224.9 | −37.8 | 479 | 194.4 | −46.2 | |
| Amendolea | 163.7 | 473 | 184.3 | 12.6 | 485 | 159.1 | −2.8 | |
| Tuccio | 206.5 | 482 | 297.4 | 44.0 | 494 | 384.3 | 86.1 | |
| Savuto | 163.7 | 653 | 170.3 | 1.7 | 662 | 178.2 | 8.9 | |
| Mean | 17.6 | 20.2 | ||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nicotra, A.; Zema, D.A.; D’Agostino, D.; Zimbone, S.M. Equivalent Small Hydro Power: A Simple Method to Evaluate Energy Production by Small Turbines in Collective Irrigation Systems. Water 2018, 10, 1390. https://doi.org/10.3390/w10101390
Nicotra A, Zema DA, D’Agostino D, Zimbone SM. Equivalent Small Hydro Power: A Simple Method to Evaluate Energy Production by Small Turbines in Collective Irrigation Systems. Water. 2018; 10(10):1390. https://doi.org/10.3390/w10101390
Chicago/Turabian StyleNicotra, Angelo, Demetrio Antonio Zema, Daniela D’Agostino, and Santo Marcello Zimbone. 2018. "Equivalent Small Hydro Power: A Simple Method to Evaluate Energy Production by Small Turbines in Collective Irrigation Systems" Water 10, no. 10: 1390. https://doi.org/10.3390/w10101390
APA StyleNicotra, A., Zema, D. A., D’Agostino, D., & Zimbone, S. M. (2018). Equivalent Small Hydro Power: A Simple Method to Evaluate Energy Production by Small Turbines in Collective Irrigation Systems. Water, 10(10), 1390. https://doi.org/10.3390/w10101390







