Evaluating Glacier Volume Changes since the Little Ice Age Maximum and Consequences for Stream Flow by Integrating Models of Glacier Flow and Hydrology in the Cordillera Blanca, Peruvian Andes
Abstract
:1. Introduction
2. Study Site and Geographic Setting
3. Data and Method
3.1. Remote Sensing Imagery
3.2. Paleoglacier Extent
3.3. Glacier Mass Balance Model: Cellular Automata
3.4. Cellular Automata Model Setup
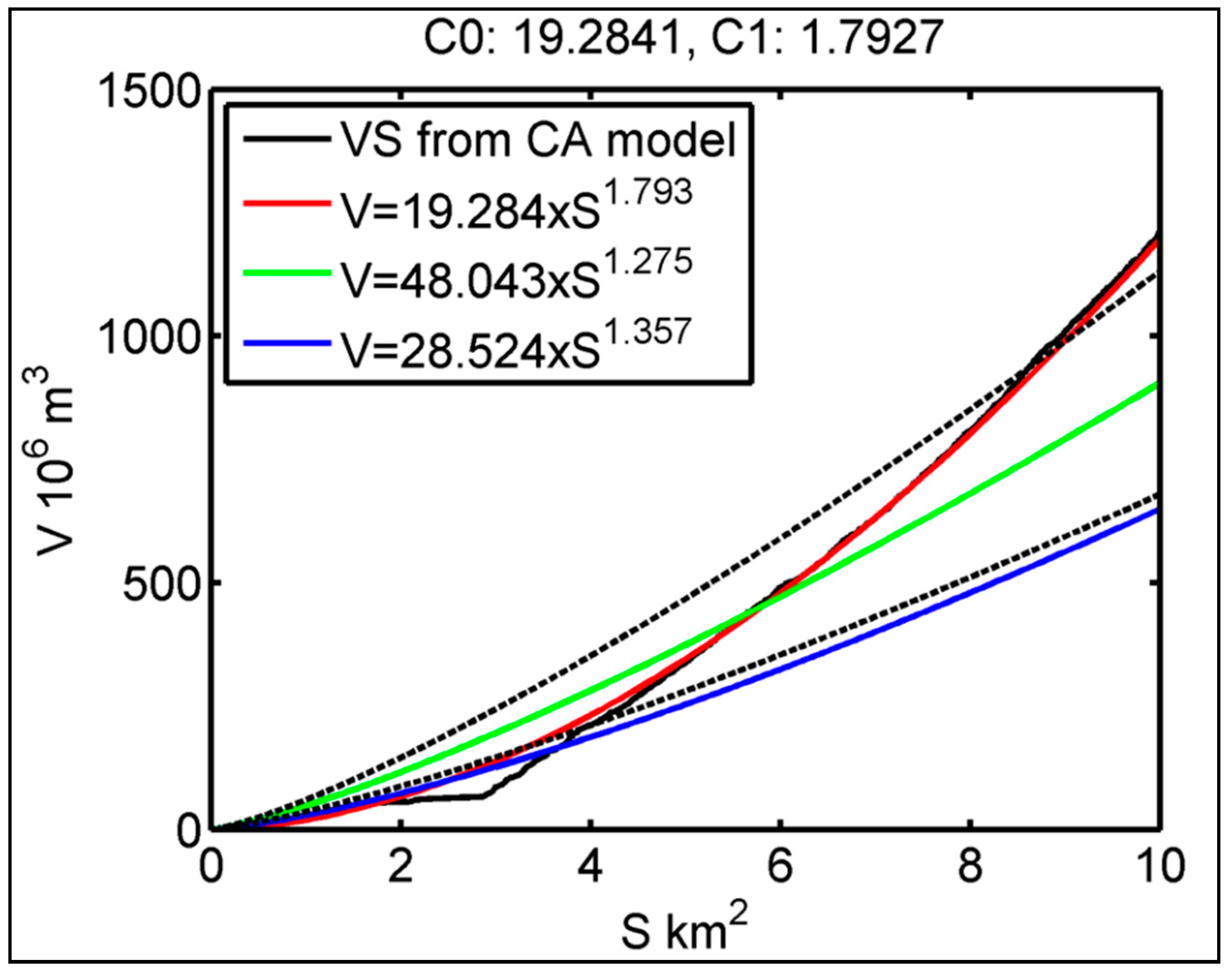
3.5. Volume and Surface Area (V-S) Scaling from the Model
3.6. Hydrology Model
4. Results and Discussion
4.1. Cellular Automata Model
4.1.1. Modeling Test: 50 Years Back (2011 through 1962)
4.1.2. Modeling through LIA Maximum (1850 AD)
4.2. Model vs. Previous Research on YAN
4.3. Volume Reconstruction from the Model vs. V-S Scaling Fit
4.3.1. The V-S Scaling of YAN from the Cellular Automata Model
4.3.2. The V-S Scaling of QUE from the Cellular Automata (CA) Model
4.4. Hydrology Model
4.4.1. The Yanamarey Glacier (YAN)
4.4.2. The Queshque Glacier (QUE)
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baraër, M.; Mark, B.G.; McKenzie, J.M.; Condom, T.; Bury, J.; Huh, K.I.; Portocarrero, C.; Gómez, J. Glacier recession and water resources in Peru’s Cordillera Blanca. J. Glaciol. 2012, 58, 134–150. [Google Scholar] [CrossRef]
- Mark, B.G.; Seltzer, G.O. Tropical Glacier Meltwater Contribution to Stream Discharge: A Case Study in the Cordillera Blanca, Peru. J. Glaciol. 2003, 49, 271–281. [Google Scholar] [CrossRef]
- Mark, B.G.; McKenzie, J.M.; Gomez, J. Hydrolochemical evaluation of changing glacier meltwater contribution to stream discharge: Callejon de Huaylas, Peru. Hydrol. Sci. J. 2005, 50, 975–987. [Google Scholar] [CrossRef]
- Mark, B.G.; McKenzie, J.M. Tracing increasing tropical Andean glacier melt with stable isotopes in water. Environ. Sci. Technol. 2007, 41, 6955–6960. [Google Scholar] [CrossRef] [PubMed]
- Huss, M.; Farinotti, D.; Bauder, A.; Funk, M. Modelling runoff from highly glacierized alpine drainage basins in a changing climate. Hydrol. Process. 2008, 22, 3888–3902. [Google Scholar] [CrossRef]
- Juen, I.; Kaser, G.; Georges, C. Modelling observed and future runoff from a glacierized tropical catchment (Cordillera Blanca, Peru). Glob. Planet. Chang. 2007, 59, 37–48. [Google Scholar] [CrossRef]
- Vuille, M.; Francou, B.; Wagnon, P.; Juen, I.; Kaser, G.; Mark, B.G.; Bradley, R.S. Climate change and tropical Andean glaciers: Past, present and future. Earth Sci. Rev. 2008, 89, 79–96. [Google Scholar] [CrossRef]
- Vergara, W.; Deeb, A.; Valencia, A.M.; Raymond, B.; Francou, B.; Zarzar, A.; Grünwaldt, A.; Haeussling, S.M. Economic Impacts of Rapid Glacier Retreat in the Andes. Eos Trans. Am. Geophys. Union 2007, 88, 261–264. [Google Scholar] [CrossRef]
- Mark, B.G.; Bury, J.; McKenzie, J.M.; French, A.; Baraër, M. Climate Change and Tropical Andean Glacier Recession: Evaluating Hydrologic Changes and Livelihood Vulnerability in the Cordillera Blanca, Peru. Ann. Assoc. Am. Geogr. 2010, 100, 794–805. [Google Scholar] [CrossRef]
- Bury, J.T.; Mark, B.G.; McKenzie, J.M.; French, A.; Baraër, M.; Huh, K.; Zapata, M.A.; Gomez, J. Glacier recession and human vulnerability in the Yanamarey watershed of the Cordillera Blanca, Peru. Clim. Chang. 2011, 105, 179–206. [Google Scholar] [CrossRef]
- Dowdeswell, J.A.; Benham, T.J.; Gorman, M.R.; Burgess, D.; Sharp, M. Form and flow of the Devon Island ice cap, Canadian Arctic. J. Geophs. Res. 2004, 109, F02002. [Google Scholar] [CrossRef]
- Conway, H.; Smith, B.; Vaswani, P.; Matsuoka, K.; Rignot, E.L.; Claus, P. A low-frequency ice-penetrating radar system adapted for use from an airplane: Test results from Bering and Malaspina Glaciers, Alaska, USA. Ann. Glaciol. 2009, 50, 93–97. [Google Scholar] [CrossRef]
- Thomas, R.; Frederick, E.; Krabill, W.; Manizade, S.; Martin, C. Recent changes on Greenland outlet glaciers. J. Glaciol. 2009, 55, 147–161. [Google Scholar] [CrossRef]
- Azam, M.F.; Wagnon, P.; Ramanathan, A.; Vincent, C.; Sharma, P.; Arnaud, Y.; Linda, A.; Pottakkal, J.G.; Chevallier, P.; Singh, V.B.; et al. From balance to imbalance: A shift in the dynamic behavior of Chota Shigri glacier, western Himalaya, India. J. Glaciol. 2012, 58, 315–324. [Google Scholar] [CrossRef]
- Harper, J.T.; Bradford, J.H. Snow stratigraphy over a uniform depositional surface: Spatial variability and measurement tools. Cold Reg. Sci. Technol. 2003, 37, 289–298. [Google Scholar] [CrossRef]
- Bradford, J.H.; Harper, J.T. Wave field migration as a tool for estimating spatially continuous radar velocity and water content in glaciers. Geophys. Res. Lett. 2005, 32, L08502. [Google Scholar] [CrossRef]
- Jol, H.M. Ground Penetrating Radar: Theory and Applications, 1st ed.; Elsevier Science: Amsterdam, The Netherlands, 2008; p. 544. ISBN 9780444533487. [Google Scholar]
- Mingo, L.; Flowers, G.E. An integrated lightweight ice-penetrating radar system. J. Glaciol. 2010, 56, 709–714. [Google Scholar] [CrossRef]
- Chen, J.; Ohmura, A. Estimation of Alpine glacier water resources and their change since the 1870s. IAHS Publ. 1990, 193, 127–135. [Google Scholar]
- Bahr, D.B.; Meier, M.F.; Peckham, S.D. The physical basis of glacier volume-area scaling. J. Geophys. Res. 1997, 102, 20355–20362. [Google Scholar] [CrossRef] [Green Version]
- Van de Wal, R.S.; Wild, M. Modelling the response of glaciers to climate change by applying volume-area scaling in combination with a high resolution GCM. Clim. Dyn. 2001, 18, 359–366. [Google Scholar] [CrossRef]
- Farinotti, D.; Huss, M.; Bauder, A.; Funk, M.; Truffer, M. A method to estimate the ice volume in Swiss Alps. Glob. Planet. Chang. 2009, 68, 225–231. [Google Scholar] [CrossRef]
- Braun, L.N.; Weber, M.; Schulz, M. Consequences of climate change for runoff from Alpine regions. Ann. Glaciol. 2000, 31, 19–25. [Google Scholar] [CrossRef]
- Jansson, P.; Hock, R.; Schneider, T. The concept of glacier storage: A review. J. Hydrol. 2003, 282, 116–129. [Google Scholar] [CrossRef]
- Brown, L.E.; Milner, A.M.; Hannah, D.M. Predicting river ecosystem response to glacial meltwater dynamics: A case study of quantitative water sourcing and glaciality index approaches. Aquat. Sci. 2010, 72, 325–334. [Google Scholar] [CrossRef]
- Uehlinger, U.; Robinson, C.T.; Hieber, M.; Zah, R. The physic-chemical habitat template for periphyton in alpine glacial streams under a changing climate. Hydrobiologia 2010, 657, 107–121. [Google Scholar] [CrossRef]
- Huss, M. Present and future contribution of glacier storage change to runoff from macroscale drainage basins in Europe. Water Resour. Res. 2011, 47, W07511. [Google Scholar] [CrossRef]
- Jomelli, V.; Favier, V.; Rabatel, A.; Runstein, D.; Hoffmann, G.; Francou, B. Fluctuations of glacier in the tropical Andes over the last millennium palaeoclimatic implications: A review. Palaeogeogr. Palaeocl. 2009, 281, 269–282. [Google Scholar] [CrossRef]
- Rodbell, D.T. Lichenometric and radiocarbon dating of Holocene glaciation, Cordillera Blanca. Holocene 1992, 2, 19–29. [Google Scholar] [CrossRef]
- Rodbell, D.T. Subdivision of Late Pleistocene Moraines in the Cordillera Blanca, Peru, Based on Rock-Weathering Features, Soils and Radiocarbon Dates. Quatern. Res. 1993, 39, 133–143. [Google Scholar] [CrossRef]
- Jomelli, V.; Grancher, D.; Brunstein, D.; Solomina, O. Recalibration of the Rhizocarpon growth curve in Cordillera Blanca (Peru) and LIA chronology implication. Geomorphology 2008, 93, 201–212. [Google Scholar] [CrossRef]
- Jomelli, V.; Argollo, J.; Brunstein, D.; Favier, V.; Hoffmann, G.; Ledru, M.P.; Sicart, J.E. Multiproxy analysis of climate variability for the last millennium in the tropical Andes (Chapitre 3). In Climate Change Research Progress; Peretz, L.N., Ed.; Nova Science Publisher: Hauppauge, NY, USA, 2008; pp. 127–159. [Google Scholar]
- Kaser, G.; George, C. Changes of the equilibrium-line altitude in the tropical Cordillera Blanca, Peru, 1930–1950, and their spatial variation. Ann. Glaciol. 1997, 24, 344–349. [Google Scholar] [CrossRef]
- Kaser, G.; Osmaston, H. Tropical Glaciers; Cambridge University Press: Cambridge, UK, 2001; p. 206. ISBN 0521633338. [Google Scholar]
- Rabatel, A.; Jomelli, V.; Naveau, P.; Francou, B.; Grancher, D. Dating of Little Ice Age glacier fluctuations in the tropical AndesL Charquini glaciers, Bolivia, 16°S. C. R. Geosci. 2005, 337, 1311–1322. [Google Scholar] [CrossRef]
- Rabatel, A.; Machaca, A.; Francou, B.; Jomelli, V. Glacier recession on the Cerro Charquini (Bolivia 16°S) since the maximum of the Little Ice Age (17th century). J. Glaciol. 2006, 52, 110–118. [Google Scholar] [CrossRef]
- Rabatel, A.; Francou, B.; Jomelli, V.; Naveau, P.; Grancher, D. A chronology of the Little Ice Age in the tropical Andes of Bolivia (16°S) and its implications for climate reconstruction. Quatern. Res. 2008, 70, 198–212. [Google Scholar] [CrossRef]
- Solomina, O.; Jomelli, V.; Kaser, G.; Ames, A.; Berger, B.; Pouyaud, B. Lichenometry in the Cordillera Blanca, Peru: “Little Ice Age” moraine chronology. Glob. Planet. Chang. 2007, 59, 225–235. [Google Scholar] [CrossRef]
- Thompson, L.G.; Mosley-Thompson, E.; Dansgaard, W.; Grootes, P.M. The Little Ice Age as recorded in the stratigraphy of the tropical Quelccaya ice cap. Science 1986, 234, 361–364. [Google Scholar] [CrossRef] [PubMed]
- Georges, C. 20th-Centry Glacier Fluctuations in the Tropical Cordillera Blanca, Peru. Arct. Antarct. Alp. Res. 2004, 36, 100–107. [Google Scholar] [CrossRef]
- Benn, D.I.; Owen, L.A.; Osmaston, H.A.; Seltzer, G.O.; Porter, S.C.; Mark, B.G. Reconstruction of equilibrium-line altitudes for tropical and sub-tropical glaciers. Quatern. Int. 2005, 138–139, 8–21. [Google Scholar] [CrossRef]
- Ramage, J.M.; Smith, J.A.; Rodbell, D.T.; Seltzer, G.O. Comparing reconstructed Pleistocene equilibrium-line altitudes in the tropical Andes of central Peru. J. Quatern. Sci. 2005, 20, 777–788. [Google Scholar] [CrossRef]
- Braithwaite, R.J.; Raper, S.C.B. Estimating equilibrium-line altitude (ELA) from glacier inventory data. Ann. Glaciol. 2009, 50, 127–132. [Google Scholar] [CrossRef]
- Everitt, B.S.; Skrondal, A. The Cambridge Dictionary of Statistics, 4th ed.; Cambridge University Press: Cambridge, UK, 2010; p. 480. ISBN 9780521766999. [Google Scholar]
- Raper, S.C.B.; Braithwaite, R.J. Glacier volume response time and its links to climate and topography based on a conceptual model of glacier hypsometry. Cryosphere 2009, 3, 183–194. [Google Scholar] [CrossRef] [Green Version]
- Evans, I.S.; Cox, N.J. Global variations of local asymmetry in glacier altitude: Separation of north-south and east-west components. J. Glaciol. 2005, 51, 469–482. [Google Scholar] [CrossRef] [Green Version]
- Machguth, H.; Haeberli, W.; Paul, F. Mass-balance parameters derived from a synthetic network of mass-balance glaciers. J. Glaciol. 2012, 58, 965–979. [Google Scholar] [CrossRef] [Green Version]
- Gómez, J.; Cochachi, A.; Gonzales, G.; Tournoud, M.; Quijano, J. Informe de mediciones effectuadas en el Glacial Artesonraju. Cordillera Blanca (Peru). INRENA. Unpublished.
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Fujita, K.; Sakai, A. Reconstructing river runoff over the past 2000 years in the arid Heihe River Basin, northwestern China. PAGES News 2012, 20, 76–77. [Google Scholar] [CrossRef]
- Kaser, G.; Hastenrath, S.; Ames, A. Mass balance profiles on tropical glaciers. Z. Gletscher. Glaziageol. 1996, 32, 75–81. [Google Scholar]
- Kaser, G.; Georges, C.; Ames, A. Modern glacier fluctuations in the Huascaran-Chopicalqui massif of the Cordillera Blanca, Peru. Z. Gletscher. Glaziageol. 1996, 32, 91–99. [Google Scholar]
- Ames, A. A documentation of glacier tongue variations and lake developments in the Cordillera Blanca. Z. Gletscher. Glaziageol. 1998, 34, 1–26. [Google Scholar]
- Mark, B.G.; Seltzer, G.O. Evaluation of recent glacier recession in the Cordillera Blanca, Peru (AD 1962–1999): Spatial distribution of mass loss and climatic forcing. Quatern. Sci. Rev. 2005, 24, 2265–2280. [Google Scholar] [CrossRef]
- ASTER Validation Team ASTER Global Digital Elevation Model Version 2—Summary of Validation Results. METI and NASA Report. Available online: https://lpdaacaster.cr.usgs.gov/GDEM/Summary_GDEM2_validation_report_final.pdf (accessed on 15 September 2014).
- Hastenrath, S.; Ames, A. Recession of Yanamarey Glacier in Cordillera Blanca, Peru, during the 20th century. J. Glaciol. 1995, 41, 191–196. [Google Scholar] [CrossRef]
- Hastenrath, S.; Ames, A. Diagnosing the imbalance of Yanamarey Glacier in the Cordillera Blanca, Peru. J. Geophys. Res. 1995, 100, 5105–5112. [Google Scholar] [CrossRef]
- Harper, J.T.; Humphrey, N.F. High altitude Himalayan climate inferred from glacial ice flux. Geophys. Res. Lett. 2003, 30, 1764. [Google Scholar] [CrossRef]
- Nye, J.F. The flow of glaciers and ice-sheets as a problem in plasticity. Proc. R. Soc. Lond. Ser. A 1951, 207, 554–572. [Google Scholar] [CrossRef]
- Paterson, W.S.B. The Physics of Glaciers, 4th ed.; Academic Press: Cambridge, MA, USA, 2010; p. 496. ISBN 9781493300761. [Google Scholar]
- Harper, J.T.; Humphrey, N.F.; Pfeffer, W.T.; Huzurbazar, S.V.; Bahr, D.B.; Welch, B.C. Spatial variability in the flow of a valley glacier: Deformation of a large array of boreholes. J. Geophys. Res. 2001, 106, 8547–8562. [Google Scholar] [CrossRef] [Green Version]
- Macheret, Y.Y.; Cherkasov, P.A.; Bobrova, L.I. The thickness and volume of Dzhungarskiy Alatau glaciers from airborne radio echo-sounding data. Mater. Glyatsiol. Issled. 1988, 62, 59–70. [Google Scholar]
- Meier, M.F.; Bahr, D.B. Counting glaciers: Use of scaling methods to estimate the number and size distribution of the glaciers of the world. In Glaciers, Ice Sheets and Volcanoes; Colbeck, S., Ed.; Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1996; Volume 96. [Google Scholar]
- Huh, K.; Mark, B.G.; Ahn, Y.; Hopkinson, C. Volume change of tropical Peruvian glaciers from multi-temporal digital elevation models and volume-surface area scaling. Geogr. Ann. A 2017, 99, 222–239. [Google Scholar] [CrossRef]
- Bevington, P.R.; Robinson, D.K. Data Reduction and Error Analysis for the Physical Sciences, 3rd ed.; McGraw-Hill: New York, NY, USA, 2003; p. 320. ISBN 9780072472271. [Google Scholar]
- Baraër, M.; McKenzie, J.M.; Mark, B.G.; Bury, J.; Knox, S. Characterizing contributions of glacier melt and groundwater during the dry season in a poorly gauged catchment of the Cordillera Blanca (Peru). Adv. Geosci. 2009, 22, 41–49. [Google Scholar] [CrossRef] [Green Version]
- Ames, A.; Hastenrath, S. Diagnosing the imbalance of Glaciar Santa Rosa, Cordillera Raura, Peru. J. Glaciol. 1996, 42, 212–218. [Google Scholar] [CrossRef] [Green Version]
- Ames, A.; Hastenrath, S. Mass Balance and flow of the Uruashraju glacier, Cordillera Blanca, Peru. Z. Gletscher. Glaziageol. 1996, 32, 83–89. [Google Scholar]
- Rabatel, A.; Francou, B.; Soruco, J.; Gómez, J.; Cáceres, B.; Ceballos, J.L.; Basantes, R.; Vuille, M.; Sicart, J.-E.; Huggel, C.; et al. Current state of glaciers in the tropical Andes: A multi-century perspective on glacier evolution and climate change. Cryosphere 2013, 7, 81–102. [Google Scholar] [CrossRef] [Green Version]
- Rodbell, D.T.; Seltzer, G.O. Rapid ice margin fluctuations during the Younger Dryas in the tropical Andes. Quatern. Res. 2000, 54, 328–338. [Google Scholar] [CrossRef]
- Smith, J.A.; Seltzer, G.O.; Farber, D.L.; Rodbell, D.T.; Finkel, R.C. Early Local Last Glacial Maximum in the Tropical Andes. Science 2005, 308, 678–681. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smith, J.A.; Finkel, R.C.; Farber, D.L.; Rodbell, D.T.; Seltzer, G.O. Moraine preservation and boulder erosion in the tropical Andes: Interpreting old surface exposure ages in glaciated valleys. J. Quatern. Sci. 2005, 20, 735–758. [Google Scholar] [CrossRef]
- Gómez, J.; (Parque Nacional Huascarán, Servicio Nacional de Áreas, Huaraz, Peru). Personal communication, 2014.
- CONAM. Escenario Climaticos Futuros y Disponsiblidad del Recurso hidrico en la Cuenca del Rio Santa; CONAM/SENAMHI: Lima, Peru, 2005; pp. 1–32. ISBN 9972824195.
- Baraër, M.; (Département de génie de la construction, École de technologie supérieure, Montréal, QC, Canada). Personal communication, 2014.
- Francou, B.; Ribstein, P.; Semiond, H.; Portocarrero, C.; Rodriguez, A. Balances de glaciares y clima en Bolivia y Peru: Impacto de los eventos ENSO. Bull. Inst. Fr. Etud. Andines. 1995, 24, 661–670. [Google Scholar]
- Immerzeel, W.W.; van Beek, L.P.H.; Bierkens, F.P. Climate change will affect the Asian water towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef] [PubMed]
- Kaser, G.; Ames, A.; Zamora, M. Glacier fluctuations and climate in the Cordillera Blanca, Peru. Ann. Glaciol. 1990, 14, 136–140. [Google Scholar] [CrossRef]













| Parameters | YAN | QUE |
|---|---|---|
| Median height (m) from DEM | 4898 | 5057 |
| Equilibrium Line Altitude (ELA) for model (m) | 4780 | 4950 |
| Net balance in ablation (103 kg m−2 year−1) | 6 | 6 |
| Max mass balance (103 kg m−2 year−1) | 1 | 1 |
| Total time (year) (test: 2011 to 1962) | 49 | 49 |
| Total time (year) (2011 to 1850) | 161 | 161 |
| Distance from Headwall to Terminus (m) | Terminus Elevation (m) | Surface Area (106m2) | Volume (106m3) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Year | Model | H&A | Diff. | Model | H&A | Model | H&A | Model | H&A |
| 1988 | 991.65 | 1250 | 258.35 | 4631.3 | 4630 | 0.86 | 0.8 | 32.29 | 25 |
| 1982 | 1098.28 | 1350 | 251.72 | 4625.92 | 4600 | 0.91 | 0.87 | 35.04 | 32 |
| 1973 | 1268.88 | 1500 | 231.12 | 4618.86 | 4595 | 0.97 | 0.95 | 38.43 | - |
| 1962 | 1432.62 | 1550 | 117.38 | 4624.55 | 4600 | 1.05 | 1.02 | 43.09 | - |
| 1948 | 1695.40 | 1600 | −95.40 | 4600 | 4590 | 1.20 | 1.0 | 52.27 | 54 |
| 1939 | 1855.34 | 1850 | −5.34 | 4530.34 | 4520 | 1.22 | 1.2 | 59.99 | - |
| 1850 | 2991.60 | 2800 | −191.60 | 4348.13 | 4420 | 1.73 | 1.7 | 88.71 | 89 |
| Year | Size (km2) | Volume from V-S Scaling CA (106m3) | Volume from V-S Scaling CB6 (106m3) | Volume from V-S Scaling C&O (106m3) | Volume Diff. (CB6 vs. CA) (%) | Volume Diff. (CA vs. C&O) (%) | Volume Diff. (CB6 vs. C&O) (%) |
|---|---|---|---|---|---|---|---|
| 1850 | 1.73 | 88.71 | 96.64 | 60.01 | 8.20 | 32.35 | 37.90 |
| 1962 | 1.16 | 49.46 | 57.73 | 34.68 | 14.33 | 29.88 | 39.93 |
| 2001 | 0.66 | 22.02 | 28.28 | 16.23 | 22.15 | 26.29 | 42.62 |
| Year | Size (km2) | Volume from V-S Scaling CA (106m3) | Volume from V-S Scaling CB6 (106m3) | Volume from V-S Scaling C&O (106m3) | Volume Diff. (CB6 vs. CA) (%) | Volume Diff. (CA vs. C&O) (%) | Volume Diff. (CB6 vs. C&O) (%) |
|---|---|---|---|---|---|---|---|
| 1850 | 3.55 | 186.96 | 241.64 | 159.17 | 22.63 | 14.86 | 34.13 |
| 1962 | 2.55 | 103.3 | 158.47 | 101.59 | 34.82 | 1.65 | 35.89 |
| 2001 | 1.57 | 43.3 | 85.39 | 52.61 | 49.29 | −21.50 | 38.39 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huh, K.I.; Baraër, M.; Mark, B.G.; Ahn, Y. Evaluating Glacier Volume Changes since the Little Ice Age Maximum and Consequences for Stream Flow by Integrating Models of Glacier Flow and Hydrology in the Cordillera Blanca, Peruvian Andes. Water 2018, 10, 1732. https://doi.org/10.3390/w10121732
Huh KI, Baraër M, Mark BG, Ahn Y. Evaluating Glacier Volume Changes since the Little Ice Age Maximum and Consequences for Stream Flow by Integrating Models of Glacier Flow and Hydrology in the Cordillera Blanca, Peruvian Andes. Water. 2018; 10(12):1732. https://doi.org/10.3390/w10121732
Chicago/Turabian StyleHuh, Kyung In, Michel Baraër, Bryan G. Mark, and Yushin Ahn. 2018. "Evaluating Glacier Volume Changes since the Little Ice Age Maximum and Consequences for Stream Flow by Integrating Models of Glacier Flow and Hydrology in the Cordillera Blanca, Peruvian Andes" Water 10, no. 12: 1732. https://doi.org/10.3390/w10121732
APA StyleHuh, K. I., Baraër, M., Mark, B. G., & Ahn, Y. (2018). Evaluating Glacier Volume Changes since the Little Ice Age Maximum and Consequences for Stream Flow by Integrating Models of Glacier Flow and Hydrology in the Cordillera Blanca, Peruvian Andes. Water, 10(12), 1732. https://doi.org/10.3390/w10121732





