Numerical Investigations of Tsunami Run-Up and Flow Structure on Coastal Vegetated Beaches
Abstract
1. Introduction
2. Numerical Method
2.1. Governing Equations
2.2. Vegetation Drag Force
2.3. Finite Volume Method
2.4. Evaluation of Numerical Fluxes
2.5. Treatment of Wetting and Drying Fronts
- Wet edge (see Figure 1a): two adjacent cells are wet, in which water depth of left cell hL > ε and water depth of right cell hR > ε.
- Partially wet edge (with flux), as presented in Figure 1b: a wet cell (left) links to a dry cell on the right, and the water level of the wet cell is higher than that of the dry cell, where hL > ε, hR ≤ ε and water level of left cell ηL > water level of left cell ηR.
- Partially wet edge (no flux), as shown in Figure 1c: a wet cell (left) links to a dry cell on the right, and the water level of the wet cell is lower than that of the dry cell, where hL > ε, hR ≤ ε, and ηL < ηR. To eliminate the non-physical flux problem produced in the interface, the water level ηR and bed level ZbR for the dry cell were temporarily replaced by a value which equaled to the water level ηL in the wet cell.
- Wet cell: all the edges of this cell consisted of a wet or partially wet edges (with flux) and all the nodes of the cell are flooded.
- Dry cell: all the edges of this cell consist of dry or partially wet edges (no flux).
- Partially wet cell: all other cells do not satisfy the criteria of either a wet or dry cell, as defined above.
3. Numerical Simulation and Experimental Validation
3.1. Solitary Wave Run-up on a Bare Sloping Beach
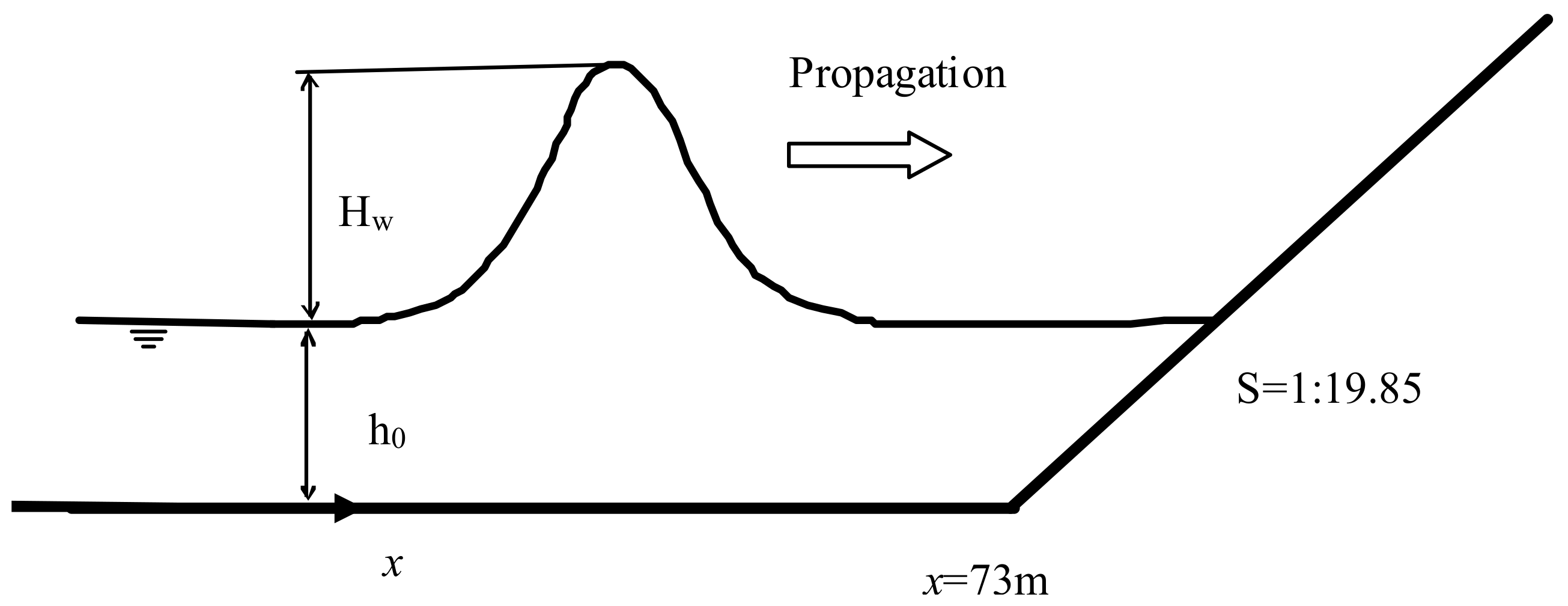
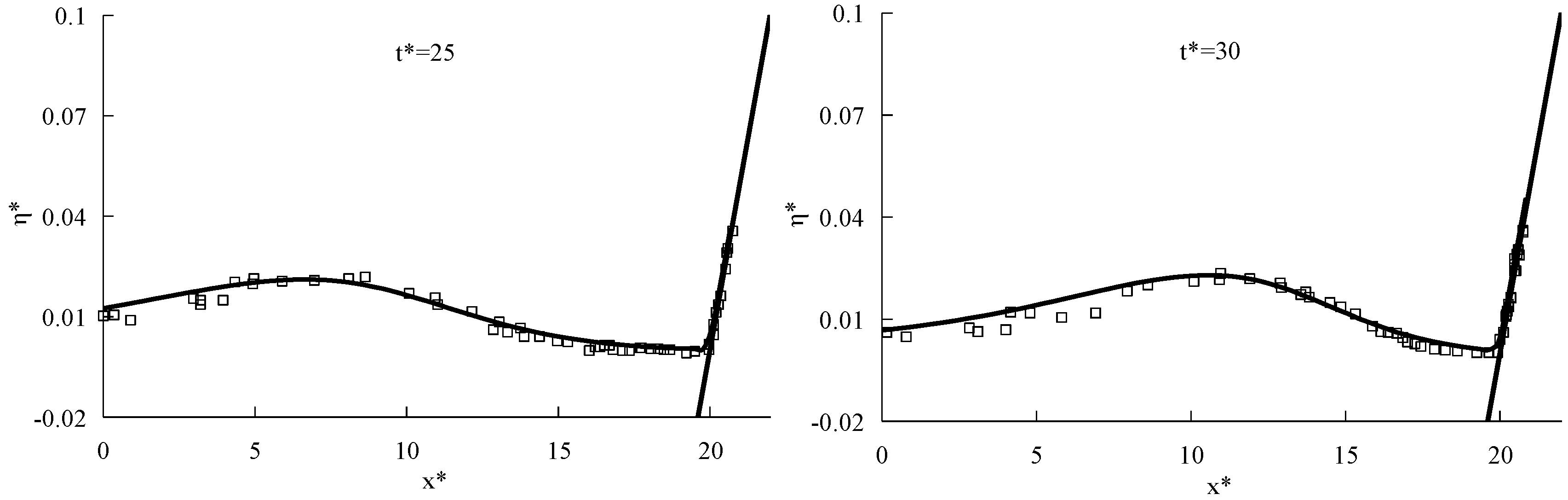
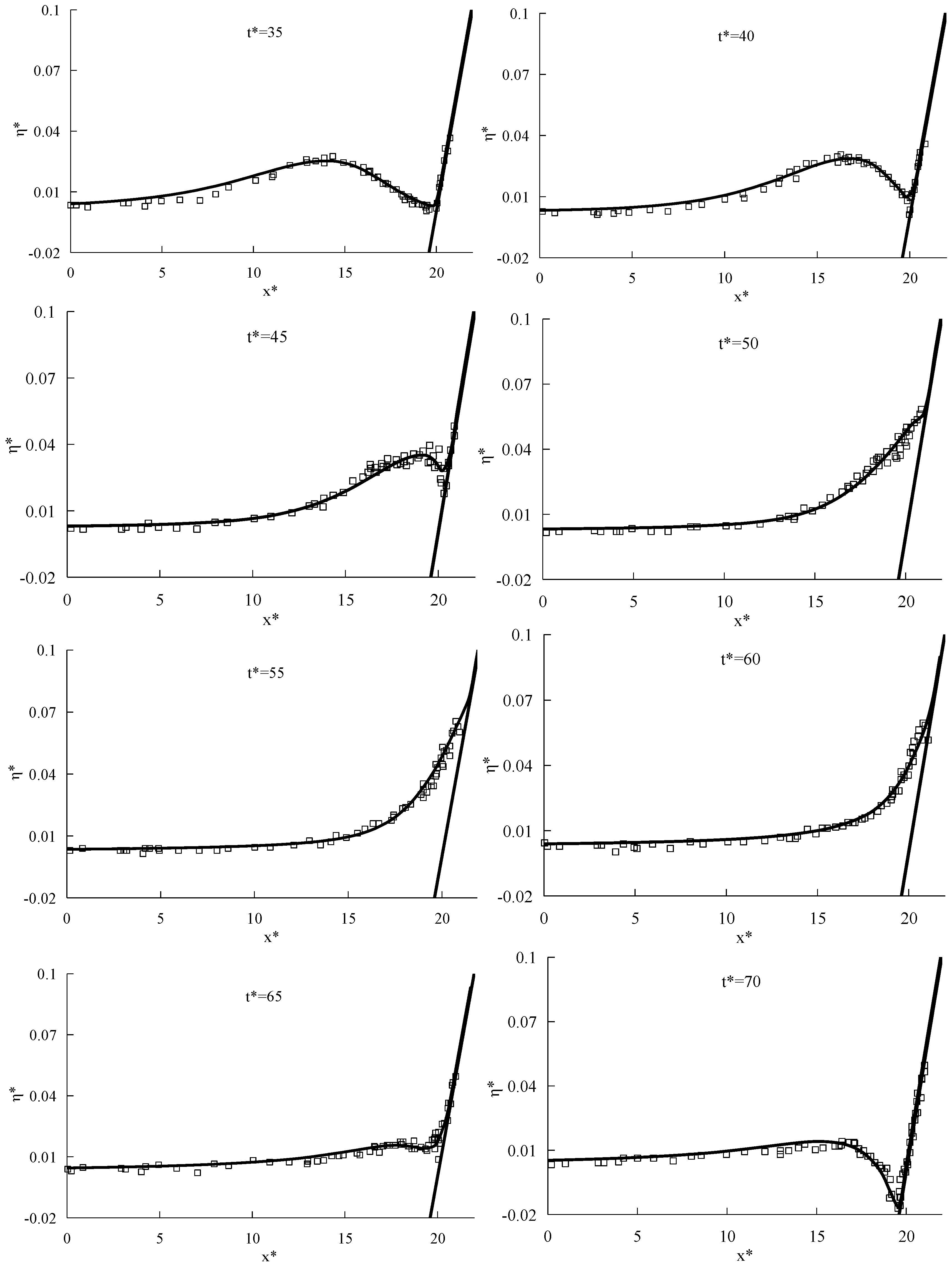
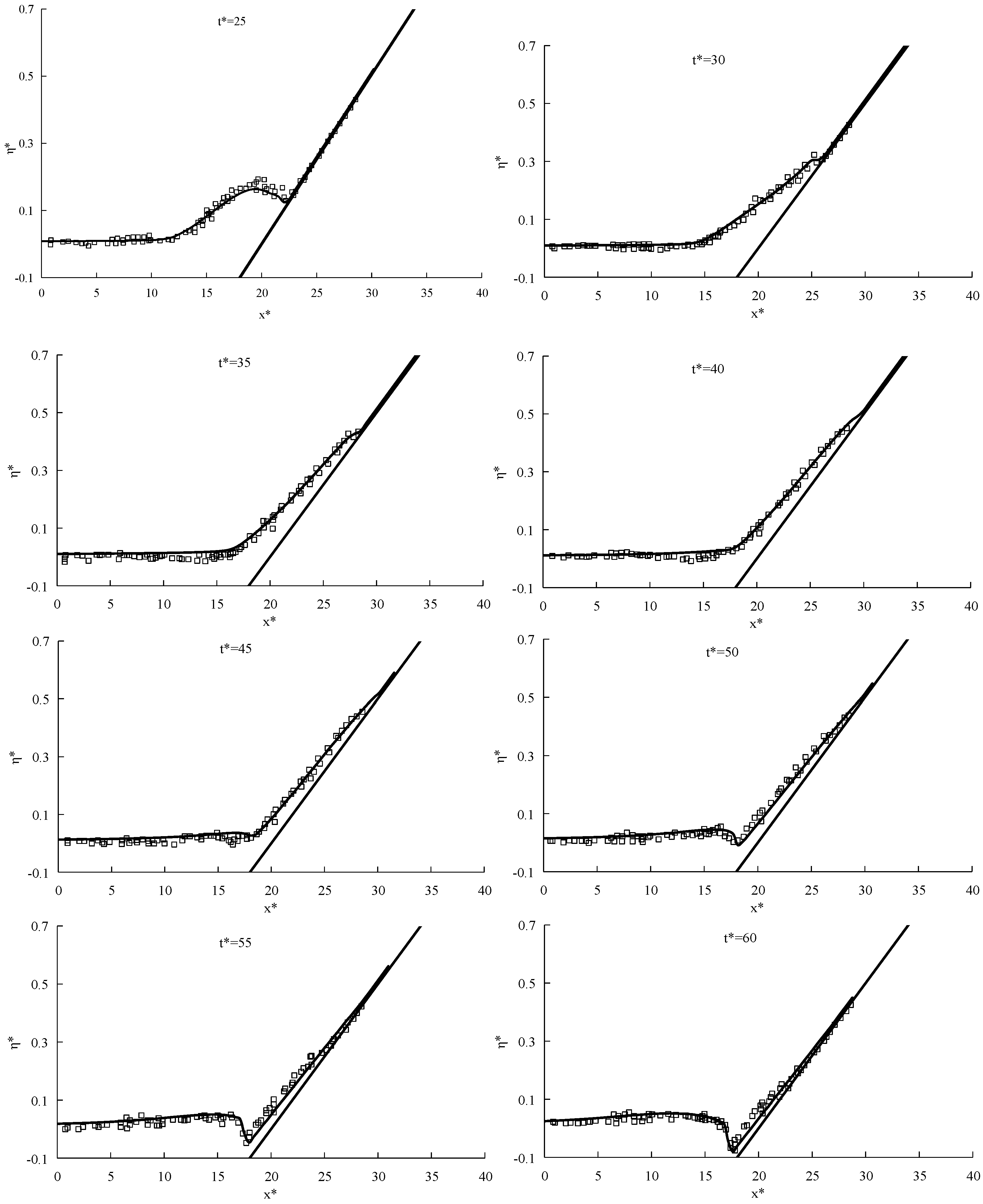
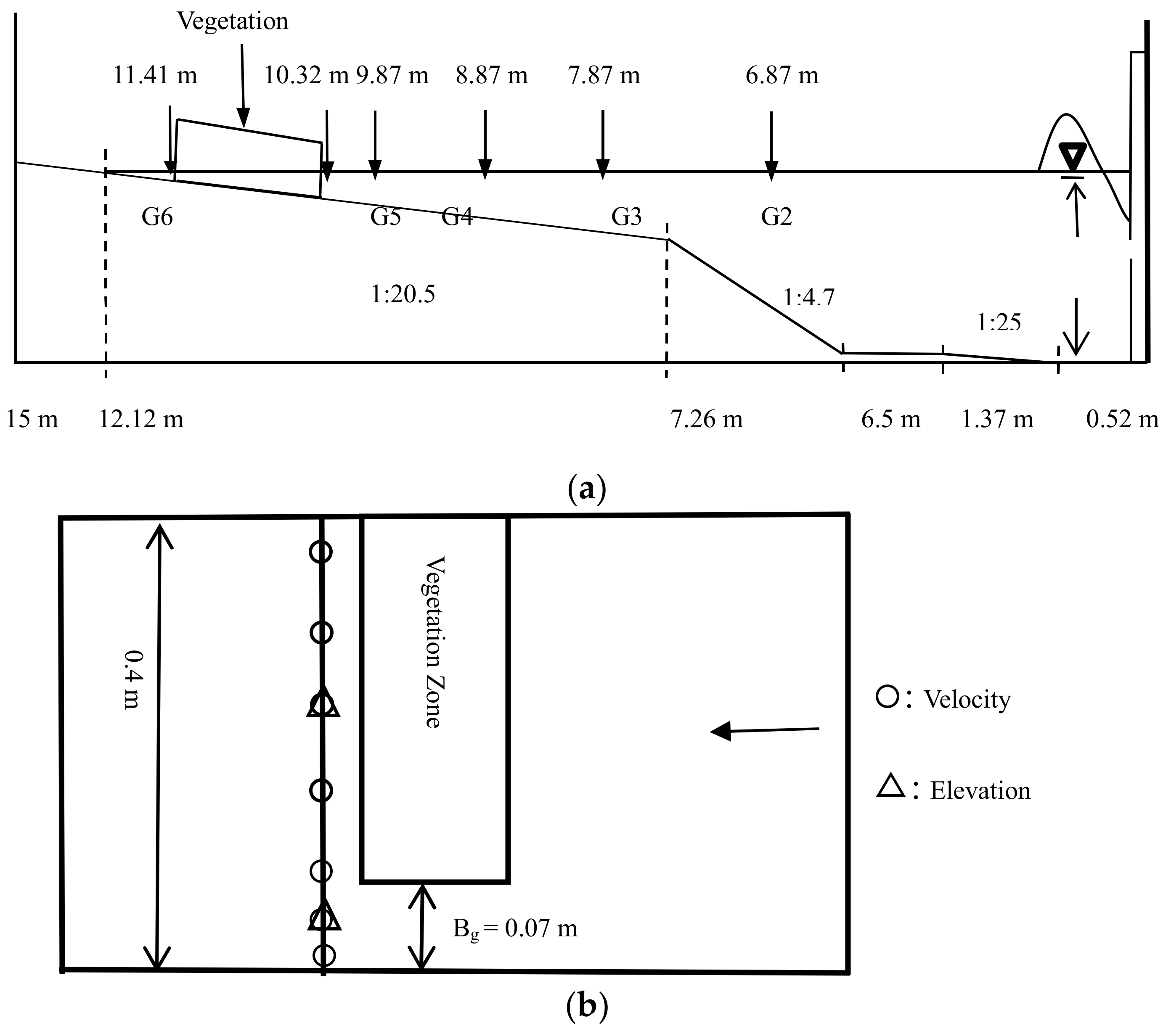
3.2. Propagation of Long Periodic Waves on a Partially Vegetated Sloping Beach
3.3. Effects of Forest on Tsunami Run-up at Actual Scale
3.3.1. Coastal Topography and Forest Conditions
3.3.2. Effects of Forest with a Straight Open Gap on Tsunami Run-up
3.3.3. Effects of Arrangements of Vegetation Patches and Open Gaps
3.3.4. Effects of Forest Parameters on Tsunami Run-up
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gopinath, G.; Løvholt, F.; Kaiser, G.; Harbitz, C.B.; Srinivasa, R.K.; Ramalingam, M.; Singh, B. Impact of the 2004 Indian ocean tsunami along the Tamil Nadu coastline: field survey review and numerical simulations. Nat. Hazards 2014, 72, 743–769. [Google Scholar] [CrossRef]
- Gelfenbaum, G.; Apotsos, A.; Stevens, A.W.; Jaffe, B. Effects of fringing reefs on tsunami inundation American Samoa. Earth Sci. Rev. 2011, 107, 12–22. [Google Scholar] [CrossRef]
- Liu, H.; Shimozono, T.; Takagawa, T.; Okayasu, A.; Fritz, H.; Sato, S.; Tajima, Y. The 11 March 2011 Tohoku tsunami survey in rikuzentakata and comparison with historical event. Pure Appl. Geophys. 2013, 170, 1033–1046. [Google Scholar] [CrossRef]
- Sarfaraz, M.; Pak, A. SPH numerical simulation of tsunami wave forces impinged on bridge superstructures. Coast. Eng. 2017, 121, 145–157. [Google Scholar] [CrossRef]
- Touhami, H.E.; Khellaf, M.C. Laboratory study on effects of submerged obstacles on tsunami wave and run-up. Nat. Hazards 2017, 87, 757–771. [Google Scholar] [CrossRef]
- Hsiao, S.C.; Lin, T.C. Tsunami-like solitary waves impinging and overtopping an impermeable seawall: experiment and RANS modeling. Coast. Eng. 2010, 57, 1–18. [Google Scholar] [CrossRef]
- Irish, J.L.; Weiss, R.; Yang, Y.; Yang, Y.; Song, Y.; Zainali, A.; Marivela-Colmenarejo, R. Laboratory experiments of tsunami run-up and withdrawal in patchy coastal forest on a steep beach. Nat. Hazards 2014, 74, 1933–1949. [Google Scholar] [CrossRef]
- Ko, H.T.S.; Yeh, H. On the splash-up of tsunami bore impact. Coast. Eng. 2018, 131, 1–11. [Google Scholar] [CrossRef]
- Witt, D.L.; Yin, L.Y.; Yim, S.C. Field investigation of tsunami impact on coral reefs and coastal sandy slopes. Mar. Geol. 2011, 289, 159–163. [Google Scholar] [CrossRef]
- Fritz, H.M.; Petroff, C.M.; Catalán, P.A.; Cienfuegos, R.; Winckler, P.; Kalligeris, N.; Weiss, R.; Barrientos, S.E.; Meneses, G.; Valderas-Bermejo, C.; et al. Field Survey of the 27 February 2010 Chile Tsunami. Pure Appl. Geophys. 2011, 168, 1989–2010. [Google Scholar] [CrossRef]
- Shuto, N. Numerical simulation of tsunamis-Its present and near future. Nat. Hazards 1991, 4, 171–191. [Google Scholar] [CrossRef]
- Li, L.; Qiu, Q.; Huang, Z. Numerical modeling of the morphological change in Lhok Nga, west banda aceh, during the 2004 Indian ocean tsunami: Understanding tsunami deposits using a forward modeling method. Nat. Hazards 2012, 64, 1549–1574. [Google Scholar] [CrossRef]
- Suppasri, A.; Imamura, F.; Koshimura, S. Effects of the rupture velocity of fault motion, ocean current and initial sea level on the transoceanic propagation of tsunami. Coast. Eng. J. 2010, 52, 107–132. [Google Scholar] [CrossRef]
- Ryan, K.J.; Geist, E.L.; Barall, M.; Oglesby, D.D. Dynamic models of an earthquake and tsunami offshore Ventura, California. Geophys. Res. Lett. 2015, 42, 6599–6606. [Google Scholar] [CrossRef]
- Maris, F.; Kitikidou, K. Tsunami hazard assessment in Greece-Review of numerical modeling (numerical simulations) from twelve different studies. Renew. Sust. Energ. Rev. 2016, 59, 1563–1569. [Google Scholar] [CrossRef]
- Qu, K.; Ren, X.; Kraatz, S. Numerical investigation of tsunami-like wave hydrodynamic characterics and its comparison with solitary wave. Appl. Ocean Res. 2017, 63, 36–48. [Google Scholar] [CrossRef]
- Kerr, A.M.; Baird, H.B. Natural barriers to natural disasters. Bioscience 2017, 57, 102–103. [Google Scholar] [CrossRef]
- Okal, E.; Fritz, H.M.; Synolakis, C.E.; Borrero, J.C. Field survey of the Samoa tsunami of 29 September. Seismol. Res. Lett. 2010, 81, 577–591. [Google Scholar] [CrossRef]
- Augustin, L.N.; Irish, J.L.; Lynett, P. Laboratory and numerical studies of wave damping by emergent and near-emergent wetland vegetation. Coast. Eng. 2009, 5, 332–340. [Google Scholar] [CrossRef]
- Yang, Z.; Tang, J.; Shen, Y. Numerical study for vegetation effects on coastal wave propagation by using nonlinear Boussinesq model. Appl. Ocean Res. 2018, 70, 32–40. [Google Scholar] [CrossRef]
- Tanaka, N.; Ogino, K. Comparison of reduction of tsunami fluid force and additional force due to impact and accumulation after collision of tsunami-produced driftwood from a coastal forest with houses during the Great East Japan tsunami. Landscape Ecol. Eng. 2017, 13, 287–304. [Google Scholar] [CrossRef]
- Feagin, R.A.; Mukherjee, N.; Shanker, S.; Baird, A.H.; Cinner, J.; Kerr, A.M.; Koedam, N.; Sridhar, A.; Arthur, R.; Jayatissa, L.P.; et al. Shelter from the storm? Use and misuse of coastal vegetation bioshields for managing natural disasters. Conserv. Lett. 2010, 3, 1–11. [Google Scholar] [CrossRef]
- Bayas, J.C.L.; Marohn, C.; Dercon, G.; Dewi, S.; Piepho, H.P.; Joshi, L.; Noordwijk, M.V.; Cadisch, G. Influence of coastal vegetation on the 2004 tsunami wave impact in west Aceh. Proc. Natl. Acad. Sci. USA 2011, 108, 18612–18617. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, N.; Nandasena, N.A.K.; Jinadasa, K.S.B.N.; Sasaki, Y.; Tanimoto, K.; Mowjood, M.I.M. Developing effective vegetation bioshield for tsunami protection. J. Civ. Environ. Eng. Syst. 2009, 26, 163–180. [Google Scholar] [CrossRef]
- Thuy, N.B.; Tanaka, N.; Tanimoto, K. Tsunami mitigation by coastal vegetation considering the effect of tree breaking. J. Coast. Conserv. 2012, 16, 111–121. [Google Scholar] [CrossRef]
- Iimura, K.; Tanaka, N. Numerical simulation estimating effects of tree density distribution in coastal forest on tsunami mitigation. Ocean Eng. 2012, 54, 223–232. [Google Scholar] [CrossRef]
- Yang, Y.Q.; Irish, J.L.; Weiss, R. Impact of patchy vegetation on tsunami dynamics. Waterw. Port Coastal Ocean Eng. 2017, 143, 04017005. [Google Scholar] [CrossRef]
- Tanaka, N.; Yasuda, S.; Iimura, K.; Yagisawa, J. Combined effects of coastal forest and sea embankment on reducing the washout region of houses in the Great East Japan tsunami. J. Hydro-Environ. Res. 2014, 8, 270–280. [Google Scholar] [CrossRef]
- Mascarenhas, A.; Jayakumar, S. An environmental perspective of the post-tsunami scenario along the coast of Tamil Nadu, India: Role of sand dunes and forests. J. Environ. Manag. 2008, 89, 24–34. [Google Scholar] [CrossRef]
- Tanimoto, K.; Tanaka, N.; Thuy, N.B.; Nandasena, N.A.K.; Iimura, K. Effect of open gap in coastal forest on tsunami run-up—investigation by 2-dimensional numerical simulation. Ocean Eng. 2008, 24, 87–92. (In Japanese) [Google Scholar]
- Thuy, N.B.; Tanimoto, K.; Tanaka, N.; Harada, K.; Iimura, K. Effect of open gap in coastal forest on tsunami run-up-investigations by experiment and numerical simulation. Ocean Eng. 2009, 36, 1258–1269. [Google Scholar] [CrossRef]
- Nandasena, N.A.K.; Sasaki, Y.; Tanaka, N. Modeling field observations of the 2011 Great East Japan tsunami: Efficacy of artificial and natural structures on tsunami mitigation. Coast. Eng. 2012, 67, 1–13. [Google Scholar] [CrossRef]
- Zhang, M.; Li, C.; Shen, Y. Depth-averaged modeling of free surface flow in open channels with emerged and submerged vegetation. Appl. Math. Model. 2013, 37, 540–553. [Google Scholar] [CrossRef]
- Liang, Q.; Borthwick, A.G.L. Adaptive quadtree simulation of shallow flows with wet-dry fronts over complex topography. Comput. Fluids 2009, 38, 221–234. [Google Scholar] [CrossRef]
- Brufau, P.; García-Navarro, P.; Vázquez-Cendón, M.E. Zero mass error using unsteady wetting-drying conditions in shallow flows over dry irregular topography. Int. J. Numer. Methods Fluids 2004, 45, 1047–1082. [Google Scholar] [CrossRef]
- Synolakis, C.E. The run-up of long waves. Ph D Thesis, California Institute of Technology, Pasadena, CA, USA, January 1986. [Google Scholar]
- Wu, W.; Marsooli, R. A depth-averaged 2D shallow water model for breaking and non-breaking long waves affected by rigid vegetation. J. Hydraul. Res. 2012, 50, 558–575. [Google Scholar] [CrossRef]
- Tang, J.; Causon, D.; Mingham, C.; Qian, L. Numerical study of vegetation damping effects on solitary wave run-up using the nonlinear shallow water equations. Coast. Eng. 2013, 75, 21–28. [Google Scholar] [CrossRef]



















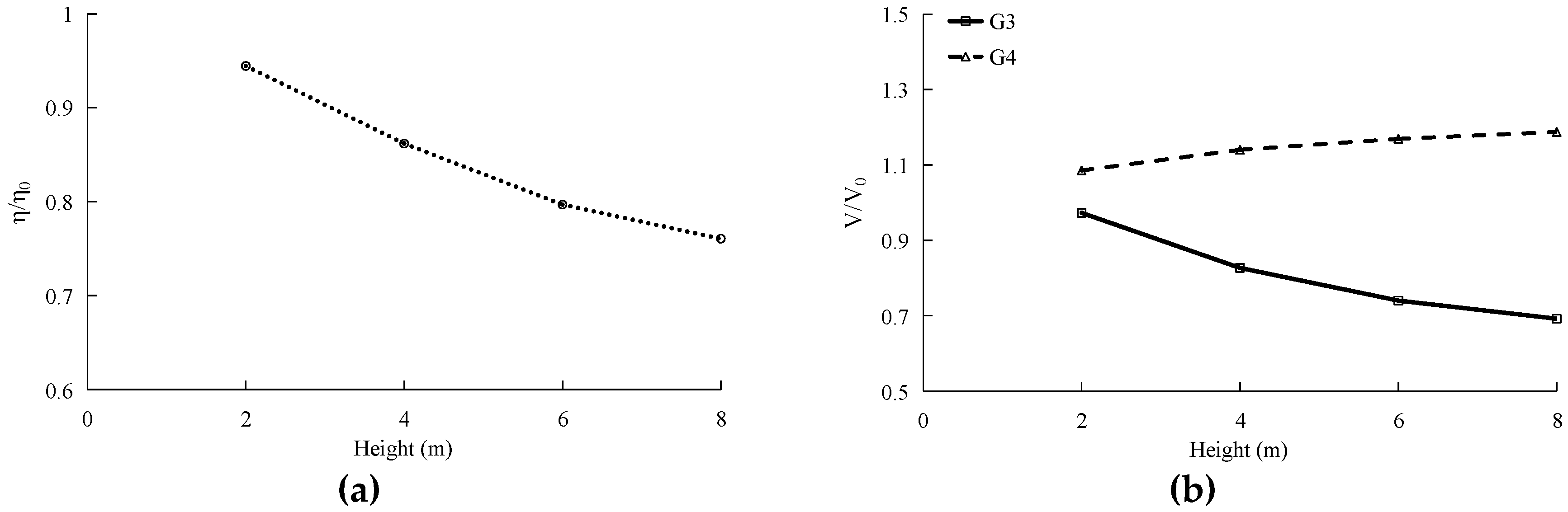
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Zhang, M.; Xu, T.; Tang, J. Numerical Investigations of Tsunami Run-Up and Flow Structure on Coastal Vegetated Beaches. Water 2018, 10, 1776. https://doi.org/10.3390/w10121776
Zhang H, Zhang M, Xu T, Tang J. Numerical Investigations of Tsunami Run-Up and Flow Structure on Coastal Vegetated Beaches. Water. 2018; 10(12):1776. https://doi.org/10.3390/w10121776
Chicago/Turabian StyleZhang, Hongxing, Mingliang Zhang, Tianping Xu, and Jun Tang. 2018. "Numerical Investigations of Tsunami Run-Up and Flow Structure on Coastal Vegetated Beaches" Water 10, no. 12: 1776. https://doi.org/10.3390/w10121776
APA StyleZhang, H., Zhang, M., Xu, T., & Tang, J. (2018). Numerical Investigations of Tsunami Run-Up and Flow Structure on Coastal Vegetated Beaches. Water, 10(12), 1776. https://doi.org/10.3390/w10121776



