A Method for Determining the Discharge of Closed-End Furrow Irrigation Based on the Representative Value of Manning’s Roughness and Field Mean Infiltration Parameters Estimated Using the PTF at Regional Scale
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experiments with Closed-End Furrow Irrigation
2.2. SIPAR_ID and WinSRFR Descriptions
2.3. Influence of Manning’s Roughness on Advance Trajectory and Performance Indicators of Furrow Irrigation
2.4. Functional Normalization of the Kostiakov Equation and PTF Development
2.5. Optimization of Inflow Discharge Based on Manning’s Roughness Representative Values and PTF to Estimate the Mean Infiltration Parameters
2.6. Criteria for Evaluation
3. Results and Discussion
3.1. Reliability Analysis of Field Mean Infiltration Parameters and Manning’s Roughness
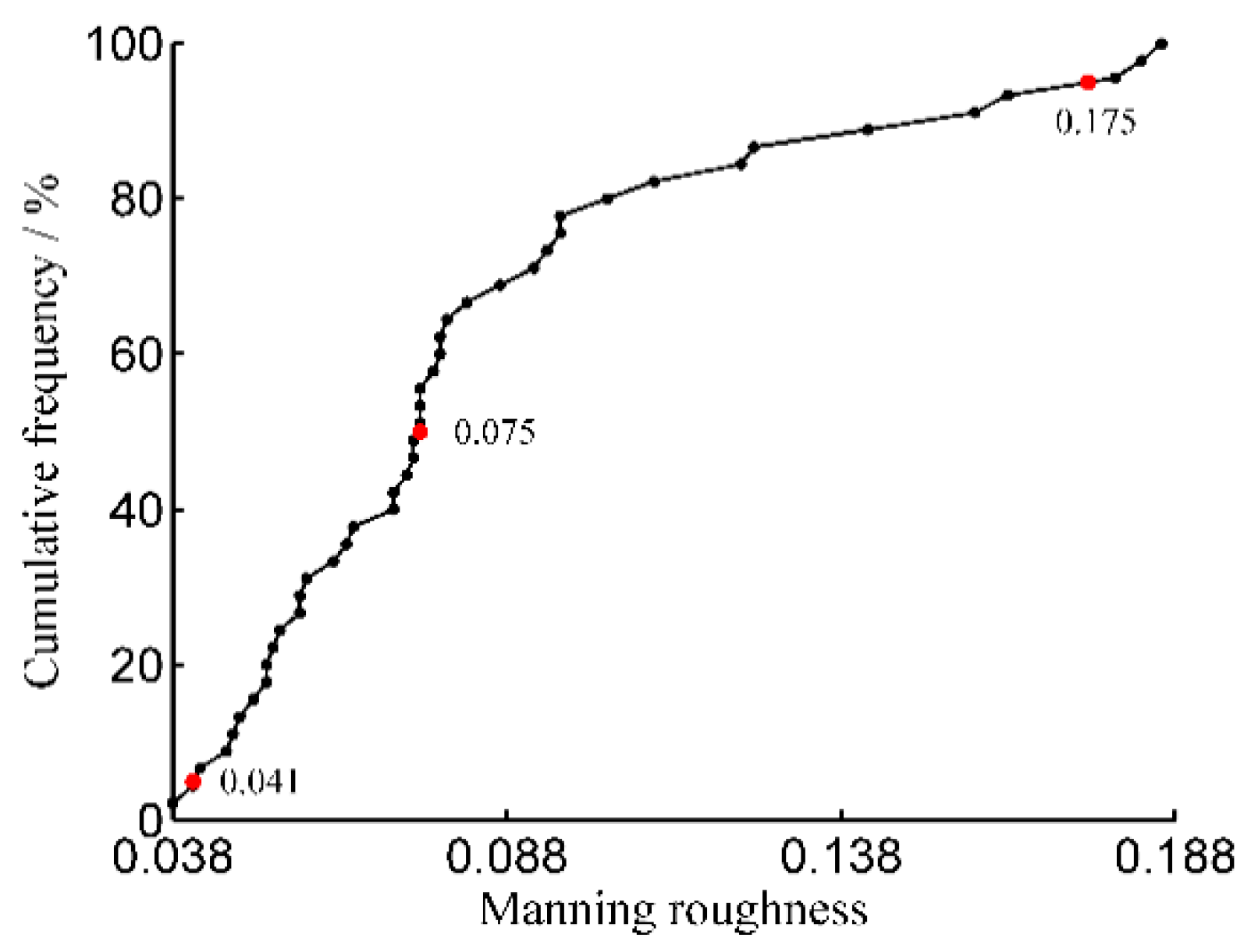
3.2. Evaluation of the Influence of Manning’s Roughness on Advance Trajectory and Irrigation Performance, and the Determination of its Representative Value in a Maize Field
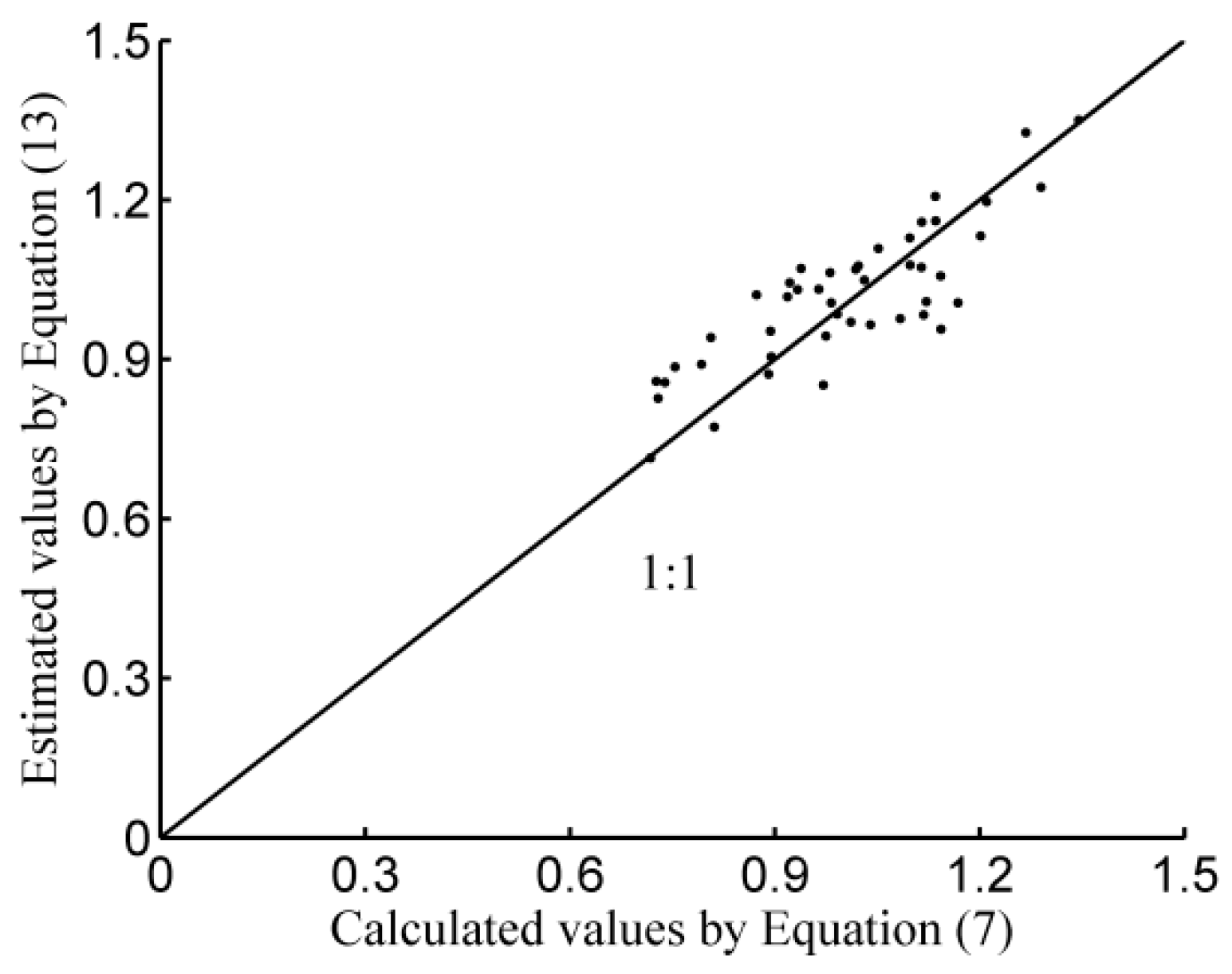
3.3. Establishment of the Normalization Function and PTF and Verification
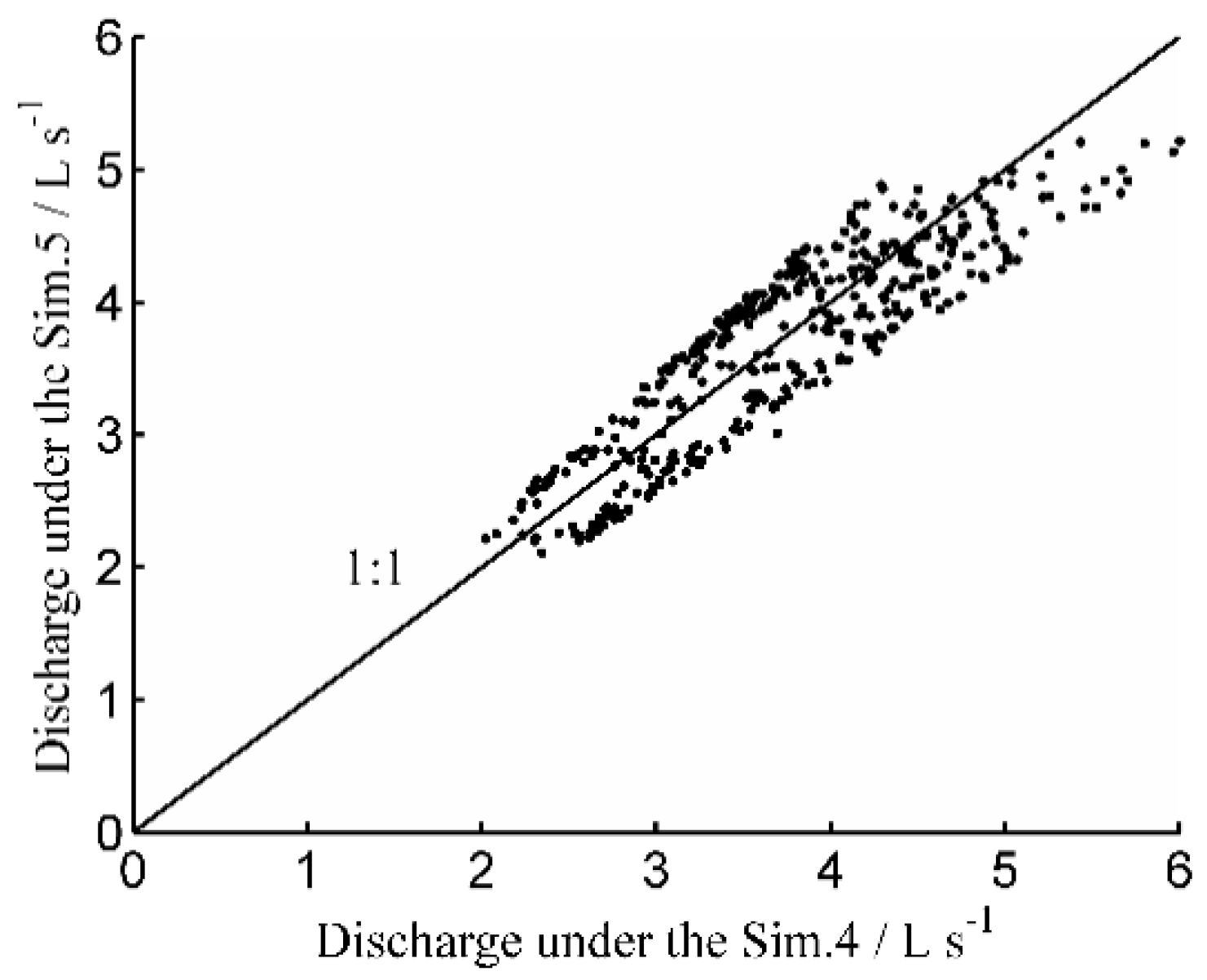
3.4. Reliability Verification of the Proposed Method for Determining the Inflow Discharge at a Regional Scale
3.5. General Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Akbari, M.; Gheysari, M.; Mostafazadeh-Fard, B.; Shayannejad, M. Surface irrigation simulation-optimization model based on meta-heuristic algorithms. Agric. Water Manag. 2018, 201, 46–57. [Google Scholar] [CrossRef]
- Smith, R.J.; Uddin, M.J.; Gillies, M.H. Estimating irrigation duration for high performance furrow irrigation on cracking clay soils. Agric. Water Manag. 2018, 206, 78–85. [Google Scholar] [CrossRef]
- Bautista, E.; Clemmens, A.J.; Strelkoff, T.S.; Schlegel, J. Modern analysis of surface irrigation systems with WinSRFR. Agric. Water Manag. 2009, 96, 1146–1154. [Google Scholar] [CrossRef]
- Gillies, M.H.; Smith, R.J. SISCO—Surface irrigation simulation calibration and optimisation. Irrig. Sci. 2015, 33, 339–355. [Google Scholar] [CrossRef]
- Salahou, M.K.; Jiao, X.Y.; Lü, H.S. Border irrigation performance with distance-based cut-off. Agric. Water Manag. 2018, 201, 27–37. [Google Scholar] [CrossRef]
- Miao, Q.F.; Shi, H.B.; Goncalves, J.M.; Pereira, L.S. Field assessment of basin irrigation performance and water saving in Hetao, Yellow River basin: Issues to support irrigation systems modernization. Biosyst. Eng. 2015, 136, 102–116. [Google Scholar] [CrossRef]
- Strelkoff, T.S.; Clemmens, A.J.; Bautista, E. Estimation of soil and crop hydraulic properties. J. Irrig. Drain. Eng. ASCE 2009, 135, 537–555. [Google Scholar] [CrossRef]
- Bautista, E.; Clemmens, A.J.; Strelkoff, T.S. Structured application of the two-point method for the estimation of infiltration parameters in surface irrigation. J. Irrig. Drain. Eng. ASCE 2009, 135, 566–578. [Google Scholar] [CrossRef]
- Chow, V.T. Open Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Li, Z.; Zhang, J. Calculation of field Manning’s roughness coefficient. Agric. Water Manag. 2001, 49, 46–57. [Google Scholar] [CrossRef]
- Zhang, S.H.; Xu, D.; Li, Y.N.; Cai, L.G. An optimized inverse model used to estimate Kostiakov infiltration parameters and Manning’s roughness coefficient based on SGA and SRFR model: (I) establishment. J. Hydraul. Eng. 2006, 37, 1297–1302. (In Chinese) [Google Scholar]
- Bautista, E.; Clemmens, A.J.; Strelkoff, T.S.; Niblack, M. Analysis of surface irrigation systems with WinSRFR—Example application. Agric. Water Manag. 2009, 96, 1162–1169. [Google Scholar] [CrossRef]
- Anwar, A.A.; Ahmad, W.; Bhatti, M.T.; Ul Haq, Z. The potential of precision surface irrigation in the Indus basin irrigation system. Irrig. Sci. 2016, 34, 379–396. [Google Scholar] [CrossRef]
- Eldeiry, A.; García, L.; Ei-Zaher, A.S.A.; Kiwan, M.E. Furrow irrigation system design for clay soils in arid regions. Appl. Eng. Agric. 2005, 21, 411–420. [Google Scholar] [CrossRef]
- Sánchez, C.A.; Zerihun, D.; Farrell-Poe, K.L. Management guidelines for efficient irrigation of vegetables using closed-end level furrows. Agric. Water Manag. 2009, 96, 43–52. [Google Scholar] [CrossRef]
- Reddy, M.; Jumaboev, K.; Matyakubov, B.; Eshmuratov, D. Evaluation of furrow irrigation practices in Fergana Valley of Uzbekistan. Agric. Water Manag. 2013, 117, 133–144. [Google Scholar] [CrossRef]
- Morris, M.R.; Hussaina, A.; Gillies, M.H.; O’Halloran, N.J. Inflow rate and border irrigation performance. Agric. Water Manag. 2015, 155, 76–86. [Google Scholar] [CrossRef]
- Nie, W.B.; Huang, H.; Ma, X.Y.; Fei, L.J. Evaluation of closed-end border irrigation accounting for soil infiltration variability. J. Irrig. Drain. Eng. ASCE 2017, 143. [Google Scholar] [CrossRef]
- Nie, W.B.; Fei, L.J.; Ma, X.Y. Impact of infiltration parameters and Manning roughness on the advance trajectory and irrigation performance for closed-end furrows. Span. J. Agric. Res. 2014, 12, 1180–1191. [Google Scholar] [CrossRef]
- Gillies, M.H. Managing the Effect of Infiltration Variability on the Performance of Surface Irrigation. Ph.D. Thesis, University of Southern Queensland, Toowoomba, Queensland, Australia, 2008. [Google Scholar]
- Duan, R.; Fedler, C.B.; Borrelli, J. Field evaluation of infiltration models in lawn soils. Irrig. Sci. 2011, 29, 379–389. [Google Scholar] [CrossRef]
- Tarboton, K.C.; Wallender, W.W. Field-wide furrow infiltration variability. Trans. ASAE 1989, 32, 913–918. [Google Scholar] [CrossRef]
- Schwankl, L.J.; Raghuwanshi, N.S.; Wallender, W.W. Furrow irrigation performance under spatially varying conditions. J. Irrig. Drain. Eng. ASCE 2000, 126, 355–361. [Google Scholar] [CrossRef]
- Machiwal, D.; Jha, M.K.; Mal, B.C. Modelling infiltration and quantifying spatial soil variability in a wasteland of Kharagpur, India. Biosyst. Eng. 2006, 95, 569–582. [Google Scholar] [CrossRef]
- Zapata, N.; Playán, E. Elevation and infiltration in a level basin. I. Characterizing variability. Irrig. Sci. 2018, 19, 155–164. [Google Scholar] [CrossRef]
- Zeleke, T.B.; Si, B.C. Characterizing scale-dependent spatial relationships between soil properties using multifractal techniques. Geoderma 2006, 134, 440–452. [Google Scholar] [CrossRef]
- Mubarak, I.; Jaramillo, R.A.; Mailhol, J.C.; Ruelle, P.; Khaledian, M.; Vauclin, M. Spatial analysis of soil surface hydraulic properties: Is infiltration method dependent? Agric. Water Manag. 2010, 97, 1517–1526. [Google Scholar] [CrossRef]
- Bautista, E.; Wallender, W.W. Spatial variability of infiltration in furrows. Trans. ASAE 1985, 28, 1846–1851. [Google Scholar] [CrossRef]
- Playán, E.; Rodriguez, J.A.; García-Navarro, P. Simulation model for level furrows. I: Analysis of field experiments. J. Irrig. Drain. Eng. ASCE 2004, 130, 106–112. [Google Scholar] [CrossRef]
- Khatri, K.L.; Smith, R.J. Toward a simple real-time control system for efficient management of furrow irrigation. Irrig. Drain. 2007, 56, 463–475. [Google Scholar] [CrossRef] [Green Version]
- Uddin, J.; Smith, R.J.; Gillies, M.H.; Moller, P.; Robson, D. Smart automated furrow irrigation of cotton. J. Irrig. Drain. Eng. ASCE 2018, 144. [Google Scholar] [CrossRef]
- Walk, W.R. Multilevel calibration of furrow infiltration and roughness. J. Irrig. Drain. Eng. ASCE 2005, 131, 129–136. [Google Scholar] [CrossRef]
- Nie, W.B.; Fei, L.J.; Ma, X.Y. Estimated infiltration parameters and manning roughness in border irrigation. Irrig. Drain. 2012, 61, 231–239. [Google Scholar]
- Philip, J.R. The theory of infiltration: 1. The infiltration equation and its solution. Soil Sci. 1957, 83, 345–357. [Google Scholar] [CrossRef]
- Rodríguez, J.A.; Martos, J.C. SIPAR_ID: Freeware for surface irrigation parameter identification. Environ. Model. Softw. 2010, 25, 1487–1488. [Google Scholar] [CrossRef]
- Etedail, H.R.; Ebrahimian, H.; Abbasi, F.; Liaghat, A. Evaluating models for the estimation of furrow irrigation infiltration and roughness. Span. J. Agric. Res. 2011, 9, 641–649. [Google Scholar] [Green Version]
- Kamali, P.; Ebrahimian, H.; Parsinejad, M. Estimation of Manning roughness coefficient for vegetated furrows. Irrig. Sci. 2018. [Google Scholar] [CrossRef]
- Wosten, J.H.M.; van Genuchten, M.T. Using texture and other soil properties to predict the unsaturated soil hydraulic functions. Soil Sci. Soc. Am. J. 1988, 52, 1762–1770. [Google Scholar] [CrossRef]
- Ghorbani, D.S.H.; Mahdi, H. Estimating soil water infiltration parameters using pedotransfer functions. Int. Assoc. Sci. Hydro. Bull. 2015, 61, 1477–1488. [Google Scholar] [CrossRef]
- Nie, W.B.; Ma, X.Y.; Fei, L.J. Evaluation of infiltration models and variability of soil infiltration properties at multiple scales. Irrig. Drain. 2017, 66, 589–599. [Google Scholar] [CrossRef]
- Chen, B.; Ouyang, Z.; Sun, Z.; Wu, L.; Li, F. Evaluation on the potential of improving border irrigation performance through border dimensions optimization: A case study on the irrigation districts along the lower Yellow River. Irrig. Sci. 2013, 31, 715–728. [Google Scholar] [CrossRef]
- Alvarez, J.A.R. Estimation of advance and infiltration equations in furrow irrigation for untested discharges. Agric. Water Manag. 2003, 60, 227–239. [Google Scholar] [CrossRef]
- Amer, A.M. Effects of water infiltration and storage in cultivated soil on surface irrigation. Agric. Water Manag. 2011, 98, 815–822. [Google Scholar] [CrossRef]
- Burguete, J.; Zapata, N.; García-Navarro, P.; Maïkaka, M.; Playán, E.; Murillo, J. Fertigation in furrows and level furrow systems. I: Model description and numerical tests. J. Irrig. Drain. Eng. ASCE 2009, 135, 401–412. [Google Scholar] [CrossRef]
- Holzapfel, E.A.; Jara, J.; Zuniga, C.; Marino, M.A.; Paredes, J.; Billib, M. Infiltration parameters for furrow irrigation. Agric. Water Manag. 2004, 68, 19–32. [Google Scholar] [CrossRef]
- Bautista, E. Effect of infiltration modeling approach on operational solutions for furrow irrigation. J. Irrig. Drain. Eng. ASCE 2016, 142. [Google Scholar] [CrossRef]
- Katopodes, N.D.; Tang, J.H.; Clemmens, A.J. Estimation of surface irrigation parameters. J. Irrig. Drain. Eng. ASCE 1990, 116, 676–696. [Google Scholar] [CrossRef]
- Tillotson, P.M.; Nielsen, D.R. Scale factors in soil science. Soil Sci. Soc. Am. J. 1984, 48, 953–959. [Google Scholar] [CrossRef]
- Wang, W.H.; Jiao, X.Y.; Peng, S.Z.; Chen, X.D. Sensitivity analysis of border irrigation performance using robust design theory. Trans. CSAE 2010, 26, 37–42. (In Chinese) [Google Scholar]
- Wattenburger, P.L.; Clyma, W. Level basin design and management in the absence of water control. Part I: Evaluation of completion-of-advance irrigation. Trans. ASAE 1989, 32, 838–843. [Google Scholar] [CrossRef]
- Pereira, L.S.; Goncalves, J.M.; Dong, B.; Mao, Z.; Fang, S.X. Assessing basin irrigation and scheduling strategies for saving irrigation water and controlling salinity in the upper Yellow River Basin, China. Agric. Water Manag. 2007, 93, 109–122. [Google Scholar] [CrossRef]
- Moriasi, D.; Arnold, J.; Liew, M.W.V.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Jacovides, C.P.; Kontoyiannis, H. Statistical procedures for the evaluation of evapotranspiration computing models. Agric. Water Manag. 1995, 27, 365–371. [Google Scholar] [CrossRef]
- Trout, T.J. Furrow irrigation erosion and sedimentation: On-field distribution. Trans. ASAE 1996, 39, 1717–1723. [Google Scholar] [CrossRef]
- Jaynes, D.B.; Clemmens, A.J. Accounting for spatially variable infiltration in border irrigation models. Water Resour. Res. 1986, 22, 1257–1262. [Google Scholar] [CrossRef]
- Oyonarte, N.A.; Mateos, L.; Palomo, M.J. Infiltration variability in furrow irrigation. J. Irrig. Drain. Eng. ASCE 2002, 128, 26–33. [Google Scholar] [CrossRef]
- Khatri, K.L.; Smith, R.J. Real-time prediction of soil infiltration characteristics for the management of furrow irrigation. Irrig. Sci. 2006, 25, 33–43. [Google Scholar] [CrossRef]
- Bai, M.J.; Xu, D.; Li, Y.N.; Li, J.S. Evaluating spatial and temporal variability of infiltration on field-scale under surface irrigation. J. Soil Water Conserv. 2005, 19, 120–123. (In Chinese) [Google Scholar]




| No. | q (L s−1) | t (min) | L (m) | BW (m) | FD (m) | FS (m) | S0 (‰) | γd (g cm−3) | θ0 (%) | Soil Particle Proportions (%) | Soil Texture | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cl | Si | Sa | |||||||||||
| F1 | 2.95 | 42.0 | 90 | 0.28 | 0.16 | 0.68 | 2.5 | 1.33 | 10.7 | 28.6 | 29.5 | 41.9 | Loamy clay |
| F2 | 2.42 | 34.0 | 82 | 0.15 | 0.15 | 0.60 | 1.9 | 1.40 | 11.0 | 29.7 | 29.3 | 41.0 | Loamy clay |
| F3 | 2.95 | 31.0 | 88 | 0.25 | 0.14 | 0.70 | 1.7 | 1.38 | 12.8 | 28.0 | 32.7 | 39.3 | Loamy clay |
| F4 | 2.69 | 59.0 | 115 | 0.27 | 0.13 | 0.65 | 2.7 | 1.26 | 10.7 | 27.8 | 29.0 | 43.2 | Loamy clay |
| F5 | 2.51 | 40.0 | 86 | 0.26 | 0.15 | 0.65 | 1.5 | 1.34 | 16.1 | 32.8 | 34.7 | 32.5 | Loamy clay |
| F6 | 2.46 | 29.0 | 88 | 0.25 | 0.16 | 0.63 | 2.9 | 1.32 | 13.3 | 32.7 | 32.5 | 34.8 | Loamy clay |
| F7 | 3.31 | 38.0 | 97 | 0.26 | 0.12 | 0.67 | 1.9 | 1.25 | 10.9 | 20.7 | 33.2 | 46.1 | Clay loam |
| F8 | 2.09 | 51.0 | 89 | 0.20 | 0.15 | 0.63 | 2.3 | 1.25 | 12.1 | 25.0 | 33.4 | 41.6 | Clay loam |
| F9 | 2.33 | 34.0 | 86 | 0.24 | 0.12 | 0.60 | 1.8 | 1.35 | 15.5 | 30.1 | 33.2 | 36.7 | Loamy clay |
| F10 | 2.29 | 58.0 | 93 | 0.29 | 0.12 | 0.68 | 2.4 | 1.40 | 13.5 | 27.0 | 34.5 | 38.5 | Loamy clay |
| F11 | 2.78 | 53.0 | 89 | 0.21 | 0.13 | 0.70 | 2.3 | 1.26 | 14.9 | 30.3 | 31.2 | 38.5 | Loamy clay |
| F12 | 2.12 | 35.0 | 87 | 0.28 | 0.20 | 0.70 | 4.3 | 1.49 | 16.0 | 35.6 | 33.4 | 31.0 | Loamy clay |
| F13 | 4.43 | 17.0 | 136 | 0.27 | 0.13 | 0.78 | 3.0 | 1.35 | 13.7 | 29.8 | 31.6 | 38.6 | Loamy clay |
| F14 | 3.53 | 53.0 | 128 | 0.20 | 0.19 | 0.62 | 3.3 | 1.23 | 9.1 | 20.5 | 33.8 | 45.7 | Clay loam |
| F15 | 3.10 | 40.0 | 104 | 0.25 | 0.12 | 0.65 | 2.3 | 1.36 | 13.9 | 30.2 | 34.8 | 35.0 | Loamy clay |
| F16 | 2.98 | 53.0 | 113 | 0.25 | 0.17 | 0.75 | 2.3 | 1.28 | 16.2 | 28.2 | 32.8 | 39.0 | Loamy clay |
| F17 | 3.40 | 39.0 | 127 | 0.27 | 0.10 | 0.62 | 3.3 | 1.34 | 17.0 | 28.0 | 31.8 | 40.2 | Loamy clay |
| F18 | 3.98 | 29.0 | 134 | 0.21 | 0.13 | 0.65 | 3.4 | 1.41 | 14.8 | 30.9 | 35.8 | 33.3 | Loamy clay |
| F19 | 2.09 | 40.0 | 84 | 0.15 | 0.15 | 0.65 | 2.1 | 1.46 | 16.7 | 29.6 | 32.2 | 38.2 | Loamy clay |
| F20 | 2.16 | 34.0 | 92 | 0.23 | 0.13 | 0.63 | 2.0 | 1.38 | 14.0 | 28.0 | 32.0 | 40.0 | Loamy clay |
| F21 | 2.70 | 43.0 | 106 | 0.23 | 0.12 | 0.60 | 2.1 | 1.26 | 15.4 | 25.4 | 33.0 | 41.6 | Loamy clay |
| F22 | 2.95 | 49.0 | 114 | 0.26 | 0.13 | 0.62 | 0.9 | 1.40 | 11.4 | 27.4 | 30.6 | 42.0 | Loamy clay |
| F23 | 2.17 | 66.0 | 107 | 0.26 | 0.12 | 0.70 | 2.6 | 1.39 | 11.4 | 22.3 | 33.8 | 43.9 | Clay loam |
| F24 | 2.43 | 60.0 | 106 | 0.19 | 0.15 | 0.70 | 1.2 | 1.38 | 11.3 | 27.4 | 29.8 | 42.8 | Loamy clay |
| F25 | 2.85 | 43.0 | 93 | 0.25 | 0.17 | 0.65 | 3.6 | 1.27 | 13.3 | 28.2 | 30.9 | 40.9 | Loamy clay |
| F26 | 2.20 | 47.0 | 82 | 0.28 | 0.15 | 0.68 | 4.1 | 1.30 | 12.3 | 30.5 | 31.3 | 38.2 | Loamy clay |
| F27 | 2.78 | 42.0 | 86 | 0.23 | 0.15 | 0.68 | 1.8 | 1.33 | 14.3 | 30.9 | 33.1 | 36.0 | Loamy clay |
| F28 | 2.97 | 25.0 | 87 | 0.19 | 0.12 | 0.65 | 2.6 | 1.33 | 14.2 | 30.0 | 31.7 | 38.3 | Loamy clay |
| F29 | 2.81 | 48.0 | 96 | 0.23 | 0.12 | 0.65 | 3.1 | 1.30 | 12.5 | 22.0 | 34.0 | 44.0 | Clay loam |
| F30 | 2.40 | 53.0 | 99 | 0.25 | 0.13 | 0.65 | 2.0 | 1.42 | 14.9 | 30.1 | 31.3 | 38.6 | Loamy clay |
| F31 | 3.53 | 17.0 | 97 | 0.20 | 0.15 | 0.62 | 1.9 | 1.37 | 16.7 | 32.8 | 32.2 | 35.0 | Loamy clay |
| F32 | 2.53 | 44.0 | 93 | 0.23 | 0.15 | 0.65 | 2.1 | 1.27 | 16.0 | 31.5 | 32.1 | 36.4 | Loamy clay |
| F33 | 4.43 | 21.0 | 118 | 0.22 | 0.12 | 0.60 | 1.8 | 1.40 | 17.7 | 30.1 | 36.3 | 33.6 | Loamy clay |
| F34 | 3.21 | 28.0 | 109 | 0.20 | 0.14 | 0.60 | 2.9 | 1.38 | 14.1 | 28.0 | 34.6 | 37.4 | Loamy clay |
| F35 | 3.51 | 35.0 | 107 | 0.16 | 0.12 | 0.60 | 2.4 | 1.43 | 14.9 | 34.6 | 31.4 | 34.0 | Loamy clay |
| F36 | 2.31 | 35.0 | 93 | 0.18 | 0.15 | 0.63 | 1.8 | 1.37 | 14.1 | 35.2 | 30.2 | 34.6 | Loamy clay |
| F37 | 3.24 | 42.0 | 116 | 0.18 | 0.13 | 0.64 | 2.5 | 1.34 | 12.0 | 27.3 | 33.4 | 39.3 | Loamy clay |
| F38 | 2.33 | 58.0 | 104 | 0.20 | 0.13 | 0.63 | 0.8 | 1.30 | 15.6 | 31.6 | 32.9 | 35.5 | Loamy clay |
| F39 | 2.61 | 39.5 | 86 | 0.20 | 0.15 | 0.62 | 1.7 | 1.31 | 16.3 | 32.0 | 33.0 | 35.0 | Loamy clay |
| F40 | 2.50 | 39.0 | 94 | 0.15 | 0.16 | 0.61 | 1.3 | 1.33 | 15.3 | 31.3 | 31.3 | 37.4 | Loamy clay |
| F41 | 2.51 | 35.5 | 83 | 0.25 | 0.15 | 0.68 | 1.9 | 1.42 | 11.6 | 23.2 | 36.0 | 40.8 | Clay loam |
| F42 | 2.20 | 51.0 | 96 | 0.19 | 0.12 | 0.60 | 2.7 | 1.35 | 11.9 | 30.4 | 32.1 | 37.5 | Loamy clay |
| F43 | 2.24 | 35.0 | 92 | 0.20 | 0.15 | 0.60 | 0.8 | 1.46 | 16.4 | 32.7 | 35.2 | 32.1 | Loamy clay |
| F44 | 2.90 | 27.0 | 89 | 0.20 | 0.15 | 0.65 | 4.5 | 1.43 | 16.4 | 32.2 | 32.8 | 35.0 | Loamy clay |
| F45 | 2.54 | 42.0 | 84 | 0.23 | 0.15 | 0.64 | 2.6 | 1.39 | 11.4 | 27.8 | 31.3 | 40.9 | Loamy clay |
| Mean value | 98.8 | 0.23 | 0.14 | 0.65 | 2.4 | 1.35 | 13.9 | ||||||
| No. | Field Mean Infiltration Parameters | n | Fc | MAPRE (%) | ||
|---|---|---|---|---|---|---|
| A | k (mm h−α) | Advance Time | Water Depth | |||
| F1 | 0.756 | 147.37 | 0.142 | 1.10 | 5.1 | 7.2 |
| F2 | 0.642 | 129.67 | 0.096 | 1.03 | 10.3 | 5.9 |
| F3 | 0.434 | 102.39 | 0.075 | 0.93 | 5.4 | 6.2 |
| F4 | 0.443 | 125.26 | 0.103 | 1.13 | 4.0 | 13.9 |
| F5 | 0.521 | 103.75 | 0.123 | 0.89 | 4.1 | 8.2 |
| F6 | 0.435 | 98.06 | 0.038 | 0.89 | 5.1 | 17.7 |
| F7 | 0.417 | 137.34 | 0.042 | 1.27 | 4.5 | 10.3 |
| F8 | 0.464 | 135.56 | 0.079 | 1.21 | 3.2 | 7.0 |
| F9 | 0.735 | 138.07 | 0.074 | 1.04 | 4.4 | 7.5 |
| F10 | 0.438 | 128.51 | 0.078 | 1.17 | 2.9 | 14.5 |
| F11 | 0.605 | 137.04 | 0.158 | 1.11 | 4.6 | 8.1 |
| F12 | 0.223 | 66.83 | 0.057 | 0.72 | 6.0 | 15.3 |
| F13 | 0.673 | 117.65 | 0.110 | 0.92 | 5.6 | 15.1 |
| F14 | 0.561 | 160.79 | 0.048 | 1.34 | 6.1 | 9.4 |
| F15 | 0.550 | 95.71 | 0.186 | 0.81 | 6.5 | 10.7 |
| F16 | 0.415 | 101.50 | 0.087 | 0.94 | 5.8 | 16.0 |
| F17 | 0.375 | 96.81 | 0.052 | 0.92 | 6.4 | 16.1 |
| F18 | 0.613 | 89.71 | 0.071 | 0.73 | 7.1 | 10.3 |
| F19 | 0.209 | 82.29 | 0.082 | 0.89 | 6.0 | 7.9 |
| F20 | 0.452 | 107.12 | 0.064 | 0.96 | 4.6 | 3.0 |
| F21 | 0.374 | 117.06 | 0.074 | 1.12 | 4.6 | 10.0 |
| F22 | 0.275 | 106.68 | 0.041 | 1.10 | 6.3 | 23.6 |
| F23 | 0.254 | 108.47 | 0.053 | 1.14 | 4.0 | 13.2 |
| F24 | 0.468 | 118.16 | 0.062 | 1.05 | 2.2 | 9.2 |
| F25 | 0.258 | 115.09 | 0.075 | 1.20 | 3.7 | 8.7 |
| F26 | 0.211 | 105.29 | 0.065 | 1.14 | 4.6 | 14.8 |
| F27 | 0.308 | 108.10 | 0.096 | 1.08 | 3.7 | 17.9 |
| F28 | 0.562 | 104.44 | 0.077 | 0.87 | 7.2 | 8.3 |
| F29 | 0.584 | 156.45 | 0.071 | 1.29 | 3.3 | 11.3 |
| F30 | 0.225 | 106.57 | 0.047 | 1.14 | 6.0 | 13.2 |
| F31 | 0.701 | 103.19 | 0.050 | 0.79 | 7.6 | 7.8 |
| F32 | 0.806 | 135.57 | 0.125 | 0.98 | 3.7 | 5.3 |
| F33 | 0.592 | 90.09 | 0.057 | 0.74 | 5.5 | 15.1 |
| F34 | 0.677 | 127.31 | 0.058 | 0.99 | 5.7 | 10.4 |
| F35 | 0.645 | 91.85 | 0.183 | 0.73 | 4.2 | 8.1 |
| F36 | 0.412 | 81.36 | 0.094 | 0.75 | 4.4 | 3.5 |
| F37 | 0.632 | 127.32 | 0.092 | 1.02 | 5.4 | 10.2 |
| F38 | 0.700 | 131.58 | 0.078 | 1.01 | 3.8 | 9.0 |
| F39 | 0.673 | 124.89 | 0.179 | 0.98 | 3.5 | 8.0 |
| F40 | 0.513 | 129.49 | 0.046 | 1.12 | 3.6 | 8.3 |
| F41 | 0.330 | 103.77 | 0.075 | 1.02 | 3.0 | 9.4 |
| F42 | 0.299 | 111.13 | 0.073 | 1.12 | 2.8 | 9.2 |
| F43 | 0.207 | 74.47 | 0.052 | 0.81 | 3.6 | 10.1 |
| F44 | 0.861 | 137.81 | 0.054 | 0.97 | 6.1 | 18.0 |
| F45 | 0.311 | 98.07 | 0.163 | 0.98 | 2.0 | 13.1 |
| Mean value | 0.485 | 113.68 | 0.085 | 1.00 | 4.8 | 10.8 |
| S0 (‰) | L (m) | Simulated Values of Y under Sim.4 | Simulated Values of Y under Sim.5 | ||||
|---|---|---|---|---|---|---|---|
| Min. | Max. | Mean | Min. | Max. | Mean | ||
| 1.0 | 80 | 0.87 | 0.98 | 0.93 (0.03) | 0.83 | 0.98 | 0.90 (0.05) |
| 105 | 0.83 | 0.97 | 0.89 (0.03) | 0.80 | 0.98 | 0.88 (0.05) | |
| 130 | 0.80 | 0.93 | 0.86 (0.03) | 0.80 | 0.96 | 0.86 (0.06) | |
| 2.5 | 80 | 0.87 | 0.98 | 0.93 (0.03) | 0.82 | 0.97 | 0.89 (0.05) |
| 105 | 0.85 | 0.96 | 0.90 (0.03) | 0.81 | 0.96 | 0.88 (0.05) | |
| 130 | 0.80 | 0.95 | 0.88 (0.03) | 0.81 | 0.97 | 0.87 (0.05) | |
| 4.0 | 80 | 0.82 | 0.96 | 0.93 (0.03) | 0.84 | 0.97 | 0.90 (0.05) |
| 105 | 0.85 | 0.95 | 0.90 (0.03) | 0.82 | 0.96 | 0.88 (0.05) | |
| 130 | 0.82 | 0.93 | 0.88 (0.03) | 0.80 | 0.94 | 0.87 (0.05) | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, W.-B.; Li, Y.-B.; Zhang, F.; Dong, S.-X.; Wang, H.; Ma, X.-Y. A Method for Determining the Discharge of Closed-End Furrow Irrigation Based on the Representative Value of Manning’s Roughness and Field Mean Infiltration Parameters Estimated Using the PTF at Regional Scale. Water 2018, 10, 1825. https://doi.org/10.3390/w10121825
Nie W-B, Li Y-B, Zhang F, Dong S-X, Wang H, Ma X-Y. A Method for Determining the Discharge of Closed-End Furrow Irrigation Based on the Representative Value of Manning’s Roughness and Field Mean Infiltration Parameters Estimated Using the PTF at Regional Scale. Water. 2018; 10(12):1825. https://doi.org/10.3390/w10121825
Chicago/Turabian StyleNie, Wei-Bo, Yi-Bo Li, Fan Zhang, Shu-Xin Dong, Heng Wang, and Xiao-Yi Ma. 2018. "A Method for Determining the Discharge of Closed-End Furrow Irrigation Based on the Representative Value of Manning’s Roughness and Field Mean Infiltration Parameters Estimated Using the PTF at Regional Scale" Water 10, no. 12: 1825. https://doi.org/10.3390/w10121825
APA StyleNie, W.-B., Li, Y.-B., Zhang, F., Dong, S.-X., Wang, H., & Ma, X.-Y. (2018). A Method for Determining the Discharge of Closed-End Furrow Irrigation Based on the Representative Value of Manning’s Roughness and Field Mean Infiltration Parameters Estimated Using the PTF at Regional Scale. Water, 10(12), 1825. https://doi.org/10.3390/w10121825




