Ranking of CMIP5 GCM Skills in Simulating Observed Precipitation over the Lower Mekong Basin, Using an Improved Score-Based Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. GCM Data
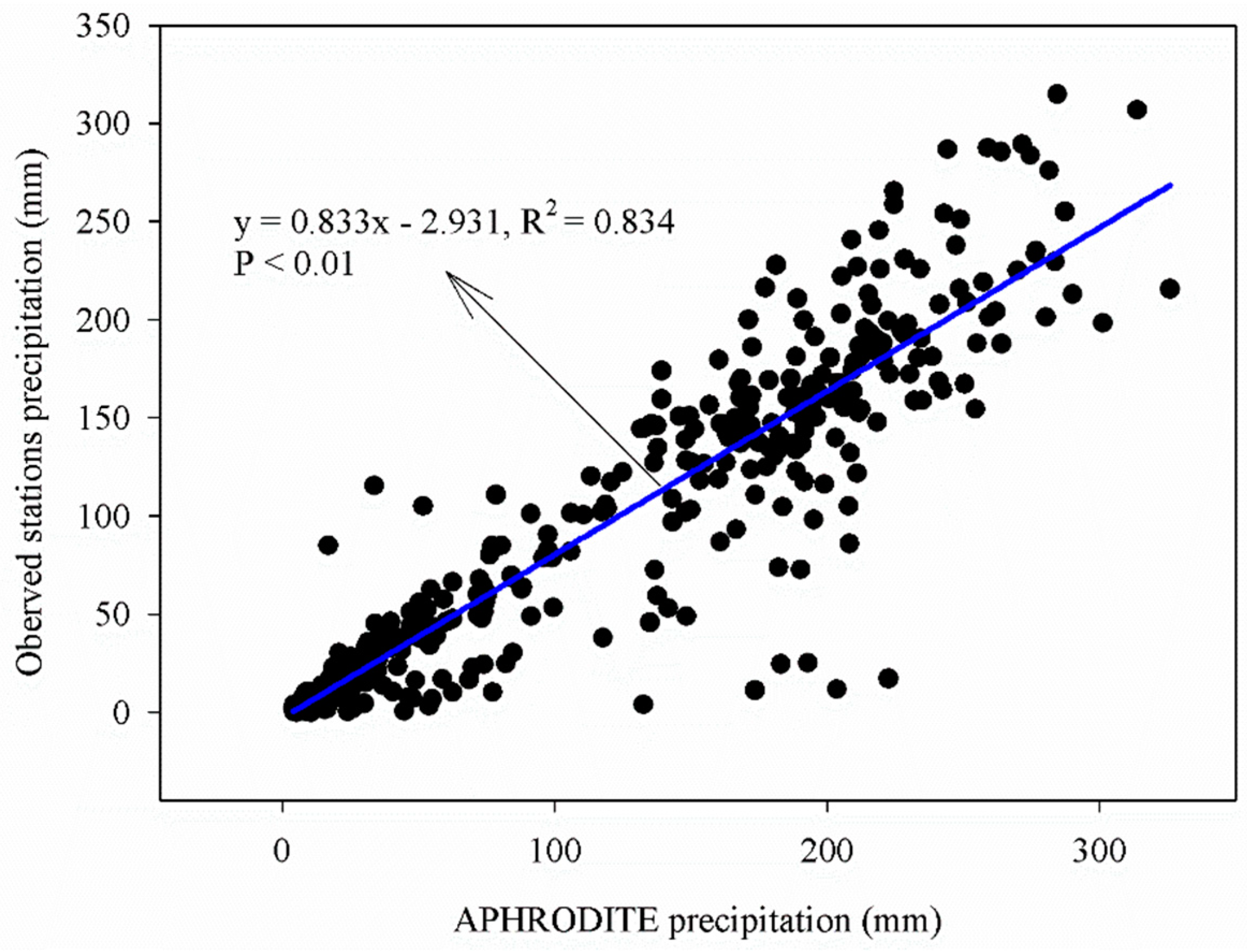
2.3. Precipitation Data
2.4. National Centers for Environmental Prediction (NCEP) Reanalysis Data
2.5. Methods
3. Results
3.1. Annual Cycle of Precipitation
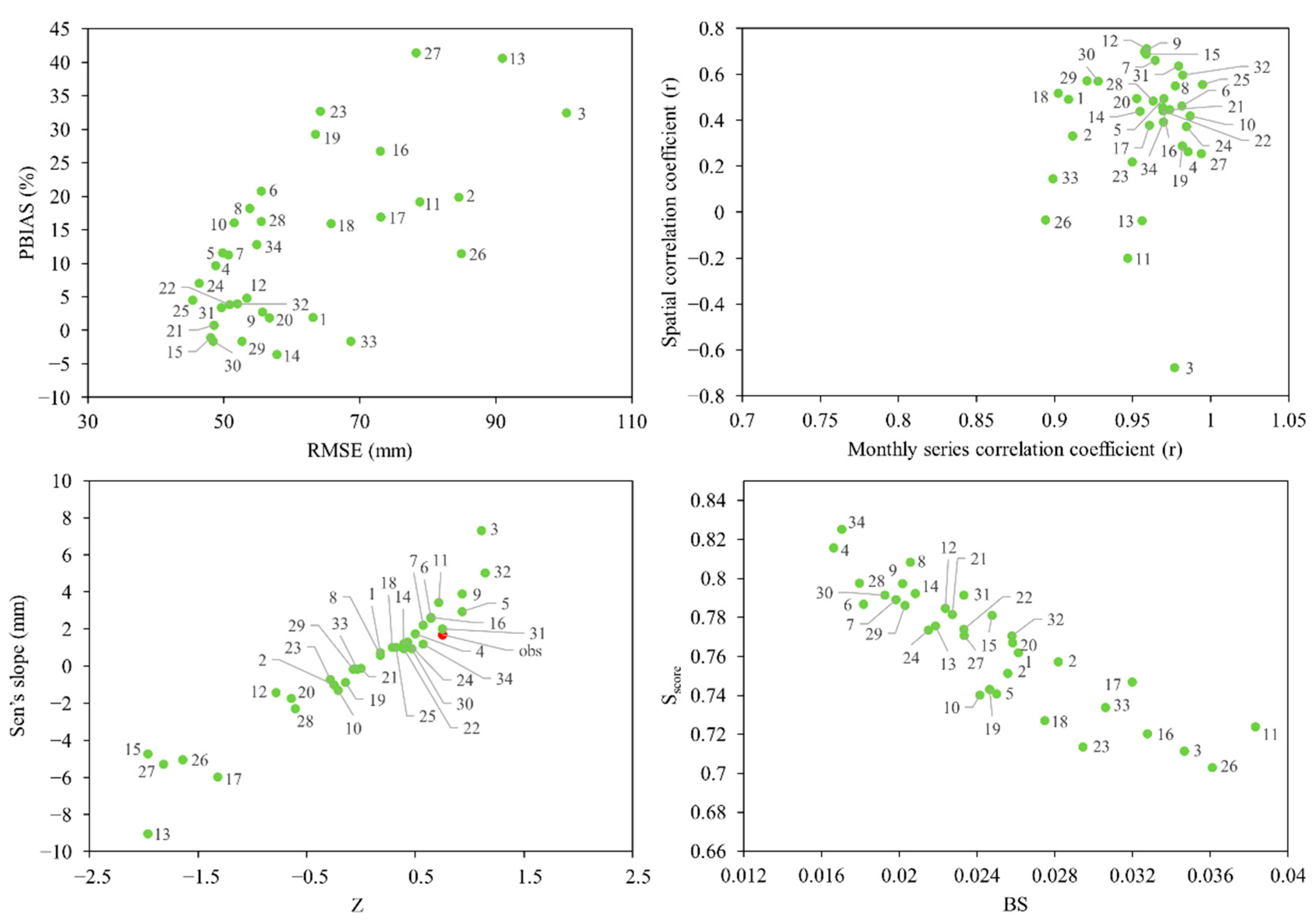
3.2. Characteristics of the Statistics of the Criteria
3.3. Comparison of Ranking Scores of the GCMs’ Performances by a Single Criterion
3.4. Overall Ranking Scores of the GCMs’ Performances by Multiple Criteria
3.5. Sensitivity Analysis of Ranking Scores of the GCMs’ Performances
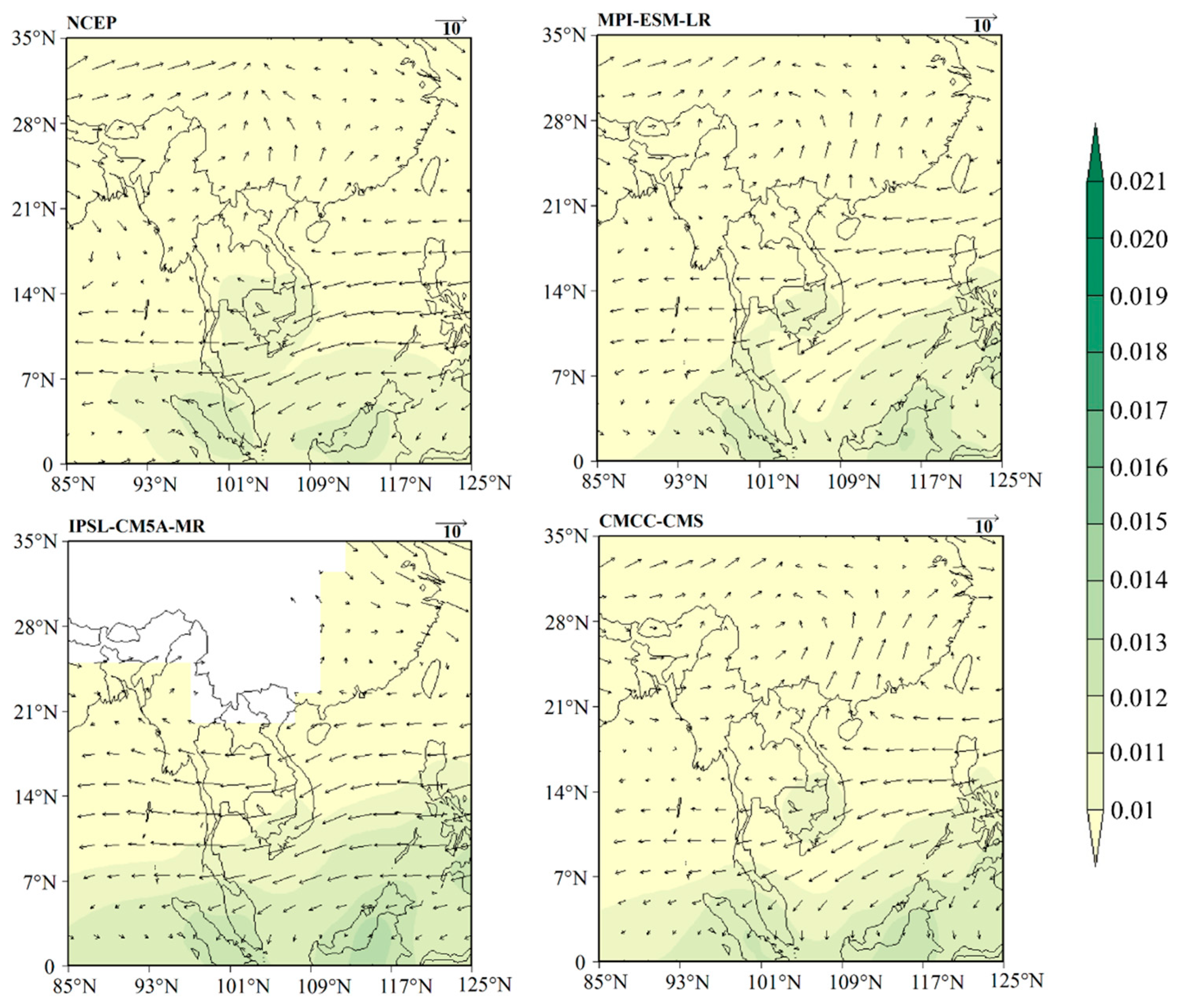
3.6. Atmospheric Circulation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Busuioc, A.; Chen, D.; Hellström, C. Performance of statistical downscaling models in GCM validation and regional climate change estimates: Application for Swedish precipitation. Int. J. Climatol. 2001, 21, 557–578. [Google Scholar] [CrossRef]
- Wilk, J.; Andersson, L.; Plermkamon, V. Hydrological impacts of forest conversion to agriculture in a large river basin in northeast Thailand. Hydrol. Process. 2001, 15, 2729–2748. [Google Scholar] [CrossRef]
- Alavian, V.; Qaddumi, H.M.; Dickson, E.; Diez, S.M.; Danilenko, A.D.; Hirji, R.F.; Puz, G.; Pizarro, C.; Jacobsen, M.; Blankespoor, B. Water and Climate Change: Understanding the Risks and Making Climate-Smart Investment Decisions. Washington, D.C, the World Bank. 2009. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.734.5926&rep=rep1&type=pdf (accessed on 10 September 2018).
- IPCC Secretariat. Climate Change and Water: Technical Paper of The Intergovernmental Panel on Climate Change; Bates, B.C., Kundzewicz, Z.W., Wu, S., Palutikof, J.P., Eds.; IPCC: Geneva, Switzerland, 2008. [Google Scholar]
- Eastham, J.; Mpelasoka, F.; Mainuddin, M.; Ticehurst, C.; Dyce, P.; Hodgson, G.; Ali, R.; Kirby, M. Mekong River Basin Water Resources Assessment: Impacts of climate change, CSIRO: Water for a Healthy Country National Research Flagship, 2008. Available online: http://www.clw.csiro.au/publications/waterforahealthycountry/2008/wfhc-MekongWaterResourcesAssessment.pdf (accessed on 20 September 2018).
- 2030 WRG (2030 Water Resources Group). Charting Our Water Future: Economic Frameworks to Inform Decision-Making; McKinsey & Company: New York, NY, USA, 2009. [Google Scholar]
- Xu, Y.; Xu, C.H.; Gao, X.J.; Luo, Y. Projected changes in temperature and precipitation extremes over the Yangtze River basin of China in the 21st century. Quat. Int. 2009, 208, 44–52. [Google Scholar] [CrossRef]
- Ramesh, K.V.; Goswami, P. Assessing reliability of regional climate projections: The case of Indian monsoon. Sci. Rep. 2014, 4, 4071. [Google Scholar] [CrossRef] [PubMed]
- Sperber, K.R.; Annamalai, H.; Kang, I.S.; Kitoh, A.; Moise, A.; Turner, A.; Wang, B.; Zhou, T. The Asian summer monsoon: An intercomparison of CMIP5 vs. CMIP3 simulations of the late 20th century. Clim. Dynam. 2013, 41, 2711–2744. [Google Scholar] [CrossRef]
- Sillmann, J.; Kharin, V.V.; Zhang, X.; Zwiers, F.W.; Bronaugh, D. Climate extremes indices in the CMIP5 multimodel ensemble: Part 1. Model evaluation in the present climate. J. Geophys. Res.-Atmos. 2013, 118, 1716–1733. [Google Scholar] [CrossRef]
- Sun, Q.H.; Miao, C.Y.; Duan, Q.Y. Comparative analysis of CMIP3 and CMIP5 global climate models for simulating the daily mean, maximum, and minimum temperatures and daily precipitation over China. J. Geophys. Res.-Atmos. 2015, 120, 4806–4824. [Google Scholar] [CrossRef]
- Meher, J.K.; Das, L.; Akhter, J.; Benestad, R.E.; Mezghani, A. Performance of CMIP3 and CMIP5 GCMs to Simulate Observed Rainfall Characteristics over the Western Himalayan Region. J. Clim. 2017, 30, 7777–7799. [Google Scholar] [CrossRef]
- Hasson, S.; Pascale, S.; Lucarini, S.; Böhner, J. Seasonal cycle of precipitation over major river basins in South and Southeast Asia: A review of the CMIP5 climate models data for present climate and future climate projections. Atmos. Res. 2016, 180, 42–63. [Google Scholar] [CrossRef]
- Kumar, S.; Merwade, V.; Kinter III, J.L.; Niyogi, D. Evaluation of Temperature and Precipitation Trends and Long-Term Persistence in CMIP5 Twentieth-Century Climate Simulations. J. Clim. 2013, 26, 4168–4185. [Google Scholar] [CrossRef]
- Kumar, D.; Kodra, E.; Ganguly, A.R. Regional and seasonal intercomparison of CMIP3 and CMIP5 climate model ensembles for temperature and precipitation. Clim. Dynam. 2014, 43, 2491–2518. [Google Scholar] [CrossRef]
- Koutroulis, A.G.; Grillakis, M.G.; Tsanis, I.K.; Papadimitriou, L. Evaluation of precipitation and temperature simulation performance of the CMIP3 and CMIP5 historical experiments. Clim. Dynam. 2016, 47, 1881–1898. [Google Scholar] [CrossRef]
- Nguyen, P.; Thorstensen, A.; Sorooshian, S.; Zhu, Q.; Tran, H.; Ashouri, H.; Miao, C.Y.; Hsu, K.L.; Gao, X.G. Evaluation of CMIP5 model precipitation using PERSIANN-CDR. J. Hydrometeorol. 2017, 18, 2313–2330. [Google Scholar] [CrossRef]
- Yoo, C.; Cho, E. Comparison of GCM precipitation predictions with their RMSEs and pattern correlation coefficients. Water. 2018, 10, 28. [Google Scholar]
- Zhou, B.T.; Wen, Q.Z.H.; Xu, Y.; Song, L.C.; Zhang, X.B. Projected changes in temperature and precipitation extremes in China by the CMIP5 multimodel ensembles. J. Clim. 2014, 27, 6591–6611. [Google Scholar] [CrossRef]
- Almazroui, M.; Islam, M.N.; Saeed, S.; Alkhalaf, A.K.; Dambul, R. Assessment of uncertainties in projected temperature and precipitation over the Arabian Peninsula using three categories of CMIP5 multimodel ensembles. Earth. Syst. Environ. 2017. [Google Scholar] [CrossRef]
- Abbasian, M.; Moghim, S.; Abrishamchi, A. Performance of the general circulation models in simulating temperature and precipitation over Iran. Theor. Appl. Climatol. 2018. [Google Scholar] [CrossRef]
- Hussain, M.; Yusof, K.W.; Mustafa, M.R.U.; Mahmood, R.; Jia, S.F. Evaluation of CMIP5 models for projection of future precipitation change in Bornean tropical rainforests. Theor. Appl. Climatol. 2017, 134, 1–18. [Google Scholar] [CrossRef]
- Kadel, I.; Yamazaki, T.; Iwasaki, T.; Abdillah, M.R. Projection of future monsoon precipitation over the central Himalayas by CMIP5 models under warming scenarios. Clim. Res. 2018, 75, l–21. [Google Scholar] [CrossRef]
- Lovino, M.A.; Müller, O.V.; Berbery, E.H.; Müller, G.V. Evaluation of CMIP5 retrospective simulations of temperature and precipitation in northeastern Argentina. Int. J. Climatol. 2018, 38, e1158–e1175. [Google Scholar] [CrossRef]
- Miao, C.Y.; Duan, Q.Y.; Sun, Q.H.; Huang, Y.; Kong, D.X.; Yang, T.T.; Ye, A.Z.; Di, Z.H.; Gong, W. Assessment of CMIP5 climate models and projected temperature changes over Northern Eurasia. Environ. Res. Lett. 2014, 9, 055007. [Google Scholar] [CrossRef]
- Penalba, O.; Rivera, J. Regional aspects of future precipitation and meteorological drought characteristics over southern South America projected by a CMIP5 multi-model ensemble. Int. J. Climatol. 2016, 36, 974–986. [Google Scholar] [CrossRef]
- IPCC (Intergovernmental Panel on Climate Change), Climate Change 2014: Impacts, Adaptation, and Vulnerability. Working Group II Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge/New York, Cambridge University Press. 2014. Available online: https://www.ipcc.ch/site/assets/uploads/2018/02/WGIIAR5-PartA_FINAL.pdf (accessed on 10 August 2018).
- Jacobs, J.W. The mekong river commission: Transboundary water resources planning and regional security. Geogr. J. 2002, 168, 354–364. [Google Scholar] [CrossRef]
- MRC: State of the Basin Report. Mekong River Commission, Vientiane, Lao PDR. 2010. Available online: http://www.mrcmekong.org/assets/Publications/basin-reports/MRC-SOB-report-2010full-report.pdf (accessed on 15 August 2018).
- Thilakarathne, M.; Sridhar, V. Characterization of future drought conditions in the Lower Mekong River Basin. Weather Clim. Extrem. 2017, 17, 47–58. [Google Scholar] [CrossRef]
- Trisurat, Y.; Aekakkararungroj, A.; Ma, H.; Johnston, J.M. Basin-wide impacts of climate change on ecosystem services in the Lower Mekong Basin. Ecol. Res. 2018, 33, 73–86. [Google Scholar] [CrossRef] [PubMed]
- Hirota, N.; Takayabu, Y.N. Reproducibility of precipitation distribution over the tropical oceans in CMIP5 multi-climate models compared to CMIP3. Clim. Dynam. 2013, 41, 2909–2920. [Google Scholar] [CrossRef]
- Zazulie, N.; Rusticucci, M.; Raga, G.B. Regional climate of the subtropical central Andes using high-resolution CMIP5 models—Part I: Past performance (1980–2005). Clim. Dynam. 2017, 49, 3937–3957. [Google Scholar] [CrossRef]
- Lutz, A.; Terink, W.; Droogers, P.; Immerzeel, W.; Piman, T. Development of Baseline Climate Data Set and Trend Analysis in the Mekong Basin. Wageningen, The Netherlands. 2014, pp. 1–127. Available online: https://www.futurewater.eu/wp-content/uploads/2014/04/MRC_baseline_climate_report_v14.pdf (accessed on 2 September 2018).
- Yatagai, A.; Kamiguchi, K.; Arakawa, O.; Hamada, A.; Yasutomi, N.; Kitoh, A. APHRODITE: Constructing a long-term daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Bull. Am. Meteorol. Soc. 2012, 93, 1401–1415. [Google Scholar] [CrossRef]
- MRC: Adaptation to climate change in the countries of the Lower Mekong Basin. Regional Synthesis Report. Mekong River Commission, Vientiane, Lao PDR. 2009. Available online: http://www.mrcmekong.org/assets/Publications/report-management-develop/MRC-IM-No1-Adaptation-to-climate-change-in-LMB.pdf (accessed on 15 September 2018).
- MRC: Planning atlas of the Lower Mekong River Basin. Basin Development Plan Programme. Mekong River Commission, Vientiane, Lao PDR. 2011. Available online: http://www.mrcmekong.org/assets/Publications/basin-reports/BDP-Atlas-Final-2011.pdf (accessed on 1 October 2018).
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Liu, Z.F.; Wang, R.; Yao, Z.J. Air temperature and precipitation over the Mongolian Plateau and assessment of CMIP5 climate models. Resour. Sci. 2016, 38, 956–969. (In Chinese) [Google Scholar]
- Hirsch, R.M.; Alexander, R.B.; Smith, R.A. Selection of methods for the detection and estimation of trends in water quality. Water Resour. Res. 1991, 27, 803–813. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Hirsch, R.M.; Slack, J.R.; Smith, R.A. Techniques of trend analysis for monthly water quality. Water Resour. Res. 1982, 18, 107–121. [Google Scholar] [CrossRef]
- Brier, G.W. Verification of forecasts expressed in terms of probability. Mon. Weather Rev. 1950, 78, 1–3. [Google Scholar] [CrossRef]
- Perkins, S.E.; Pitman, A.J.; Holbrook, N.J.; McAneney, J. Evaluation of the AR4 climate models’ simulated daily maximum temperature, minimum temperature, and precipitation over Australia using probability density functions. J. Clim. 2007, 20, 4356–4376. [Google Scholar] [CrossRef]
- Fu, G.B.; Liu, Z.F.; Charles, S.P.; Xu, Z.X.; Yao, Z.J. A score-based method for assessing the performance of GCMs: A case study of southeastern Australia. J. Geophys. Res.-Atmos. 2013, 118, 4154–4167. [Google Scholar] [CrossRef]
- Bannister, D.; Herzog, M.; Graf, H.; Hosking, J.S.; Short, C.A. An assessment of recent and future temperature change over the Sichuan Basin, China, Using CMIP5 Climate Models. J. Clim. 2017, 30, 6701–6722. [Google Scholar] [CrossRef]
- Wang, X.; Chen, M.Y.; Wang, C.Z.; Yeh, S.W.; Tan, W. Evaluation of performance of CMIP5 models in simulating the North Pacific Oscillation and El Niño Modoki. Clim. Dynam. 2018, 1–12. [Google Scholar] [CrossRef]
- Harris, I.; Jones, P.D.; Osborn, T.J.; Lister, D.H. Updated high-resolution grids of monthly climatic observations—The CRU TS3.10 Dataset. Int. J. Climatol. 2013, 34, 623–642. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M.; Rudolf, B. GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 2013, 115, 15–40. [Google Scholar] [CrossRef]









| Model Name | ID | Institution | Resolution (Lon × Lat) | Time Range |
|---|---|---|---|---|
| ACCESS1.0 | 1 | Commonwealth Scientific and Industrial Research Organization/Bureau of Meteorology, Australia | 1.88° × 1.25° | 1850–2005 |
| ACCESS1.3 | 2 | 1.88° × 1.25° | 1850–2005 | |
| BCC-CSM1.1 | 3 | Beijing Climate Center, China Meteorological Administration, China | 2.81° × 2.79° | 1850–2012 |
| BNU-ESM | 4 | College of Global Change and Earth System Science, Beijing Normal University, China | 2.81° × 2.79° | 1850–2005 |
| CanESM2 | 5 | Canadian Centre for Climate Modelling and Analysis, Canada | 2.81° × 2.79° | 1850–2005 |
| CCSM4 | 6 | National Center for Atmospheric Research, USA | 1.25° × 0.94° | 1850–2005 |
| CESM1(CAM5) | 7 | 1.25° × 0.94° | 1850–2005 | |
| CESM1(WACCM) | 8 | 2.50° × 1.88° | 1850–2005 | |
| CMCC-CMS | 9 | Centro Euro-Mediterraneo sui Cambiamenti Climatici, Italy | 1.88° × 1.88° | 1850–2005 |
| CNRM-CM5 | 10 | Centre National de Recherches Météorologiques Centre Européen de Recherche et Formation Avancée en Calcul Scientifique, France | 1.41° × 1.40° | 1850–2005 |
| CSIRO-Mk3.6.0 | 11 | Commonwealth Scientific and Industrial Research Organization/Queensland Climate Change Centre of Excellence, Australia | 1.88° × 1.88° | 1850–2005 |
| EC-EARTH | 12 | EC-EARTH consortium published at the Irish Centre for High-End Computing, Netherlands/Ireland | 1.13° × 1.13° | 1850–2009 |
| FGOALS-g2 | 13 | Institute of Atmospheric Physics, Chinese Academy of Sciences, China | 2.81° × 2.81° | 1850–2005 |
| FIO-ESM | 14 | The First Institute of Oceanography, SOA, China | 2.80° × 2.80° | 1850–2005 |
| GFDL-CM3 | 15 | NOAA Geophysical Fluid Dynamics Laboratory, USA | 2.50° × 2.00° | 1860–2005 |
| GFDL-ESM2G | 16 | 2.00° × 2.02° | 1861–2005 | |
| GFDL-ESM2M | 17 | 2.50° × 2.02° | 1861–2005 | |
| GISS-E2-H | 18 | NASA/GISS Goddard Institute for Space Studies, USA | 2.50° × 2.00° | 1850–2005 |
| GISS-E2-R | 19 | 2.50° × 2.00° | 1850–2005 | |
| HadGEM2-AO | 20 | National Institute of Meteorological Research, Korea Meteorological Administration, Korea | 1.88° × 1.25° | 1860–2005 |
| HadGEM2-CC | 21 | Met Office Hadley Center, UK | 1.88° × 1.25° | 1859–2005 |
| HadGEM2-ES | 22 | 1.88° × 1.25° | 1859–2005 | |
| INMCM4.0 | 23 | Russian Academy of Sciences, Institute for Numerical Mathematics, Russia | 2.00° × 1.50° | 1850–2005 |
| IPSL-CM5A-LR | 24 | Institute Pierre-Simon Laplace, France | 3.75° × 1.89° | 1850–2005 |
| IPSL-CM5A-MR | 25 | 2.50° × 1.27° | 1850–2005 | |
| IPSL-CM5B-LR | 26 | 3.75° × 1.89° | 1850–2005 | |
| MIROC4h | 27 | Atmosphere and Ocean Research Institute (the University of Tokyo), National Institute for Environmental Studies, and Japan Agency for Marine-Earth Science and Technology, Japan | 0.56° × 0.56° | 1950–2005 |
| MIROC5 | 28 | 1.41° × 1.40° | 1850–2012 | |
| MIROC-ESM | 29 | 2.81° × 2.79° | 1850–2005 | |
| MIROC-ESM-CHEM | 30 | 2.81° × 2.79° | 1850–2005 | |
| MPI-ESM-LR | 31 | Max Planck Institute for Meteorology, Germany | 1.88° × 1.87° | 1850–2005 |
| MPI-ESM-MR | 32 | 1.88° × 1.87° | 1850–2005 | |
| MRI-CGCM3 | 33 | Meteorological Research Institute, Japan | 1.13° × 1.12° | 1850–2005 |
| NorESM1-M | 34 | Bjerknes Centre for Climate Research, Norwegian Climate Center, Norway | 2.50° × 1.89° | 1850–2005 |
| GCMs | ID | Wet | Dry | Annual | Overall |
|---|---|---|---|---|---|
| ACCESS1.0 | 1 | 0.753 | 0.633 | 0.640 | 0.667 |
| ACCESS1.3 | 2 | 0.546 | 0.614 | 0.429 | 0.505 |
| BCC-CSM1.1 | 3 | 0.310 | 0.740 | 0.464 | 0.494 |
| BNU-ESM | 4 | 0.757 | 0.760 | 0.814 | 0.786 |
| CanESM2 | 5 | 0.726 | 0.595 | 0.743 | 0.702 |
| CCSM4 | 6 | 0.720 | 0.780 | 0.762 | 0.756 |
| CESM1(CAM5) | 7 | 0.842 | 0.672 | 0.832 | 0.795 |
| CESM1(WACCM) | 8 | 0.779 | 0.468 | 0.781 | 0.702 |
| CMCC-CMS | 9 | 0.864 | 0.735 | 0.841 | 0.820 |
| CNRM-CM5 | 10 | 0.698 | 0.613 | 0.694 | 0.675 |
| CSIRO-Mk3.6.0 | 11 | 0.430 | 0.622 | 0.451 | 0.489 |
| EC-EARTH | 12 | 0.738 | 0.690 | 0.779 | 0.746 |
| FGOALS-g2 | 13 | 0.379 | 0.540 | 0.248 | 0.353 |
| FIO-ESM | 14 | 0.738 | 0.745 | 0.764 | 0.753 |
| GFDL-CM3 | 15 | 0.747 | 0.656 | 0.731 | 0.716 |
| GFDL-ESM2G | 16 | 0.447 | 0.622 | 0.560 | 0.548 |
| GFDL-ESM2M | 17 | 0.481 | 0.670 | 0.476 | 0.526 |
| GISS-E2-H | 18 | 0.571 | 0.606 | 0.547 | 0.568 |
| GISS-E2-R | 19 | 0.602 | 0.511 | 0.569 | 0.563 |
| HadGEM2-AO | 20 | 0.754 | 0.621 | 0.694 | 0.691 |
| HadGEM2-CC | 21 | 0.847 | 0.634 | 0.800 | 0.770 |
| HadGEM2-ES | 22 | 0.791 | 0.741 | 0.785 | 0.776 |
| INMCM4.0 | 23 | 0.763 | 0.244 | 0.440 | 0.472 |
| IPSL-CM5A-LR | 24 | 0.726 | 0.738 | 0.804 | 0.768 |
| IPSL-CM5A-MR | 25 | 0.790 | 0.821 | 0.844 | 0.824 |
| IPSL-CM5B-LR | 26 | 0.331 | 0.661 | 0.219 | 0.358 |
| MIROC4h | 27 | 0.491 | 0.623 | 0.424 | 0.491 |
| MIROC5 | 28 | 0.640 | 0.688 | 0.701 | 0.682 |
| MIROC-ESM | 29 | 0.743 | 0.515 | 0.737 | 0.683 |
| MIROC-ESM-CHEM | 30 | 0.745 | 0.592 | 0.794 | 0.731 |
| MPI-ESM-LR | 31 | 0.879 | 0.733 | 0.882 | 0.844 |
| MPI-ESM-MR | 32 | 0.709 | 0.751 | 0.807 | 0.769 |
| MRI-CGCM3 | 33 | 0.609 | 0.853 | 0.473 | 0.602 |
| NorESM1-M | 34 | 0.734 | 0.684 | 0.791 | 0.750 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruan, Y.; Yao, Z.; Wang, R.; Liu, Z. Ranking of CMIP5 GCM Skills in Simulating Observed Precipitation over the Lower Mekong Basin, Using an Improved Score-Based Method. Water 2018, 10, 1868. https://doi.org/10.3390/w10121868
Ruan Y, Yao Z, Wang R, Liu Z. Ranking of CMIP5 GCM Skills in Simulating Observed Precipitation over the Lower Mekong Basin, Using an Improved Score-Based Method. Water. 2018; 10(12):1868. https://doi.org/10.3390/w10121868
Chicago/Turabian StyleRuan, Yunfeng, Zhijun Yao, Rui Wang, and Zhaofei Liu. 2018. "Ranking of CMIP5 GCM Skills in Simulating Observed Precipitation over the Lower Mekong Basin, Using an Improved Score-Based Method" Water 10, no. 12: 1868. https://doi.org/10.3390/w10121868
APA StyleRuan, Y., Yao, Z., Wang, R., & Liu, Z. (2018). Ranking of CMIP5 GCM Skills in Simulating Observed Precipitation over the Lower Mekong Basin, Using an Improved Score-Based Method. Water, 10(12), 1868. https://doi.org/10.3390/w10121868





