Sensitivity Analyses for Modeling Evolving Reactivity of Granular Iron for the Treatment of Trichloroethylene
Abstract
:1. Introduction
2. Methods
2.1. Model
2.2. Model Parameters
2.3. Sensitivity Analysis
3. Results and Discussion
3.1. Iron Corrosion Rate
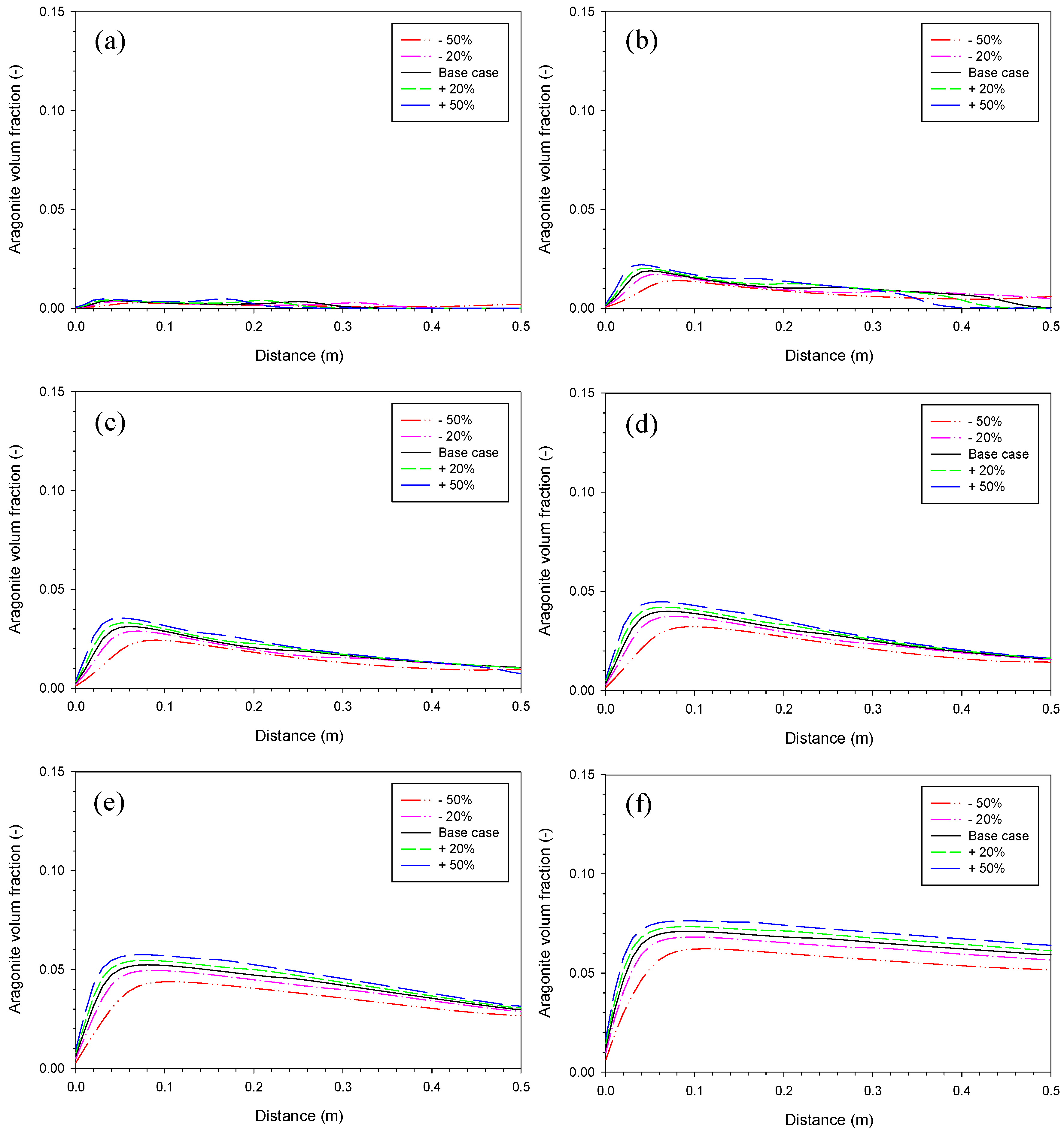
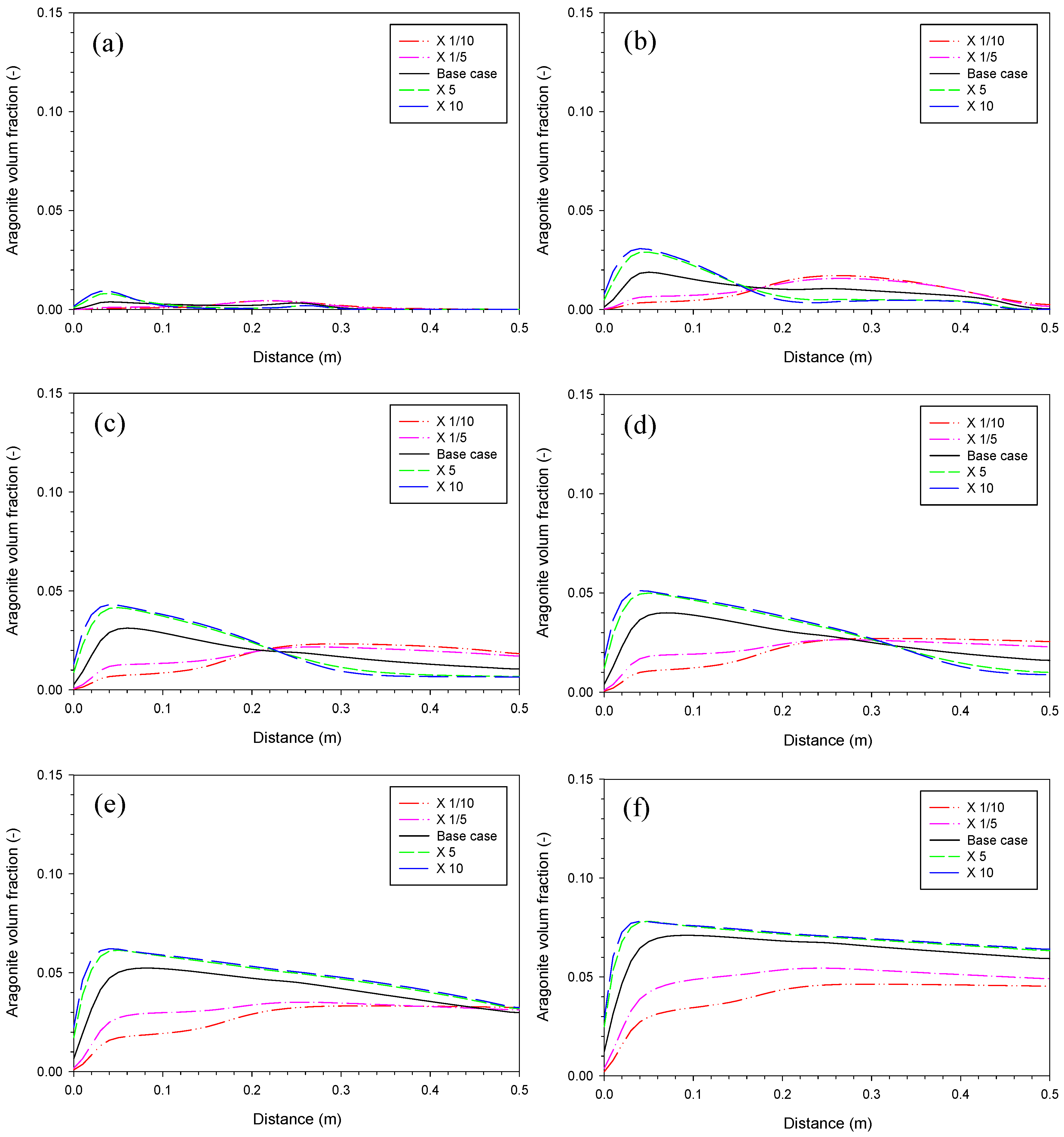
3.2. Aragonite Precipitation Rate
3.3. Fe2(OH)2CO3 Precipitation Rate
3.4. Proportionality Constant for Aragonite
3.5. Proportionality Constant for Fe2(OH)2CO3
4. Conclusions
Funding
Conflicts of Interest
References
- O’Hannesin, S.F.; Gillham, R.W. Long-term performance of an in-situ “iron wall” for remediation of VOCs. Ground Water 1998, 36, 164–170. [Google Scholar] [CrossRef]
- Blowes, D.W.; Ptacek, C.J.; Benner, S.G.; McRae, C.W.T.; Puls, R.W. Treatment of dissolved metals and nutrients using permeable reactive barriers. J. Contam. Hydrol. 2000, 45, 123–137. [Google Scholar] [CrossRef]
- Wilkin, R.T.; Acree, S.D.; Ross, R.R.; Beak, D.G.; Lee, T.R. Performance of a zerovalent iron reactive barrier for the treatment of arsenic in groundwater: Part 1. Hydrogeochemical studies. J. Contam. Hydrol. 2009, 106, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Obiri-Nyarko, F.; Grajales-Mesa, S.J.; Malina, G. An overview of permeable reactive barriers for in situ sustainable groundwater remediation. Chemosphere 2014, 111, 243–259. [Google Scholar] [CrossRef]
- Li, J.; Dou, X.; Qin, H.; Sun, Y.; Yin, D.; Guan, X. Characterization methods of zerovalent iron for water treatment and remediation. Water Res. 2018, 148, 70–85. [Google Scholar] [CrossRef]
- Phillips, D.H.; Van Nooten, T.; Bastiaens, L.; Russell, M.I.; Dickson, K.; Plant, S.; Ahad, J.M.E.; Newton, T.; Elliot, T.; Kalin, R.M. Ten year performance evaluation of a field-scale zero-valent iron permeable reactive barrier installed to remediate trichloroethene contaminated groundwater. Environ. Sci. Technol. 2010, 44, 3861–3869. [Google Scholar] [CrossRef]
- Dong, J.; Ding, L.; Wen, C.; Hong, M.; Zhao, Y. Effects of geochemical constituents on the zero-valent iron reductive removal of nitrobenzene in groundwater. Water Environ. J. 2013, 27, 20–28. [Google Scholar] [CrossRef]
- Jeen, S.-W.; Yang, Y.; Gui, L.; Gillham, R.W. Treatment of trichloroethene and hexavalent chromium by granular iron in the presence of dissolved CaCO3. J. Contam. Hydrol. 2013, 144, 108–121. [Google Scholar] [CrossRef]
- Guan, X.; Sun, Y.; Qin, H.; Li, J.; Lo, I.M.C.; He, D.; Dong, H. The limitations of applying zero-valent iron technology in contaminants sequestration and the corresponding countermeasures: the development in zero-valent iron technology in the last two decades (1994–2014). Water Res. 2015, 75, 224–248. [Google Scholar] [CrossRef]
- Ansaf, K.V.K.; Ambika, S.; Nambi, I.M. Performance enhancement of zero valent iron based systems using depassivators: Optimization and kinetic mechanisms. Water Res. 2016, 102, 436–444. [Google Scholar] [CrossRef]
- Tang, F.; Xin, J.; Zheng, T.; Zheng, X.; Yang, X. Individual and combined effects of humic acid, bicarbonate and calcium on TCE removal kinetics, aging behavior and electron efficiency of mZVI particles. Chem. Eng. J. 2017, 324, 324–335. [Google Scholar] [CrossRef]
- Flury, B.; Frommer, J.; Eggenberger, U.; Mäder, U.; Nachtegaal, M.; Kretzschmar, R. Assessment of long-term performance and chromate reduction mechanisms in a field scale permeable reactive barrier. Environ. Sci. Technol. 2009, 43, 6786–6792. [Google Scholar] [CrossRef] [PubMed]
- Yabusaki, S.; Cantrell, K.; Sass, B.; Steefel, C. Multicomponent reactive transport in an in situ zero-valent iron cell. Environ. Sci. Technol. 2001, 35, 1493–1503. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Benson, C.H. Evaluation of five strategies to limit the impact of fouling in permeable reactive barriers. J. Hazard. Mater. 2010, 181, 170–180. [Google Scholar] [CrossRef] [PubMed]
- Weber, A.; Ruhl, A.S.; Amos, R.T. Investigating dominant processes in ZVI permeable reactive barriers using reactive transport modeling. J. Contam. Hydrol. 2013, 151, 68–82. [Google Scholar] [CrossRef] [PubMed]
- Jeen, S.-W.; Mayer, K.U.; Gillham, R.W.; Blowes, D.W. Reactive transport modeling of trichloroethene treatment with declining reactivity of iron. Environ. Sci. Technol. 2007, 41, 1432–1438. [Google Scholar] [CrossRef]
- Jeen, S.-W.; Amos, R.T.; Blowes, D.W. Modeling gas formation and mineral precipitation in a granular iron column. Environ. Sci. Technol. 2012, 46, 6742–6749. [Google Scholar] [CrossRef]
- Jeong, H.Y.; Jeen, S.-W. Geochemical interactions of mine seepage water with an aquifer: Laboratory tests and reactive transport modeling. Environ. Earth Sci. 2016, 2016. 75, 1333. [Google Scholar] [CrossRef]
- Jeen, S.-W. Reactive transport modeling for mobilization of arsenic in a sediment downgradient from an iron permeable reactive barrier. Water 2017, 9, 890. [Google Scholar] [CrossRef]
- Jeen, S.-W.; Gillham, R.W.; Przepiora, A. Predictions of long-term performance of granular iron permeable reactive barriers: Field-scale evaluation. J. Contam. Hydrol. 2011, 123, 50–64. [Google Scholar] [CrossRef]
- Mayer, K.U.; Frind, E.O.; Blowes, D.W. Multicomponent reactive transport modeling in variably saturated porous media using a generalized formulation for kinetically controlled reactions. Water Resour Res. 2002, 38, 1174. [Google Scholar] [CrossRef]
- Steefel, C.I.; Lasaga, A.C. A coupled model for transport of multiple chemical species and kinetic precipitation/dissolution reactions with application to reactive flow in single phase hydrothermal systems. Am. J. Sci. 1994, 294, 529–592. [Google Scholar] [CrossRef]
- Lichtner, P.C. Continuum Formulation of Multicomponent-Multiphase Reactive Transport. In Reactive Transport in Porous Media. Review in Mineralogy, vol. 34; Lichtner, P.C., Steefel, C.I., Oelkers, E.H., Eds.; Mineralogical Society of America: Washington, DC, USA, 1996; pp. 1–81. [Google Scholar]
- Lichtner, P.C. Continuum model for simultaneous chemical reactions and mass transport in hydrothermal systems. Geochim. Cosmochim. Ac. 1985, 49, 779–800. [Google Scholar] [CrossRef]
- Sevougian, S.D.; Schechter, R.S.; Lake, W. Effect of partial local equilibrium on the propagation of precipitation/dissolution waves. Ind. Eng. Chem. Res. 1993, 32, 2281–2304. [Google Scholar] [CrossRef]
- Zhang, Y.; Gillham, R.W. Effects of gas generation and precipitates on performance of Fe0 RRBs. Ground Water 2005, 43, 113–121. [Google Scholar] [CrossRef] [PubMed]
- Lu, Q.; Jeen, S.-W.; Gui, L.; Gillham, R.W. Nitrate reduction and its effects on trichloroethylene degradation by granular iron. Water Res. 2017, 112, 48–57. [Google Scholar] [CrossRef] [PubMed]
- Jeen, S.-W.; Gillham, R.W.; Blowes, D.W. Effects of carbonate precipitates on long-term performance of granular iron for reductive dechlorination of TCE. Environ. Sci. Technol. 2006, 40, 6432–6437. [Google Scholar] [CrossRef] [PubMed]
- Allison, J.D.; Brown, D.S.; Novo-Gradac, K.J. MINTEQA2/PRODEFA2, A Geochemical Assessment Model for Environmental Systems: Version 3.0 User’s Manual; EPA-600/3-91-021; U.S. Environmental Protection Agency: Athens, GA, USA, 1991.
- Ball, J.W.; Nordstrom, D.K. User’s Manual for WATEQ4F, with Revised Thermodynamic Database and Test Cases for Calculating Speciation of Major, Trace, and Redox Elements in Natural Waters; Open-File Report 91-183; U.S. Geological Survey: Menlo Park, CA, USA, 1991.
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice-Hall: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Mayer, K.U.; Blowes, D.W.; Frind, E.O. Reactive transport modeling of an in situ reactive barrier for the treatment of hexavalent chromium and trichloroethylene in groundwater. Water Resour. Res. 2001, 37, 3091–3103. [Google Scholar] [CrossRef] [Green Version]








| Model Input Parameter | Value |
|---|---|
| Column length (m) | 0.50 |
| Fe0 volume fraction (-) | 0.49 |
| Porosity (-) | 0.51 |
| Hydraulic conductivity (m s−1) | 3.49 × 10−5 |
| Diffusion coefficient (m2 s) | 1.5 × 10−9 |
| Longitudinal dispersivity (m) | 9.9 × 10−4 |
| Running time (days) | 410 |
| Flow rate (m s−1) | 1.38 × 10−5 |
| pH | 6.66 |
| Ca2+ (mol L−1) | 5.0 × 10−3 |
| CO3 Total (mol L−1) | 1.57 × 10−2 |
| TCE (mol L−1) | 7.6 × 10−5 |
| Parameter | Base Case | Sensitivity Analysis | |
|---|---|---|---|
| Initial reactive surface area (m2 iron L−1 bulk) | 8.37 × 103 | Fixed | |
| log a (mol m−2 iron s-1) | −10.95 | Fixed | |
| b (mol L−1 H2O) | 1.83 × 10−5 | Fixed | |
| log c (mol m−2 iron s−1) | −9.90 | −50%, −20%, +20%, +50% | |
| log d (mol L−1 H2O s−1) | CaCO3(s) (aragonite) | −6.93 | ×1/10, ×1/5, ×5, ×10 |
| Fe2(OH)2CO3(s) | −9.75 | ×1/10, ×1/5, ×5, ×10 | |
| e (for aragonite) | 55 | −50%, −20%, +20%, +50% | |
| f (for Fe2(OH)2CO3(s)) | 2 | −100%, −50%, +50%, +100% | |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeen, S.-W. Sensitivity Analyses for Modeling Evolving Reactivity of Granular Iron for the Treatment of Trichloroethylene. Water 2018, 10, 1878. https://doi.org/10.3390/w10121878
Jeen S-W. Sensitivity Analyses for Modeling Evolving Reactivity of Granular Iron for the Treatment of Trichloroethylene. Water. 2018; 10(12):1878. https://doi.org/10.3390/w10121878
Chicago/Turabian StyleJeen, Sung-Wook. 2018. "Sensitivity Analyses for Modeling Evolving Reactivity of Granular Iron for the Treatment of Trichloroethylene" Water 10, no. 12: 1878. https://doi.org/10.3390/w10121878
APA StyleJeen, S.-W. (2018). Sensitivity Analyses for Modeling Evolving Reactivity of Granular Iron for the Treatment of Trichloroethylene. Water, 10(12), 1878. https://doi.org/10.3390/w10121878





