Quantifying Climatic Impact on Reference Evapotranspiration Trends in the Huai River Basin of Eastern China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Source
2.3. Reference Evapotranspiration Calculation
2.4. Trend Analysis
2.5. Spatial Interpolation Method
2.6. Sensitivity Coefficient Estimation
2.7. Contributions of Climate Factors on ETref
3. Results
3.1. Variations of Climate Factors and Their Trend Analysis
3.2. Variations of ETref and Their Trend Analysis
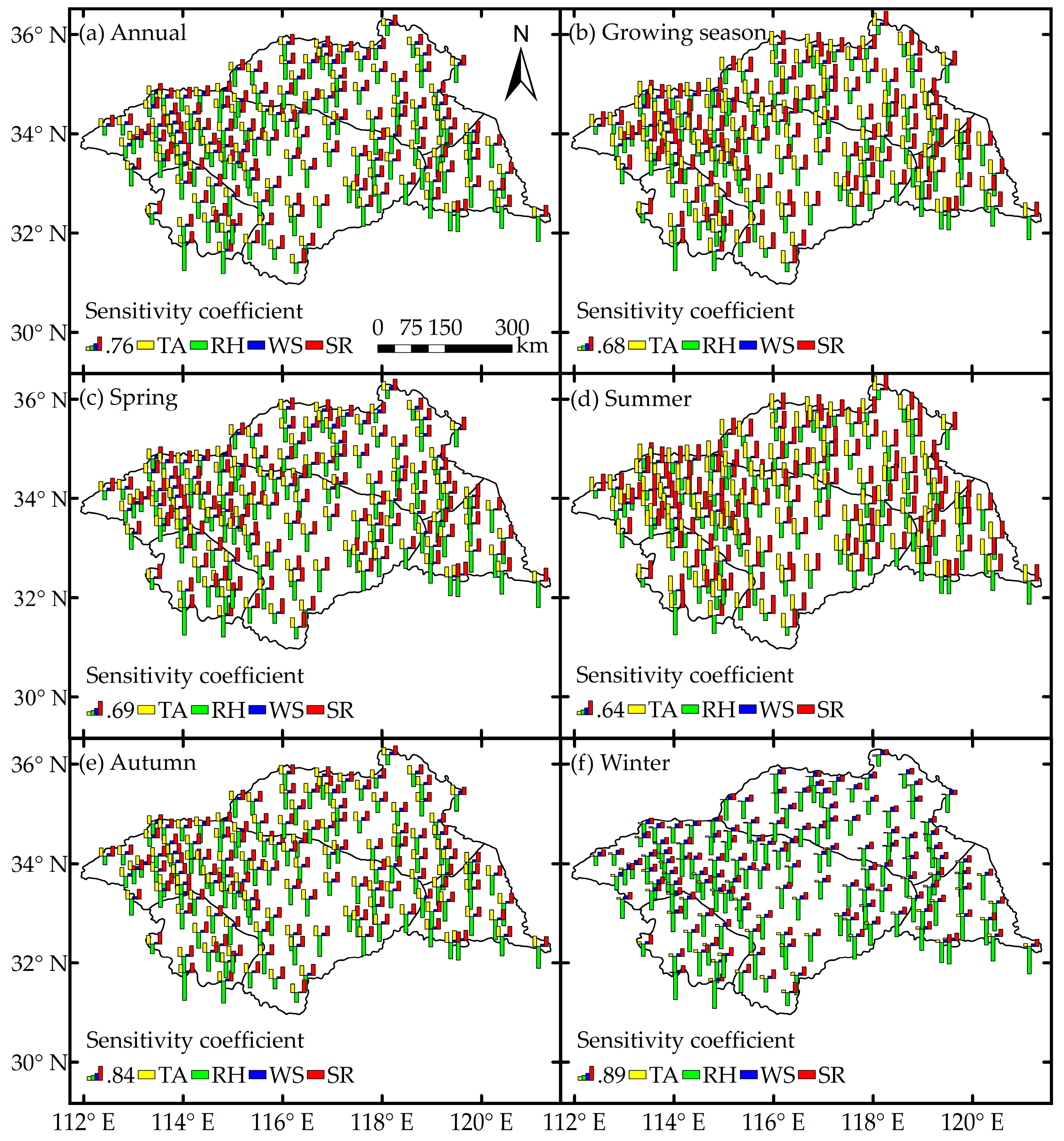
3.3. Sensitivity Coefficient of ETref to Climate Factors
3.4. Quantitative Contributions of Climate Factors to ETref
4. Discussion
4.1. Temporal Change Trends of ETref and Climate Factors in HRB
4.2. Impact of Climate Factors to ETref Trends
4.3. Uncertainties
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Validation of the Hargreaves–Samani Method for Estimating Solar Radiation

References
- Xu, C.Y.; Gong, L.; Jiang, T.; Chen, D.; Singh, V.P. Analysis of spatial distribution and temporal trend of reference evapotranspiration and pan evaporation in Changjiang (Yangtze River) catchment. J. Hydrol. 2006, 327, 81–93. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Zhao, L.; Xia, J.; Sobkowiak, L.; Li, Z. Climatic Characteristics of Reference Evapotranspiration in the Hai River Basin and Their Attribution. Water 2014, 6, 1482–1499. [Google Scholar] [CrossRef]
- Thomas, A. Development and properties of 0.25-degree gridded evapotranspiration data fields of China for hydrological studies. J. Hydrol. 2008, 358, 145–158. [Google Scholar] [CrossRef]
- Jhajharia, D.; Shrivastava, S.K.; Sarkar, D.; Sarkar, S. Temporal characteristics of pan evaporation trends under the humid conditions of northeast India. Agric. For. Meteorol. 2009, 149, 763–770. [Google Scholar] [CrossRef]
- Zuo, H.; Chen, B.; Wang, S.; Guo, Y.; Zuo, B.; Wu, L.; Gao, X. Observational study on complementary relationship between pan evaporation and actual evapotranspiration and its variation with pan type. Agric. For. Meteorol. 2016, 222, 1–9. [Google Scholar] [CrossRef]
- Alexander, L.V.; Allen, S.K.; Bindoff, N.L.; Bréon, F.-M.; Church, J.A.; Cubasch, U.; Emori, S.; Forster, P.; Friedlingstein, P.; Gillett, N.; et al. Climate change 2013: The physical science basis, in contribution of Working Group I (WGI) to the Fifth Assessment Report (AR5) of the Intergovernmental Panel on Climate Change (IPCC). Science 2013, 129, 83–103. [Google Scholar]
- Xu, L.; Shi, Z.; Wang, Y.; Zhang, S.; Chu, X.; Yu, P.; Xiong, W.; Zuo, H.; Wang, Y. Spatiotemporal variation and driving forces of reference evapotranspiration in Jing River Basin, northwest China. Hydrol. Process. 2015, 29, 4846–4862. [Google Scholar] [CrossRef]
- McMahon, T.A.; Finlayson, B.L.; Peel, M.C. Historical developments of models for estimating evaporation using standard meteorological data. WIREs Water 2016, 3, 788–818. [Google Scholar] [CrossRef]
- Cong, Z.T.; Yang, D.W.; Ni, G.H. Does evaporation paradox exist in China? Hydrol. Earth Syst. Sci. 2009, 13, 357–366. [Google Scholar] [CrossRef]
- Limjirakan, S.; Limsakul, A. Trends in Thailand pan evaporation from 1970 to 2007. Atmos. Res. 2012, 108, 122–127. [Google Scholar] [CrossRef]
- Breña-Naranjo, J.A.; Laverde-Barajas, M.Á.; Pedrozo-Acuña, A. Changes in pan evaporation in Mexico from 1961 to 2010. Int. J. Climatol. 2016, 23, 361–387. [Google Scholar] [CrossRef]
- Brutsaert, W.; Parlange, M.B. Hydrologic cycle explains the evaporation paradox. Nature 1998, 396, 30. [Google Scholar] [CrossRef]
- Huo, Z.; Dai, X.; Feng, S.; Kang, S.; Huang, G. Effect of climate change on reference evapotranspiration and aridity index in arid region of China. J. Hydrol. 2013, 492, 24–34. [Google Scholar] [CrossRef]
- Thomas, A. Spatial and temporal characteristics of potential evapotranspiration trends over China. Int. J. Climatol. 2000, 20, 381–396. [Google Scholar] [CrossRef]
- Chu, R.; Li, M.; Shen, S.; Islam, A.R.M.T.; Cao, W.; Tao, S.; Gao, P. Changes in reference evapotranspiration and its contributing factors in Jiangsu, a major economic and agricultural province of eastern China. Water 2017, 9, 486. [Google Scholar] [CrossRef]
- Dinpashoh, Y.; Jhajharia, D.; Fard, A.F.; Singh, V.P.; Kahya, E. Trends in reference crop evapotranspiration over Iran. J. Hydrol. 2011, 399, 422–433. [Google Scholar] [CrossRef]
- Tabari, H.; Aghajanloo, M.B. Temporal pattern of aridity index in Iran with considering precipitation and evapotranspiration trends. Int. J. Climatol. 2013, 33, 396–409. [Google Scholar] [CrossRef]
- Chaouche, K.; Neppel, L.; Dieulin, C.; Pujol, N.; Ladouche, B.; Martin, E.; Salas, D.; Caballero, Y. Analyses of precipitation, temperature and evapotranspiration in a French Mediterranean region in the context of climate change. Comptes Rendus Geosci. 2010, 342, 234–243. [Google Scholar] [CrossRef]
- Palumbo, A.D.; Vitale, D.; Campi, P.; Mastrorilli, M. Time trend in reference evapotranspiration: Analysis of a long series of agrometeorological measurements in Southern Italy. Irrig. Drain. Syst. 2011, 25, 395–411. [Google Scholar] [CrossRef]
- Liu, Q.; Yang, Z.; Cui, B.; Sun, T. The temporal trends of reference evapotranspiration and its sensitivity to key meteorological variables in the Yellow River Basin, China. Hydrol. Process. 2010, 24, 2171–2181. [Google Scholar] [CrossRef]
- Zuo, D.; Xu, Z.; Yang, H.; Liu, X. Spatiotemporal variations and abrupt changes of potential evapotranspiration and its sensitivity to key meteorological variables in the Wei River basin, China. Hydrol. Process. 2012, 26, 1149–1160. [Google Scholar] [CrossRef]
- Vörösmarty, C.J.; Sahagian, D. Anthropogenic disturbance of the terrestrial water cycle. Bioscience 2000, 50, 753–765. [Google Scholar] [CrossRef]
- Rezaei, M.; Valipour, M.; Valipour, M. Modelling evapotranspiration to increase the accuracy of the estimations based on the climatic parameters. Water Conserv. Sci. Eng. 2016, 1, 197–207. [Google Scholar] [CrossRef]
- Valipour, M.; Sefidkouhi, M.A.G.; Sarjaz, M.R. Selecting the best model to estimate potential evapotranspiration with respect to climate change and magnitudes of extreme events. Agric. Water Manag. 2017, 180, 50–60. [Google Scholar] [CrossRef]
- Tegos, A.; Malamos, N.; Efstratiadis, A.; Tsoukalas, I.; Karanasios, A.; Koutsoyiannis, D. Parametric Modelling of Potential Evapotranspiration: A Global Survey. Water 2017, 9, 795. [Google Scholar] [CrossRef]
- McCuen, R.H. A sensitivity and error analysis of procedures used for estimating evaporation. J. Am. Water Resour. Assoc. 1974, 10, 486–497. [Google Scholar] [CrossRef]
- Yin, Y.; Wu, S.; Chen, G.; Dai, E. Attribution analyses of potential evapotranspiration changes in China since the 1960s. Theor. Appl. Climatol. 2010, 101, 19–28. [Google Scholar] [CrossRef]
- Fan, J.; Wu, L.; Zhang, F.; Xiang, Y.; Zheng, J. Climate change effects on reference crop evapotranspiration across different climatic zones of China during 1956–2015. J. Hydrol. 2016, 542, 923–937. [Google Scholar] [CrossRef]
- Gao, Z.; He, J.; Dong, K.; Bian, X.; Li, X. Sensitivity study of reference crop evapotranspiration during growing season in the West Liao River basin, China. Theor. Appl. Climatol. 2016, 124, 1–17. [Google Scholar] [CrossRef]
- Li, C.; Wu, P.T.; Li, X.L.; Zhou, T.W.; Sun, S.K.; Wang, Y.B.; Luan, X.B.; Yu, X. Spatial and temporal evolution of climatic factors and its impacts on potential evapotranspiration in Loess Plateau of Northern Shaanxi, China. Sci. Total Environ. 2017, 589, 165–172. [Google Scholar] [CrossRef] [PubMed]
- Ye, X.; Li, X.; Liu, J.; Xu, C.; Zhang, Q. Variation of reference evapotranspiration and its contributing climatic factors in the Poyang Lake catchment, China. Hydrol. Process. 2015, 28, 6151–6162. [Google Scholar] [CrossRef]
- Shan, N.; Shi, Z.; Yang, X.; Gao, J.; Cai, D. Spatiotemporal trends of reference evapotranspiration and its driving factors in the Beijing-Tianjin Sand Source Control Project Region, China. Agric. For. Meteorol. 2015, 200, 322–333. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, P.; Lai, C.; Chen, X.; Wu, X.; Zeng, Z.; Li, J. Spatiotemporal variability of reference evapotranspiration and contributing climatic factors in China during 1961–2013. J. Hydrol. 2017, 544, 97–108. [Google Scholar] [CrossRef]
- Gao, Z.; He, J.; Dong, K.; Li, X. Trends in reference evapotranspiration and their causative factors in the West Liao River basin, China. Agric. For. Meteorol. 2017, 232, 106–177. [Google Scholar] [CrossRef]
- Li, Z.; Li, Z.; Xu, Z.; Zhou, X. Temporal variations of reference evapotranspiration in Heihe River basin of China. Hydrol. Res. 2013, 44, 904–916. [Google Scholar] [CrossRef]
- Wang, W.; Shao, Q.; Peng, S.; Xing, W.; Yang, T.; Luo, Y.; Yong, B.; Xu, J. Reference evapotranspiration change and the causes across the Yellow River Basin during 1957–2008 and their spatial and seasonal differences. Water Resour. Res. 2012, 48, 1–27. [Google Scholar] [CrossRef]
- Nouri, M.; Homaee, M.; Bannayan, M. Quantitative trend, sensitivity and contribution analyses of reference evapotranspiration in some arid environments under climate change. Water Resour. Manag. 2017, 31, 2207–2224. [Google Scholar] [CrossRef]
- Roderick, M.L.; Rotstayn, L.D.; Farquhar, G.D.; Hobbins, M.T. On the attribution of changing pan evaporation. Geophys. Res. Lett. 2007, 34, 251–270. [Google Scholar] [CrossRef]
- Zheng, H.; Liu, X.; Liu, C.; Dai, X.; Zhu, R. Assessing contributions to panevaporation trends in Haihe River Basin, China. J. Geophys. Res. 2009, 114, 144–153. [Google Scholar] [CrossRef]
- Liu, Q.; Mcvicar, T.R. Assessing climate change induced modification of Penman potential evaporation and runoff sensitivity in a large water-limited basin. J. Hydrol. 2012, 464–465, 352–362. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, J.; Zhao, Y.; Li, H.; Zhai, J.; Yu, Z.; Zhang, S. Reference evapotranspiration trends from 1980 to 2012 and their attribution to meteorological drivers in the three-river source region, China. Int. J. Climatol. 2016, 36, 3759–3769. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, D. Trend analysis of reference evapotranspiration in Northwest China: The roles of changing wind speed and surface air temperature. Hydrol. Process. 2013, 27, 3941–3948. [Google Scholar] [CrossRef]
- Ye, J.; He, Y.; Pappenberger, F.; Cloke, H.L.; Manful, D.; Li, Z. Evaluation of ECMWF medium-range ensemble forecasts of precipitation for river basins. Q. J. R. Meteorol. Soc. 2013, 140, 1615–1628. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.; Yu, J.; Tao, G.; Vos, J.; Bouman, B.A.M.; Xie, G.H.; Meinke, H. Yield formation and tillering dynamics of direct-seeded rice in flooded and nonflooded soils in the Huai River Basin of China. Field Crop. Res. 2010, 116, 252–259. [Google Scholar] [CrossRef]
- Angstrom, A. Solar and terrestrial radiation. Report to the international commission for solar research on actinometric investigations of solar and atmospheric radiation. Q. J. R. Meteorol. Soc. 1924, 50, 121–126. [Google Scholar] [CrossRef]
- Chen, R.; Kang, E.; Yang, J.; Lu, S.; Zhao, W. Validation of five global radiation models with measured daily data in China. Energy Convers. Manag. 2004, 45, 1759–1769. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Estimating potential evapotranspiration. J. Irrig. Drain. Div. 1982, 108, 225–230. [Google Scholar]
- Hargreaves, G.H.; Allen, R.G. History and evaluation of Hargreaves evapotranspiration equation. J. Irrig. Drain. Eng. 2003, 129, 53–63. [Google Scholar] [CrossRef]
- Allen, R.G. Self-Calibrating Method for Estimating Solar Radiation from Air Temperature. J. Hydrol. Eng. 1997, 2, 56–67. [Google Scholar] [CrossRef]
- Tabari, H.; Somee, B.S.; Zadeh, M.R. Testing for long-term trends in climatic variables in Iran. Atmos. Res. 2011, 100, 132–140. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, C.; Xu, C.; Xu, Y.; Jiang, T. Observed trends of annual maximum water level and streamflow during past 130 years in the Yangtze River basin, China. J. Hydrol. 2006, 324, 255–265. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric test against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1975. [Google Scholar]
- Theil, H. A Rank Invariant Method of Linear and Polynomial Regression Analysis; Nederlandse Akademie Van Wetenschappen: Amsterdam, The Netherlands, 1950. [Google Scholar]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Von Storch, H.; Navarra, A. Analysis of Climate Variability: Applications of Statistical Techniques, Misuses of Statistical Analysis in Climate Research; Springer: Berlin, Germany, 1995. [Google Scholar]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Kumar, S.; Merwade, V.; Kam, J.; Thurner, K. Streamflow trends in Indiana: Effects of long term persistence, precipitation and subsurface drains. J. Hydrol. 2009, 374, 171–183. [Google Scholar] [CrossRef]
- Tegos, A.; Malamos, N.; Koutsoyiannis, D. A parsimonious regional parametric evapotranspiration model based on a simplification of the Penman-Monteith formula. J. Hydrol. 2015, 524, 708–717. [Google Scholar] [CrossRef]
- Zhao, C.; Nan, Z.; Cheng, G. Methods for modelling of temporal and spatial distribution of air temperature at landscape scale in the southern Qilian mountains, China. Ecol. Model. 2005, 189, 209–220. [Google Scholar]
- Sun, F.; Yang, X.; Lu, S.; Yang, S. The contrast analysis on the average and extremum temperature trend in Northeast China. Sci. Meteorol. Sin. 2006, 26, 157–163. [Google Scholar]
- McVicar, T.R.; Roderick, M.L.; Donohue, R.J.; Li, L.T.; Niel, T.G.V.; Thomas, A.; Grieser, J.; Jhajharia, D.; Himri, Y.; Mahowald, N.M.; et al. Global review and synthesis of trends in observed terrestrial near-surface wind speeds: Implications for evaporation. J. Hydrol. 2012, 416–417, 182–205. [Google Scholar] [CrossRef]
- Guo, H.; Xu, M.; Hu, Q. Changes in near-surface wind speed in China: 1969–2005. Int. J. Climatol. 2015, 31, 349–358. [Google Scholar] [CrossRef]
- Mcvicar, T.R.; Roderick, M.L. Atmospheric science: Winds of change. Nat. Geosci. 2010, 3, 747–748. [Google Scholar] [CrossRef]
- Song, Z.W.; Zhang, H.L.; Snyder, R.L.; Anderson, F.E.; Chen, F. Distribution and trends in reference evapotranspiration in the North China Plain. J. Irrig. Drain. Eng. 2010, 136, 240–247. [Google Scholar] [CrossRef]
- Vautard, R.; Cattiaux, J.; Yiou, P.; Thépaut, J.-N.; Ciais, P. Northern Hemisphere atmospheric stilling partly attributed to an increase in surface roughness. Nat. Geosci. 2010, 3, 756–761. [Google Scholar] [CrossRef]
- Shi, Z.; Xu, L.; Yang, X.; Guo, H.; Dong, L.; Song, A.; Zhang, X.; Shan, N. Trends in reference evapotranspiration and its attribution over the past 50 years in the Loess Plateau, China: Implications for ecological projects and agricultural production. Stoch. Environ. Res. Risk Assess. 2017, 31, 257–273. [Google Scholar] [CrossRef]
- Xu, M.; Chang, C.-P.; Fu, C.; Qi, Y.; Robock, A.; Robinson, D.; Zhang, H.-M. Steady decline of East Asian monsoon winds, 1969–2000: Evidence from direct ground measurements of wind speed. J. Geophys. Res. 2006, 111, 906–910. [Google Scholar] [CrossRef]
- You, Q.; Kang, S.; Flügel, W.-A.; Pepin, N.; Yan, Y.; Huang, J. Decreasing wind speed and weakening latitudinal surface pressure gradients in the Tibetan Plateau. Clim. Res. 2010, 42, 57–64. [Google Scholar] [CrossRef]
- Lin, C.; Yang, K.; Qin, J. Observed surface and upper-air wind speed changes over China since 1960. J. Clim. 2012, 26, 2891–2903. [Google Scholar] [CrossRef]
- Kwon, M.H.; Jhun, J.G.; Ha, K.J. Decadal change in East Asian summer monsoon circulation in the mid-1990s. Geophys. Res. Lett. 2007, 34, 377–390. [Google Scholar] [CrossRef]
- Teh, C.B.S. Introduction to Mathematical Modeling of Crop Growth: How the Equations Are Derived and Assembled into a Computer Program; BrownWalker Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Stanhill, G.; Cohen, S. Global dimming: A review of the evidence for a widespread and significant reduction in global radiation with discussion of its probable causes and possible agricultural consequences. Agric. For. Meteorol. 2001, 107, 255–278. [Google Scholar] [CrossRef]
- Liepert, B.G. Observed reductions of surface solar radiation at sites in the United States and worldwide from 1961 to 1990. Geophys. Res. Lett. 2002, 29, 1–4. [Google Scholar] [CrossRef]
- Wild, M.; Gilgen, H.; Roesch, A.; Ohmura, A.; Long, C.N.; Dutton, E.G.; Forgan, B.; Kallis, A.; Russak, V.; Tsvetkov, A. From dimming to brightening: Decadal changes in solar radiation at Earth’s surface. Science 2005, 308, 847–850. [Google Scholar] [CrossRef] [PubMed]
- Stjern, C.W.; Ansson, J.E.K.; Hansen, A.W. Global dimming and global brightening-an analysis of surface radiation and cloud cover data in northern Europe. Int. J. Climatol. 2008, 29, 643–653. [Google Scholar] [CrossRef]
- Qian, Y.; Wang, W.; Leung, L.R.; Kaiser, D.P. Variability of solar radiation under cloud-free skies in China: The role of aerosols. Geophys. Res. Lett. 2007, 34, 1–5. [Google Scholar] [CrossRef]
- Che, H.Z.; Shi, G.Y.; Zhang, X.Y.; Arimoto, R.; Zhao, J.Q.; Xu, L.; Wang, B.; Chen, Z.H. Analysis of 40 years of solar radiation data from China, 1961–2000. Geophys. Res. Lett. 2005, 32, 1–5. [Google Scholar] [CrossRef]
- Yang, Y.H.; Zhao, N.; Hu, Y.K.; Zhou, X.Y. Effect of wind speed on sunshine hours in three cities in northern China. Clim. Res. 2009, 39, 149–157. [Google Scholar] [CrossRef]
- Peterson, T.C.; Golubev, V.S.; Groisman, P.Y. Evaporation losing its strength. Nature 1995, 377, 687–688. [Google Scholar] [CrossRef]
- Goyal, R.K. Sensitivity of evapotranspiration to global warming: A case study of arid zone of Rajasthan (India). Agric. Water Manag. 2004, 69, 1–11. [Google Scholar] [CrossRef]
- Hulme, M.; Zhao, Z.; Jiang, T. Recent and future climate change in East Asia. Int. J. Climatol. 1994, 14, 637–658. [Google Scholar] [CrossRef]
- Tang, B.; Tong, L.; Kang, S.; Zhang, L. Impacts of climate variability on reference evapotranspiration over 58 years in the Haihe river basin of north China. Agric. Water Manag. 2011, 97, 1506–1516. [Google Scholar] [CrossRef]
- Roderick, M.L.; Farquhar, G.D. Changes in Australian pan evaporation from 1970 to 2002. Int. J. Climatol. 2004, 24, 1077–1090. [Google Scholar] [CrossRef]
- Gong, L.; Xu, C.-Y.; Chen, D.; Halldin, S.; Chen, Y.D. Sensitivity of the Penman-Monteith reference evapotranspiration to key climatic variables in the Changjiang (Yangtze River) basin. J. Hydrol. 2006, 329, 620–629. [Google Scholar] [CrossRef]
- Estévez, J.; Gavilán, P.; Berengena, J. Sensitivity analysis of a Penman–Monteith ttype equation to estimate reference evapotranspiration in Southern Spain. Hydrol. Process. 2009, 23, 3342–3353. [Google Scholar] [CrossRef]
- Irmak, S.; Payero, J.; Martin, D.; Irmak, A.; Howell, T. Sensitivity analyses and sensitivity coefficients of standardized daily ASCE-Penman-Monteith equation. J. Irrig. Drain. Eng. 2006, 132, 564–578. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, C.; Tan, Y.; Yang, Y. Trends in pan evaporation and reference and actual evapotranspiration across the Tibetan Plateau. J. Geophys. Res. 2007, 112, 1–12. [Google Scholar] [CrossRef]
- Li, M.; Chu, R.; Shen, S.; Islam, A.R.M.T. Dynamic analysis of pan evaporation variations in the Huai River Basin, a climate transition zone in eastern China. Sci. Total Environ. 2018, 625, 496–509. [Google Scholar] [CrossRef] [PubMed]







| Region | Climatic Factor | Annual | Growing Season | Spring | Summer | Autumn | Winter | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Z | β | Z | β | Z | β | Z | β | Z | β | Z | β | ||
| Upper | TA (°C) | 3.48 | 0.01 *** | 2.18 | 0.010 * | 3.76 | 0.034 *** | −0.91 | −0.007 | 2.51 | 0.015 * | 2.76 | 0.025 ** |
| RH (%) | −1.55 | −0.035 | −0.79 | −0.027 | −2.81 | −0.133 ** | 2.09 | 0.056 * | −1.79 | −0.065 | −0.85 | −0.051 | |
| WS (m·s−1) | −9.37 | −0.019 *** | −9.13 | −0.019 *** | −8.30 | −0.020 *** | −8.16 | −0.019 *** | −8.31 | −0.020 *** | −8.18 | −0.020 *** | |
| SR (MJ·m−2·day−1) | −5.09 | −0.030 *** | −4.36 | −0.038 *** | −0.39 | −0.005 | −5.13 | −0.062 *** | −2.27 | −0.018 * | −3.52 | −0.023 *** | |
| Middle | TA (°C) | 3.57 | 0.018 *** | 2.04 | 0.010 * | 3.57 | 0.030 *** | −0.60 | −0.004 | 3.18 | 0.016 ** | 3.49 | 0.032 *** |
| RH (%) | −0.55 | −0.015 | −0.13 | −0.005 | −1.33 | −0.064 | 1.39 | 0.040 | −1.61 | −0.061 | −0.64 | −0.039 | |
| WS (m·s−1) | −9.71 | −0.022 *** | −9.58 | −0.021 *** | −9.04 | −0.024 *** | −9.09 | −0.020 *** | −8.94 | −0.021 *** | −8.56 | −0.023 *** | |
| SR (MJ·m−2·day−1) | −6.01 | −0.035 *** | −5.42 | −0.045 *** | −1.09 | −0.012 | −5.82 | −0.072 *** | −3.10 | −0.026 *** | −4.15 | −0.029 *** | |
| Yi-Shu-Si | TA (°C) | 4.86 | 0.025 *** | 3.63 | 0.017 *** | 4.46 | 0.035 *** | 1.03 | 0.006 | 3.67 | 0.021 *** | 4.43 | 0.040 *** |
| RH (%) | −1.79 | −0.042 | −1.60 | −0.035 | −1.66 | −0.075 | −0.57 | −0.012 | −1.31 | −0.050 | −1.01 | −0.053 | |
| WS (m·s−1) | −8.97 | −0.021 *** | −8.85 | −0.021 *** | −8.55 | −0.025 *** | −8.46 | −0.019 *** | −7.80 | −0.019 *** | −7.58 | −0.020 *** | |
| SR (MJ·m−2·day−1) | −5.82 | −0.030 *** | −5.18 | −0.038 *** | −1.34 | −0.010 | −5.82 | −0.062 *** | −3.27 | −0.025 ** | −3.83 | −0.023 *** | |
| Lower | TA (°C) | 4.67 | 0.027 *** | 3.88 | 0.023 *** | 4.79 | 0.039 *** | 1.31 | 0.012 | 4.07 | 0.026 *** | 3.89 | 0.034 *** |
| RH (%) | −4.79 | −0.109 *** | −4.74 | −0.120 *** | −4.01 | −0.178 *** | −3.36 | −0.085 *** | −3.60 | −0.107 *** | −2.95 | −0.098 ** | |
| WS (m·s−1) | −8.76 | −0.021 *** | −8.27 | −0.019 *** | −8.58 | −0.025 *** | −7.46 | −0.017 *** | −7.33 | −0.019 *** | −7.88 | −0.022 *** | |
| SR (MJ·m−2·day−1) | −4.10 | −0.018 *** | −3.27 | −0.023 ** | 0.95 | 0.009 | −4.18 | −0.056 *** | −1.45 | −0.009 | −2.42 | −0.017 * | |
| Whole | TA (°C) | 4.06 | 0.021 *** | 2.78 | 0.013 ** | 3.88 | 0.032 *** | 0.10 | 0.001 | 3.52 | 0.018 *** | 3.77 | 0.035 *** |
| RH (%) | −1.64 | −0.038 | −1.28 | −0.028 | −1.76 | −0.083 | 0.18 | 0.005 | −1.87 | −0.062 | −0.97 | −0.054 | |
| WS (m·s−1) | −9.64 | −0.021 *** | −9.50 | −0.020 *** | −8.98 | −0.024 *** | −9.00 | −0.019 *** | −8.64 | −0.020 *** | −8.40 | −0.022 *** | |
| SR (MJ·m−2·day−1) | −5.73 | −0.030 *** | −5.25 | −0.040 *** | −0.72 | −0.007 | −5.79 | −0.066 *** | −3.07 | −0.022 ** | −3.80 | −0.025 *** | |
| Region | Annual | Growing Season | Spring | Summer | Autumn | Winter | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Z | β | Z | β | Z | β | Z | β | Z | β | Z | β | |
| Upper | −3.49 | −1.787 *** | −3.55 | −1.578 *** | 0.69 | 0.197 | −4.97 | −1.567 *** | −1.76 | −0.253 | −1.12 | −0.138 |
| Middle | −4.74 | −2.561 *** | −4.92 | −2.287 *** | −1.06 | −0.331 | −5.43 | −1.596 *** | −2.73 | −0.400 ** | −1.82 | −0.235 |
| Yi-Shu-Si | −3.88 | −1.556 *** | −3.83 | −1.446 *** | −0.60 | −0.153 | −4.43 | −1.094 *** | −2.25 | −0.276 * | −0.39 | −0.044 |
| Lower | 0.45 | 0.177 | 0.15 | 0.062 | 3.04 | 0.660 ** | −1.97 | −0.498 * | 0.91 | 0.100 | 0.93 | 0.075 |
| Whole | −4.09 | −1.894 *** | −4.25 | −1.772 *** | −0.39 | −0.122 | −4.64 | −1.307 *** | −2.40 | −0.308 * | −1.24 | −0.143 |
| Region | Sensitivity Coefficient | Annual | Growing Season | Spring | Summer | Autumn | Winter |
|---|---|---|---|---|---|---|---|
| Upper | S(TA) | 0.463 | 0.634 | 0.493 | 0.695 | 0.541 | 0.122 |
| S(RH) | −0.963 | −0.764 | −0.853 | −0.675 | −1.032 | −1.301 | |
| S(WS) | 0.115 | 0.077 | 0.089 | 0.055 | 0.131 | 0.184 | |
| S(SR) | 0.642 | 0.737 | 0.666 | 0.793 | 0.630 | 0.480 | |
| Middle | S(TA) | 0.461 | 0.640 | 0.498 | 0.700 | 0.544 | 0.102 |
| S(RH) | −0.850 | −0.669 | −0.739 | −0.597 | −0.907 | −1.165 | |
| S(WS) | 0.140 | 0.095 | 0.114 | 0.073 | 0.152 | 0.222 | |
| S(SR) | 0.615 | 0.720 | 0.637 | 0.779 | 0.609 | 0.436 | |
| Yi-Shu-Si | S(TA) | 0.436 | 0.639 | 0.480 | 0.699 | 0.536 | 0.028 |
| S(RH) | −0.813 | −0.663 | −0.678 | −0.642 | −0.852 | −1.082 | |
| S(WS) | 0.156 | 0.100 | 0.138 | 0.065 | 0.169 | 0.253 | |
| S(SR) | 0.582 | 0.701 | 0.591 | 0.778 | 0.577 | 0.383 | |
| Lower | S(TA) | 0.481 | 0.662 | 0.488 | 0.724 | 0.588 | 0.122 |
| S(RH) | −1.128 | −0.929 | −1.037 | −0.864 | −1.135 | −1.478 | |
| S(WS) | 0.111 | 0.067 | 0.074 | 0.042 | 0.138 | 0.191 | |
| S(SR) | 0.614 | 0.718 | 0.636 | 0.783 | 0.602 | 0.433 | |
| Whole | S(TA) | 0.459 | 0.643 | 0.493 | 0.703 | 0.549 | 0.091 |
| S(RH) | −0.892 | −0.713 | −0.777 | −0.653 | −0.939 | −1.204 | |
| S(WS) | 0.138 | 0.090 | 0.112 | 0.065 | 0.152 | 0.222 | |
| S(SR) | 0.610 | 0.717 | 0.629 | 0.781 | 0.602 | 0.427 |
| Region | Contribution | Annual | Growing Season | Spring | Summer | Autumn | Winter |
|---|---|---|---|---|---|---|---|
| Upper | C(TA) | 0.572 | 0.248 | 0.324 | −0.056 | 0.103 | 0.133 |
| C(RH) | 0.236 | 0.111 | 0.296 | −0.153 | 0.121 | 0.066 | |
| C(WS) | −1.300 | −0.775 | −0.334 | −0.281 | −0.386 | −0.289 | |
| C(SR) | −1.217 | −1.203 | −0.057 | −1.028 | −0.191 | −0.122 | |
| C_ETref | −1.710 | −1.619 | 0.228 | −1.517 | −0.353 | −0.211 | |
| T_ETref | −1.787 | −1.578 | 0.197 | −1.567 | −0.253 | −0.138 | |
| Middle | C(TA) | 0.584 | 0.225 | 0.297 | −0.039 | 0.121 | 0.158 |
| C(RH) | 0.054 | 0.008 | 0.141 | −0.123 | 0.105 | 0.047 | |
| C(WS) | −1.777 | −1.038 | −0.488 | −0.405 | −0.446 | −0.389 | |
| C(SR) | −1.383 | −1.358 | −0.115 | −1.123 | −0.257 | −0.125 | |
| C_ETref | −2.523 | −2.163 | −0.166 | −1.690 | −0.476 | −0.309 | |
| T_ETref | −2.561 | −2.287 | −0.331 | −1.596 | −0.400 | −0.235 | |
| Yi-Shu-Si | C(TA) | 0.831 | 0.417 | 0.375 | 0.065 | 0.159 | 0.200 |
| C(RH) | 0.289 | 0.153 | 0.177 | 0.020 | 0.092 | 0.078 | |
| C(WS) | −1.622 | −0.977 | −0.567 | −0.321 | −0.395 | −0.325 | |
| C(SR) | −1.133 | −1.130 | −0.096 | −0.986 | −0.224 | −0.087 | |
| C_ETref | −1.635 | −1.537 | −0.112 | −1.223 | −0.368 | −0.134 | |
| T_ETref | −1.556 | −1.446 | −0.153 | −1.094 | −0.276 | −0.044 | |
| Lower | C(TA) | 0.878 | 0.523 | 0.379 | 0.119 | 0.189 | 0.168 |
| C(RH) | 1.012 | 0.768 | 0.467 | 0.242 | 0.243 | 0.154 | |
| C(WS) | −0.983 | −0.540 | −0.285 | −0.157 | −0.285 | −0.241 | |
| C(SR) | −0.753 | −0.720 | 0.056 | −0.869 | −0.109 | −0.069 | |
| C_ETref | 0.155 | 0.031 | 0.617 | −0.665 | 0.039 | 0.012 | |
| T_ETref | 0.177 | 0.062 | 0.660 | −0.498 | 0.100 | 0.075 | |
| Whole | C(TA) | 0.679 | 0.310 | 0.329 | 0.004 | 0.137 | 0.167 |
| C(RH) | 0.254 | 0.151 | 0.207 | −0.046 | 0.122 | 0.071 | |
| C(WS) | −1.608 | −0.944 | −0.473 | −0.345 | −0.411 | −0.347 | |
| C(SR) | −1.222 | −1.204 | −0.080 | −1.047 | −0.223 | −0.108 | |
| C_ETref | −1.897 | −1.687 | −0.018 | −1.434 | −0.374 | −0.217 | |
| T_ETref | −1.894 | −1.772 | −0.122 | −1.307 | −0.308 | −0.143 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Chu, R.; Shen, S.; Islam, A.R.M.T. Quantifying Climatic Impact on Reference Evapotranspiration Trends in the Huai River Basin of Eastern China. Water 2018, 10, 144. https://doi.org/10.3390/w10020144
Li M, Chu R, Shen S, Islam ARMT. Quantifying Climatic Impact on Reference Evapotranspiration Trends in the Huai River Basin of Eastern China. Water. 2018; 10(2):144. https://doi.org/10.3390/w10020144
Chicago/Turabian StyleLi, Meng, Ronghao Chu, Shuanghe Shen, and Abu Reza Md. Towfiqul Islam. 2018. "Quantifying Climatic Impact on Reference Evapotranspiration Trends in the Huai River Basin of Eastern China" Water 10, no. 2: 144. https://doi.org/10.3390/w10020144
APA StyleLi, M., Chu, R., Shen, S., & Islam, A. R. M. T. (2018). Quantifying Climatic Impact on Reference Evapotranspiration Trends in the Huai River Basin of Eastern China. Water, 10(2), 144. https://doi.org/10.3390/w10020144






