Towards Development of an Optimization Model to Identify Contamination Source in a Water Distribution Network
Abstract
:1. Introduction
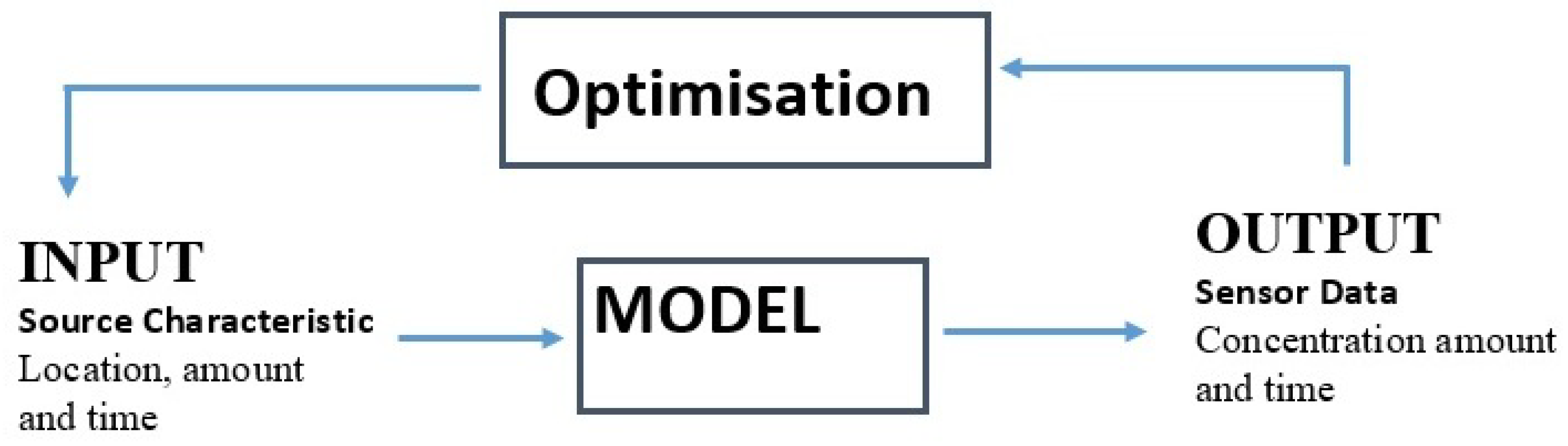
2. Contamination Source Identification (CSI) Problem
3. Water Quality Models
4. Solution Approaches to the Pipe Network Problem
5. Water Quality Modelling Approach
6. Available Simulation Tools
6.1. EPANET
EPANET MSX
6.2. PORTEAU
6.3. Piccolo
6.4. Synergi Water
6.5. WaterGEMS
6.6. H2ONET
7. Solution Approaches to Source Identification Problems
7.1. Simulation–Optimisation Approach
7.2. Probabilistic Approach
7.3. Other Approaches
8. Summary of Existing Approaches
9. Challenges, Suggested Solutions and Future Directions
10. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Swamee, P.K.; Sharma, A.K. Design of Water Supply Pipe Networks; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Yazdani, A.; Otoo, R.A.; Jeffrey, P. Resilience enhancing expansion strategies for water distribution systems: A network theory approach. Environ. Model. Softw. 2011, 26, 1574–1582. [Google Scholar] [CrossRef]
- Collins, M.; Cooper, L.; Helgason, R.; Kennington, J.; LeBlanc, L. Solving the pipe network analysis problem using optimization techniques. Manag. Sci. 1978, 24, 747–760. [Google Scholar] [CrossRef]
- Clark, R.M.; Grayman, W.M.; Males, R.M.; Hess, A.F. Modeling contaminant propagation in drinking-water distribution systems. J. Environ. Eng. 1993, 119, 349–364. [Google Scholar] [CrossRef]
- Clark, R.M.; Grayman, W.M.; Goodrich, J.A.; Deininger, R.A.; Skov, K. Measuring and modeling chlorine propagation in water distribution systems. J. Water Resour. Plan. Manag. 1994, 120, 871–887. [Google Scholar] [CrossRef]
- Clark, R.M.; Grayman, W.M.; Males, R.M. Contaminant propagation in distribution systems. J. Environ. Eng. 1988, 114, 929–943. [Google Scholar] [CrossRef]
- Clark, R.M.; Deininger, R.A. Protecting the nation’s critical infrastructure: The vulnerability of US water supply systems. J. Conting. Crisis Manag. 2000, 8, 73–80. [Google Scholar] [CrossRef]
- Kirmeyer, G.J.; Martel, K. Pathogen Intrusion into the Distribution System; American Water Works Association: Denver, CO, USA, 2001. [Google Scholar]
- Mac Kenzie, W.R.; Hoxie, N.J.; Proctor, M.E.; Gradus, M.S.; Blair, K.A.; Peterson, D.E.; Kazmierczak, J.J.; Addiss, D.G.; Fox, K.R.; Rose, J.B.; et al. A massive outbreak in Milwaukee of Cryptosporidium infection transmitted through the public water supply. N. Engl. J. Med. 1994, 331, 161–167. [Google Scholar] [CrossRef] [PubMed]
- Corso, P.S.; Kramer, M.H.; Blair, K.A.; Addiss, D.G.; Davis, J.P.; Haddix, A.C. Costs of illness in the 1993 waterborne Cryptosporidium outbreak, Milwaukee, Wisconsin. Emerg. Infect. Dis. 2003, 9, 426. [Google Scholar] [CrossRef] [PubMed]
- Cooper, W.J. Responding to crisis: The West Virginia chemical spill. Environ. Sci. Technol. 2014, 48, 3095. [Google Scholar] [CrossRef] [PubMed]
- Berry, J.W.; Fleischer, L.; Hart, W.E.; Phillips, C.A.; Watson, J.P. Sensor placement in municipal water networks. J. Water Resour. Plan. Manag. 2005, 131, 237–243. [Google Scholar] [CrossRef]
- Berry, J.W.; Hart, W.E.; Phillips, C.A.; Uber, J.G.; Watson, J.P. Validation and assessment of integer programming sensor placement models. In Impacts of Global Climate Change; American Society of Civil Engineers: Reston, VA, USA, 2005; pp. 1–11. [Google Scholar]
- Berry, J.; Hart, W.E.; Phillips, C.A.; Uber, J.G.; Watson, J.P. Sensor placement in municipal water networks with temporal integer programming models. J. Water Resour. Plan. Manag. 2006, 132, 218–224. [Google Scholar] [CrossRef]
- Berry, J.; Carr, R.D.; Hart, W.E.; Leung, V.J.; Phillips, C.A.; Watson, J.P. Designing contamination warning systems for municipal water networks using imperfect sensors. J. Water Resour. Plan. Manag. 2009, 135, 253–263. [Google Scholar] [CrossRef]
- Ostfeld, A.; Salomons, E. Optimal layout of early warning detection stations for water distribution systems security. J. Water Resour. Plan. Manag. 2004, 130, 377–385. [Google Scholar] [CrossRef]
- Ostfeld, A.; Salomons, E. Optimal early warning monitoring system layout for water networks security: Inclusion of sensors sensitivities and response delays. Civ. Eng. Environ. Syst. 2005, 22, 151–169. [Google Scholar] [CrossRef]
- Ostfeld, A.; Salomons, E. Securing water distribution systems using online contamination monitoring. J. Water Resour. Plan. Manag. 2005, 131, 402–405. [Google Scholar] [CrossRef]
- Ostfeld, A.; Uber, J.G.; Salomons, E.; Berry, J.W.; Hart, W.E.; Phillips, C.A.; Watson, J.P.; Dorini, G.; Jonkergouw, P.; Kapelan, Z.; et al. The battle of the water sensor networks (BWSN): A design challenge for engineers and algorithms. J. Water Resour. Plan. Manag. 2008, 134, 556–568. [Google Scholar] [CrossRef]
- Propato, M. Contamination warning in water networks: General mixed-integer linear models for sensor location design. J. Water Resour. Plan. Manag. 2006, 132, 225–233. [Google Scholar] [CrossRef]
- Kansal, M.; Dorji, T.; Chandniha, S.K. Design scheme for water quality monitoring in a distribution network. Int. J. Environ. Dev. 2012, 9, 69–81. [Google Scholar]
- Krause, A.; Leskovec, J.; Guestrin, C.; VanBriesen, J.; Faloutsos, C. Efficient sensor placement optimization for securing large water distribution networks. J. Water Resour. Plan. Manag. 2008, 134, 516–526. [Google Scholar] [CrossRef]
- Afshar, A.; Mariño, M.A. Multi-objective coverage-based ACO model for quality monitoring in large water networks. Water Resour. Manag. 2012, 26, 2159–2176. [Google Scholar] [CrossRef]
- Afshar, A.; Khombi, S.M. Multiobjective Optimization of Sensor Placement in Water Distribution Networks; Dual Use Benefit Approach. Int. J. Optim. Civ. Eng. 2015, 5, 315–331. [Google Scholar]
- Woo, H.M.; Yoon, J.H.; Choi, D.Y. Optimal monitoring sites based on water quality and quantity in water distribution systems. In Bridging the Gap: Meeting the World’s Water and Environmental Resources Challenges; American Society of Civil Engineers: Reston, VA, USA, 2001; pp. 1–9. [Google Scholar]
- Cozzolino, L.; Mucherino, C.; Pianese, D.; Pirozzi, F. Positioning, within water distribution networks, of monitoring stations aiming at an early detection of intentional contamination. Civ. Eng. Environ. Syst. 2006, 23, 161–174. [Google Scholar] [CrossRef]
- Adedeji, K.B.; Hamam, Y.; Abe, B.T.; Abu-Mahfouz, A.M. Leakage Detection and Estimation Algorithm for Loss Reduction in Water Piping Networks. Water 2017, 9, 773. [Google Scholar] [CrossRef]
- Hindi, K.; Hamam, Y. Locating pressure control elements for leakage minimization in water supply networks: An optimization model. Eng. Optim. 1991, 17, 281–291. [Google Scholar] [CrossRef]
- Hindi, K.; Hamam, Y. Pressure control for leakage minimization in water supply networks Part 1: Single period models. Int. J. Syst. Sci. 1991, 22, 1573–1585. [Google Scholar] [CrossRef]
- Hindi, K.; Hamam, Y. Locating pressure control elements for leakage minimisation in water supply networks by genetic algorithms. In Artificial Neural Nets and Genetic Algorithms; Springer: Vienna, Austria, 1993; pp. 583–587. [Google Scholar]
- Sun, N.Z. Inverse Problems in Groundwater Modeling; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Laird, C.D.; Biegler, L.T.; van Bloemen Waanders, B.G.; Bartlett, R.A. Contamination source determination for water networks. J. Water Resour. Plan. Manag. 2005, 131, 125–134. [Google Scholar] [CrossRef]
- De Sanctis, A.E.; Shang, F.; Uber, J.G. Real-time identification of possible contamination sources using network backtracking methods. J. Water Resour. Plan. Manag. 2009, 136, 444–453. [Google Scholar] [CrossRef]
- Wang, H.; Harrison, K.W. Improving efficiency of the Bayesian approach to water distribution contaminant source characterization with support vector regression. J. Water Resour. Plan. Manag. 2012, 140, 3–11. [Google Scholar] [CrossRef]
- Huang, J.J.; McBean, E.A.; James, W. Multi-objective optimization for monitoring sensor placement in water distribution systems. In Water Distribution Systems Analysis Symposium 2006; American Society of Civil Engineers: Reston, VA, USA, 2008; pp. 1–14. [Google Scholar]
- Tsitsifli, S.; Kanakoudis, V. Drinking water quality and safety assessment—A review. In Proceedings of the 6th International Conference on Environmental Management, Planning, Engineering (CEMEPE2017), Thessaloniki, Greece, 25–30 June 2017; pp. 403–416. [Google Scholar]
- Kanakoudis, V.; Tsitsifli, S. Potable water security assessment—A review on monitoring, modelling and optimization techniques, applied to water distribution networks. Desalin. Water Treat. 2017, 99, 18–26. [Google Scholar] [CrossRef]
- Deng, W.; Wang, G. A novel water quality data analysis framework based on time-series data mining. J. Environ. Manag. 2017, 196, 365–375. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.; Zhao, J.; Yan, X.; Zeng, D.; Guo, S. A MapReduce based parallel niche genetic algorithm for contaminant source identification in water distribution network. Ad Hoc Netw. 2015, 35, 116–126. [Google Scholar] [CrossRef]
- Perelman, L.; Ostfeld, A. Bayesian networks for source intrusion detection. J. Water Resour. Plan. Manag. 2012, 139, 426–432. [Google Scholar] [CrossRef]
- Wagner, D.; Neupauer, R. Probabilistic contaminant source identification in water distribution systems with incomplete mixing at pipe junctions. In World Environmental and Water Resources Congress 2013: Showcasing the Future; American Society of Civil Engineers: Reston, VA, USA, 2013; pp. 930–935. [Google Scholar]
- Guan, J.; Aral, M.M.; Maslia, M.L.; Grayman, W.M. Identification of contaminant sources in water distribution systems using simulation-optimization method: Case study. J. Water Resour. Plan. Manag. 2006, 132, 252–262. [Google Scholar] [CrossRef]
- Liu, L.; Ranjithan, S.R.; Mahinthakumar, G. Contamination source identification in water distribution systems using an adaptive dynamic optimization procedure. J. Water Resour. Plan. Manag. 2010, 137, 183–192. [Google Scholar] [CrossRef]
- Liu, L.; Zechman, E.M.; Brill, E.D., Jr.; Mahinthakumar, G.; Ranjithan, S.; Uber, J. Adaptive contamination source identification in water distribution systems using an evolutionary algorithm-based dynamic optimization procedure. In Water Distribution Systems Analysis Symposium 2006; American Society of Civil Engineers: Reston, VA, USA, 2008; pp. 1–9. [Google Scholar]
- Shang, F.; Uber, J.; Murray, R. Uncertainty of contamination source characterization within water distribution systems. In World Environmental and Water Resources Congress 2007: Restoring Our Natural Habitat; American Society of Civil Engineers: Reston, VA, USA, 2007; pp. 1–8. [Google Scholar]
- Murray, R.; Haxton, T.; Janke, R.; Hart, W.E.; Berry, J.; Phillips, C. Sensor Network Design for Drinking Water Contamination Warning Systems: A Compendium of Research Results and Case Studies Using the TEVA-SPOT Software; National Homeland Security Research Center, US Environmental Protection Agency: Cincinnati, OH, USA, 2010.
- Rossman, L.A. EPANET 2: Users Manual; National Risk Management Research Laboratory: Cincinnati, OH, USA, 2000. [Google Scholar]
- Tinelli, S.; Creaco, E.; Ciaponi, C. Sampling significant contamination events for optimal sensor placement in water distribution systems. J. Water Resour. Plan. Manag. 2017, 143, 04017058. [Google Scholar] [CrossRef]
- Davidson, J.; Bouchart, F.; Cavill, S.; Jowitt, P. Real-time connectivity modeling of water distribution networks to predict contamination spread. J. Comput. Civ. Eng. 2005, 19, 377–386. [Google Scholar] [CrossRef]
- Boulus, P.F.; Altman, T.; Sadhal, K.S. Computer modeling of water quality in large multiple-source networks. Appl. Math. Model. 1992, 16, 439–445. [Google Scholar] [CrossRef]
- Males, R.M.; Clark, R.M.; Wehrman, P.J.; Gates, W.E. Algorithm for mixing problems in water systems. J. Hydraul. Eng. 1985, 111, 206–219. [Google Scholar] [CrossRef]
- Wood, D.J.; Ormsbee, L.E. Supply identification for water distribution systems. J. Am. Water Works Assoc. 1989, 81, 74–80. [Google Scholar] [CrossRef]
- Bhave, P.R. Extended period simulation of water systems—Direct solution. J. Environ. Eng. 1988, 114, 1146–1159. [Google Scholar] [CrossRef]
- Creaco, E.; Pezzinga, G. Embedding linear programming in multi objective genetic algorithms for reducing the size of the search space with application to leakage minimization in water distribution networks. Environ. Model. Softw. 2015, 69, 308–318. [Google Scholar] [CrossRef]
- Giustolisi, O.; Kapelan, Z.; Savic, D. Extended period simulation analysis considering valve shutdowns. J. Water Resour. Plan. Manag. 2008, 134, 527–537. [Google Scholar] [CrossRef]
- Giustolisi, O.; Laucelli, D.; Berardi, L.; Savić, D.A. Computationally efficient modeling method for large water network analysis. J. Hydraul. Eng. 2011, 138, 313–326. [Google Scholar] [CrossRef]
- Todini, E. A more realistic approach to the extended period simulation of water distribution networks. Adv. Water Supply Manag. 2003, 173–184. [Google Scholar]
- Rossman, L.A.; Boulos, P.F. Numerical methods for modeling water quality in distribution systems: A comparison. J. Water Resour. Plan. Manag. 1996, 122, 137–146. [Google Scholar] [CrossRef]
- Liou, C.; Kroon, J. Modeling the propagation of waterborne substances in distribution networks. J. Am. Water Works Assoc. 1987, 79, 54–58. [Google Scholar] [CrossRef]
- Boulos, P.F.; Altman, T.; Jarrige, P.A.; Collevati, F. Discrete simulation approach for network-water-quality models. J. Water Resour. Plan. Manag. 1995, 121, 49–60. [Google Scholar] [CrossRef]
- Boulos, P.F.; Altman, T.; Jarrige, P.A.; Collevati, F. An event-driven method for modelling contaminant propagation in water networks. Appl. Math. Model. 1994, 18, 84–92. [Google Scholar] [CrossRef]
- Islam, M.R.; Chaudhry, M.H. Modeling of constituent transport in unsteady flows in pipe networks. J. Hydraul. Eng. 1998, 124, 1115–1124. [Google Scholar] [CrossRef]
- Grayman, W.M.; Clark, R.M.; Males, R.M. Modeling distribution-system water quality; dynamic approach. J. Water Resour. Plan. Manag. 1988, 114, 295–312. [Google Scholar] [CrossRef]
- Rossman, L.A.; Boulos, P.F.; Altman, T. Discrete volume-element method for network water-quality models. J. Water Resour. Plan. Manag. 1993, 119, 505–517. [Google Scholar] [CrossRef]
- Rossman, L.A.; Clark, R.M.; Grayman, W.M. Modeling chlorine residuals in drinking-water distribution systems. J. Environ. Eng. 1994, 120, 803–820. [Google Scholar] [CrossRef]
- Mansour-Rezaei, S.; Naser, G.; Malekpour, A.; Karney, B.W. Contaminant intrusion in water distribution systems. J. Am. Water Works Assoc. 2013, 105, E278–E290. [Google Scholar] [CrossRef]
- Fernandes, C.; Karney, B. Modelling the advection equation under water hammer conditions. Urban Water J. 2004, 1, 97–112. [Google Scholar] [CrossRef]
- Tzatchkov, V.G.; Aldama, A.A.; Arreguin, F.I. Advection-dispersion-reaction modeling in water distribution networks. J. Water Resour. Plan. Manag. 2002, 128, 334–342. [Google Scholar] [CrossRef]
- Basha, H.; Malaeb, L. Eulerian-Lagrangian method for constituent transport in water distribution networks. J. Hydraul. Eng. 2007, 133, 1155–1166. [Google Scholar] [CrossRef]
- Munavalli, G.; Kumar, M.M. Modified Lagrangian method for modeling water quality in distribution systems. Water Res. 2004, 38, 2973–2988. [Google Scholar] [CrossRef] [PubMed]
- Cross, H. Analysis of Flow in Networks of Conduits or Conductors. In Analysis of Flow in Networks of Conduits or Conductors; Technical Report; University of Illinois at Urbana Champaign, College of Engineering, Engineering Experiment Station: Champaign, IL, USA, 1936. [Google Scholar]
- Martin, D.; Peters, G. The application of Newtons method to network analysis by digital computer. J. Inst. Water Eng. 1963, 17, 115–129. [Google Scholar]
- Epp, R.; Fowler, A.G. Efficient code for steady-state flows in networks. J. Hydraul. Div. 1970, 96, 43–56. [Google Scholar]
- Hamam, Y.; Brameller, A. Hybrid method for the solution of piping networks. Proc. Inst. Electr. Eng. 1971, 118, 1607–1612. [Google Scholar] [CrossRef]
- Wood, D.J.; Charles, C.O. Hydraulic network analysis using linear theory. J. Hydraul. Div. 1972, 98, 1157–1170. [Google Scholar]
- Todini, E.; Pilati, S. A gradient method for the analysis of pipe networks. In Proceedings of the International Conference on Computer Applications for Water Supply and Distribution, Leicester Polytechnic, UK, 8–10 September 1987. [Google Scholar]
- Todini, E. A unifying view on the different looped pipe network analysis algorithms. In Computing and Control for the Water Industry; Research Studies Press Ltd.: Baldock, UK, 1999; pp. 63–80. [Google Scholar]
- Todini, E.; Rossman, L.A. Unified framework for deriving simultaneous equation algorithms for water distribution networks. J. Hydraul. Eng. 2012, 139, 511–526. [Google Scholar] [CrossRef]
- Walski, T.M.; Chase, D.V.; Savic, D.A.; Grayman, W.; Beckwith, S.; Koelle, E. Advanced Water Distribution Modeling and Management. Civ. Environ. Eng. Eng. Mech. Fac. Publ. 2003, 18. [Google Scholar]
- Strafaci, A. Advanced Water Distribution Modeling and Management. Ed; Haestad Press: Waterbury, CT, USA, 2003; pp. 577–583. [Google Scholar]
- Clark, R.M.; Rossman, L.A.; Wymer, L.J. Modeling distribution system water quality: Regulatory implications. J. Water Resour. Plan. Manag. 1995, 121, 423–428. [Google Scholar] [CrossRef]
- Ozdemir, O.N.; Ger, A.M. Unsteady 2-D chlorine transport in water supply pipes. Water Res. 1999, 33, 3637–3645. [Google Scholar] [CrossRef]
- Al-Omari, A.S.; Chaudhry, M.H. Unsteady-state inverse chlorine modeling in pipe networks. J. Hydraul. Eng. 2001, 127, 669–677. [Google Scholar] [CrossRef]
- Ozdemir, O.N.; Ucak, A. Simulation of chlorine decay in drinking-water distribution systems. J. Environ. Eng. 2002, 128, 31–39. [Google Scholar] [CrossRef]
- Boulos, P.; Altman, T. Explicit calculation of water quality parameters in pipe distribution systems. Civ. Eng. Syst. 1993, 10, 187–206. [Google Scholar] [CrossRef]
- Mau, R.E.; Boulos, P.F.; Bowcock, R.W. Modelling distribution storage water quality: An analytical approach. Appl. Math. Model. 1996, 20, 329–338. [Google Scholar] [CrossRef]
- Islam, M.R.; Chaudhry, M.H. Numerical solution of transport equation for applications in environmental hydraulics and hydrology. J. Hydrol. 1997, 191, 106–121. [Google Scholar] [CrossRef]
- Islam, M.R.; Chaudhry, M.H.; Clark, R.M. Inverse modeling of chlorine concentration in pipe networks under dynamic condition. J. Environ. Eng. 1997, 123, 1033–1040. [Google Scholar] [CrossRef]
- Zierolf, M.L.; Polycarpou, M.M.; Uber, J.G. Development and autocalibration of an input-output model of chlorine transport in drinking water distribution systems. IEEE Trans. Control Syst. Technol. 1998, 6, 543–553. [Google Scholar] [CrossRef]
- Shang, F.; Uber, J.G.; Polycarpou, M.M. Particle backtracking algorithm for water distribution system analysis. J. Environ. Eng. 2002, 128, 441–450. [Google Scholar] [CrossRef]
- Al-Zahrani, M.A.; Moied, K. Optimizing water quality monitoring stations using genetic algorithms. Arab. J. Sci. Eng. 2003, 28, 57–75. [Google Scholar]
- Ewing, R.E.; Wang, H. A summary of numerical methods for time-dependent advection-dominated partial differential equations. In Partial Differential Equations; Elsevier: New York, NY, USA, 2001; pp. 423–445. [Google Scholar]
- Alhumaizi, K. Comparison of finite difference methods for the numerical simulation of reacting flow. Comput. Chem. Eng. 2004, 28, 1759–1769. [Google Scholar] [CrossRef]
- Alhumaizi, K. Flux-limiting solution techniques for simulation of reaction–diffusion–convection system. Commun. Nonlinear Sci. Numer. Simul. 2007, 12, 953–965. [Google Scholar] [CrossRef]
- Hallam, N.; West, J.; Forster, C.; Powell, J.; Spencer, I. The decay of chlorine associated with the pipe wall in water distribution systems. Water Res. 2002, 36, 3479–3488. [Google Scholar] [CrossRef]
- Munavalli, G.; Kumar, M.M. Water quality parameter estimation in steady-state distribution system. J. Water Resour. Plan. Manag. 2003, 129, 124–134. [Google Scholar] [CrossRef]
- Munavalli, G.; Kumar, M.M. Water quality parameter estimation in a distribution system under dynamic state. Water Res. 2005, 39, 4287–4298. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.J.; Haught, R.C.; Goodrich, J.A. Real-time contaminant detection and classification in a drinking water pipe using conventional water quality sensors: Techniques and experimental results. J. Environ. Manag. 2009, 90, 2494–2506. [Google Scholar] [CrossRef] [PubMed]
- Gancel, G.; Mortazavi, I.; Piller, O. Coupled numerical simulation and sensitivity assessment for quality modelling for water distribution systems. Appl. Math. Lett. 2006, 19, 1313–1319. [Google Scholar] [CrossRef]
- Siew, C.; Tanyimboh, T.T. Pressure-dependent EPANET extension: Extended period simulation. In Water Distribution Systems Analysis 2010; American Society of Civil Engineers: Reston, VA, USA, 2010; pp. 85–95. [Google Scholar]
- Jun, L.; Guoping, Y. Iterative methodology of pressure-dependent demand based on EPANET for pressure-deficient water distribution analysis. J. Water Resour. Plan. Manag. 2012, 139, 34–44. [Google Scholar] [CrossRef]
- Muranho, J.; Ferreira, A.; Sousa, J.; Gomes, A.; Marques, A.S. Pressure-dependent demand and leakage modelling with an EPANET extension—WaterNetGen. Proc. Eng. 2014, 89, 632–639. [Google Scholar] [CrossRef]
- Conejos, M.P.; Alzamora, F.M.; Alonso, J.C. A water distribution system model to simulate critical scenarios by considering both leakage and pressure dependent demands. Proc. Eng. 2017, 186, 380–387. [Google Scholar] [CrossRef]
- Zhang, G.Y. Real-Time Simulation of Pipe Network Based on EPANET. In Applied Mechanics and Materials; Trans Tech Publications: Zürich, Switzerland, 2014; Volume 548, pp. 1800–1803. [Google Scholar]
- Seyoum, A.G.; Tanyimboh, T.T. Investigation into the pressure-driven extension of the EPANET hydraulic simulation model for water distribution systems. Water Resour. Manag. 2016, 30, 5351–5367. [Google Scholar] [CrossRef]
- Puri, D.; Borel, K.; Vance, C.; Karthikeyan, R. Optimization of a Water Quality Monitoring Network Using a Spatially Referenced Water Quality Model and a Genetic Algorithm. Water 2017, 9, 704. [Google Scholar] [CrossRef]
- Huang, L.; Wang, L.; Zhang, Y.; Xing, L.; Hao, Q.; Xiao, Y.; Yang, L.; Zhu, H. Identification of Groundwater Pollution Sources by a SCE-UA Algorithm-Based Simulation/Optimization Model. Water 2018, 10, 193. [Google Scholar] [CrossRef]
- Huang, P.S.; Chiu, Y.C. A Simulation-Optimization Model for Seawater Intrusion Management at Pingtung Coastal Area, Taiwan. Water 2018, 10, 251. [Google Scholar] [CrossRef]
- Anele, A.O.; Hamam, Y.; Abu-Mahfouz, A.M.; Todini, E. Overview, Comparative Assessment and Recommendations of Forecasting Models for Short-Term Water Demand Prediction. Water 2017, 9, 887. [Google Scholar] [CrossRef]
- Letting, L.K.; Hamam, Y.; Abu-Mahfouz, A.M. Estimation of Water Demand in Water Distribution Systems Using Particle Swarm Optimization. Water 2017, 9, 593. [Google Scholar] [CrossRef]
- Lee, Y.J.; Park, C.; Lee, M.L. Identification of a Contaminant Source Location in a River System Using Random Forest Models. Water 2018, 10, 391. [Google Scholar] [CrossRef]
- van Bloemen Waanders, B.G.; Bartlett, R.A.; Biegler, L.T.; Laird, C.D. Nonlinear programming strategies for source detection of municipal water networks. In World Water & Environmental Resources Congress 2003; American Society of Civil Engineers: Reston, VA, USA, 2003; pp. 1–10. [Google Scholar]
- Laird, C.D.; Biegler, L.T.; van Bloemen Waanders, B.G. Real-time, large-scale optimization of water network systems using a subdomain approach. In Real-Time PDE-Constrained Optimization; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2007; pp. 289–306. [Google Scholar]
- Preis, A.; Ostfeld, A. A contamination source identification model for water distribution system security. Eng. Optim. 2007, 39, 941–947. [Google Scholar] [CrossRef]
- Preis, A.; Ostfeld, A. Multiobjective sensor design for water distribution systems security. In Water Distribution Systems Analysis Symposium 2006; American Society of Civil Engineers: Reston, VA, USA, 2008; pp. 1–17. [Google Scholar]
- Preis, A.; Ostfeld, A. Genetic algorithm for contaminant source characterization using imperfect sensors. Civ. Eng. Environ. Syst. 2008, 25, 29–39. [Google Scholar] [CrossRef]
- Prasad, T.D.; Park, N.S. Multiobjective genetic algorithms for design of water distribution networks. J. Water Resour. Plan. Manag. 2004, 130, 73–82. [Google Scholar] [CrossRef]
- Van Thienen, P. Alternative strategies for optimal water quality sensor placement in drinking water distribution networks. In Proceedings of the 11th International Conference on Hydroinformatics, New York, NY, USA, 16–21 August 2014. [Google Scholar]
- Chung, G.; Lansey, K.; Bayraksan, G. Reliable water supply system design under uncertainty. Environ. Model. Softw. 2009, 24, 449–462. [Google Scholar] [CrossRef]
- Li, Y.; Huang, G.; Nie, S. Planning water resources management systems using a fuzzy-boundary interval-stochastic programming method. Adv. Water Resour. 2010, 33, 1105–1117. [Google Scholar] [CrossRef]
- Li, Y.; Huang, G.; Nie, S.; Chen, X. A robust modeling approach for regional water management under multiple uncertainties. Agric. Water Manag. 2011, 98, 1577–1588. [Google Scholar] [CrossRef]
- Torres, J.M.; Brumbelow, K.; Guikema, S.D. Risk classification and uncertainty propagation for virtual water distribution systems. Reliab. Eng. Syst. Saf. 2009, 94, 1259–1273. [Google Scholar] [CrossRef]
- Preis, A.; Ostfeld, A. Hydraulic uncertainty inclusion in water distribution systems contamination source identification. Urban Water J. 2011, 8, 267–277. [Google Scholar] [CrossRef]
- Vankayala, P.; Sankarasubramanian, A.; Ranjithan, S.R.; Mahinthakumar, G. Contaminant source identification in water distribution networks under conditions of demand uncertainty. Environ. Forensics 2009, 10, 253–263. [Google Scholar] [CrossRef]
- Yan, X.; Zhao, J.; Hu, C. Research on Multimodal Optimization Algorithm for the Contamination Source Identification of City Water Distribution Networks. In Bio-Inspired Computing-Theories and Applications; Springer: Singapore, 2016; pp. 80–85. [Google Scholar]
- Hill, J.; van Bloemen Waanders, B.; Laird, C. Source inversion with uncertain sensor measurements. In Proceedings of the Water Distribution System Analysis Symposium 2006, Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar]
- Cristo, C.D.; Leopardi, A. Pollution source identification of accidental contamination in water distribution networks. J. Water Resour. Plan. Manag. 2008, 134, 197–202. [Google Scholar] [CrossRef]
- Mou, L.; Menglin, W.; Jie, L.; Shen, D. Notice of Retraction Investigation on backward tracking of contamination sources in water supply systems—Case study. In Proceedings of the 2010 The 2nd Conference on Environmental Science and Information Application Technology, Wuhan, China, 17–18 July 2010; Volume 3, pp. 484–487. [Google Scholar]
- Tryby, M.E.; Propato, M.; Ranjithan, S.R. Monitoring design for source identification in water distribution systems. J. Water Resour. Plan. Manag. 2010, 136, 637–646. [Google Scholar] [CrossRef]
- Gugat, M. Contamination source determination in water distribution networks. SIAM J. Appl. Math. 2012, 72, 1772–1791. [Google Scholar] [CrossRef]
- Yan, X.; Gong, W.; Wu, Q. Contaminant source identification of water distribution networks using cultural algorithm. Concurr. Comput. Pract. Exp. 2017, 29. [Google Scholar] [CrossRef]
- Yan, X.; Zhao, J.; Hu, C.; Wu, Q. Contaminant source identification in water distribution network based on hybrid encoding. J. Comput. Methods Sci. Eng. 2016, 16, 379–390. [Google Scholar] [CrossRef]
- Xuesong, Y.; Jie, S.; Chengyu, H. Research on contaminant sources identification of uncertainty water demand using genetic algorithm. Cluster Comput. 2017, 20, 1007–1016. [Google Scholar] [CrossRef]
- Neupauer, R.M.; Wilson, J.L. Adjoint method for obtaining backward-in-time location and travel time probabilities of a conservative groundwater contaminant. Water Resour. Res. 1999, 35, 3389–3398. [Google Scholar] [CrossRef]
- Neupauer, R.M. Adjoint sensitivity analysis of contaminant concentrations in water distribution systems. J. Eng. Mech. 2010, 137, 31–39. [Google Scholar] [CrossRef]
- Austin, R.; Waanders, B.v.B.; McKenna, S.; Choi, C. Mixing at cross junctions in water distribution systems. II: Experimental study. J. Water Resour. Plan. Manag. 2008, 134, 295–302. [Google Scholar] [CrossRef]
- Wang, H.; Jin, X. Characterization of groundwater contaminant source using Bayesian method. Stoch. Environ. Res. Risk Assess. 2013, 27, 867–876. [Google Scholar] [CrossRef]
- Ung, H.; Piller, O.; Gilbert, D.; Mortazavi, I. Accurate and Optimal Sensor Placement for Source Identification of Water Distribution Networks. J. Water Resour. Plan. Manag. 2017, 143, 04017032. [Google Scholar] [CrossRef]
- Hobbs, B.F. Bayesian methods for analysing climate change and water resource uncertainties. J. Environ. Manag. 1997, 49, 53–72. [Google Scholar] [CrossRef]
- Bates, B.C.; Campbell, E.P. A Markov chain Monte Carlo scheme for parameter estimation and inference in conceptual rainfall-runoff modeling. Water Resour. Res. 2001, 37, 937–947. [Google Scholar] [CrossRef]
- Marshall, L.; Nott, D.; Sharma, A. A comparative study of Markov chain Monte Carlo methods for conceptual rainfall-runoff modeling. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Boccelli, D.; Uber, J. Incorporating spatial correlation in a Markov chain Monte Carlo approach for network model calibration. Impacts Glob. Clim. Chang. 2005, 1–8. [Google Scholar] [CrossRef]
- Soldevila, A.; Fernandez-Canti, R.M.; Blesa, J.; Tornil-Sin, S.; Puig, V. Leak localization in water distribution networks using Bayesian classifiers. J. Process Control 2017, 55, 1–9. [Google Scholar] [CrossRef]
- Gargano, R.; Tricarico, C.; Granata, F.; Santopietro, S.; de Marinis, G. Probabilistic models for the peak residential water demand. Water 2017, 9, 417. [Google Scholar] [CrossRef]
- Candelieri, A. Clustering and Support Vector Regression for Water Demand Forecasting and Anomaly Detection. Water 2017, 9, 224. [Google Scholar] [CrossRef]
- Shabani, S.; Candelieri, A.; Archetti, F.; Naser, G. Gene Expression Programming Coupled with Unsupervised Learning: A Two-Stage Learning Process in Multi-Scale, Short-Term Water Demand Forecasts. Water 2018, 10, 142. [Google Scholar] [CrossRef]
- Candelieri, A.; Perego, R.; Archetti, F. Bayesian optimization of pump operations in water distribution systems. J. Glob. Optim. 2018, 1–23. [Google Scholar] [CrossRef]
- Zhang, J.; Zeng, L.; Chen, C.; Chen, D.; Wu, L. Efficient Bayesian experimental design for contaminant source identification. Water Resour. Res. 2015, 51, 576–598. [Google Scholar] [CrossRef]
- Dawsey, W.J.; Minsker, B.S.; VanBlaricum, V.L. Bayesian belief networks to integrate monitoring evidence of water distribution system contamination. J. Water Resour. Plan. Manag. 2006, 132, 234–241. [Google Scholar] [CrossRef]
- Dawsey, W.J. Bayesian Belief Networks to Integrate Monitoring Evidence of Water Distribution System Contamination. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 2012. [Google Scholar]
- Tao, T.; Huang, H.D.; Xin, K.L.; Liu, S.M. Identification of contamination source in water distribution network based on consumer complaints. J. Central South Univ. Technol. 2012, 19, 1600–1609. [Google Scholar] [CrossRef]
- De Sanctis, A.; Boccelli, D.; Shang, F.; Uber, J. Probabilistic approach to characterize contamination sources with imperfect sensors. In Proceedings of the World Environmental and Water Resources Congress 2008: Ahupua’A, Honolulu, HI, USA, 12–13 May 2008; pp. 1–10. [Google Scholar]
- Yang, X.; Boccelli, D.L. Bayesian approach for real-time probabilistic contamination source identification. J. Water Resour. Plan. Manag. 2013, 140, 04014019. [Google Scholar] [CrossRef]
- Perelman, L.; Ostfeld, A. Bayesian networks for estimating contaminant source and propagation in a water distribution system using cluster structure. In Water Distribution Systems Analysis 2010; American Society of Civil Engineers: Reston, VA, USA, 2010; pp. 426–435. [Google Scholar]
- Neupauer, R.M.; Records, M.K.; Ashwood, W.H. Backward probabilistic modeling to identify contaminant sources in water distribution systems. J. Water Resour. Plan. Manag. 2009, 136, 587–591. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, S. Contamination source identification based on sequential Bayesian approach for water distribution network with stochastic demands. IISE Trans. 2017, 49, 899–910. [Google Scholar] [CrossRef]
- Barandouzi, M.; Kerachian, R. Probabilistic Contaminant Source Identification in Water Distribution Infrastructure Systems. Civ. Eng. Infrastruct. J. 2016, 49, 311–326. [Google Scholar]
- Di Nardo, A.; Di Natale, M.; Guida, M.; Musmarra, D. Water network protection from intentional contamination by sectorization. Water Resour. Manag. 2013, 27, 1837–1850. [Google Scholar] [CrossRef]
- Zechman, E.M.; Ranjithan, S.R. Evolutionary computation-based methods for characterizing contaminant sources in a water distribution system. J. Water Resour. Plan. Manag. 2009, 135, 334–343. [Google Scholar] [CrossRef]
- Kim, M.; Choi, C.Y.; Gerba, C.P. Source tracking of microbial intrusion in water systems using artificial neural networks. Water Res. 2008, 42, 1308–1314. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Zechman, E.M.; Mahinthakumar, G.; Ranji Ranjithan, S. Identifying contaminant sources for water distribution systems using a hybrid method. Civ. Eng. Environ. Syst. 2012, 29, 123–136. [Google Scholar] [CrossRef]
- Liu, L.; Zechman, E.M.; Mahinthakumar, G.; Ranjithan, S.R. Coupling of logistic regression analysis and local search methods for characterization of water distribution system contaminant source. Eng. Appl. Artif. Intell. 2012, 25, 309–316. [Google Scholar] [CrossRef]
- Shen, H.; McBean, E. False negative/positive issues in contaminant source identification for water-distribution systems. J. Water Resour. Plan. Manag. 2011, 138, 230–236. [Google Scholar] [CrossRef]
- Eliades, D.; Lambrou, T.; Panayiotou, C.; Polycarpou, M. Contamination event detection in water distribution systems using a model-based approach. Proc. Eng. 2014, 89, 1089–1096. [Google Scholar] [CrossRef]
- Hamam, Y.; Hindi, K. Optimised on-line leakage minimisation in water piping networks using neural nets. Proc. IFIP Work. Conf. 1992, 28, 57–64. [Google Scholar]
- Koch, M.W.; McKenna, S.A. Distributed sensor fusion in water quality event detection. J. Water Resour. Plan. Manag. 2010, 137, 10–19. [Google Scholar] [CrossRef]
- Eliades, D.G.; Polycarpou, M.M. Water contamination impact evaluation and source-area isolation using decision trees. J. Water Resour. Plan. Manag. 2011, 138, 562–570. [Google Scholar] [CrossRef]
- Brumbelow, K.; Torres, J.; Guikema, S.; Bristow, E.; Kanta, L. Virtual cities for water distribution and infrastructure system research. In Proceedings of the World Environmental and Water Resources Congress 2007: Restoring Our Natural Habitat, Tampa, FL, USA, 15–19 May 2007; pp. 1–7. [Google Scholar]
- Costa, D.; Melo, L.; Martins, F. Localization of contamination sources in drinking water distribution Systems: A method based on successive positive readings of sensors. Water Resour. Manag. 2013, 27, 4623–4635. [Google Scholar] [CrossRef]
- Laird, C.; Biegler, L.; van Bloemen Waanders, B.; Bartlett, R. Time dependent contamination source determination for municipal water networks using large scale optimization. J. Water Resour. Plan. Manag. 2003. Available online: https://www.researchgate.net/publication/266407494_T (accessed on 23 November 2017).
- Laird, C.D.; Biegler, L.T.; van Bloemen Waanders, B.G. Mixed-integer approach for obtaining unique solutions in source inversion of water networks. J. Water Resour. Plan. Manag. 2006, 132, 242–251. [Google Scholar] [CrossRef]
- Laird, C.D.; Biegler, L.T.; van Bloemen Waanders, B.G.; Bartlett, R.A. Time dependent contamination source determination: A network subdomain approach for very large water networks. In Critical Transitions in Water and Environmental Resources Management; American Society of Civil Engineers: Reston, VA, USA, 2004; pp. 1–10. [Google Scholar]
- Preis, A.; Ostfeld, A. Contamination source identification in water systems: A hybrid model trees-linear programming scheme. J. Water Resour. Plan. Manag. 2006, 132, 263–273. [Google Scholar] [CrossRef]
- Nazarovs, S.; Dejus, S.; Juhna, T. Modelling water quality in drinking water distribution networks from real-time direction data. Drink. Water Eng. Sci. 2012, 5, 39–45. [Google Scholar] [CrossRef]
- Quesson, B.; Sheldon-Robert, M.; Vloerbergh, I.; Vreeburg, J.G. Acoustic monitoring of terrorist intrusion in a drinking water network. In Water Distribution Systems Analysis 2008; American Society of Civil Engineers: Reston, VA, USA, 2008; pp. 1–12. [Google Scholar]
- Tabaa, Y.; Medouri, A.; Tetouan, M. Towards a next generation of scientific computing in the cloud. Int. J. Comput. Sci. 2012, 9, 177–183. [Google Scholar]
- Creaco, E.; Pezzinga, G.; Savic, D. On the choice of the demand and hydraulic modeling approach to WDN real-time simulation. Water Resour. Res. 2017, 53, 6159–6177. [Google Scholar] [CrossRef]
- Creaco, E.; Blokker, M.; Buchberger, S. Models for generating household water demand pulses: Literature review and comparison. J. Water Resour. Plan. Manag. 2017, 143, 04017013. [Google Scholar] [CrossRef]

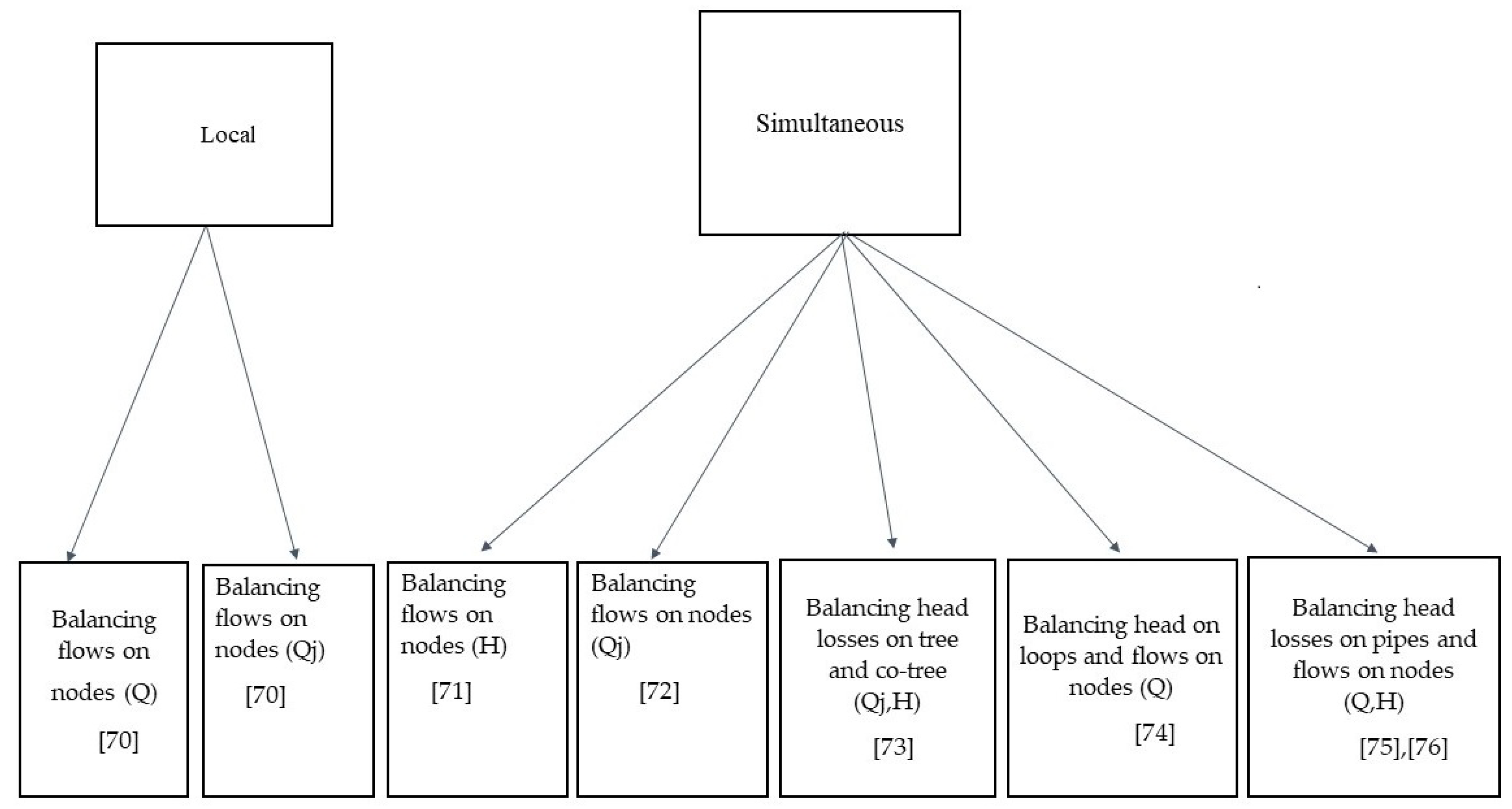
| Numerical Model | Governing Equation | Hydraulic Model | Citations |
|---|---|---|---|
| E-FDM | Advection-reaction equation | SSM | [58] |
| E-DVM | Advection-reaction equation | DA | [64] |
| E-FDM | Advection-reaction equation | TA | [67] |
| Eulerian-Langragian method | Advection-diffusion-reaction equation | SSM | [68,69] |
| L-MEDM | Advection-reaction equation | SSM | [70] |
| L-EDM | Advection-reaction equation | SSM | [61] |
| Specific Method | Classification | Remarks | Citations |
|---|---|---|---|
| NLP | Optimisation | Performance affected by source location and not up to large network | [32,112,170] |
| PB | Optimisation | Explicit mathematical computation | [89,90] |
| MIQP | Optimisation | Show positive result | [171] |
| SO | Optimisation | Show robustness | [42,124,128,170,172] |
| LSF | Optimisation | Show potential to reveal location | [126] |
| MTLPA | Optimisation | Show efficiency | [173] |
| GA | Optimisation | Revealed approximation time of injection | [114,116] |
| FMC | Optimisation | Show applicability | [127] |
| ADOPT | Optimisation | Converges to best solution | [43,44] |
| QRLS | Optimisation | Show potential usage of the procedure | [130] |
| RTM | Others | Fundamentals path was more efficient computationally | [49,174] |
| BBN | Probability | Effective for steady flow condition for single instantaneous source | [40,149,150,151,153,154] |
| ASA | Others | Show promising result | [175] |
| ANN | Others | Positive correlation | [160] |
| DMA | Others | [98] | |
| ESHA | Others | Algorithm had good performance | [159] |
| KST | Others | Indicates potential to detect source location | [166] |
| DT | Others | Required further investigations | [158] |
| MBA | Others | Show capability | [167] |
| CSMHSM | Others | Demonstrated to identify location and evaluating degree of non-uniqueness | [162] |
| HM | Others | Show robustness | [161] |
| RP | Others | Show robustness | [151] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adedoja, O.S.; Hamam, Y.; Khalaf, B.; Sadiku, R. Towards Development of an Optimization Model to Identify Contamination Source in a Water Distribution Network. Water 2018, 10, 579. https://doi.org/10.3390/w10050579
Adedoja OS, Hamam Y, Khalaf B, Sadiku R. Towards Development of an Optimization Model to Identify Contamination Source in a Water Distribution Network. Water. 2018; 10(5):579. https://doi.org/10.3390/w10050579
Chicago/Turabian StyleAdedoja, Oluwaseye Samson, Yskandar Hamam, Baset Khalaf, and Rotimi Sadiku. 2018. "Towards Development of an Optimization Model to Identify Contamination Source in a Water Distribution Network" Water 10, no. 5: 579. https://doi.org/10.3390/w10050579
APA StyleAdedoja, O. S., Hamam, Y., Khalaf, B., & Sadiku, R. (2018). Towards Development of an Optimization Model to Identify Contamination Source in a Water Distribution Network. Water, 10(5), 579. https://doi.org/10.3390/w10050579






