Evaluation of Multiple Satellite Precipitation Products and Their Use in Hydrological Modelling over the Luanhe River Basin, China
Abstract
:1. Introduction
2. Study Area and Datasets
2.1. Study Area
2.2. Datasets
3. Methods
3.1. Statistical Metrics
3.2. SWAT Model
3.2.1. Model Setup
3.2.2. Model Calibration, Validation, and Uncertainty Analysis
4. Results and Discussions
4.1. Evaluation of Satellite Precipitation Products Against Gauge Observations
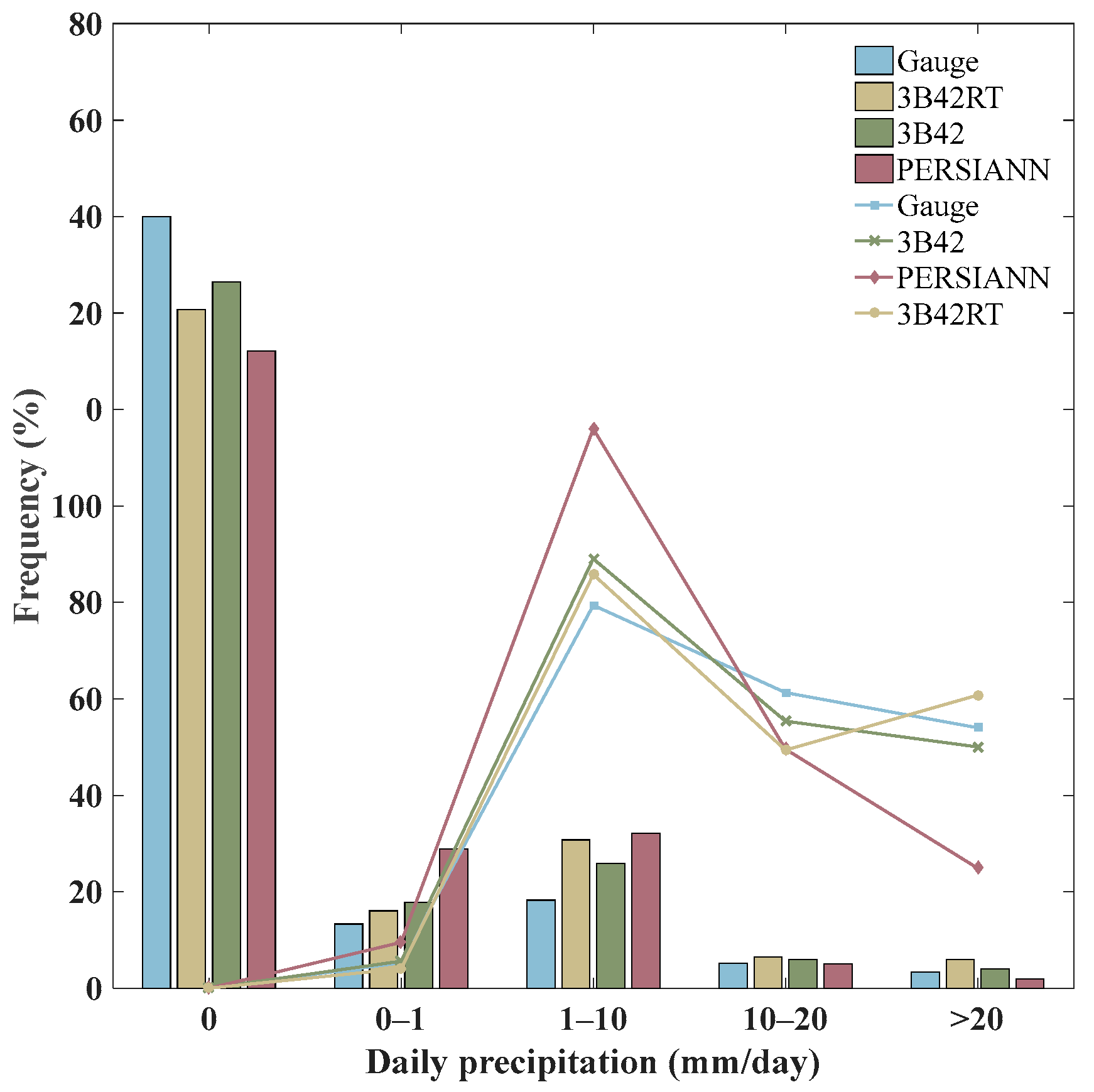
4.1.1. Daily Comparison
4.1.2. Monthly Comparison
4.1.3. Seasonal (Rainy/Dry Spells) and Annual Comparisons
4.2. Hydrological Evaluation
4.2.1. Hydrological Modelling Performance
4.2.2. Parameter Uncertainty
4.2.3. Prediction Uncertainty
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Kidd, C.; Huffman, G. Global Precipitation Measurement. Meteorol. Appl. 2011, 18, 334–353. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Alijanian, M.; Rakhshandehroo, G.R.; Mishra, A.K.; Dehghani, M. Evaluation of Satellite Rainfall Climatology Using CMORPH, PERSIANN-CDR, PERSIANN, TRMM, MSWEP Over Iran. Int. J. Climatol. 2017, 37, 4896–4914. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Y.; Yang, D.; Bin Farhan, S. Precipitation Bias Variability Versus Various Gauges Under Different Climatic Conditions over the Third Pole Environment (TPE) Region. Int. J. Climatol. 2015, 35, 1201–1211. [Google Scholar] [CrossRef]
- Chao, L.; Zhang, K.; Li, Z.; Zhu, Y.; Wang, J.; Yu, Z. Geographically Weighted Regression Based Methods for Merging Satellite and Gauge Precipitation. J. Hydrol. 2018, 558, 275–289. [Google Scholar] [CrossRef]
- Strauch, M.; Kumar, R.; Eisner, S.; Mulligan, M.; Reinhardt, J.; Santini, W.; Vetter, T.; Friesen, J. Adjustment of Global Precipitation Data for Enhanced Hydrologic Modeling of Tropical Andean Watersheds. Clim. Chang. 2017, 141, 547–560. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Behrangi, A.; Sorooshian, S.; Hsu, K.; Amitai, E. Evaluation of Satellite-Retrieved Extreme Precipitation Rates Across the Central United States. J. Geophys. Res. Atmos. 2011, 116, D02115. [Google Scholar] [CrossRef]
- Yang, T.; Feng, L.; Chang, L. Improving Radar Estimates of Rainfall Using an Input Subset of Artificial Neural Networks. J. Appl. Remote Sens. 2016, 10, 026013. [Google Scholar] [CrossRef]
- Kidd, C.; Levizzani, V. Status of Satellite Precipitation Retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 1109–1116. [Google Scholar] [CrossRef] [Green Version]
- Tang, G.; Zeng, Z.; Long, D.; Guo, X.; Yong, B.; Zhang, W.; Hong, Y. Statistical and Hydrological Comparisons between TRMM and GPM Level-3 Products over a Midlatitude Basin: Is Day-1 IMERG a Good Successor for TMPA 3B42V7? J. Hydrometeorol. 2015, 17, 121–137. [Google Scholar] [CrossRef]
- Sun, R.; Yuan, H.; Liu, X.; Jiang, X. Evaluation of the Latest Satellite-Gauge Precipitation Products and their Hydrologic Applications over the Huaihe River Basin. J. Hydrol. 2016, 536, 302–319. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T. TRMM and Other Data Precipitation Data Set Documentation; NASA: Greenbelt, MD, USA, 2013.
- Sorooshian, S.; Hsu, K.L.; Gao, X.; Gupta, H.V.; Imam, B.; Braithwaite, D. Evaluation of PERSIANN System Satellite-Based Estimates of Tropical Rainfall. Bull. Am. Meteorol. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef]
- Kubota, T.; Shige, S.; Hashizurne, H.; Aonashi, K.; Takahashi, N.; Seto, S.; Hirose, M.; Takayabu, Y.N.; Ushio, T.; Nakagawa, K.; et al. Global Precipitation Map Using Satellite-Borne Microwave Radiometers by the GSMap Project: Production and Validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2259–2275. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P.P. CMORPH: A Method that Produces Global Precipitation Estimates From Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Omranian, E.; Sharif, H.O. Evaluation of the Global Precipitation Measurement (GPM) Satellite Rainfall Products over the Lower Colorado River Basin, Texas. JAWRA J. Am. Water Resour. Assoc. 2018. [Google Scholar] [CrossRef]
- Dinku, T.; Ruiz, F.; Connor, S.J.; Ceccato, P. Validation and Intercomparison of Satellite Rainfall Estimates Over Colombia. J. Appl. Meteorol. Clim. 2010, 49, 1004–1014. [Google Scholar] [CrossRef]
- Vergara, H.; Hong, Y.; Gourley, J.J.; Anagnostou, E.N.; Maggioni, V.; Stampoulis, D.; Kirstetter, P. Effects of Resolution of Satellite-Based Rainfall Estimates on Hydrologic Modeling Skill at Different Scales. J. Hydrometeorol. 2014, 15, 593–613. [Google Scholar] [CrossRef]
- Thiemig, V.; Rojas, R.; Zambrano-Bigiarini, M.; De Roo, A. Hydrological Evaluation of Satellite-Based Rainfall Estimates over the Volta and Baro-Akobo Basin. J. Hydrol. 2013, 499, 324–338. [Google Scholar] [CrossRef]
- Grimes, D.; Diop, M. Satellite-Based Rainfall Estimation for River Flow Forecasting in Africa. I: Rainfall Estimates and Hydrological Forecasts. J. Hydrol. Sci. 2003, 48, 567–584. [Google Scholar] [CrossRef]
- Wilk, J.; Kniveton, D.; Andersson, L.; Layberry, R.; Todd, M.C.; Hughes, D.; Ringrose, S.; Vanderpost, C. Estimating Rainfall and Water Balance over the Okavango River Basin for Hydrological Applications. J. Hydrol. 2006, 331, 18–29. [Google Scholar] [CrossRef]
- Ebert, E.E.; Janowiak, J.E.; Kidd, C. Comparison of Near-Real-Time Precipitation Estimates from Satellite Observations and Numerical Models. Bull. Am. Meteorol. Soc. 2007, 88, 47–64. [Google Scholar] [CrossRef]
- Artan, G.; Gadain, H.; Smith, J.L.; Asante, K.; Bandaragoda, C.J.; Verdin, J.P. Adequacy of Satellite Derived Rainfall Data for Stream Flow Modeling. Nat. Hazards 2007, 43, 167–185. [Google Scholar] [CrossRef]
- Mashingia, F.; Mtalo, F.; Bruen, M. Validation of Remotely Sensed Rainfall over Major Climatic Regions in Northeast Tanzania. Phys. Chem. Earth 2014, 67–69, 55–63. [Google Scholar] [CrossRef]
- Tan, M.L.; Ibrahim, A.L.; Duan, Z.; Cracknell, A.P.; Chaplot, V. Evaluation of Six High-Resolution Satellite and Ground-Based Precipitation Products over Malaysia. Remote Sens. 2015, 7, 1504–1528. [Google Scholar] [CrossRef]
- Tuo, Y.; Duan, Z.; Disse, M.; Chiogna, G. Evaluation of Precipitation Input for SWAT Modeling in Alpine Catchment: A Case Study in the Adige River Basin (Italy). Sci. Total Environ. 2016, 573, 66–82. [Google Scholar] [CrossRef] [PubMed]
- Alazzy, A.A.; Lu, H.; Chen, R.; Ali, A.B.; Zhu, Y.; Su, J. Evaluation of Satellite Precipitation Products and Their Potential Influence on Hydrological Modeling over the Ganzi River Basin of the Tibetan Plateau. Adv. Meteorol. 2017, 2017, 3695285. [Google Scholar] [CrossRef]
- Sorooshian, S.; AghaKouchak, A.; Arkin, P.; Eylander, J.; Foufoula-Georgiou, E.; Harmon, R.; Hendrickx, J.M.H.; Imam, B.; Kuligowski, R.; Skahill, B.; et al. Advanced Concepts on Remote Sensing of Precipitation at Multiple Scales. Bull. Am. Meteorol. Soc. 2011, 92, 1353–1357. [Google Scholar] [CrossRef]
- Li, Z.; Yang, D.; Hong, Y. The Opportunities and Challenges: Statistical and Hydrological Evaluation of High-Resolution Multisensor Blended Global Precipitation Products over the Yangtze River Basin, China. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 3–7 December 2012. [Google Scholar]
- Jiang, S.; Ren, L.; Hong, Y.; Yong, B.; Yang, X.; Yuan, F.; Ma, M. Comprehensive Evaluation of Multi-Satellite Precipitation Products with a Dense Rain Gauge Network and Optimally Merging their Simulated Hydrological Flows Using the Bayesian Model Averaging Method. J. Hydrol. 2012, 452, 213–225. [Google Scholar] [CrossRef]
- Gao, Y.C.; Liu, M.F. Evaluation of High-Resolution Satellite Precipitation Products Using Rain Gauge Observations over the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2013, 17, 837–849. [Google Scholar] [CrossRef]
- Zhu, Q.; Xuan, W.; Liu, L.; Xu, Y. Evaluation and Hydrological Application of Precipitation Estimates Derived From PERSIANN-CDR, TRMM 3B42V7, and NCEP-CFSR over Humid Regions in China. Hydrol. Process. 2016, 30, 3061–3083. [Google Scholar] [CrossRef]
- Li, J.; Li, G.; Zhou, S.; Chen, F. Quantifying the Effects of Land Surface Change on Annual Runoff Considering Precipitation Variability by SWAT. Water Resour. Manag. 2016, 30, 1071–1084. [Google Scholar] [CrossRef]
- Hsu, K.L.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation Estimation from Remotely Sensed Information Using Artificial Neural Networks. J. Appl. Meteorol. 1996, 36, 1176–1190. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large Area Hydrologic Modeling and Assessment—Part 1: Model Development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Dile, Y.T.; Karlberg, L.; Daggupati, P.; Srinivasan, R.; Wiberg, D.; Rockstrom, J. Assessing the Implications of Water Harvesting Intensification on Upstream-Downstream Ecosystem Services: A Case Study in the Lake Tana Basin. Sci. Total Environ. 2016, 542, 22–35. [Google Scholar] [CrossRef] [PubMed]
- Teshager, A.D.; Gassman, P.W.; Secchi, S.; Schoof, J.T. Simulation of Targeted Pollutant-Mitigation-Strategies to Reduce Nitrate and Sediment Hotspots in Agricultural Watershed. Sci. Total Environ. 2017, 607, 1188–1200. [Google Scholar] [CrossRef] [PubMed]
- Abbaspour, K.C.; Vejdani, M.; Haghighat, S. SWAT-CUP Calibration and Uncertainty Programs for SWAT. In Proceedings of the Modsim International Congress on Modelling & Simulation Land Water & Environmental Management Integrated Systems for Sustainability, Hobart, Australian, 3–8 December 2017; pp. 1603–1609. [Google Scholar]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Klove, B. A Continental-Scale Hydrology and Water Quality Model for Europe: Calibration and Uncertainty of a High-Resolution Large-Scale SWAT Model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Gomiz-Pascual, J.J.; Bolado-Penagos, M.; Vazquez, A. Soil and Water Assessment Tool. Sea Technol. 2016, 57, 19–21. [Google Scholar]
- Sun, Z.; Lotz, T.; Chang, N. Assessing the Long-Term Effects of Land Use Changes On Runoff Patterns and Food Production in a Large Lake Watershed with Policy Implications. J. Environ. Manag. 2017, 204, 92–101. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Li, J. Quantifying Drought and Water Scarcity: A Case Study in the Luanhe River Basin. Nat. Hazards 2016, 81, 1913–1927. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Chen, H.; Luo, Y.; Potter, C.; Moran, P.J.; Grieneisen, M.L.; Zhang, M. Modeling Pesticide Diuron Loading From the San Joaquin Watershed Into the Sacramento-San Joaquin Delta Using SWAT. Water Res. 2017, 121, 374–385. [Google Scholar] [CrossRef] [PubMed]
- Afshari, S.; Tavakoly, A.A.; Rajib, A.; Zheng, X.; Follum, M.L.; Omranian, E. Comparison of New Generation Low-complexity Flood Inundation Mapping Tools with a Hydrodynamic Model. J. Hydrol. 2017, 556, 539–556. [Google Scholar] [CrossRef]
- Bitew, M.M.; Gebremichael, M. Evaluation of Satellite Rainfall Products through Hydrologic Simulation in a Fully Distributed Hydrologic Model. Water Resour. Res. 2011, 47, 6. [Google Scholar] [CrossRef]
- Javaheri, A.; Nabatian, M.; Omranian, E.; Babbar-Sebens, M.; Noh, S.J. Merging Real-time Channel Sensor Networks with Continental-scale Hydrologic Models: A Data Assimilation Approach for Improving Accuracy in Flood Depth Predictions. Hydrology 2018, 5, 9. [Google Scholar] [CrossRef]
- Evensen, G. Sequential Data Assimilation with a Nonlinear Quasi-geostrophic Model Using Monte Carlo Methods to Forecast Error Statistics. J. Geophys. Res. Oceans 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Srinivasan, R.; Williams, J.R. Soil and Water Assessment Tool Input/output File Documentation: Version 2009; Texas Water Resources Institute Technical Report 365; Texas A&M University System: College Station, TX, USA, 2011. [Google Scholar]









| Data Type | Products | Time Resolution | Time Extent | Spatial Resolution | Spatial Extent | Availability after the Events | Data Source |
|---|---|---|---|---|---|---|---|
| Meteorology | Rain gauges observations | daily | 2001–2012 | point | - | - | China Meteorological Administration (CMA) |
| TRMM_3B42V7 | 3 h | 31 December 1997 to present | 0.25° × 0.25° | 50° N to 50° S 180° E to 180° W | 10–15 days | NASA Goddard Earth Sciences Data and Information Services Center (GES DISC) | |
| TRMM_3B42RTV7 | 3 h | 29 February 2000 to present | 0.25° × 0.25° | 60° N to 60° S 180° E to 180° W | 9 h | NASA Goddard Earth Sciences Data and Information Services Center (GES DISC) | |
| PERSIANN | 3 h | 1 March 2000 to present | 0.25° × 0.25° | 60° N to 60° S 180° E to 180° W | 2 days | The Center for Hydrometeorology and Remote Sensing (CHRS) at the University of California, Irvine (UCI) | |
| Other Meteorological data | daily | 2001–2012 | point | - | - | China Meteorological Administration (CMA) | |
| Streamflow | Hydrological station | monthly | 2001–2011 | point | - | - | Haihe River Water Conservancy Commission (MWR) |
| Geography | Digital Elevation Model (DEM) | - | - | 30 m × 30 m | Luanhe River basin | - | Geospatial Data Cloud |
| Land use | - | - | 30 m | Luanhe River basin | - | GlobeLand30 | |
| Soil | - | - | 1 km | Luanhe River basin | - | Environmental and Ecological Science Data Center for West China, National Natural Science Foundation of China |
| Index | Unit | Equation | Perfect Value |
|---|---|---|---|
| Correlation coefficient (CC) | - | 1 | |
| Root mean squared error (RMSE) | mm | 0 | |
| Mean absolute error (MAE) | mm | 0 | |
| Relative bias (BIAs) | % | 0 | |
| Coefficient of determination (R2) | - | 1 | |
| Nash-Sutcliffe efficiency coefficient (NS) | - | 1 | |
| Probability of detection (POD) | - | 1 | |
| False alarm ratio (FAR) | - | 0 | |
| Critical success index (CSI) | - | 1 |
| Parameters | Unit | Description | Calibration Range |
|---|---|---|---|
| r_CN2.mgt | - | Initial soil conservation service runoff | [−0.3, 0.3] |
| v_ALPHA_BF.gw | days | Baseflow alpha factor | [0, 1] |
| v_GW_DELAY.gw | days | Groundwater delay | [0, 500] |
| v_GWQMN.gw | mm | Threshold depth of water in the shallow aquifer required for return flow to occur | [0, 5000] |
| v_GW_REVAP.gw | - | Groundwater “revap” coefficient | [0.02, 0.2] |
| v_ESCO.hru | - | Soil evaporation compensation factor | [0.01, 0.1] |
| v_CH_N2.rte | - | Channel hydraulic conductivity | [0, 0.3] |
| v_ALPHA_BNK.rte | - | Baseflow alpha factor for bank storage | [0, 1] |
| r_SOL_AWC().sol | - | Available soil water capacity | [−0.95, 0.95] |
| r_SOL_K().sol | mm/h | Saturated hydraulic conductivity of the soil | [−0.95, 0.95] |
| Time Scale | Precipitation Types | Mean (mm) | RMSE (mm) | MAE (mm) | CC | BIAs (%) | POD | FAR | CSI |
|---|---|---|---|---|---|---|---|---|---|
| Daily | Gauge | 1.36 | - | - | - | - | - | - | - |
| 3B42RT | 2.20 | 5.91 | 1.77 | 0.64 | 62.80 | 0.75 | 0.29 | 0.74 | |
| 3B42 | 1.63 | 4.60 | 1.36 | 0.67 | 20.17 | 0.79 | 0.24 | 0.78 | |
| PERSIANN | 1.27 | 4.79 | 1.53 | 0.55 | −6.38 | 0.63 | 0.37 | 0.62 | |
| Monthly | Gauge | 41.55 | - | - | - | - | - | - | - |
| 3B42RT | 67.21 | 49.34 | 30.29 | 0.86 | 62.80 | - | - | - | |
| 3B42 | 49.85 | 21.91 | 13.08 | 0.94 | 20.17 | - | - | - | |
| PERSIANN | 38.63 | 30.82 | 19.68 | 0.80 | −6.38 | - | - | - |
| Satellite Precipitation Products | Water Components | Period (Year) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | ||
| Rain gauge | Total precipitation (mm) | 461 | 480 | 489 | 494 | 464 | 541 | 322 | 612 | 451 | 522 |
| Evapotranspiration (mm) | 296 | 312 | 282 | 270 | 246 | 315 | 220 | 313 | 269 | 263 | |
| Runoff depth (mm) | 66 | 70 | 90 | 77 | 73 | 83 | 57 | 102 | 86 | 89 | |
| 3B42RT | Total precipitation (mm) | 875 | 634 | 1086 | 619 | 749 | 726 | 643 | 869 | 745 | 810 |
| Evapotranspiration (mm) | 536 | 446 | 587 | 471 | 446 | 415 | 415 | 494 | 413 | 503 | |
| Runoff depth (mm) | 59 | 77 | 120 | 49 | 59 | 65 | 71 | 64 | 70 | 80 | |
| 3B42 | Total precipitation (mm) | 562 | 558 | 594 | 461 | 502 | 611 | 406 | 647 | 533 | 643 |
| Evapotranspiration (mm) | 446 | 399 | 368 | 353 | 363 | 372 | 276 | 319 | 327 | 330 | |
| Runoff depth (mm) | 62 | 68 | 93 | 55 | 56 | 81 | 64 | 95 | 84 | 90 | |
| PERSIANN | Total precipitation (mm) | 526 | 385 | 516 | 436 | 623 | 356 | 364 | 479 | 416 | 573 |
| Evapotranspiration (mm) | 468 | 335 | 381 | 335 | 467 | 322 | 322 | 359 | 352 | 440 | |
| Runoff depth (mm) | 46 | 38 | 66 | 44 | 68 | 34 | 29 | 65 | 44 | 76 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, P.; Li, J.; Feng, P.; Guo, Y.; Ma, Q. Evaluation of Multiple Satellite Precipitation Products and Their Use in Hydrological Modelling over the Luanhe River Basin, China. Water 2018, 10, 677. https://doi.org/10.3390/w10060677
Ren P, Li J, Feng P, Guo Y, Ma Q. Evaluation of Multiple Satellite Precipitation Products and Their Use in Hydrological Modelling over the Luanhe River Basin, China. Water. 2018; 10(6):677. https://doi.org/10.3390/w10060677
Chicago/Turabian StyleRen, Peizhen, Jianzhu Li, Ping Feng, Yuangang Guo, and Qiushuang Ma. 2018. "Evaluation of Multiple Satellite Precipitation Products and Their Use in Hydrological Modelling over the Luanhe River Basin, China" Water 10, no. 6: 677. https://doi.org/10.3390/w10060677
APA StyleRen, P., Li, J., Feng, P., Guo, Y., & Ma, Q. (2018). Evaluation of Multiple Satellite Precipitation Products and Their Use in Hydrological Modelling over the Luanhe River Basin, China. Water, 10(6), 677. https://doi.org/10.3390/w10060677




