Spatial and Temporal Trend Analysis of Precipitation and Drought in South Korea
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. Standardized Precipitation Index (SPI)
2.3. Commonly Used Statistical Tests for Trend Detection
2.3.1. Mann-Kendall (MK) Test
2.3.2. Theil–Sen’s Estimator
2.3.3. Linear Regression Estimator
2.4. Principal Component Analysis (PCA)
2.5. Statistical Tests Considering the Effect of Serial Correlation for Trend Detection
2.5.1. Pre-Whitening (PW)
2.5.2. Trend-Free Pre-Whitening (TFPW)
2.5.3. Variance Correction (VC) Approach
2.6. Field Significance
3. Results and Discussion
3.1. Spatial Variability of Annual and Monthly Precipitation
3.2. Autocorrelation of Annual and Monthly Precipitation
3.3. Spatial Patterns of Temporal Trends in Precipitation
3.4. Spatial Variability of Drought Using PCA
3.5. Spatial Patterns of Temporal Trends in Drought
3.6. Spatial Patterns of Drought Frequency
4. Conclusions
- The MAP and MMP showed high quantities of rainfall in the north and south part of South Korea, and low quantities in the south coastal areas. High spatial variation of rainfall (CV) was observed on the south coast for MAP and the south and southwest coast for MMP.
- Most of the stations did not show any significant lag-1 serial correlation coefficient for monthly and annual precipitation series, whereas autocorrelations of SPI-12 series were all significant and positive up to a time lag of 7 months for 55 stations across South Korea.
- The spatial patterns of monthly precipitation trends revealed that most of the significant trends were detected along the south coast of South Korea, especially during winter (February, December), late spring (May) and summer (June, August), whereas no significant trend was detected in annual precipitation. The magnitude of the trends increased from January to August and decreased from August onward. Moreover, annual precipitation tends to show similar trends to summer precipitation. When field significance was considered, none of the stations showed trends above the limit of field significance.
- Principal component analysis applied on SPI-12 series indicated that the whole of South Korea could be divided into four subregions with the different temporal drought behavior, and corresponding representative stations were identified for future drought monitoring.
- Removing the serial correlation using the tfpwMK test led to more than 90% of stations having significant trends, which indicates its inability to consider high-order dependencies by imposing the AR(1) structure. Furthermore, the tfpwMK test has serious problems in terms of preserving the nominal significance level. These results match well with previous studies [75]. The pwMK approach showed the lowest value of the Z statistic because of its adverse effect on the true slope of the drought time series. This observation is in agreement with the findings of [76]. VC approaches can handle not only the AR(1) structure, but also higher-order dependencies, and therefore has broader applications. MK, modMK2, modMK2 lag-1 and tfpwMK showed trends above the limit of field significance.
- Trend analysis applied on SPI-12 time series showed significant increasing or increasing trends of drought severity at the stations located at northeast coast, inland mid-latitude west and southeast coastal areas of South Korea. The four representative stations identified by rotated loadings of the leading four principal components were located nearly at the same location.
- Monthly drought frequencies showed that the areas with the highest drought frequencies were in the southwest coastal areas. Drought events were expected to occur more frequently in the late winter, early spring and early autumn, while droughts were expected to occur least frequently in summer.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Paulo, A.A.; Rosa, R.D.; Pereira, L.S. Climate trends and behaviour of drought indices based on precipitation and evapotranspiration in Portugal. Nat. Hazards Earth Syst. Sci. 2012, 12, 1481–1491. [Google Scholar] [CrossRef]
- Güner Bacanli, Ü. Trend analysis of precipitation and drought in the Aegean region, Turkey. Meteorol. Appl. 2017, 24, 239–249. [Google Scholar] [CrossRef]
- Azam, M.; Maeng, S.; Kim, H.S.; Murtazaev, A. Copula-Based Stochastic Simulation for Regional Drought Risk Assessment in South Korea. Water 2018, 10, 359. [Google Scholar] [CrossRef]
- Azam, M.; Park, H.; Maeng, S.J.; Kim, H.S. Regionalization of Drought across South Korea Using Multivariate Methods. Water 2017, 10, 24. [Google Scholar] [CrossRef]
- Maeng, S.J.; Azam, M.; Kim, H.S.; Hwang, J.H. Analysis of changes in spatio-temporal patterns of drought across South Korea. Water 2017, 9, 679. [Google Scholar] [CrossRef]
- Azam, M.; Kim, H.S.; Maeng, S.J. Development of flood alert application in Mushim stream watershed Korea. Int. J. Disaster Risk Reduct. 2017, 21, 11–26. [Google Scholar] [CrossRef]
- Kim, H.S.; Muhammad, A.; Maeng, S.-J. Hydrologic Modeling for Simulation of Rainfall-Runoff at Major Control Points of Geum River Watershed. Procedia Eng. 2016, 154, 504–512. [Google Scholar] [CrossRef]
- Tabari, H.; Abghari, H.; Hosseinzadeh Talaee, P. Temporal trends and spatial characteristics of drought and rainfall in arid and semiarid regions of Iran. Hydrol. Process. 2012, 26, 3351–3361. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of precipitation and drought data in Serbia over the period 1980–2010. J. Hydrol. 2013, 494, 32–42. [Google Scholar] [CrossRef]
- Zhang, Y.; Cai, W.; Chen, Q.; Yao, Y.; Liu, K. Analysis of changes in precipitation and drought in Aksu River Basin, Northwest China. Adv. Meteorol. 2015, 2015, 215840. [Google Scholar] [CrossRef]
- Hamed, K.H. Trend detection in hydrologic data: The Mann-Kendall trend test under the scaling hypothesis. J. Hydrol. 2008, 349, 350–363. [Google Scholar] [CrossRef]
- Chang, H.; Kwon, W.-T. Spatial variations of summer precipitation trends in South Korea, 1973–2005. Environ. Res. Lett. 2007, 2, 45012. [Google Scholar] [CrossRef]
- Jung, I.W.; Bae, D.H.; Kim, G. Recent trends of mean and extreme precipitation in Korea. Int. J. Climatol. 2011, 31, 359–370. [Google Scholar] [CrossRef]
- Kim, J.S.; Jain, S. Precipitation trends over the Korean peninsula: Typhoon-induced changes and a typology for characterizing climate-related risk. Environ. Res. Lett. 2011, 6, 034033. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G.; Lombardo, F. Untenable nonstationarity: An assessment of the fitness for purpose of trend tests in hydrology. Adv. Water Resour. 2018, 111, 132–155. [Google Scholar] [CrossRef]
- Clarke, R.T. On the (mis)use of statistical methods in hydro-climatological research. Hydrol. Sci. J. 2010, 55, 139–144. [Google Scholar] [CrossRef]
- Lee, S.K.W. A variation of summer rainfall in Korea. J. Korean Geogr. Soc. 2004, 39, 819–832. (In Korean) [Google Scholar]
- Kim, B.J.; Kripalani, R.H.; Oh, J.H.; Moon, S.E. Summer monsoon rainfall patterns over South Korea and associated circulation features. Theor. Appl. Climatol. 2002, 72, 65–74. [Google Scholar] [CrossRef]
- Baek, H.J.; Kim, M.K.; Kwon, W.T. Observed short- and long-term changes in summer precipitation over South Korea and their links to large-scale circulation anomalies. Int. J. Climatol. 2017, 37, 972–986. [Google Scholar] [CrossRef]
- Lee, J.J.; Kwon, H.H.; Kim, T.W. Spatio-temporal analysis of extreme precipitation regimes across South Korea and its application to regionalization. J. Hydrol. Environ. Res. 2012, 6, 101–110. [Google Scholar] [CrossRef]
- Im, E.S.; Jung, I.W.; Bae, D.H. The temporal and spatial structures of recent and future trends in extreme indices over Korea from a regional climate projection. Int. J. Climatol. 2011, 31, 72–86. [Google Scholar] [CrossRef]
- Bae, D.H.; Jung, I.W.; Chang, H. Long-term trend of precipitation and runoff in Korean river basins. Hydrol. Process. 2008, 22, 2644–2656. [Google Scholar] [CrossRef]
- Park, J.S.; Kang, H.S.; Lee, Y.S.; Kim, M.K. Changes in the extreme daily rainfall in South Korea. Int. J. Climatol. 2011, 31, 2290–2299. [Google Scholar] [CrossRef]
- Choi, G.; Kwon, W.-T.; Boo, K.-O.; Cha, Y.-M. Recent Spatial and Temporal Changes in Means and Extreme Events of Temperature and Precipitation across the Republic of Korea. J. Korean Geogr. Soc. 2008, 43, 681–700. [Google Scholar]
- Chung, Y.-S.; Yoon, M.-B.; Kim, H.-S. On Climate Variations and Changes Observed in South Korea. Clim. Chang. 2004, 66, 151–161. [Google Scholar] [CrossRef]
- Von Storch, H. Misuses of Statistical Analysis in Climate. In Analysis of Climate Variability; Springer: Berlin/Heidelberg, Germany, 1995; pp. 11–26. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C.Y. Applicability of prewhitening to eliminate the influence of serial correlation on the Mann-Kendall test. Water Resour. Res. 2002, 38, 4-1–4-7. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C.Y. The Mann-Kendall test modified by effective sample size to detect trend in serially correlated hydrological series. Water Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Khaliq, M.N.; Ouarda, T.B.M.J.; Gachon, P.; Sushama, L.; St-Hilaire, A. Identification of hydrological trends in the presence of serial and cross correlations: A review of selected methods and their application to annual flow regimes of Canadian rivers. J. Hydrol. 2009, 368, 117–130. [Google Scholar] [CrossRef]
- Adeloye, A.J.; Montaseri, M. Preliminary streamflow data analyses prior to water resources planning study. Hydrol. Sci. 2003, 47, 679–692. [Google Scholar] [CrossRef]
- Mckee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the AMS 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–184. [Google Scholar]
- Hayes, M.J.; Svoboda, M.D.; Wilhite, D.A.; Vanyarkho, O.V. Monitoring the 1996 Drought Using the Standardized Precipitation Index. Bull. Am. Meteorol. Soc. 1999, 80, 429–438. [Google Scholar] [CrossRef]
- Lee, J.H.; Seo, J.W.; Kim, C.J. Analysis on trends, periodicities and frequencies of Korean drought using drought indices. J. Korea Water Resour. Assoc. 2012, 45, 75–89. [Google Scholar] [CrossRef]
- Thorn, H.C.S. Some methods of climatological analysis. WMO Tech. Note 1966, 81, 16–22. [Google Scholar]
- Kim, C.J.; Park, M.J.; Lee, J.H. Analysis of climate change impacts on the spatial and frequency patterns of drought using a potential drought hazard mapping approach. Int. J. Climatol. 2014, 34, 61–80. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, C.J. A multimodel assessment of the climate change effect on the drought severity-duration-frequency relationship. Hydrol. Process. 2013, 27, 2800–2813. [Google Scholar] [CrossRef]
- Kao, S.C.; Govindaraju, R.S. A copula-based joint deficit index for droughts. J. Hydrol. 2010, 380, 121–134. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Charles Griffin: London, UK, 1975. [Google Scholar]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis, Part I. Proc. R. Neth. Acad. Sci. 1950, 53, 386–392. [Google Scholar]
- Singh, P.K.; Kumar, V.; Purohit, R.C.; Kothari, M.; Dashora, P.K. Application of Principal Component Analysis in Grouping Geomorphic Parameters for Hydrologic Modeling. Water Resour. Manag. 2009, 23, 325–339. [Google Scholar] [CrossRef]
- Kahya, E.; Kalaycı, S.; Piechota, T.C. Streamflow Regionalization : Case Study of Turkey. J. Hydrol. Eng. 2008, 13, 205–214. [Google Scholar] [CrossRef]
- Raziei, T.; Bordi, I.; Pereira, L.S.; Sutera, A. Space-time variability of hydrological drought and wetness in Iran using NCEP/NCAR and GPCC datasets. Hydrol. Earth Syst. Sci. 2010, 14, 1919–1930. [Google Scholar] [CrossRef]
- Kalayci, S.; Kahya, E. Assessment of streamflow variability modes in Turkey: 1964–1994. J. Hydrol. 2006, 324, 163–177. [Google Scholar] [CrossRef]
- Von Storch, H.; Zwiers, F.W. Statistical Analysis in Climate Research. J. Am. Stat. Assoc. 1999, 95, 1375. [Google Scholar] [CrossRef]
- North, G.R.; Bell, T.L.; Cahalan, R.F. Sampling Errors in the Estimation of Empirical Orthogonal Funtions. Mon. Weather Rev. 1982, 110, 699–706. [Google Scholar] [CrossRef]
- Raziei, T.; Saghafian, B.; Paulo, A.A.; Pereira, L.S.; Bordi, I. Spatial patterns and temporal variability of drought in Western Iran. Water Resour. Manag. 2009, 23, 439–455. [Google Scholar] [CrossRef]
- Kulkarni, A.; Von Storch, H. Monte Carlo experiments on the effect of serial correlation on the Mann-Kendall test of trend. Meteorol. Z. 1995, 4, 82–85. [Google Scholar]
- Zhang, X.; David Harvey, K.; Hogg, W.D.; Yuzyk, T.R. Trends in Canadian streamflow. Water Resour. Res. 2001, 37, 987–998. [Google Scholar] [CrossRef]
- Zhang, X.; Vincent, L.A.; Hogg, W.D.; Niitsoo, A. Temperature and precipitation trends in Canada during the 20th century. Atmos. Ocean 2000, 38, 395–429. [Google Scholar] [CrossRef]
- Salas, J. Applied Modeling of Hydrologic Time Series; Water Resources Publication: Littleton, CO, USA, 1980. [Google Scholar]
- Fleming, S.W.; Clarke, G.K.C. Autoregressive Noise, Deserialization, and Trend Detection and Quantification in Annual River Discharge Time Series. Can. Water Resour. J. 2002, 27, 335–354. [Google Scholar] [CrossRef]
- Bayley, A.G.V.; Hammersley, J.M.; Supplement, S.; Society, S. The “Effective” Number of Independent Observations in an Autocorrelated Time Series. Suppl. J. R. Stat. Soc. 1946, 8, 184–197. [Google Scholar] [CrossRef]
- Hamed, K.H.; Ramachandra Rao, A. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Ramachandra Rao, A.; Hamed, K.H.; Chen, H.-L. Nonstationarities in Hydrologic and Environmental Time Series; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003; Volume 45, ISBN 978-94-010-3979-6. [Google Scholar]
- Dinpashoh, Y.; Mirabbasi, R.; Jhajharia, D.; Abianeh, H.Z.; Mostafaeipour, A. Effect of Short-Term and Long-Term Persistence on Identification of Temporal Trends. J. Hydrol. Eng. 2014, 19, 617–625. [Google Scholar] [CrossRef]
- Kumar, S.; Merwade, V.; Kam, J.; Thurner, K. Streamflow trends in Indiana: Effects of long term persistence, precipitation and subsurface drains. J. Hydrol. 2009, 374, 171–183. [Google Scholar] [CrossRef]
- Sagarika, S.; Kalra, A.; Ahmad, S. Evaluating the effect of persistence on long-term trends and analyzing step changes in streamflows of the continental United States. J. Hydrol. 2014, 517, 36–53. [Google Scholar] [CrossRef]
- Wilks, D.S. On “field significance” and the false discovery rate. J. Appl. Meteorol. Climatol. 2006, 45, 1181–1189. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Phinney, B. Canadian streamflow trend detection: Impacts of serial and cross-correlation. Hydrol. Sci. J. 2003, 48, 51–64. [Google Scholar] [CrossRef]
- El Kenawy, A.; Lopez-Moreno, J.I.; Vicente-Serrano, S.M. Recent trends in daily temperature extremes over northeastern Spain (1960–2006). Nat. Hazards Earth Syst. Sci. 2011, 11, 2583–2603. [Google Scholar] [CrossRef]
- Douglas, E.M.; Vogel, R.M.; Kroll, C.N. Trends in floods and low flows in the United States: Impact of spatial correlation. J. Hydrol. 2000, 240, 90–105. [Google Scholar] [CrossRef]
- Tabari, H.; Talaee, P.H. Temporal variability of precipitation over Iran: 1966–2005. J. Hydrol. 2011, 396, 313–320. [Google Scholar] [CrossRef]
- Ho, C.H.; Lee, J.Y.; Ahn, M.H.; Lee, H.S. A sudden change in summer rainfall characteristics in Korea during the late 1970s. Int. J. Climatol. 2003, 23, 117–128. [Google Scholar] [CrossRef]
- Oh, J.-H.; Kwon, W.-T.; Ryoo, S.-B. Review of the researches on Changma and future observational study (KORMEX). Adv. Atmos. Sci. 1997, 14, 207–222. [Google Scholar] [CrossRef]
- Webster, P.J.; Holland, G.J.; Curry, J.A.; Chang, H.R. Atmospheric science: Changes in tropical cyclone number, duration, and intensity in a warming environment. Science 2005, 309, 1844–1846. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Wang, Y.; Shao, M.; Jia, X.; Li, X. Spatiotemporal analysis of multiscalar drought characteristics across the Loess Plateau of China. J. Hydrol. 2016, 534, 281–299. [Google Scholar] [CrossRef]
- Shao, Q.; Li, M. A new trend analysis for seasonal time series with consideration of data dependence. J. Hydrol. 2011, 396, 104–112. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. The importance of prewhitening in change point analysis under persistence. Stoch. Environ. Res. Risk Assess. 2016, 30, 763–777. [Google Scholar] [CrossRef]
- Tan, X.; Gan, T.Y.; Shao, D. Effects of persistence and large-scale climate anomalies on trends and change points in extreme precipitation of Canada. J. Hydrol. 2017, 550, 453–465. [Google Scholar] [CrossRef]
- Kim, J.S.; Jain, S.; Moon, Y., II. Atmospheric teleconnection-based conditional streamflow distributions for the Han River and its sub-watersheds in Korea. Int. J. Climatol. 2012, 32, 1466–1474. [Google Scholar] [CrossRef]
- Kim, J.S.; Jain, S.; Yoon, S.K. Warm season streamflow variability in the Korean Han River Basin: Links with atmospheric teleconnections. Int. J. Climatol. 2012, 32, 635–640. [Google Scholar] [CrossRef]
- Khaliq, M.N.; Ouarda, T.B.M.J.; Gachon, P. Identification of temporal trends in annual and seasonal low flows occurring in Canadian rivers: The effect of short- and long-term persistence. J. Hydrol. 2009, 369, 183–197. [Google Scholar] [CrossRef]
- Bayazit, M.; Önöz, B. To prewhiten or not to prewhiten in trend analysis? Hydrol. Sci. J. 2007, 52, 611–624. [Google Scholar] [CrossRef]





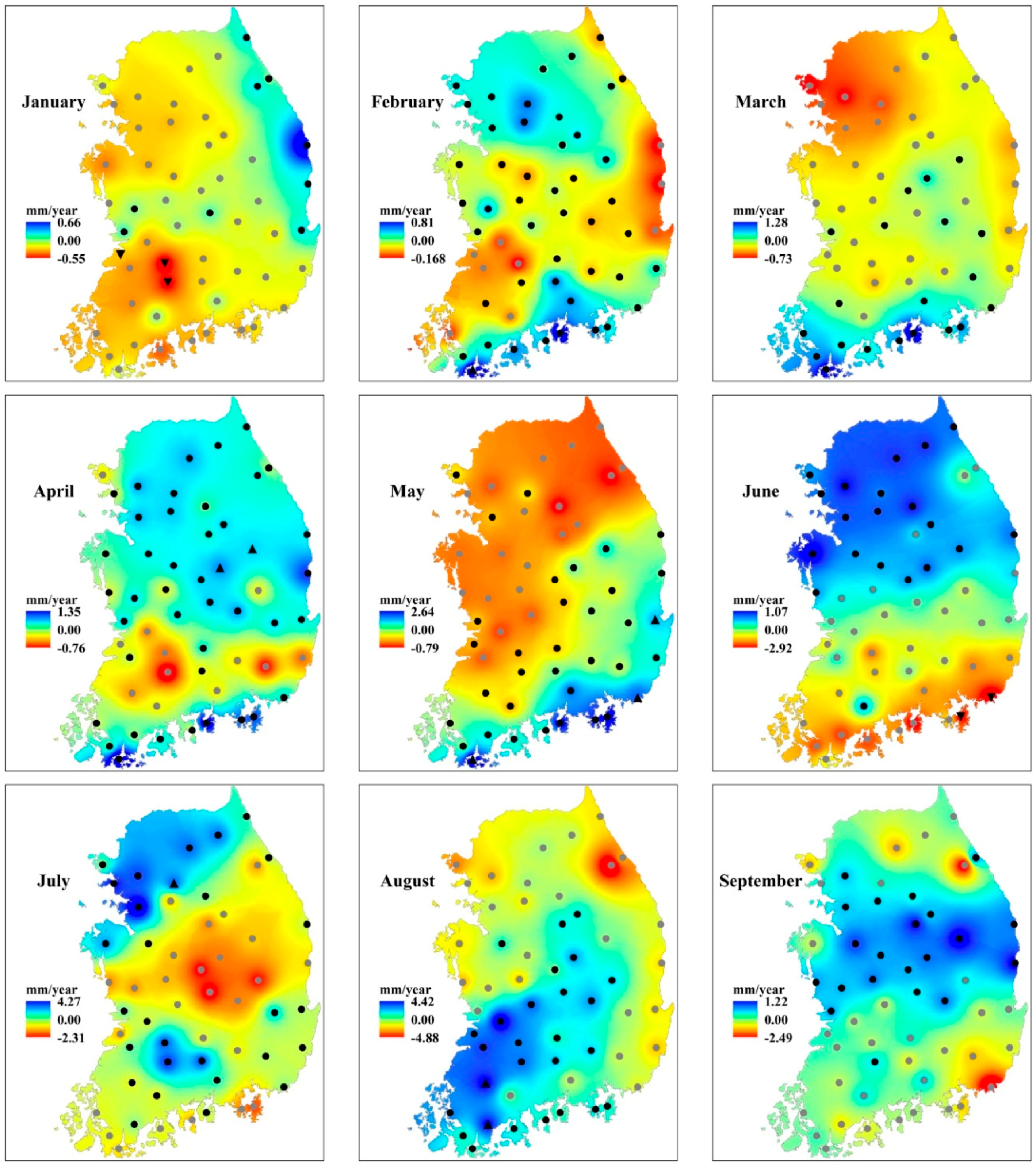








| Variable | Significant Autocorrelation | No Significant Autocorrelation | Significant Trends | No Significant Trends | |||
|---|---|---|---|---|---|---|---|
| + | - | Increasing | Decreasing | Increasing | Decreasing | ||
| January | 1 | 1 | 53 | 0 | 3 | 9 | 43 |
| February | 0 | 1 | 54 | 1 | 0 | 46 | 8 |
| March | 0 | 7 | 48 | 0 | 0 | 20 | 35 |
| April | 0 | 0 | 55 | 2 | 0 | 41 | 12 |
| May | 0 | 1 | 54 | 3 | 0 | 32 | 20 |
| June | 1 | 0 | 54 | 0 | 2 | 20 | 33 |
| July | 2 | 1 | 52 | 1 | 0 | 28 | 26 |
| August | 0 | 4 | 51 | 2 | 0 | 25 | 28 |
| September | 0 | 1 | 54 | 0 | 0 | 21 | 34 |
| October | 0 | 0 | 55 | 1 | 0 | 32 | 22 |
| November | 0 | 0 | 55 | 0 | 0 | 40 | 15 |
| December | 0 | 2 | 53 | 6 | 0 | 41 | 8 |
| Annual | 5 | 1 | 49 | 0 | 0 | 38 | 17 |
| Principal Components | Eigen Value for Unrotated | % Variance Explained Unrotated | Eigen Value for Rotated | % Variance Explained Rotated |
|---|---|---|---|---|
| PC1 | 31.958 | 58.106 | 18.628 | 33.901 |
| PC2 | 7.753 | 14.097 | 12.292 | 22.3 |
| PC3 | 3.267 | 5.940 | 9.238 | 16.8 |
| PC4 | 2.005 | 3.645 | 4.826 | 8.8 |
| Cumulative variance | 81.8 | 81.8 |
| Trend Approach | Significant Trends | No Significant Trends | ||
|---|---|---|---|---|
| Increasing | Decreasing | Increasing | Decreasing | |
| MK | 25 | 1 | 25 | 4 |
| modMK1 | 8 | 0 | 42 | 5 |
| modMK1 lag-3 | 7 | 0 | 43 | 5 |
| modMK2 | 19 | 0 | 31 | 5 |
| modMK2 lag-1 | 16 | 1 | 34 | 4 |
| pwMK | 0 | 0 | 44 | 11 |
| tfpwMK | 48 | 2 | 2 | 3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azam, M.; Maeng, S.J.; Kim, H.S.; Lee, S.W.; Lee, J.E. Spatial and Temporal Trend Analysis of Precipitation and Drought in South Korea. Water 2018, 10, 765. https://doi.org/10.3390/w10060765
Azam M, Maeng SJ, Kim HS, Lee SW, Lee JE. Spatial and Temporal Trend Analysis of Precipitation and Drought in South Korea. Water. 2018; 10(6):765. https://doi.org/10.3390/w10060765
Chicago/Turabian StyleAzam, Muhammad, Seung Jin Maeng, Hyung San Kim, Seung Wook Lee, and Jae Eun Lee. 2018. "Spatial and Temporal Trend Analysis of Precipitation and Drought in South Korea" Water 10, no. 6: 765. https://doi.org/10.3390/w10060765
APA StyleAzam, M., Maeng, S. J., Kim, H. S., Lee, S. W., & Lee, J. E. (2018). Spatial and Temporal Trend Analysis of Precipitation and Drought in South Korea. Water, 10(6), 765. https://doi.org/10.3390/w10060765






