Drought Prediction for Areas with Sparse Monitoring Networks: A Case Study for Fiji
Abstract
:1. Introduction
2. Study Area
3. Materials
3.1. In-Situ Data
3.2. WRF Model Outputs
3.3. SPI
3.4. APCC MME Seasonal Climate Forecast
3.5. Remote Sensing Data
3.5.1. PERSIANN-CDR
3.5.2. TRMM
3.5.3. GPM
3.5.4. MODIS Land Surface Temperature
3.5.5. MODIS Vegetation Indices
3.5.6. Elevation Data
3.6. Large-Scale Climate Index
3.6.1. SPCZ
3.6.2. MEI
4. Methods
4.1. Drought Modeling
4.2. Machine Learning Model Design
4.3. Data Pre-Processing
4.4. Performance Measures
5. Results and Discussion
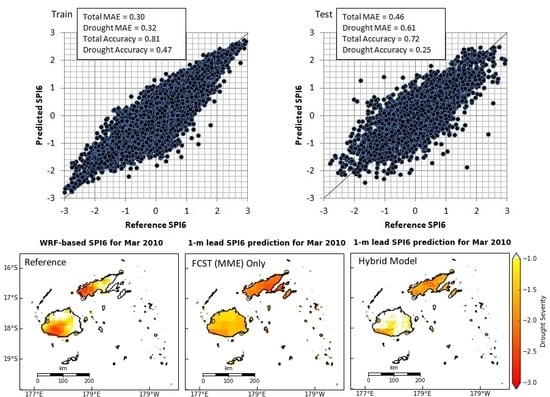
5.1. Training of the Models
5.2. Test of the Models
5.3. Spatial Distribution Maps of SPI6 Predictions
5.4. Relative Importance of Input Variables to Machine Learning Models
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Intergovernmental Panel on Climate Change. Climate Change 2007: The Physical Science Basis: Working Group I Contribution to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007; 996p. [Google Scholar]
- Hay, J.E.; Mimura, N.; Campbell, J.; Fifita, S.; Koshy, K.; McLean, R.F.; Nakalevu, T.; Nunn, P.; de Wet, N. Climate Variability and Change and Sea-Level Rise in the Pacific Islands Region: A Resource Book for Policy and Decision Makers, Educators and Other Stakeholders; South Pacific Regional Environment Programme: Apia, Samoa, 2003; 108p. [Google Scholar]
- Trenberth, K.E.; Hoar, T.J. The 1990–1995 El Niño-Southern Oscillation event: Longest on record. Geophys. Res. Lett. 1996, 23, 57–60. [Google Scholar] [CrossRef]
- Mantua, N.J.; Hare, S.R.; Zhang, Y.; Wallace, J.M.; Francis, R.C. A Pacific interdecadal climate oscillation with impacts on salmon production. Bull. Am. Meteorol. Soc. 1997, 78, 1069–1079. [Google Scholar] [CrossRef]
- Mantua, N.J.; Hare, S.R. The Pacific decadal oscillation. J. Oceanogr. 2002, 58, 35–44. [Google Scholar] [CrossRef]
- Bergeron, T. Richtlinien einer dynamischen Klimatologie. Meteorol. Z. 1930, 47, 246–262. [Google Scholar]
- Trenberth, K.E. Spatial and temporal variations of the Southern Oscillation. Q. J. R. Meteorol. Soc. 1976, 102, 639–653. [Google Scholar] [CrossRef]
- Folland, C.K.; Renwick, J.A.; Salinger, M.J.; Mullan, A.B. Relative influences of the interdecadal Pacific oscillation and ENSO on the South Pacific convergence zone. Geophys. Res. Lett. 2002, 29, 1643. [Google Scholar] [CrossRef]
- Hu, Z.-Z.; Huang, B. Interferential impact of ENSO and PDO on dry and wet conditions in the US Great Plains. J. Clim. 2009, 22, 6047–6065. [Google Scholar] [CrossRef]
- Nicholls, N.; Wong, K.K. Dependence of rainfall variability on mean rainfall, latitude, and the Southern Oscillation. J. Clim. 1990, 3, 163–170. [Google Scholar] [CrossRef]
- Deo, R.C. On meteorological droughts in tropical Pacific Islands: Time-series analysis of observed rainfall using Fiji as a case study. Meteorol. Appl. 2011, 18, 171–180. [Google Scholar] [CrossRef]
- Mataki, M.; Koshy, K.C.; Lal, M. Baseline climatology of Viti Levu (Fiji) and current climatic trends. Pac. Sci. 2006, 60, 49–68. [Google Scholar] [CrossRef]
- Kumar, R.; Stephens, M.; Weir, T. Rainfall trends in Fiji. Int. J. Climatol. 2014, 34, 1501–1510. [Google Scholar] [CrossRef]
- Kumar, R.; Stephens, M.; Weir, T. Temperature trends in Fiji: A clear signal of climate change. S. Pac. J. Nat. Appl. Sci. 2013, 31, 27–38. [Google Scholar]
- Risbey, J.S.; Lamb, P.J.; Miller, R.L.; Morgan, M.C.; Roe, G.H. Exploring the structure of regional climate scenarios by combining synoptic and dynamic guidance and GCM output. J. Clim. 2002, 15, 1036–1050. [Google Scholar] [CrossRef]
- Feresi, J.; Kenny, G.J.; de Wet, N.; Limalevu, L.; Bhusan, J.; Ratukalou, I. Climate Change Vulnerability and Adaptation Assessment for Fiji; Technical Report; The International Global Change Institute, University of Waikato: Hamilton, New Zealand, 2000; 135p. [Google Scholar]
- Agrawala, S.; Ota, T.; Risbey, J.; Hagenstad, M.; Smith, J.; van Aalst, M.; Koshy, K.; Prasad, B. Development and Climate Change in Fiji: Focus on Coastal Mangroves; Organisation for Economic Co-operation and Development: Paris, France, 2003; 56p. [Google Scholar]
- Intergovernmental Panel on Climate Change. Climate Change 2013: The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; 1535p. [Google Scholar]
- Terry, J.P.; Raj, R. The 1997–98 El Niño and drought in the Fiji Islands. In Hydrology and Water Management in the Humid Tropics, Proceedings of the Second International Colloquium, Panama, Republic of Panama, 22–26 March 1999; UNESCO: Paris, France, 2002; pp. 80–93. [Google Scholar]
- ENSO Update. Available online: http://www.met.gov.fj/ENSO_Update.pdf (accessed on 3 November 2017).
- Yin, H.; Donat, M.G.; Alexander, L.V.; Sun, Y. Multi-dataset comparison of gridded observed temperature and precipitation extremes over China. Int. J. Climatol. 2015, 35, 2809–2827. [Google Scholar] [CrossRef]
- Derrick, R.A. The Fiji Islands: A Geographical Handbook; Fiji Government Printing Department: Suva, Fiji, 1957; 68p.
- Terry, J.P.; Raj, R. Hydrological drought in western Fiji and the contribution of tropical cyclones. In Climate and Environmental Change in the Pacific; Terry, J.P., Ed.; School of Social and Economic Development, University of the South Pacific: Suva, Fiji, 1998; pp. 73–85. [Google Scholar]
- Rhee, J.; Yang, H. Development of a Drought Forecast Model for Fiji Based on High-Resolution Dynamic Downscaling of Climate Data and Machine Learning of Long-Range Climate Forecast and Remote Sensing Data; APEC Climate Center Research Report 2017-04; APEC Climate Center: Busan, South Korea, 2018; 63p. [Google Scholar]
- Guttman, N.B. Accepting the standardized precipitation index: A calculation algorithm. J. Am. Water Resour. Assoc. 1999, 35, 311–322. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; American Meteorological Society: Boston, MA, USA, 1993; pp. 179–183. [Google Scholar]
- Fiji Meteorological Service. Personal communication, 2017.
- APEC Climate Data Service System (ADSS). Available online: http://adss.apcc21.org (accessed on 7 July 2017).
- Ashouri, H.; Hsu, K.-L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily precipitation climate data record from multisatellite observations for hydrological and climate studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote. Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.Q.; Huete, A. A feedback based modification of the NDVI to minimize canopy background and atmospheric noise. IEEE Trans. Geosci. Remote 1995, 33, 457–465. [Google Scholar]
- Borlace, S.; Santoso, A.; Cai, W.; Collins, M. Extreme swings of the South Pacific Convergence Zone and the different types of El Niño events. Geophys. Res. Lett. 2014, 41, 4695–4703. [Google Scholar] [CrossRef] [Green Version]
- Cai, W.; Lengaigne, M.; Borlace, S.; Collins, M.; Cowan, T.; McPhaden, M.J.; Timmermann, A.; Power, S.; Brown, J.; Menkes, C.; et al. More extreme swings of the South Pacific convergence zone due to greenhouse warming. Nature 2012, 488, 365–369. [Google Scholar] [CrossRef] [PubMed]
- Kidwell, A.; Lee, T.; Jo, Y.-H.; Yan, X.-H. Characterization of the variability of the South Pacific convergence zone using satellite and reanalysis wind products. J. Clim. 2016, 29, 1717–1732. [Google Scholar] [CrossRef]
- Vincent, E.M.; Lengaigne, M.; Menkes, C.E.; Jourdain, N.C.; Marchesiello, P.; Madec, G. Interannual variability of the South Pacific Convergence Zone and implications for tropical cyclone genesis. Clim. Dyn. 2011, 36, 1881–1896. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought modeling–A review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- Leilah, A.A.; Al-Khateeb, S.A. Statistical analysis of wheat yield under drought conditions. J. Arid Environ. 2005, 61, 483–496. [Google Scholar] [CrossRef]
- Steinemann, A.C. Using climate forecasts for drought management. J. Appl. Meteorol. Climatol. 2006, 45, 1353–1361. [Google Scholar] [CrossRef]
- Morid, S.; Smakhtin, V.; Bagherzadeh, K. Drought forecasting using artificial neural networks and time series of drought indices. Int. J. Climatol. 2007, 27, 2103–2111. [Google Scholar] [CrossRef] [Green Version]
- Han, P.; Wang, P.X.; Zhang, S.Y.; Zhu, D.H. Drought forecasting based on the remote sensing data using ARIMA models. Math. Comput. Model. 2010, 51, 1398–1403. [Google Scholar] [CrossRef]
- Ribeiro, A.; Pires, C.A. Seasonal drought predictability in Portugal using statistical-dynamical techniques. Phys. Chem. Earth 2016, 94, 155–166. [Google Scholar] [CrossRef]
- Tadesse, T.; Brown, J.F.; Hayes, M.J. A new approach for predicting drought-related vegetation stress: Integrating satellite, climate, and biophysical data over the US central plains. ISPRS J. Photogramm. 2005, 59, 244–253. [Google Scholar] [CrossRef]
- Rhee, J.; Im, J. Meteorological drought forecasting for ungauged areas based on machine learning: Using long-range climate forecast and remote sensing data. Agric. For. Meteorol. 2017, 237, 105–122. [Google Scholar] [CrossRef]
- Jensen, J.R.; Lulla, K. Introductory Digital Image Processing: A Remote Sensing Perspective; Taylor & Francis: Milton Park, UK, 1987; 65p. [Google Scholar]
- Quan, X.-W.; Hoerling, M.P.; Lyon, B.; Kumar, A.; Bell, M.A.; Tippett, M.K.; Wang, H. Prospects for dynamical prediction of meteorological drought. J. Appl. Meteorol. Clim. 2012, 51, 1238–1252. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef] [Green Version]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Rhee, J.; Im, J.; Carbone, G.J. Monitoring agricultural drought for arid and humid regions using multi-sensor remote sensing data. Remote Sens. Environ. 2010, 114, 2875–2887. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar drought index sensitive to global warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Kim, D.; Rhee, J. A drought index based on actual evapotranspiration from the Bouchet hypothesis. Geophys. Res. Lett. 2016, 43, 10277–10285. [Google Scholar] [CrossRef]











| Observation Sites | Latitude | Longitude |
|---|---|---|
| Udu Point (91652) | 16.13° S | 180.02° E |
| Nabouwalu (91659) | 16.98° S | 178.70° E |
| Nadi (91680) | 17.75° S | 177.45° E |
| Suva (91690) | 18.15° S | 178.45° E |
| Classification | Index Value |
|---|---|
| Extremely wet (EW) | ≥2.00 |
| Very wet (VW) | 1.50 to 1.99 |
| Moderately wet (MW) | 1.00 to 1.49 |
| Near Normal (NN) | 0.99 to −0.99 |
| Moderate drought (MD) | −1.00 to −1.49 |
| Severe drought (SD) | −1.50 to −1.99 |
| Extreme drought (ED) | ≤−2.00 |
| Source | Type | Lead Time (Month) | Number of Samples | |
|---|---|---|---|---|
| All Categories | Three Drier Categories | |||
| WRF model output | Train (80%) | 1 | 16,693 | 1767 |
| 2 | 16,545 | 1787 | ||
| 3 | 16,379 | 1776 | ||
| 4 | 16,211 | 1762 | ||
| 5 | 16,043 | 1761 | ||
| 6 | 15,875 | 1792 | ||
| Test (20%) | 1 | 4169 | 470 | |
| 2 | 4132 | 445 | ||
| 3 | 4091 | 445 | ||
| 4 | 4049 | 447 | ||
| 5 | 4006 | 456 | ||
| 6 | 3964 | 424 | ||
| In-situ data | All | 1 | 266 | 37 |
| 2 | 264 | 37 | ||
| 3 | 262 | 37 | ||
| 4 | 260 | 37 | ||
| 5 | 258 | 37 | ||
| 6 | 256 | 36 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rhee, J.; Yang, H. Drought Prediction for Areas with Sparse Monitoring Networks: A Case Study for Fiji. Water 2018, 10, 788. https://doi.org/10.3390/w10060788
Rhee J, Yang H. Drought Prediction for Areas with Sparse Monitoring Networks: A Case Study for Fiji. Water. 2018; 10(6):788. https://doi.org/10.3390/w10060788
Chicago/Turabian StyleRhee, Jinyoung, and Hongwei Yang. 2018. "Drought Prediction for Areas with Sparse Monitoring Networks: A Case Study for Fiji" Water 10, no. 6: 788. https://doi.org/10.3390/w10060788
APA StyleRhee, J., & Yang, H. (2018). Drought Prediction for Areas with Sparse Monitoring Networks: A Case Study for Fiji. Water, 10(6), 788. https://doi.org/10.3390/w10060788