Applicability of a Spatially Semi-Distributed Hydrological Model for Watershed Scale Runoff Estimation in Northwest Ethiopia
Abstract
:1. Introduction
2. Study Area and Methods
2.1. Description of Study Area
2.2. Data Collection
2.2.1. Rainfall Data
2.2.2. Discharge Data
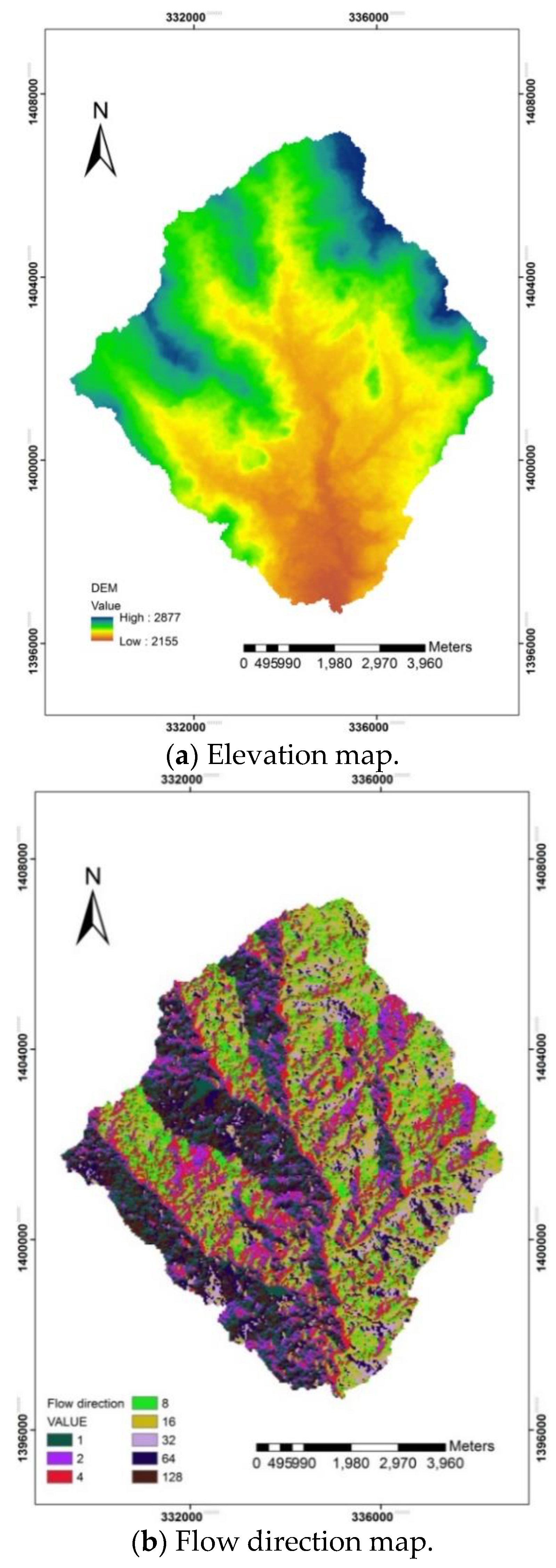
2.2.3. DEM Data Processing Using HEC-GeoHMS Tool in ArcGIS Programme
2.3. HEC-HMS Mode
2.3.1. Loss Methods
2.3.2. The Transform Method
2.3.3. A Base Flow Separation Method
2.3.4. Model Calibration and Validation
3. Results and Discussion
3.1. Physiographic Characteristics of the Catchment
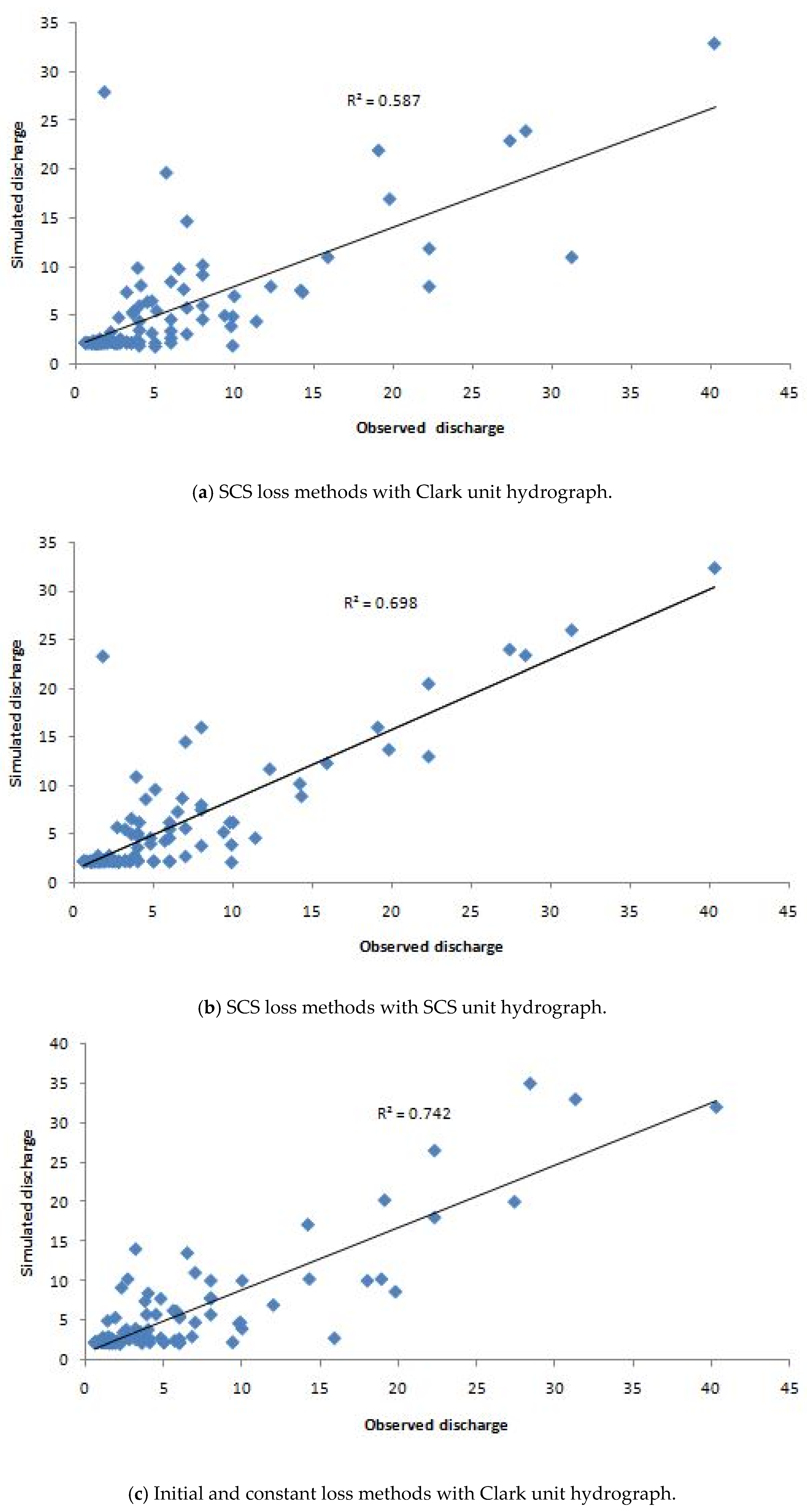
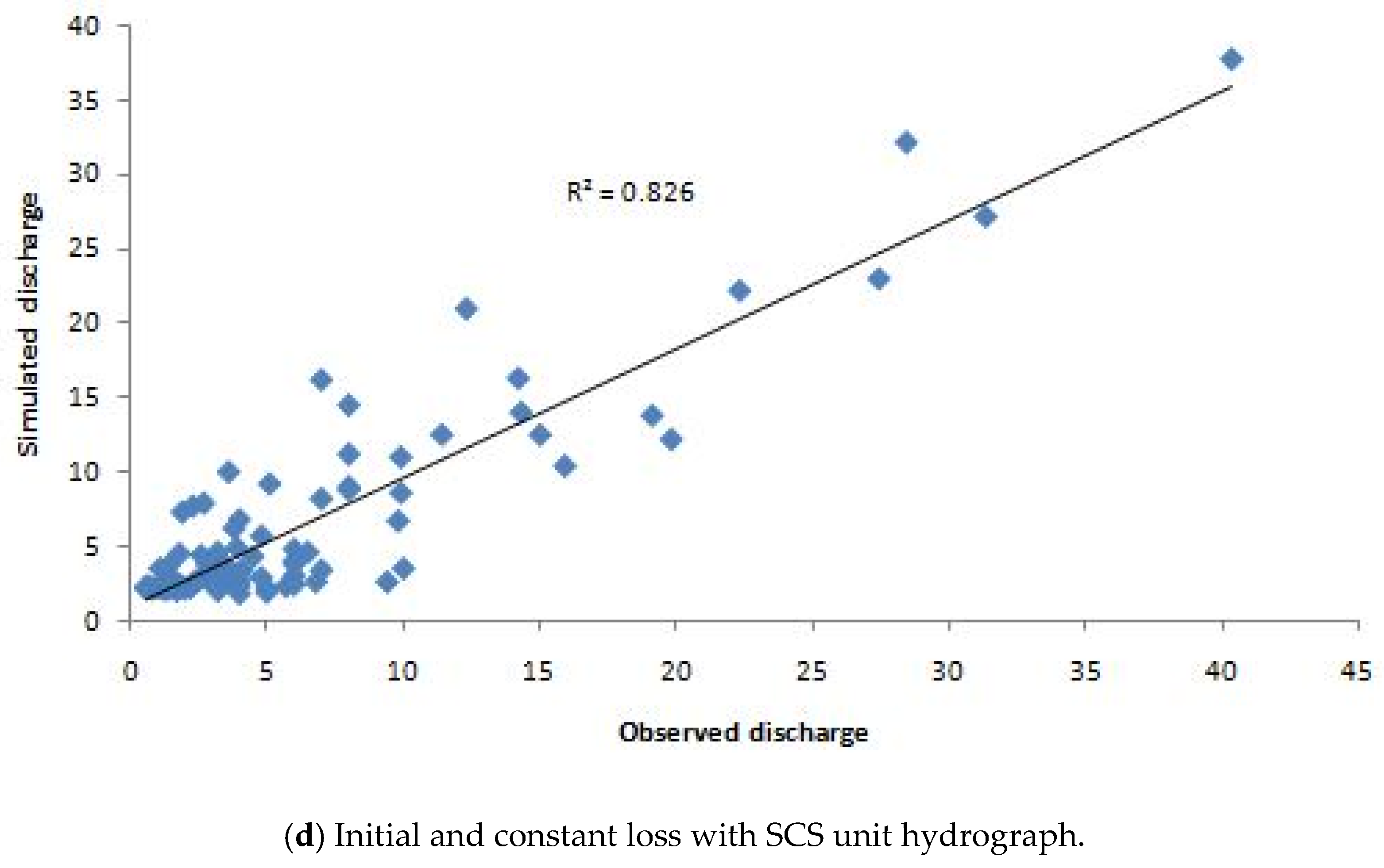
3.2. Simulation Results of The HEC-HMS Model
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Putty, M.R.Y.; Prasad, R. Understanding runoff processes using a watershed model: A case study in the Western Ghats in South India. J. Hydrol. 2000, 228, 215–227. [Google Scholar] [CrossRef]
- Oleyiblo, J.O.; Li, Z. Application of HEC-HMS for flood forecasting in Misai and Wan’an catchments in China. Water Sci. Eng. 2010, 3, 14–22. [Google Scholar] [CrossRef]
- Beven, K.J.; Kirkby, M.J. A physically based variable contributing area model of basin hydrology. Hydrol. Sci. Bull. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Zhao, W.W.; FU, B.J.; Meng, Q.H.; Zhang, Q.J.; Zhang, Y.H. Effects of land-use pattern change on rainfall-runoff and runoff-sediment relations: A case study in Zichang watershed of the Loess Plateau of China. J. Environ. Sci. 2004, 16, 436–442. [Google Scholar]
- Todini, E. The ARNO rainfall-runoff model. J. Hydrol. 1996, 175, 339–382. [Google Scholar] [CrossRef]
- Sugawara, M. Automatic calibration of the tank model. Hydrol. Sci. Bull. 1979, 24, 375–388. [Google Scholar] [CrossRef]
- Singh, V.P.; Woolhiser, D.A. Mathematical modelling of watershed hydrology. J. Hydrol. Eng. 2002, 7, 270–292. [Google Scholar] [CrossRef]
- Pilgrim, D.H.; Cordery, I. Flood runoff. In Handbook of Hydrology; McGraw-Hill Inc.: New York, NY, USA, 1993. [Google Scholar]
- Singh, V.P. Applied Modeling in Catchment Hydrology; Water Resources Publications: Littleton, CO, USA, 1982. [Google Scholar]
- Beven, K.J. Rainfall-Runoff Modelling: The Primer; John Wiley& Sons: Chichester, UK; Wiley-Blackwell: Hoboken, NJ, USA, 2012. [Google Scholar]
- Jin, X.; Xu, C.Y.; Zhang, Q.; Chen, Y.D. Regionalization study of a conceptual hydrological model in Dongjiang basin, south China. Quat. Int. 2009, 208, 129–137. [Google Scholar] [CrossRef]
- Majidi, A.; Shahedi, K. Simulation of Rainfall-Runoff Process Using Green-Ampt Method and HEC-HMS Model (Case Study: Abnama Watershed, Iran). Int. J. Hydraul. Eng. 2012, 1, 5–9. [Google Scholar] [CrossRef]
- Verma, A.K.; Jha, M.K.; Mahana, R.K. Evaluation of HEC-HMS and WEPP for simulating watershed runoff using remote sensing and geographical information system. Paddy Water Environ. 2010, 8, 131–144. [Google Scholar] [CrossRef]
- Hesbon, O.; Dawei, H. Comparative Study on Water Resources Assessment between Kenya and England. In Proceedings of the 11th International Conference on Hydroinformatics HIC, New York, NY, USA, 17–21 August 2014. [Google Scholar]
- Skhakhfa, I.D.; Ouerdachi, L. Hydrological modelling of wadiRessoul watershed, Algeria, by HECHMS model. J. Water Land Dev. 2016, 31, 139–147. [Google Scholar] [CrossRef]
- Feldman, A.D. Hydrologic Modeling System HEC-HMS. In Technical Reference Manual; U.S. Army Corps of Engineers, Hydrologic Engineering Center: Davis, CA, USA, 2000. [Google Scholar]
- U.S. Army Corps of Engineers. Hydrologic Modeling System (HEC-HMS) Applications Guide: Version 3.1.0; Hydrologic Engineers Center: Davis, CA, USA, 2008. [Google Scholar]
- Halwatura, D.; Najim, M.M. Application of the HEC-HMS model for runoff simulation in a tropical catchment. Environ. Model. Softw. 2013, 46, 155–162. [Google Scholar] [CrossRef]
- Kathol, J.P.; Werner, H.D.; Trooien, T.P. Runoff for Frequency Based Storm Using a Prediction- Runoff Model; ASAE: Washington, DC, USA, 2003. [Google Scholar]
- Knebl, M.; Yang, Z.; Hutchison, K.; Maidment, D.R. Regional scale flood modeling using NEXRAD rainfall, GIS, and HEC-HMS / HEC-RAS: A case study for the San Antonio River Basin Summer 2002 storm event. J. Environ. Manag. 2005, 75, 325–336. [Google Scholar] [CrossRef] [PubMed]
- McColl, C.; Aggett, G. Land use forecasting and hydrologic model integration for improved land use decision support. J. Environ. Manag. 2006, 84, 494–512. [Google Scholar] [CrossRef] [PubMed]
- Momcilo, M.; Angle, Y.L.; Hejazi, M. Changing estimates for design precipitation in northeastern Illinois. Comparison between different sources and sensitivity analysis. J. Hydrol. 2007, 347, 211–222. [Google Scholar]
- Amengual, A.; Romero, R.A. Hydrometeorological modeling study of a flash-flood event over Catalonia, Spain. J. Hydrol. 2007, 8, 282–303. [Google Scholar] [CrossRef]
- Yusop, Z.; Chan, C.H.; Katimon, A. Runoff characteristics and application of HEC-HMS for modelling storm flow hydrograph in an oil palm catchment. J. Water Sci. Technol. 2007, 56, 41–48. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Garcia, A.; Sainz, A.; Revilla, J.; Alvarez, C. Surface water resources assessment in scarcely gauged basins in the north of Spain. J. Hydrol. 2008, 356, 312–326. [Google Scholar] [CrossRef]
- Jin, H.; Liang, R.; Wang, Y.; Tumula, P. Flood-Runoff in Semi-Arid and Sub-Humid Regions, a Case Study: A Simulation of Jianghe Watershed in Northern China. Water 2015, 7, 5155–5172. [Google Scholar] [CrossRef] [Green Version]
- Arekhi, S.; Rostamizad, G.; Rostami, N. Evaluation of HEC-HMS Methods in Surface Runoff Simulation (Case Study: Kan Watershed, Iran). Adv. Environ. Biol. 2011, 5, 1316–1321. [Google Scholar]
- Haberlandt, U.; Radtke, I. Hydrological model calibration for derived flood frequency analysis. Hydrol. Earth Syst. Sci. 2014, 18, 353–365. [Google Scholar] [CrossRef] [Green Version]
- Gumindoga, W.; Makurira, H.; Phiri, M.; Nhapi, I. Estimating runoff from ungauged catchments for reservoir water balance in the Lower Middle Zambezi Basin. Water SA 2016, 42, 641–649. [Google Scholar] [CrossRef]
- Azam, M.; Kim, H.S.; Maeng, S.J. Development of flood alert application in Mushim stream watershed Korea. Int. J. Disaster Risk Reduct. 2017, 21, 11–26. [Google Scholar] [CrossRef]
- Yilma, H.; Moges, S.A. Application of semi-distributed conceptual hydrological model for flow forecasting on upland catchments of Blue Nile River Basin, a case study of Gilgel Abbay catchment. Catchment Lake Res. 2007, 6, 1–200. [Google Scholar]
- Merrey, D.J.; Gebreselassie, T. Promoting Improved Rainwater and Land Management in the Blue Nile (Abay) Basin of Ethiopia; NBDC Technical Report 1; International Livestock Research Institute: Nairobi, Kenya, 2011. [Google Scholar]
- Blöschl, G. Rainfall-runoff modeling of un-gauged catchments. Encycl. Hydrol. Sci. 2005, 5, 1–19. [Google Scholar] [CrossRef]
- Chow, V.; Maidment, D.; Mays, L. Applied Hydrology; McGraw-Hill Science/Engineering/Math: New York, NY, USA, 1998. [Google Scholar]
- Najim, M.M.; Babel, M.S.; Loof, R. AGNPS model assessment for a mixed forested watershed in Thailand. Sci. Asia 2006, 32, 53–61. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutclife, J.V. River flow forecasting through conceptual models Part 1: A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Neter, J.; Wasserman, W.; Kutner, M.H. Applied Linear Models: Regression, Analysis of Variance, and Experimental Designs, 3rd ed.; Irwin: Homewood, IL, USA, 1990. [Google Scholar]
- Sabzevari, T.; Ardakanian, R.; Shamsaee, A.; Talebi, A. Estimation of flood hydrograph in no statistical watersheds using HEC-HMS model and GIS (Case study: Kasilian watershed). J. Water Eng. 2009, 4, 1–11. [Google Scholar]
- Zou, K.H.; Tuncali, K.; Silverman, S.G. Correlation and simple linear regression. Radiology 2003, 227, 617–622. [Google Scholar] [CrossRef] [PubMed]
- Sharma, K.D. Modified runoff curve numbers for bare crust forming sandy soils. Aust. J. Soil Res. 1987, 25, 541–545. [Google Scholar] [CrossRef]
- Hawkins, R.H. Asymptotic determination of runoff curve numbers from data. J. Irrig. Drain. Eng. 1993, 119, 334–345. [Google Scholar] [CrossRef]
- Zelelew, D.G. Spatial mapping and testing the applicability of the curve number method for un-gauged catchments in Northern Ethiopia. Int. Soil Water Conserv. Res. 2017, 5, 293–301. [Google Scholar] [CrossRef]
- Burn, D.H.; Boorman, D.B. Estimation of hydrological parameters at un-gauged catchments. J. Hydrol. 1993, 143, 429–454. [Google Scholar] [CrossRef]




| Parameters | Values |
|---|---|
| Area | 55.2 km2 |
| Perimeter | 45,076 m |
| Max. Elevation | 2877 m |
| Min. Elevation | 2155 m |
| Mean slope of the basin | 25.6% |
| Main channel length | 12,485 m |
| Main channel mean slope | 2.81% |
| Drainage density | 0.94 km/km2 |
| Sub-Basins | Area (km2) | Perimeter (m) | Basin Slope (%) | Main River Flow | Curve Number | Constant Loss Rate (mm/h) | |||
|---|---|---|---|---|---|---|---|---|---|
| Flow Length (m) | Slope (m/m) | Initial Values | Optimized Values | Initial Values | Optimized Values | ||||
| Sub-basin 1 | 13.76 | 25,757 | 26.5 | 7877 | 0.045 | 78 | 86 | 3.8 | 2.2 |
| Sub-basin 2 | 24.08 | 31,018 | 26.2 | 9030 | 0.035 | 75 | 90 | 4.3 | 3.1 |
| Sub-basin 3 | 11.55 | 23,345 | 26.3 | 6424 | 0.051 | 72 | 82 | 6.7 | 4.4 |
| Sub-basin 4 | 5.77 | 17,776 | 19.8 | 3455 | 0.021 | 68 | 68 | 7.8 | 5.2 |
| Element | X | Muskinghum (K), K(h) | ||
|---|---|---|---|---|
| Initial Values | Optimized Values | Initial Values | Optimized Values | |
| Reach 1 | 0.2 | 0.145 | 1 | 0.65 |
| Reach 2 | 0.2 | 0.145 | 1 | 0.65 |
| Simulation Event | Observed Runoff Depth (mm) | Outflow (SCS-ClarkHy) | Change in % | Outflow (SCS-SCSHy) | Change in % | Outflow (InCo-SCSHy) | Change in % | Outflow (InCo-ClarkHy) | Change in % |
|---|---|---|---|---|---|---|---|---|---|
| Before calibration | 614.83 | 378.25 | −38.48 | 407.8 | −33.67 | 462.98 | −24.70 | 485.07 | −21.11 |
| For model calibration | 420.41 | 350.71 | −16.58 | 352.04 | −16.26 | 373.87 | −11.07 | 359.48 | −14.49 |
| For model validation | 975.92 | 801.58 | −17.92 | 798.32 | −18.20 | 910.13 | −6.74 | 877.00 | −10.14 |
| (a) Uncalibrated | |||||||||
| Date | Observed Flow (m3/s) | Outflow (SCS-ClarkUH) | Change in % | Outflow (SCS-SCSUH) | Change in % | Outflow (InCo-SCSUH) | Change in % | Outflow (InCo-ClarkUH) | Change in % |
| 8 September 1992 | 15.9 | 7.8 | −50.94 | 8.3 | −47.80 | 10.8 | −32.08 | 9.6 | −39.62 |
| 27 March 1993 | 8.1 | 3.8 | −53.09 | 4.3 | −46.91 | 5.6 | −30.86 | 6.6 | −18.52 |
| 12 July 1993 | 30.2 | 17.3 | −42.72 | 19.2 | −36.42 | 22.4 | −25.83 | 19.2 | −36.42 |
| 8 September 1994 | 32.9 | 13.1 | −60.18 | 17.2 | −47.72 | 24.2 | −26.44 | 22.5 | −31.61 |
| 9 May 1995 | 25.4 | 11.2 | −55.91 | 11.7 | −53.94 | 17.6 | −30.71 | 15.6 | −38.58 |
| 2 August 1995 | 18.4 | 11.5 | −37.5 | 10.4 | −43.48 | 12.1 | −34.23 | 10.0 | −45.65 |
| Average | −50.06 | −46.05 | −30.03 | −35.07 | |||||
| (b) Calibrated | |||||||||
| Date | Observed Flow (m3/s) | Outflow (SCS-ClarkHy) | Change in % | Outflow (SCS-SCSHy) | Change in % | Outflow (InCo-SCSHy) | Change in % | Outflow (InCo-ClarkHy) | Change in % |
| 12 July 1996 | 24.6 | 14.7 | −40.24 | 17.8 | −27.64 | 21.8 | −11.38 | 20.4 | −17.07 |
| 21 August 1996 | 20.4 | 16 | −21.57 | 15.6 | −23.53 | 18.2 | −10.78 | 18.2 | −10.78 |
| 16 August 2003 | 32.8 | 23.7 | −27.74 | 24.2 | −26.22 | 28.6 | −12.80 | 25.2 | −23.17 |
| 22 August 2003 | 27.4 | 20.7 | −24.45 | 22 | −19.71 | 24.3 | −11.31 | 20.9 | −23.72 |
| 26 August 2003 | 36.2 | 26.7 | −26.24 | 26.2 | −27.62 | 33.2 | −8.29 | 31.1 | −14.09 |
| 4 July 2004 | 35.2 | 24 | −31.82 | 27.8 | −21.02 | 31.8 | −9.66 | 29.8 | −15.34 |
| Average | −28.68 | −24.29 | −10.70 | −17.36 | |||||
| Statistical Evaluation Criteria | Loss Methods | |||
|---|---|---|---|---|
| SCS Loss Method | Initial and Constant Loss Method | |||
| SCS Unit Hydrograph | Clark Unit Hydrograph | SCS Unit Hydrograph | SCS Unit Hydrograph | |
| Relative bias errors (%) | 24.29 ns | 28.68 ns | 17.36 ** | 10.71 *** |
| Coefficient of determination (R2) | 0.70 * | 0.59 * | 0.74 ** | 0.83 *** |
| Nash-Sutcliffe Efficiency (%) | 64.7 * | 57.8 ns | 71.8 ** | 82.8 *** |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zelelew, D.G.; Melesse, A.M. Applicability of a Spatially Semi-Distributed Hydrological Model for Watershed Scale Runoff Estimation in Northwest Ethiopia. Water 2018, 10, 923. https://doi.org/10.3390/w10070923
Zelelew DG, Melesse AM. Applicability of a Spatially Semi-Distributed Hydrological Model for Watershed Scale Runoff Estimation in Northwest Ethiopia. Water. 2018; 10(7):923. https://doi.org/10.3390/w10070923
Chicago/Turabian StyleZelelew, Demlie G., and Assefa M. Melesse. 2018. "Applicability of a Spatially Semi-Distributed Hydrological Model for Watershed Scale Runoff Estimation in Northwest Ethiopia" Water 10, no. 7: 923. https://doi.org/10.3390/w10070923
APA StyleZelelew, D. G., & Melesse, A. M. (2018). Applicability of a Spatially Semi-Distributed Hydrological Model for Watershed Scale Runoff Estimation in Northwest Ethiopia. Water, 10(7), 923. https://doi.org/10.3390/w10070923






