Next Article in Journal
A Comparative Analysis of the Wind and Wave Climate in the Black Sea Along the Shipping Routes
Next Article in Special Issue
Improving Reservoir Operation Criteria to Stabilize Water Supplies in a Multipurpose Dam: Focused on Nakdong River Basin in Korea
Previous Article in Journal
Willingness to Pay for Recreational Benefit Evaluation in a Wastewater Reuse Project. Analysis of a Case Study
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 10
Issue 7
10.3390/w10070923
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Applicability of a Spatially Semi-Distributed Hydrological Model for Watershed Scale Runoff Estimation in Northwest Ethiopia

by
Demlie G. Zelelew
1,* and
Assefa M. Melesse
2
1
Amhara Agricultural Research Institute, Sirinka Agricultural Research Centre, P.O. Box 74, North Wollo, Woldia, Ethiopia
2
Department of Earth and Environment, Florida International University, Miami, FL 33199, USA
*
Author to whom correspondence should be addressed.
Water 2018, 10(7), 923; https://doi.org/10.3390/w10070923
Submission received: 11 June 2018 / Revised: 1 July 2018 / Accepted: 9 July 2018 / Published: 12 July 2018
(This article belongs to the Special Issue GIS-Based Hydrology and Water Quality Modeling)
Browse Figures
Versions Notes

Abstract

:
Estimation of runoff is vital forplanning activities in relation to integrated watershed management and flood protection measures. This research was conducted at one of the catchments in Abbay River (upper Blue Nile River) basin to assess the applicabilityof the Hydrologic Engineering Centre Hydrological Modelling Software (HEC-HMS) modelfor simulation of runoff. It was aimed at selecting the best loss and transform methods in the model, as well as testing the applicability of the calibrated model to ungauged watersheds. Two loss methods such as soil conservation service (SCS) and initial and constant methods with two transform methods including SCS and Clark unit hydrographs were considered in the study for selecting the best combinations applicable in the area. While comparing the simulation results of each combination, better results were obtained in the model set containing the initial and constant loss method and SCS unit hydrograph with a Nash-Sutcliff Efficiency (NSE) of 82.8%, R2 of 0.83, and 10.71% of relative bias errors, followed by initial and constant with Clarks unit hydrograph, and it can be used for similar ungauged watersheds.

1. Introduction

An adequate knowledge of runoff within a given catchment is important for the planning and designing of many water resources development and related projects. An actual estimation of runoff volume and peaks is also important for planning different interventions in integrated watershed management and many flood protectionprojects [1,2]. The tasks in relation to estimation runoff volumes and flood peaks can be, however, easily simplified by adopting a modelling concept understanding rainfall partitioning and the principal factors triggering runoff [3,4,5]. The rainfall-runoff modelling approach is most frequently used in hydrology for estimating the runoff signal which leaves the catchment from the rainfall signal received by the basin [6,7]. Different techniques of the hydrologic modelling approach have been so far adopted in different studies, with some of them focused on an empiricalbasis and other modelling approaches based on the distributed modelling concept [1,8].The type of the modelling approach normally depends on the purposes, data availability, and ease of use [9,10].
Measurement of all parameters affecting catchmentrunoff is impossible, especially for remote catchments. It is thus imperative to choose a suitable model with a simple structure, minimum input data requirements, and a reasonable precision [1,10,11,12]. Considering the lack of sufficient data on one hand and the complexity of hydrological systems on the other, a lot of computer-based hydrological models have been developed, such as Soil Water & Assessment Tool (SWAT), Hydrologic Engineering Center-Hydrologic Modeling System (HEC-HMS), Topography based hydrological model (TOPMODEL), The Water Erosion Prediction Project (WEPP) Model, and Annualized Non Point Source Pollution Model (AnnAGNPS) [13,14,15].Those models were developed based on different situations of data availability and ease of complexity. HEC-HMS is one of those models significantly used in different parts of the world for estimating runoff by considering different modelling approaches, in which both lumped and distributed modelling approaches and concepts are embedded in the programme [16,17].HEC-HMS is hydrological modelling software developed by the US Army Corps of Engineers Hydrologic Engineering Centre (HEC), which is designed to simulate the precipitation runoff processes within a wide range of geographic areas, such as large river basins and small urban or natural watersheds [17,18]. Because of its ability in the simulation of runoff both in short and long time events, ease to use, and use of common methods, HEC-HMS has become very popular and been adopted in many hydrological studiesin relation to the simulation of runoff volume in integrated water resources and watershed management projects and for estimating flood peaks in flood forecasting, irrespective of the size of the catchment [12,18,19,20,21,22,23,24,25,26,27,28,29,30]. A special extension programme of the HEC-GeoHMS in ArcGIS has been applied in some of the studies and allowed researchers to generate relevant spatial data in relation to terrain characteristics which cloud be used as input data for HEC-HMS mode [2,12,21,24,25,26,27,28,29,30]. After appropriate calibration and validation tasks in each selected loss, transform methods, and routing reaches in the HEC-HMS programme, reasonable and reliable simulation results of runoff volume and peak values were obtained as compared to observational data in all the studies. It is, however, clearly indicated that the results of the model were location specific in that different combinations of a model set containing the loss methods, runoff transform methods, and base flow separation techniques were found to respond variably in simulating the basic components of runoff hydrographs in various studies. According to the study by Oleyibl et al. [2], for example, credible results were obtained by usinginitial and constant as the loss method, a Soil Conservation Services (SCS) unit hydrograph as the transform method, and the exponential recession model as a base separation model, whereas Halwatura and Najjim [18] obtained better simulation results from the combination of deficit constant loss methods and Snyder Unit Hydrograph, and a combination of the modified SCS loss method, Clarks unit hydrograph, and recession model in the study by Azam et al. [30].
Though huge tasks made for testing and calibrating the HEC-HMS on a global scale, little effort has been made in the context of Ethiopian catchments [31]. Abbay River basin is a significant part of Ethiopia, covering an area of 199,812 km2. Due to extensive agricultural practices and unpredicted flood events in the basin, it has been seriously affected by land degradation and flood problems, especially in the lowlands [32]. This study isconducted in one of the catchments at Abbay River (upper Blue Nile River) in Northwest Ethiopia. An accurate estimation of runoff in volume and peak values for the corresponding rainfall occurrence is critically important for designing appropriateintegrated watershed managementactivities and taking appropriate flood protection measures in time, as described earlier. This study aimed to assess the runoff potential using a spatial distributed hydrological model in the targeted area.
This study is primarily conducted to test the applicability of the HEC-HMS model through selecting the best combinations of the loss and transform methods applicable to the targeted catchment. The study also aimed at fixing the corresponding calibrated values of those sensitive parameters in the selected loss and transform methods and characterizing the basic parameters of the catchment for further and future hydrological investigations in similar catchments and other nearby un-gauged catchments in the basin.

2. Study Area and Methods

2.1. Description of Study Area

The targeted catchment (Angreb sub basin) selected for this study is found within Abbay river basin in Northwest Ethiopia, and covers a total area of about 55 km2 (Figure 1). Geographically, the sub-basin is found between 12°37′49″ N and 12°43′29″ N latitude and 37°25′38″ E and 37°30′52″ E longitude. The annual rainfall of the sub-basin ranges from 700 mm to 1900 mm, with a mean annual rainfall value of about 1150 mm. Besides, the sub-basin has a mean maximum temperature of 29 °C and minimum temperature of 10 °C.

2.2. Data Collection

2.2.1. Rainfall Data

The rainfall data is the basic input data for any hydrological modelling study, including HEC-HMS. The rainfall data for the two nearby stations were collected from the national meteorological agency of Ethiopia.

2.2.2. Discharge Data

Calibration and validation tasks are fundamental operations in many modelling studies, including hydrological studies [6,9,10,21,28]. Hydrological models basically need a series of runoff data for model calibration and validation purposes [20,30,33].The runoff data for this study (1992–2005) was taken from the Ethiopian Ministry of Water, Irrigation and Electricity and implemented while calibrating the parameters in the HEC-HMS model.

2.2.3. DEM Data Processing Using HEC-GeoHMS Tool in ArcGIS Programme

A 30 × 30 m resolution DEM (digital elevation model) of the targeted catchment from the US Geological Survey was used for extracting relevant basic information on physiographic characteristics of the catchment, including elevation and slope information (Figure 2). The DEMs data were further processed using the geographic information system (GIS) interface of the HEC-GeoHMS model in an ArcGIS programme. Terrain pre-processing and basin processing tools were used to generate basin characteristic parameters and input files for HEC-HMS including a stream network, sub-basin boundaries, and the connectivity of various hydrologic elements.

2.3. HEC-HMS Mode

HEC-HMS easily operates huge tasks in relation to hydrological studies, including losses, runoff transform, open channel routing, analysis of meteorological data, rainfall-runoff simulation, and parameter estimation [16,17]. It uses separate models to represent each component of the runoff process, including models that compute runoff volume, models of direct runoff, and models of base flow. For each of the hydrological models, estimation tools have been defined in the programme. The details of model structures and various processes involved are given in the technical reference HEC-HMS manual in Feldman [16] and the user’s manual in U.S. Army Corps of Engineers-The Hydrologic Engineering Center (USACE-HEC) [14]. Before running the model, a basin model, a meteorological model, and control specifications were created and defined in advance in this study. The basin model and basin features which derived from HEC-GeoHMS were taken as a background map file and imported to HEC-HMS 3.5. As every sub-basin has no observation station within it, the precipitation values for each sub basin were then estimated by interpolating using the Inverse Distance Weighing (IDW) method with respect to the centroid point of each sub-basin, and both an hourly and daily simulation time step were used while calibrating the parameters of the selected methods in the model.

2.3.1. Loss Methods

The loss models in HEC-HMS normally compute runoff volume by computing the volume of water that is intercepted, infiltrated, stored, evaporated, or transpired, and subtracting it from the precipitation. Around 11 kinds of loss estimation methods are embedded in the programme considering different modelling concepts on the relation of precipitation and runoff trigging factors like soil properties, land covers, canopy cover, etc. In this study, two kinds of loss methods were selected for simulating the runoff volume and peak flood, considering ease of applicability and low data requirement, like Soil Curve Number (SCS Curve Number) and initial and constant loss methods [16]. A detailed description of the modelling concepts and the corresponding equation behind each loss method can be found in the technical reference manual in Feldman [16] and the User’s Manual of USACE-HEC [17].

2.3.2. The Transform Method

The transform prediction models in HEC-HMS simulate the process of the direct runoff of excess precipitation on the watershed, and they transform the precipitation excess into point runoff. The models transform the rainfall excess into direct surface runoff through a unit hydrograph, and the SCS and Clarks unit hydrograph method were used as the transform models in this study. The basic concepts and assumptions behind each unit hydrograph method can be also found in the HEC-HMS technical manual in Feldman [16]. Besides, a Kirpich method shown in Equation (1) and a relation shown in Equation (2) were also jointly applied in this study for estimating the initial values for the time of concentration and lag time in each sub-basin, which were used as input data in the selected transform methods.
TC = 0.0195 × L0.77 × S−0.385
where TC is the time of concentration (min), L is the length of the main river (m), and S is the mean slope of the main river (m/m).
TL = 0.6 × TC
where TL is the lag time (min) and TC is the time of concentration.

2.3.3. A Base Flow Separation Method

While the total runoff is transformed into direct runoff, basic information in relation to base flow is required, and a monthly constant base flow separation technique was adopted in this study. In order to separate the overland flow and base flow, a methodology proposed by Chow et al. [34] was used in this study. Using this technique, a line that slopes upwards is drawn from the initial hydrograph rise and extends until it intercepts the hydrograph downward. The hydrographs developed using daily data were then used for undertaking the base flow separation techniques in this study. Besides, the Muskingum routing model was employed to model the reach elements.

2.3.4. Model Calibration and Validation

Sensitive analysis is usually undertaken in most modelling studies [22,24,25,27,30]. This operation is mainly carried out for selecting the most trigging input factor that affects the output of the model. Both manual and automatic calibration were used in this study, where the manual calibration was undertaken through conducting a sensitive analysis in each simulation on the parameters in the selected methods in each sub-basin through changing their value in the range of ±30% with 5% intervals until the best fit between the observed and simulated parameters in the given hydrograph was obtained. The sensitive parameters were then selected based on their effect on peak discharge and runoff volume and the model calibration task was then later performed using the optimization method. In this study, the selected flood events from 1992 to 1995 were used for model testing and the remaining data from 1996 and 2005 for calibration and validation purposes. Homogeneity and stationarity tests were primarily undertaken in the data setprior to any analysis in this study. The missing data and outliers were then adjusted accordingly for those data sets which did not satisfy the tests. Lastly, statistical evaluation techniques such as the objective function of relative bias errors proposed by Najim et al. [35], Nash-Sutcliffe Efficiency (NSE) by Nash and Sutclife [36], and coefficient of determination (R2) as described in Neter et al. [37] were applied to evaluate the performance of the model and the selected loss and transform methods by comparing the relation between the simulated and observed direct runoff values.

3. Results and Discussion

3.1. Physiographic Characteristics of the Catchment

The outlet point of the catchment (the geographical reference point of the hydrological gauging station) was considered in this study to delineate the boundary of the catchment area using the HEC-GeoHMS extension in ArcGIS. Further processing of the DEM using HEC-GeoHMS also resulted in generating four sub-basins, two routing reaches, and the major physiographic characteristics of the catchments, as shown in Figure 3 and Table 1.

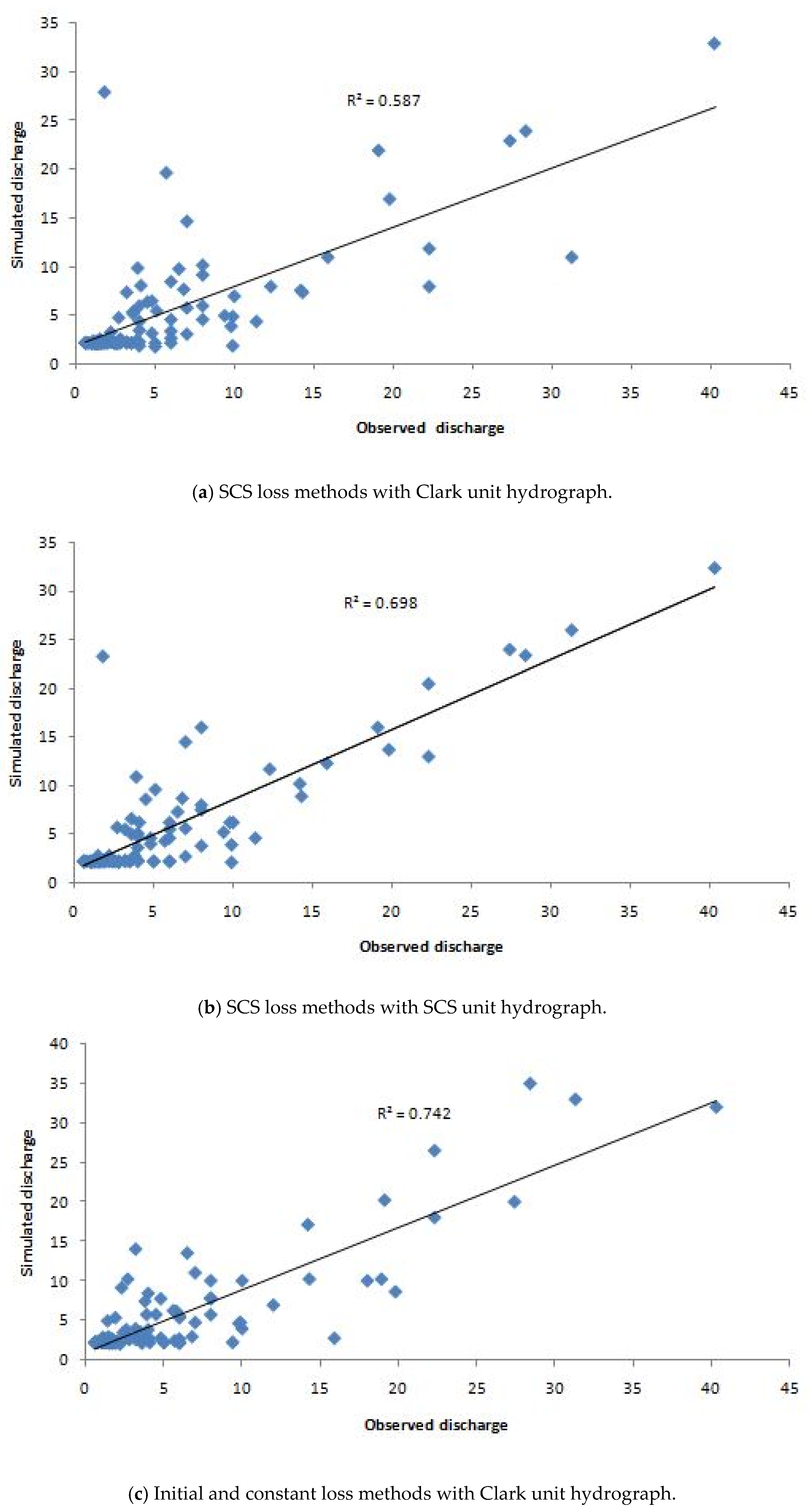
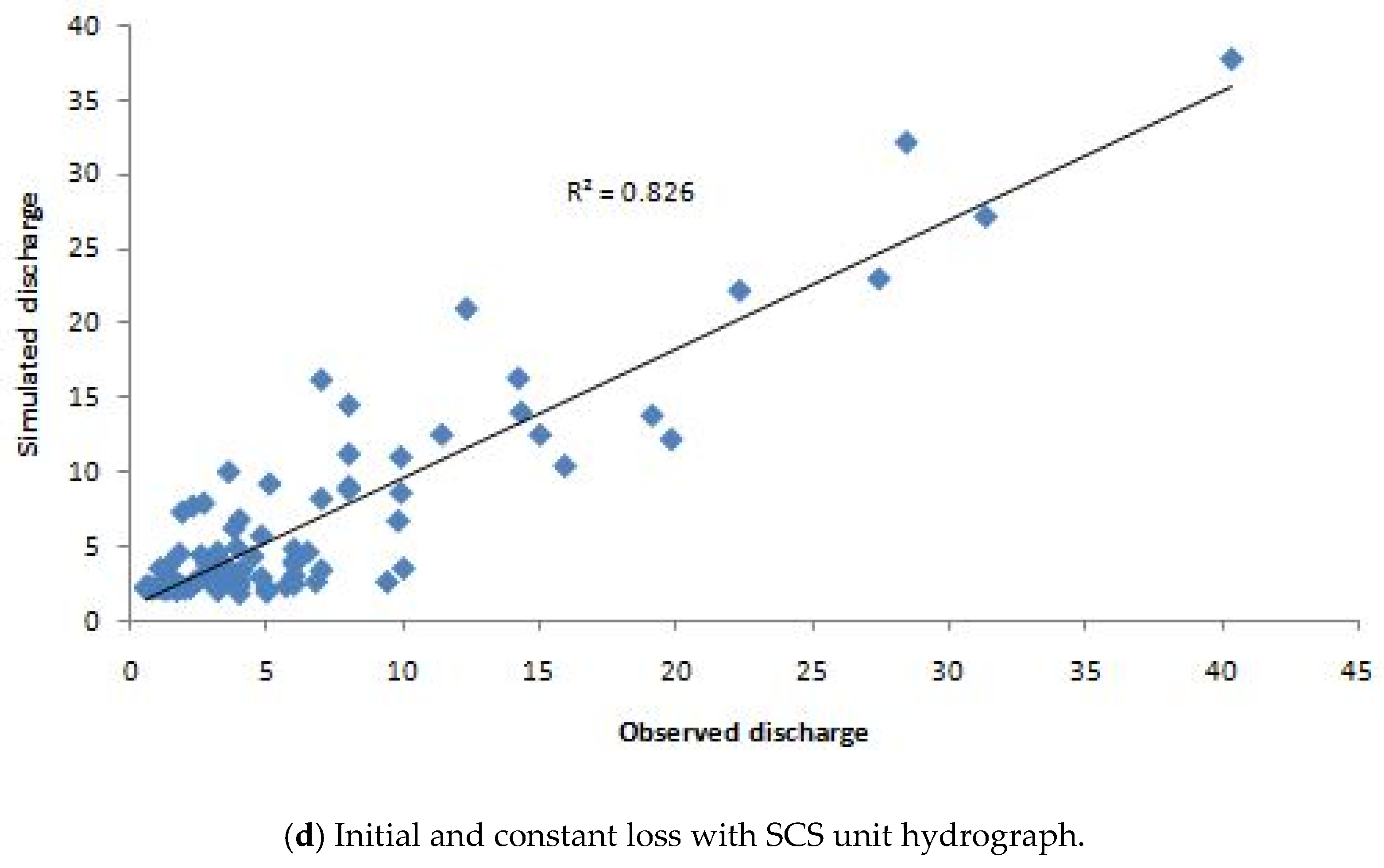
3.2. Simulation Results of The HEC-HMS Model

Using a procedure described in Section 2.3.4 the basin model was created in the HEC-HMS by using four sub-basins and two routing reaches which were imported from the HEC-GeoHMS model. To begin the simulation task, calculated and assumed initial values for the sensitive parameter of the sub-basins shown in Table 2 and Table 3 were first used in the HEC-HMS model for simulating the runoff depth and peak discharge for some selected events.
In this study, selected flood events that occurred from 1996 to 2000 were used for model calibration, and flood events that occurred between 2001 and 2005 were used for model verification. Figure 4 and Table 4 and Table 5 summarize the simulation results of the selected loss methods before calibration and the simulation results after calibration and for validation. Figure 4a shows the runoff hydrograph simulation results of the HEC-HMS model for some selected events before calibration by loss methods and transform models. As indicated in the figure, a difference between the observed and simulated hydrographs is clearly observed in all combinations of loss and transform methods, and underestimated values were obtained both in flood peaks and runoff volume in all simulation run. As shown in Table 4, higher values for percent errors in total runoff depth were recorded between the simulated and observed value in all simulations before calibration, which falls in the range between 21% and 38%. Table 5 also indicates an objective function for percent errors in peak discharge values for some selected events before and after calibration. As shown in the Table 5a, the percentage of variation ranges from 37.5% to 60.2%, with a mean value of 50.1%; for example, for a model set containing the SCS loss method with Clarks unit hydrographs, respectively. However, according to Najim et al. [35] and Sabzevari et al. [38], the acceptable ranges of relative percent errors between the observed and simulated values should be below ±20%. In this statistical evaluation criteria, the negative percentage of relative errors indicated under prediction, while the positive values represented over prediction of the simulation outcome. Considering the percentages of relative bias errors found in Table 5a, all the simulation results are almost beyond the allowable limit, and an effort was then made to undertake the sensitive analysis for selecting the sensitive parametersin the selected loss methods, transform models, and routing reach elements. While calibrating the model, it was found that the curve number and the constant loss rate were the most sensitive parameters for the SCS and initial and constant loss methods, respectively. Once selecting the sensitive parameters, the parameters were then calibrated accordingly through adjusting the values of those sensitive parameters using techniques described in Section 2.3.4 until a good agreement between the observed and simulated hydrographs was achieved. The corresponding calibrated values of those parameters are shown in Table 2 and Table 3. With the help of these optimized parameters, the hydrographs were again simulated for selected flow events. Figure 4b,c indicates the simulation results of the model validation for some selected events after the calibration. As shown in the figures, the hydrographs developed for the selected events indicated relatively close values to the observed hydrograph, both in peak discharge values and runoff volume. As it can also be seenin Table 4 and Table 5, it is found that the optimized values of the sensitive parameters had closer values in terms of total runoff depth and peak discharge values compared to the observed one. As it is also shown in Table 4, the percentage of errors in total runoff depth for model calibration and validation simulations fell in the acceptable range between 7% and 18% in the simulation, with a relatively lower percentage of errors in the model set containing an initial and constant as a loss method and SCS unit hydrograph as the transform model. Moreover, the mean percentage variation of the peak discharge between the observed and simulated values was found to get reduced to 28.7% and 10.7%; for example, for a model set containing the SCS loss method with Clarks unit hydrograph and initial and constant loss method with SCS unit hydrograph, respectively (Table 5b).Based on the results of the objective functions of relative bias errors shown in the Table 4 and Table 5, it is possible to conclude that better simulation results were obtained in the model set containing the initial and constant loss method with SCS transform methods followed by a model containing the initial and constant as a loss method withClark unit hydrograph, in which the percentage of each relative bias error in each case was almost found within the acceptable limit, whereas unacceptable values for the remaining set combinations were revealed based on descriptions in the studies by Najim et al. [35] and Sabzevari et al. [38].
As shown in Figure 5 and Table 6, a model set containing the initial and constant loss method and SCS unit hydrograph displayeda relatively closer agreement between the observed and simulated discharge values (R2 = 0.83), followed by a combination of the initial and constant loss method with Clarks unit hydrograph and SCS loss method with SCS unit hydrograph, with R2 values of 0.742 and 0.698, respectively. Based on the classification range explained in Zou et al. [39], the coefficients obtained in this study can therefore be considered as highly strong and moderately strong, respectively, whereas the correlation coefficients obtained in the SCS loss method in either of the transform models had relatively low values for the correlation between the simulated and observed discharge values. Better results were also obtained in the Nash-Sutcliffe Efficiency (NSE) criteria by the initial and constant loss method as compared to the SCS loss method, particularly a model set containing initial and constant loss methods with SCS unit hydrograph, which showed better simulations between the estimated and observed values, with an NSE of 82.8% (Table 6). As it can be seen in the table, the overall results indicated that better values were obtained in the initial and constant loss method as compared to the SCS loss method, particularly a model set containing initial and constant loss methods with SCS unit hydrograph, which showed better simulations between the estimated and observed values in almost three criteria sets in the study.

3.3. Discussion

When summarizing the overall simulation results for the events selected for validation, it was foundthat there was a possibility of obtaining a good performance of the HEC-HMS model in predicting both the runoff depth and peak values provided that an appropriate selection in the loss and transform methods is executed. Similar studies by Oleyibl et al. [2], Majidi and Shahedi [12], McColl and Aggett [18], Amengual and Romero [20], Yusop et al. [21], Jin et al. [23], and Arekhi et al. [24] also obtained credible simulation results of peak flood and runoff depth runoff in the HEC-HMS model containing a combination of the selected loss methods and unit hydrograph transform methods. While considering the results of the above three model comparison criteria, the HEC-HMS model set that contained the initial and constant as a loss method and SCS unit hydrograph as a transform method was found to be the best model combination for an effective simulation of both runoff volume and flood peaks in the study area. Besides, based on the results of the three statistical evaluation criteria described earlier obtained in this study, a moderately convincible performance of the HEC-HMS model in simulating the runoff was obtained in this study with the model set combination containing the SCS loss method with the selected transform methods. However, the optimized curve number values used during calibration procedures, as shown in Table 2, are too high and beyond the ranges of the recommended tabulated standard CN values, which may indicate inappropriateness of the loss methods to be used for further application in the study area. The results might, however, give a hint on the urgency of determination of the actual CN values from local and regional studies rather than using the tabulated standardized CN value while simulating runoff, as was also stated in Sharma [40], Hawikins [41], and Zelelew [42].
Overall, it is believed that the result of this study can give basic information on the extent of runoff volume and flood peak generated in the catchment for the corresponding rainfall events, which are in turn important for the planning and designing of appropriate watershed management activities and formulating suitable management strategies for reducing the recurrent problems of soil erosion by water and flood risks in the low lying areas by managing the surface runoff generated in the catchment. It is also believed that the results of this finding can be taken as basic input data for further hydrological investigations in the nearby un-gauged catchments by transferring the values of the calibrated parameters through applying parameter transposing and regionalization techniques described in Jin et al. [11], Bloschl [33], and Burn and Boorman [43]. It is finally suggested that the methodology of the study should be adopted to test the HEC-HMS and other related computer-based hydrological models for a coherent simulation of the fundamental components of the runoff hydrograph, and calibration of the basic parameters while applying different rainfall-runoff modelling concepts in similar un-gauged catchments around the world.

4. Conclusions

The applicability test of the HEC-HMS model was undertaken in a catchment at Abbay River basin. The ArcGIS spatial analysis tool was used to generate spatial data inputs for the model. A DEM analysis of HEC-GeoHMSin ArcGIS provided relevant basic information on basin characteristics of the targeted catchment and the initial calculated values of the parameters for starting the model calibration task. Considering the optimization trail test for parameters in the selected models, it was found that the curve number and constant loss rate were the most sensitive parameters in the study. While considering the overall performance of the HEC-HMS model, it was found that the model showed reasonable results in terms of the percentages of the error objective function, correlation relation, and Nash-Sutcliffe Efficiency, provided that suitable selection in the loss and transform methods adaptable to the area had been undertaken. Based on the results of the selected statistical evaluation criteria, the initial and constant loss method showed a relatively better performance. Simulated flood peaks and total runoff depth values using the SCS loss method were in good agreement with observed values, and the SCS unit hydrograph was a relatively better transforming model compared to the Clark unit hydrograph. It is also suggested that the values of the calibrated parameters are considered for further hydrological investigations in the study catchment and other nearby catchments, in the river basin, and that the methodology is adopted for other ungauged similar catchments around the world. As a remark, investigations in relation to parameter transposing and regionalization, localized determination of the curve numbers, and further applicability tests of the HEC-HMS in the other loss and transform methods in large scale catchments within Abbay River basin and other nearby river basins in Ethiopia are highly appreciated.

Author Contributions

D.G.Z. had the original idea, and conducted data preparation, model setup, results analysis and discussion and writing of the first draft of the article; A.M.M. contributed to the writing, discussion, editing tasks of the manuscript. All authors reviewed the article.

Funding

This research received no external funding.

Acknowledgments

The authors would like to acknowledge the Ethiopian Ministry of Water, Irrigation and Electricity and the National Meteorology Agency of Ethiopia for providing the required discharge and rainfall data, respectively.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Putty, M.R.Y.; Prasad, R. Understanding runoff processes using a watershed model: A case study in the Western Ghats in South India. J. Hydrol. 2000, 228, 215–227. [Google Scholar] [CrossRef]
  2. Oleyiblo, J.O.; Li, Z. Application of HEC-HMS for flood forecasting in Misai and Wan’an catchments in China. Water Sci. Eng. 2010, 3, 14–22. [Google Scholar] [CrossRef]
  3. Beven, K.J.; Kirkby, M.J. A physically based variable contributing area model of basin hydrology. Hydrol. Sci. Bull. 1979, 24, 43–69. [Google Scholar] [CrossRef]
  4. Zhao, W.W.; FU, B.J.; Meng, Q.H.; Zhang, Q.J.; Zhang, Y.H. Effects of land-use pattern change on rainfall-runoff and runoff-sediment relations: A case study in Zichang watershed of the Loess Plateau of China. J. Environ. Sci. 2004, 16, 436–442. [Google Scholar]
  5. Todini, E. The ARNO rainfall-runoff model. J. Hydrol. 1996, 175, 339–382. [Google Scholar] [CrossRef]
  6. Sugawara, M. Automatic calibration of the tank model. Hydrol. Sci. Bull. 1979, 24, 375–388. [Google Scholar] [CrossRef]
  7. Singh, V.P.; Woolhiser, D.A. Mathematical modelling of watershed hydrology. J. Hydrol. Eng. 2002, 7, 270–292. [Google Scholar] [CrossRef]
  8. Pilgrim, D.H.; Cordery, I. Flood runoff. In Handbook of Hydrology; McGraw-Hill Inc.: New York, NY, USA, 1993. [Google Scholar]
  9. Singh, V.P. Applied Modeling in Catchment Hydrology; Water Resources Publications: Littleton, CO, USA, 1982. [Google Scholar]
  10. Beven, K.J. Rainfall-Runoff Modelling: The Primer; John Wiley& Sons: Chichester, UK; Wiley-Blackwell: Hoboken, NJ, USA, 2012. [Google Scholar]
  11. Jin, X.; Xu, C.Y.; Zhang, Q.; Chen, Y.D. Regionalization study of a conceptual hydrological model in Dongjiang basin, south China. Quat. Int. 2009, 208, 129–137. [Google Scholar] [CrossRef]
  12. Majidi, A.; Shahedi, K. Simulation of Rainfall-Runoff Process Using Green-Ampt Method and HEC-HMS Model (Case Study: Abnama Watershed, Iran). Int. J. Hydraul. Eng. 2012, 1, 5–9. [Google Scholar] [CrossRef]
  13. Verma, A.K.; Jha, M.K.; Mahana, R.K. Evaluation of HEC-HMS and WEPP for simulating watershed runoff using remote sensing and geographical information system. Paddy Water Environ. 2010, 8, 131–144. [Google Scholar] [CrossRef]
  14. Hesbon, O.; Dawei, H. Comparative Study on Water Resources Assessment between Kenya and England. In Proceedings of the 11th International Conference on Hydroinformatics HIC, New York, NY, USA, 17–21 August 2014. [Google Scholar]
  15. Skhakhfa, I.D.; Ouerdachi, L. Hydrological modelling of wadiRessoul watershed, Algeria, by HECHMS model. J. Water Land Dev. 2016, 31, 139–147. [Google Scholar] [CrossRef]
  16. Feldman, A.D. Hydrologic Modeling System HEC-HMS. In Technical Reference Manual; U.S. Army Corps of Engineers, Hydrologic Engineering Center: Davis, CA, USA, 2000. [Google Scholar]
  17. U.S. Army Corps of Engineers. Hydrologic Modeling System (HEC-HMS) Applications Guide: Version 3.1.0; Hydrologic Engineers Center: Davis, CA, USA, 2008. [Google Scholar]
  18. Halwatura, D.; Najim, M.M. Application of the HEC-HMS model for runoff simulation in a tropical catchment. Environ. Model. Softw. 2013, 46, 155–162. [Google Scholar] [CrossRef]
  19. Kathol, J.P.; Werner, H.D.; Trooien, T.P. Runoff for Frequency Based Storm Using a Prediction- Runoff Model; ASAE: Washington, DC, USA, 2003. [Google Scholar]
  20. Knebl, M.; Yang, Z.; Hutchison, K.; Maidment, D.R. Regional scale flood modeling using NEXRAD rainfall, GIS, and HEC-HMS / HEC-RAS: A case study for the San Antonio River Basin Summer 2002 storm event. J. Environ. Manag. 2005, 75, 325–336. [Google Scholar] [CrossRef] [PubMed]
  21. McColl, C.; Aggett, G. Land use forecasting and hydrologic model integration for improved land use decision support. J. Environ. Manag. 2006, 84, 494–512. [Google Scholar] [CrossRef] [PubMed]
  22. Momcilo, M.; Angle, Y.L.; Hejazi, M. Changing estimates for design precipitation in northeastern Illinois. Comparison between different sources and sensitivity analysis. J. Hydrol. 2007, 347, 211–222. [Google Scholar]
  23. Amengual, A.; Romero, R.A. Hydrometeorological modeling study of a flash-flood event over Catalonia, Spain. J. Hydrol. 2007, 8, 282–303. [Google Scholar] [CrossRef]
  24. Yusop, Z.; Chan, C.H.; Katimon, A. Runoff characteristics and application of HEC-HMS for modelling storm flow hydrograph in an oil palm catchment. J. Water Sci. Technol. 2007, 56, 41–48. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  25. Garcia, A.; Sainz, A.; Revilla, J.; Alvarez, C. Surface water resources assessment in scarcely gauged basins in the north of Spain. J. Hydrol. 2008, 356, 312–326. [Google Scholar] [CrossRef]
  26. Jin, H.; Liang, R.; Wang, Y.; Tumula, P. Flood-Runoff in Semi-Arid and Sub-Humid Regions, a Case Study: A Simulation of Jianghe Watershed in Northern China. Water 2015, 7, 5155–5172. [Google Scholar] [CrossRef] [Green Version]
  27. Arekhi, S.; Rostamizad, G.; Rostami, N. Evaluation of HEC-HMS Methods in Surface Runoff Simulation (Case Study: Kan Watershed, Iran). Adv. Environ. Biol. 2011, 5, 1316–1321. [Google Scholar]
  28. Haberlandt, U.; Radtke, I. Hydrological model calibration for derived flood frequency analysis. Hydrol. Earth Syst. Sci. 2014, 18, 353–365. [Google Scholar] [CrossRef] [Green Version]
  29. Gumindoga, W.; Makurira, H.; Phiri, M.; Nhapi, I. Estimating runoff from ungauged catchments for reservoir water balance in the Lower Middle Zambezi Basin. Water SA 2016, 42, 641–649. [Google Scholar] [CrossRef]
  30. Azam, M.; Kim, H.S.; Maeng, S.J. Development of flood alert application in Mushim stream watershed Korea. Int. J. Disaster Risk Reduct. 2017, 21, 11–26. [Google Scholar] [CrossRef]
  31. Yilma, H.; Moges, S.A. Application of semi-distributed conceptual hydrological model for flow forecasting on upland catchments of Blue Nile River Basin, a case study of Gilgel Abbay catchment. Catchment Lake Res. 2007, 6, 1–200. [Google Scholar]
  32. Merrey, D.J.; Gebreselassie, T. Promoting Improved Rainwater and Land Management in the Blue Nile (Abay) Basin of Ethiopia; NBDC Technical Report 1; International Livestock Research Institute: Nairobi, Kenya, 2011. [Google Scholar]
  33. Blöschl, G. Rainfall-runoff modeling of un-gauged catchments. Encycl. Hydrol. Sci. 2005, 5, 1–19. [Google Scholar] [CrossRef]
  34. Chow, V.; Maidment, D.; Mays, L. Applied Hydrology; McGraw-Hill Science/Engineering/Math: New York, NY, USA, 1998. [Google Scholar]
  35. Najim, M.M.; Babel, M.S.; Loof, R. AGNPS model assessment for a mixed forested watershed in Thailand. Sci. Asia 2006, 32, 53–61. [Google Scholar] [CrossRef]
  36. Nash, J.E.; Sutclife, J.V. River flow forecasting through conceptual models Part 1: A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
  37. Neter, J.; Wasserman, W.; Kutner, M.H. Applied Linear Models: Regression, Analysis of Variance, and Experimental Designs, 3rd ed.; Irwin: Homewood, IL, USA, 1990. [Google Scholar]
  38. Sabzevari, T.; Ardakanian, R.; Shamsaee, A.; Talebi, A. Estimation of flood hydrograph in no statistical watersheds using HEC-HMS model and GIS (Case study: Kasilian watershed). J. Water Eng. 2009, 4, 1–11. [Google Scholar]
  39. Zou, K.H.; Tuncali, K.; Silverman, S.G. Correlation and simple linear regression. Radiology 2003, 227, 617–622. [Google Scholar] [CrossRef] [PubMed]
  40. Sharma, K.D. Modified runoff curve numbers for bare crust forming sandy soils. Aust. J. Soil Res. 1987, 25, 541–545. [Google Scholar] [CrossRef]
  41. Hawkins, R.H. Asymptotic determination of runoff curve numbers from data. J. Irrig. Drain. Eng. 1993, 119, 334–345. [Google Scholar] [CrossRef]
  42. Zelelew, D.G. Spatial mapping and testing the applicability of the curve number method for un-gauged catchments in Northern Ethiopia. Int. Soil Water Conserv. Res. 2017, 5, 293–301. [Google Scholar] [CrossRef]
  43. Burn, D.H.; Boorman, D.B. Estimation of hydrological parameters at un-gauged catchments. J. Hydrol. 1993, 143, 429–454. [Google Scholar] [CrossRef]
Water 10 00923 g001 550
Figure 1. Location of the targeted catchment (Angreb sub-basin) in reference to Blue Nile River, map of Ethiopia, and Abbay River Basin.
Figure 1. Location of the targeted catchment (Angreb sub-basin) in reference to Blue Nile River, map of Ethiopia, and Abbay River Basin.
Water 10 00923 g001
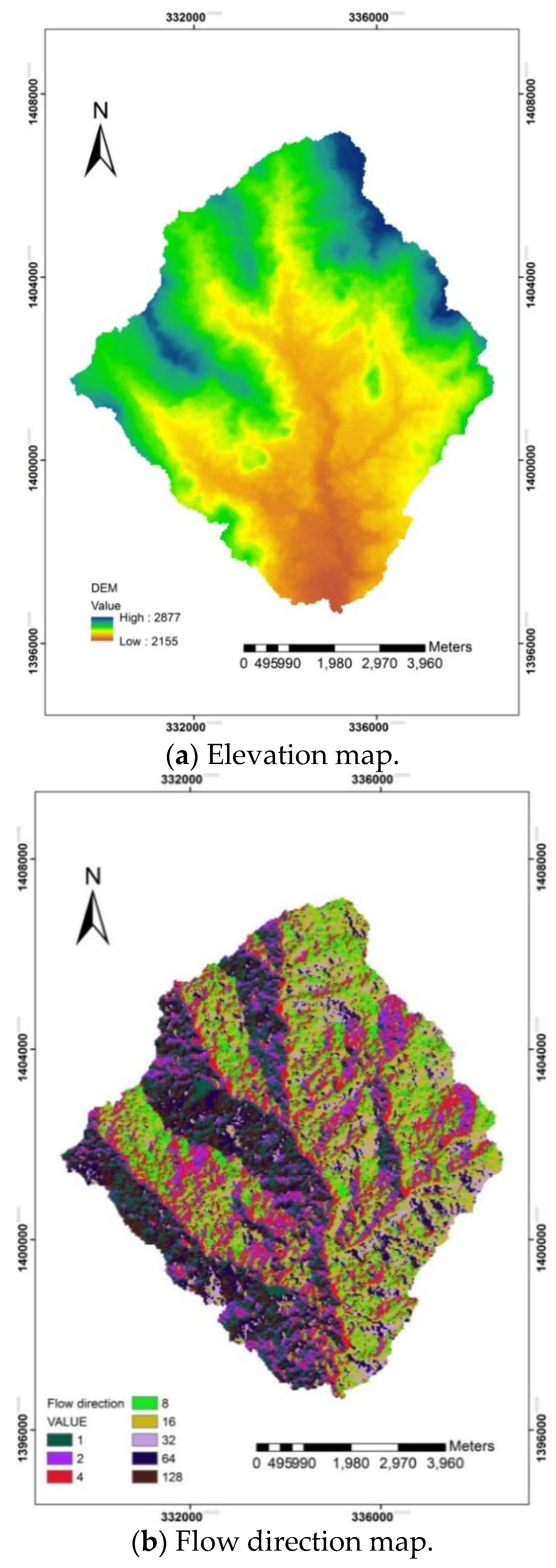
Water 10 00923 g002 550
Figure 2. Terrain characteristics of the study catchment (Elevation and flow direction map).
Figure 2. Terrain characteristics of the study catchment (Elevation and flow direction map).
Water 10 00923 g002
Water 10 00923 g003 550
Figure 3. Basin characteristics and sub-basins of the catchment.
Figure 3. Basin characteristics and sub-basins of the catchment.
Water 10 00923 g003
Water 10 00923 g004a 550Water 10 00923 g004b 550
Figure 4. Hydrograph comparison between observed and simulated discharge in different model combinations: (a) Uncalibrated; (b) calibration; (c) validation.
Figure 4. Hydrograph comparison between observed and simulated discharge in different model combinations: (a) Uncalibrated; (b) calibration; (c) validation.
Water 10 00923 g004aWater 10 00923 g004b
Water 10 00923 g005a 550Water 10 00923 g005b 550
Figure 5. Correlation between observed and simulated discharge values (m3 / s ) : (a) SCS loss method withClark unit hydrograph; (b) SCS loss method with SCS unit hydrograph; (c) Initial and constant loss method with Clark unit hydrograph; (d) Initial and constant loss method with SCS unit hydrograph.
Figure 5. Correlation between observed and simulated discharge values (m3 / s ) : (a) SCS loss method withClark unit hydrograph; (b) SCS loss method with SCS unit hydrograph; (c) Initial and constant loss method with Clark unit hydrograph; (d) Initial and constant loss method with SCS unit hydrograph.
Water 10 00923 g005aWater 10 00923 g005b
Table
Table 1. Physiographic characteristics of the catchment.
Table 1. Physiographic characteristics of the catchment.
ParametersValues
Area55.2 km2
Perimeter45,076 m
Max. Elevation2877 m
Min. Elevation2155 m
Mean slope of the basin25.6%
Main channel length12,485 m
Main channel mean slope2.81%
Drainage density0.94 km/km2
Table
Table 2. Initial and calibrated values of sensitive parameters.
Table 2. Initial and calibrated values of sensitive parameters.
Sub-BasinsArea (km2)Perimeter (m)Basin Slope (%)Main River FlowCurve NumberConstant Loss Rate
(mm/h)
Flow Length (m)Slope (m/m)Initial ValuesOptimized ValuesInitial ValuesOptimized Values
Sub-basin 113.7625,75726.578770.04578863.82.2
Sub-basin 224.0831,01826.290300.03575904.33.1
Sub-basin 311.5523,34526.364240.05172826.74.4
Sub-basin 45.7717,77619.834550.02168687.85.2
Table
Table 3. Initial and optimized X and K parameters in the routing reaches element.
Table 3. Initial and optimized X and K parameters in the routing reaches element.
ElementXMuskinghum (K), K(h)
Initial ValuesOptimized ValuesInitial ValuesOptimized Values
Reach 10.20.14510.65
Reach 20.20.14510.65
Table
Table 4. Comparison of simulated and observed total runoff depth for the above selected hydrographs.
Table 4. Comparison of simulated and observed total runoff depth for the above selected hydrographs.
Simulation EventObserved Runoff Depth (mm)Outflow
(SCS-ClarkHy)		Change in %Outflow
(SCS-SCSHy)		Change in %Outflow
(InCo-SCSHy)		Change in %Outflow
(InCo-ClarkHy)		Change in %
Before calibration614.83378.25−38.48407.8−33.67462.98−24.70485.07−21.11
For model calibration420.41350.71−16.58352.04−16.26373.87−11.07359.48−14.49
For model validation975.92801.58−17.92798.32−18.20910.13−6.74877.00−10.14
Table
Table 5. Comparison of simulated and observed peak discharge values (a) Uncalibrated, (b) Calibrated.
Table 5. Comparison of simulated and observed peak discharge values (a) Uncalibrated, (b) Calibrated.
(a) Uncalibrated
DateObserved Flow
(m3/s)		Outflow (SCS-ClarkUH)Change in %Outflow
(SCS-SCSUH)		Change in %Outflow
(InCo-SCSUH)		Change in %Outflow
(InCo-ClarkUH)		Change in %
8 September 199215.97.8−50.948.3−47.8010.8−32.089.6−39.62
27 March 19938.13.8−53.094.3−46.915.6−30.866.6−18.52
12 July 199330.217.3−42.7219.2−36.4222.4−25.8319.2−36.42
8 September 199432.913.1−60.1817.2−47.7224.2−26.4422.5−31.61
9 May 199525.411.2−55.9111.7−53.9417.6−30.7115.6−38.58
2 August 199518.411.5−37.510.4−43.4812.1−34.2310.0−45.65
Average −50.06 −46.05 −30.03 −35.07
(b) Calibrated
DateObserved Flow (m3/s)Outflow
(SCS-ClarkHy)		Change in %Outflow
(SCS-SCSHy)		Change in %Outflow
(InCo-SCSHy)		Change in %Outflow
(InCo-ClarkHy)		Change in %
12 July 199624.614.7−40.2417.8−27.6421.8−11.3820.4−17.07
21 August 199620.416−21.5715.6−23.5318.2−10.7818.2−10.78
16 August 200332.823.7−27.7424.2−26.2228.6−12.8025.2−23.17
22 August 200327.420.7−24.4522−19.7124.3−11.3120.9−23.72
26 August 200336.226.7−26.2426.2−27.6233.2−8.2931.1−14.09
4 July 200435.224−31.8227.8−21.0231.8−9.6629.8−15.34
Average −28.68 −24.29 −10.70 −17.36
Table
Table 6. The summary table for comparison between the two loss methods in simulating flood peaks based on the three statistical evaluation criteria.
Table 6. The summary table for comparison between the two loss methods in simulating flood peaks based on the three statistical evaluation criteria.
Statistical Evaluation CriteriaLoss Methods
SCS Loss MethodInitial and Constant Loss Method
SCS Unit Hydrograph Clark Unit HydrographSCS Unit HydrographSCS Unit Hydrograph
Relative bias errors (%)24.29 ns28.68 ns17.36 **10.71 ***
Coefficient of determination (R2)0.70 *0.59 *0.74 **0.83 ***
Nash-Sutcliffe Efficiency (%)64.7 *57.8 ns71.8 **82.8 ***
Notes: *** Highly satisfactory, ** Satisfactory, * moderately satisfactory, ns not satisfactory.

Share and Cite

MDPI and ACS Style

Zelelew, D.G.; Melesse, A.M. Applicability of a Spatially Semi-Distributed Hydrological Model for Watershed Scale Runoff Estimation in Northwest Ethiopia. Water 2018, 10, 923. https://doi.org/10.3390/w10070923

AMA Style

Zelelew DG, Melesse AM. Applicability of a Spatially Semi-Distributed Hydrological Model for Watershed Scale Runoff Estimation in Northwest Ethiopia. Water. 2018; 10(7):923. https://doi.org/10.3390/w10070923

Chicago/Turabian Style

Zelelew, Demlie G., and Assefa M. Melesse. 2018. "Applicability of a Spatially Semi-Distributed Hydrological Model for Watershed Scale Runoff Estimation in Northwest Ethiopia" Water 10, no. 7: 923. https://doi.org/10.3390/w10070923

APA Style

Zelelew, D. G., & Melesse, A. M. (2018). Applicability of a Spatially Semi-Distributed Hydrological Model for Watershed Scale Runoff Estimation in Northwest Ethiopia. Water, 10(7), 923. https://doi.org/10.3390/w10070923

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop