A Study on Optimization of CBM Water Drainage by Well-Test Deconvolution in the Early Development Stage
Abstract
:1. Introduction
2. The Division of Production Stages
3. Deconvolution of Well-Test for CBM Wells
3.1. Improvement of Deconvolution Algorithm
3.2. Well-Test Analysis System
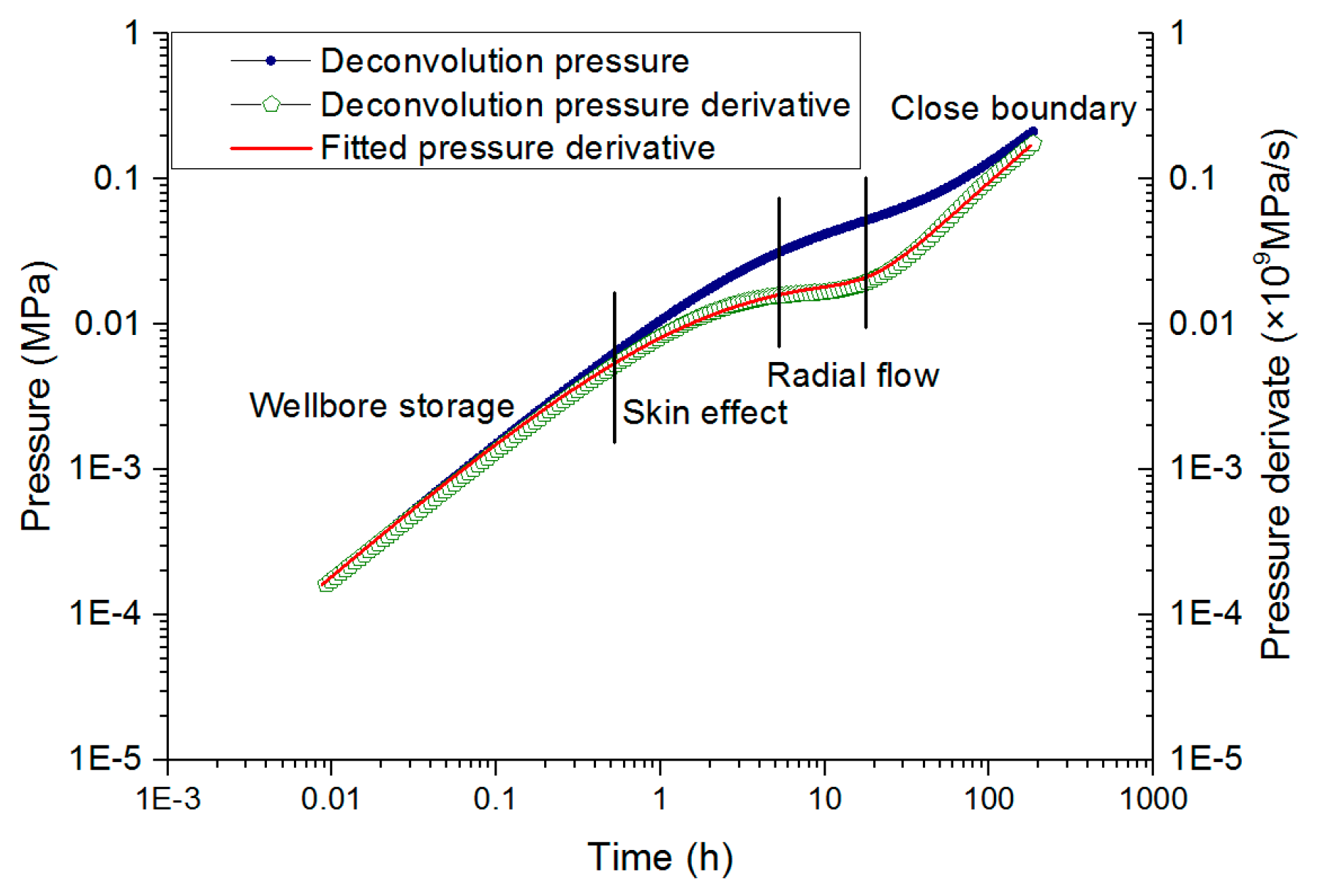
3.3. Method Validation
4. Field Application—A Case of Hancheng Block
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, X.F.; Pu, Y.C.; Sun, C.Y.; Ren, W.N.; Li, Y.Y.; Zhang, Y.Q.; Li, J.; Zang, J.L.; Hu, A.M.; Wen, S.M.; et al. Recognition of absorption/desorption theory in coalbed methane reservoir and shale gas reservoir. Acta Pet. Sin. 2014, 35, 1113–1129. (In Chinese) [Google Scholar]
- Han, G.P.; Ling, K.G.; Zhang, H. Smart de-watering and production system through real-time water level surveillance for Coal-Bed Methane wells. J. Nat. Gas Sci. Eng. 2016, 31, 769–778. [Google Scholar] [CrossRef]
- Li, J.H.; Su, X.B.; Lin, X.Y.; Guo, H.Y. Relationship between discharge rate and productivity of coalbed methane wells. J. China Coal Soc. 2009, 34, 376–380. [Google Scholar]
- Liu, S.Q.; Sang, S.X.; Li, M.X.; Liu, H.H.; Wang, L.L. Control factors of coalbed methane well desorption cone under drainage well network in southern Qinshui basin. J. China Univ. Min. Technol. 2012, 41, 943–950. [Google Scholar]
- Kang, Y.Y.; Shao, X.J.; Wang, C.F. Production characteristics and affecting factors of high-mid rank coalbed methane wells: Taking Fanzhuang and Hancheng mining areas as examples. Petrol. Explor. Dev. 2012, 39, 728–732. [Google Scholar] [CrossRef]
- Shao, X.J.; Wang, C.F.; Tang, D.Z.; Sun, Y.B.; Xu, H. Productivity mode and control factors of coalbed methane wells: A case from Hancheng region. J. China Coal Soc. 2013, 38, 271–276. [Google Scholar]
- Fu, X.H.; Ge, Y.Y.; Liang, W.Q.; Li, S. Pressure control and fluid effect of progressive drainage of multiple superposed CBM systems. Nat. Gas Ind. 2013, 33, 35–39. (In Chinese) [Google Scholar]
- Zhang, S.A.; Cao, L.H.; Du, C.X. Study on CBM production mechanism and control theory of bottom-hole pressure and coal fines during CBM well production. J. China Coal Soc. 2014, 39, 1927–1931. [Google Scholar]
- Wan, Y.Z.; Liu, Y.W.; Ouyang, W.P.; Liu, W.C.; Han, G.F. Desorption area and pressure-drop region of wells in a homogeneous coalbed. J. Nat. Gas Sci. Eng. 2016, 28, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Von Schroeter, T.; Gringarten, A.C. Superposition principle and reciprocity for pressure transient analysis of data from interfering wells. SPE J. 2009, 14, 488–495. [Google Scholar] [CrossRef]
- Von Schroeter, T.; Hollaender, F.; Gringarten, A.C. Analysis of well test data from permanent downhole gauges by deconvolution. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 29 September–2 October 2002. [Google Scholar]
- Von Schroeter, T.; Hollaender, F.; Gringarten, A.C. Deconvolution of well-test data as a nonlinear total least-squares problem. SPE J. 2009, 9, 375–390. [Google Scholar] [CrossRef]
- Setiawan, A.; Hird, K.; Bennett, C.O. Enhancement of Vorwata Field reservoir model by integration of pressure transient analysis with real-time downhole pressure data. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Jakarta, Indonesia, 20–22 September 2011. [Google Scholar]
- Gringarten, A.C. From straight lines to deconvolution: The evolution of the state of the art in well test analysis. SPE Reserv. Eval. Eng. 2008, 11, 41–62. [Google Scholar] [CrossRef]
- Cheng, Y.; Lee, W.J.; Mcvay, D.A. Fast-fourier-transform-based deconvolution for interpretation of pressure transient test data dominated by wellbore storage. SPE Reserv. Eval. Eng. 2005, 8, 224–239. [Google Scholar] [CrossRef]
- Saevareid, O. Wavelet based regularization of the well test deconvolution problem. In Proceedings of the 10th European Conference on the Mathematics of Oil Recovery, Amsterdam, The Netherlands, 4–7 September 2006. [Google Scholar]
- Pimonov, E.A.; Onur, M.; Kuchuk, F.J. A new robust algorithm for solution of pressure/rate deconvolution problem. J. Inverse Ill-posed Probl. 2009, 17, 611–627. [Google Scholar] [CrossRef]
- Onur, M.; Kuchuk, F.J. A new deconvolution technique based on pressure-derivative data for pressure-transient-test interpretation. SPE J. 2012, 17, 307–320. [Google Scholar] [CrossRef]
- Vasin, V.; Skorik, G.; Pimonov, E.; Kuchuk, F. New regularization algorithms for solving the deconvolution problem in well test data interpretation. Appl. Math. 2010, 1, 387–399. [Google Scholar] [CrossRef]
- Skorik, G.G.; Vasin, V.V.; Kuchuk, F. A new technique for solving pressure-rate deconvolution problem in pressure transient testing. J. Eng. Math. 2016, 101, 1–12. [Google Scholar] [CrossRef]
- Conislla, J.W.Q.; Quinones, V.A.H.; Quispe, D. Numerical transient-testing deconvolution as a reservoir-modeling tool for gas fields in early development phase. In Proceedings of the SPE Latin American and Caribbean Petroleum Engineering Conference, Lima, Peru, 1–3 December 2010. [Google Scholar]
- Moore, T.A. Coalbed methane: A review. Int. J. Coal Geol. 2015, 101, 36–81. [Google Scholar] [CrossRef]
- Salmachi, A.; Yarmohammadtooski, Z. Production data analysis of coalbed methane wells to estimate the time required to reach to peak of gas production. Int. J. Coal Geol. 2015, 141, 33–41. [Google Scholar] [CrossRef]
- Liu, W.C.; Liu, Y.W.; Zhu, W.Y.; Sun, H.D. A stability-improved efficient deconvolution algorithm based on B-splines by appending a nonlinear regularization. J. Petrol. Sci. Eng. 2018, 164, 400–416. [Google Scholar] [CrossRef]
- Ilk, D.; Valko, P.P.; Blasingame, T.A. Deconvolution of Variable-Rate Reservoir Performance Data Using B-Splines. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 9–12 October 2005. [Google Scholar]
- Burden, R.L.; Faires, J.D. Numerical Analysis. In Interpolation & Polynomial Approximation Cubic Spline Interpolation III, 9th ed.; Cengage Learning: Boston, MA, USA, 2010. [Google Scholar]
- Liu, N.Q. A new definition of investigation radius. Well Test. 2006, 15, 42–43. (In Chinese) [Google Scholar]
- Akhondzadeh, H.; Keshavarz, A.; Sayyafzadeh, M.; Kalantariasl, A. Investigating the relative impact of key reservoir parameters on performance of coalbed methane reservoirs by an efficient statistical approach. J. Nat. Gas Sci. Eng. 2018, 53, 416–428. [Google Scholar] [CrossRef]
- Sun, Z.; Shi, J.; Wang, K.; Miao, Y.; Zhang, T.; Li, X.F. The gas-water two phase flow behavior in low-permeability CBM reservoirs with multiple mechanisms coupling. J. Nat. Gas Sci. Eng. 2018, 52, 82–83. [Google Scholar] [CrossRef]
- Xu, B.X.; Li, X.F.; Ren, W.N.; Chen, D.; Bai, Y.H. Dewatering rate optimization for coal-bed methane well based on the characteristics of pressure propagation. Fuel 2016, 188, 11–18. [Google Scholar] [CrossRef]











| Well | Well-Test Analysis Method | Initial Pressure | Permeability | Skin Factor | Wellbore Storage Factor | Investigation Radius | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Fitted Value/MPa | Relative Error | Fitted Value/10−3 μm2 | Relative Error | Fitted Value | Relative Error | Fitted Value/m3·MPa−1 | Relative Error | Fitted Value/m | Relative Error | ||
| H3-1 | Pressure drop well-test | 0.302 | - | 9.38 | - | −6.65 | - | 4.58 | - | 348 | - |
| Deconvolution well-test | 0.302 | 0% | 9.3 | 1.0% | −6.79 | 2.1% | 4.34 | 5.5% | 352 | 1.1% | |
| H3-2 | Pressure build-up well-test | 5.24 | - | 3.54 | - | 1.1 | - | 34.7 | - | 929 | - |
| Deconvolution well-test | 5.25 | 0.2% | 3.5 | 1.1% | 0.79 | 28% | 33.6 | 3.2% | 1000 | 7.1% | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, D.; Liu, Y.; Guo, Z.; Han, J.; Lin, J.; Fang, H.; Ma, H.; Tsai, S.-B. A Study on Optimization of CBM Water Drainage by Well-Test Deconvolution in the Early Development Stage. Water 2018, 10, 929. https://doi.org/10.3390/w10070929
Gao D, Liu Y, Guo Z, Han J, Lin J, Fang H, Ma H, Tsai S-B. A Study on Optimization of CBM Water Drainage by Well-Test Deconvolution in the Early Development Stage. Water. 2018; 10(7):929. https://doi.org/10.3390/w10070929
Chicago/Turabian StyleGao, Dapeng, Yuewu Liu, Zhidong Guo, Jun Han, Jingde Lin, Huijun Fang, Hailing Ma, and Sang-Bing Tsai. 2018. "A Study on Optimization of CBM Water Drainage by Well-Test Deconvolution in the Early Development Stage" Water 10, no. 7: 929. https://doi.org/10.3390/w10070929
APA StyleGao, D., Liu, Y., Guo, Z., Han, J., Lin, J., Fang, H., Ma, H., & Tsai, S.-B. (2018). A Study on Optimization of CBM Water Drainage by Well-Test Deconvolution in the Early Development Stage. Water, 10(7), 929. https://doi.org/10.3390/w10070929







