Model-Based Analysis of Macrophytes Role in the Flow Distribution in the Anastomosing River System
Abstract
1. Introduction
2. Materials and Methods
2.1. Site Description
2.2. Fieldwork and Modeling Tool
2.3. Model Performance
2.4. Model Sensitivity Analysis
2.5. Vegetation Changes Impact on Water Flow
3. Results
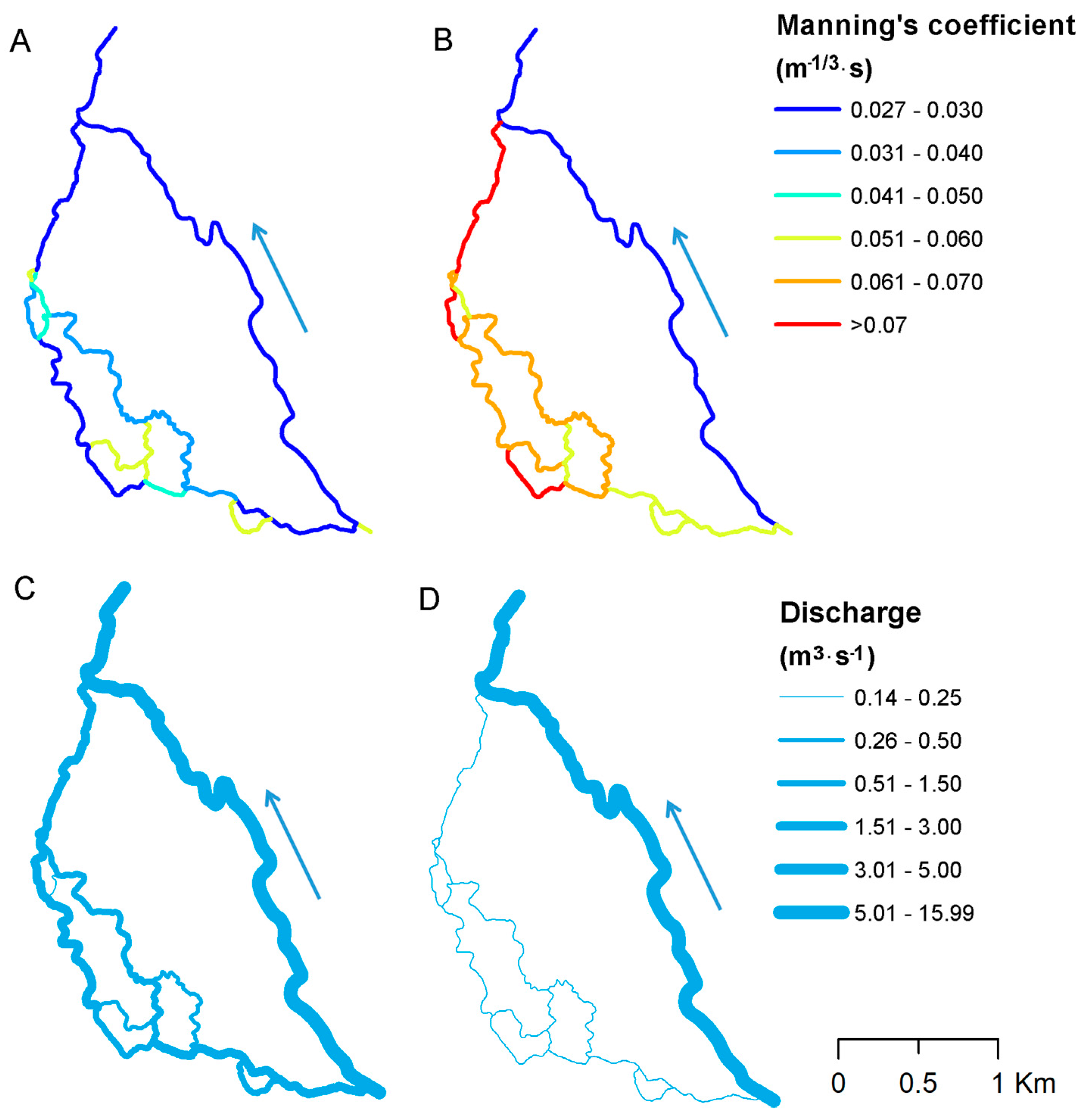
3.1. Model Sensitivity Analysis
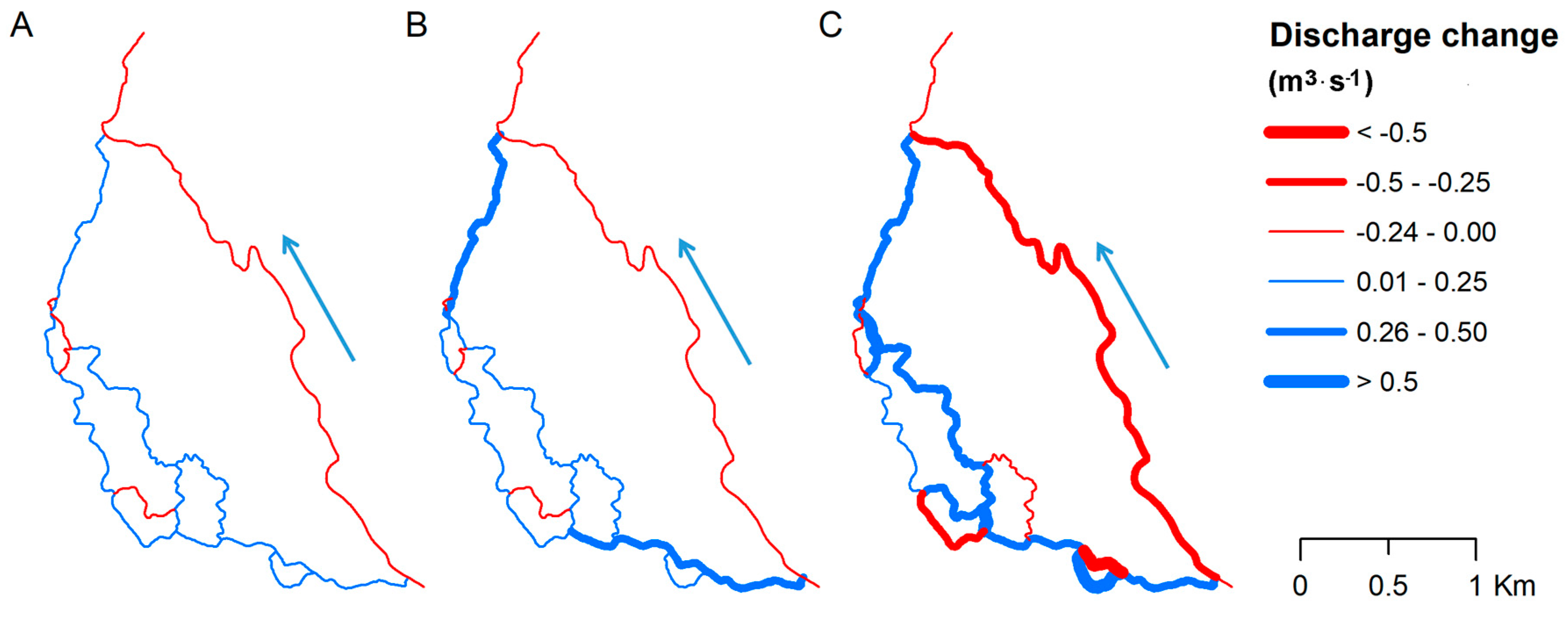
3.2. Impact of Vegetation Changes on Water Flow Distribution
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gurnell, A. Plants as river system engineers: Further comments. Earth Surf. Process. Landf. 2014, 40, 135–137. [Google Scholar] [CrossRef]
- Gurnell, A.M.; Corenblit, D.; García de Jalón, D.; González del Tánago, M.; Grabowski, R.C.; O’Hare, M.T.; Szewczyk, M. A conceptual model of vegetation-hydrogeomorphology interactions within river corridors. River Res. Appl. 2016, 32, 142–163. [Google Scholar] [CrossRef]
- Schoelynck, J.; Creëlle, S.; Buis, K.; De Mulder, T.; Emsens, W.; Hein, T.; Meire, D.; Meire, P.; Okruszko, T.; Preiner, S.; et al. What is a macrophyte patch? Patch identification in aquatic ecosystems and guidelines for consistent delineation. Ecohydrol. Hydrobiol. 2017, 18, 1–9. [Google Scholar] [CrossRef]
- Zong, L.; Nepf, H. Spatial distribution of deposition within a patch of vegetation. Water Resour. Res. 2011, 47, 1–12. [Google Scholar] [CrossRef]
- Solari, L.; Van Oorschot, M.; Belletti, B.; Hendriks, D.; Rinaldi, M.; Vargas-Luna, A. Advances on modelling riparian vegetation-hydromorphology interactions. River Res. Appl. 2016, 2, 164–178. [Google Scholar] [CrossRef]
- Verschoren, V.; Meire, D.; Schoelynck, J.; Buis, K.; Bal, K.D.; Troch, P.; Meire, P.; Temmerman, S. Resistance and reconfiguration of natural flexible submerged vegetation in hydrodynamic river modelling. Environ. Fluid Mech. 2016, 16, 245–265. [Google Scholar] [CrossRef]
- Corenblit, D.; Baas, A.C.W.; Bornette, G.; Darrozes, J.; Delmotte, S.; Francis, R.A.; Gurnell, A.M.; Julien, F.; Naiman, R.J.; Steiger, J. Feedbacks between geomorphology and biota controlling Earth surface processes and landforms: A review of foundation concepts and current understandings. Earth Sci. Rev. 2011, 106, 307–331. [Google Scholar] [CrossRef]
- Gurnell, A. Plants as river system engineers. Earth Surf. Process. Landf. 2014, 39, 4–25. [Google Scholar] [CrossRef]
- Vaughan, I.P.; Diamond, M.; Gurnell, A.M.; Hall, K.A.; Jenkins, A.; Milner, N.J.; Naylor, L.A.; Sear, D.A.; Woodward, G.; Ormerod, S.J. Integrating ecology with hydromorphology: A priority for river science and management. Aquat. Conserv. Mar. Freshw. Ecosyst. 2009, 19, 113–125. [Google Scholar] [CrossRef]
- Oorschot, M.; Kleinhans, M.; Geerling, G.; Middelkoop, H. Distinct patterns of interaction between vegetation and morphodynamics. Earth Surf. Process. Landf. 2016, 41, 791–808. [Google Scholar] [CrossRef]
- Schuurman, F.; Marra, W.A.; Kleinhans, M.G. Physics-based modeling of large braided sand-bed rivers: Bar pattern formation, dynamics, and sensitivity. J. Geophys. Res. Earth Surf. 2013, 118, 2509–2527. [Google Scholar] [CrossRef]
- Lotsari, E.; Wainwright, D.; Corner, G.D.; Alho, P.; Käyhkö, J. Surveyed and modelled one-year morphodynamics in the braided lower Tana River. Hydrol. Process. 2013, 28, 2685–2716. [Google Scholar] [CrossRef]
- Williams, R.D.; Brasington, J.; Hicks, M.; Measures, R.; Rennie, C.D.; Vericat, D. Hydraulic validation of two-dimensional simulations of braided river flow with spatially continuous aDcp data. Water Resour. Res. 2013, 49, 5183–5205. [Google Scholar] [CrossRef]
- Nicholas, A. Morphodynamic diversity of the world’s largest rivers. Geology 2013, 41, 475–478. [Google Scholar] [CrossRef]
- Bertoldi, W.; Siviglia, A.; Tettamanti, S.; Toffolon, M.; Vetsch, D.; Francalanci, S. Modeling vegetation controls on fluvial morphological trajectories. Geophys. Res. Lett. 2014, 41, 7167–7175. [Google Scholar] [CrossRef]
- Williams, R.D.; Brasington, J.; Hicks, D.M. Numerical modelling of braided river morphodynamics: Review and future challenges. Geogr. Compass 2016, 10, 102–127. [Google Scholar] [CrossRef]
- Jowett, J.G.; Duncan, M.J. Effectiveness of 1D and 2D hydraulic models for instream habitat analysis in a braided river. Ecol. Eng. 2012, 48, 92–100. [Google Scholar] [CrossRef]
- Nanson, G.C.; Croke, J.C. A genetic classification of floodplains. Geomorphology 1992, 4, 459–486. [Google Scholar] [CrossRef]
- Nanson, G.C.; Knighton, A.D. Anabranching rivers: Their cause, character and classification. Earth Surf. Process. Landf. 1996, 21, 217–239. [Google Scholar] [CrossRef]
- Gradziński, R.; Baryła, J.; Doktor, M.; Gmur, D.; Gradziński, M.; Kędzior, A.; Paszkowski, M.; Soja, R.; Zieliński, T.; Żurek, S. Vegetation-controlled modern anastomosing system of the upper Narew River (NE Poland) and its sediments. Sediment. Geol. 2003, 157, 253–276. [Google Scholar] [CrossRef]
- Makaske, B.; Lavooi, E.; de Haas, T.; Kleinhans, M.G.; Smith, D.G. Upstream control of river anastomosis by sediment overloading, upper Columbia River, British Columbia, Canada. Sedimentology 2017, 64, 1488–1510. [Google Scholar] [CrossRef]
- McCarthy, T.S.; Ellery, W.N.; Stanistreet, I.G. Avulsion mechanisms on the Okavango fan, Botswana: The control of a fluvial system by vegetation. Sedimentology 1992, 39, 779–795. [Google Scholar] [CrossRef]
- Schumann, R.R. Morphology of Red Creek, Wyoming, an arid-region anastomosing channel system. Earth Surf. Process. Landf. 1989, 14, 277–288. [Google Scholar] [CrossRef]
- Smith, N.D.; Cross, T.A.; Dufficy, J.; Clough, S.R. Anatomy of avulsion. Sedimentology 1989, 36, 1–23. [Google Scholar] [CrossRef]
- Tooth, S.; Nanson, G.C. The role of vegetation in the formation of anabranching channels in an ephemeral river, Northern plains, arid central Australia. Hydrol. Process. 2000, 14, 3099–3117. [Google Scholar] [CrossRef]
- McCarthy, T.S.; Ellery, W.N.; Rogers, K.H.; Cairncross, B.; Ellery, K. The roles of sedimentation and plant growth in changing flow patterns in the Okavango Delta, Botswana. S. Afr. J. Sci. 1986, 82, 579–585. [Google Scholar]
- Ellery, W.N.; Ellery, K.; Rogers, K.H.; McCarthy, T.S.; Walker, B.H. Vegetation, hydrology and sedimentation processes as determinants of channel form and dynamics in the northeastern Okavango Delta, Botswana. Afr. J. Ecol. 1993, 31, 10–25. [Google Scholar] [CrossRef]
- Stanistreet, I.G.; Cairncross, B.; McCarthy, T.S. Low sinuosity and meandering bedload rivers of the Okavango Fan: Channel confinement by vegetated levées without fine sediment. Sediment. Geol. 1993, 85, 135–156. [Google Scholar] [CrossRef]
- Wende, R.; Nanson, G.C. Anabranching rivers: Ridge-form alluvial channels in tropical northern Australia. Geomorphology 1998, 22, 205–224. [Google Scholar] [CrossRef]
- Tabata, K.K.; Hickin, E.J. Intrachannel hydraulic geometry and hydraulic efficiency of the anastomosing Columbia river, southeastern British Columbia, Canada. Earth Surf. Process. Landf. 2003, 28, 837–852. [Google Scholar] [CrossRef]
- Jansen, J.D.; Nanson, G.C. Anabranching and maximum flow efficiency in Magela Creek, northern Australia. Water Resour. Res. 2004, 40, W04503. [Google Scholar] [CrossRef]
- Van, T.P.D.; Carling, P.A.; Atkinson, P.M. Modelling the bulk flow of a bedrock-constrained, multi-channel reach of the Mekong River, Siphandone, southern Laos. Earth Surf. Process. Landf. 2012, 37, 533–545. [Google Scholar] [CrossRef]
- Gibson, S.A.; Pasternack, G.B. Selecting between one-dimensional and two-dimensional hydrodynamic models for ecohydraulic analysis. River Res. Appl. 2016, 32, 1365–1381. [Google Scholar] [CrossRef]
- Romanowicz, R.; Kiczko, A.; Napiórkowski, J. Stochastic transfer function simulator of a 1-D flow routing. Publ. Inst. Geophys. Pol. Acad. Sci. 2008, E-10, 151–160. [Google Scholar]
- Romanowicz, R.; Kiczko, A.; Napiórkowski, J. Stochastic transfer function model applied to combined reservoir management and flow routing. Hydrol. Sci. J. 2010, 55, 27–44. [Google Scholar] [CrossRef]
- Mashriqui, H.S.; Halgren, J.S.; Reed, S.M. 1D river hydraulic model for operational flood forecasting in the tidal Potomac: Evaluation for freshwater, tidal, and wind-driven events. J. Hydraul. Eng. 2014, 140, 04014005. [Google Scholar] [CrossRef]
- Horritt, M.S.; Bates, P.D. Evaluation of 1D and 2D numerical models for predicting river flood inundation. J. Hydrol. 2002, 268, 87–99. [Google Scholar] [CrossRef]
- Jordanova, A.A.; James, C.S. Experimental study of bed load transport through emergent vegetation. J. Hydraul. Eng. 2003, 129, 474–478. [Google Scholar] [CrossRef]
- Wilson, C.A.M.E. Flow resistance models for flexible submerged vegetation. J. Hydrol. 2007, 342, 213–222. [Google Scholar] [CrossRef]
- Abu-Aly, T.R.; Pasternack, G.B.; Wyrick, J.R.; Barker, R.; Massa, D.; Johnson, T. Effects of LiDAR-derived, spatially distributed vegetation roughness on two-dimensional hydraulics in a gravel-cobble river at flows of 0.2 to 20 times bankfull. Geomorphology 2014, 206, 468–482. [Google Scholar] [CrossRef]
- Curran, J.W.; Hession, W.C. Vegetative impacts on hydraulics and sediment processes across the fluvial system. J. Hydrol. 2013, 505, 364–376. [Google Scholar] [CrossRef]
- Manners, R.; Schmidt, J.; Wheaton, J.M. Multiscalar model for the determination of spatially explicit riparian vegetation roughness. J. Geophys. Res. Earth Surf. 2013, 118, 65–83. [Google Scholar] [CrossRef]
- Bywater-Reyes, S.; Diehl, R.M.; Wilcox, A.C. The influence of a vegetated bar on channel-bend flow dynamics. Earth Surf. Dynam. 2018, 6, 487–503. [Google Scholar] [CrossRef]
- Baptist, M.J.; Van Den Bosch, L.V.; Dijkstra, J.T.; Kapinga, S. Modelling the effects of vegetation on flow and morphology in rivers. Large Rivers 2003, 15, 339–357. [Google Scholar] [CrossRef]
- James, C.; Birkhead, A.; Jordanova, A. Flow resistance of emergent vegetation. J. Hydraul. Res. 2004, 42, 390–398. [Google Scholar] [CrossRef]
- Song, S.; Schmalz, B.; Xu, Y.P.; Fohrer, M. Seasonality of roughness—The indicator of annual river flow resistance condition in a lowland catchment. Water Resour. Manag. 2017, 31, 3299–3312. [Google Scholar] [CrossRef]
- O’Hare, M.T.; McGahey, C.; Bissett, N.; Cailes, C.; Henville, P.; Scarlett, P. Variability in roughness measurements for vegetated rivers near base flow, in England and Scotland. J. Hydrol 2010, 385, 361–370. [Google Scholar] [CrossRef]
- Parhi, P.K.; Sankhua, R.; Roy, G.P. Calibration of channel roughness for Mahanadi River, (India) using HEC-RAS model. J. Water Resour. Prot. 2012, 4, 847–850. [Google Scholar] [CrossRef]
- Yang, T.H.; Wang, Y.C.; Tsung, S.C.; Guo, W.D. Applying micro-genetic algorithm in the one-dimensional unsteady hydraulic model for parameter optimization. J. Hydroinform. 2014, 16, 772–783. [Google Scholar] [CrossRef]
- Frias, C.E.; Abad, J.D.; Mendoza, A.; Paredes, J.; Ortals, C.; Montoro, H. Planform evolution of two anabranching structures in the Upper Peruvian Amazon River. Water Resour. Res. 2015, 51, 2742–2759. [Google Scholar] [CrossRef]
- Green, J. Effect of macrophyte spatial variability on channel resistance. Adv. Water Resour. 2006, 29, 426–438. [Google Scholar] [CrossRef]
- Kiczko, A.; Romanowicz, R.J.; Osuch, M.; Karamuz, E. Maximising the usefulness of flood risk assessment for the river vistula in warsaw. Nat. Hazards Earth Syst. Sci. 2013, 13, 3443–3455. [Google Scholar] [CrossRef]
- Romanowicz, R.J.; Kiczko, A. An event simulation approach to the assessment of flood level frequencies: Risk maps for the Warsaw reach of the river Vistula. Hydrol. Process. 2016, 30, 2451–2462. [Google Scholar] [CrossRef]
- De Doncker, L.; Troch, P.; Verhoeven, R.; Buis, K. Deriving the relationship among discharge, biomass and Manning’s coefficient through a calibration approach. Hydrol. Process. 2011, 25, 1979–1995. [Google Scholar] [CrossRef]
- Pappenberger, F.; Beven, K.; Morrit, H.; Blazkova, S. Uncertainty in the calibration of effective roughness parameters in hec-ras using inundation and downstream level observations. J. Hydrol. 2005, 302, 46–69. [Google Scholar] [CrossRef]
- De Pauw, D.J.W.; Vanrolleghem, P.A. Practical aspects of sensitivity function approximation for dynamic models. Math. Comput. Model. Dyn. Syst. 2006, 12, 395–414. [Google Scholar] [CrossRef]
- Haaker, M.P.R.; Verheijen, P.J.T. Local and global sensitivity analysis for a reactor design with parameter uncertainty. Chem. Eng. Res. Des. 2004, 82, 591–598. [Google Scholar] [CrossRef]
- Morio, J. Global and local sensitivity analysis methods for a physical system. Eur. J. Phys. 2011, 32, 1577–1583. [Google Scholar] [CrossRef]
- Wright, K.A.; Goodman, D.H.; Som, N.A.; Alvarez, J.; Martin, A.; Hardy, T.B. Improving hydrodynamic modelling: An analytical framework for assessment of two-dimensional hydrodynamic models. River Res. Appl. 2017, 33, 170–181. [Google Scholar] [CrossRef]
- Neal, J.C.; Odoni, N.A.; Trigg, M.A.; Freer, J.E.; Garcia-Pintado, J.; Mason, D.C.; Wood, M.; Bates, P.D. Efficient incorporation of channel cross-section geometry uncertainty into regional and global scale flood inundation models. J. Hydrol. 2015, 529, 169–183. [Google Scholar] [CrossRef]
- Marcinkowski, P.; Grygoruk, M. Long-term downstream effects of a dam on a lowland river flow regime: Case study of the upper Narew. Water 2017, 9, 783. [Google Scholar] [CrossRef]
- Próchnicki, P. The expansion of common reed (phragmites australis (cav.) trin. ex steud.) in the anastomosing river valley after cessation of agriculture use (narew river valley, NE Poland). Pol. J. Ecol. 2005, 53, 353–364. [Google Scholar]
- Marcinkowski, P.; Grabowski, R.C.; Okruszko, T. Controls on anastomosis in lowland river systems: Towards process-based solutions to habitat conservation. Sci. Total Environ. 2017, 609, 1544–1555. [Google Scholar] [CrossRef] [PubMed]
- Marcinkowski, P.; Giełczewski, M.; Okruszko, T. Where Might the Hands-off Protection Strategy of Anastomosing Rivers Lead? A Case Study of Narew National Park. Pol. J. Environ. Stud. 2018, 27, 2647–2658. [Google Scholar] [CrossRef]
- Marcinkowski, P.; Kiczko, A.; Okruszko, T. Modeling of water flow in multi-channel river system in the Narew National Park. Ann. Warsaw Univ. Life Sci. SGGW Land Reclam. 2017, 49, 167–177. [Google Scholar] [CrossRef]
- Nepf, H.M. Hydrodynamics of vegetated channels. J. Hydraul. Res. 2012, 50, 262–279. [Google Scholar] [CrossRef]
- Shields, F.D.; Coulton, K.G.; Nepf, H. Representation of vegetation in two-dimensional hydrodynamic models. J. Hydraul. Eng. 2017, 143, 02517002. [Google Scholar] [CrossRef]
- Arcement, G.J.; Schneider, V.R. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains; United States Government Printing Office: Denver, CO, USA, 1989.
- Green, J.C. Comparison of blockage factors in modelling the resistance of channels containing submerged macrophytes. River Res. Appl. 2005, 21, 671–686. [Google Scholar] [CrossRef]
- Luhar, M.; Nepf, H.M. From the blade scale to the reach scale: A characterization of aquatic vegetative drag. Adv. Water Resour. 2013, 51, 305–316. [Google Scholar] [CrossRef]
- Rhee, D.P.; Woo, H.; Kwon, B.A.; Ahn, H.K. Hydraulic resistance of some selected vegetation in open channel flows. River Res. Appl. 2008, 24, 673–687. [Google Scholar] [CrossRef]
- Kale, V.S.; Baker, V.R.; Mishra, S. Multi-channel patterns of bedrock rivers: An example from the central Narmada basin, India. Catena 1996, 26, 85–98. [Google Scholar] [CrossRef]
- Merwade, V.M.; Olivera, F.; Arabi, M.; Edleman, S. Uncertainty in flood inundation mapping—Current issues and future directions. ASCE J. Hydrol. Eng. 2008, 13, 608–620. [Google Scholar] [CrossRef]
- Luhar, M.; Rominger, J.; Nepf, H. Interaction between flow, transport and vegetation spatial structure. Environ. Fluid Mech. 2008, 8, 423–439. [Google Scholar] [CrossRef]
- Katul, G.; Wiberg, P.; Albertson, J.; Hornberger, G. A mixing layer theory for flow resistance in shallow streams. Water Resour. Res. 2002, 38, 321–328. [Google Scholar] [CrossRef]
- Baptist, M.J.; Babovic, C.; Uthurburu, J.R.; Mynett, A.; Verwey, A. On inducing equations for vegetation resistance. J. Hydraul. Res. 2007, 45, 435–450. [Google Scholar] [CrossRef]
- Whittaker, P.; Wilson, C.A.M.E.; Aberle, J. An improved Cauchy number approach for predicting the drag and reconfiguration of flexible vegetation. Adv. Water Resour. 2015, 83, 28–35. [Google Scholar] [CrossRef]
- Jarvela, J. Determination of flow resistance caused by non-submerged woody vegetation. Int. J. River Basin Manag. 2004, 2, 61–70. [Google Scholar] [CrossRef]






| Junction Number | Difference in Energy Level between Parallel Branches—Winter Conditions (m) | Difference between Measured and Computed Water Level—Winter Conditions (m) | Difference in Energy Level between Parallel Branches—Summer Conditions (m) | Difference between Measured and Computed Water Level—Summer Conditions (m) |
|---|---|---|---|---|
| Calibration | ||||
| 1 | 1.7 × 10−8 | 0.053 | 5.1 × 10−4 | 0.018 |
| 2 | 3.7 × 10−8 | 0.017 | 2.1 × 10−4 | 0.023 |
| 3 | - | 0.041 | - | 0.058 |
| 4 | 2.3 × 10−8 | 0.002 | 5.3 × 10−4 | 0.014 |
| 5 | - | 0.008 | - | 0.019 |
| 6 | 1.7 × 10−8 | 0.018 | 0.0 | 0.079 |
| 7 | - | 0.002 | - | 0.075 |
| 8 | - | 0.013 | - | 0.058 |
| 9 | 3.2 × 10−8 | 0.010 | 6.7 × 10−4 | 0.058 |
| 10 | - | 0.016 | - | 0.038 |
| 11 | - | 0.050 | - | 0.030 |
| 12 | 3.0 × 10−8 | 0.031 | 6.7 × 10−4 | 0.091 |
| 13 | - | 0.021 | - | 0.072 |
| 14 | 3.7 × 10−8 | 0.001 | 6.7 × 10−4 | 0.033 |
| Validation | ||||
| 1 | - | - | 1.5 × 10−5 | 0.020 |
| 2 | - | - | 7.8 × 10−6 | 0.017 |
| 3 | - | - | - | 0.020 |
| 4 | - | - | 1.1 × 10−5 | 0.026 |
| 5 | - | - | - | 0.070 |
| 6 | - | - | 0.0 | 0.083 |
| 7 | - | - | - | 0.080 |
| 8 | - | - | - | 0.063 |
| 9 | - | - | 4.3 × 10−5 | 0.063 |
| 10 | - | - | - | 0.157 |
| 11 | - | - | - | 0.017 |
| 12 | - | - | 2.6 × 10−5 | 0.130 |
| 13 | - | - | - | 0.111 |
| 14 | - | - | 4.3 × 10−5 | 0.072 |
| Group Number | Vegetation Type | Manning’s Coefficient Value (m−1/3·s) |
|---|---|---|
| 1 | Short submerged grasses along the banks with no significant vegetation evident along the channel bottoms (Figure 3C,D and Figure 4D). | 0.025 |
| 2 | Submerged grass or weed growing where the average depth of flow is about equal to the height of the vegetation (Figure 3A,B and Figure 4A) | 0.050 |
| 3 | Emergent grass, weed or reed growing where the average depth of flow is less than half the height of the vegetation along channel bottom (Figure 4B,C). | 0.075 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marcinkowski, P.; Kiczko, A.; Okruszko, T. Model-Based Analysis of Macrophytes Role in the Flow Distribution in the Anastomosing River System. Water 2018, 10, 953. https://doi.org/10.3390/w10070953
Marcinkowski P, Kiczko A, Okruszko T. Model-Based Analysis of Macrophytes Role in the Flow Distribution in the Anastomosing River System. Water. 2018; 10(7):953. https://doi.org/10.3390/w10070953
Chicago/Turabian StyleMarcinkowski, Paweł, Adam Kiczko, and Tomasz Okruszko. 2018. "Model-Based Analysis of Macrophytes Role in the Flow Distribution in the Anastomosing River System" Water 10, no. 7: 953. https://doi.org/10.3390/w10070953
APA StyleMarcinkowski, P., Kiczko, A., & Okruszko, T. (2018). Model-Based Analysis of Macrophytes Role in the Flow Distribution in the Anastomosing River System. Water, 10(7), 953. https://doi.org/10.3390/w10070953






